Classical Collapse to Black Holes and Quantum Bounces: A Review
Abstract
:1. Introduction
2. Classical Collapse...
- Scale factor given by: .
- Mass function given by: .
- Velocity profile given by: .
2.1. Dust, Homogeneous Fluids and Null Shells
2.2. Toy Models vs. Realistic Models
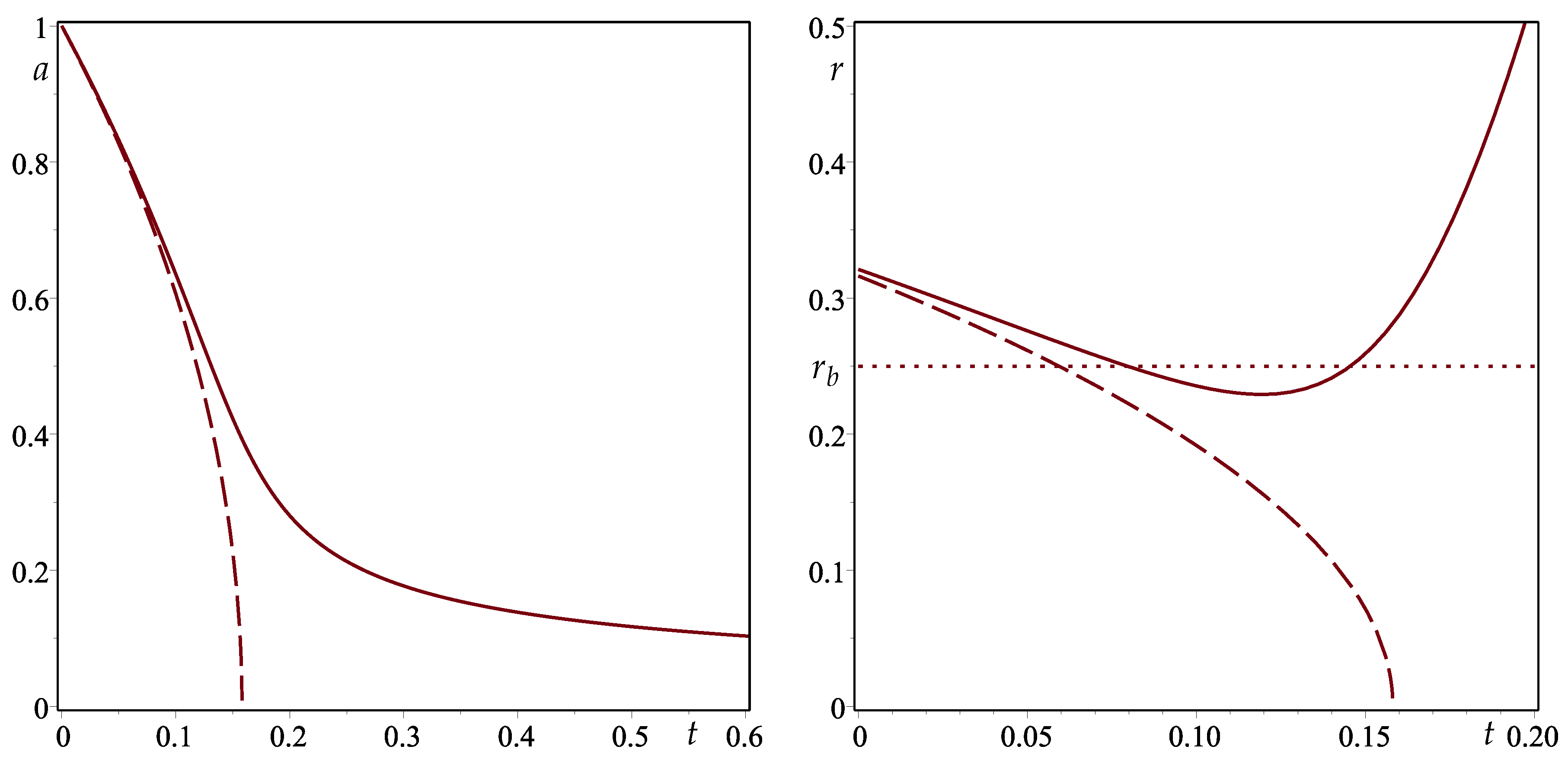
2.3. Numerical Simulations
3. ...And Quantum Bounces
3.1. A Brief History of Collapse Models with Quantum Corrected Interiors
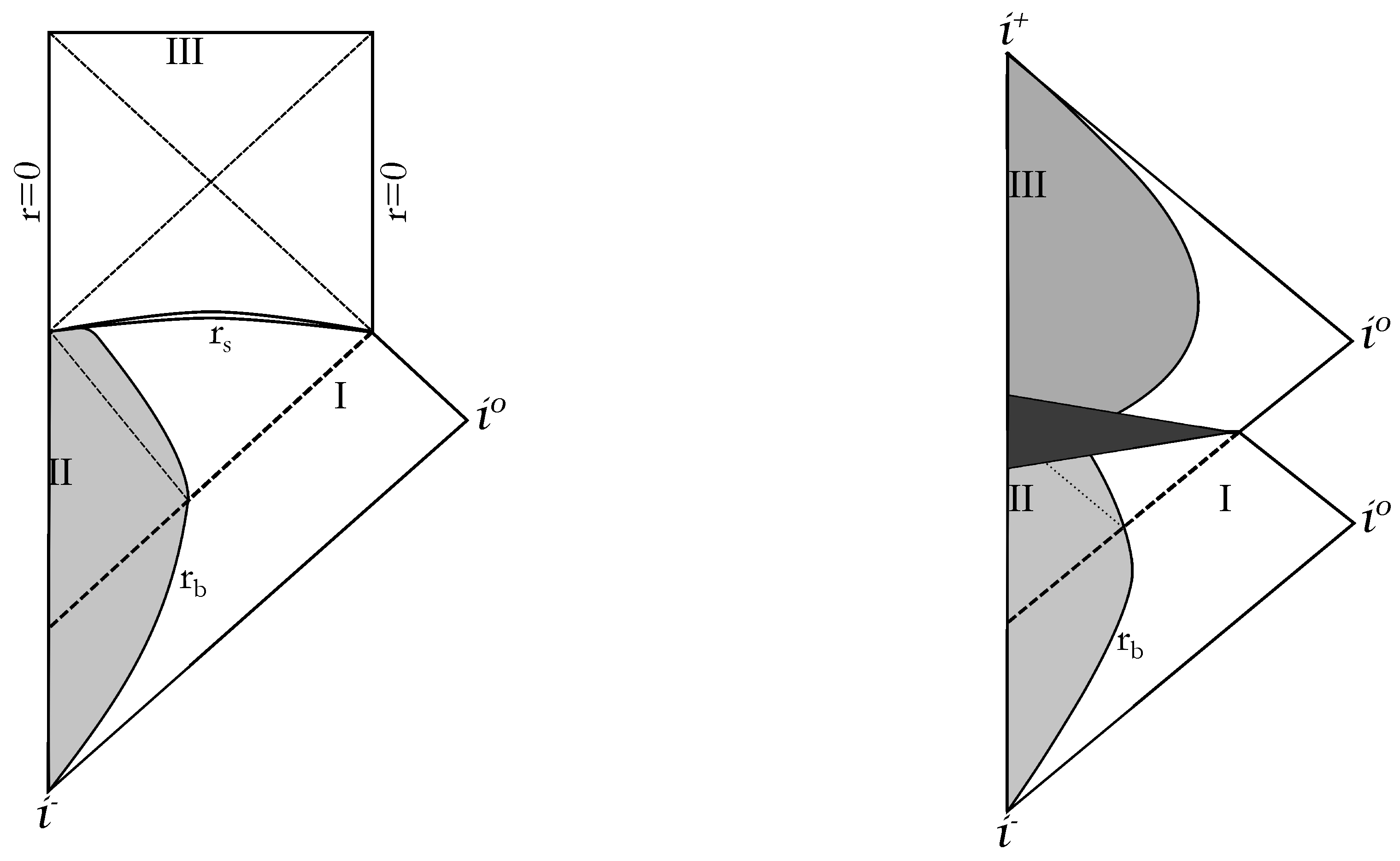
3.2. The Exterior Geometry
4. Open Issues
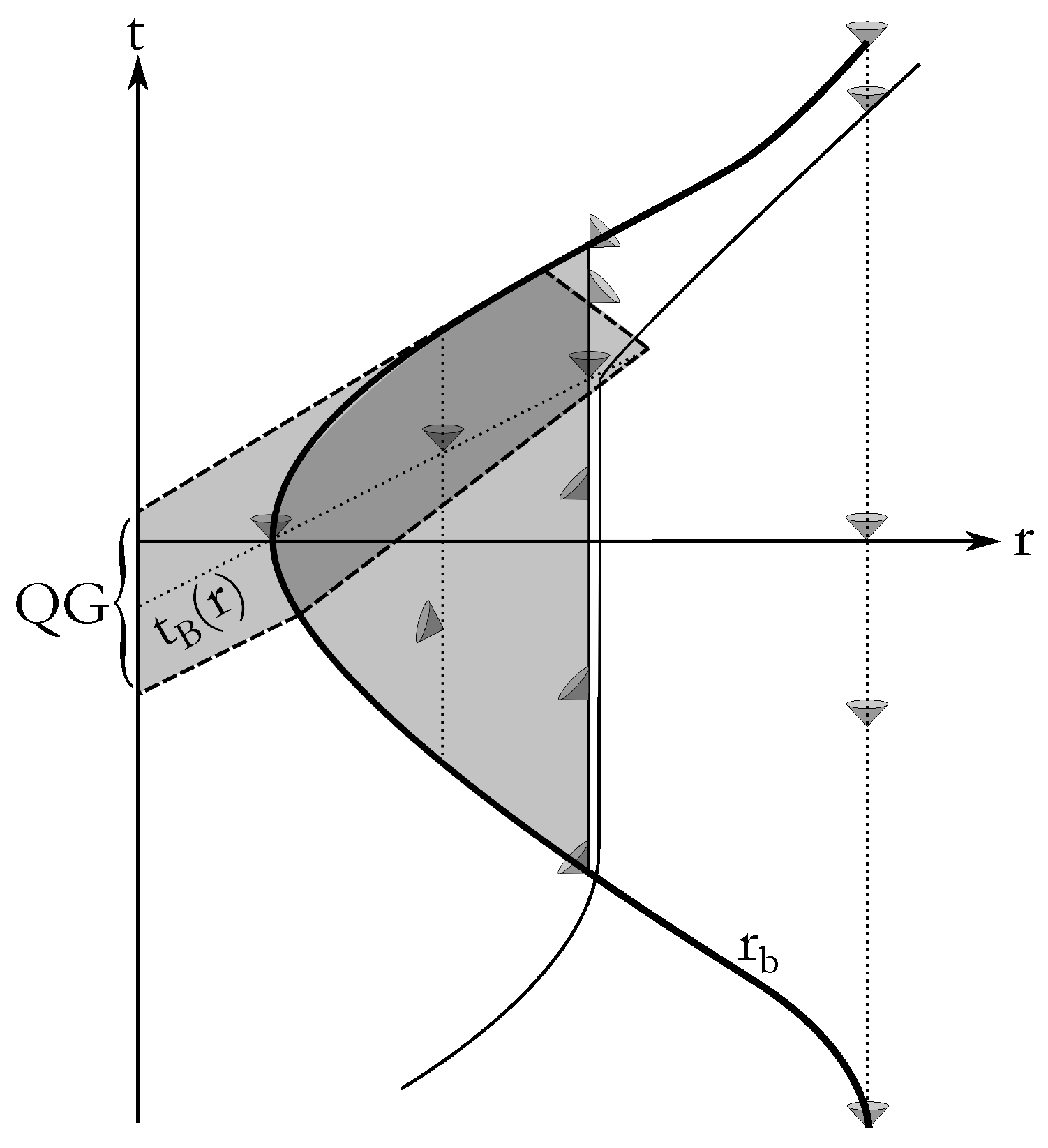
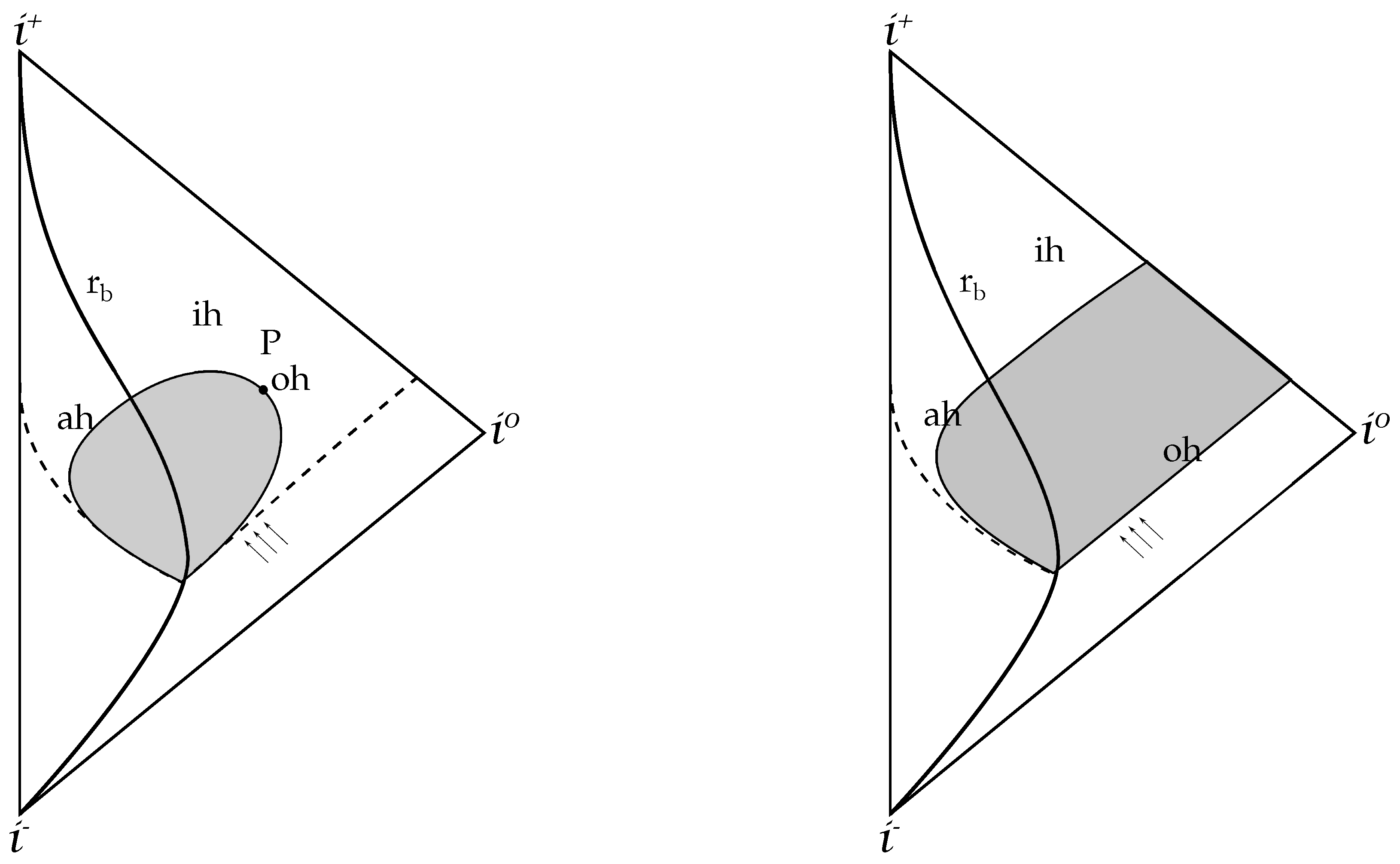
4.1. The Horizon in the Exterior
4.2. The Black Hole to White Hole Transition
4.3. Lifespan of the Black Hole
4.4. Hawking Radiation and Time Symmetry
4.5. Matter Models
4.6. Other Possibilities
5. Remnants and Phenomenology
5.1. Compact Objects
5.2. A Toy Model of Collapse to a Dark Energy Star
5.3. Future Observations
6. Discussion
Conflicts of Interest
References
- Penrose, R. Gravitational Collapse and Space-Time Singularities. Phys. Rev. Lett. 1965, 14, 57–59. [Google Scholar] [CrossRef]
- Hawking, S.W.; Penrose, R. The Singularities of Gravitational Collapse and Cosmology. Proc. R. Soc. Lond. A 1970, 314, 529–548. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Zurek, W.H. John Wheeler, relativity, and quantum information. Phys. Today 2009, 1638, 40–46. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Snyder, H. On continued gravitational contraction. Phys. Rev. 1939, 56, 455–459. [Google Scholar] [CrossRef]
- Datt, S. Über eine Klasse von Lösungen der Gravitationsgleichungen der Relativität. Z. Phys. 1938, 108, 314–321. [Google Scholar] [CrossRef]
- Bardeen, J.M. Non singular general relativistic gravitational collapse. In Proceedings of the International Conference GR5; USSR: Tiblisi, Georgia, 1968. [Google Scholar]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
- Frolov, V.P. Notes on non-singular models of black holes. Phys. Rev. D 2016, 94, 104056. [Google Scholar] [CrossRef]
- Bojowald, M. Non-singular black holes and degrees of freedom in quantum gravity. Phys. Rev. Lett. 2005, 95, 061301. [Google Scholar] [CrossRef] [PubMed]
- Bambi, C.; Modesto, L. Rotating regular black holes. Phys. Lett. B 2013, 721, 329–334. [Google Scholar] [CrossRef]
- Toshmatov, B.; Ahmedov, B.; Abdujabbarov, A.; Stuchlik, Z. Rotating Regular Black Hole Solution. Phys. Rev. D 2014, 89, 104017. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Amir, M.; Ahmedov, B.; Ghosh, S.G. Shadow of rotating regular black holes. Phys. Rev. D 2016, 93, 104004. [Google Scholar] [CrossRef]
- Neves, J.C.S.; Saa, A. Regular rotating black holes and the weak energy condition. Phys. Lett. B 2014, 734, 44–48. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M. Quantum geometry and the Schwarzschild singularity. Class. Quantum Gravity 2006, 23, 391–411. [Google Scholar] [CrossRef]
- Bojowald, M. Quantum Geometry and its Implications for Black Holes. Int. J. Mod. Phys. D 2006, 15, 1545–1559. [Google Scholar] [CrossRef]
- Gambini, R.; Pullin, J. Loop quantization of the Schwarzschild black hole. Phys. Rev. Lett. 2013, 110, 211301. [Google Scholar] [CrossRef] [PubMed]
- Hossenfelder, S.; Modesto, L.; Premont-Schwarz, I. A Model for non-singular black hole collapse and evaporation. Phys. Rev. D 2010, 81, 044036. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Renormalization group improved black hole spacetimes. Phys. Rev. D 2000, 62, 043008. [Google Scholar] [CrossRef]
- Gegenberg, J.; Kunstatter, G.; Small, R.D. Quantum Structure of Space Near a Black Hole Horizon. Class. Quantum Gravity 2006, 23, 6087–6100. [Google Scholar] [CrossRef]
- Casadio, R.; Giugno, A.; Micu, O. Horizon Quantum Mechanics: A hitchhiker’s guide to quantum black holes. Int. J. Mod. Phys. D 2016, 25, 1630006. [Google Scholar] [CrossRef]
- Torres, R. On the interior of (Quantum) Black Holes. Phys. Lett. B 2013, 724, 338–345. [Google Scholar] [CrossRef]
- Torres, R. Non-Singular Black Holes, the Cosmological Constant and Asymptotic Safety. arXiv, 2017; arXiv:1703.09997. [Google Scholar]
- Mazur, P.O.; Mottola, E. Gravitational Condensate Stars: An Alternative to Black Holes. arXiv, 2002; arXiv:gr-qc/0109035. [Google Scholar]
- Baccetti, V.; Mann, R.B.; Terno, D.R. Role of evaporation in gravitational collapse. arXiv, 2016; arXiv:1610.07839. [Google Scholar]
- Baccetti, V.; Mann, R.B.; Terno, D.R. Horizon avoidance in spherically-symmetric collapse. arXiv, 2017; arXiv:1703.09369. [Google Scholar]
- Mersini-Houghton, L. Backreaction of Hawking Radiation on a Gravitationally Collapsing Star I: Black Holes? Phys. Lett. B 2014, 738, 61–67. [Google Scholar] [CrossRef]
- Kawai, H.; Yokokura, Y. Interior of black holes and information recovery. Phys. Rev. D 2016, 93, 044011. [Google Scholar] [CrossRef]
- Kawai, H.; Yokokura, Y. A model of black hole evaporation and 4D Weyl anomaly. arXiv, 2017; arXiv:1701.03455. [Google Scholar]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Mutiny at the white-hole district. Int. J. Mod. Phys. D 2014, 23, 1442022. [Google Scholar] [CrossRef]
- Haggard, H.M.; Rovelli, C. Black hole fireworks: Quantum-gravity effects outside the horizon spark black to white hole tunneling. Phys. Rev. D 2015, 92, 104020. [Google Scholar] [CrossRef]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J.; Jannes, G. The lifetime problem of evaporating black holes: Mutiny or resignation. Class. Quantum Gravity 2015, 32, 035012. [Google Scholar] [CrossRef]
- Frolov, V.P.; Vilkovisky, G.A. Quantum Gravity removes classical singularities and shortens the life of a black hole. In Proceedings of the Second Marcel Grossmann Meeting on General Relativity, Trieste, Italy, 5–11 July 1979. [Google Scholar]
- Frolov, V.P.; Vilkovisky, G.A. Spherically Symmetric Collapse in Quantum Gravity. Phys. Lett. B 1981, 106, 307–313. [Google Scholar] [CrossRef]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the big bang. Phys. Rev. Lett. 2006, 96, 141301. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Pawlowski, T.; Singh, P.; Vandersloot, K. Loop quantum cosmology of k = 1 FRW models. Phys. Rev. D 2007, 75, 24035. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of Singularity in Loop Quantum Cosmology. Phys. Rev. Lett. 2001, 86, 5227–5230. [Google Scholar] [CrossRef] [PubMed]
- Bojowald, M.; Goswami, R.; Maartens, R.; Singh, P. Black hole mass threshold from nonsingular quantum gravitational collapse. Phys. Rev. Lett. 2005, 95, 091302. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhu, Y.; Modesto, L.; Bambi, C. Can static regular black holes form from gravitational collapse? Eur. Phys. J. C 2015, 75, 96. [Google Scholar] [CrossRef]
- Barrau, A.; Bolliet, B.; Vidotto, F.; Weimer, C. Phenomenology of bouncing black holes in quantum gravity: A closer look. J. Cosmol. Astropart. Phys. 2016, 2016, 022. [Google Scholar] [CrossRef]
- Hawking, S.W. Gravitationally collapsed objects of very low mass. Mon. Not. R. Astron. Soc. 1971, 152, 75–78. [Google Scholar] [CrossRef]
- Visser, M.; Wiltshire, D.L. Stable gravastars—An alternative to black holes? Class. Quantum Gravity 2004, 21, 1135–1152. [Google Scholar] [CrossRef]
- Barceló, C.; Liberati, S.; Sonego, S.; Visser, M. Fate of gravitational collapse in semiclassical gravity. Phys. Rev. D 2008, 77, 044032. [Google Scholar] [CrossRef]
- Itoh, N. Hydrostatic Equilibrium of Hypothetical Quark Stars. Prog. Theor. Phys. 1970, 44, 291–292. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Ruffini, R.; Bonazzola, S. Systems of Self-Gravitating Particles in General Relativity and the Concept of an Equation of State. Phys. Rev. 1969, 187, 1767–1783. [Google Scholar] [CrossRef]
- Schunck, F.E.; Mielke, E.W. General relativistic boson stars. Class. Quantum Gravity 2003, 20, R301–R356. [Google Scholar] [CrossRef]
- Giddings, S.B. Black holes and massive remnants. Phys. Rev. D 1992, 46, 1347–1352. [Google Scholar] [CrossRef]
- Chen, P.; Ong, Y.C.; Yeom, D. Black Hole Remnants and the Information Loss Paradox. Phys. Rep. 2015, 603, 1–45. [Google Scholar] [CrossRef]
- Lochan, K.; Chakraborty, S.; Padmanabhan, T. Information retrieval from black holes. Phys. Rev. D 2016, 94, 044056. [Google Scholar] [CrossRef]
- Israel, W. Singular hypersurfaces and thin shells in general relativity. Il Nuovo Cimento B (1965–1970) 1966, 44, 1–4. [Google Scholar] [CrossRef]
- Fayos, F.; Jaen, X.; Llanta, E.; Senovilla, J.M.M. Matching of the Vaidya and Robertson-Walker metric. Class. Quantum Gravity 1991, 8, 2057–2068. [Google Scholar] [CrossRef]
- Fayos, F.; Jaen, X.; Llanta, E.; Senovilla, J.M.M. Interiors of Vaidya’s radiating metric: Gravitational collapse. Phys. Rev. D 1992, 45, 2732–2738. [Google Scholar] [CrossRef]
- Fayos, F.; Senovilla, J.M.M.; Torres, R. General matching of two spherically symmetric spacetimes. Phys. Rev. D 1996, 54, 4862–4872. [Google Scholar] [CrossRef]
- Misner, C.; Sharp, D. Relativistic Equations for Adiabatic, Spherically Symmetric Gravitational Collapse. Phys. Rev. 1964, 136, B571–B576. [Google Scholar] [CrossRef]
- Tooper, R.F. General Relativistic Polytropic Fluid Spheres. Astrophys. J. 1964, 140, 434–459. [Google Scholar] [CrossRef]
- Joshi, P.S.; Malafarina, D. Recent developments in gravitational collapse and spacetime singularities. Int. J. Mod. Phys. D 2011, 20, 2641–2729. [Google Scholar] [CrossRef]
- Martin-Moruno, P.; Visser, M. Semiclassical energy conditions for quantum vacuum states. J. High Energy Phys. 2013, 2013, 050. [Google Scholar] [CrossRef]
- Senovilla, J.M.M.; Garfinkle, D. The 1965 Penrose singularity theorem. Class. Quantum Gravity 2015, 32, 124008. [Google Scholar] [CrossRef]
- Roman, T.A.; Bergmann, P.G. Stellar collapse without singularities? Phys. Rev. D 1983, 28, 1265–1277. [Google Scholar] [CrossRef]
- Vaidya, P. The Gravitational Field of a Radiating Star. Proc. Math. Sci. 1951, 33, 264–276. [Google Scholar]
- Joshi, P.S. Gravitational Collapse and Spacetime Singularities; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Where does the physics of extreme gravitational collapse reside? Universe 2016, 2, 7. [Google Scholar] [CrossRef]
- Ziprick, J.; Kunstatter, G. Spherically Symmetric Black Hole Formation in Painlevé-Gullstrand Coordinates. Phys. Rev. D 2009, 79, 101503. [Google Scholar] [CrossRef]
- Silk, J.; Wright, J.P. The gravitational collapse of a slowly rotating relativistic star. Mon. Not. R. Astron. Soc. 1969, 143, 55–71. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Miller, J.C. On slowly rotating homogeneous masses in general relativity. Mon. Not. R. Astron. Soc. 1974, 167, 63–80. [Google Scholar] [CrossRef]
- Hartle, J.B.; Thorne, K.S. Slowly Rotating Relativistic Stars. II. Models for Neutron Stars and Supermassive Stars. Astrophys. J. 1968, 153, 807–834. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L. Numerical Relativity: Solving Einstein’s Equations on the Computer; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- May, M.M.; White, R.H. Hydrodynamic Calculations of General-Relativistic Collapse. Phys. Rev. 1966, 141, 1232–1241. [Google Scholar] [CrossRef]
- Stark, R.F.; Piran, T. Gravitational-wave emission from rotating gravitational collapse. Phys. Rev. Lett. 1985, 55, 891–894. [Google Scholar] [CrossRef] [PubMed]
- Eardley, D.M.; Smarr, L. Time functions in numerical relativity: Marginally bound dust collapse. Phys. Rev. D 1979, 19, 2239–2259. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Formation of naked singularities: The violation of cosmic censorship. Phys. Rev. Lett. 1991, 66, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Baiotti, L.; Hawke, I.; Montero, P.J.; Loffler, F.; Rezzolla, L.; Stergioulas, N.; Font, J.A.; Seidel, E. Three-dimensional relativistic simulations of rotating neutron-star collapse to a Kerr black hole. Phys. Rev. D 2005, 71, 024035. [Google Scholar] [CrossRef]
- Giacomazzo, B.; Rezzolla, L.; Stergioulas, N. Collapse of differentially rotating neutron stars and cosmic censorship. Phys. Rev. D 2011, 84, 024022. [Google Scholar] [CrossRef]
- Nathanail, A.; Most, E.R.; Rezzolla, L. Gravitational collapse to a Kerr–Newman black hole. Mon. Not. R. Astron. Soc. Lett. 2017, 469, L31–L35. [Google Scholar] [CrossRef]
- Hajicek, P. Unitary dynamics of spherical null gravitating shells. Nucl. Phys. B 2001, 603, 555–577. [Google Scholar] [CrossRef]
- Hajicek, P.; Kiefer, C. Singularity avoidance by collapsing shells in quantum gravity. Int. J. Mod. Phys. D 2001, 10, 775–779. [Google Scholar] [CrossRef]
- Vaz, C.; Witten, L.; Singh, T.P. Towards a quantization of null dust collapse. Phys. Rev. D 2002, 65, 104016. [Google Scholar] [CrossRef]
- Vaz, C. Quantum gravitational collapse does not result in a black hole. Nucl. Phys. B 2015, 891, 558–569. [Google Scholar] [CrossRef]
- Kiefer, C.; Múller-Hill, J.; Vaz, C. Classical and quantum LTB model for the non-marginal case. Phys. Rev. D 2006, 73, 044025. [Google Scholar] [CrossRef]
- Tippett, B.K.; Husain, V. Gravitational collapse of quantum matter. Phys. Rev. D 2011, 84, 104031. [Google Scholar] [CrossRef]
- Husain, V.; Winkler, O. Quantum resolution of black hole singularities. Class. Quantum Gravity 2005, 22, L127–L134. [Google Scholar] [CrossRef]
- Husain, V.; Winkler, O. Quantum black holes from null expansion operators. Class. Quantum Gravity 2005, 22, L135–L141. [Google Scholar] [CrossRef]
- Husain, V.; Winkler, O. Flat slice Hamiltonian formalism for dynamical black holes. Phys. Rev. D 2005, 71, 104001. [Google Scholar] [CrossRef]
- Husain, V.; Winkler, O. Quantum Hamiltonian for gravitational collapse. Phys. Rev. D 2006, 73, 124007. [Google Scholar] [CrossRef]
- Husain, V.; Winkler, O. Semiclassical states for quantum cosmology. Phys. Rev. D 2007, 75, 024014. [Google Scholar] [CrossRef]
- Husain, V.; Terno, D.R. Dynamics and entanglement in spherically symmetric quantum gravity. Phys. Rev. D 2010, 81, 044039. [Google Scholar] [CrossRef]
- Ziprick, J.; Kunstatter, G. Dynamical Singularity Resolution in Spherically Symmetric Black Hole Formation. Phys. Rev. D 2009, 80, 024032. [Google Scholar] [CrossRef]
- Ziprick, J.; Kunstatter, G. Quantum Corrected Spherical Collapse: A Phenomenological Framework. Phys. Rev. D 2010, 82, 044031. [Google Scholar] [CrossRef]
- Abedi, J.; Arfaei, H. Obstruction of black hole singularity by quantum field theory effects. J. High Energy Phys. 2016, 2016, 135. [Google Scholar] [CrossRef]
- Arfaei, H.; Noorikuhani, M. Quantum vacuum effects on the final fate of a collapsing ball of dust. J. High Energy Phys. 2017, 2017, 124. [Google Scholar] [CrossRef]
- Koch, B.; Saueressig, F. Black holes within Asymptotic Safety. Int. J. Mod. Phys. A 2014, 29, 1430011. [Google Scholar] [CrossRef]
- Saueressig, F.; Alkofer, N.; D’Odorico, G.; Vidotto, F. Black holes in Asymptotically Safe Gravity. arXiv, 2015; arXiv:1503.06472. [Google Scholar]
- Bonanno, A.; Reuter, M. Spacetime structure of an evaporating black hole in quantum gravity. Phys. Rev. D 2006, 73, 083005. [Google Scholar] [CrossRef]
- Fayos, F.; Torres, R. A quantum improvement to the gravitational collapse of radiating stars. Class. Quantum Gravity 2011, 28, 105004. [Google Scholar] [CrossRef]
- Casadio, R.; Hsu, S.D.H.; Mirza, B. Asymptotic Safety, Singularities, and Gravitational Collapse. Phys. Lett. B 2011, 695, 317–319. [Google Scholar] [CrossRef]
- Bambi, C.; Malafarina, D.; Modesto, L. Terminating black holes in asymptotically free quantum gravity. Eur. Phys. J. C 2014, 74, 2767. [Google Scholar] [CrossRef]
- Barcelò, C.; Garay, L.J.; Jannes, G. Quantum Non-Gravity and Stellar Collapse. Found. Phys. 2011, 41, 1532–1541. [Google Scholar] [CrossRef]
- Ashtekar, A. Loop Quantum Cosmology: An Overview. Gen. Relativ. Gravit. 2009, 41, 707–741. [Google Scholar] [CrossRef]
- Goswami, R.; Joshi, P.S.; Singh, P. Quantum evaporation of a naked singularity. Phys. Rev. Lett. 2006, 96, 031302. [Google Scholar] [CrossRef] [PubMed]
- Bambi, C.; Malafarina, D.; Modesto, L. Non-singular quantum-inspired gravitational collapse. Phys. Rev. D 2013, 88, 044009. [Google Scholar] [CrossRef]
- Torres, R.; Fayos, F. Singularity free gravitational collapse in an effective dynamical quantum spacetime. Phys. Lett. B 2014, 733, 169–175. [Google Scholar] [CrossRef]
- Torres, R. Singularity-free gravitational collapse and asymptotic safety. Phys. Lett. B 2014, 733, 21–24. [Google Scholar] [CrossRef]
- Bambi, C.; Malafarina, D.; Modesto, L. Black supernovae and black holes in non-local gravity. J. High Energy Phys. 2016, 2016, 147. [Google Scholar] [CrossRef]
- Ziaie, A.H.; Moniz, P.V.; Ranjbar, A.; Sepangi, H.R. Einstein-Cartan gravitational collapse of a homogeneous Weyssenhoff fluid. Eur. Phys. J. C 2014, 74, 3154. [Google Scholar] [CrossRef]
- Bambi, C.; Cardenas-Avendano, A.; Olmo, G.J.; Rubiera-Garcia, D. Wormholes and nonsingular space-times in Palatini f(R) gravity. Phys. Rev. D 2016, 93, 064016. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Martinez-Asencio, J.; Olmo, G.J.; Rubiera-Garcia, D. Dynamical generation of wormholes with charged fluids in quadratic Palatini gravity. Phys. Rev. D 2014, 90, 024033. [Google Scholar] [CrossRef]
- Kreienbuehl, A.; Husain, V.; Seahra, S.S. Modified general relativity as a model for quantum gravitational collapse. Class. Quantum Gravity 2012, 29, 095008. [Google Scholar] [CrossRef]
- Choptuik, M.W. Universality and scaling in gravitational collapse of a massless scalar field. Phys. Rev. Lett. 1993, 70, 9–12. [Google Scholar] [CrossRef] [PubMed]
- Casadio, R.; Micu, O.; Nicolini, P. Minimum length effects in black hole physics. In Quantum Aspects of Black Holes; Calmet, X., Ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Bambi, C.; Malafarina, D.; Marcianò, A.; Modesto, L. Singularity avoidance in classical gravity from four-fermion interaction. Phys. Lett. B 2014, 734, 27–30. [Google Scholar] [CrossRef]
- Markov, M.A. Limiting density of matter as a universal law of nature. J. Exp. Theor. Phys. Lett. 1982, 36, 265–267. [Google Scholar]
- Markov, M.A. Problems of a perpetually oscillating universe. Ann. Phys. 1984, 155, 333–357. [Google Scholar] [CrossRef]
- Hawking, S.W. Information Preservation and Weather Forecasting for Black Holes. arXiv, 2014; arXiv:1401.5761. [Google Scholar]
- Ambrus, M.; Hajicek, P. Quantum superposition principle and graviational collapse: Scattering times for spherical shells. Phys. Rev. D 2005, 72, 064025. [Google Scholar] [CrossRef]
- Joshi, P.S.; Dwivedi, I.H. Naked singularities in spherically symmetric inhomogeneous Tolman-Bondi dust cloud collapse. Phys. Rev. D 1993, 47, 5357–5369. [Google Scholar] [CrossRef]
- Helou, A.; Musco, I.; Miller, J.C. Causal Nature and Dynamics of Trapping Horizons in Black Hole Collapse. arXiv, 2016; arXiv:1601.05109. [Google Scholar]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Black holes turn white fast, otherwise stay black: No half measures. J. High Energy Phys. 2016, 2016, 157. [Google Scholar] [CrossRef]
- Visser, M. Physical observability of horizons. Phys. Rev. D 2014, 90, 127502. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Exponential fading to white of black holes in quantum gravity. Class. Quantum Gravity 2017, 34, 105007. [Google Scholar] [CrossRef]
- Christodoulou, M.; Rovelli, C.; Speziale, S.; Vilensky, I. Realistic Observable in Background-Free Quantum Gravity: The Planck-Star Tunnelling-Time. Phys. Rev. D 2016, 94, 084035. [Google Scholar] [CrossRef]
- Eardley, D.M. Death of white holes in the early universe. Phys. Rev. Lett. 1974, 33, 442–444. [Google Scholar] [CrossRef]
- Barrabès, C.; Brady, P.R.; Poisson, E. Death of white holes. Phys. Rev. D 1993, 47, 2383–2387. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M. Black hole evaporation: A paradigm. Class. Quantum Gravity 2005, 22, 3349–3362. [Google Scholar] [CrossRef]
- Gerlach, U.H. The mechanism of blackbody radiation from an incipient black hole. Phys. Rev. D 1976, 14, 1479–1508. [Google Scholar] [CrossRef]
- Torres, R.; Fayos, F. On the quantum corrected gravitational collapse. arXiv, 2015. [Google Scholar] [CrossRef]
- Giddings, S.B. Hawking radiation, the Stefan-Boltzmann law, and unitarization. Phys. Lett. B 2016, 754, 39–42. [Google Scholar] [CrossRef]
- Dey, R.; Liberati, S.; Pranzetti, D. The black hole quantum atmosphere. arXiv, 2017; arXiv:1701.06161. [Google Scholar]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- De Lorenzo, T.; Perez, A. Improved Black Hole Fireworks: Asymmetric Black-Hole-to-White-Hole Tunneling Scenario. Phys. Rev. D 2016, 93, 124018. [Google Scholar] [CrossRef]
- Booth, I.; Brits, L.; Gonzalez, J.A.; van den Broeck, C. Marginally trapped tubes and dynamical horizons. Class. Quantum Gravity 2006, 23, 413–440. [Google Scholar] [CrossRef]
- Brizuela, D.; Marugán, G.A.M.; Pawlowski, T. Effective dynamics of the hybrid quantization of the Gowdy T3 universe. Phys. Rev. D 2011, 84, 124017. [Google Scholar] [CrossRef]
- Fernandez-Mendez, M.; Marugán, G.A.M. Effective dynamics of scalar perturbations in a flat Friedmann-Robertson-Walker spacetime in loop quantum cosmology. Phys. Rev. D 2014, 89, 044041. [Google Scholar] [CrossRef]
- Liu, Y.; Malafarina, D.; Modesto, L.; Bambi, C. Singularity avoidance in quantum-inspired inhomogeneous dust collapse. Phys. Rev. D 2014, 90, 044040. [Google Scholar] [CrossRef]
- Bojowald, M.; Harada, T.; Tibrewala, R. Lemaitre-Tolman-Bondi collapse from the perspective of loop quantum gravity. Phys. Rev. D 2008, 78, 064057. [Google Scholar] [CrossRef]
- Ford, L.H.; Roman, T.A. Averaged Energy Conditions and Quantum Inequalities. Phys. Rev. D 1995, 51, 4277–4286. [Google Scholar] [CrossRef]
- Abreu, G.; Barceló, C.; Visser, M. Entropy bounds in terms of the w parameter. J. High Energy Phys. 2011, 2011, 092. [Google Scholar] [CrossRef]
- Martin-Moruno, P.; Visser, M. Classical and quantum flux energy conditions for vacuum quantum states. Phys. Rev. D 2013, 88, 061701. [Google Scholar] [CrossRef]
- Barceló, C.; Visser, M. Twilight for the energy conditions? Int. J. Mod. Phys. D 2002, 11, 1553–1560. [Google Scholar] [CrossRef]
- Weber, F. Strange Quark Matter and Compact Stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. The Equation of State at Ultrahigh Densities and Its Relativistic Limitations. J. Exp. Theor. Phys. 1962, 14, 1143–1147. [Google Scholar]
- Sakharov, A.D. The initial stage of an expanding universe and the appearance of a nonuniform distribution of matter. J. Exp. Theor. Phys. 1966, 22, 241–249. [Google Scholar]
- Hagedorn, R. Thermodynamics of strong interactions at high energy and its consequences for astrophysics. Astron. Astrophys. 1970, 5, 184–205. [Google Scholar]
- Bahcall, J.N.; Frautschi, S. The hadron barrier in cosmology and gravitational collapse. Astrophys. J. 1971, 170, L81–L84. [Google Scholar] [CrossRef]
- Malafarina, D. Gravitational collapse of Hagedorn fluids. Phys. Rev. D 2016, 93, 104042. [Google Scholar] [CrossRef]
- Harko, T. Gravitational collapse of a Hagedorn fluid in Vaidya geometry. Phys. Rev. D 2003, 68, 064005. [Google Scholar] [CrossRef]
- Frolov, V.P.; Markov, M.A.; Mukhanov, V.F. Black Holes as Possible Sources of Closed and Semiclosed Worlds. Phys. Rev. D 1990, 41, 383–394. [Google Scholar] [CrossRef]
- Poplawski, N. Universe in a black hole in Einstein-Cartan gravity. Astrophys. J. 2016, 832, 96. [Google Scholar] [CrossRef]
- Hsu, S.D.H. Spacetime topology change and black hole information. Phys. Lett. B 2007, 644, 67–71. [Google Scholar] [CrossRef]
- Smolin, L. Did the univrese evolve? Class. Quantum Gravity 1992, 9, 173–191. [Google Scholar] [CrossRef]
- Campiglia, M.; Gambini, R.; Olmedo, J.; Pullin, J. Quantum self-gravitating collapsing matter in a quantum geometry. Class. Quantum Gravity 2016, 33, 18LT01. [Google Scholar] [CrossRef]
- Singh, P.; Vidotto, F. Exotic singularities and spatially curved Loop Quantum Cosmology. Phys. Rev. D 2011, 83, 064027. [Google Scholar] [CrossRef]
- Hossenfelder, S.; Smolin, L. Conservative solutions to the black hole information problem. Phys. Rev. D 2010, 81, 064009. [Google Scholar] [CrossRef]
- Hawking, S.W.; Laflamme, R. Baby Universes and the Non-renormalizability of Gravity. Phys. Lett. B 1988, 209, 39–41. [Google Scholar] [CrossRef]
- Hawking, S.W. Wormholes in Space-Time. Phys. Rev. D 1988, 37, 904–910. [Google Scholar] [CrossRef]
- Hellaby, C.; Dray, T. Failure of standard conservation laws at a classical change of signature. Phys. Rev. D 1994, 49, 5096–5104. [Google Scholar] [CrossRef]
- Liberati, S.; Maccione, L. Quantum gravity phenomenology: Achievements and challenges. J. Phys. Conf. Ser. 2011, 314, 012007. [Google Scholar] [CrossRef]
- Ashtekar, A.; Gupt, B. Quantum gravity in the sky: Interplay between fundamental theory and observations. Class. Quantum Gravity 2017, 34, 014002. [Google Scholar] [CrossRef]
- Narlikar, J.V.; Rao, K.A.; Dadhich, N. High energy radiation from white holes. Nature 1974, 251, 590–591. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The maximum mass of ideal white dwarfs. Astrophys. J. 1931, 74, 81–82. [Google Scholar] [CrossRef]
- Visser, M.; Barcelo, C.; Liberati, S.; Sonego, S. Small, dark, and heavy: But is it a black hole? In Proceedings of the Black Holes in General Relativity and String Theory, Veli Losinj, Croatia, 24–30 August 2008. [Google Scholar]
- Mazur, P.O.; Mottola, E. Surface tension and negative pressure interior of a non-singular ’black hole’. Class. Quantum Gravity 2015, 32, 215024. [Google Scholar] [CrossRef]
- Cattoen, C.; Faber, T.; Visser, M. Gravastars must have anisotropic pressures. Class. Quantum Gravity 2005, 22, 4189–4202. [Google Scholar] [CrossRef]
- Chirenti, C.B.M.H.; Rezzolla, L. How to tell a gravastar from a black hole. Class. Quantum Gravity 2007, 24, 4191–4206. [Google Scholar] [CrossRef]
- Cardoso, V.; Franzin, E.; Pani, P. Is the Gravitational-Wave Ringdown a Probe of the Event Horizon? Phys. Rev. Lett. 2016, 116, 171101. [Google Scholar] [CrossRef] [PubMed]
- Sakai, N.; Saida, H.; Tamaki, T. Gravastar shadows. Phys. Rev. D 2014, 90, 104013. [Google Scholar] [CrossRef]
- Barcelò, C.; Liberati, S.; Sonego, S.; Visser, M. Hawking-like radiation does not require a trapped region. Phys. Rev. Lett. 2006, 97, 171301. [Google Scholar] [CrossRef] [PubMed]
- Husain, V.; Winkler, O. How red is a quantum black hole? Int. J. Mod. Phys. D 2005, 14, 2233–2238. [Google Scholar] [CrossRef]
- Rovelli, C.; Vidotto, F. Planck stars. Int. J. Mod. Phys. D 2014, 23, 1442026. [Google Scholar] [CrossRef]
- De Lorenzo, T.; Pacilio, C.; Rovelli, C.; Speziale, S. On the Effective Metric of a Planck Star. Gen. Relativ. Gravit. 2015, 47, 41. [Google Scholar] [CrossRef]
- Barrau, A.; Rovelli, C. Planck star phenomenology. Phys. Lett. B 2014, 739, 405–409. [Google Scholar] [CrossRef]
- Lobo, F.S.N. Stable dark energy stars. Class. Quantum Gravity 2006, 23, 1525–1541. [Google Scholar] [CrossRef]
- DeBenedictis, A.; Garattini, R.; Lobo, F.S.N. Phantom stars and topology change. Phys. Rev. D 2008, 78, 104003. [Google Scholar] [CrossRef]
- Rahaman, F.; Yadav, A.K.; Ray, S.; Maulick, R.; Sharma, R. Singularity-free dark energy star. Gen. Relativ. Gravit. 2012, 44, 107–124. [Google Scholar] [CrossRef]
- Giddings, S.B. Possible observational windows for quantum effects from black holes. Phys. Rev. D 2014, 90, 124033. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J. Circular geodesic of Bardeen and Ayon–Beato–Garcia regular black-hole and no-horizon spacetimes. Int. J. Mod. Phys. D 2015, 24, 1550020. [Google Scholar] [CrossRef]
- Eiroa, E.F.; Sendra, C.M. Gravitational lensing by a regular black hole. Class. Quantum Gravity 2011, 28, 085008. [Google Scholar] [CrossRef]
- Chiba, T.; Kimura, M. A Note on Geodesics in the Hayward Metric. Prog. Theor. Exp. Phys. 2017, 2017, 043E01. [Google Scholar] [CrossRef]
- Bambi, C.; Malafarina, D. Kα iron line profile from accretion disks around regular and singular exotic compact objects. Phys. Rev. D 2013, 88, 064022. [Google Scholar] [CrossRef]
- Doeleman, S.; Agol, E.; Backer, D.; Baganoff, F.; Bower, G.C.; Broderick, A.; Fabian, A.; Fish, V.; Gammie, C.; Ho, P.; et al. Imaging an Event Horizon: Submm-VLBI of a Super Massive Black Hole. arXiv, 2009; arXiv:0906.3899. [Google Scholar]
- Goddi, C.; Falcke, H.; Kramer, M.; Rezzolla, L.; Brinkerink, C.; Bronzwaer, T.; Davelaar, J.R.; Deane, R.; de Laurentis, M.; Desvignes, G.; et al. BlackHoleCam: Fundamental physics of the Galactic center. Int. J. Mod. Phys. D 2016, 26, 1730001. [Google Scholar] [CrossRef]
- Johannsen, T. Sgr A* and General Relativity. Class. Quantum Gravity 2016, 33, 113001. [Google Scholar] [CrossRef]
- Bambi, C.; Jiang, J.; Steiner, J.F. Testing the no-hair theorem with the continuum-fitting and the iron line methods: A short review. Class. Quantum Gravity 2016, 33, 064001. [Google Scholar] [CrossRef]
- Haggard, H.; Rovelli, C. Quantum gravity effects around Sagittarius A*. Int. J. Mod. Phys. D 2016, 25, 1644021. [Google Scholar] [CrossRef]
- Barrau, A.; Rovelli, C.; Vidotto, F. Fast Radio Bursts and White Hole Signals. Phys. Rev. D 2014, 90, 127503. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Giddings, S.B. Gravitational wave tests of quantum modifications to black hole structure—With post-GW150914 update. Class. Quantum Gravity 2016, 33, 235010. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Detection of gravitational waves from black holes: Is there a window for alternative theories? Phys. Lett. B 2016, 756, 350–353. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Wormholes versus black holes: Quasinormal ringing at early and late times. J. Cosmol. Astropart. Phys. 2016, 2016, 043. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, 83, 793. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. Generation of Waves by a Rotating Body. J. Exp. Theor. Phys. Lett. 1971, 14, 180–181. [Google Scholar]
- Starobinsky, A. Amplification of waves during reection from a black hole. J. Exp. Theor. Phys. 1973, 37, 28. [Google Scholar]
- Bekenstein, J.D.; Schiffer, M. The many faces of superradiance. Phys. Rev. D 1998, 58, 064014. [Google Scholar] [CrossRef]
- Marolf, D. The Black Hole information problem: Past, present, and future. arXiv, 2017; arXiv:1703.02143. [Google Scholar]
- Unruh, W.G.; Wald, R.M. Information Loss. arXiv, 2017; arXiv:1703.02140. [Google Scholar]
- Chakraborty, S.; Lochan, K. Black Holes: Eliminating Information or Illuminating New Physics? arXiv, 2017. [Google Scholar]
- Cardoso, V.; Hopper, S.; Macedo, C.F.B.; Palenzuela, C.; Pani, P. Gravitational-wave signatures of exotic compact objects and of quantum corrections at the horizon scale. Phys. Rev. D 2016, 94, 084031. [Google Scholar] [CrossRef]
- Abedi, J.; Dykaar, H.; Afshordi, N. Echoes from the Abyss: Evidence for Planck-scale structure at black hole horizons. arXiv, 2016; arXiv:1612.00266. [Google Scholar]
- Barceló, C.; Carballo-Rubio, R.; Garay, L.J. Gravitational echoes from macroscopic quantum gravity effects. arXiv, 2017; arXiv:1701.09156. [Google Scholar]
- Price, R.; Khanna, G. Gravitational wave sources: Reflections and echoes. arXiv, 2017; arXiv:1702.04833. [Google Scholar]
- Giddings, S.B.; Psaltis, D. Event Horizon Telescope Observations as Probes for Quantum Structure of Astrophysical Black Holes. arXiv, 2016; arXiv:1606.07814. [Google Scholar]
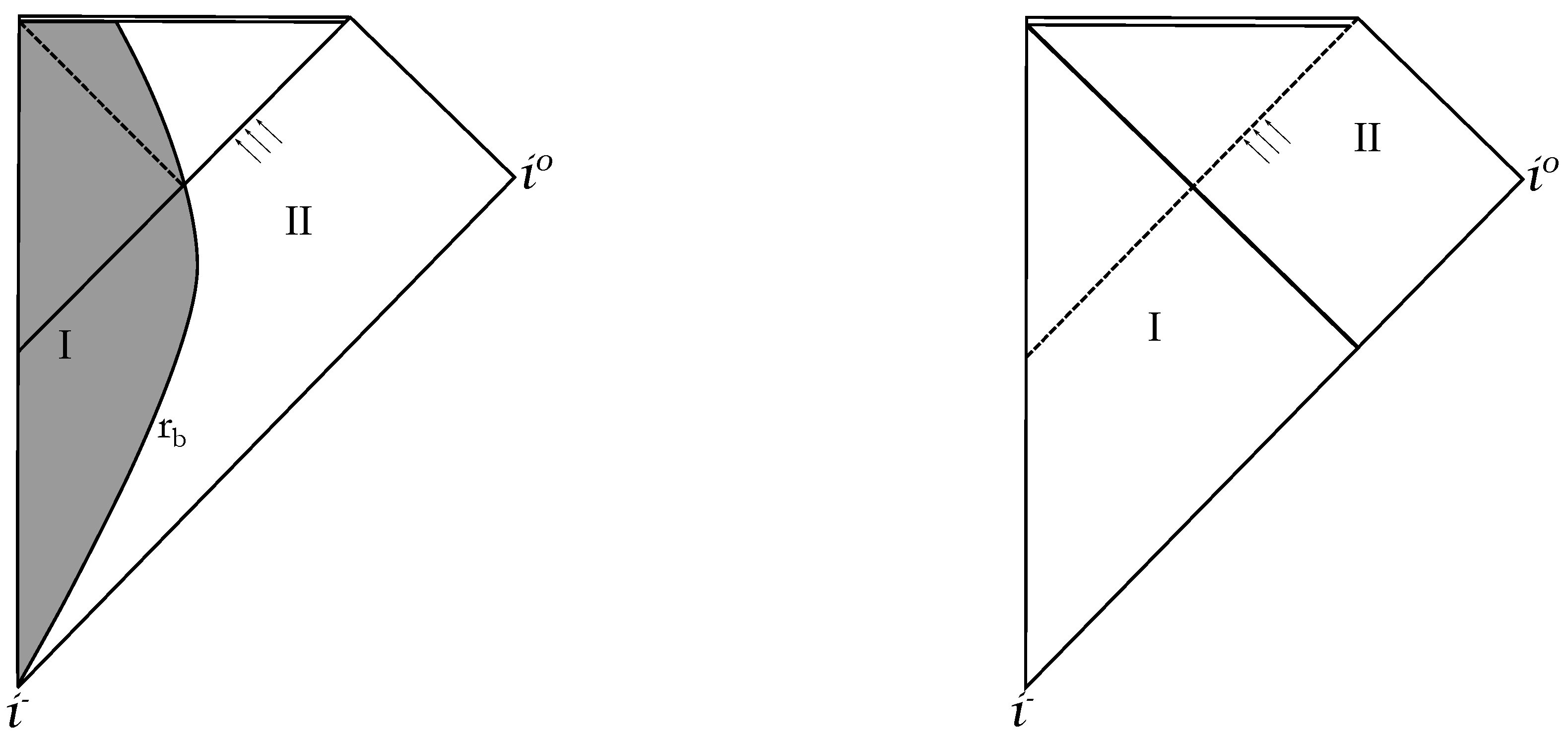
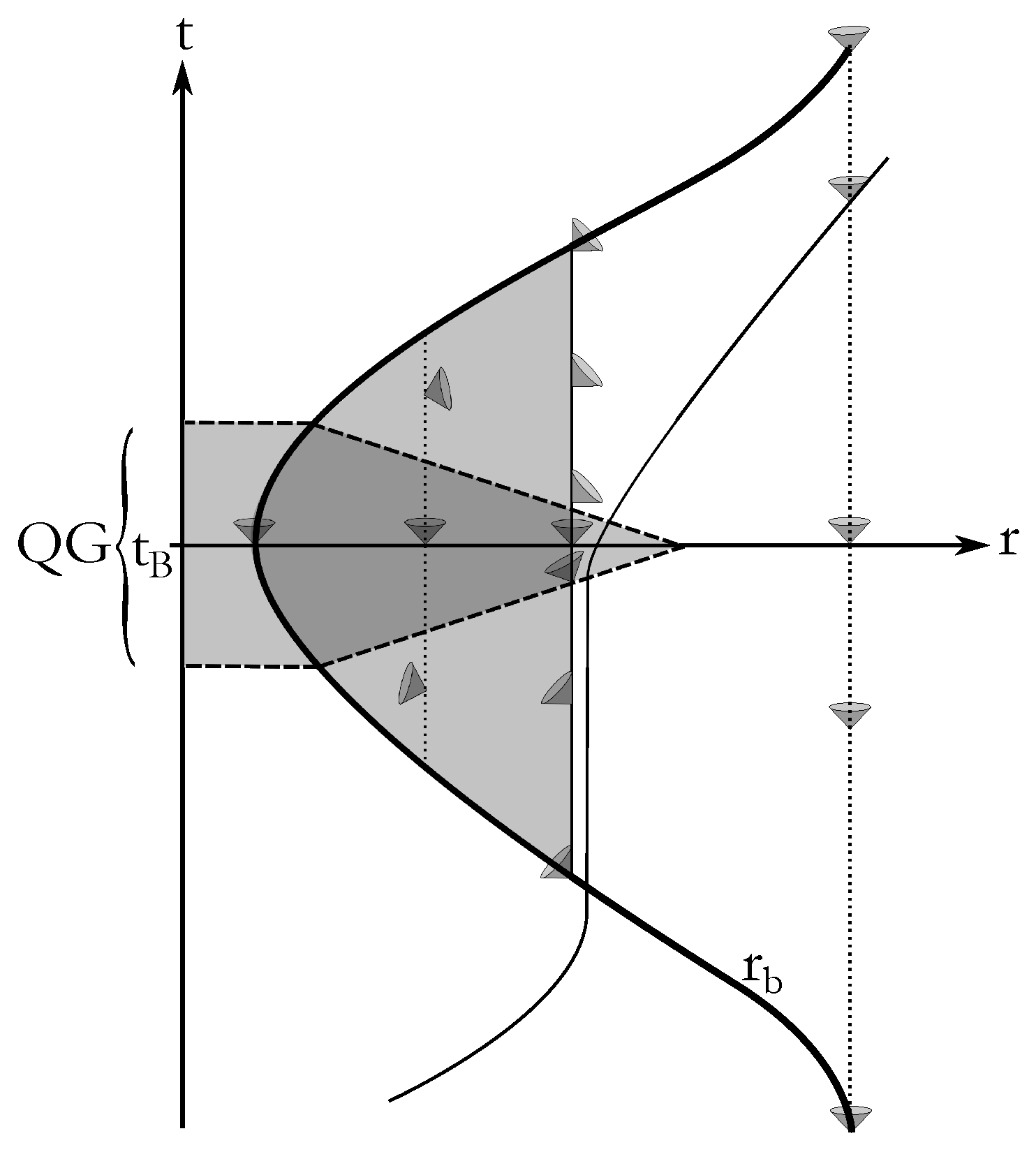
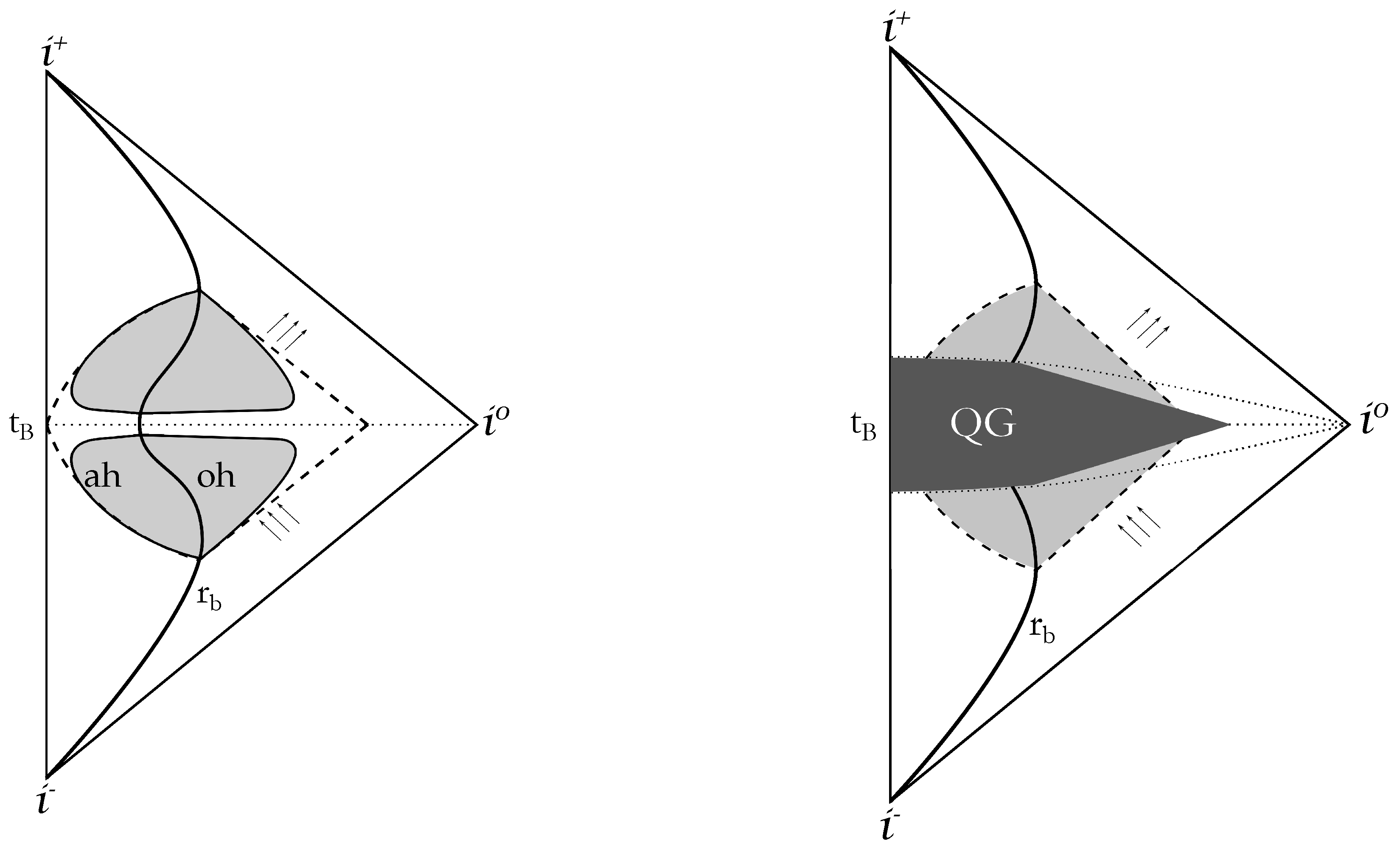
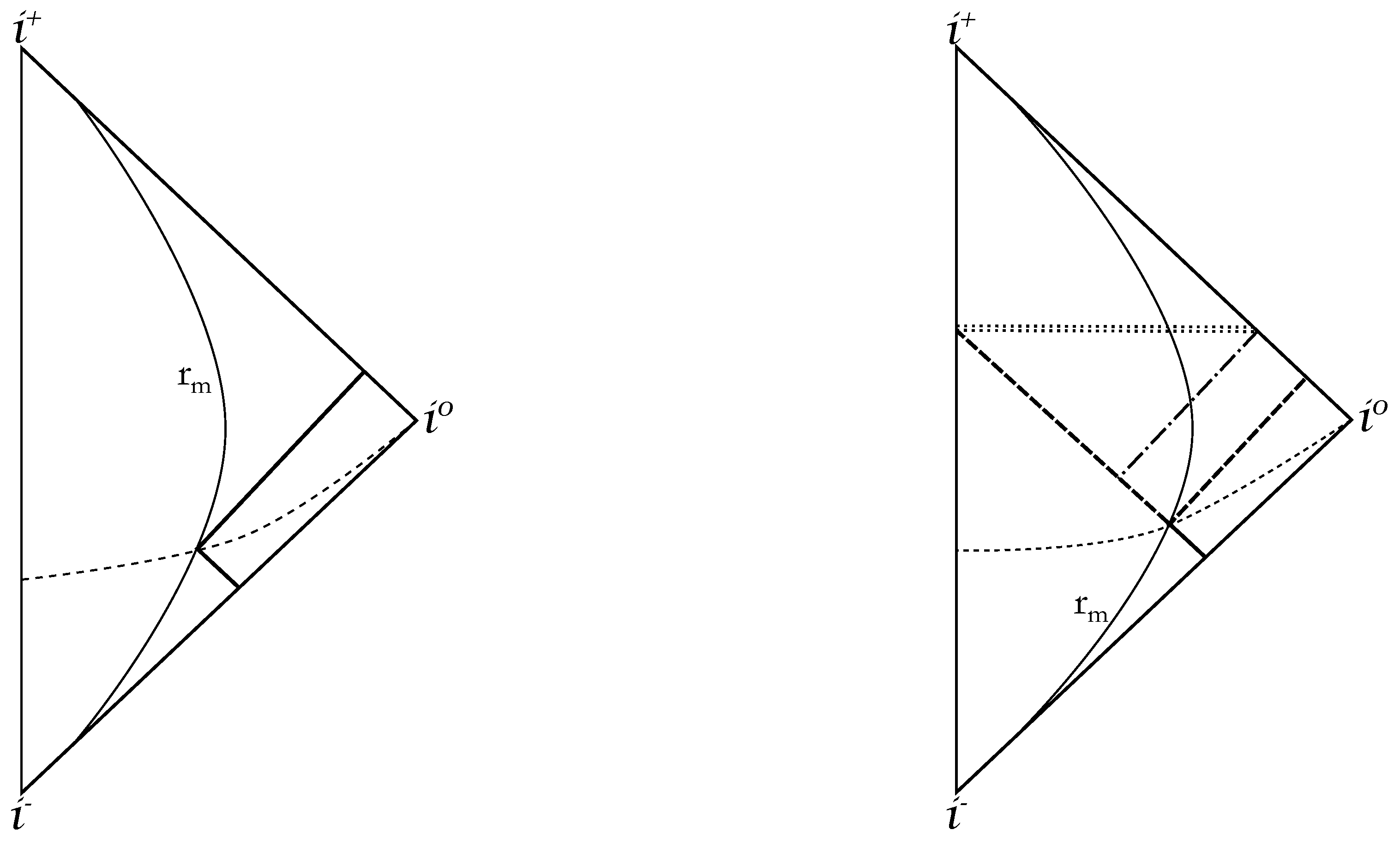
| 1. | The choice of Painlevé-Gullstrand coordinates is particularly well suited for describing collapse that starts from rest at a finite radius (see [65] for a detailed discussion). |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malafarina, D. Classical Collapse to Black Holes and Quantum Bounces: A Review. Universe 2017, 3, 48. https://doi.org/10.3390/universe3020048
Malafarina D. Classical Collapse to Black Holes and Quantum Bounces: A Review. Universe. 2017; 3(2):48. https://doi.org/10.3390/universe3020048
Chicago/Turabian StyleMalafarina, Daniele. 2017. "Classical Collapse to Black Holes and Quantum Bounces: A Review" Universe 3, no. 2: 48. https://doi.org/10.3390/universe3020048
APA StyleMalafarina, D. (2017). Classical Collapse to Black Holes and Quantum Bounces: A Review. Universe, 3(2), 48. https://doi.org/10.3390/universe3020048





