Quantum Cosmology of the Big Rip: Within GR and in a Modified Theory of Gravity
Abstract
:1. Introduction
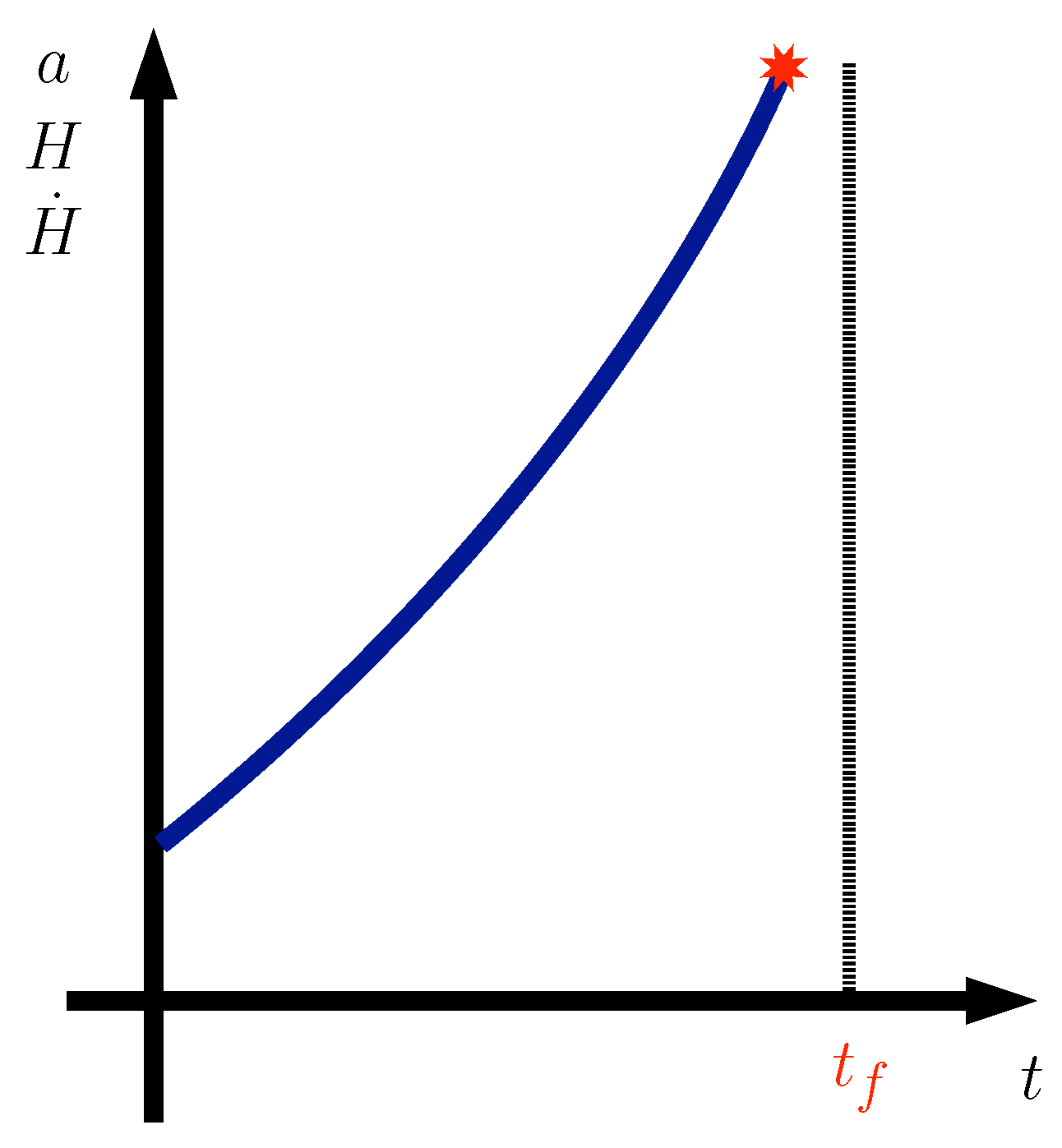
2. The Classical Big Rip Singularity
3. Quantum Cosmology of the Big Rip within the Holographic Ricci Dark Energy
4. Quantum Cosmology of the Big Rip Model within the Eddington-Inspired Born-Infeld Model
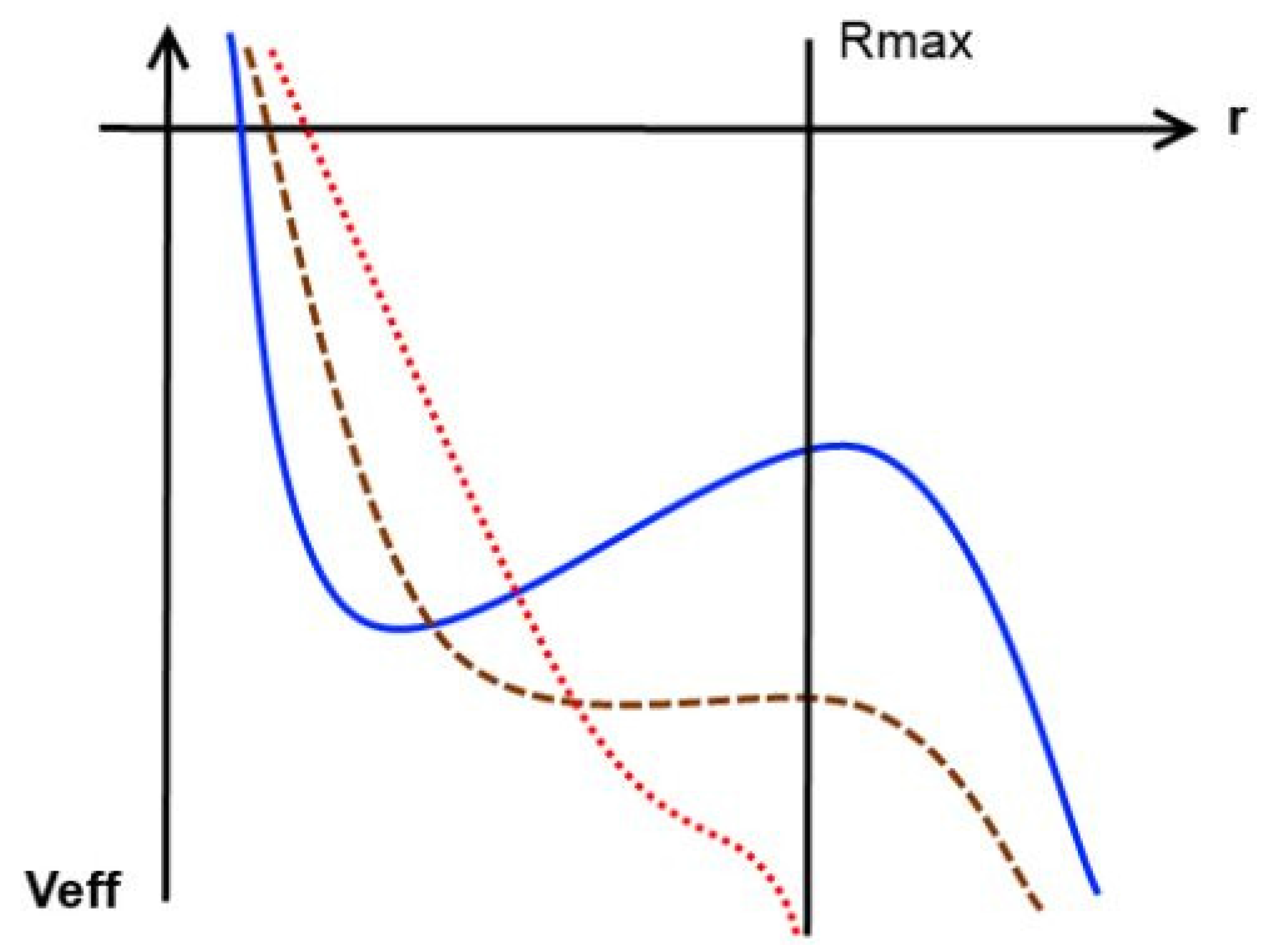
- If diverges slower than (i.e., ), the second term in the bracket in (15) is negligible compared with the first term. However, whether the first term dominates over the third term depends on the exact form of and . In either case, the potential reaches positive infinite values when both a and x go to infinity.
- If diverges faster than (i.e., ), the potential can be approximated aswhen a goes to infinity.
- If diverges comparably with , the potential can also be approximated as in Equation (16), because the phantom energy density blows up when .
5. Conclusions and Further Discussions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BR | Big Rip |
| DE | dark energy |
| DM | dark matter |
| FLRW | Friedmann–Lemaître–Robertson–Walker |
| HRDE | holographic Ricci dark energy |
| EiBI | Eddington-Inspired-Born-Infeld |
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astrophys. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Battaner, E.; et al. Planck 2015 results. XIV. Dark energy and modified gravity. Astron. Astrophys. 2016, 594, A14. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Sahni, V.; Starobinsky, A.A. The Case for a positive cosmological Lambda term. Int. J. Mod. Phys. D 2000, 9, 373. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological constant. Living Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Padmanabhan, T. Cosmological constant: The Weight of the vacuum. Phys. Rep. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Tsujikawa, S. Dark energy: Investigation and modeling. In Dark Matter and Dark Energy: A Challenge for Modern Cosmology; Matarrese, S., Colpi, M., Gorini, V., Moschella, U., Eds.; Springer: New York, NY, USA, 2011; pp. 331–342. [Google Scholar]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Springer Science & Business Media: New York, NY, USA, 2011; Volume 170. [Google Scholar]
- Morais, J.; Bouhmadi-López, M.; Capozziello, S. Can f(R) gravity contribute to (dark) radiation? J. Cosmol. Astropart. Phys. 2015, 2015, 41. [Google Scholar] [CrossRef]
- Susskind, L. The World as a hologam. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Cohen, A.G.; Kaplan, D.B.; Nelson, A.E. Effective field theory, black holes, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 4971–4974. [Google Scholar] [CrossRef]
- Li, M. A Model of holographic dark energy. Phys. Lett. B 2004, 603, 1–5. [Google Scholar] [CrossRef]
- Hsu, S.D.H. Entropy bounds and dark energy. Phys. Lett. B 2004, 594, 13–16. [Google Scholar] [CrossRef]
- Gao, C.; Wu, F.Q.; Chen, X.; Shen, Y.G. A Holographic Dark Energy Model from Ricci Scalar Curvature. Phys. Rev. D 2009, 79, 043511. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Future and origin of our universe: Modern view. Gravit. Cosmol. 2000, 6, 157–163. [Google Scholar]
- Caldwell, R.R. A Phantom menace? Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom energy and cosmic doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar] [CrossRef] [PubMed]
- Suwa, M.; Kobayashi, K.; Oshima, H. The interacting generalized Ricci dark energy model in non-flat universe. J. Mod. Phys. 2015, 6, 327–334. [Google Scholar] [CrossRef]
- Xu, L.; Wang, Y. Observational Constraints to Ricci Dark Energy Model by Using: SN, BAO, OHD, fgas Data Sets. J. Cosmol. Astropart. Phys. 2010, 2010, 2. [Google Scholar] [CrossRef]
- Fernández-Jambrina, L.; Lazkoz, R. Classification of cosmological milestones. Phys. Rev. D 2006, 74, 064030. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Bañados, M.; Ferreira, P.G. Eddington’s theory of gravity and its progeny. Phys. Rev. Lett. 2010, 105, 011101. [Google Scholar] [CrossRef] [PubMed]
- Deser, S.; Gibbons, G.W. Born-Infeld-Einstein actions? Class. Quantum Gravity 1998, 15, L35–L39. [Google Scholar] [CrossRef]
- Delsate, T.; Steinhoff, J. New insights on the matter-gravity coupling paradigm. Phys. Rev. Lett. 2012, 109, 021101. [Google Scholar] [CrossRef] [PubMed]
- Bouhmadi-López, M.; Chen, C.Y. Towards the Quantization of Eddington-inspired-Born-Infeld Theory. J. Cosmol. Astropart. Phys. 2016, 2016, 23. [Google Scholar] [CrossRef]
- Pani, P.; Sotiriou, T.P. Surface singularities in Eddington-inspired Born-Infeld gravity. Phys. Rev. Lett. 2012, 109, 251102. [Google Scholar] [CrossRef] [PubMed]
- Pani, P.; Cardoso, V.; Delsate, T. Compact stars in Eddington inspired gravity. Phys. Rev. Lett. 2011, 107, 031101. [Google Scholar] [CrossRef] [PubMed]
- Olmo, G.J.; Rubiera-Garcia, D.; Sanchis-Alepuz, H. Geonic black holes and remnants in Eddington-inspired Born-Infeld gravity. Eur. Phys. J. C 2014, 74, 2804. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Du, X.-L.; Liu, Y.-X. Linear perturbations in Eddington-inspired Born-Infeld gravity. Phys. Rev. D 2013, 88, 124037. [Google Scholar] [CrossRef]
- Avelino, P.P. Eddington-inspired Born-Infeld gravity: Nuclear physics constraints and the validity of the continuous fluid approximation. J. Cosmol. Astropart. Phys. 2012, 2012, 22. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Chen, C.-Y.; Chen, P. Is Eddington-Born-Infeld theory really free of cosmological singularities? Eur. Phys. J. C 2014, 74, 2802. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Chen, C.Y.; Chen, P. Eddington-Born-Infeld cosmology: A cosmographic approach, a tale of doomsdays and the fate of bound structures. Eur. Phys. J. C 2015, 2, 90. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Chen, C.Y.; Chen, P. Cosmological singularities in Born-Infeld determinantal gravity. Phys. Rev. D 2014, 90, 123518. [Google Scholar] [CrossRef]
- Chen, C.Y.; Bouhmadi-López, M.; Chen, P. Modified Eddington-inspired-Born-Infeld Gravity with a Trace Term. Eur. Phys. J. C 2016, 76, 40. [Google Scholar] [CrossRef]
- Beltrán Jiménez, J.; Lazkoz, R.; Sáez-Gómez, D.; Salzano, V. Observational constraints on cosmological future singularities. Eur. Phys. J. C 2016, 76, 631. [Google Scholar] [CrossRef]
- Nesseris, S.; Perivolaropoulos, L. The Fate of bound systems in phantom and quintessence cosmologies. Phys. Rev. D 2004, 70, 123529. [Google Scholar] [CrossRef]
- Faraoni, V.; Jacques, A. Cosmological expansion and local physics. Phys. Rev. D 2007, 76, 063510. [Google Scholar] [CrossRef]
- Albarran, I.; Bouhmadi-López, M. Quantisation of the holographic Ricci dark energy model. J. Cosmol. Astropart. Phys. 2015, 2015, 51. [Google Scholar] [CrossRef]
- Da̧browski, M.P.; Kiefer, C.; Sandhöfer, B. Quantum phantom cosmology. Phys. Rev. D 2006, 74, 044022. [Google Scholar] [CrossRef]
- Barbaoza, E.M., Jr.; Lemos, N.A. Does the Big Rip survive quantization? Gen. Relativ. Gravit. 2006, 38, 1609–1622. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Pantoja, D.M. Bohmian quantization of the big rip. Phys. Rev. D 2009, 80, 083509. [Google Scholar] [CrossRef]
- Tretyakov, P.; Toporensky, A.; Shtanov, Y.; Sahni, V. Quantum effects, soft singularities and the fate of the universe in a braneworld cosmology. Class. Quantum Gravity 2006, 23, 3259–3274. [Google Scholar] [CrossRef]
- Sami, M.; Singh, P.; Tsujikawa, S. Avoidance of future singularities in loop quantum cosmology. Phys. Rev. D 2006, 74, 043514. [Google Scholar] [CrossRef]
- Barvinsky, A.O.; Kamenshchik, A.Y. Selection rules for the Wheeler-DeWitt equation in quantum cosmology. Phys. Rev. D 2014, 89, 043526. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouhmadi-López, M.; Albarran, I.; Chen, C.-Y. Quantum Cosmology of the Big Rip: Within GR and in a Modified Theory of Gravity. Universe 2017, 3, 36. https://doi.org/10.3390/universe3020036
Bouhmadi-López M, Albarran I, Chen C-Y. Quantum Cosmology of the Big Rip: Within GR and in a Modified Theory of Gravity. Universe. 2017; 3(2):36. https://doi.org/10.3390/universe3020036
Chicago/Turabian StyleBouhmadi-López, Mariam, Imanol Albarran, and Che-Yu Chen. 2017. "Quantum Cosmology of the Big Rip: Within GR and in a Modified Theory of Gravity" Universe 3, no. 2: 36. https://doi.org/10.3390/universe3020036
APA StyleBouhmadi-López, M., Albarran, I., & Chen, C.-Y. (2017). Quantum Cosmology of the Big Rip: Within GR and in a Modified Theory of Gravity. Universe, 3(2), 36. https://doi.org/10.3390/universe3020036





