Abstract
Recent developments in gravitation theory indicate that the classic general relativity is an effective macroscopic theory which will be eventually replaced with a more fundamental theory based on thermodynamics of yet unknown microscopic degrees of freedom. Here we consider thermodynamics of an effective spacetime which may be formed under the influence of an external magnetic field in a cobalt ferrofluid. It appears that the extraordinary photons propagating inside the ferrofluid perceive thermal gradients in the ferrofluid as an effective gravitational field, which obeys the Newton law. Moreover, the effective de Sitter spacetime behaviour near the metric signature transition may mimic various cosmological inflation scenarios, which may be visualized directly using an optical microscope. Thus, some features of the hypothetic microscopic theory of gravity are illustrated in the ferrofluid-based analogue models of inflation.
1. Introduction
Modern advances in gravitation theory [1,2] strongly indicate that the classic general relativity description of gravity results from a more fundamental theory based on thermodynamics of yet unknown microscopic degrees of freedom. These true microscopic degrees of freedom cannot be probed directly because they are far out of reach of terrestrial experiments and astronomical observations. Therefore, it is instructive to look at various examples of emergent gravity in various analogue spacetimes, which appear in several condensed matter systems [3]. By probing such systems, we may gain valuable insights into the relationship between the macroscopic effective gravity and the thermodynamics of well-known microscopic atomic degrees of freedom.
Ferrofluid-based self-assembled hyperbolic metamaterials have emerged recently as an interesting example of a condensed matter system, which may be described by an emergent effective Minkowski spacetime, and which exhibits gravity-like nonlinear optical interactions [4,5,6]. If a ferrofluid is subjected to a strong enough external magnetic field, it self-assembles into a “wire array” hyperbolic metamaterial [7] (see Figure 1), which may exhibit rich physics associated with topological defects [8] and metric signature transitions [9]. Moreover, such a self-assembly may occur even without the external field at low enough temperature, due to spontaneous magnetization of the ferrofluid. As was pointed out recently by Mielczarek and Bojowald [10,11], such self-assembled magnetic nanoparticle-based hyperbolic metamaterials exhibit strong similarities with the properties of some microscopic quantum gravity models, such as loop quantum cosmology.
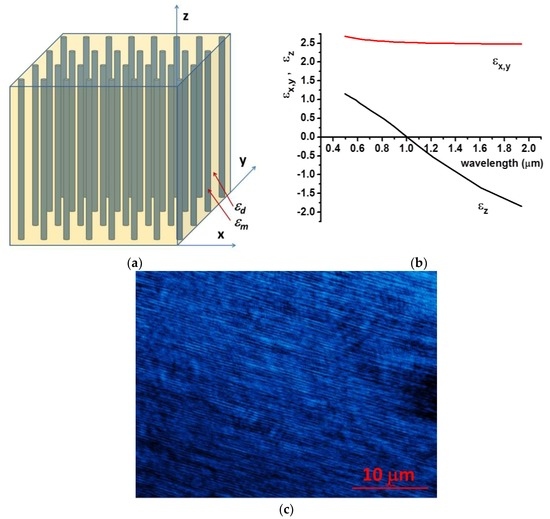
Figure 1.
(a) Schematic geometry of the metal nanowire-based hyperbolic metamaterial; (b) Wavelength dependencies of the real parts of εz and εx = εy for a cobalt nanoparticle-based ferrofluid at α = 8.2% volume fraction of nanoparticles. While εx = εy stays positive and almost constant, εz changes sign to negative around λ = 1 µm; (c) Microscopic image of cobalt nanoparticle-based ferrofluid in external magnetic field reveals nanoparticle alignment along the field direction.
Here, we will consider thermodynamics of the effective spacetime in a ferrofluid. It appears that the extraordinary photons propagating inside the ferrofluid perceive thermal gradients in the ferrofluid as an effective gravitational field, which obeys the Newton law. Moreover, the effective spacetime behaviour near the metric signature transition may mimic various inflationary cosmological Big Bang scenarios. Thus, some important features of the hypothetic microscopic theory of gravity are reproduced in the ferrofluid-based analogue model. Even though the relationship between the thermodynamics and the effective gravity in 3D ferrofluid spacetime does not completely match the behaviour of general relativity in four spacetime dimensions, this model system is quite interesting. It permits direct theoretical analysis at the level of well-defined microscopic degrees of freedom, and it enables direct visualization of these microscopic degrees of freedom using standard optical tools. It is interesting that inflation-like behaviors emerge naturally within the scope of this model.
2. Materials and Methods
As a starting point, let us consider the electromagnetic properties of self-assembled ferrofluids based on their microscopic degrees of freedom. As an example, let us choose the cobalt magnetic fluid 27-0001 from Strem Chemicals (Newburyport, MA, USA) used in experimental studies reported in [4,7,8], which is composed of 10 nm magnetic cobalt nanoparticles in kerosene. The nanoparticles are coated with sodium dioctylsulfosuccinate and a monolayer of LP4 fatty acid condensation polymer. The average volume fraction of cobalt nanoparticles in this ferrofluid is p = 8.2%. Magnetic nanoparticles in this ferrofluid are known to form nanocolumns aligned along the magnetic field [7]. Macroscopic electromagnetic properties of such a ferrofluid may be understood based on the Maxwell-Garnett approximation via the dielectric permittivities εm and εd of cobalt and kerosene, respectively. The volume fraction of cobalt nanoparticles aligned into nanocolumns by the external magnetic field, α(H,T), depends on the temperature and the field magnitude. At very large magnetic fields, all nanoparticles are aligned into nanocolumns, so that α(∞,T) = p = 8.2%, and a 3D wire array hyperbolic metamaterial [4,5] is formed as shown schematically in Figure 1a. We will assume that, at smaller fields, the difference α(∞,T)–α(H,T) describes cobalt nanoparticles, which are not aligned and distributed homogeneously inside the ferrofluid. Dielectric polarizability of these nanoparticles may be included into εd, leading to slight increase in its value. Using this model, the diagonal components of the ferrofluid permittivity may be calculated using the Maxwell-Garnett approximation as follows [12]:
Calculated wavelength dependencies of ε2 and ε1 at α(∞,T) = p = 8.2% are plotted in Figure 1b. These calculations are based on the optical properties of cobalt in the infrared range [13]. While ε1 stays positive and almost constant, ε2 changes sign to negative around λ = 1 µm. If the volume fraction of cobalt nanoparticles varies, this change of sign occurs at some critical value αH:
so that the ferrofluid becomes a hyperbolic metamaterial [4,5]. Alignment of cobalt nanoparticle chains along the direction of the external magnetic field is clearly revealed by microscopic images of the ferrofluid, as shown in Figure 1c. As far as magnetic permeability is concerned, at the visible and infrared frequencies, the ferrofluid may be considered as a non-magnetic (µ = 1) medium.
As a second step, let us demonstrate that the wave equation describing propagation of monochromatic extraordinary light inside a hyperbolic metamaterial exhibits 2 + 1 dimensional Lorentz symmetry. A detailed derivation of this result may be found in [5]. Since the ferrofluid in the external magnetic field may be characterized as a uniaxial dielectric material, the electromagnetic field inside the ferrofluid may be separated into ordinary and extraordinary waves. As a reminder, vector of the extraordinary light wave is parallel to the plane defined by the k-vector of the wave and the optical axis of the metamaterial. Propagation of monochromatic extraordinary light may be described by a coordinate-dependent wave function ϕ = Ez obeying the wave equation:
This wave equation coincides with the Klein-Gordon equation for a massive scalar field ϕϖ in 3D Minkowski spacetime:
in which the spatial coordinate z behaves as a “timelike” variable. Equation (5) exhibits effective Lorentz invariance under the coordinate transformation
where β is the effective boost. Similar to our own Minkowski spacetime, the effective Lorentz transformations in the xz and yz planes form the Poincare group together with translations along x-, y-, and z-axis, and rotations in the xy plane. Thus, the wave Equation (5) describes world lines of massive particles (with an effective mass m* = ħϖ0/c2), which propagate in an effective 2 + 1 dimensional Minkowski spacetime. Note that the components of the metamaterial dielectric tensor define the effective metric gik of this spacetime: g00 = −ε1 and g11 = g22 = −ε2.
When the nonlinear optical effects become important, they are described in terms of various order nonlinear susceptibilities χ(υ) of the metamaterial:
Taking into account these nonlinear terms, the dielectric tensor of the metamaterial (which defines its effective metric) may be written as
In a centrosymmetric material, all the second order nonlinear susceptibilities χ(2)ijl must be equal to zero. It is clear that Equation (8) provides coupling between the matter content (photons) and the effective metric of the metamaterial spacetime. Nonlinear optical effects “bend” this effective Minkowski spacetime, resulting in gravity-like interaction of extraordinary light rays. It appears that, in the weak field limit, the nonlinear optics of hyperbolic metamaterials may indeed be formulated as an effective gravity [5]. In such a limit, the Einstein equation
is reduced to
where φ is the gravitational potential [14]. Therefore, the third order terms in Equation (8) may provide a correct coupling between the effective metric and the energy-momentum tensor. These terms are associated with the optical Kerr effect. The detailed analysis in [5] indeed indicates that the Kerr effect in a hyperbolic metamaterial leads to effective gravity.
Let us briefly reproduce this analysis, since it is important for the discussion of the connection between the effective gravity and the thermodynamics of a magnetized ferrofluid. Since the z-coordinate plays the role of time, while g00 is identified with −ε1, Equation (10) may be re-written as
where ∆(2) is the 2D Laplacian operating in the xy plane, γ* is the effective “gravitation constant”, and σzz is the zz component of the Maxwell stress tensor of the electromagnetic field in the medium:
Taking into account Equation (4), for a single plane wave, Equation (11) may be rewritten as [5]
where without a loss of generality we have assumed that the B field of the wave is oriented along the y-direction. We also assumed that the nonlinear corrections to ε1 are small, so that we can separate ε1 into the constant background value ε1(0) and the weak nonlinear corrections. These nonlinear corrections do indeed look like the Kerr effect assuming that the extraordinary photon wave vector components are large compared to ω/c:
This assumption has to be the case if extraordinary photons may be considered as classic “particles”. Unlike the usual “elliptic” optical materials, this assumption is justified by the hyperbolic dispersion relation of the extraordinary photons:
which follows from Equation (4). Equation (14) establishes a connection between the effective gravitation constant γ* and the third order nonlinear susceptibility χ(3) of the hyperbolic metamaterial. Since ε2 < 0, the sign of χ(3) must be negative for the effective gravity to be attractive. This condition is satisfied naturally in most liquids, and, in particular, in kerosene. Because of the large and negative thermo-optic coefficient inherent to most liquids, heating produced by partial absorption of the propagating beam translates into a significant decrease of the refractive index at higher light intensity. For example, the reported thermo-optic coefficient of water reaches ∆n/∆T = −5.7 × 10−4 K−1 [15]. Moreover, introduction of nanoparticles or absorbent dye into the liquid allows for further increase of the thermal nonlinear response [16]. Therefore, a ferrofluid-based self-assembled hyperbolic metamaterial naturally exhibits a potentially interesting version of effective gravity. The thermal origin of this effective gravity looks interesting in light of the modern advances in gravitation theory [1,2], which strongly indicate that the classic general relativity description of gravity results from thermodynamic effects.
3. Results
As a next step, let us consider the effect of a thermal gradient in the ferrofluid on its effective metric. It appears that the extraordinary photons propagating inside the ferrofluid perceive thermal gradients as an effective gravitational field. Indeed, Equations (1) and (2) imply that ε2 and ε1 (which may be understood as the effective metric coefficients g00 =−ε1 and g11 = g22 = −ε2 of the metamaterial spacetime) depend on the volume fraction α(H,T) of cobalt nanoparticles aligned into nanocolumns by the external magnetic field, which, in turn, depends on the local temperature of the ferrofluid. Since ferrofluids subjected to an external magnetic field are known to exhibit classical superparamagnetic behaviour [17], well established results from the theory of magnetism may be used to calculate α(H,T). Superparamagnetism is a form of magnetism that is exhibited by magnetic materials, which consist of small ferromagnetic or ferrimagnetic nanoparticles. Superparamagnetism occurs in nanoparticles which are single-domain, which is possible when their diameter is below ~50 nm, depending on the material. Since the typical size of magnetic nanoparticles in ferrofluids is ~10 nm, magnetic ferrofluids also belong to the class of superparamagnetic materials. When an external magnetic field is applied to an assembly of superparamagnetic nanoparticles, their magnetic moments tend to align along the applied field, leading to a net magnetization. If all the particles may be considered to be roughly identical (as in the case of a homogeneous ferrofluid), and the temperature is low enough, then the magnetization of the assembly is [17]
where n is the nanoparticle concentration and µ is their magnetic moment. Therefore, within the scope of our model of the dielectric response of the ferrofluid (see Equations (1) and (2)), we may assume that
where α∞ = 0.082. Let us consider the typical case of −εm >> εd and assume that α(H,T) is small (which is typically required for the Maxwell-Garnett approximation to be valid). In such a case, the effective metric coefficients are:
(note that εm is negative). The effective spacetime appears to have the correct signature if the temperature is low enough, so that
Thus, in the weak field limit, the effective gravitational potential (see Equation (10)) is
where the value of the effective potential at T = 0 is chosen as a reference, and the effective gravitational field is
where we have assumed that the external magnetic field H to be constant. Thus, the extraordinary photons propagating inside the ferrofluid perceive thermal gradients in the ferrofluid as an effective gravitational field. This observation correlates nicely with the thermal origin of gravity-like nonlinear optical interaction of the extraordinary light rays due to photo-thermal Kerr effect, which was noted above.
Let us consider a linear source of heat q (see Figure 2) placed inside the ferrofluid, which is constant in time and aligned parallel to the external magnetic field H (and, therefore, it is also parallel to the nanoparticle chains). Let us also assume that the ferrofluid is kept at a constant temperature T0. The temperature distribution around the source is defined by the two-dimensional heat conductance equation
where σ is the thermal diffusivity, cp is the heat capacity and ρ is the density of the ferrofluid. If the linear source of heat is weak enough, so that the temperature-dependent terms in the denominator of Equation (22) may be considered constant, Equation (23) may be re-written as an equation for the effective gravitational field :
which has the form of the Newton law of gravity. As evident from Equation (24), the heat source q plays the role of a gravitational mass. Thus, a linear source of heat parallel to the external magnetic field H behaves as a world line of a massive gravitating object in the metamaterial Minkowski spacetime. It is interesting that, unlike the quantum mechanical derivation based on the holographic principle reported in [2], the Newton law in a ferrofluid arises in a purely classical Boltzmann system. In principle, a similar approach may be applied to other magnetic systems at lower temperatures, where the thermodynamics description becomes explicitly quantum mechanical [18]. However, direct visualization of gravity-like effects in such systems appears to be much more difficult.
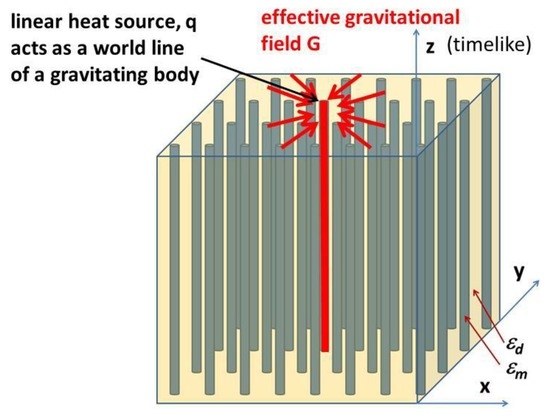
Figure 2.
Schematic geometry of the Newton law derivation for effective gravity in a ferrofluid.
As far as the strong field limit is concerned (where the temperature may not be considered almost constant) it was pointed out in Ref. [5] that large enough power gravitational self-interaction of the extraordinary rays is strong enough, so that spatial solitons may be formed. These spatial solitons also behave as world lines of compact self-gravitating bodies in the effective 2 + 1 dimensional spacetime. This is not surprising since, due to the photo-thermal effect, solitons may also be considered as linear sources of heat. Moreover, upon increase of the optical power, a spatial soliton may collapse into a black hole analogue [5]. Indeed, in the presence of self-defocusing negative Kerr effect in the dielectric host εd, the wave equation (Equation (5)) must be modified. Assuming a spatial soliton-like solution that conserves energy per unit length W~P/c (where P is the laser power), the soliton width ρ and the magnetic field amplitude B of the extraordinary wave are related as
As a result, Equation (5) must be re-written as
where ε1(0) is the dielectric permittivity component at P = 0 (note that the nonlinear contribution to may be neglected). Equation (26) looks like a Klein-Gordon equation in a spacetime with a metric coefficient , which has a black hole-like horizon at
The critical soliton radius at P = 100 W was estimated to be ~20 nm [5], which does not look completely unrealistic from the fabrication standpoint. While achieving such critical values with continuous wave (CW) lasers seems implausible, a using pulsed laser definitely looks like a realistic option since thermal damage produced by a pulsed laser typically depends on the pulse energy and not the pulse power.
Another “strong field” situation corresponds to the ferrofluid behavior near the metric signature transition. It appears that “melting” of the effective spacetime in such a case may mimic various cosmological Big Bang scenarios. This is not surprising since symmetry breaking in a magnetic systems is typically described by the Mexican hat potential. Moreover, such a Big Bang-like behavior may be observed directly using an optical microscope. Indeed, based on Equation (5) and Figure 1b, it is clear that the factor (−ε2) plays the role of a scale factor of the effective spacetime
since, according to Equation (19), ε1 is positive and almost constant, as plotted in Figure 3b. The scale factor of the effective spacetime calculated using Equation (18) is plotted in Figure 3a as a function of kT/µH at different values of . Let us assume that the temperature distribution inside the ferrofluid may be described as
where Tc is the temperature of the metric signature transition (the ε2 = 0 point). Since the z-coordinate plays the role of time in the effective spacetime described by Equation (28), such a temperature gradient η will result in a Big Bang-like spacetime expansion described by the scale factor –ε2(Tc − ηz) plotted in Figure 3a. Indeed, as the ferrofluid temperature falls away from the Tc boundary at z = 0, the spacetime scale factor increases sharply as a function of z. Note that, at larger values of , expansion of the effective spacetime “accelerates” at lower temperatures (compare the slopes of the red and black curves in Figure 3a near the metric signature transitions marked by the arrows and at lower temperatures). As demonstrated below, this “cosmological” spacetime expansion may be visualized directly using an optical microscope.
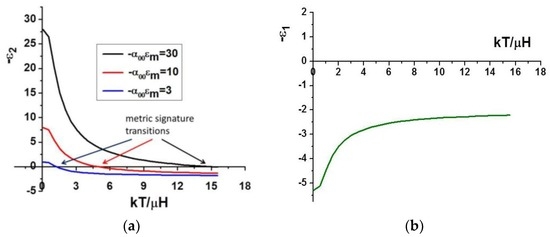
Figure 3.
(a) Scale factor of the effective de Sitter spacetime g11 = g22 = −ε2 (calculated using Equation (18)) plotted as a function of kT/µH at different values of . It is assumed that εd = 2; (b) Metric coefficient g00 = −ε1 of the effective de Sitter spacetime calculated using Equation (19).
We should also note that, in the case of non-constant z-dependent ε1 = εx = εy and ε2 = εz, the electromagnetic field separation into the ordinary and the extraordinary components remains well defined [19,20]. Taking into account z derivatives of ε1 and ε2, Equation (5) becomes
Since ε1 remains almost constant in a very broad temperature range far from T = 0 (as evident from Figure 3b), its derivatives may be neglected. If we also neglect the second derivative of ε2, the wave equation for the extraordinary field ϕω = Ez may be re-written as
It is easy to verify that the latter equation coincides with the Klein-Gordon equation [21] for a massive particle in a gravitational field described by the metric coefficients g00 = −ε1 and g11 = g22 = −ε2:
Indeed, for a wave field , Equation (31) is reproduced if we also neglect the second derivative terms.
As demonstrated by Figure 1c, the alignment of cobalt nanoparticles along the timelike z-direction is easy to visualize. Moreover, as demonstrated in [22], visibility of the filaments in such images, which may be assessed quantitatively by Fourier analysis, provides measurements of the relative value of α(H,T) compared to . A natural way to study ferrofluid behaviour near the metric signature transition is to gradually reduce the external magnetic field H until the periodic alignment of cobalt nanoparticles begins to disappear. Since thermal and/or magnetic field gradients are unavoidable in such an experiment, a ferrofluid region showing gradual disappearance of filament periodicity across the image is relatively easy to find. A microscopic transmission image of such a region taken using illumination with λ =1.5 µm light is presented in Figure 4b. The filament periodicity (compare Figure 4a,b) gradually disappears towards the top of the image, which is verified by Fourier analysis in Figure 4c (note that the contrast in these Fourier images is internal). The measured dependence of the spacetime scale factor –ε2 on the effective time calculated at λ = 1.4 µm is shown in Figure 4d. This wavelength is close enough to the λ = 1.5 µm illumination wavelength used in the experiment, while the experimental data for the electromagnetic properties of cobalt [13] may also be used. Calculated values of –ε2 are based on the Fourier analysis of smaller regions in Figure 4b (shown by the yellow boxes). The measured behaviour of the scale factor in this experiment corresponds to small values of , which is expected at λ = 1.4 µm based on the optical properties of cobalt [13]. As evident from Figure 4d, the measured data show good agreement with theoretical calculations based on Equation (18).

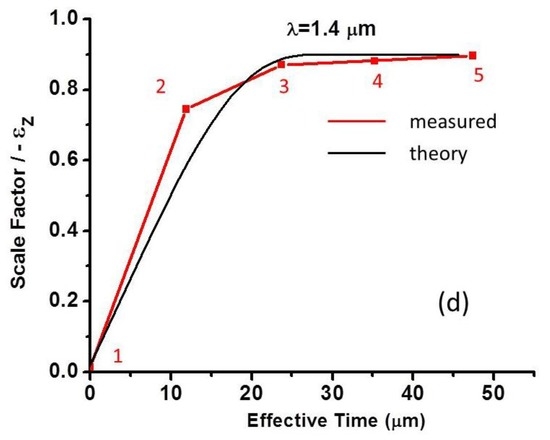
Figure 4.
(a) Microscopic transmission image of the cobalt nanoparticle-based ferrofluid taken in external magnetic field H using illumination with λ = 1.5 µm light; (b) Analysis of gradual melting of the effective Minkowski spacetime within a single microscopic image of the ferrofluid. This image was obtained while the magnitude of external magnetic field H was decreased gradually. The effective time direction is indicated by the red arrow. The effective spacetime expansion is shown schematically by the yellow cone: the scale factor is proportional to –ε2, and it vanishes at the point of metric signature transition (see Equation (1)) where the ferrofluid periodicity is no longer visible; and (d) Measured dependence of the spacetime scale factor –ε2 on the effective time calculated at λ = 1.4 µm. These calculations are based on the Fourier analysis (c) of smaller regions of Figure 4b shown by the yellow boxes. The measured data are compared with theoretical calculations based on Equation (18).
4. Discussion
The observed measured experimental behaviour of the scale factor is somewhat similar to the cosmological inflation: the initial very fast spacetime expansion is followed by a drastic slowdown. Together with the analogy to some microscopic quantum gravity models (such as the loop quantum cosmology) noted by Mielczarek and Bojowald [10,11], the considered experimental model appears to be interesting and relevant for research in inflationary cosmology. Furthermore, the modest success of this rudimentary model may justify further investigation of more refined models based on quantum hyperbolic metamaterials [18].
Unfortunately, the described analogy between the extraordinary light propagation inside the ferrofluid and the dynamics of massive particles in Minkowski spacetime is in no way perfect. The main difficulty comes from the cross-coupling between extraordinary and ordinary light inside the ferrofluid, which may be caused by internal defects and strong gradients of the dielectric permittivity tensor components. Since ordinary light “lives” in Euclidean space, such a cross-coupling breaks the effective Lorentz symmetry (6) of the system. In addition, such a model is necessarily limited to 2 + 1 spacetime dimensions. Nevertheless, these limitations notwithstanding, it is interesting to trace the appearance of macroscopic “gravity” (even though imperfect) to thermal behavior of well understood microscopic degrees of freedom of the ferrofluid.
5. Conclusions
In conclusion, we have considered thermodynamics of the effective spacetime that may be formed under the influence of an external magnetic field in a cobalt ferrofluid. It appears that the extraordinary photons propagating inside the ferrofluid perceive thermal gradients in the ferrofluid as an effective gravitational field, which obeys the Newton law. Unlike a quantum mechanical derivation based on the holographic principle reported in [2], the Newton law in a ferrofluid arises in a purely classical Boltzmann system. The effective spacetime behaviour near the metric signature transition may mimic various inflationary cosmological Big Bang scenarios, which may be observed directly using an optical microscope. Even though the considered model is applicable only to the extraordinary photons, it is quite interesting since it permits both direct theoretical analysis at the level of well-defined microscopic degrees of freedom, and it enables direct visualization of these microscopic degrees of freedom using standard optical tools.
Conflicts of Interest
The author declares no conflict of interest.
References
- Jacobson, T. Thermodynamics of spacetime: The Einstein equation of state. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed]
- Verlinde, E.P. On the origin of gravity and the laws of Newton. J. High Energy Phys. 2011, 2011, 29. [Google Scholar] [CrossRef]
- Barcelo, C.; Liberati, S.; Visser, M. Analogue Gravity. Living Rev. Relativ. 2005, 8, 12. [Google Scholar] [CrossRef] [PubMed]
- Smolyaninov, I.I.; Yost, B.; Bates, E.; Smolyaninova, V.N. Experimental demonstration of metamaterial “multiverse” in a ferrofluid. Opt. Express 2013, 21, 14918–14925. [Google Scholar] [CrossRef] [PubMed]
- Smolyaninov, I.I. Analogue gravity in hyperbolic metamaterials. Phys. Rev. A 2013, 88, 033843. [Google Scholar] [CrossRef]
- Smolyaninov, I.I. Holographic duality in nonlinear hyperbolic metamaterials. J. Opt. 2014, 16, 075101. [Google Scholar] [CrossRef]
- Smolyaninova, V.N.; Yost, B.; Lahneman, D.; Narimanov, E.; Smolyaninov, I.I. Self-assembled tunable photonic hyper-crystals. Sci. Rep. 2014, 4, 5706. [Google Scholar] [CrossRef] [PubMed]
- Smolyaninov, I.I.; Smolyaninova, V.N.; Smolyaninov, A.I. Experimental model of topological defects in Minkowski spacetime based on disordered ferrofluid: Magnetic monopoles, cosmic strings and the spacetime cloak. Philos. Trans. R. Soc. A 2015, 373, 20140360. [Google Scholar] [CrossRef] [PubMed]
- Smolyaninov, I.I.; Narimanov, E.E. Metric signature transitions in optical metamaterials. Phys. Rev. Lett. 2010, 105, 067402. [Google Scholar] [CrossRef] [PubMed]
- Mielczarek, J. Signature change in loop quantum cosmology. In Relativity and Gravitation; Springer: Cham, Switzerland, 2014; pp. 555–562. [Google Scholar]
- Bojowald, M.; Mielczarek, J. Some implications of signature-change in cosmological models of loop quantum gravity. J. Cosmol. Astropart. Phys. 2015, 2015, 52. [Google Scholar] [CrossRef]
- Wangberg, R.; Elser, J.; Narimanov, E.E.; Podolskiy, V.A. Nonmagnetic nanocomposites for optical and infrared negative-refractive-index media. J. Opt. Soc. Am. B 2006, 23, 498–505. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of transition metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd. Phys. Rev. B 1974, 9, 5056–5070. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Field Theory; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Brochard, P.; Grolier-Mazza, V.; Cabanel, R. Thermal nonlinear refraction in dye solutions: A study of the transient regime. J. Opt. Soc. Am. B 1997, 14, 405–414. [Google Scholar] [CrossRef]
- Alkeskjold, T.T.; Lægsgaard, J.; Bjarklev, A.; Hermann, D.S.; Anawati, A.; Broeng, J.; Li, J.; Wu, S.T. All-optical modulation in dye-doped nematic liquid crystal photonic bandgap fibers. Opt. Express 2004, 12, 5857–5871. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Introduction to Solid State Physics; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Smolyaninov, I.I. Quantum topological transition in hyperbolic metamaterials based on high Tc superconductors. J. Phys. Condens. Matter 2014, 26, 305701. [Google Scholar] [CrossRef] [PubMed]
- Smolyaninov, I.I.; Hung, Y.J.; Hwang, E. Experimental modeling of cosmological inflation with metamaterials. Phys. Lett. A 2012, 376, 2575–2579. [Google Scholar] [CrossRef]
- Smolyaninov, I.I.; Hwang, E.; Narimanov, E.E. Hyperbolic metamaterial interfaces: Hawking radiation from Rindler horizons and spacetime signature transtions. Phys. Rev. B 2012, 85, 235122. [Google Scholar] [CrossRef]
- Davydov, A.S. Quantum Mechanics; Elsevier Ltd.: Pergamon, Turkey, 1976. [Google Scholar]
- Smolyaninov, I.I.; Smolyaninova, V.N. Experimental observation of melting of the effective Minkowski spacetime. In Reviews in Plasmonics; Springer: Berlin, Germany, 2016. [Google Scholar]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).