1. Introduction
When doing macroscopic physics, a tacit assumption is that all mathematical tools we use are founded on some theory of sets. When we want to be more sophisticated, we could say that they are situated in the environment of the category of sets and morphisms as functions between them (SET category). Both formulations can be made equivalent, but the latter focuses on transformations between sets rather than on sets themselves. General relativity is a macroscopic theory, and it is not an exception in this respect. Only when we start thinking on quantising gravity might we suspect that it could be reasonable to make the above assumption “non-tacit” and submit it to critical evaluation. Our suspicion is strengthened by the fact that already on the quantum mechanical level replacing set theoretic environment by the topos environment could lead to the correct interpretation of quantum mechanics (see works of Isham and his co-workers [
1,
2,
3,
4] and also [
5,
6]). In the present work, we want to take up this challenge and to treat this suspicion as a serious working hypothesis.
Category theorists have elaborated a categorical version of differential geometry—the so-called Synthetic Differential Geometry (SDG)—which almost exactly parallels the usual differential geometry employed in relativistic calculations. One of the essential differences between them is that in SDG, infinitesimals appear which substantially enrich the usual real line. Owing to this fact, geometry acquires a tool to penetrate infinitesimally small portions of a given manifold, which are invisible in the usual approach (in SET, they simply do not exist). This creates an invaluable opportunity for physical applications. The first that comes to mind is to test this method on the singularity problem in general relativity. The existence of strong curvature singularity (such as the Big Bang singularity or central Schwarzschild singularity) strongly depends on the behaviour of curvature on “infinitesimal portions” of space-time. In the present work, we show that the components of the curvature tensor on the “infinitesimal neighbourhood” in the “categorically generalised” manifold are themselves infinitesimal, and construct a toy model of the contracting universe demonstrating that the final singularity in this model disappears. This should be regarded as only a preliminary result. More work would be required To obtain a more reliable solution and more realistic examples. One should also study the transition (a suitable functor) from the SET environment of standard general relativity to a suitable topos providing the logic of the “infinitesimal behaviour”. Some work in this respect is underway.
In the present “classical singularity paradigm”, when we want to identify a singularity in space-time, we are looking for the incomplete maximal extension of this space-time—the signature of which is the existence of an inextendible causal (timelike or null) geodesic. In general, the extension is not unique, and most often obstacles to extendability consist of failures of various degrees of differentiability required to assure the unique extension (see [
7,
8,
9] or [
10] for a more popular account). It is clear that the appearance of infinitesimals via the SDC strategy can drastically change the situation in this respect, but the study of this highly interesting aspect of the problem has to be postponed to another occasion.
We should also mention a price one should pay for the possibility of using the “method of infinitesimals”. In the topos theory, together with the weakening of arithmetic (the existence of invertible infinitesimals), one must also face the weakening of logic. The internal logic of topoi is intuitionistic logic in which the excluded middle law and the axiom of choice are forbidden. Is this too high a price for the acquisition of a new method of solving unsolved problems in physics? Without trying, we shall never know the answer.
Our line of reasoning develops in the following way. In
Section 2, we give a quick tour through categories that could be considered as providing a suitable environment for physical theories of space-time. In
Section 3, we define the concept of formal manifold and that of locally formal manifold. On such manifolds, SDG can be done in a way parallel to the ordinary differential geometry. In
Section 4, we prove our main result, stating that the components of the curvature tensor are infinitesimal (if not zero) on the locally infinitesimal formal manifold. In
Section 5, we present a toy model of a contracting universe in which the above result is employed to get rid of singularity. Finally, in
Section 6, we collect our conclusions and comment on future perspectives.
The present essay is based on our previous works [
11,
12]. We presuppose only an elementary knowledge of category theory.
2. Categorically Generalised Theory of Manifolds
Several attempts have been made to employ categorical methods to general relativity (e.g., [
13,
14,
15,
16,
17,
18]). Our approach is based on the assumption that when going to smaller and smaller space-time distances (or higher and higher energies), we could encounter a region on which the SET category changes into another suitable topos. The richness of possibilities is strongly constrained by the demand that the candidate-topos should contain (as its subcategory) the category of manifolds and smooth mappings between them, and the inclusion should be full and faithful. This demand distinguishes the following scheme:
where
is the category of smooth manifolds and smooth mappings (a subcategory of SET),
is the so-called category of “loci”,
is the presheaves category on
; and
s and
Y are suitable functors to be defined below. To explain the above scheme, we must immerse ourselves in a few technicalities (in this section, we follow [
19]).
Let us first define the category of finitely-generated -rings. Its objects are smooth rings represented by , where I is an ideal in . Its morphisms , where , are equivalence classes of smooth functions such that if , then . Smooth functions and are equivalent if for every projection .
The category of “loci” is the opposite category with respect to the category ; i.e., . If , A as an object of is denoted by .
The functor
is defined by
. It is
full and faithful, but the image
is essentially richer than
M. Let us consider an object
which we denote by
R. We thus have
In
, in place of
, we have all smooth functions
. Constant functions correspond to real numbers from
, all other functions are something new. Among them there are “infinitesimals”; e.g., nilpotent infinitesimals
We see how the change of categories can modify mathematics.
Unfortunately,
is not Cartesian closed (not all its objects are exponentiable). Therefore, manifolds with singularities of some type are excluded. To remove this difficulty, we consider the functor
given by
This is the so-called Yoneda embedding (of in ). Here, is the category of presheaves. Manifolds sit in it fully and faithfully.
However, this category also has some “unwanted” properties; e.g., the “smooth line” R is not a local ring (the sum of two irreversible elements can be reversible). Again, we can improve the situation. Let us consider a subcategory of consisting of those functors which are sheaves (sheafification procedure). To do so, we introduce a Grothendieck topology on . This can be done in several ways, which leads to various topoi. Two of them are especially interesting: the Zariski topos and the Basel topos . In both of them, is embedded fully and faithfully.
Internal logic of topoi is intuitionistic logic, and the double negation law is not permitted. Consequently, from , we cannot infer that x exists, but only that it is not true that x does not exist. Therefore, in there can exist nonempty objects, but we cannot claim that they have some elements. Such objects are called noninhabited. This “strange behaviour” can be removed by improving the Grothendieck topology on . In this way, a new topos is defined. It is called the Basel topos, denoted by . In many respects, it is similar to the Zariski topos. It can be regarded as the best environment the topos theory can offer to develop a categorically generalised theory of manifolds.
In principle, each of the above-mentioned topoi could be tried as providing a categorical environment for submicrophysics (as well as a few others not mentioned here, such as the topos of germ-determined ideals ([
19] [p. 08-112])). Of course, it is too early to speculate about details. In the following, we conduct our analysis in a “generic” topos
, about which we assume that it is a
smooth topos. By a smooth topos, we understand—after Moerdijk and Reyes ([
19] [p. 7])—a topos that contains the category of manifolds and smooth functions between them in a full and faithful manner. In such topoi, inverse limits of spaces and function spaces can be adequately constructed (including infinitesimal spaces). They can also be models of SDG.
Smooth topoi can be regarded as vast generalisations of the usual smooth spaces. To make differential geometry on them (SDG) even more similar to the standard differential geometry (by enabling local coordinates on them), one introduces the formal manifold concept.
3. Formal Manifolds
To define formal manifold requires quite a bit of technical machinery (see [
20], (pp. 68–75, [
21]), (pp. 66–75, [
22])). To go into all of these details would blow up the limits of the present paper; instead, we will indicate steps leading to this concept. First, we must ensure that at each point of a given space (we treat objects of a considered smooth category as spaces) should exist a well-behaved tangent space with the vector space structure (or, more generally, the
R-module structure). Spaces with these properties are called microlinear. Then, we should ensure the existence of a basis on each of such tangent spaces (or
R-modules). This would prepare a way for defining “local coordinates” on our spaces. Finally, our construction should guarantee the local isomorphism between any tangent space and
. This is guaranteed if corresponding mappings are “étale” mappings. Now, we shall briefly comment on each of the above steps.
If
M is a smooth manifold (in SET), and
the tangent bundle over
M, then the fiber
, over each
, has the vector space structure over
. To generalise this fact to a smooth topos
(with the real line object
R), let
, where
X is an object of
and
D an infinitesimal interval, be a tangent bundle. If each fibre of this tangent bundle has the structure of an
R-module, the object (space)
X is called microlinear (for a strict definition, see for example [
19], pp. 182–185).
On such a fibre we want to introduce a basis. A basis in an
R-module
V is a finite collection of mutually free vectors of
V, such that every vector in
V can be expressed as a finite combination of vectors from this collection. In SDG, linear combination of vectors that is involved in this definition differs from the standard definition of linear independence by replacing the “equal to zero” phrase by the “apart from zero” phrase. Let
. We say that
are apart,
, if
is invertible in
R. We have:
. A finite collection of vectors
of
V is mutually free if
where
(for details, see [
22], pp. 66–67).
The local isomorphism between any tangent space (
R-module) and
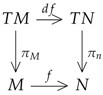
is achieved with the help of the so-called étale morphisms. A morphism
from an object
M to an object
N is said to be a formal étale morphism if, for any small object
and the canonical map
called the base point of this small object, the diagram
is a pullback.
denotes the spectrum of the Weil algebra
W, and represents a space of formal infinitesimals (for details, see [
22]). To intuitively see that this indeed determines a local isomorphism to
, let us consider the above diagram for tangent spaces to
M and
N, respectively, when the canonical base point is zero. We then have TM df TN
From the commutativity of this diagram, we easily deduce , which is in fact what we are after.
Now we are ready do give the formal n-dimensional manifold definition.
Definition 1. If is a monic (“injective”) formal étale morphism, then U is said to be an n-dimensional model object. A formal n-dimensional manifold is an object M such that there exists a regular epic (“surjective”) morphism , where each is a monic étale formal morphism such that every is an n-dimensional model object.
Let us notice that is a covering family of M by jointly epic class of morphisms. On such formal manifolds, topology can be defined. However, for our purposes, no topology is required. The possibility to develop differential geometry on formal manifolds without any topology is a typical feature of SDG.
We are interested in properties of formal manifolds on the smallest possible scale. In SDG, besides
D, we meet some other kinds of infinitesimals; among others,
We have the following important result:
Proposition 1. ([23] [Proposition 17.1]) The inclusion (a monic map) is an étale morphism. This result justifies the following definition:
Definition 2. An infinitesimal
n-dimensional formal manifold
is an object M for which there exists a “jointly epic” class of monic étale maps If , then M is called locally -formal manifold by analogy with locally manifolds in SET.
Having the above concepts at our disposal, we can develop SDG on the very small (infinitesimal) scale. In the next section, we focus on the behaviour of curvature on this scale.
5. A Model
According to our main assumption, macroscopic space (or space-time) is described (as usual) within the SET environment, but on a sufficiently small scale (supposedly beneath the Planck scale), one should change from SET to a suitable topos .
Let us consider a model
where—in analogy with the closed Friedman–Lemaître cosmological model—
can be interpreted as a cosmic time, and
as a three-dimensional instantaneous time section. Let us further assume that the diameter
of
contracts to the zero size (i.e., to a point which we call “singularity”) and situate it at
, for example. It is a simple cone singularity rather than a curvature singularity met in the standard cosmological models. This construction can be considered as a toy model of a contracting universe ending its evolution in the singularity as it is seen from the SET perspective. However, when the diameter
of
reaches sufficiently small values, the environment changes from SET to
, and we have
We should notice that
because
is now enriched by infinitesimals, and
becomes a locally
-infinitesimal formal manifold below some (infinitesimal) scale
h. If
contracts, its 3-curvature grows, but when its radius reaches infinitesimal size, then—on the strength of Theorem 1—the components of the curvature become infinitesimal (if not zero). In this way, the conic singularity is avoided, and the evolution can eventually be prolonged beyond 0 of
R. The delicate point is the transition from rapidly growing curvature to its infinitesimal values. This could be connected with the transition from SET to another topos. In [
12], we have studied this process in the Basel topos.
6. Conclusions and Comments
In this short paper, we tried to pave the way towards a broader use of categorical methods—in particular, those related to synthetic differential geometry—in general relativity. In this theory, there is a number of fundamental problems which so far have resisted many attempts to cope with them. It seems that even to weaken the standard logic (as enforced by categorical methods) is not too high a price for the hope of progress. The great advantage of SDG is the existence of infinitesimals; they offer a unique opportunity to deal with all these questions in which very small scales of space-time (on or beneath the Planck scale) are involved. Quantum gravity and the singularity problem are obvious candidates to be approached with the help of this method. In the present paper, we have chosen to test the method on the classical singularity problem. We have shown that the infinitesimal formal manifold concept is a good tool to deal with “infinitesimal scales” of space-time. This creates a potential field of applications to general relativity, but as for now is nothing more than just a test of the fruitfulness of this method. Nevertheless, our result is relevant as far as all curvature singularities are concerned (finite time singularities included; see [
24]). However, strictly speaking, we have not proven that the appearance of infinitesimals always removes all curvature singularities, but only that in the SDG approach, the components of the curvature tensor on any infinitesimal neigbourhood are themselves infinitesimal.
Our toy model of
Section 5 is certainly not enough. One should construct more realistic models. In this respect, only some preliminary work has been done [
14,
15,
16], and as far as we know, no concrete solution has been analysed with respect to the singularity problem.
Let us notice that the strategy adopted in the present work is independent of any dynamical equations of the underlying theory of gravity. Just as in the case of the well-known singularity theorems [
7], the method is applicable to a broad class of space-time models satisfying certain general conditions.
To fully cope with the singularity problem requires much more than is presented in this essay . First of all, one should elaborate a “categorical space-time model” admitting a change of categories as one goes from the macroscopic description gradually to smaller and smaller space-time distances. Suitable functors should be identified that are responsible for these changes. The choice of a category—providing a conceptual environment on the fundamental level—should be made on the basis of physical phenomena predicted by various possibilities, Zariski or Basel topoi (mentioned in
Section 2) being the first candidates. We should be open to such a change of the “conceptual environment” when moving along the ladder of higher and higher energy levels. This could have a powerful impact on our thinking about some frontier problems of contemporary theoretical physics, quantising of gravity in particular.
Moreover, there already exist some important conceptual problems that deserve serious reconsideration in the light of possibilities opened by categorical methods. As was noticed by Heunen, Landsman, and Spitters [
17], the principle of general covariance requires a substantial generalisation in the context of the topos theory
1. Another cornerstone of relativity is the principle of equivalence, stating that all reference frames are locally equivalent. In view of the fact that any formal manifold is infinitesimally linear [
21] (Proposition 17.6), the principle should be strengthened to the statement that all reference frames are infinitesimally “linearly equivalent”, which is more than just “equivalent”. The physical meaning of this statement should be subject to detailed analysis. This is clearly related to the main plot of the present study.