Prospects for Multimessenger Observations of the Shapley Supercluster

Abstract

The Shapley Supercluster, one of the largest and most massive structures in the nearby (redshift $z\le 0.1$) Universe, located approximately 200 Mpc away, is a unique laboratory for high-energy astrophysics. Galaxy clusters that comprise it are promising targets for multimessenger study due to the presence in the intracluster medium of the necessary conditions for the acceleration of cosmic rays up to ultra-high energies and the generation by them of non-thermal electromagnetic and neutrino emission. Using the Shapley Supercluster’s observational data from the recent eROSITA-DE Data Release, we recover the physical parameters of 45 X-ray luminous galaxy clusters and calculate the expected multiwavelength—from radio to very-high-energy γ-ray as well as neutrino emission, with a particular focus on hadronic interactions of accelerated cosmic ray nuclei with the nuclei of the intracluster medium. The results obtained allow verification of cluster models based on multimessenger observations of clusters, especially in $\gamma$-ray (Fermi-LAT, H.E.S.S., CTAO-South for the Shapley Supercluster case), and neutrino (Ice Cube, KM3NeT). We also estimate the ability of the Shapley Supercluster to manifest as cosmic Zevatrons and show that it can contribute to the PAO Hot Spot in the Cen A region at UHECR energies over 50 EeV.

1. Introduction

According to the Standard Model of the Big Bang cosmology, the observed large-scale structure of the Universe—the spatially inhomogeneous distribution of baryonic and dark matter (DM) structures, such as galaxies, their groups, clusters, and superclusters—is the result of gravitational instability and the growth of primordial cosmological perturbations on the background of the Hubble expansion [1,2,3].

Galaxy superclusters (GSCs), with masses of the order of ${10}^{15}$–${10}^{16}{M}_{\odot }$ and extents reaching up to ∼100 Mpc, are conglomerates of compact (spatially close) smaller-scale structures—galaxy clusters (GCs) [4,5,6]. GCs represent the most massive and largest cosmological perturbations that have undergone gravitational collapse and rapid relaxation, forming gravitationally bound, virialized systems of galaxies and intracluster medium (ICM) within the gravitational potential of dominant DM halos [3,7,8].

At the same time, the scale of the uniformity of the distribution of GSCs determines the characteristic size of uniformity in the Universe—the size of the nearby Universe up to redshift $z\le 0.1$ or to luminosity distance $d_L\le 400$ Mpc—a “mini-Universe” that will reflect the structure of the entire Universe [9,10,11].

The structure and evolution of GSCs and their components—GCs with masses of the order of $M_{cl}={10}^{14}$–${10}^{15}{M}_{\odot }$ and virial radii of approximately $R_{vir}$ = 1–2 Mpc—are determined by the parameters of the cosmological model and the interaction of their main components: DM (85% of the total mass), baryonic intercluster gas (14%), and the stellar component of galaxies (1–2%) [10,12]. At the same time, the dominance of DM in the gravitational potential of the GCs leads to the hydrostatic equilibrium of the plasma, with a virial temperature $k_{B}T\approx m_{p}G{M}_{cl}/R_{vir}\approx$ 2–10 keV. Therefore, the thermal X-ray emission of the intracluster plasma in the GCs is an important diagnostic tool of the physical conditions within them [13]. Additional information about the distribution of the thermal electron pressure in the GCs is provided by observations of the thermal Sunyaev–Zeldovich effect—the Comptonization of the cosmic microwave background (CMB) spectrum (resulting in a slight increase in temperature) [13,14]. Multiwavelength observations—particularly in the radio, optical, and $\gamma$-ray bands—are crucial for studying processes such as star formation, dynamic activity in the ICM (e.g., relaxation and mergers of substructures), the manifestations of active galactic nuclei (AGN) and their influence on the cluster gas [15,16].

At the same time, the unique properties of GSCs and GCs—as record-holding objects in terms of the masses and sizes of their DM halos and their thermal energy reserves—make them unique laboratories for studying the physics of fundamental interactions. First and foremost, DM particles are representatives of new physics beyond the Standard Model (SM) of particle physics, which so far have revealed themselves only through gravitational interactions [17]. If they are also capable of decaying or self-annihilating into SM particles—in particular, photons or neutrinos with energies of the order of (0.001–0.5) of DM mass $m_{dm}$—then GCs are among the primary candidate sources for such signals [18]. New observational programs are already being implemented and planned to search for manifestations of annihilation or decay of DM candidates—weakly interacting massive particles (WIMPs) with masses in the range of 0.1–100 TeV—through high and very-high-energy $\gamma$-ray emission from dwarf galaxies, the central region of our Galaxy, and GCs [19,20].

Moreover, the late nonlinear stages of GC formation are associated with the accretion of intergalactic gas and DM onto protoclusters. An accretion shock wavewith Mach number $\mathcal{M}\sim 10$ and radius $R_{sw}\approx 2R_{vir}\approx$ 3–5 Mpc acts as an effective “Zevatron”—an accelerator of cosmic rays (CRs) up to energies of the order of $1\mathrm{ZeV}$ = ${10}^{21}\mathrm{eV}$ [21]. In this case, CRs with energies below ∼${10}^{15}$ eV have diffusion escape times from the GCs longer than the age of the Universe, resulting in their accumulation within GCs with a total energy reserve amounting to 3–10% of the thermal energy. Observationally, these CRs manifest as sources of high- and very-high-energy $\gamma$-ray and neutrino emission through pp-collisions with the ICM plasma, producing neutral and charged pions, which subsequently decay into $\gamma$-rays and neutrinos. Ultra-high-energy cosmic rays (UHECRs) accelerated to energies above ${10}^{18}$ eV—including extreme-energy cosmic rays (EECRs) with $E>{10}^{20}$ eV—can escape from GCs and GSCs and contribute to the UHECR flux observed on Earth [22].

In our work, we investigate multimessenger manifestations of the Shapley Supercluster (SSC) and its GCs [23,24,25,26]. Using observational data from the eROSITA-DE Data Release 1 (DR1) [27], we recover the physical parameters of the 45 most massive GCs and calculate the expected non-thermal multiwavelength emission—from radio to very-high-energy $\gamma$-rays—as well as neutrino and UHECR fluxes. We also determine the range of GC parameters required for the detection of their multimessenger signatures by current and upcoming observatories. The text is organized as follows. In Section 2, we outline the structure and main parameters of GCs in the SSC. Section 3 and Section 4 present the results of calculation of the non-thermal $\gamma$-ray and radio emission from GCs in the SSC. In Section 5 and Section 6 neutrino fluxes from GCs and signatures of UHECRs from the SSC region are presented. Finally, in Section 7, we summarize and discuss the obtained results. Throughout the paper, we assume a flat ΛCDM cosmology, with Hubble constant $H_0=100h=70h_{70}$ km s⁻¹ Mpc⁻¹, $h=0.70$, matter density ${\Omega }_m=0.3$, and dark energy density ${\Omega }_{\Lambda }=0.7$. This corresponds to a luminosity distance of $d_L$ = 222 Mpc, and an angular scale of 0.977 kpc/$1^{″}$=3.52 Mpc/$1^{\circ }$ at the mean SSC redshift z = 0.05.

2. Structure and Main Parameters of Galaxy Clusters in the Shapley Supercluster

The SSC, originally discovered by Harlow Shapley in 1930, is the richest supercluster in the nearby Universe [10]. It spans a region of approximately ${19}^{\circ }\times {13}^{\circ }$ in the sky, centered at $\mathrm{RA}\sim {13}^{\mathrm{h}}{25}^{\mathrm{m}}$, $\mathrm{Dec}\sim -{30}^{\circ }$, and includes over 45 X-ray luminous galaxy clusters within the velocity range 9000 $\mathrm{km}{\mathrm{s}}^{-1}<cz<$ 18,000 $\mathrm{km}{\mathrm{s}}^{-1}$, corresponding to a luminosity distance of ∼129–$261\mathrm{Mpc}$ [24]. The SSC location in relation to other luminous objects is shown in Figure 1. With a mass of $M\approx 5\times {10}^{16} h^{-1}$$M_{\odot }$ SSC is also the most massive supercluster [10] and as a new “Great Attractor” (the old GA was the Hydra-Centaurus supercluster at ∼40 $h^{-1}$ Mpc [23]) determines the dipole-type peculiar velocity field in the nearby Universe [3].

Contrary to individual GCs, the SSC is not a gravitationally bound system as a whole. Only three GC groups—the A3558, A3528, and A3571 complexes—are gravitationally bound and form the cores of the SSC. The total energy of these cores—the sum of kinetic (thermal) and gravitational energy—is negative at $z=0.05$, indicating that they are bound and, by $z=0.0$, should have already undergone collapse [28]. Three main components of GCs, as virialized structures, determine their multimessenger signatures: DM, baryonic intracluster plasma (including both thermal plasma and CRs), and intracluster magnetic fields. The thermal plasma, with typical temperatures of $k_{B}T\sim 2$–10 keV determined by the gravitational potential of the DM, manifests itself through thermal X-rays. CRs—both hadrons (protons and heavier nuclei) and leptons (electrons)—give rise to non-thermal synchrotron radiation, high-energy and very-high-energy $\gamma$-ray emission, as well as neutrino production [15]. The maximum energies of these messengers are limited by the maximum energies of long-lived (i.e., non-escaping) intracluster CRs, of the order of ${10}^{15}$–${10}^{16}$ eV. Meanwhile, accretion shocks at the boundaries of GCs are expected to accelerate CRs up to the ultra-high-energy (UHE) regime, with CR energies exceeding ${10}^{18}$ eV. Such UHECRs originating from GCs may contribute to the flux of UHECRs observed by the Telescope Array (TA) and Pierre Auger Observatory (PAO) [29].

2.1. Intracluster Gas in GCs of SSC

The internal structure and physical conditions of the ICM in virialised GCs can be recovered from the equations of the hydrostatic equilibrium of the ICM plasma in the gravitational field of the main GC components: DM, ICM plasma, and stellar (galactic) components [10]. A fundamental method for determining GC parameters involves the analysis of thermal X-ray emission and the thermal Sunyaev–Zeldovich effect, which together allow the reconstruction of the gravitational potential and the mass distribution—both dark and baryonic—within the cluster [13,14].

Accurate modeling of the thermal component of GCs typically requires detailed X-ray observations and analysis for each individual system. However, in our study, we adopt the framework of self-similar modeling [30], which assumes that GCs evolve in a homologous manner across different masses and redshifts, with gravity being the dominant force governing their dynamics. Under this assumption, clusters can be treated as scaled versions of one another.

The key parameter characterizing a GC is its total mass, $M_{500}$, enclosed within a radius $R_{500}$. This radius defines the region where the mean density is 500 times the critical density ${\rho }_c\left(z\right)$ of the Universe at a given redshift z. The radius $R_{500}$ is calculated from $M_{500}$ using the following relation:

$$R_{500}={\left({\displaystyle \frac{3M_{500}}{4\pi 500{\rho }_c\left(z\right)}}\right)}^{1/3}$$

(1)

The thermal pressure profile is parametrized using the generalized Navarro–Frenk–White model [31]:

$$p\left(x\right)={\displaystyle \frac{P_0}{{\left(c_{500}x\right)}^{\gamma }{\left[1+{\left(c_{500}x\right)}^{\alpha }\right]}^{(\beta -\gamma )/\alpha }}},$$

(2)

where $x=r/R_{500}$. Assuming the self-similar scaling of GCs, and following [30], the physical pressure profile is expressed as:

$$P\left(r\right)=P_{500}\times f_M\times p\left(x\right),$$

(3)

with the self-similar normalization factor given by:

$$P_{500}=1.65\times {10}^{-3}E{\left(z\right)}^{8/3}{h}_{70}^2{\left({\displaystyle \frac{M_{500}}{3\times {10}^{14}{h}_{70}^{-1}{M}_{\odot }}}\right)}^{2/3},$$

(4)

and the redshift evolution function is:

$$E\left(z\right)=\sqrt{{\Omega }_M{(1+z)}^3+{\Omega }_{\Lambda }},$$

(5)

while a small correction for mass dependence is applied as:

$$f_M={\left({\displaystyle \frac{M_{500}}{3\times {10}^{14}{h}_{70}^{-1}{M}_{\odot }}}\right)}^{0.12}.$$

(6)

Table 1. Best-fit parameters for the thermal pressure profile in Equation (2), adapted from [30].

Sample	P0	c500	$\mathit{\gamma }$	$\mathit{\alpha }$	$\mathit{\beta }$
All	8.403	1.177	0.3081	1.0510	5.4905
CC	3.249	1.128	0.7736	1.2223	5.4905
NCC	3.202	1.083	0.3798	1.4063	5.4905

presents the best-fit parameters for the pressure profiles of all 33 local GCs from the REXCESS sample [32] and also for subsamples consisting only of cool-core (CC) and non-cool-core (NCC) clusters.

The thermal proton $n_p\left(r\right)$ and electron $n_e\left(r\right)$ density profiles are described using a modified $\beta$-model introduced by [33]:

$$n_p\left(r\right)n_e\left(r\right)=0.85n_e^2\left(r\right)=n_0^2{\displaystyle \frac{{(r/r_c)}^{-\alpha }}{{(1+r^2/r_c^2)}^{3\beta -\alpha /2}}}·{\displaystyle \frac{1}{{(1+r^{\gamma }/r_s^{\gamma })}^{ϵ/\gamma }}},$$

(7)

where $r_c$ and $r_s$ are two free parameters and $\gamma =3$.

The corresponding thermal barion gas density profile is

$${\rho }_{gas}={\mu }_e{m}_p{n}_e\left(r\right),$$

(8)

where ${\mu }_e={(1-0.5Y-0.5Z)}^{-1}=1.15$ is the mean electron molecular weight, assuming the helium mass fraction $Y=0.27$, the heavy element mass fraction $Z=0.005$, and where $m_p$ is the proton mass [13].

Equation (7) was used in [34] to fit X-ray density profiles of 16 GCs from the first Planck SZ catalogue [35], which includes both CC and NCC systems. The results of these fits are summarized in

Table 2. Best-fit parameters for the density profile (Equation (7)), adapted from [34].

Sample	$lg({\mathit{n}}_0/{\mathbf{cm}}^{-3})$	$lg({\mathit{r}}_{\mathit{c}}/{\mathit{R}}_{500})$	$lg({\mathit{r}}_{\mathit{s}}/{\mathit{R}}_{500})$	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{ϵ}$
All	−4.4	−3.0	−0.29	0.89	0.43	2.86
CC	−3.9	−3.2	0.17	0.80	0.49	4.67
NCC	−4.9	−2.7	−0.51	0.70	0.39	2.60

. The first row presents the best-fit parameters for the entire sample, while the second and third rows correspond to the CC and NCC subsamples, respectively.

2.2. Magnetic Fields in GCs

The ICM in GCs is turbulent and magnetized [36,37]. Typical values of the ICM magnetic field are of the order of 1–10 μG in the central regions, decreasing radially toward the periphery of the cluster. Turbulence is sustained by cluster merger, AGN activity, ICM shocks, etc. Radio observations of SSC have revealed a diffuse, non-thermal component within the ICM, generated by cosmic ray electrons (CRe) not directly associated with individual radio galaxies [38]. One of the most effective methods for probing these fields is through Faraday Rotation Measure studies. Using this technique, refs. [39,40] estimated the central magnetic field strengths in the nearby Coma and Perseus GCs to be approximately 4.7 μG and 25 μG, respectively, on spatial scales of around 10 kpc.

We assume that the magnetic field in SSC GCs scales with the thermal gas density, following the relation:

$$\langle B\rangle \left(r\right)=\langle B_{ref}\rangle {\left({\displaystyle \frac{n_e\left(r\right)}{n_{\mathrm{e},\mathrm{ref}}}}\right)}^{{\eta }_B}$$

(9)

where $\langle B_{\mathrm{ref}}\rangle$ and $n_{\mathrm{e},\mathrm{ref}}$ are the normalization parameters for the magnetic field and electron density, respectively.

For CC clusters, we adopt the model from [18,40], which yields $\langle B\rangle$ (10 kpc) ∼25 μG with a scaling index of ${\eta }_B=2/3$. In the case of NCC clusters, we follow [39,41], where $\langle B_{\mathrm{ref}}\rangle$ = 4.7 μG and ${\eta }_B=0.5$.

2.3. Cosmic Rays in GCs of the SSC

Similarly to the interstellar medium of our Galaxy, the ICM of GCs in the SSC is filled with CRs—relativistic protons, nuclei, and electrons. CRs are accelerated by several mechanisms within GCs. One of the key processes is the formation of shock waves, which arise both from mergers between and inside clusters and from the continuous accretion of matter from the surrounding large-scale structure. These shocks not only contribute to the heating and thermalization of the ICM but also serve as efficient sites for CR acceleration via diffusive shock acceleration. The efficiency of this process primarily depends on the shock’s Mach number $\mathcal{M}$ and the magnetic field structure at the shock front [42]. Additional contributions to the CR population in GCs come from AGNs and supernova explosions, which inject CRs into the ICM.

Since the diffusion timescale of CRs with energies below 1–10 PeV exceeds the Hubble timescale, accelerated CRs can accumulate in the cluster volume over cosmological timescales, forming a potentially significant non-thermal component of the ICM [15,43,44]. These accumulated CRs—protons and nuclei—interact with the ICM via pp collision and produce $\gamma$-ray and neutrino emission [45]. Meanwhile, CR electrons produce synchrotron emission in the ICM magnetic fields. Therefore, non-thermal multiwavelength emission from GCs serves as a key signature of CR acceleration within these systems.

The CR proton (CRp) population is especially relevant for modeling $\gamma$-ray and neutrino emission, whereas the CR primary electron (CRe1) population mainly contributes to synchrotron radio emission. It is essential to distinguish CRe1, which are injected directly (e.g., by AGNs or shocks), from secondary electrons (CRe2), which are generated through pion decay in hadronic interactions. In this section, we focus on modeling only the CRp and CRe1 populations. The number density of CRp (i = p) and CRe1 (i = e) is computed similarly and given by:

$$-{\displaystyle \frac{d{N}_{cr,i}(r,>E)}{dE}}=N_{cr,i}(r,E)=N_{cr,i,0}\left(E_0\right)f_1\left(E\right)f_2\left(r\right)$$

(10)

where the differential energy spectrum $N_{cr,i}(r,E)$ is expressed as the product of the energy spectrum $f_1\left(E\right)$, the radial distribution $f_2\left(r\right)$, and the normalization factor $N_{cr,i,0}\left(E_0\right)$.

The energy spectrum of CRp, as expected from Fermi diffusive shock acceleration, follows a power-law distribution with spectral index $\alpha$ and exponential cut-off [46]:

$$f_1\left(E\right)={\left({\displaystyle \frac{E}{E_{cr,p,0}}}\right)}^{-\alpha }exp\left(-{\displaystyle \frac{E}{E_{cr,p,cut}}}\right)$$

(11)

The radial dependence of the CR distribution is modeled under the assumption that the CRe number density scales with the thermal gas density [13]:

$$f_2\left(r\right)={(n_e\left(r\right)/n_e\left(0\right))}^{\eta }$$

(12)

For CRe1, we need also to account for energy losses by using a continuous injection model:

$$f_1\left(E\right)={\left({\displaystyle \frac{E}{E_{cr,e,0}}}\right)}^{-(\alpha +1)}\left\{\begin{array}{cc}1-{\left(1-{\displaystyle \frac{E}{E_{cr,e,cut}}}\right)}^{\alpha -1},\hfill & E<E_{cr,e,cut}\hfill \\ 1,\hfill & E\ge E_{cr,e,cut}\hfill \end{array}\right.$$

(13)

In this framework, the CRe1 population evolves under the balance between injection and radiative losses.

For the determination of normalization $N_{cr,p,0}\left(E_0\right)$, we adopt the parameter

$$X_{cr,p}(<r)=ϵ\left(r\right)={\displaystyle \frac{U_{cr,p}(<r)}{U_{th}(<r)}},$$

(14)

for the case $r=R_{500}$ [13]. Here, $U_{cr,p}(<r)$ denotes the total CR proton energy within radius r, and $U_{th}(<r)$ is the total thermal energy within the same radius. In our modeling, we assume a typical shock acceleration electron-to-proton energy ratio: $X_{cr,e}={10}^{-3}{X}_{CR,p}$. Additionally, we use the same spectral index $\alpha$ and radial scaling parameter $\eta$ for both CRp and CRe1 populations. The CR content within GCs remains poorly constrained. Therefore, in our modeling, we explore a range of values for the key parameters $X_{cr,p}$, $\alpha$, and $\eta$, guided by the limits presented in the literature and summarized in the theoretical overview sections. For the spectral index, we consider values $\alpha =(2.0,2.3,2.5)$, while for the spatial scaling index, we use $\eta =(0,0.5,1)$. The normalization of the CR energy density relative to the thermal energy density, $X_{cr,p}\left(R_{500}\right)$, is set to $(0.05,0.1)$ for CC clusters and to $(0.02,0.045)$ for NCC clusters.

2.4. Thermal X-Ray Emission and Models of GCs in the SSC

Thermal X-ray emission of GCs is the dominant contributor to the electromagnetic spectrum. Their X-ray luminosity allows estimation of the total barionic and DM mass. Using universal scaling, we can recover the model parameters of GCs in SSC.

The hot intracluster medium can undergo significant cooling in regions where the gas density reaches sufficiently high values. The efficiency of this cooling process can be quantified through the cooling time, which represents the characteristic timescale over which the thermal energy of the gas would be radiated away [46]:

$$t_{\mathrm{cool}}\approx {10}^{10}{\displaystyle \frac{T^{1/2}}{N}}\mathrm{yr},$$

(15)

In this expression, T represents the gas temperature in kelvin, while N denotes the number density of ions in the plasma. For a typical intracluster gas with temperatures ranging from ${10}^7\mathrm{to}{10}^8$ K, the cooling time becomes shorter than the Hubble time (∼${10}^{10}$ years) when the electron density exceeds approximately $3\times {10}^{-3}$–${10}^{-2}$ cm⁻³.

Such high-density conditions are frequently encountered in the central regions of X-ray luminous galaxy clusters. As these dense central regions radiate away their thermal energy, the cooling gas must contract to maintain pressure equilibrium with the surrounding medium [47]. However, this straightforward cooling flow model encountered significant challenges when high-resolution X-ray spectroscopy revealed a surprising absence of the expected cool gas in cluster cores. These observations indicated that the simple cooling flow picture was incomplete, suggesting the presence of additional heating mechanisms that counterbalance radiative cooling. Several mechanisms have been proposed to explain this “cooling flow problem,” including thermal conduction from outer regions, heating from central active galactic nuclei through direct cosmic ray interactions with the ICM, dissipation of turbulent energy, and various other processes [47,48,49]. The interplay between cooling processes and these heating mechanisms creates diverse thermal structures within cluster cores and provides the framework for classifying GCs into two primary categories: cool-core (CC) and non-cool-core (NCC) clusters. It is important to note that the distinction between CC and NCC clusters extends beyond simply measuring cooling times (see [50]).

CC clusters are characterized primarily by their remarkably short central cooling times, typically less than $1h_{70}^{-1/2}$ Gyr, coupled with minimal central entropy values of $K_0\lesssim 30$ $h_{70}^{-1/3}$ keV cm².

While the central temperature decline relative to the virial temperature $(T_0/T_{vir})$ is frequently employed as a CC cluster identifier, ref. [50] revealed that this temperature drop lacks clear correlation with the central cooling time. Indeed, several NCC clusters exhibit central temperature decreases, potentially indicating recent merger activity where the original core structure remains partially intact. Another notable characteristic of CC clusters is their tendency to host a brightest cluster galaxy positioned precisely at the X-ray emission peak. The research also uncovered an intriguing relationship suggesting that lower-temperature clusters (galaxy groups) typically display smaller $r_c/r_{500}$ ($r_c$—core radius) compared to their hotter counterparts. In contrast, NCC clusters demonstrate substantially longer central cooling times, exceeding $7.7h_{70}^{-1/2}$ Gyr, alongside greater central entropy values of $K_0\gtrsim 110$ $h_{70}^{-1/3}$ keV cm². Their temperature profiles typically exhibit either flat distributions or central increases, distinguishing them structurally from the CC population.

DR1 data allow estimation of the parameters of X-ray active GCs (presented in Appendix A). Using these data, we utilize in our modeling the global properties of GCs, such as $M_{500}$ and z, derived from the first catalogue of superclusters in the western Galactic hemisphere [27], for the whole GCs sample. In this catalogue, the SSC is identified as the richest system, comprising 45 GCs with total mass of $(2.58\pm 0.51)\times {10}^{16}{M}_{\odot }$.

In this section, we model the ICM of 45 X-ray GCs located in the SSC region, as identified in the first catalog of superclusters in the western Galactic hemisphere based on the SRG/eROSITA All-Sky Survey [27]. For this purpose, we employ the Python 3-compatible version of the software (tested with Python 3.12.2) MINOT (Available at https://github.com/remi-adam/minot (accessed on 17 July 2025)) [13]. The modeling incorporates a range of parameters, generally divided into two categories: global properties that characterize the entire cluster (e.g., mass, redshift, and coordinates), and parameters that vary with radius or energy. The individual global properties of the GC sample are summarized in

Table A1. Global properties of the GCs in the area of the SSC from [27].

Cluster	z	RA J2000 (Degree)	Dec J2000 (Degree)	${\mathit{M}}_{500}/{10}^{14}{\mathit{M}}_{\odot }$
J135003.4-345543	0.0492	207.5140	−34.9266	0.116
J130708.2-314108	0.0515	196.7925	−31.6893	0.652
J132240.7-323137	0.0440	200.6716	−32.5241	0.062
J125234.8-311556	0.0537	193.1463	−31.2661	3.519
J120731.0-341822	0.0581	181.8798	−34.3048	0.179
J132404.7-314125	0.0484	200.9987	−31.7008	1.664
J133948.9-340714	0.0497	204.9548	−34.1241	0.160
J125422.3-290045	0.0535	193.5936	−29.0132	3.367
J130948.9-245129	0.0458	197.4513	−24.8580	0.198
J125440.6-291341	0.0535	193.6703	−29.2273	4.245
J120917.3-343138	0.0581	182.3230	−34.5277	0.263
J125536.9-302039	0.0549	193.9013	−30.3425	2.969
J132655.1-270951	0.0458	201.7413	−27.1621	3.622
J125653.4-311934	0.0558	194.2442	−31.3299	1.409
J125710.6-172444	0.0464	194.2933	−17.4120	3.855
J132755.9-312929	0.0487	201.9934	−31.5014	6.403
J125716.2-302355	0.0556	194.3367	−30.3674	4.079
J131339.7-325022	0.0518	198.4143	−32.8418	0.180
J132807.1-340339	0.0495	202.0337	−34.0576	0.852
J125721.6-154734	0.0494	194.3406	−15.7935	0.573
J131407.7-334612	0.0509	198.5358	−33.7751	0.652
J125748.9-171625	0.0496	194.453	−17.2752	1.57
J132830.4-245442	0.0456	202.1258	−24.9128	0.088
J124426.6-323242	0.0541	191.1123	−32.5477	0.253
J131419.8-332903	0.0491	198.5851	−33.4849	0.144
J125113.4-223227	0.0464	192.8015	−22.537	0.239
J125950.7-334019	0.0515	194.9575	−33.6715	0.401
J132947.4-313643	0.0489	202.4557	−31.6118	3.232
J132949.1-331024	0.0511	202.4537	−33.1751	0.237
J132952.4-293039	0.0493	202.4707	−29.5077	0.961
J133127.0-314940	0.0479	202.877	−31.8162	2.528
J123115.5-334626	0.0571	187.815	−33.7759	0.287
J133209.4-330026	0.0491	203.0394	−33.0064	1.851
J131857.6-371408	0.0503	199.7722	−37.2345	1.628
J123235.7-311251	0.0522	188.1509	−31.2147	0.351
J133226.0-330740	0.049	203.1206	−33.1296	2.903
J124857.4-120707	0.0446	192.2399	−12.1184	0.412
J123325.9-312205	0.0514	188.3528	−31.3726	0.537
J131933.0-332922	0.0474	199.8881	−33.4938	1.492
J133336.1-314026	0.0492	203.4009	−31.6715	4.33
J125030.2-142534	0.0427	192.6264	−14.4242	1.008
J132035.9-410200	0.0506	200.1557	−41.0348	1.73
J123507.7-330217	0.0549	188.7824	−33.0434	0.343
J130557.6-374005	0.0501	196.4826	−37.6473	2.332
J132124.1-354738	0.0478	200.3602	−35.795	0.963

.

Among GCs detected by eROSITA, the A3558 and A3528 complexes—which constitute primary targets for this research—have been previously investigated through X-ray observations. The A3528 complex features two interacting components: A3528N and A3528S. Ref. [51] revealed that A3528 displays definitive CC characteristics, including peaked X-ray surface brightness profiles, steep metallicity gradients and cooling time ∼1 Gyr for both subclumps. Their XMM-Newton observations also revealed an extended region of soft X-ray emission connecting the two subclusters, forming a narrow bridge-like structure between A3528-N and A3528-S. Notably, the observations show no evidence of shock-heated gas, either in surface brightness measurements or temperature mapping. The asymmetric surface brightness distribution suggests specific directional movement of the subclusters: A3528-N appears to be moving from the northwest toward the southeast, while A3528-S shows motion from the northeast toward the southwest. These observational characteristics collectively support a post-merger scenario rather than a pre-merger phase for these subclusters, with the closest core encounter estimated to have occurred approximately 1–2 billion years ago. The A3558 cluster complex is a central core of the SSC composed of three Abell clusters: A3556, A3558, and A3562 and a few smaller GGs. Among them, A3558 stands out as the most massive and dominant cluster, initially classified with a richness class of 4. According to [52], A3558 exhibits properties that place it between CC and NCC. Its central cooling time is approximately ∼5 Gyr, and it hosts a brightest cluster galaxy (BCG) at its center. The central electron density is estimated to be $n_0\simeq 1.5\times {10}^{-2}{\mathrm{cm}}^{-3}$. Despite its seemingly relaxed state, several features indicate a more complex dynamical history. Thermodynamic maps reveal notable deviations from spherical symmetry, and the presence of a low-entropy tail suggests recent or ongoing merging activity. A particularly intriguing characteristic of A3558 is the presence of a cold front, further complicating its dynamical interpretation. This cold front may be linked to nearby structures, such as the adjacent A3562 cluster and the GGs SC 1329–313 and SC 1327–312. The authors of [52] proposed that the cluster’s relaxation could have been disrupted by either the passage of the smaller group SC 1327–312 or an off-axis merger involving a more massive system, whose remnants now constitute A3562 and the nearby subgroups between A3558 and A3562. Further insights into the complexity of A3558 were provided by [53], who reported the presence of at least two additional large-scale cold fronts based on XMM-Newton observations. This discovery positions A3558 among the few known clusters that exhibit three or more cold fronts. Notably, the outermost northwestern cold front is located at a projected distance of 1.2 Mpc from the cluster core, making it one of the most distant cold fronts ever detected in a galaxy cluster. A comprehensive understanding of the formation and dynamical evolution of this system necessitates multiwavelength observations, as the interplay between its thermal structure, merger history, and surrounding environment remains highly complex.

3. Non-Thermal γ-Ray Emission of GCs in the SSC

Despite a long history of observations, there is still no reliable detection of high-energy and very-high-energy $\gamma$-ray emissions from GCs (see [54] and reference therein). This makes the search for such emissions from the SSC particularly important. As shown in [54,55], the $\gamma$-ray emissivity per unit volume of the ICM in the hadronic scenario (i.e., via pp collisions) is given by:

$${\varphi }_{\gamma }(E_{\gamma },\mathbf{r})=c{n}_{ICM,p}\left(\mathbf{r}\right){\int }_{E_{\gamma }}^{\infty }{\sigma }_{pp}\left(E_p\right)N_{cr,p}(E_p,\mathbf{r})F_{\gamma }(E_{\gamma }/E_p,E_p)d{E}_p/E_p,$$

(16)

where ${\sigma }_{pp}\left(E_p\right)$ is the total inelastic cross-section of pp interactions, and $F_{\gamma }(E_{\gamma }/E_p,E_p)$ is the spectrum of the secondary $\gamma$-ray photons in a single pp collision. The corresponding neutrino emissivity for three flavors after the oscillation is connected with the $\gamma$-ray emissivity:

$$E_{\gamma }^2{\varphi }_{\gamma }\left(E_{\gamma }\right)\approx 2E_{\nu }^2{\varphi }_{\nu }\left(E_{\nu }\right){|}_{E_{\nu }=E_{\gamma }/2},$$

(17)

and after integrating over the total extent of the galaxy cluster, the total photon (i = $\gamma$) or muon neutrino (i = $\nu$) flux from an individual galaxy cluster at luminosity distance $d_L$ can be calculated as [54,55]:

$$E_i^2{F}_i\left(E_i\right)={\int }_V{\displaystyle \frac{E_i^2{\varphi }_i(E_i,\mathbf{r})}{4\pi d_L^2\left(z\right)}}dV$$

(18)

where $dV=r^{2}drsin\theta d\theta d\phi$ is the differential volume element of the radius-vector $\mathbf{r}=(r,\theta ,\phi )$.

3.1. Hadronic Mechanism of GC γ-Ray Emission

In GCs, $\gamma$-rays are predicted as secondary products of hadronic interactions between CRp and the ICM proton and heavier nuclei plasma. These processes primarily involve the production and subsequent decay of neutral pions:

$$\begin{array}{cc}\hfill p+p/\gamma & \to p/n+{\pi }^{\pm }+{\pi }^0+K^{\pm }+\dots \hfill \end{array}$$

$$\begin{array}{cc}\hfill {\pi }^{+}& \to {\mu }^{+}+{\nu }_{\mu }\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\mu }^{+}& \to e^{+}+{\nu }_e+{\overline{\nu }}_{\mu }\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\pi }^{-}& \to {\mu }^{-}+{\overline{\nu }}_{\mu }\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\mu }^{-}& \to e^{-}+{\overline{\nu }}_e+{\nu }_{\mu }\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\pi }^0& \to \gamma +\gamma \hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill K^{\pm }& \to {\mu }^{\pm }+{\nu }_{\mu }/{\overline{\nu }}_{\mu }\hfill \end{array}$$

(24)

The $\gamma$-ray spectral luminosity of GC is determined as the integral of the $\gamma$-ray emissivity (Equation (16)) over the volume of the cluster inside the GC accretion shock at truncated radius $r_{tr}\sim 3R_{500}$ [56]

$$L\left(E_{\gamma }\right)=4\pi {\int }_0^{r_{tr}}{\varphi }_{\gamma }(E_{\gamma },r)r^{2}dr$$

(25)

Additionally, a smaller contribution to the $\gamma$-ray emission arises from inverse Compton scattering, where relativistic electrons upscatter low-energy background (mainly CMB) photons.

The $\gamma$-ray spectrum is affected by absorption due to extragalactic background light (EBL), particularly at multi-TeV energies. High-energy photons interact with the EBL through electron–positron pair production and following electromagnetic cascade, leading to an attenuation and energy-degrading of the high energy and ultra-high-energy $\gamma$-ray flux. This absorption is characterized by a redshift- and energy-dependent optical depth $\tau (z,E)$ (the SSC lies at a mean redshift of ∼0.05), modifying the observable spectrum by a multiplier $exp(-\tau (z,E)$. In our modeling, the EBL model adopted is based on [57]. The maximum energy of CRe and CRp is set to 10 PeV, while the minimum energies are 1 MeV for CRe and ∼1.217 GeV for CRp. The latter corresponds to the kinematic threshold energy for pion production in proton–proton interactions.

Over the past twenty years, numerous efforts have been made to detect $\gamma$-ray emission from GCs. These include both studies targeting individual clusters [41] and statistical stacking analyses that combine data from multiple systems [58,59]. Although no definitive detection of cluster-origin $\gamma$-rays has been confirmed so far, these investigations have played a critical role in constraining the CRp energy density within clusters. The upper limits derived from $\gamma$-ray observations suggest that CRps contribute less than approximately ten percent to the total thermal energy of the ICM.

One of the most extensively studied targets is the Coma cluster. According to [41], $\gamma$-ray emission has been detected in its direction using twelve years of data from the Fermi-LAT. The detection significance depends on the specific modeling assumptions, yielding a test statistic (TS) in the range of approximately 24–34. This corresponds to a detection significance of about $4.9\sigma$ to $5.8\sigma$, indicating a potentially significant signal.

In [59], a stacking analysis of ∼8 years of Fermi-LAT data in the 1–100 GeV energy range is conducted, focusing on 112 of the most massive and spatially extended GCs located at high Galactic latitudes. By radially binning the $\gamma$-ray counts around each cluster, the study revealed statistically significant excess emission. The observed central excess is spatially unresolved and constrained within the inner $0.5R_{500}$ region of the clusters, exhibiting a detection significance in the range of approximately $6\sigma$–$7\sigma$. This feature is consistent with a point-like $\gamma$-ray source situated near the cluster centers. Additionally, a peripheral ring-like excess was detected at radii between $2.0R_{500}$ and $2.5R_{500}$, with a significance of about $4.2\sigma$. This outer feature aligns with theoretical expectations for inverse Compton $\gamma$-ray emission, generated by CRe accelerated at the GC’s virial shocks. The analysis has recently been refined in [60], where the updated 4FGL-DR4 LAT source catalog was employed to assemble a cleaner sample of 75 high-latitude GCs with angular sizes ${\theta }_{500}>0.2^{\circ }$. This study focused on the central regions ($r_{500}=r/R_{500}<0.5$), reporting a stacked excess $\gamma$-ray signal with a significance of $4.7\sigma$. A backward model fit of the emission within $r_{500}=1$ yielded a mean cluster brightness at $E_{\gamma }=10$ GeV of $E_{\gamma }^{2}dI/d{E}_{\gamma }={10}^{-9.2\pm 0.2}\mathrm{erg}{\mathrm{s}}^{-1}{\mathrm{cm}}^{-2}{\mathrm{sr}}^{-1}$, which shows good consistency with the results reported in [41] for individual cluster detections.

Assuming a flat $\gamma$-ray spectrum, GCs are considered to be significant contributors to the diffuse $\gamma$-ray flux at TeV energies. Upcoming next-generation observatories, such as the Cherenkov Telescope Array Observatory (CTAO), are designed with enhanced sensitivity specifically in this energy range [61,62]. These technological advancements are expected to significantly improve the prospects of detecting individual clusters, potentially making such detections more frequent and robust.

3.2. Testing the GC Parameter Scaling Efficiency

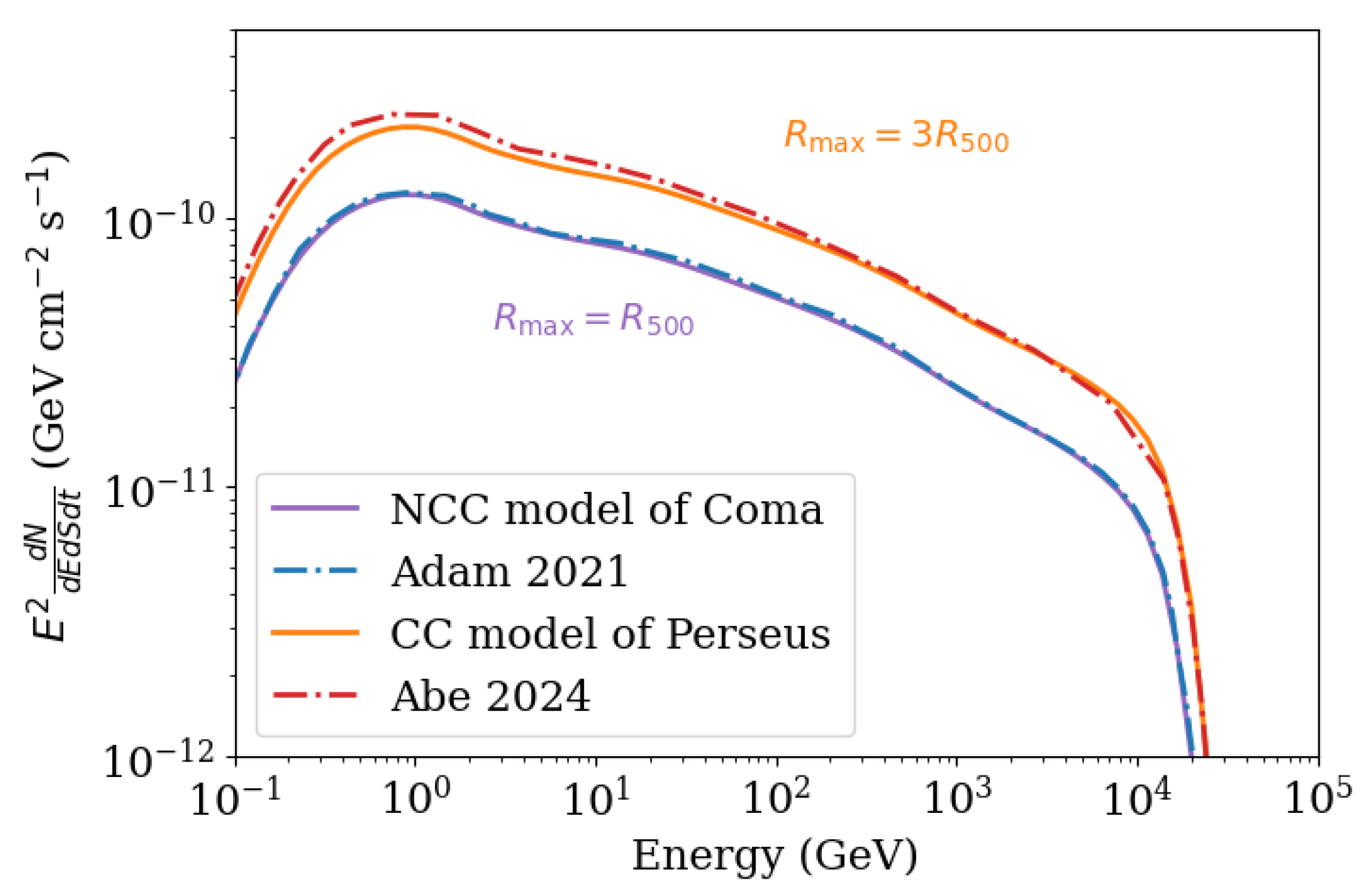
With all models now defined, we can test our modeling using data from well-studied clusters, such as the NCC Coma cluster [41] and the CC Perseus cluster [18]. In Figure 2, we present a comparison of the $\gamma$-ray spectra of these GCs as modeled in the literature and the spectra obtained using the profiles defined earlier from self-similar modeling. To match the integrated spectra from the literature, we set the upper integration limit for CC clusters at $3R_{500}$, which corresponds to the physical boundaries of the GC, while for NCC clusters, we integrate up to $R_{500}$.

3.3. Non-Thermal γ-Ray Emission of the SSC Region

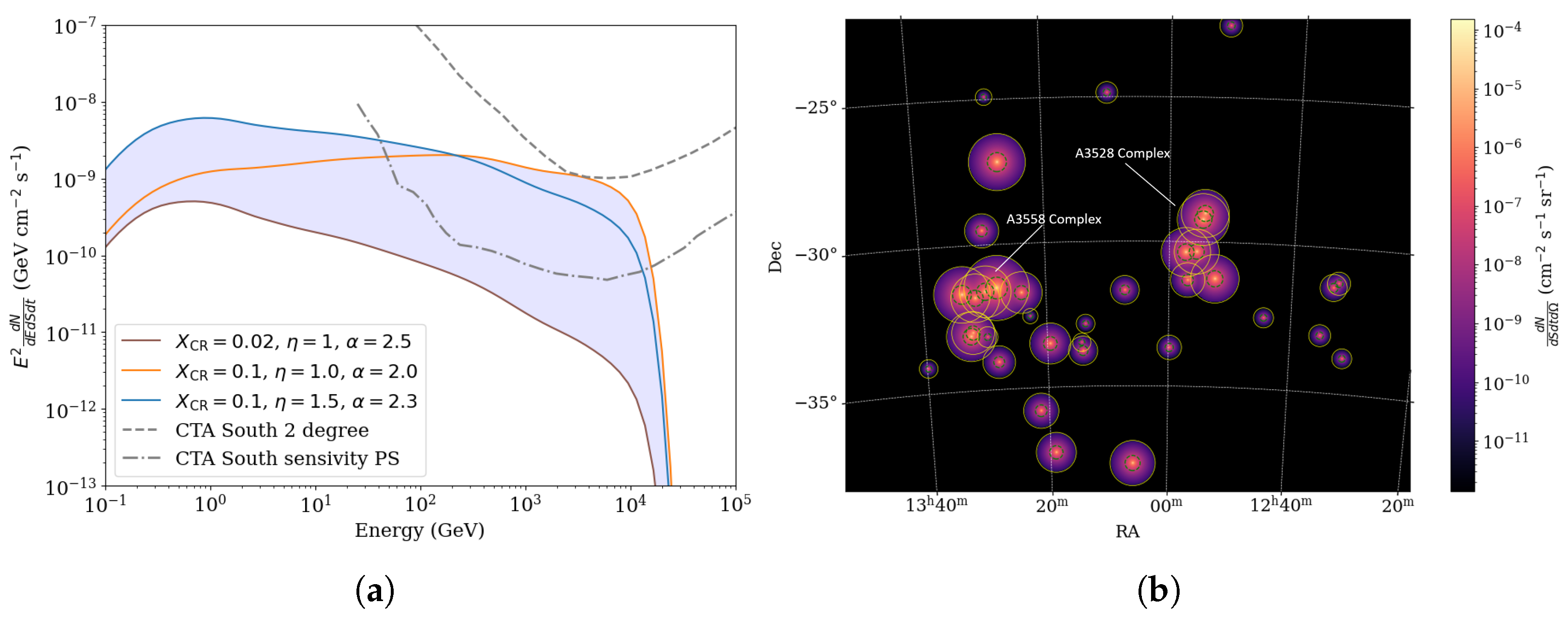
Superclusters are extended structures. GCs of the SSC in the eROSITA survey are located within ${12}^{\mathrm{h}}{07}^{\mathrm{m}}<\mathrm{RA}<{13}^{\mathrm{h}}{50}^{\mathrm{m}}$ and $-{41}^{\circ }<\mathrm{Dec}<-{25}^{\circ }$. Observing $\gamma$-ray emission from such a large region of the sky (Figure 3) by Imaging Atmospheric Cherenkov Telescopes (IACT) with ∼$5^{\circ }$ field of view is unfeasible. For this reason, we focus on smaller structures within the SSC—its cores. A core is defined here as a large, gravitationally bound structure, composed of two or more clusters and groups, with sufficient matter density to survive cosmic expansion and eventually virialize. Ref. [28] confirms the presence of two additional cores within the SSC, in addition to the central A3558 complex.

The results of our $\gamma$-ray modeling for the A3528 and A3558 complexes are shown in Figure 4 and Figure 5, respectively. In both cases, we consider only regions with angular sizes up to 1 degree, as the sensitivity of CTAO decreases significantly for extended sources of larger size. In the A3528 complex, we model the A3528N and A3528S components as two separate GCs.

For the A3558 complex, the model includes the A3558 cluster and the two closest groups, SC1327-312 and SC1329-314. Since the properties of the A3558 cluster are not fully understood—and it exhibits characteristics of both CC and NCC clusters—we present the results for both scenarios. As seen from the results, the NCC models yield a notably lower $\gamma$-ray flux compared to the CC scenario. There are significant uncertainties in the TeV energy range, primarily due to variations in the spectral index $\alpha$.

The most optimistic set of CR parameters for CTAO-South observations corresponds to $(\eta ,\alpha )=(1,2.0)$. These results suggest that even with $X_{\mathrm{CRp}}=0.1$, the predicted flux approaches but does not exceed the CTAO-South sensitivity, indicating that longer exposure times will be required. Regarding Fermi-LAT observations, we find that for the A3528 cluster, the minimum CR parameter set required to reach the sensitivity threshold is $(X_{\mathrm{CRp}},\eta ,\alpha )=(0.05,1.5,2.3)$. For the A3558 complex in the CC scenario, all models with $X_{\mathrm{CRp}}=0.1$ reach or exceed the Fermi-LAT sensitivity. In contrast, under the NCC scenario, Fermi-LAT detection is less likely.

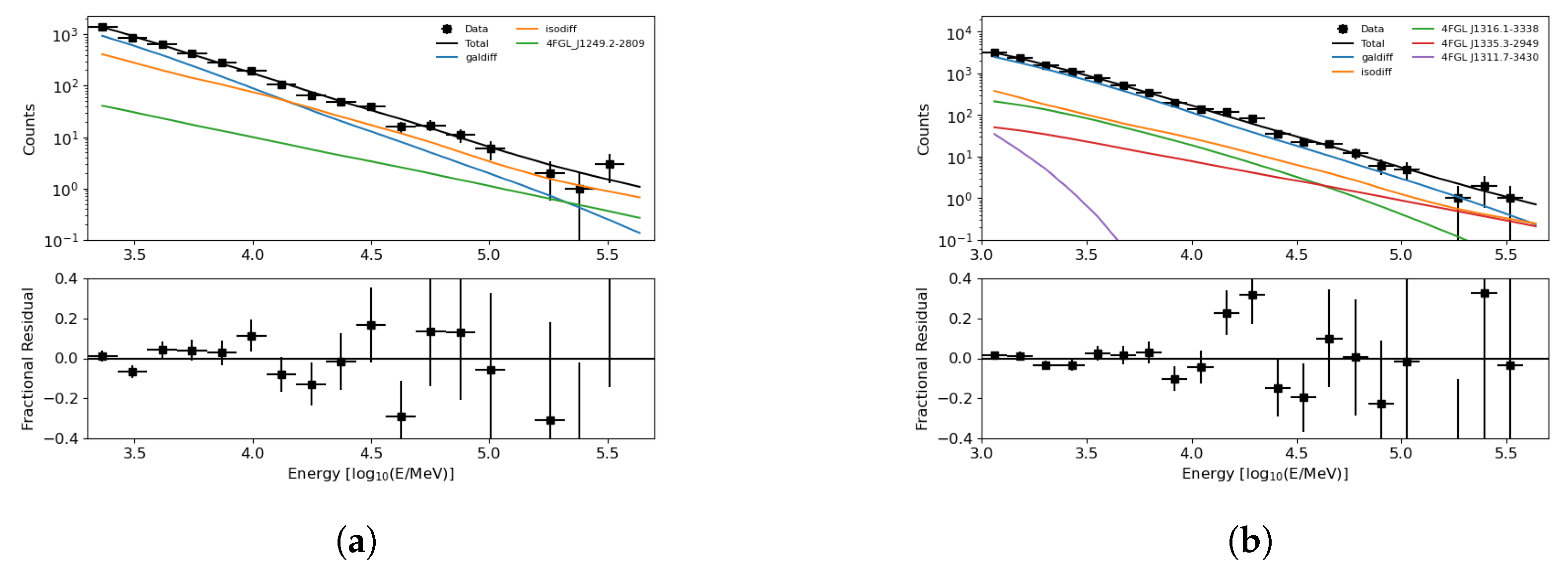
To analyze the high-energy $\gamma$-ray emission near the A3528 and A3558 GC complexes, we employed the Fermipy (available at https://github.com/fermiPy/fermipy (accessed on 17 July 2025)) framework—a Python-based interface built on the Fermi Science Tools [64]. The analysis was performed for two separate regions of interest (ROIs), each centered on the corresponding cluster. In the case of the A3528 complex, we identify a single source in the region: 4FGL J1249.2-2809, which is classified as a BL Lac object. According to [65], this source is modeled with a power-law spectrum with a photon index of 2.14. As for the A3558 complex ROI, we identify three sources that significantly influence our model:

(i) 4FGLJ1316.1-3338 quasar, spectrum type LogParabola with photon index 2.24 and curvature 0.07;

(ii) 4FGL J1311.7-3430 pulsar, spectrum type PLSuperExpCutoff with power law index 1.66, exponential index 0.67;

(iii) 4FGL J1335.3-2949 BL Lac, spectrum type PowerLaw with photon index 2.03.

The results of our spectral fit are presented in Figure 6. We note that the model provides a good fit to the data up to energies of approximately 10 GeV. Beyond this energy, the model tends to underpredict the photon counts in the higher-energy bins.

In addition to the spectral fit, we also examine the residual maps Figure 7, which represent the difference between the observed and modeled photon counts in each spatial bin.

In the vicinity of the GCs, we observe an excess at the ∼2$\sigma$ level within ${\theta }_{500}$ of A3528S and A3528N. In the A3558 complex, we trace filamentary-like emission within the SC1327-312 and SC1329-314 groups as well as at the $\sigma$∼2 level. While this is not sufficient to claim a detection, it suggests a potential signal that warrants further investigation with improved modeling and/or deeper data.

4. Non-Thermal Radio Emission from the SSC Region

Radio observations have revealed the presence of a diffuse, non-thermal component within the ICM, produced by CRe that are not directly linked to individual radio galaxies.

The population of CRe in ICM is commonly modeled using a power-law energy distribution:

$$N_{cr,e}\left(E\right)=N_{cr,e,0}\left(E_0\right){(E/E_0)}^{-{\gamma }_e}$$

(26)

The corresponding spectral flux of synchrotron emission is of power-law type $F_{\nu }\propto {\nu }^s$ as well as with radio spectral index $s=-({\gamma }_e-1)/2$. In the case of strong non-relativistic shock with ${\gamma }_e\approx$ 2.0–2.4, the radio spectral index is $s\approx -$(0.5–0.7). But in GCs, this index is typically steep, with $s\lesssim -1$. The shape of the spectrum is influenced by both the mechanisms responsible for particle acceleration and the subsequent energy losses due to synchrotron radiation and inverse Compton scattering. Over time, these losses lead to a steepening of the initial power-law spectrum above a characteristic break frequency, which depends on the time elapsed since the electrons were last accelerated [46].

According to [66], diffuse radio emission in clusters is broadly categorized into three main types:

(i) Radio halos are large-scale, centrally located spots found in merging clusters;

(ii) Mini radio halos are compact and appear in relaxed, CC clusters, usually surrounding an active radio galaxy at the center, often associated with the BCG;

(iii) Radio relics are elongated, highly polarized structures (≳10% at GHz frequencies) located in the outskirts of clusters. Like halos, relics do not show any optical counterparts, and their morphology and location suggest a strong connection to shock waves generated during cluster mergers.

In the SSC area, a total of 28 radio galaxies have been identified within the cluster A3562, which lies at the eastern end of the SSC chain [25]. Interestingly, seven of these radio galaxies are concentrated along the eastern edge of the cluster. Among them, J1333-3141 and J1335-3153 exhibit extended radio emission, while two additional extended sources—J1322-3146 and J1324-3138—are located in the nearby cluster A3556, part of the broader A3558 complex. More recent observations by [67] provide a detailed view of the diffuse radio features in the central core region of the SSC. Their analysis reveals several distinct structures extending between A3562 and SC1329-313. The radio properties of GC A3558 are particularly noteworthy. The central diffuse emission reported by [67] is atypical when compared to classical radio halos observed in merging clusters. It spans only ∼400 × 200 kpc—smaller than standard radio halos—and its radio power is extremely low, with $P_{1.283\mathrm{GHz}}=6.85\times {10}^{22}\mathrm{W}{\mathrm{Hz}}^{-1}$. Moreover, the spectral index is exceptionally steep, with $s_{887\mathrm{MHz}}^{1283\mathrm{MHz}}=-2.3\pm 0.4$, suggesting an aging electron population or weak reacceleration mechanisms. These unusual characteristics may support the interpretation that the observed X-ray features in A3558 are not the result of a major merger, but rather of gas sloshing triggered by a nearby perturber—likely the adjacent SC1327-312 cluster [52].

The A3528 complex has been thoroughly examined in recent work by [26]. In A3528N, tailed radio galaxies exhibit a typical spectral index gradient, ranging from approximately s∼$-0.4$ at the head to s∼$-1.0$ at the end of the tail. This trend aligns well with predictions from standard ageing models, such as the Jaffe–Perola (JP) model. In contrast, the extended head–tail structure in A3528S follows the JP model only within the first ∼60 kpc. Beyond this region, deviations in the spectral index may suggest either re-acceleration processes—possibly induced by sloshing in the cluster core—or changes in the galaxy’s projected velocity relative to the ICM. Additionally, distinctive “mushroom”-shaped radio features were identified, likely corresponding to AGN-inflated bubbles originating from the central galaxy J1254-2913. Of particular interest to this study is the detection of a separate diffuse radio component, approximately 200 kpc in extent, oriented along the northwest–southeast axis. This emission does not coincide with the peak of the thermal X-ray signal and may represent a displaced or fossil mini-halo. Its central surface brightness was measured as $I_0^{410\mathrm{MHz}}=6.2\pm 0.4$ $\mathrm{\mu Jy}{\mathrm{arcsec}}^{-2}$ and $I_0^{700\mathrm{MHz}}=3.4\pm 0.2$ $\mathrm{\mu Jy}{\mathrm{arcsec}}^{-2}$.

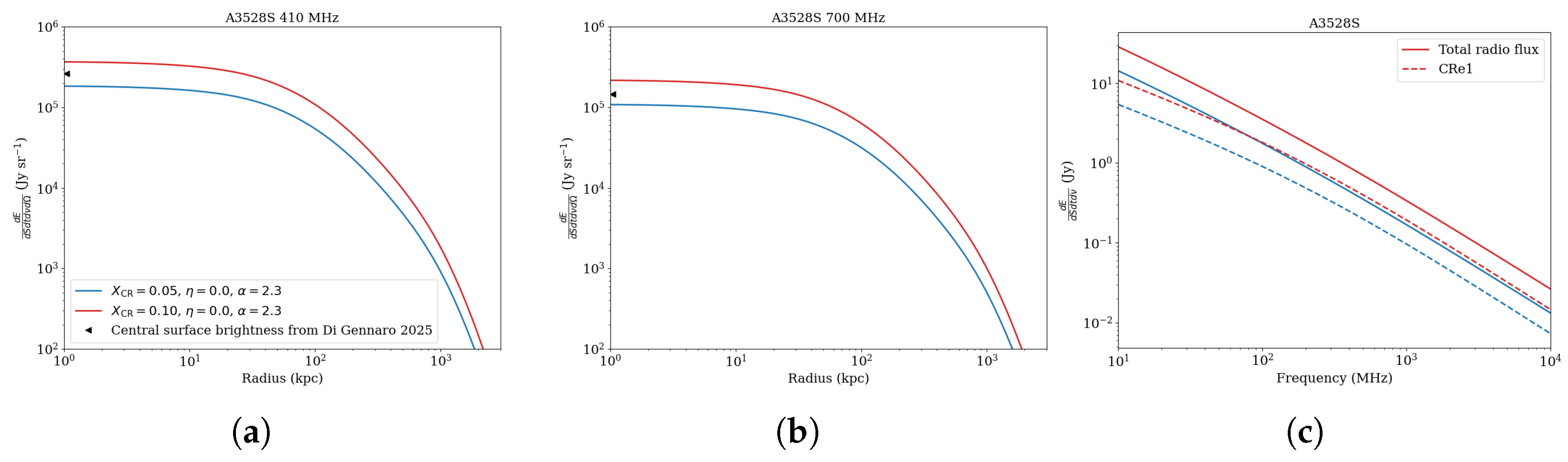
As we have already defined the properties of the CRe1 population, MINOT code allows us to compute the synchrotron radio emission associated with radio halos. In [26], a candidate mini radio halo in the subcluster A3528S was reported, along with central surface brightness values of $I_0^{410\mathrm{MHz}}=2.637\times {10}^5$ Jy sr⁻¹ and $I_0^{700\mathrm{MHz}}=1.446\times {10}^5$ Jy sr⁻¹. The results of our synchrotron modeling are presented in

Table 3. Calculated lower ($X_{\mathrm{CR}}=0.05$) and upper ($X_{\mathrm{CR}}=0.1$) limits on the central surface brightness $I_0$ at frequencies of 410 and 700 MHz for the subcluster A3528S.

Model	${\mathit{I}}_0^{410\mathbf{MHz}}$ [Jy sr−1]	${\mathit{I}}_0^{700\mathbf{MHz}}$ [Jy sr−1]
$\eta =1.5$, $\alpha =2.3$	[$1.1\times {10}^8$; $2.2\times {10}^8$]	[$6.5\times {10}^7$; $1.3\times {10}^8$]
$\eta =1.0$, $\alpha =2.3$	[$1.4\times {10}^7$; $2.8\times {10}^7$]	[$8.2\times {10}^6$; $1.6\times {10}^7$]
$\eta =0.5$, $\alpha =2.3$	[$1.6\times {10}^6$; $3.1\times {10}^6$]	[$9.2\times {10}^5$; $1.8\times {10}^6$]
$\eta =0.0$, $\alpha =2.3$	[$1.8\times {10}^5$; $3.7\times {10}^5$]	[$1.1\times {10}^5$; $2.2\times {10}^5$]
$\eta =1.0$, $\alpha =2.0$	[$1.9\times {10}^7$; $3.7\times {10}^7$]	[$1.3\times {10}^7$; $2.6\times {10}^7$]
$\eta =1.0$, $\alpha =2.5$	[$9.5\times {10}^6$; $1.9\times {10}^7$]	[$5.3\times {10}^6$; $1.1\times {10}^7$]

and Figure 8. We find that the reported central brightness lies within the limits predicted by our model for the parameter set $(\eta ,\alpha )=(0.0,2.3)$, which corresponds to a spatially flat CR distribution.

We also examine all our models using simulated radio maps, where variations in the spatial dependence parameter $\eta$ lead to changes in the observed extent of the radio emission (see Figure 9).

Figure 8 shows the predicted total synchrotron spectrum of the radio halo in A3528S for the selected parameter set. The resulting spectrum is in good agreement with the radio spectra of individual galaxies reported in [26]. However, further radio observations are necessary to better constrain the CR parameters. In this work, we assume a single magnetic field model based on the Perseus cluster; given the strong dependence of synchrotron emission on the magnetic field structure, a more accurate model specific to A3528S would be essential for improving the precision of the results.

As discussed in Section 2, the A3558 complex appears to be mostly composed of relaxed GCs, although there are signs of renewed merging activity. Figure 10 presents the results of our radio emission modeling. For A3562, we used an NCC model and adopted a magnetic field configuration with a mean value of $\langle B_{\mathrm{ref}}\rangle$ = 3 μG and ${\eta }_B=2/3$ in order to better fit the observational data from [67]. The adopted CR parameters were $(\eta ,\alpha )=(1.0,2.5)$. The value $\eta =1.0$ implies that the spatial distribution of CRe closely follows the thermal electron density profile, leading to a relatively centrally concentrated CR population. This is consistent with the observed compactness of the radio halo, whose extent is limited to the central region of the cluster. Such a distribution suggests that either the seed CRs are injected in or transported toward the cluster core—possibly along magnetic field lines connected to a head–tail radio galaxy—as proposed by [67]. The situation with the A3558 cluster appears even more puzzling. Based on its X-ray properties, one would naturally expect the presence of a radio mini-halo. Surprisingly, however, much fainter radio emission was detected, which can be reproduced by again lowering the magnetic field strength to $B_0$ = 2 μG, using the same spectral index as in A3562—$\alpha =2.5$ and $\eta =0.5$.

Given the complex dynamical history of the A3558 region, we hypothesize that the radio halo, if present, may be spatially offset and thus not correlated with the X-ray peak—similar to the case of the A3528 cluster. Given the very low radio surface brightness of $4.25\times {10}^3$ Jy sr⁻¹ at 1.283 GHz, we consider the NCC scenario to be a more realistic assumption in our modeling. Although we present our results in Figure 10, we again reduce the magnetic field, this time to $\langle B_{\mathrm{ref}}\rangle$ = 2 μG. With this configuration, we obtain a central brightness of $4.98\times {10}^3$ Jy sr⁻¹ using a CR parameter set of $(\eta ,\alpha )=(0.0,2.3)$.

5. Neutrino Fluxes from GCS of the SSC

High-energy neutrinos are also expected as secondary products of hadronic interactions between CRp and the ICM. These interactions produce charged pions, which decay via the following channel:

$${\pi }^{\pm }\to {\mu }^{\pm }+{\nu }_{\mu }/\overline{{\nu }_{\mu }}\to e^{\pm }+{\nu }_e/\overline{{\nu }_e}+{\nu }_{\mu }+\overline{{\nu }_{\mu }}$$

(27)

Due to their weak interaction cross-section and lack of electric charge, they travel straight from their source without being deflected. Therefore, detecting neutrinos originating from GCs would provide direct evidence of CR interactions within these structures.

In the [68] IceCube Collaboration, a stacking analysis was conducted of 1094 GCs with masses $\gtrsim {10}^{14}{M}_{\odot }$ and redshifts up to $z\lesssim 1.0$. Based on this analysis, the researchers derived upper limits on the cluster contribution to the diffuse astrophysical neutrino flux. In their most realistic scenario, the clusters account for no more than approximately 4.6% of the observed neutrino flux at 100 TeV. In contrast, recent theoretical work by [69] suggests a much higher potential contribution. Using three-dimensional cosmological magneto-hydrodynamic simulations combined with Monte Carlo modeling of CR propagation and secondary particle production, the authors predict that GCs could contribute a substantial fraction of the IceCube—detected diffuse neutrino background—possibly up to 100%, depending on assumptions about the CR spectral index and energy distribution. Their findings suggest that the latest IceCube constraints are compatible with models involving hard spectra, with spectral indices $\alpha \gtrsim 2.0$. 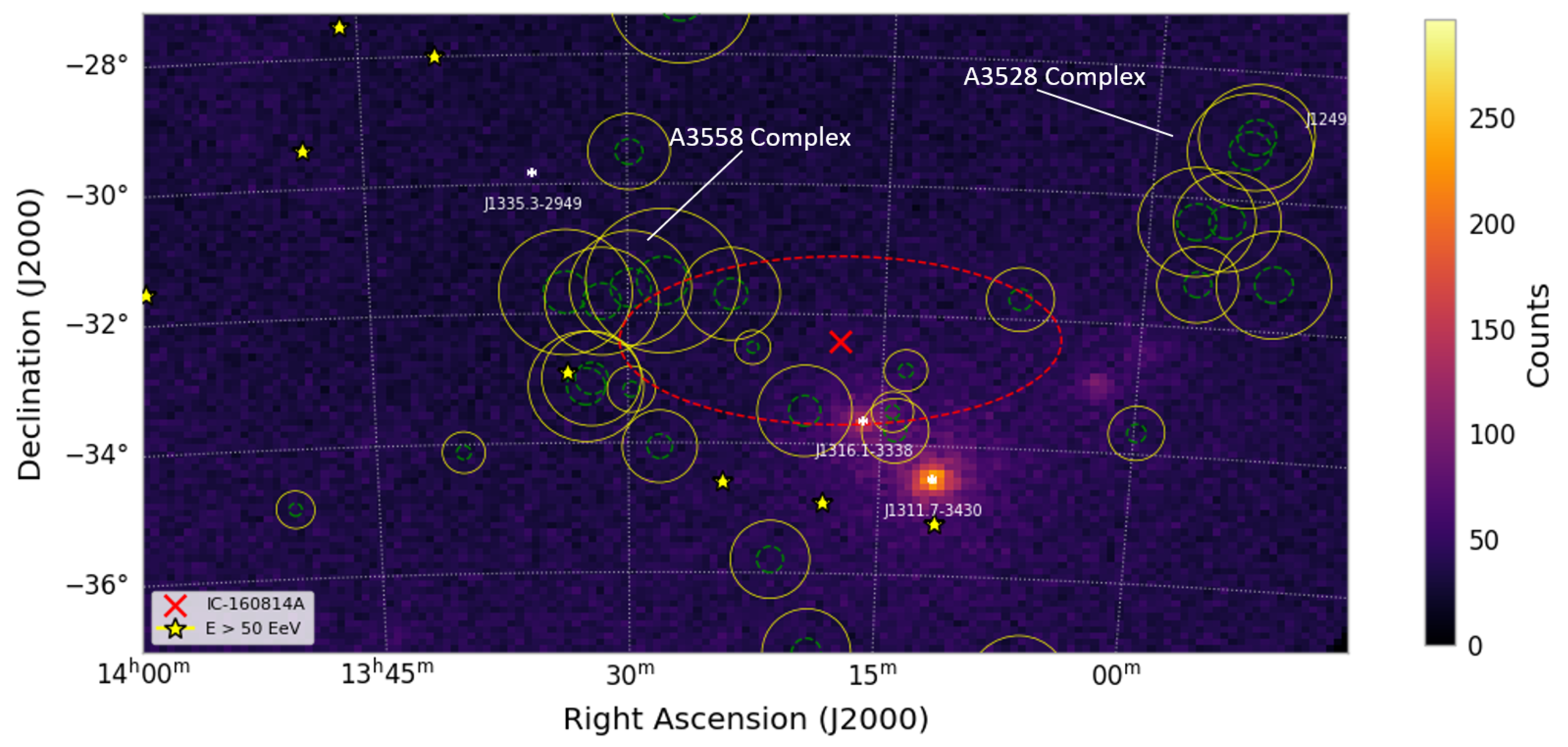In the IceCube alert track event catalog IceCat-1 [70], we identify a single neutrino event located in the region of SSC—IC-160814A. This event was previously associated with the blazar J1316.1-3338 [71]. However, due to the large positional uncertainty, we argue that it could potentially originate from a GC within the SSC (see Figure 11).

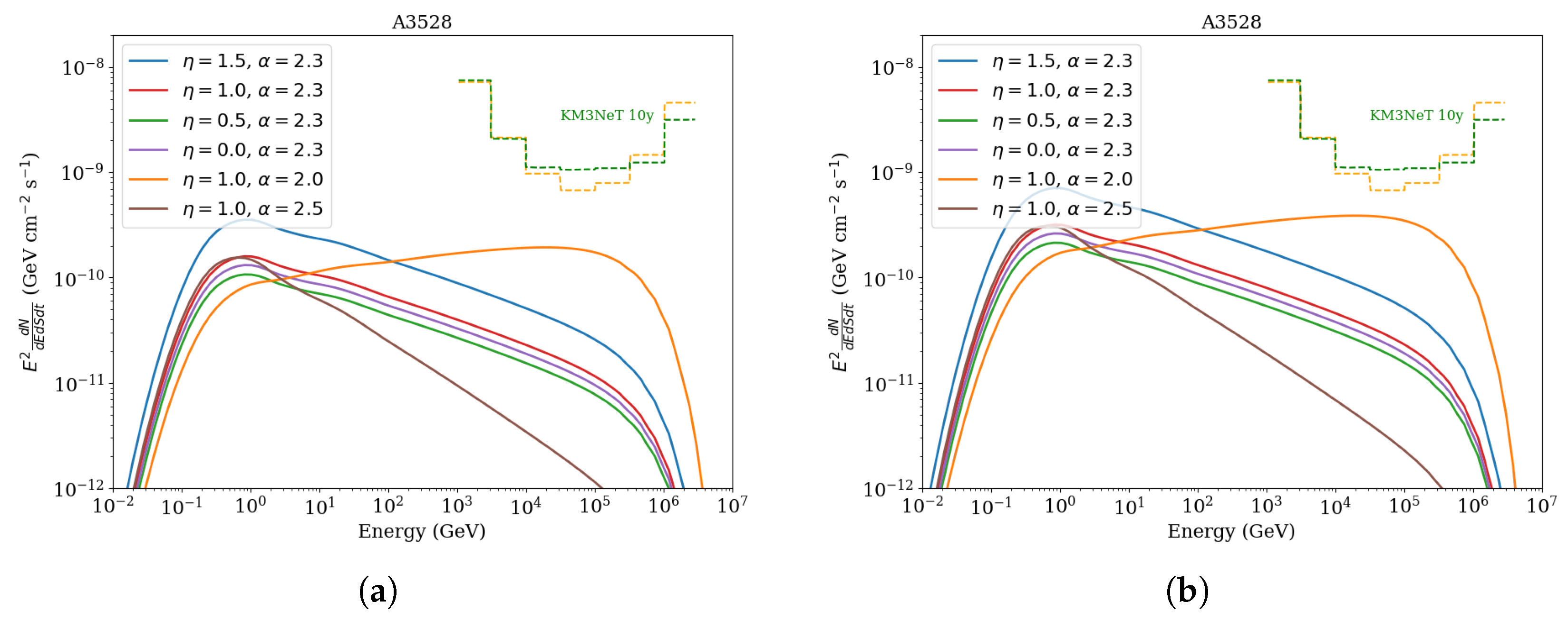
Unlike $\gamma$-rays, neutrinos are not absorbed by the EBL and can travel across cosmic distances without attenuation. They are produced in the same hadronic interactions as $\gamma$-rays, resulting in similar spectra, though with slightly lower normalization. Due to neutrino oscillations, we expect a mixed flavor ratio in the observed flux. Figure 12 and Figure 13 show the predicted spectra of neutrinos—specifically the sum of electron and muon neutrino fluxes—produced via proton–proton collisions. In this analysis, we focus on the KM3NeT observatory, as it offers optimal sensitivity for sources at declination $\mathrm{Dec}\approx -{30}^{\circ }$, whereas IceCube’s sensitivity at these declinations is significantly reduced, by roughly 1.5 orders of magnitude [72]. Similar to the $\gamma$-ray results, the total neutrino flux in the NCC scenario is lower than in the CC case. Models with a soft spectral index of $\alpha =2.3$ peak around ∼1 GeV, where the atmospheric neutrino background dominates. Prospects for detection with KM3NeT improve under the assumption of a harder spectrum, particularly for $\alpha =2.0$.

6. Ultra-High-Energy Cosmic Rays from the SSC Region

CRs in magnetized turbulent ICM propagate diffusively/quasi-ballistically with small-angle scattering if their Larmor radius

$${\displaystyle \frac{r_L}{1\mathrm{cm}}}={\displaystyle \frac{E/1\mathrm{eV}}{300Z(B/1\mathrm{G})}}$$

(28)

is smaller/larger than the coherence length $l_c$ of the magnetic field. For typical values $l_c=0.1$ Mpc and $B=1$ μG, the transition energy is

$$E_{\mathrm{CR}}={10}^{20}Z\left({\displaystyle \frac{B}{1\mu \mathrm{G}}}\right)\left({\displaystyle \frac{l_c}{0.1\mathrm{Mpc}}}\right)\mathrm{eV}.$$

(29)

In GCs, CRs with smaller energy move diffusely with a diffusion coefficient [54]

$$D_{\mathrm{cl}}\approx 1.2\times {10}^{32}{\left({\displaystyle \frac{l_c}{0.1R_{200}}}\right)}^{2/3}{\left({\displaystyle \frac{M_{200}}{{10}^{15}{M}_{\odot }}}\right)}^{2/9}{\left({\displaystyle \frac{E_{\mathrm{cr}}}{1\mathrm{PeV}}}\right)}^{1/3}{\left({\displaystyle \frac{BZ}{1\mu \mathrm{G}}}\right)}^{-1/3}{\mathrm{cm}}^2{\mathrm{s}}^{-1},$$

(30)

and the time of the diffusive exit of CRs from a GC with mass $M_{vir}={10}^{15}{M}_{\odot }$ is as follows [54]:

$$t_{\mathrm{diff}}\approx {\displaystyle \frac{R_{200}^2}{2D_{\mathrm{cl}}}}\approx 6.4{\left({\displaystyle \frac{M_{200}}{{10}^{15}{M}_{\odot }}}\right)}^{4/9}{\left({\displaystyle \frac{E_{\mathrm{cr}}}{1\mathrm{PeV}}}\right)}^{-1/3}{\left({\displaystyle \frac{BZ}{1\mu \mathrm{G}}}\right)}^{1/3}\mathrm{Gyr}$$

(31)

Therefore, CRs with rigidity $R<E/Ze\sim$ (1–10) PV—such that the diffusive time is larger than the age of the Universe—are confined in the GCs.

But GCs as cosmic ray accelerators are able to accelerate particles up to extreme energy—over the ZeV-region with $E_{cr}>{10}^{21}$ eV (see [44,74,75] and reference therein). Such CRs are not confined in the GC magnetic field and can propagate at cosmological distances with contribution to the observed terrestrial detectors UHECR flux. In [76], the PAO Collaboration detected $3.1\sigma$ excess of UHECR ($E>20$ EeV) flux in the Centaurus region.

Table 4. EECR events with energies $E>50$ EeV in the SSC area. Data from [77].

RA (Degree)	Dec (Degree)	Energy (EeV)	Catalogue
192.90	−21.20	165.000	Highest energy
211.20	−36.10	90.000	Highest energy
199.60	−34.90	86.000	Highest energy
203.40	−32.90	82.000	Highest energy
206.98	−29.16	63.809	SD 1500
197.30	−36.30	53.714	Inclined
190.30	−30.20	50.482	Inclined

presents a list of extreme energy CRs (EECRs) with $E>50$ EeV in the SSC area as a part of the Centaurus region. The event with $E=165$ EeV is one of two highest-energy events.

This Hot Spot is a serious challenge for the SSC as a potential contributor into the observed EECR flux. The main problem is the large distance to the SSC—about 200 Mpc, while the energy losses of EECRs restricted typical distances to the sources to about 40 Mpc [74]. An additional problem is connected with the considerable deflection of UHECR heavy nuclei $Z\ge 10$ in the Galactic magnetic field [78]. Nevertheless, there is some window of opportunity, when the SSC can contribute to the observed UHECR and even the EECR flux. The most favorable for the SSC model chemical composition of EECRs are protons and iron (Fe). The distance in 200 Mpc is a challenge but not critical. Once more, recent PAO data allow a possible proton component fraction of 10% above $3\times {10}^{19}$ eV [79].

In order to estimate the expected contribution of UHECR protons from the SSC to that observed by the PAO Hot Spot, we recover the trajectory of the observed $E>32$ EeV and $E>50$ EeV events, considered as protons, while protons with $E=100$ EeV in the Cen A direction are deflected by the Galactic magnetic field by about 5 degrees. Heavy nuclei are deflected more strongly and escape the Hot Spot region [78,80]. As a first step, we use CRPropa 3.2—a Monte Carlo code for simulating the propagation of high-energy particles in the Universe [81] in order to backtrack the observable events in the Galactic magnetic field up to the Galaxy boundary at 20 kpc from its centre. The next step involves modeling of the UHECR backward propagation in the extragalactic magnetic fields in the limit of their pre-diffusive (quasi-ballistic) propagation up to the maximum deflection angle $\theta \le {90}^{\circ }$.

In this case, the influence of random magnetic fields manifests as small-angle stochastic scattering around the primary direction [82]. The average angular deflection (spreading) ${\Theta }_{\mathrm{rms}}$ and the corresponding time delay ${\tau }_{\mathrm{rms}}$ of UHECRs passing a distance L in a turbulent magnetic field ${\mathrm{B}}_{\mathrm{rms}}$ with coherence length $l_{\mathrm{c}}$ are as follows [83,84]:

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Theta }_{\mathrm{rms}}(E,L)=\sqrt{{\displaystyle \frac{2}{9}}}\left({\displaystyle \frac{Ze}{E}}\right)B_{\mathrm{rms}}\sqrt{l_{\mathrm{c}}L}\hfill \\ & \simeq 0.8^{\circ }Z{\left({\displaystyle \frac{E}{{10}^{20}\mathrm{eV}}}\right)}^{-1}{\left({\displaystyle \frac{L}{10\mathrm{Mpc}}}\right)}^{{\displaystyle \frac{1}{2}}}{\left({\displaystyle \frac{l_{\mathrm{c}}}{1\mathrm{Mpc}}}\right)}^{{\displaystyle \frac{1}{2}}}\left({\displaystyle \frac{B_{\mathrm{rms}}}{{10}^{-9}\mathrm{G}}}\right)\hfill \end{array}\end{array}$$

(32)

$$\begin{array}{c}\hfill \begin{array}{cc}& {\tau }_{\mathrm{rms}}(E,L)=L{\Theta }_{\mathrm{rms}}^2(E,L)/4c\hfill \\ & \simeq 1500Z^2{\left({\displaystyle \frac{E}{{10}^{20}\mathrm{eV}}}\right)}^{-2}{\left({\displaystyle \frac{L}{10\mathrm{Mpc}}}\right)}^2\left({\displaystyle \frac{l_{\mathrm{c}}}{1\mathrm{Mpc}}}\right){\left({\displaystyle \frac{B_{\mathrm{rms}}}{{10}^{-9}\mathrm{G}}}\right)}^2\mathrm{yr}\hfill \end{array}\end{array}$$

(33)

Using the upper limit on the extragalactic magnetic field ${\mathrm{B}}_{\mathrm{rms}}$ = 1 nG and a typical correlation length $l_{\mathrm{c}}$ = 1 Mpc [85], the expected spreading of EECR protons with $E>{10}^{20}$ eV in the SSC sky region ($L=200$ Mpc) is of the order of ${\Theta }_{\mathrm{rms}}\simeq 6^{\circ }$, while for heavy nuclei ($Z>1$) spreading ${\Theta }_{\mathrm{rms}}\left(Z\right)\simeq 6^{\circ }Z$ can cause a loss of correlation with potential sources. The resulting initial (observed) and reconstructed values for the proton case at 200 Mpc away from our Galaxy Hot Spots of $E>32$ EeV and $E>50$ EeV are presented in Figure 14. In all cases, Gaussian smoothing with ${\Theta }_{\mathrm{rms}}\simeq 6^{\circ }$ was used.

As can be observed, the distributions for events with E > 32 EeV are highly multimodal, with no clearly defined density peak. However, when the energy threshold is increased to 50 EeV, the highest-density regions for both observed and simulated events become aligned with the central part of the SSC. Notably, the simulated events—after correction for deflections in the Galactic magnetic field—exhibit even stronger alignment than the observed events. This alignment disfavors the Centaurus Cluster and Cen A as potential sources of UHECR protons in favor of an SSC source.

Above, we considered the proton component of the expected UHECR flux from the SSC. But the initial accelerated (injected) material by the SSC UHECR flux, similarly to the Galactic CR flux, consists of a mix of protons and heavier He-Fe nuclei.

During their propagation, UHECRs are affected by the background radiation fields, mainly the CMB and the EBL [86]. The major interaction mechanisms include the following:

(i) Adiabatic cooling caused by the cosmological expansion of the Universe;

(ii) Photo-pair production—creation of an electron–positron pair $e^{-}{e}^{+}$ in the interaction of particle N with background photons $\gamma$:

$$N+\gamma \to N+e^{-}+e^{+},$$

(34)

(iii) Photo-disintegration. There are multiple photo-nuclear processes that all lead to the disintegration of the nucleus into two or more fragments; an example is $\alpha$-emission:

$${}_A{}^{Z}N+\gamma \to {}_A{}^{Z}N^{*}\to {}_{A-4}{}^{Z-2}N+{}^4\mathit{He}$$

(35)

(iv) Photo -pion production. The interaction of UHECRs with photons can stimulate baryonic resonances $\Delta$ at the level of individual nucleons, leading to the generation of pions ${\pi }^0$ or ${\pi }^{+}$:

$$p+\gamma \to {\Delta }^{+}\to \{\begin{array}{cc}{\pi }^0+p,\hfill & 2/3 \mathrm{of} \mathrm{all} \mathrm{cases}\hfill \\ {\pi }^{+}+n,\hfill & 1/3 \mathrm{of} \mathrm{all} \mathrm{cases}\hfill \end{array},$$

(36)

The extragalactic background photon fields are homogenous and isotropic on large scales. As a first approximation for calculation of the expected at Earth UHECR spectrum from the SSC, we use a transport equation [87]:

$${\partial }_t{Y}_i(E,z)=\underset{\mathrm{adiabatic}\mathrm{cooling}}{\underbrace{{\partial }_E\left(H\left(z\right)E{Y}_i\right)}}-\underset{\mathrm{pair}\mathrm{prod}}{\underbrace{{\partial }_E\left({\displaystyle \frac{dE}{dt}}{Y}_i\right)}}\underset{\mathrm{photo}\text{-}\mathrm{nuclear}\mathrm{interaction}}{\underbrace{-{\Gamma }_i{Y}_i+\sum _j{Q}_{j\to i}}}+\underset{\mathrm{injection}}{\underbrace{J_i}}$$

(37)

This is a coupled system of differential equations, that represents the evolution of the homogenous and isotropic co-moving CR spectrum $Y_i(E_i,z)=N_i(E_i,z)/{(1+z)}^3$, $dz=-dt(1+z)H\left(z\right)$ and the index i represents a single species—from H to Fe. The first two terms denote continuous energy losses. The third and fourth are discrete interaction terms that are described by the interaction of particles and the subsequent re-injection into secondaries at different energies. The last term stands for the external injection of particles, $J_i$. These processes are described by the interaction rate ${\Gamma }_i$ and the re-injection terms $Q_{j\to i}$. The PriNCe (Propagation including Nuclear Cascade equations) (available at https://github.com/joheinze/PriNCe (accessed on 17 July 2025)) code is applied for an extensive parameter scan of a generic source model that is described by the spectral index, the maximal rigidity, the cosmological source evolution, and the injected mass composition [87]. The main idea of PriNCe is to solve the above-mentioned system of the coupled partial differential Equation (37). The common software for UHECR-propagation, such as CRPropa and SimProp, use a Monte Carlo approach.

When analyzing the cross-section systematics or nonlinear scaling of photon fields, the Monte Carlo method can become computationally intensive and slow. PriNCe provides an alternative approach and directly solves the transport equation for the particle spectral density $Y_i(E_i,z)$.

We injected CRs at $z=0.05$. For the spectrum of injected cosmic rays (elements: H, N, Si, Fe), we used a simple power-law with $\gamma =2.5$ and an exponential cut-off $E_{cut}=2\times {10}^{21}$ eV:

$$J_i\left(E\right)=J_{i,0}{\left({\displaystyle \frac{E}{{10}^9\mathrm{GeV}}}\right)}^{-\gamma }exp\left(-{\displaystyle \frac{E}{E_{cut}}}\right)$$

(38)

As follows from Figure 15, we expect detectable contribution to PAO and future Global Cosmic Ray Observatory EECR E > 50 EeV spectra from SSC region especially due to a number of massive clusters in this direction at distances 40-80 Mpc – the Great Attractor complex, the Centaurus cluster and others.

7. Discussion and Conclusions

In the large-scale structure of the nearby Universe ($z<0.1$), the most massive and largest structure turned out to be the SSC—a conglomerate of spatially close GCs. Due to its mass (∼5 ×${10}^{16}{M}_{\odot }$) and size (∼100 Mpc), the SSC serves as a unique laboratory for cosmology, high-energy astrophysics, and particle physics. Multimessenger studies of the SSC are of great importance for the search for new physics beyond the SM, in particular, for establishing the nature of dark matter, for improving the modern cosmological model, and for high-energy astrophysics.

In our work, we carried out a comprehensive study of the physical conditions in the SSC and in its components—in 45 massive X-ray active GSs. Based on this, the expected multimessenger observational manifestations of physical processes in individual clusters and in their aggregates were calculated. Attention was mainly paid to calculation of the all-wavelength non-thermal emission of GCs as a test of the characteristics of the main components of the GCs—dominant in terms of total mass dark matter, dominant in terms of baryonic mass ICM plasma, and the relativistic component—CRs, and magnetic fields. One of the most important results of the work is the calculation of the non-thermal gamma-ray and neutrino emission of GCs due to the hadronic mechanism—collisions of relativistic protons and nuclei with protons and nuclei of the ICM plasma with the production of pions and their subsequent decay into $\gamma$-photons and neutrinos. Until now, such emission has not been reliably detected from closer GCs in the local ($z<0.02$) Universe. We found the regions of the parameters of the baryonic gas and CRs at which non-thermal gamma-ray emission can be detected by existing detectors, in particular, the CTAO-South, and neutrino emission by the KM3NeT detector. An important new result is the estimation of the non-thermal radio emission of the leptonic component of the CRs, which showed the ability of our models to explain the existing observations of radio emission from some GCs and give a forecast for the possible detection of radio emission from other GCs.

In multimessenger astronomy, only CRs have not yet been identified with astrophysical sources. At the same time, GCs and the SSC are considered to be among the most promising sources of CRs in the entire range of their energy spectrum, including the highest detected energies above ${10}^{20}$ eV. We investigate the expected fluxes of UHECRs from the SSC and show that in the UHECR flux observed by the PAO detectors, a contribution of the SSC should be expected, especially in their proton component. In particular, protons with energies above 50 EeV can contribute to the observed PAO hot spot in the Centaurus region. Therefore, future multimessenger observations of the SSC promise to yield breakthrough results in cosmology, cosmic ray astrophysics, and particle physics.