Chaos of Charged Particles in Quadrupole Magnetic Fields Under Schwarzschild Backgrounds
Abstract
1. Introduction
2. Magnetic Fields in Schwarzschild Geometries
3. Dynamics of Charged Particles in Combination of Dipole and Quadrupole Magnetic Fields
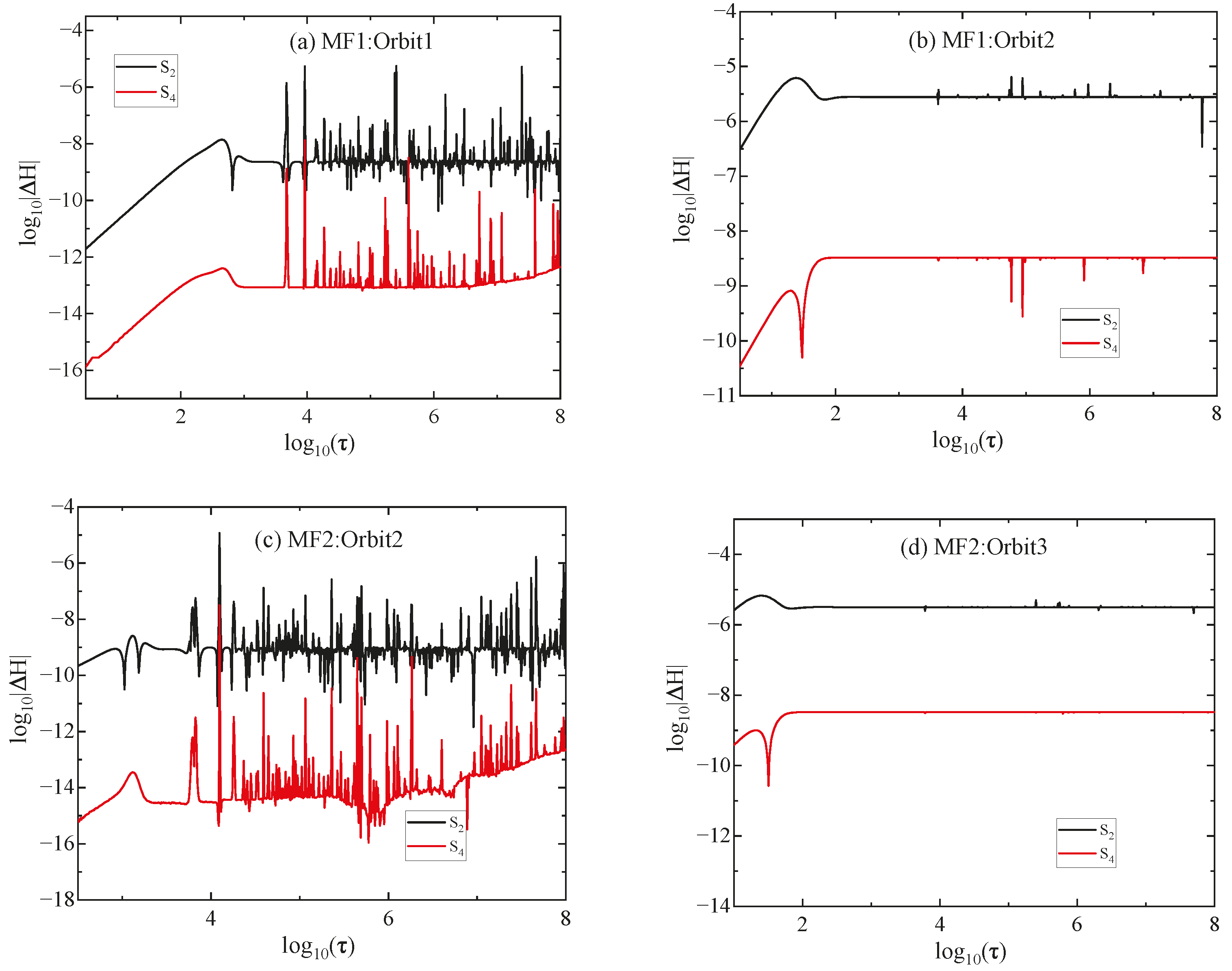
3.1. Dynamical Equations and Numerical Schemes
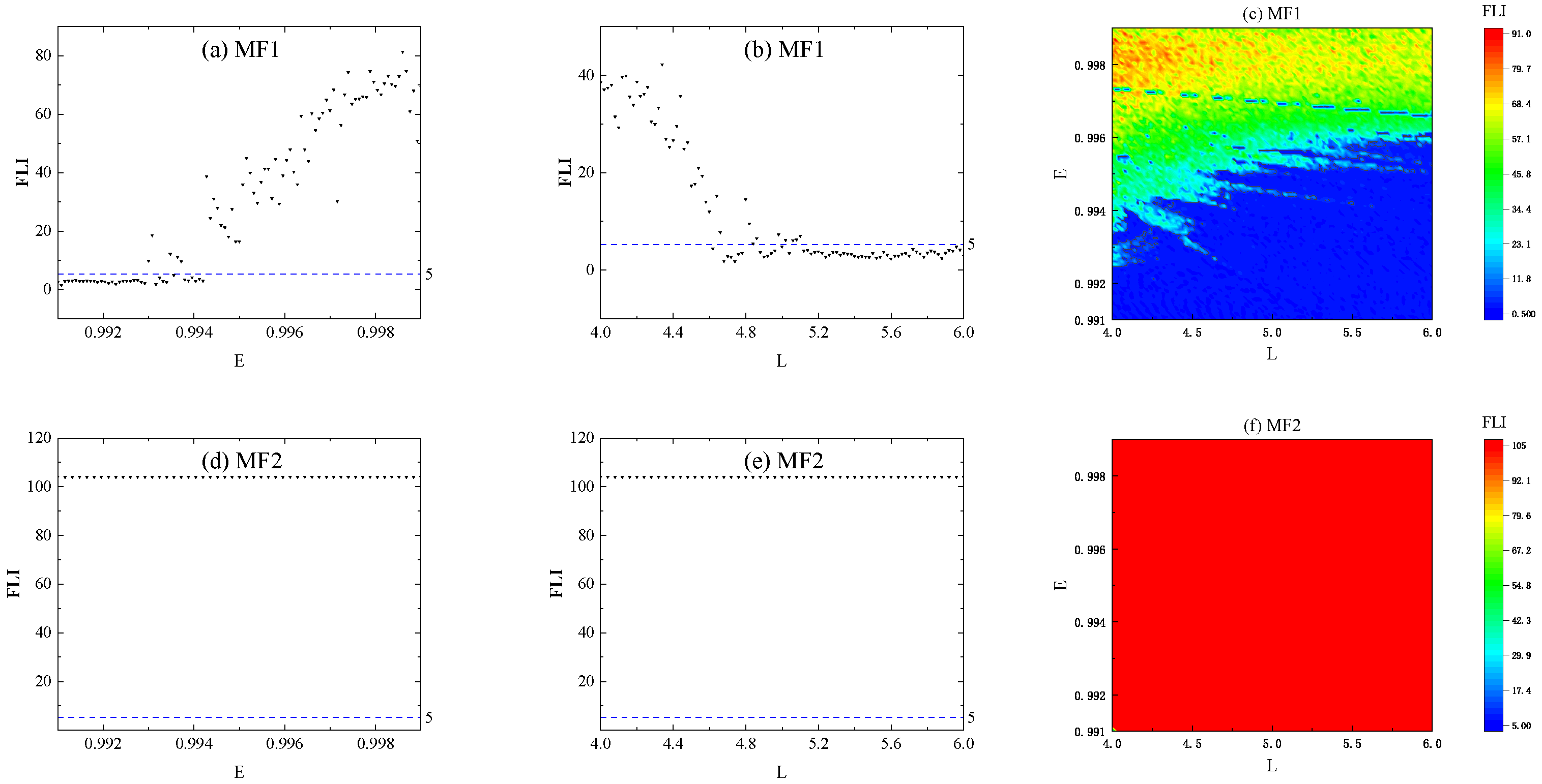
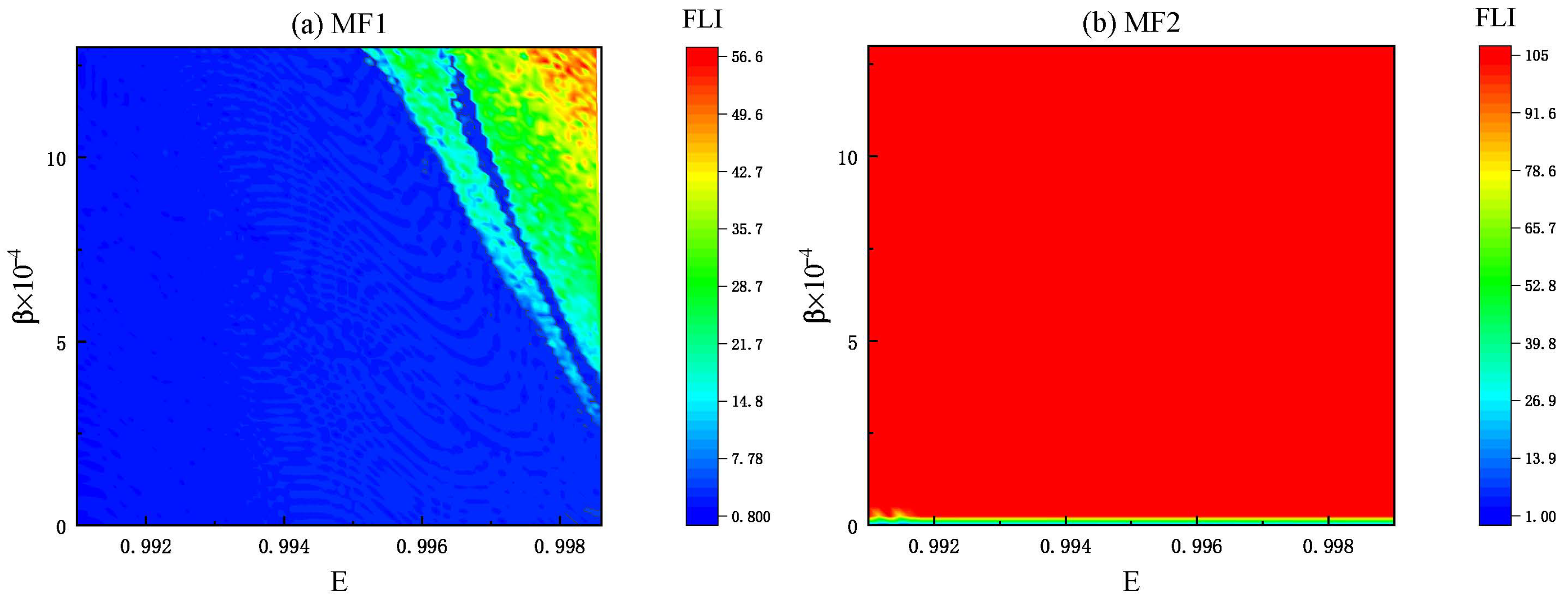
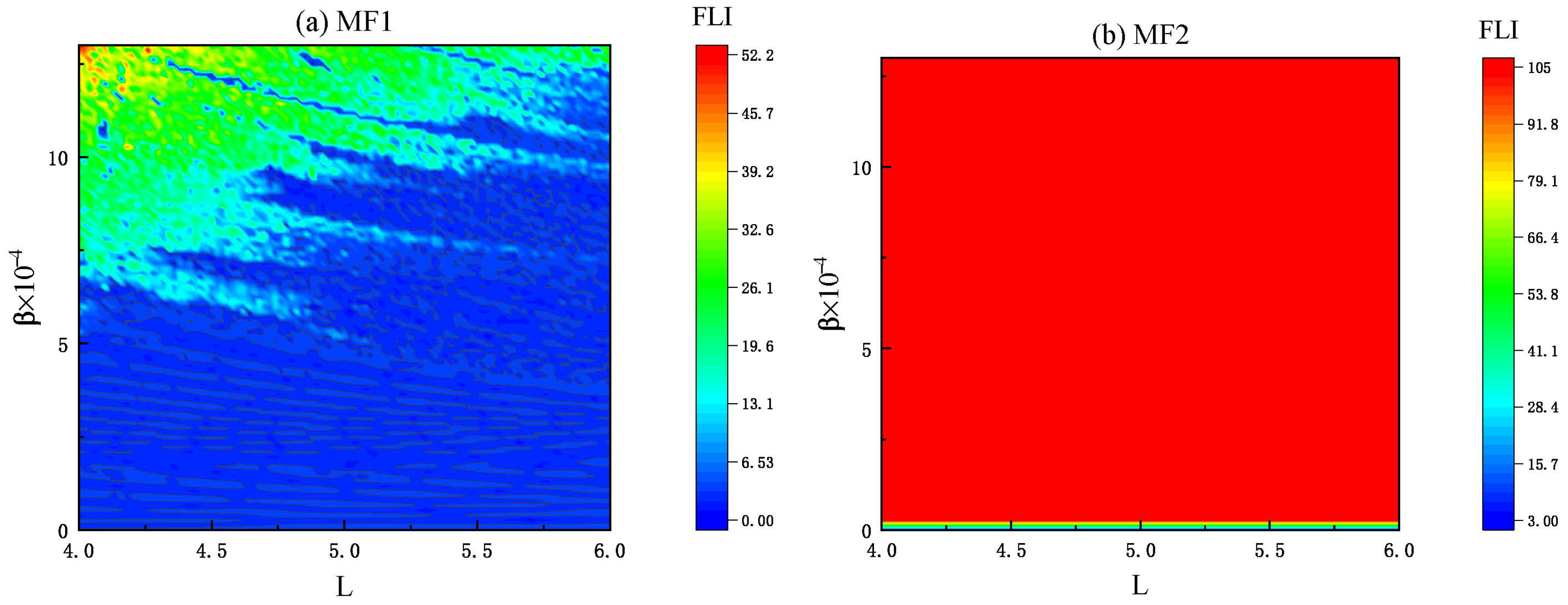
3.2. Chaotic Dynamics of Charged Particles in the Two Electromagnetic Potentials
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eatough, R.P.; Falcke, H.; Karuppusamy, R.; Lee, K.J.; Champion, D.J.; Keane, E.F.; Desvignes, G.; Schnitzeler, D.H.F.M.; Spitler, L.G.; Kramer, M.; et al. A strong magnetic field around the supermassive black hole at the centre of the Galaxy. Nature 2013, 501, 391. [Google Scholar] [CrossRef]
- Paraschos, G.F.; Kim, J.-Y.; Wielgus, M.; Röder, J.; Krichbaum, T.P.; Ros, E.; Agudo, I.; Myserlis, I.; Moscibrodzka, M.; Traianou, E.; et al. Ordered magnetic fields around the 3C 84 central black hole. Astron. Astrophys. 2024, 682, L3. [Google Scholar] [CrossRef]
- Frolov, V.P.; Shoom, A.A. Motion of charged particles near a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2010, 82, 084034. [Google Scholar] [CrossRef]
- Santoprete, M.; Cicogna, G. Chaos in Black holes Surrounded by Electromagnetic Fields. Gen. Relativ. Gravit. 2002, 34, 1107–1119. [Google Scholar] [CrossRef]
- Takahashi, M.; Koyama, H. Chaotic motion of charged particles in an electromagnetic field surrounding a rotating black hole. Astrophys. J. 2009, 693, 472. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V.; Kovář, K.; Stuchlík, Z. Transtion from regular to chaotic circulation in magnetized coronae near compact objects. Astrophys. J. 2010, 722, 1240. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V. Inducing Chaos by Breaking Axil Symmetry in a Black Hole Magenetosphere. Astrophys. J. 2014, 787, 117. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Acceleration of the charged particles due to chaotic scattering in the combined black hole gravitational field and asymptotically uniform magnetic field. Eur. Phys. J. C 2016, 76, 32. [Google Scholar] [CrossRef]
- Kopáček, O.; Karas, V. Near-horizon structure of escape zones of electrically charged particles around weakly magnetized rotating black hole. Astrophys. J. 2018, 853, 53. [Google Scholar] [CrossRef]
- Pánis, R.; Kološ, M.; Stuchlík, Z. Determination of chaotic behaviour in time series generated by charged particle motion around magnetized Schwarzschild black holes. Eur. Phys. J. C 2019, 79, 479. [Google Scholar] [CrossRef]
- Cao, W.F.; Wu, X.; Lyu, J. Electromagnetic field and chaotic charged-particle motion around hairy black holes in Horndeski gravity. Eur. Phys. J. C 2024, 84, 435. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680. [Google Scholar] [CrossRef]
- Azreg-Aïnou, M. Vacuum and nonvacuum black holes in a uniform magnetic field. Eur. Phys. J. C 2016, 76, 414. [Google Scholar] [CrossRef]
- Cohen, J.M.; Wald, R.M. Point Charge in the Vicinity of a Schwarzschild Black Hole. J. Math. Phys. 1971, 12, 1845. [Google Scholar] [CrossRef]
- Hanni, R.S.; Ruffini, R. Lines of force of a point charge near Schwarzschild Black Hole. Phys. Rev. D 1973, 8, 3259. [Google Scholar] [CrossRef]
- Petterson, J.A. Magnetic field of a current loop around a Schwarzschild black hole. Phys. Rev. D 1974, 10, 3166. [Google Scholar] [CrossRef]
- Petterson, J.A. Stationary axisymmetric electromagnetic fields around a rotating black hole. Phys. Rev. D 1975, 12, 2218. [Google Scholar] [CrossRef]
- Kerner, R.; Koekoek, G.; Schuring, J.A.; van Holten, J.W. Polar magnetic fields in black-hole space-times. arXiv 2024, arXiv:2407.04975. [Google Scholar] [CrossRef]
- Ghosh, P. The structure of black hole magnetospheres. I. Schwarzschild black holes. Mon. Not. R. Astron. Soc. 2000, 315, 89. [Google Scholar] [CrossRef]
- Kolos, M.; Stuchlík, Z.; Tursunov, A. Quasi-harmonic oscillatory motion of charged particles around a Schwarzschild black hole immersed in a uniform magnetic field. Class. Quantum Grav. 2015, 32, 165009. [Google Scholar] [CrossRef]
- Zahrani, A.M.A. Circular orbits of Charged Particles around a Weakly Charged and Magnetized Schwarzschild Black Hole. Phys. Rev. D 2021, 103, 084008. [Google Scholar] [CrossRef]
- Zahrani, A.M.A. Charged Particles Circular Orbits around Weakly Charged and Magnetized Kerr Black Holes. Astrophys. J. 2022, 937, 50. [Google Scholar] [CrossRef]
- Vrba, J.; Rayimbaev, J.; Stuchlík, Z.; Ahmedov, B. Charged particles motion and quasiperiodic oscillation in Simpson-Visser spacetime in the presence of external magnetic fields. Eur. Phys. J. C 2023, 83, 854. [Google Scholar] [CrossRef]
- Baker, N.P.; Frolov, V.P. Charged Particle Motion Near a Magnetized Black Hole: A Near-Horizon Approximation. Phys. Rev. D 2023, 108, 024045. [Google Scholar] [CrossRef]
- Uktamov, U.; Fathi, M.; Rayimbaev, J.; Abdujabbarov, A. Orbits of particles with magnetic dipole moment around magnetized Schwarzschild black holes: Applications to S2 star orbit. Phys. Rev. D 2024, 110, 084084. [Google Scholar] [CrossRef]
- Trova, A. Equilibrium of charged fluid around a Kerr black hole immersed in a magnetic field: Variation of angular momentum. International J. Mod. Phys. D 2024, 33, 2350112. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.; Wu, X. Construction of Explicit Symplectic Integrators in General Relativity. I. Schwarzschild Black Holes. Astrophys. J. 2021, 907, 66. [Google Scholar] [CrossRef]
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262. [Google Scholar] [CrossRef]
- Wu, X.; Huang, T.Y.; Zhang, H. Lyapunov indices with two nearby trajectories in a curved spacetime. Phys. Rev. D 2006, 74, 083001. [Google Scholar] [CrossRef]
- Froeschlé, C.; Lega, E. On the Structure of Symplectic Mappings. The Fast Lyapunov Indicator: A Very Sensitive Tool. Celest. Mech. Dyn. Astron. 2000, 78, 167. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Wu, X. Chaos of Charged Particles in Quadrupole Magnetic Fields Under Schwarzschild Backgrounds. Universe 2025, 11, 234. https://doi.org/10.3390/universe11070234
Zhang Q, Wu X. Chaos of Charged Particles in Quadrupole Magnetic Fields Under Schwarzschild Backgrounds. Universe. 2025; 11(7):234. https://doi.org/10.3390/universe11070234
Chicago/Turabian StyleZhang, Qihan, and Xin Wu. 2025. "Chaos of Charged Particles in Quadrupole Magnetic Fields Under Schwarzschild Backgrounds" Universe 11, no. 7: 234. https://doi.org/10.3390/universe11070234
APA StyleZhang, Q., & Wu, X. (2025). Chaos of Charged Particles in Quadrupole Magnetic Fields Under Schwarzschild Backgrounds. Universe, 11(7), 234. https://doi.org/10.3390/universe11070234






