Many Phases in a Hairy Box in Three Dimensions
Abstract
1. Introduction
2. EOM, Boundary Conditions, and Thermodynamic Quantities
3. Thermodynamics of (=Einstein–Maxwell)
3.1. Saddles
3.2. Thermodynamics
3.3. Dissimilarities
- BG entropy does not depend on temperature T.In standard gravitational thermodynamics, as we increase T, the entropy or horizon area increases. However, in this case, the entropy is given by (36). For a fixed chemical potential , no matter how we change T (above the Hawking–Page point), the horizon area does not change! (note that this does not mean that the geometry does not change).
- BG free energy is linear to T. The heat capacity is zero.Related to the previous fact, the BG free energy is a linear function of T, and thus, the heat capacity is exactly zero at the zero-loop order. This is a peculiar property since, usually, the dominant BH (or BG) saddles have positive specific heat even at the zero loop and give us well-defined thermodynamic descriptions. Although I suspect this problem can be solved by one-loop corrections, it is still a somewhat remarkable property of this saddle or system.
- No extremal horizons. The empty phase is always dominant at low temperatures.One remarkable property of charged systems is that they generally have extremal BH (or BG) saddles. Although the existence of the saddles does not necessarily imply dominance in the GPI, their phase appears when the chemical potential is sufficiently high in the EM system with the AdS boundary condition.11 As shown in Figure 2b, however, we do not have an extremal BG phase in this system. The zero and low temperature phase is always the empty phase.
4. Thermodynamics of Finite
4.1. Saddles
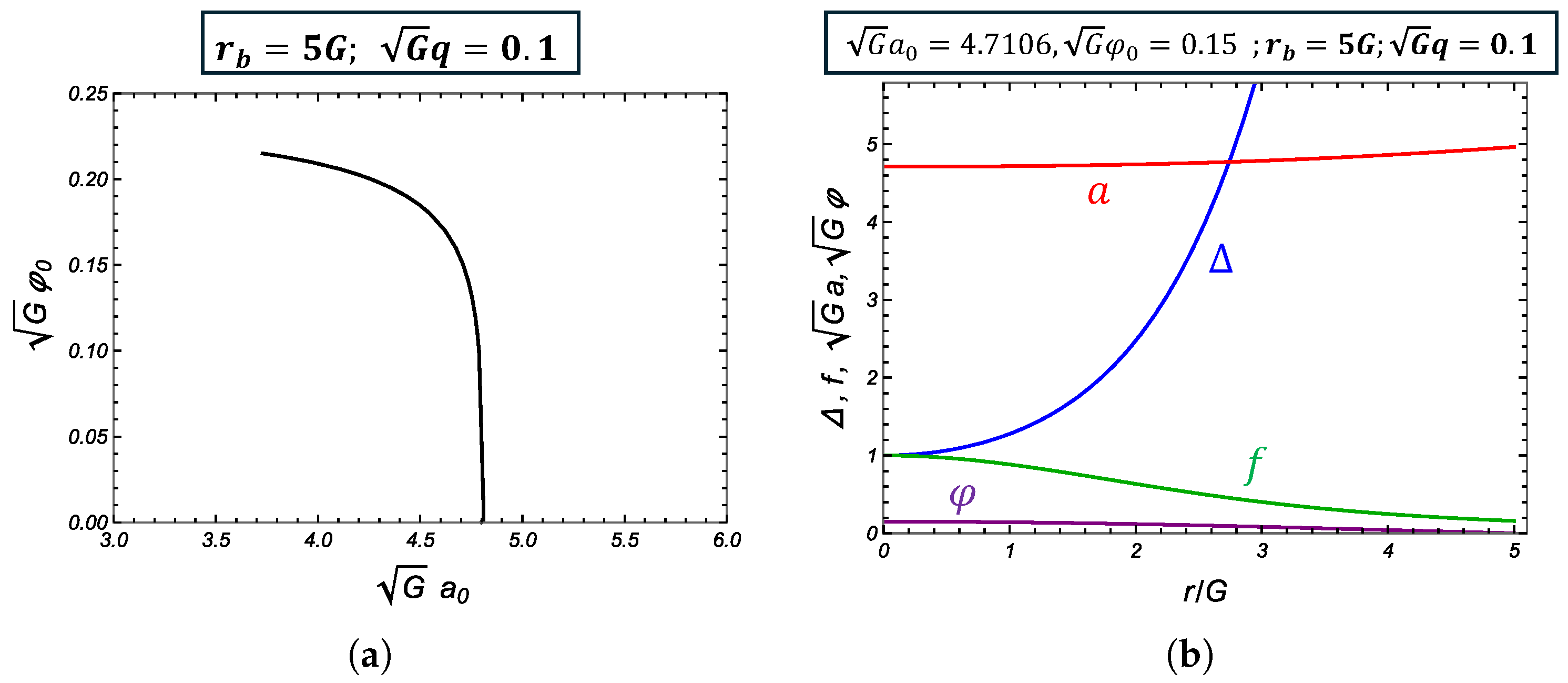
- Empty saddle (already explained in Section 3);
- BG saddle (already explained in Section 3);
- Boson star saddle (to be explained in Section 4.1.1);
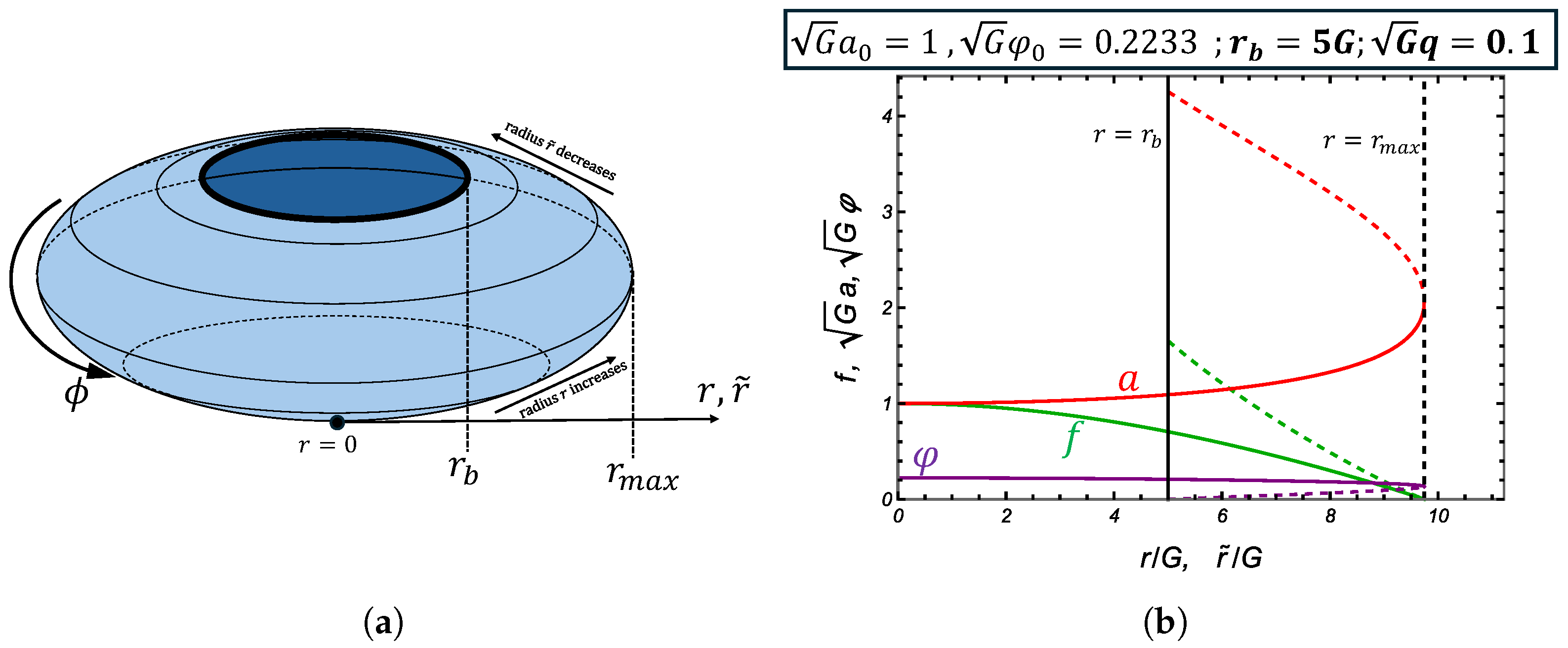
- Boson star-PL saddle (to be explained in Section 4.1.2);
- Hairy BG saddle (to be explained in Section 4.1.3).
4.1.1. Boson Star Saddle
- corresponds to the freedom of a certain simultaneous rescaling of coordinates. If we rescale , and , the metric, gauge field, and the EOM are unchanged. Therefore, we can set .12
4.1.2. Boson Star-PL Saddle (and Boson Star Saddle)
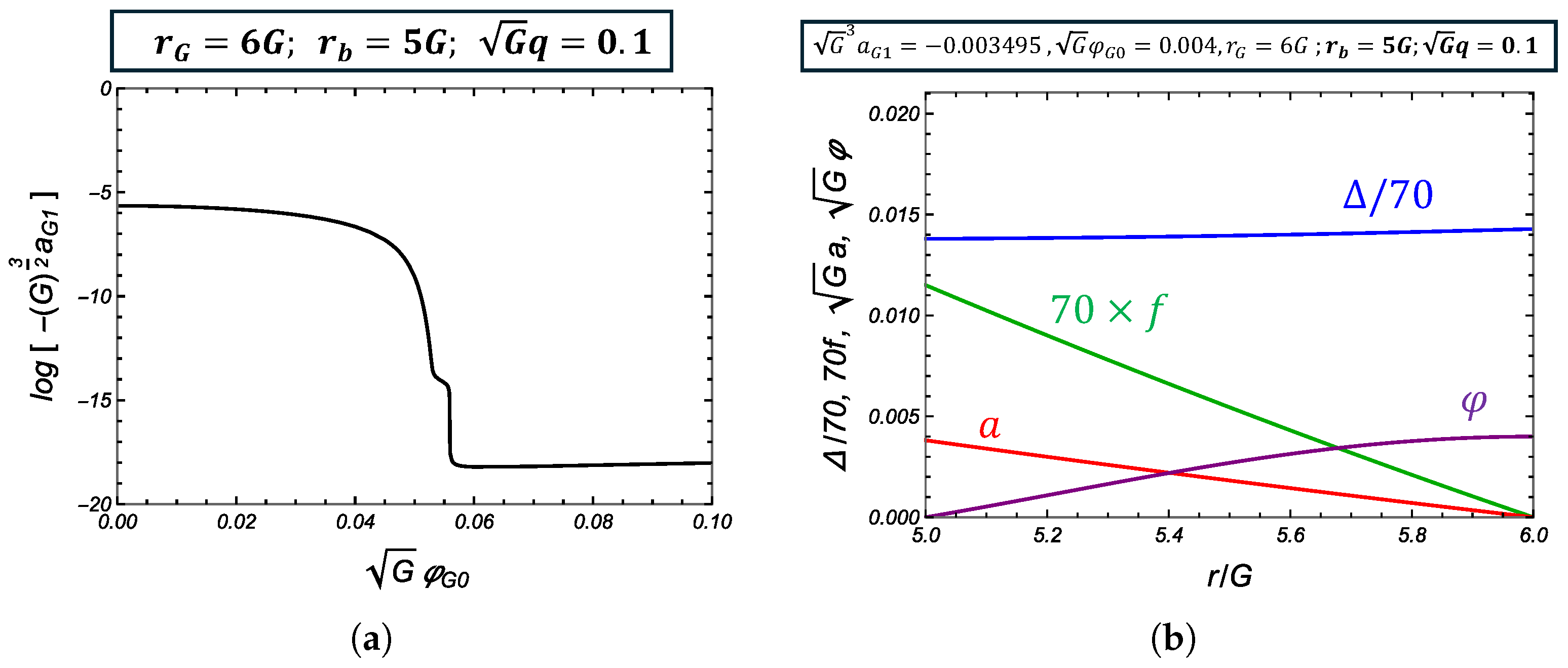
4.1.3. Hairy BG Saddle
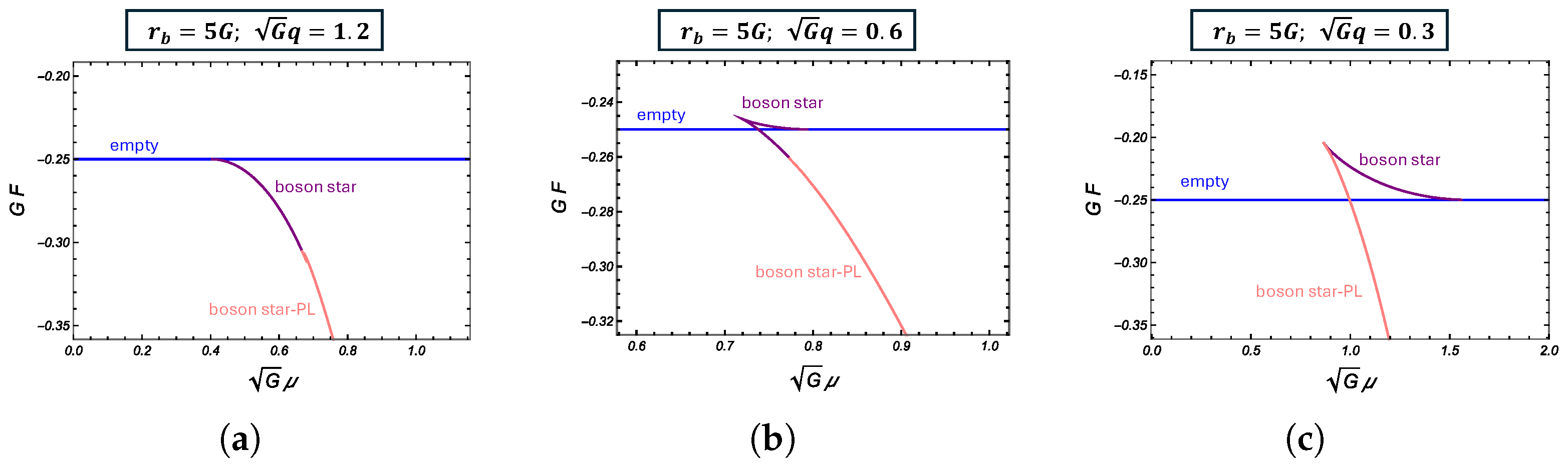
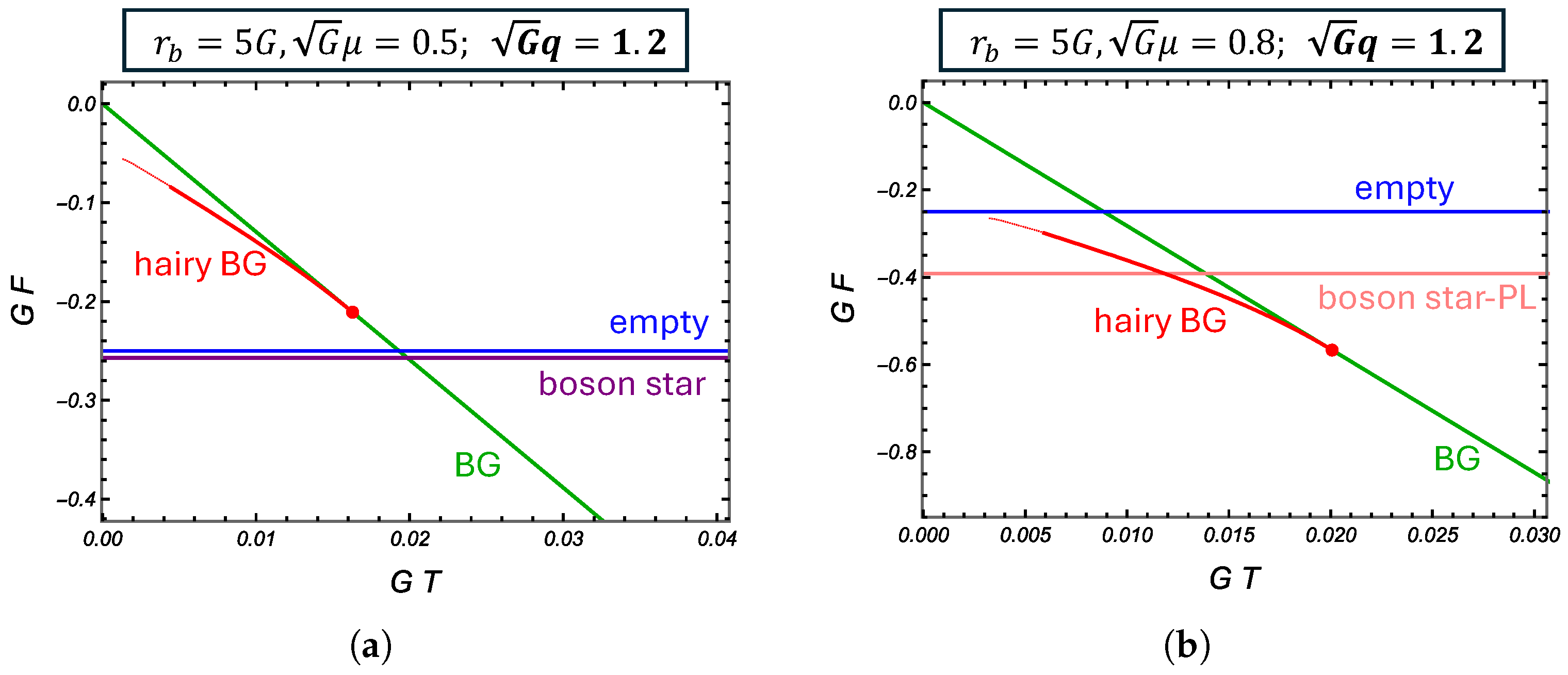
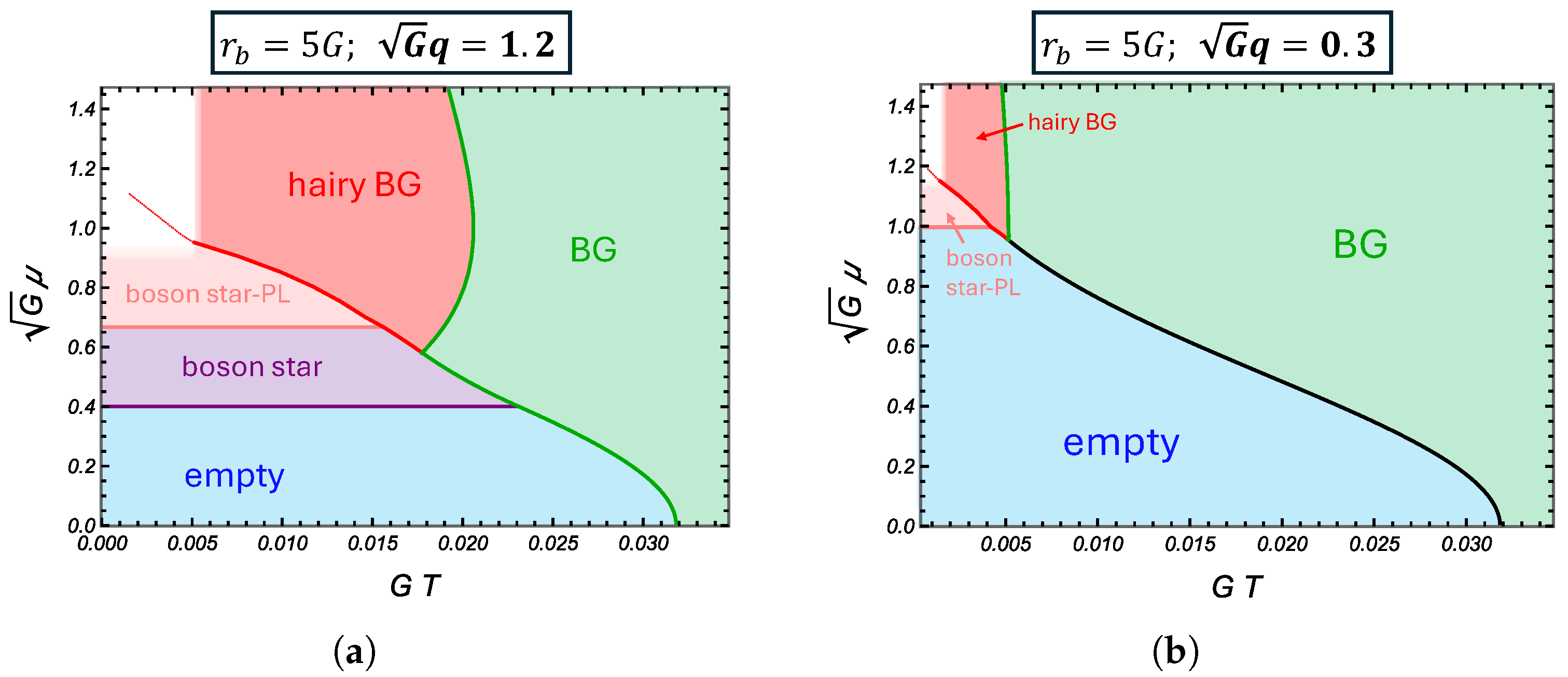
4.2. Thermodynamics
5. Summary and Discussion
Funding
Data Availability Statement
Conflicts of Interest
| 1 | In general, GPI has several problems, such as the non-renormalizability problem and the integration contour problem [2]. However, there is compelling evidence supporting the validity of this approach, including the derivation of “BH thermodynamics” [3], the AdS/CFT correspondence [4,5,6], and the derivation of the Page curve of Hawking radiation [7,8,9]. In this paper, I will assume that GPI can capture the thermodynamic properties of quantum gravity. |
| 2 | BG stands for bag of gold. For the reason (which is not important), see [32]. |
| 3 | If we assume that both the zero-loop calculation and the restriction to the simple topology sectors are sufficient to extract the thermodynamic property of gravity. |
| 4 | As long as we consider the zero-loop order and with the boundary condition . |
| 5 | Typically, the aforementioned currents and charges are defined in a Lorentzian signature. In that case, conservation is with respect to the spacelike hypersurfaces on the boundary. Consider two spacelike hypersurfaces on the boundary, denoted by , and their normal vector . Then, the following equality holds: |
| 6 | In that paper, I made a mistake about the free energy and the energy of BG saddles. The fact that the free energy is a linear function of T is not changed by this error. Therefore, the final conclusion of [31] is still true. However, the “transition temperature” and the “phase diagram” are slightly modified. |
| 7 | As I will explain shortly, this saddle is similar to, but different from, the BH saddle. That is why I use the other name for this saddle. Sometimes it is called “cosmological side” or “cosmological type”, presumably because this type of saddle was first studied in the context of dS thermodynamics [32,36,37], where the bolt corresponds to the cosmological horizon of dS spacetime. |
| 8 | In [31], the energy was wrongly set to zero, and the energy contribution to the free energy was missing. That is, the energy and the free energy in [31] are related to the true thermodynamic quantities as As I wrote in the previous footnote, the linearity of the free energy is not changed by this modification, and the conclusions of [31] are unchanged. The transition temperature and the phase diagram are slightly modified. |
| 9 | Similar to the empty saddle whose heat capacity is zero at the zero-loop order, but positive when we include the contribution of fluctuations (or ordinary matter fields). |
| 10 | |
| 11 | The case of the Dirichlet boundary condition in higher dimensions is subtle. When , the extremal horizon states appear the same as in the AdS boundary case. When , they do not appear. |
| 12 | This freedom of rescaling appears only in three dimensions, not in higher dimensions. In [33], (which is what they call in their paper) was considered as a new degree of freedom specific to three dimensions. However, I believe they missed this rescaling symmetry and just represents this redundancy. |
| 13 | Note that there are also solutions that satisfy the boundary condition (15) but have multiple nodes in the scalar configuration. Figure 3 is for the 0 node case. (For one-node solutions, see [33].) In general, hairy solutions, such as hairy soliton or hairy BH, can have multiple-node solutions. In fact, I have found multiple node solutions not only for this boson star saddle, but also for boson star-PL saddles and hairy BG saddles. However, as a rule of thumb for systems with hairy solutions, only the lowest, mostly zero, node solutions are stable in any sense; i.e., they are perturbatively stable, or thermodynamically stable, and so on. Therefore, in this paper, I will concentrate only on the 0 node solutions. |
| 14 | See note 13 above. |
| 15 | Here, the signs of the second terms in the expansions of a and differ from those in Equations (50) and (51). This discrepancy arises because the expansions in (50) and (51) are valid for under the coordinate transformation . When we instead use the coordinate transformation with , an additional minus sign appears in front of the second term due to the change in the sign of . |
| 16 | PL stands for Python’s Lunch [41]. Here, I have nothing to say about it except that the shape of the saddles is similar to the Python’s Lunch. |
| 17 | Although the definition of the thermodynamic variable and the boundary size are different, Figure 5b (or Figure 7) corresponds to Figure 7 of [33]. In particular, the boson star region of Figure 5b corresponds to the green region of their figure. According to their figure, it seems that the lowest value of q at which the boson star could be stable seems to be around , which is different from mine. I found that we should be very careful with the numerical analysis around this intersection point; otherwise, an order one error could occur. I believe this is the source of the difference (see also the caption of Figure 7). |
| 18 |
References
- Hawking, S.W.; Page, D.N. Thermodynamics of Black Holes in anti-De Sitter Space. Commun. Math. Phys. 1983, 87, 577–588. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W.; Perry, M.J. Path Integrals and the Indefniteness of the Gravitational Action. Nucl. Phys. B 1978, 138, 141–150. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Action Integrals and Partition Functions in Quantum Gravity. Phys. Rev. D 1977, 15, 2752–2756. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge Theory Correlators from Non-Critical String Theory. Phys. Lett. B 1998, 428, 105–114. [Google Scholar] [CrossRef]
- Witten, E. Anti de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Almheiri, A.; Mahajan, R.; Maldacena, J.M.; Zhao, Y. The Page curve of Hawking radiation from semiclassical geometry. J. High Energy Phys. 2020, 3, 149. [Google Scholar] [CrossRef]
- Penington, G.; Shenker, S.H.; Stanford, D.; Yang, Z. Replica wormholes and the black hole interior. J. High Energy Phys. 2022, 3, 205. [Google Scholar] [CrossRef]
- Almheiri, A.; Hartman, T.; Maldacena, J.M.; Shaghoulian, E.; Tajdini, A. Replica Wormholes and the Entropy of Hawking Radiation. J. High Energy Phys. 2020, 5, 013. [Google Scholar] [CrossRef]
- York, J.W., Jr. Black hole thermodynamics and the Euclidean Einstein action. Phys. Rev. D 1986, 33, 2092–2099. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Charged AdS black holes and catastrophic holography. Phys. Rev. D 1999, 60, 064018. [Google Scholar] [CrossRef]
- Hartnoll, S.A.; Herzog, C.P.; Horowitz, G.T. Holographic Superconductors. J. High Energy Phys. 2008, 12, 015. [Google Scholar] [CrossRef]
- Maeda, K.; Koga, J.; Fujii, S. The final fate of instability of Reissner-Nordström-anti-de Sitter black holes by charged complex scalar fields. Phys. Rev. D 2010, 81, 124020. [Google Scholar] [CrossRef]
- Basu, P.; Bhattacharya, J.; Bhattacharyya, S.; Loganayagam, R.; Minwalla, S.; Umesh, V. Small Hairy Black Holes in Global AdS Spacetime. J. High Energy Phys. 2010, 1010, 245. [Google Scholar] [CrossRef]
- Basu, P.; Krishnan, C.; Bala Subramanian, P.N. Phases of Global AdS Black Holes. J. High Energy Phys. 2016, 6, 139. [Google Scholar] [CrossRef]
- Arias, R.; Mas, J.; Serantes, A. Stability of charged global AdS4 spacetimes. J. High Energy Phys. 2016, 9, 024. [Google Scholar] [CrossRef]
- Bjoraker, J.; Hosotani, Y. Stable monopole and dyon solutions in the Einstein-Yang-Mills theory in asymptotically anti-de Sitter Space. Phys. Rev. Lett. 2000, 84, 1853–1856. [Google Scholar] [CrossRef]
- Bjoraker, J.; Hosotani, Y. Monopoles, dyons and black holes in the four-dimensional Einstein-Yang-Mills theory. Phys. Rev. D 2000, 62, 043513. [Google Scholar] [CrossRef]
- Winstanley, E. Existence of stable hairy black holes in su(2) Einstein-Yang-Mills theory with a negative cosmological constant. Class. Quantum Gravity 1999, 16, 1963–1978. [Google Scholar] [CrossRef]
- Mann, R.B.; Radu, E.; Tchrakian, E.H. Nonabelian solutions in AdS4 and d = 11 supergravity. Phys. Rev. D 2006, 74, 064015. [Google Scholar] [CrossRef]
- Kichakova, O.; Kunz, J.; Radu, E.; Shnir, Y. Thermodynamic properties of asymptotically anti-de Sitter black holes in d = 4 Einstein–Yang–Mills theory. Phys. Lett. B 2005, 747, 205–211. [Google Scholar] [CrossRef][Green Version]
- Lugo, A.R.; Moreno, E.F.; Schaposnik, F.A. Monopole Solutions in AdS Space. Phys. Lett. B 2000, 473, 35–42. [Google Scholar] [CrossRef]
- Lugo, A.R.; Schaposnik, F.A. Monopole and Dyon Solutions in AdS space. Phys. Lett. B 1999, 467, 43–53. [Google Scholar] [CrossRef]
- Lugo, A.R.; Moreno, E.F.; Schaposnik, F.A. Holographic Phase Transition from Dyons in an AdS Black Hole Background. J. High Energy Phys. 2010, 3, 013. [Google Scholar] [CrossRef]
- Lugo, A.R.; Moreno, E.F.; Schaposnik, F.A. Holography and AdS4 self-gravitating dyons. J. High Energy Phys. 2010, 11, 081. [Google Scholar] [CrossRef]
- Giordano, G.L.; Lugo, A.R. Holographic phase transitions from higgsed, non abelian charged black holes. J. High Energy Phys. 2015, 7, 172. [Google Scholar] [CrossRef]
- Miyashita, S.; Maeda, K. AdS Monopole Black Hole and Phase Transition. Phys. Rev. D 2016, 94, 124037. [Google Scholar] [CrossRef]
- Braden, H.W.; Brown, J.D.; Whiting, B.F.; York, J.W., Jr. Charged black hole in a grand canonical ensemble. Phys. Rev. D 1990, 42, 3376–3385. [Google Scholar] [CrossRef]
- Basu, P.; Krishnan, C.; Bala Subramanian, P.N. Hairy Black Holes in a Box. J. High Energy Phys. 2016, 11, 041. [Google Scholar] [CrossRef]
- Miyashita, S. Thermodynamics of the Einstein-Maxwell system. J. High Energy Phys. 2024, 4, 083. [Google Scholar] [CrossRef]
- Miyashita, S. Thermodynamics of the 3-dimensional Einstein-Maxwell system. J. High Energy Phys. 2024, 6, 134. [Google Scholar] [CrossRef]
- Miyashita, S. Gravitational and gravitoscalar thermodynamics. J. High Energy Phys. 2021, 9, 121. [Google Scholar] [CrossRef]
- Krishnan, C.; Shekhar, R.; Bala Subramanian, P.N. A hairy box in three dimensions. Nucl. Phys. B 2020, 958, 115115. [Google Scholar] [CrossRef]
- York, J.W., Jr. Role of conformal three geometry in the dynamics of gravitation. Phys. Rev. Lett. 1972, 28, 1082–1085. [Google Scholar] [CrossRef]
- Brown, J.D.; York, J.W., Jr. Quasilocal energy and conserved charges derived from the gravitational action. Phys. Rev. D 1993, 47, 1407. [Google Scholar] [CrossRef] [PubMed]
- Draper, P.; Farkas, S. Euclidean de Sitter black holes and microcanonical equilibrium. Phys. Rev. D 2022, 105, 126021. [Google Scholar] [CrossRef]
- Banihashemi, B.; Jacobson, T. Thermodynamic ensembles with cosmological horizons. J. High Energy Phys. 2022, 7, 042. [Google Scholar] [CrossRef]
- Ida, D. No black hole theorem in three-dimensional gravity. Rhys. Rev. Lett. 2000, 85, 3758–3760. [Google Scholar] [CrossRef]
- Gubser, S.S. Breaking an Abelian gauge symmetry near a black hole horizon. Phys. Rev. D 2008, 78, 065034. [Google Scholar] [CrossRef]
- Hartnoll, S.A.; Herzog, C.P.; Horowitz, G.T. Building a Holographic Superconductor. Phys. Rev. Lett. 2008, 101, 031601. [Google Scholar] [CrossRef]
- Brown, A.R.; Gharibyan, H.; Penington, G.; Susskind, L. The Python’s Lunch: Geometric obstructions to decoding Hawking radiation. J. High Energy Phys. 2020, 8, 121. [Google Scholar] [CrossRef]
- Nishioka, T.; Ryu, S.; Takayanagi, T. Holographic Superconductor/Insulator Transition at Zero Temperature. J. High Energy Phys. 2010, 3, 131. [Google Scholar] [CrossRef]
- Horowitz, G.T.; Way, B. Complete phase diagrams for a holographic superconductor/insulator system. J. High Energy Phys. 2010, 11, 011. [Google Scholar] [CrossRef]
- Horowitz, G.T.; Roberts, M.M. Zero Temperature Limit of Holographic Superconductors. J. High Energy Phys. 2009, 11, 015. [Google Scholar] [CrossRef]




| Number of Boson Star | Number of Boson Star-PL | Stable Saddle | |
|---|---|---|---|
| 1 | 1 | boson star-PL | |
| 0 | 1 | boson star-PL | |
| 2 | 0 | boson star | |
| 1 | 0 | boson star | |
| 1 | 1 | None | |
| 2 | 0 | None | |
| V | 0 | 0 | None |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miyashita, S. Many Phases in a Hairy Box in Three Dimensions. Universe 2025, 11, 208. https://doi.org/10.3390/universe11070208
Miyashita S. Many Phases in a Hairy Box in Three Dimensions. Universe. 2025; 11(7):208. https://doi.org/10.3390/universe11070208
Chicago/Turabian StyleMiyashita, Shoichiro. 2025. "Many Phases in a Hairy Box in Three Dimensions" Universe 11, no. 7: 208. https://doi.org/10.3390/universe11070208
APA StyleMiyashita, S. (2025). Many Phases in a Hairy Box in Three Dimensions. Universe, 11(7), 208. https://doi.org/10.3390/universe11070208







