Line-of-Sight Mass Estimator and the Masses of the Milky Way and Andromeda Galaxy
Abstract
1. Introduction
2. Projection Mass Method
- Biased, meaning that the average of estimates for the same group is not necessarily equal to the true mass for a finite number of particles, N;
- Inefficient with a large variance;
- Inconsistent in some cases, meaning that does not converge to the true mass as .
3. Line-of-Sight Mass Method
3.1. Milky Way Case
3.2. Nearby Group Case
3.3. Additional Notes
4. Comparison with Cosmological Simulations
5. Application to the Local Group of Galaxies
5.1. Milky Way

5.2. Andromeda Galaxy
5.3. Influence of the Distance Measurement Errors
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. List of Satellites of the Milky Way
| Name | J2000 | Method | D | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| mag | kpc | km s−1 | ||||||||
| Tucana IV | 000255.2−605100 | 18.41 | [91] | TRGB | 48.1 | 15.9 | +1.8 −1.7 | [25] | ||
| SMC | 005238.0−724801 | 18.99 | [25] | Cep | 62.8 | 158 | [92] | |||
| Sculptor | 010009.4−334233 | 19.67 | [25] | TRGB | 85.9 | 111.4 | [93] | |||
| Cetus II | 011752.8−172512 | 17.10 | [94] | CMD | 26.3 | |||||
| DELVE 2 | 015505.3−681511 | 19.26 | [95] | HB | 71.1 | |||||
| Cetus III | 020519.4−041612 | 22.00 | +0.20 −0.10 | [25] | HB | 251 | +24 −12 | |||
| Triangulum II | 021317.4+361042 | 17.27 | [96] | CMD | 28.4 | −381.70 | [25] | |||
| Segue 2 | 021916.0+201031 | 17.70 | [25] | TRGB | 34.7 | −40.20 | [26] | |||
| Eridanus III | 022245.5−521701 | 19.70 | [25] | HB | 87.1 | |||||
| DES J0225+0304 | 022542.4+030410 | 16.88 | +0.06 −0.05 | [97] | CMD | 23.8 | +0.7 −0.6 | |||
| Hydrus I | 022933.4−784128 | 17.20 | [25] | TRGB | 27.5 | 80.4 | [25] | |||
| Fornax | 023954.7−343133 | 20.84 | [25] | TRGB | 147 | 55.2 | [93] | |||
| Horologium I | 025531.7−540708 | 19.50 | [25] | HB | 79.4 | 112.8 | +2.5 −2.6 | [25] | ||
| Horologium II | 031632.1−500105 | 19.46 | [25] | HB | 78.0 | 168.7 | +12.9 −12.6 | [25] | ||
| Reticulum II | 033542.1−540257 | 17.40 | [25] | HB | 30.2 | 64.7 | +1.3 −0.8 | [25] | ||
| Reticulum III | 034526.4−602700 | 19.81 | [25] | CMD | 92 | 274.2 | +7.5 −7.4 | [25] | ||
| Pictor I | 044347.4−501659 | 20.30 | [25] | HB | 115 | |||||
| LMC | 052334.6−694522 | 18.50 | [98] | Cep | 50.1 | 278 | [99] | |||
| Columba I | 053125.7−275727 | 21.31 | [96] | BHB | 183 | 153.7 | +5 −4.8 | [25] | ||
| Carina | 064136.7−505758 | 20.11 | [25] | TRGB | 105 | 222.9 | [25] | |||
| Pictor II | 064443.2−595360 | 18.30 | +0.12 −0.15 | [25] | HB | 45.7 | +2.6 −3.3 | |||
| Carina II | 073625.6−560003 | 17.79 | [25] | HB | 36.1 | 477.2 | [25] | |||
| Carina III | 073831.2−560601 | 17.22 | [25] | HB | 27.8 | 284.6 | +3.4 −3.1 | [25] | ||
| Ursa Major II | 085130.0+630748 | 17.50 | [25] | TRGB | 31.6 | −116.5 | [25] | |||
| HYDRA 1 | 085536.0+033600 | 15.52 | [100] | MS | 12.7 | 89 | [100] | |||
| Antlia II | 093532.8−364602 | 20.6 | [101] | BHB | 132 | 288.8 | [102] | |||
| Segue 1 | 100703.2+160425 | 16.8 | [25] | CMD | 22.9 | 208.5 | [25] | |||
| Leo I | 100826.9+121829 | 22.02 | [25] | TRGB | 254 | 282.5 | [25] | |||
| Sextans dSph | 101303.0−013652 | 19.67 | [25] | TRGB | 85.9 | 224.2 | [25] | |||
| Sextans II | 102544.9−003752 | 20.50 | [103] | HB | 126 | |||||
| Ursa Major I | 103448.8+515606 | 19.93 | [25] | TRGB | 97 | −55.3 | [25] | |||
| Willman 1 | 104921.0+510260 | 17.90 | [25] | CMD | 38.0 | −12.8 | [26] | |||
| Leo II | 111329.2+220917 | 21.84 | [25] | TRGB | 233 | 78 | [25] | |||
| Leo V | 113109.6+021312 | 21.46 | [25] | TRGB | 196 | 170.9 | +2.1 −1.9 | [25] | ||
| Leo IV | 113257.0+003160 | 20.94 | [25] | HB | 154 | 132.3 | [25] | |||
| Crater | 113615.8−105240 | 20.81 | [104] | HB | 145 | 149.3 | [105] | |||
| Crater II | 114914.4−182447 | 20.35 | [25] | TRGB | 118 | 89.3 | [102] | |||
| Virgo I | 120009.6+004048 | 19.80 | [25] | HB | 91 | |||||
| Hydra II | 122142.1−315907 | 20.64 | [25] | TRGB | 134 | 303.1 | [25] | |||
| Coma Berenices | 122658.4+235442 | 18.13 | [25] | HB | 42.3 | 98.1 | [25] | |||
| Centaurus I | 123820.4−405407 | 20.33 | [106] | HB | 116 | |||||
| Canes Venatici II | 125710.0+341915 | 21.02 | [25] | HB | 160 | −129 | [25] | |||
| Canes Venatici I | 132803.5+333321 | 21.69 | [25] | TRGB | 218 | 30.9 | [107] | |||
| Bootes III | 135712.0+264800 | 18.35 | [108] | HB | 46.8 | 197.5 | [23] | |||
| Bootes II | 135808.0+125054 | 18.10 | [25] | TRGB | 41.7 | −117 | [25] | |||
| Bootes I | 140005.0+143015 | 19.11 | [25] | HB | 66.4 | 101.8 | [26] | |||
| Ursa Minor | 150911.3+671252 | 19.40 | [25] | TRGB | 75.9 | −246.9 | [25] | |||
| Bootes IV | 153445.4+434334 | 21.60 | [25] | HB | 209 | |||||
| Draco II | 155247.6+643355 | 16.67 | [25] | TRGB | 21.6 | 342.5 | +1.1 −1.2 | [25] | ||
| DELVE 1 | 163054.0+005819 | 16.39 | [106] | HB | 19.0 | |||||
| Hercules | 163103.6+124724 | 20.84 | [25] | TRGB | 147 | 46.4 | [109] | |||
| Draco | 172001.4+575434 | 19.40 | [25] | TRGB | 76 | −291 | [25] | |||
| Milky Way | 174540.0−290028 | 14.55 | [110] | Direct | 8.1 | −9.5 | [34] | |||
| Sagittarius dSph | 185503.1−302842 | 17.10 | [111] | TRGB | 26.3 | 140 | [112] | |||
| Sagittarius II | 195240.5−220405 | 19.32 | +0.03 −0.02 | [25] | CMD | 73.1 | +1.0 −0.7 | −177.2 | +0.5 −0.6 | [113] |
| Indus II | 203852.8−460936 | 21.65 | [25] | CMD | 214 | |||||
| Indus I | 210850.0−510949 | 20.00 | [25] | HB | 100 | |||||
| Segue 3 | 212131.0+190702 | 16.16 | [114] | CMD | 17.1 | −167.1 | [114] | |||
| Grus II | 220404.8−462624 | 18.62 | [25] | CMD | 53 | −110 | [25] | |||
| Pegasus III | 222422.6+052512 | 21.56 | [25] | CMD | 205 | −222.9 | [25] | |||
| Aquarius II | 223355.5−091939 | 20.16 | [25] | TRGB | 108 | −71.1 | [25] | |||
| Tucana II | 225155.1−583408 | 18.80 | [25] | HB | 58 | −129.1 | [25] | |||
| Grus I | 225642.4−500948 | 20.40 | [25] | TRGB | 120 | −140.5 | +2.4 −0.6 | [25] | ||
| Pisces II | 225831.0+055709 | 21.31 | [25] | TRGB | 183 | −226.5 | [25] | |||
| Tucana V | 233724.0−631612 | 18.71 | [25] | CMD | 55 | −36.2 | +2.5 −2.2 | [25] | ||
| Phoenix II | 233959.4−542422 | 19.60 | [25] | HB | 83 | 32.4 | +3.7 −3.8 | [115] | ||
| Tucana III | 235636.0−593600 | 17.01 | [25] | TRGB | 25.2 | −102.3 | [26] | |||
Appendix B. List of Satellites of the Andromeda Galaxy
| Name | Alt Name | J2000 | Method | D | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| mag | kpc | km s−1 | |||||||||
| PAndAS-05 | 000024.1+435535 | [116] | |||||||||
| And XVIII | 000214.5+450520 | 25.43 | +0.05 −0.03 | [117] | HB | 1219 | +28 −17 | [118] | |||
| PAndAS-04 | 000442.9+472142 | [116] | |||||||||
| And XX | 000730.7+350756 | 24.35 | [27] | RR Lyr | 741 | +3.0 −3.4 | [118] | ||||
| IC 10 | 002024.5+591730 | 24.50 | [119] | TRGB | 794 | [120] | |||||
| And XXVI | 002345.6+475558 | 24.48 | +0.06 −0.07 | [27] | RR Lyr | 787 | +22 −26 | +4.0 −3.7 | [118] | ||
| And XXV | 003008.9+465107 | 24.38 | +0.07 −0.06 | [27] | RR Lyr | 752 | +25 −21 | +1.0 −0.9 | [118] | ||
| NGC 147 | 003350.8+483028 | 24.33 | [27] | RR Lyr | 735 | [118] | |||||
| And III | 003533.8+362952 | 24.29 | [27] | RR Lyr | 721 | [118] | |||||
| Cas III | And XXXII | 003559.4+513335 | 24.52 | [27] | RR Lyr | 802 | [121] | ||||
| And XXX | 003634.9+493848 | 23.74 | [27] | RR Lyr | 560 | +5.8 −6.7 | [118] | ||||
| And XVII | 003707.0+441920 | 24.40 | [27] | RR Lyr | 759 | +1.5 −1.6 | [118] | ||||
| And XXVII | 003727.1+452313 | 24.59 | [122] | HB | 828 | +5.4 −4.9 | [118] | ||||
| NGC 185 | 003858.0+482010 | 24.06 | [27] | RR Lyr | 649 | [118] | |||||
| NGC 205 | 004022.5+414111 | 24.61 | [27] | RR Lyr | 836 | [118] | |||||
| M 32 | 004242.1+405259 | 24.44 | [27] | RR Lyr | 773 | [118] | |||||
| M 31 | 004244.5+411609 | 24.45 | [27] | RR Lyr | 776 | [118] | |||||
| And I | 004540.0+380214 | 24.45 | [27] | RR Lyr | 776 | [118] | |||||
| And XI | 004620.0+334805 | 24.38 | [27] | RR Lyr | 752 | +2.9 −2.8 | [118] | ||||
| And XII | 004727.0+342229 | 24.28 | +0.08 −0.07 | [27] | RR Lyr | 718 | +27 −24 | [118] | |||
| Bol 520 | 005042.4+325559 | 24.00 | [123] | TRGB | 631 | [124] | |||||
| And XIV | 005135.0+294149 | 24.44 | [27] | RR Lyr | 773 | [118] | |||||
| And XIII | 005151.0+330016 | 24.57 | [27] | RR Lyr | 820 | [118] | |||||
| And IX | 005252.8+431200 | 24.60 | [27] | RR Lyr | 832 | [118] | |||||
| PAndAS-48 | 005928.2+312910 | 24.57 | [125] | HB | 820 | [116] | |||||
| And XVI | 005929.8+322236 | 23.57 | [27] | RR Lyr | 518 | [118] | |||||
| PAndAS-50 | 010150.6+481819 | [116] | |||||||||
| LGS 3 | Pisces I | 010355.0+215306 | 23.91 | [27] | RR Lyr | 605 | [118] | ||||
| And X | 010633.7+444816 | 24.00 | [27] | RR Lyr | 631 | [118] | |||||
| And V | 011017.1+473741 | 24.58 | [27] | RR Lyr | 824 | [118] | |||||
| And XV | 011418.7+380703 | 24.37 | [27] | RR Lyr | 748 | [118] | |||||
| And II | 011629.8+332509 | 24.12 | [27] | RR Lyr | 667 | +16 −16 | [118] | ||||
| And XXIV | 011830.0+462258 | 23.92 | [27] | RR Lyr | 608 | +5.3 −5.4 | [118] | ||||
| And XXIX | 011830.0+304520 | 24.26 | [27] | RR Lyr | 711 | [126] | |||||
| Tri III | Pisces VII | 012141.3+262332 | 24.81 | +0.15 −0.13 | [125] | TRGB | 916 | +65 −53 | [127] | ||
| PAndAS-56 | 012303.5+415511 | [116] | |||||||||
| And XXII | 012740.0+280525 | 24.39 | [27] | RR Lyr | 755 | +2.1 −2.2 | [118] | ||||
| PAndAS-57 | 012747.5+404047 | [116] | |||||||||
| PAndAS-58 | 012902.1+404708 | [116] | |||||||||
| And XXIII | 012921.8+384308 | 24.36 | [27] | RR Lyr | 745 | [118] | |||||
| M 33 | 013350.8+303937 | 24.67 | [27] | RR Lyr | 859 | [118] | |||||
| Per I | And XXXIII | 030123.6+405918 | 24.24 | [27] | RR Lyr | 705 | [121] | ||||
| And XXVIII | 223241.2+311358 | 24.36 | [27] | RR Lyr | 745 | [126] | |||||
| Lac I | And XXXI | 225816.3+411728 | 24.36 | [27] | RR Lyr | 745 | [121] | ||||
| Cas dSph | And VII | 232631.8+504032 | 24.40 | [27] | RR Lyr | 759 | [118] | ||||
| Pegasus | Peg DIG | 232827.6+144434 | 24.74 | [27] | RR Lyr | 887 | [118] | ||||
| Peg dSph | And VI | 235146.9+243557 | 24.23 | [27] | RR Lyr | 702 | [118] | ||||
| And XXI | 235447.7+422815 | 24.44 | +0.06 −0.07 | [27] | RR Lyr | 773 | +22 −25 | [118] | |||
| PAndAS-01 | 235712.0+433308 | [116] | |||||||||
| PAndAS-02 | 235755.6+414649 | [116] | |||||||||
| And XIX | 235855.6+350237 | 24.55 | +0.09 −0.08 | [27] | RR Lyr | 813 | +34 −31 | +1.2 −1.3 | [118] | ||
Appendix C. List of the Milky Way Mass Estimates
- Escape Velocities. This method analyzes the tail of the velocity distribution of the halo stars (so-called high-velocity stars) to estimate the escape speed from the Galaxy.
- Rotation curve method bases on the measurement of the circular velocities of stars and gas. Inner regions use HI/CO gas kinematics, while outer regions rely on tracers like red giants and masers, combined with Gaia proper motions.
- Stellar streams. Tidal streams, such as GD-1 and Sagittarius, are sensitive probes of the Galactic potential. Orbit-fitting and N-body simulations model their dynamics constraining mass at intermediate radii –100 kpc. Challenges include separating the host potential’s effects from subhalo perturbations.
- Spherical Jeans Equation connects the radial velocity dispersion, , the radial density density profile, , and the velocity anisotropy, , of the mass tracers with the underlying gravitational potential. It assumes that a system is a spherically symmetric and in a steady-state.
- Distribution Function approach models the gravitational potential by reconstructing the phase–space distribution of tracers (halo stars, globular clusters) using integrals of motion or action.
- Kinematics of Satellites. The motions of satellite galaxies and globular clusters probe the outer halo mass. Methods include timing arguments (for bound systems like Leo I) and tracer mass estimators, often compared with cosmological simulations.
| Authors | kpc | Ref. | ||
|---|---|---|---|---|
| Escape Velocities | ||||
| Prudil et al. (2022) | 8.3 | +2.9 −1.6 | 20 | [42] |
| Roche et al. (2024) | 6.4 | +1.5 −1.4 | 11 | [43] |
| Rotation Curve | ||||
| McMillan (2011) | 12.6 | 8 | [44] | |
| Bovy et al. (2012) | 14 | [45] | ||
| Huang et al. (2016) | 8.5 | +0.7 −0.8 | 25 | [46] |
| Eilers et al. (2019) | 7.25 | 25 | [47] | |
| Cautun et al. (2020) | 10.8 | +2.0 −1.4 | 20 | [48] |
| Ablimit et al. (2020) | 8.22 | 19 | [49] | |
| Zhou et al. (2023) | 8.05 | 30 | [6] | |
| Sylos Labini et al. (2023) | 6.5 | 28 | [50] | |
| Klačka et al. (2024) | 13.4 | 25 | [51] | |
| Streams | ||||
| Craig et al. (2022) | 15.0 | [52] | ||
| Spherical Jeans Equation | ||||
| Gnedin et al. (2010) | 16.0 | 80 | [53] | |
| Kafle et al. (2012) | 9.0 | +4.0 −3.0 | 60 | [54] |
| Kafle et al. (2014) | 8.0 | +3.1 −1.6 | 160 | [55] |
| Zhai et al. (2018) | 10.8 | +1.7 −1.4 | 120 | [56] |
| Bird et al. (2022) | – | 70 | [57] | |
| Distribution Function | ||||
| Eadie et al. (2015) | 13.7 | +1.4 −1.0 | 261 | [58] |
| Eadie and Harris (2016) | 9.02 | +1.7 −3.3 | 200 | [59] |
| Sohn et al. (2018) | 20.5 | +9.7 −7.9 | 100 | [60] |
| Watkins et al. (2019) | 15.4 | +7.5 −4.4 | 40 | [61] |
| Vasiliev (2019) | 12 | +15 −5 | 50 | [8] |
| Posti and Helmi (2019) | 13 | 20 | [62] | |
| Li et al. (2020) | 12.3 | +2.1 −1.8 | 200 | [63] |
| Deason et al. (2021) | 10.1 | 100 | [64] | |
| Shen et al. (2022) | 10.8 | +1.2 −1.1 | 145 | [65] |
| Kinematics of Satellites | ||||
| Watkins et al. (2010) | 14.0 | 300 | [3] | |
| Busha et al. (2011) | 12.0 | +7.0 −4.0 | 300 | [66] |
| González et al. (2013) | 11.5 | +4.8 −3.4 | 200 | [67] |
| Boylan-Kolchin et al. (2013) | 16 | +8 −6 | 261 | [38] |
| Cautun et al. (2014) | 7.8 | +5.7 −3.3 | 200 | [68] |
| Barber et al. (2014) | 11.0 | +4.5 −2.9 | 200 | [69] |
| Patel et al. (2017) | 8.3 | +7.7 −5.5 | 200 | [70] |
| Patel et al. (2018) | 6.8 | +2.3 −2.6 | 200 | [71] |
| Fritz et al. (2020) | 15.1 | +4.5 −4.0 | 300 | [72] |
| RodriguezWimberly et al. (2022) | –12 | 300 | [73] | |
| Kravtsov andWinney (2024) | 9.96 | 200 | [9] | |
| this work | 7.9 | 236 | ||
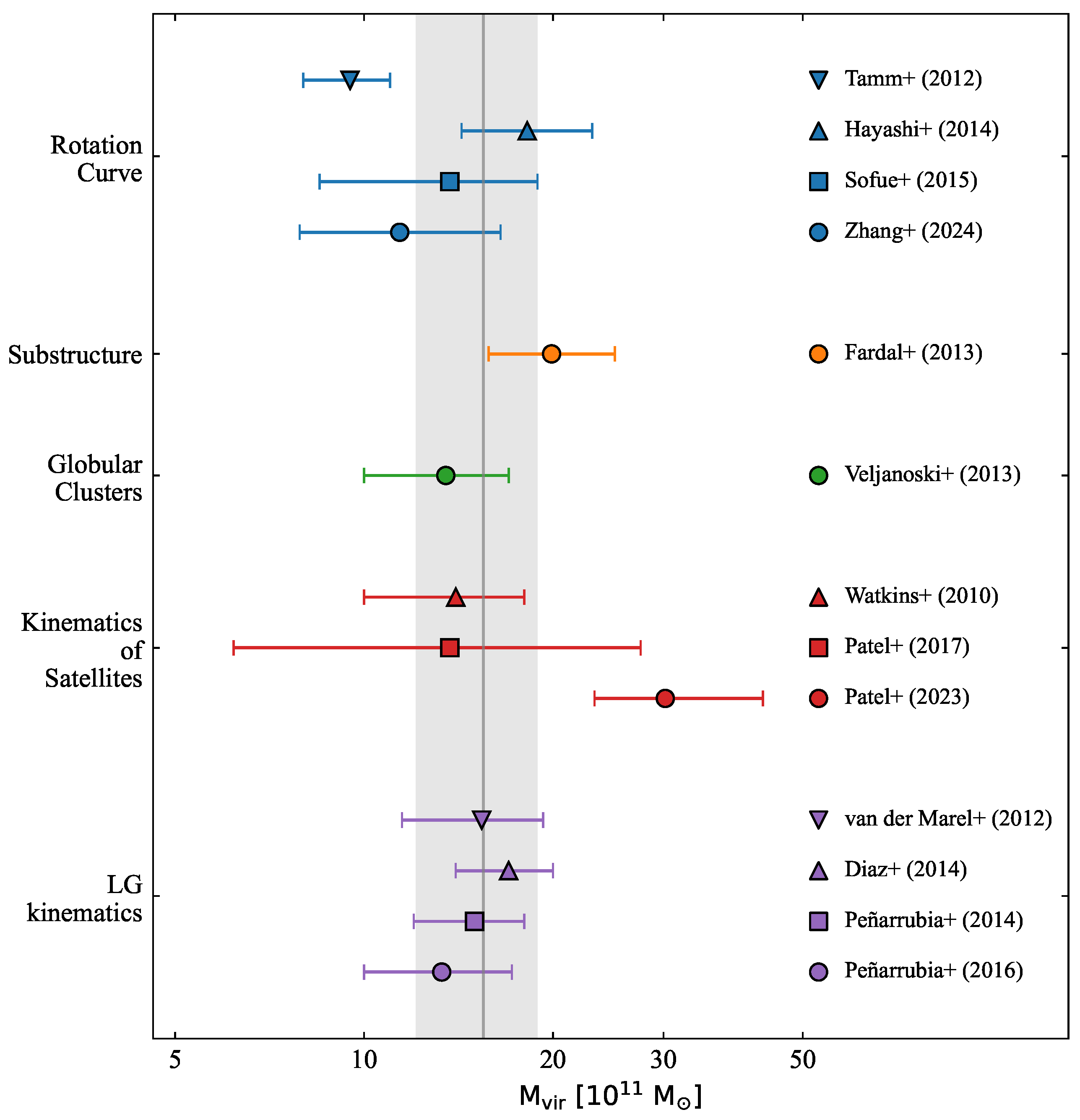
Appendix D. List of the M 31 Mass Estimates
| Authors | kpc | Ref. | ||
|---|---|---|---|---|
| Rotation Curve | ||||
| Tamm et al. (2012) | 9.5 | 25 | [81] | |
| Hayashi and Chiba (2014) | 18.2 | +4.9 −3.9 | 30 | [82] |
| Sofue (2015) | 13.7 | 31 | [83] | |
| Zhang et al. (2024) | 11.4 | +5.1 −3.5 | 125 | [84] |
| Substructure | ||||
| Fardal et al. (2013) | 19.9 | +5.2 −4.1 | [85] | |
| Globular Clusters | ||||
| Veljanoski et al. (2013) | 13.5 | 130 | [86] | |
| Kinematics of Satellites | ||||
| Watkins et al. (2010) | 14 | 300 | [3] | |
| Patel et al. (2017) | 13.7 | +13.9 −7.5 | 300 | [87] |
| Patel and Mandel (2023) | 30.2 | +13.0 −6.9 | 300 | [76] |
| this work | 15.5 | 292 | ||
| Local Group Kinematics | ||||
| van der Marel et al. (2012) | 15.4 | [88] | ||
| Diaz et al. (2014) | 17 | [89] | ||
| Peñarrubia et al. (2014) | 15 | [22] | ||
| Peñarrubia et al. (2016) | 13.3 | +3.9 −3.3 | [90] | |
- Rotation Curve measures circular velocities of tracers (stars, gas) to determine the mass distribution. In the case of M 31, HI observations extend to kpc, revealing flat rotation curves that indicate dark matter dominance. The virial mass within ∼200 kpc is based on a model of the M 31 gravitational potential.
- Subsctructure Tidal streams (e.g., the Giant Stream) constrain halo mass and shape using N-body simulations. Progenitor properties and merger history must be taken into accounted.
- Globular Clusters (GC) trace mass at intermediate radii of 20–200 kpc. The advantage is the large number of known GC. However, a major challenge lies in distinguishing between in situ and recently accreted clusters, as well as accounting for the tidal effects.
- Kinematics of Satellites uses the velocities and distances of the dwarf satellites to infer gravitational mass at 100–300 kpc. Challenges include small sample sizes (<30 satellites) and potential disequilibrium due to ongoing mergers.
- Local Group Kinematics The M 31-MW motion provides a total mass estimate using the timing argument. Modern approaches include proper motions and perturbations from the LMC, but depend on the assumed mass ratios.
| 1 | The energy, , and the angular momentum, , define the orbit of a satellite within a spherically symmetric potential, while the delta functions represent the phase–space distribution under the condition that the energy and angular momentum are constrained to these specific values. |
| 2 | Tri III has already been excluded in the previous step due to insufficient distance measurement accuracy. |
| 3 | http://leda.univ-lyon1.fr (accessed on 26 April 2025). |
References
- Bahcall, J.N.; Tremaine, S. Methods for determining the masses of spherical systems. I. Test particles around a point mass. Astrophys. J. 1981, 244, 805–819. [Google Scholar] [CrossRef]
- Heisler, J.; Tremaine, S.; Bahcall, J.N. Estimating the masses of galaxy groups: Alternatives to the virial theorem. Astrophys. J. 1985, 298, 8–17. [Google Scholar] [CrossRef]
- Watkins, L.L.; Evans, N.W.; An, J.H. The masses of the Milky Way and Andromeda galaxies. Mon. Not. R. Astron. Soc. 2010, 406, 264–278. [Google Scholar] [CrossRef]
- Anand, G.S.; Rizzi, L.; Tully, R.B.; Shaya, E.J.; Karachentsev, I.D.; Makarov, D.I.; Makarova, L.; Wu, P.F.; Dolphin, A.E.; Kourkchi, E. The Extragalactic Distance Database: The Color-Magnitude Diagrams/Tip of the Red Giant Branch Distance Catalog. Astron. J. 2021, 162, 80. [Google Scholar] [CrossRef]
- Tully, R.B.; Rizzi, L.; Shaya, E.J.; Courtois, H.M.; Makarov, D.I.; Jacobs, B.A. The Extragalactic Distance Database. Astron. J. 2009, 138, 323–331. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.; Huang, Y.; Zhang, H. The Circular Velocity Curve of the Milky Way from 5 to 25 kpc Using Luminous Red Giant Branch Stars. Astrophys. J. 2023, 946, 73. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The assembly of galaxies in a hierarchically clustering universe. Mon. Not. R. Astron. Soc. 1995, 275, 56–66. [Google Scholar] [CrossRef]
- Vasiliev, E. Proper motions and dynamics of the Milky Way globular cluster system from Gaia DR2. Mon. Not. R. Astron. Soc. 2019, 484, 2832–2850. [Google Scholar] [CrossRef]
- Kravtsov, A.; Winney, S. Effect of the Large Magellanic Cloud on the kinematics of Milky Way satellites and virial mass estimate. Open J. Astrophys. 2024, 7, 50. [Google Scholar] [CrossRef]
- Karachentsev, I.D.; Kashibadze, O.G.; Makarov, D.I.; Tully, R.B. The Hubble flow around the Local Group. Mon. Not. R. Astron. Soc. 2009, 393, 1265–1274. [Google Scholar] [CrossRef]
- Libeskind, N.I.; Carlesi, E.; Grand, R.J.J.; Khalatyan, A.; Knebe, A.; Pakmor, R.; Pilipenko, S.; Pawlowski, M.S.; Sparre, M.; Tempel, E.; et al. The HESTIA project: Simulations of the Local Group. Mon. Not. R. Astron. Soc. 2020, 498, 2968–2983. [Google Scholar] [CrossRef]
- Weinberger, R.; Springel, V.; Pakmor, R. The AREPO Public Code Release. Astrophys. J. 2020, 248, 32. [Google Scholar] [CrossRef]
- Tully, R.B.; Courtois, H.M.; Dolphin, A.E.; Fisher, J.R.; Héraudeau, P.; Jacobs, B.A.; Karachentsev, I.D.; Makarov, D.; Makarova, L.; Mitronova, S.; et al. Cosmicflows-2: The Data. Astron. J. 2013, 146, 86. [Google Scholar] [CrossRef]
- Doumler, T.; Hoffman, Y.; Courtois, H.; Gottlöber, S. Reconstructing cosmological initial conditions from galaxy peculiar velocities—I. Reverse Zeldovich Approximation. Mon. Not. R. Astron. Soc. 2013, 430, 888–901. [Google Scholar] [CrossRef]
- Grand, R.J.J.; Gómez, F.A.; Marinacci, F.; Pakmor, R.; Springel, V.; Campbell, D.J.R.; Frenk, C.S.; Jenkins, A.; White, S.D.M. The Auriga Project: The properties and formation mechanisms of disc galaxies across cosmic time. Mon. Not. R. Astron. Soc. 2017, 467, 179–207. [Google Scholar] [CrossRef]
- McCall, M.L. A Council of Giants. Mon. Not. R. Astron. Soc. 2014, 440, 405–426. [Google Scholar] [CrossRef]
- Smith, S.E.T.; Cerny, W.; Hayes, C.R.; Sestito, F.; Jensen, J.; McConnachie, A.W.; Geha, M.; Navarro, J.F.; Li, T.S.; Cuillandre, J.C.; et al. The Discovery of the Faintest Known Milky Way Satellite Using UNIONS. Astrophys. J. 2024, 961, 92. [Google Scholar] [CrossRef]
- Wang, W.; Han, J.; Cautun, M.; Li, Z.; Ishigaki, M.N. The mass of our Milky Way. Sci. China Phys. Mech. Astron. 2020, 63, 109801. [Google Scholar] [CrossRef]
- Bobylev, V.V.; Baykova, A.T. Modern Estimates of the Mass of the Milky Way. Astron. Rep. 2023, 67, 812–823. [Google Scholar] [CrossRef]
- Bhattacharya, S. Weighing Andromeda: Mass estimates of the M∼31 galaxy. arXiv 2023, arXiv:2305.03293. [Google Scholar] [CrossRef]
- Carlesi, E.; Hoffman, Y.; Libeskind, N.I. Estimation of the masses in the local group by gradient boosted decision trees. Mon. Not. R. Astron. Soc. 2022, 513, 2385–2393. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Ma, Y.Z.; Walker, M.G.; McConnachie, A. A dynamical model of the local cosmic expansion. Mon. Not. R. Astron. Soc. 2014, 443, 2204–2222. [Google Scholar] [CrossRef]
- Kaisina, E.I.; Makarov, D.I.; Karachentsev, I.D.; Kaisin, S.S. Observational database for studies of nearby universe. Astrophys. Bull. 2012, 67, 115–122. [Google Scholar] [CrossRef]
- Kashibadze, O.G.; Karachentsev, I.D. Cosmic flow around local massive galaxies. Astron. Astrophys. 2018, 609, A11. [Google Scholar] [CrossRef]
- McConnachie, A.W.; Venn, K.A. Revised and New Proper Motions for Confirmed and Candidate Milky Way Dwarf Galaxies. Astron. J. 2020, 160, 124. [Google Scholar] [CrossRef]
- Pace, A.B.; Erkal, D.; Li, T.S. Proper Motions, Orbits, and Tidal Influences of Milky Way Dwarf Spheroidal Galaxies. Astrophys. J. 2022, 940, 136. [Google Scholar] [CrossRef]
- Savino, A.; Weisz, D.R.; Skillman, E.D.; Dolphin, A.; Kallivayalil, N.; Wetzel, A.; Anderson, J.; Besla, G.; Boylan-Kolchin, M.; Bullock, J.S.; et al. The Hubble Space Telescope Survey of M31 Satellite Galaxies. I. RR Lyrae-based Distances and Refined 3D Geometric Structure. Astrophys. J. 2022, 938, 101. [Google Scholar] [CrossRef]
- Drlica-Wagner, A.; Bechtol, K.; Mau, S.; McNanna, M.; Nadler, E.O.; Pace, A.B.; Li, T.S.; Pieres, A.; Rozo, E.; Simon, J.D.; et al. Milky Way Satellite Census. I. The Observational Selection Function for Milky Way Satellites in DES Y3 and Pan-STARRS DR1. Astrophys. J. 2020, 893, 47. [Google Scholar] [CrossRef]
- Makarov, D.; Prugniel, P.; Terekhova, N.; Courtois, H.; Vauglin, I. HyperLEDA. III. The catalogue of extragalactic distances. Astron. Astrophys. 2014, 570, A13. [Google Scholar] [CrossRef]
- Pawlowski, M.S. Phase-Space Correlations among Systems of Satellite Galaxies. Galaxies 2021, 9, 66. [Google Scholar] [CrossRef]
- Conn, A.R.; Lewis, G.F.; Ibata, R.A.; Parker, Q.A.; Zucker, D.B.; McConnachie, A.W.; Martin, N.F.; Valls-Gabaud, D.; Tanvir, N.; Irwin, M.J.; et al. The Three-dimensional Structure of the M31 Satellite System; Strong Evidence for an Inhomogeneous Distribution of Satellites. Astrophys. J. 2013, 766, 120. [Google Scholar] [CrossRef]
- Gaia Collaboration; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Bailer-Jones, C.A.L.; Biermann, M.; Evans, D.W.; Eyer, L.; et al. Gaia Data Release 2. Summary of the contents and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar] [CrossRef]
- Makarov, D.; Khoperskov, S.; Makarov, D.; Makarova, L.; Libeskind, N.; Salomon, J.B. The LMC impact on the kinematics of the Milky Way satellites: Clues from the running solar apex. Mon. Not. R. Astron. Soc. 2023, 521, 3540–3552. [Google Scholar] [CrossRef]
- Akhmetov, V.S.; Bucciarelli, B.; Crosta, M.; Lattanzi, M.G.; Spagna, A.; Re Fiorentin, P.; Bannikova, E.Y. A new kinematic model of the Galaxy: Analysis of the stellar velocity field from Gaia Data Release 3. Mon. Not. R. Astron. Soc. 2024, 530, 710–729. [Google Scholar] [CrossRef]
- Reid, M.J.; Brunthaler, A. The Proper Motion of Sagittarius A*. III. The Case for a Supermassive Black Hole. Astrophys. J. 2020, 892, 39. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Clénet, Y.; Davies, R.; de Zeeuw, P.T.; et al. Improved GRAVITY astrometric accuracy from modeling optical aberrations. Astron. Astrophys. 2021, 647, A59. [Google Scholar] [CrossRef]
- Bajkova, A.T.; Bobylev, V.V. Galactic orbits of selected companions of the Milky Way. Astron. Rep. 2017, 61, 727–738. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Sohn, S.T.; Besla, G.; van der Marel, R.P. The Space Motion of Leo I: The Mass of the Milky Way’s Dark Matter Halo. Astrophys. J. 2013, 768, 140. [Google Scholar] [CrossRef]
- Pacucci, F.; Ni, Y.; Loeb, A. Extreme Tidal Stripping May Explain the Overmassive Black Hole in Leo I: A Proof of Concept. Astrophys. J. 2023, 956, L37. [Google Scholar] [CrossRef]
- Bland-Hawthorn, J.; Gerhard, O. The Galaxy in Context: Structural, Kinematic, and Integrated Properties. Annu. Rev. Astron. Astrophys. 2016, 54, 529–596. [Google Scholar] [CrossRef]
- Hunt, J.A.S.; Vasiliev, E. Milky Way dynamics in light of Gaia. New Astron. Rev. 2025, 100, 101721. [Google Scholar] [CrossRef]
- Prudil, Z.; Koch-Hansen, A.J.; Lemasle, B.; Grebel, E.K.; Marchetti, T.; Hansen, C.J.; Crestani, J.; Braga, V.F.; Bono, G.; Chaboyer, B.; et al. Milky Way archaeology using RR Lyrae and type II Cepheids. II. High-velocity RR Lyrae stars and Milky Way mass. Astron. Astrophys. 2022, 664, A148. [Google Scholar] [CrossRef]
- Roche, C.; Necib, L.; Lin, T.; Ou, X.; Nguyen, T. The Escape Velocity Profile of the Milky Way from Gaia DR3. Astrophys. J. 2024, 972, 70. [Google Scholar] [CrossRef]
- McMillan, P.J. Mass models of the Milky Way. Mon. Not. R. Astron. Soc. 2011, 414, 2446–2457. [Google Scholar] [CrossRef]
- Bovy, J.; Allende Prieto, C.; Beers, T.C.; Bizyaev, D.; da Costa, L.N.; Cunha, K.; Ebelke, G.L.; Eisenstein, D.J.; Frinchaboy, P.M.; García Pérez, A.E.; et al. The Milky Way’s Circular-velocity Curve between 4 and 14 kpc from APOGEE data. Astrophys. J. 2012, 759, 131. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, X.W.; Yuan, H.B.; Xiang, M.S.; Zhang, H.W.; Chen, B.Q.; Ren, J.J.; Wang, C.; Zhang, Y.; Hou, Y.H.; et al. The Milky Way’s rotation curve out to 100 kpc and its constraint on the Galactic mass distribution. Mon. Not. R. Astron. Soc. 2016, 463, 2623–2639. [Google Scholar] [CrossRef]
- Eilers, A.C.; Hogg, D.W.; Rix, H.W.; Ness, M.K. The Circular Velocity Curve of the Milky Way from 5 to 25 kpc. Astrophys. J. 2019, 871, 120. [Google Scholar] [CrossRef]
- Cautun, M.; Benítez-Llambay, A.; Deason, A.J.; Frenk, C.S.; Fattahi, A.; Gómez, F.A.; Grand, R.J.J.; Oman, K.A.; Navarro, J.F.; Simpson, C.M. The milky way total mass profile as inferred from Gaia DR2. Mon. Not. R. Astron. Soc. 2020, 494, 4291–4313. [Google Scholar] [CrossRef]
- Ablimit, I.; Zhao, G.; Flynn, C.; Bird, S.A. The Rotation Curve, Mass Distribution, and Dark Matter Content of the Milky Way from Classical Cepheids. Astrophys. J. 2020, 895, L12. [Google Scholar] [CrossRef]
- Sylos Labini, F.; Chrobáková, Ž.; Capuzzo-Dolcetta, R.; López-Corredoira, M. Mass Models of the Milky Way and Estimation of Its Mass from the Gaia DR3 Data Set. Astrophys. J. 2023, 945, 3. [Google Scholar] [CrossRef]
- Klačka, J.; Šturc, M.; Puha, E. Milky Way: New Galactic mass model for orbit computations. arXiv 2024, arXiv:2407.12551. [Google Scholar] [CrossRef]
- Craig, P.A.; Chakrabarti, S.; Baum, S.; Lewis, B.T. An estimate of the mass of the Milky Way from the Magellanic Stream. Mon. Not. R. Astron. Soc. 2022, 517, 1737–1749. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Brown, W.R.; Geller, M.J.; Kenyon, S.J. The Mass Profile of the Galaxy to 80 kpc. Astrophys. J. 2010, 720, L108–L112. [Google Scholar] [CrossRef]
- Kafle, P.R.; Sharma, S.; Lewis, G.F.; Bland-Hawthorn, J. Kinematics of the Stellar Halo and the Mass Distribution of the Milky Way Using Blue Horizontal Branch Stars. Astrophys. J. 2012, 761, 98. [Google Scholar] [CrossRef]
- Kafle, P.R.; Sharma, S.; Lewis, G.F.; Bland-Hawthorn, J. On the Shoulders of Giants: Properties of the Stellar Halo and the Milky Way Mass Distribution. Astrophys. J. 2014, 794, 59. [Google Scholar] [CrossRef]
- Zhai, M.; Xue, X.X.; Zhang, L.; Li, C.D.; Zhao, G.; Yang, C.Q. The mass of the Galactic dark matter halo from ∼9000 LAMOST DR5 K giants. Res. Astron. Astrophys. 2018, 18, 113. [Google Scholar] [CrossRef]
- Bird, S.A.; Xue, X.X.; Liu, C.; Flynn, C.; Shen, J.; Wang, J.; Yang, C.; Zhai, M.; Zhu, L.; Zhao, G.; et al. Milky Way mass with K giants and BHB stars using LAMOST, SDSS/SEGUE, and Gaia: 3D spherical Jeans equation and tracer mass estimator. Mon. Not. R. Astron. Soc. 2022, 516, 731–748. [Google Scholar] [CrossRef]
- Eadie, G.M.; Harris, W.E.; Widrow, L.M. Estimating the Galactic Mass Profile in the Presence of Incomplete Data. Astrophys. J. 2015, 806, 54. [Google Scholar] [CrossRef]
- Eadie, G.M.; Harris, W.E. Bayesian Mass Estimates of the Milky Way: The Dark and Light Sides of Parameter Assumptions. Astrophys. J. 2016, 829, 108. [Google Scholar] [CrossRef]
- Sohn, S.T.; Watkins, L.L.; Fardal, M.A.; van der Marel, R.P.; Deason, A.J.; Besla, G.; Bellini, A. Absolute Hubble Space Telescope Proper Motion (HSTPROMO) of Distant Milky Way Globular Clusters: Galactocentric Space Velocities and the Milky Way Mass. Astrophys. J. 2018, 862, 52. [Google Scholar] [CrossRef]
- Watkins, L.L.; van der Marel, R.P.; Sohn, S.T.; Evans, N.W. Evidence for an Intermediate-mass Milky Way from Gaia DR2 Halo Globular Cluster Motions. Astrophys. J. 2019, 873, 118. [Google Scholar] [CrossRef]
- Posti, L.; Helmi, A. Mass and shape of the Milky Way’s dark matter halo with globular clusters from Gaia and Hubble. Astron. Astrophys. 2019, 621, A56. [Google Scholar] [CrossRef]
- Li, Z.Z.; Qian, Y.Z.; Han, J.; Li, T.S.; Wang, W.; Jing, Y.P. Constraining the Milky Way Mass Profile with Phase-space Distribution of Satellite Galaxies. Astrophys. J. 2020, 894, 10. [Google Scholar] [CrossRef]
- Deason, A.J.; Erkal, D.; Belokurov, V.; Fattahi, A.; Gómez, F.A.; Grand, R.J.J.; Pakmor, R.; Xue, X.X.; Liu, C.; Yang, C.; et al. The mass of the Milky Way out to 100 kpc using halo stars. Mon. Not. R. Astron. Soc. 2021, 501, 5964–5972. [Google Scholar] [CrossRef]
- Shen, J.; Eadie, G.M.; Murray, N.; Zaritsky, D.; Speagle, J.S.; Ting, Y.S.; Conroy, C.; Cargile, P.A.; Johnson, B.D.; Naidu, R.P.; et al. The Mass of the Milky Way from the H3 Survey. Astrophys. J. 2022, 925, 1. [Google Scholar] [CrossRef]
- Busha, M.T.; Marshall, P.J.; Wechsler, R.H.; Klypin, A.; Primack, J. The Mass Distribution and Assembly of the Milky Way from the Properties of the Magellanic Clouds. Astrophys. J. 2011, 743, 40. [Google Scholar] [CrossRef]
- González, R.E.; Kravtsov, A.V.; Gnedin, N.Y. Satellites in Milky-Way-like Hosts: Environment Dependence and Close Pairs. Astrophys. J. 2013, 770, 96. [Google Scholar] [CrossRef]
- Cautun, M.; Frenk, C.S.; van de Weygaert, R.; Hellwing, W.A.; Jones, B.J.T. Milky Way mass constraints from the Galactic satellite gap. Mon. Not. R. Astron. Soc. 2014, 445, 2049–2060. [Google Scholar] [CrossRef]
- Barber, C.; Starkenburg, E.; Navarro, J.F.; McConnachie, A.W.; Fattahi, A. The orbital ellipticity of satellite galaxies and the mass of the Milky Way. Mon. Not. R. Astron. Soc. 2014, 437, 959–967. [Google Scholar] [CrossRef]
- Patel, E.; Besla, G.; Sohn, S.T. Orbits of massive satellite galaxies—I. A close look at the Large Magellanic Cloud and a new orbital history for M33. Mon. Not. R. Astron. Soc. 2017, 464, 3825–3849. [Google Scholar] [CrossRef]
- Patel, E.; Besla, G.; Mandel, K.; Sohn, S.T. Estimating the Mass of the Milky Way Using the Ensemble of Classical Satellite Galaxies. Astrophys. J. 2018, 857, 78. [Google Scholar] [CrossRef]
- Fritz, T.K.; Di Cintio, A.; Battaglia, G.; Brook, C.; Taibi, S. The mass of our Galaxy from satellite proper motions in the Gaia era. Mon. Not. R. Astron. Soc. 2020, 494, 5178–5193. [Google Scholar] [CrossRef]
- Rodriguez Wimberly, M.K.; Cooper, M.C.; Baxter, D.C.; Boylan-Kolchin, M.; Bullock, J.S.; Fillingham, S.P.; Ji, A.P.; Sales, L.V.; Simon, J.D. Sizing from the smallest scales: The mass of the Milky Way. Mon. Not. R. Astron. Soc. 2022, 513, 4968–4982. [Google Scholar] [CrossRef]
- van der Marel, R.P.; Fardal, M.A.; Sohn, S.T.; Patel, E.; Besla, G.; del Pino, A.; Sahlmann, J.; Watkins, L.L. First Gaia Dynamics of the Andromeda System: DR2 Proper Motions, Orbits, and Rotation of M31 and M33. Astrophys. J. 2019, 872, 24. [Google Scholar] [CrossRef]
- Salomon, J.B.; Ibata, R.; Reylé, C.; Famaey, B.; Libeskind, N.I.; McConnachie, A.W.; Hoffman, Y. The proper motion of Andromeda from Gaia EDR3: Confirming a nearly radial orbit. Mon. Not. R. Astron. Soc. 2021, 507, 2592–2601. [Google Scholar] [CrossRef]
- Patel, E.; Mandel, K.S. Evidence for a Massive Andromeda Galaxy Using Satellite Galaxy Proper Motions. Astrophys. J. 2023, 948, 104. [Google Scholar] [CrossRef]
- Casetti-Dinescu, D.I.; Pawlowski, M.S.; Girard, T.M.; Kanehisa, K.J.; Petroski, A.; Martone, M.; Kozhurina-Platais, V.; Platais, I. HST Proper Motion of Andromeda III. Another Satellite Coorbiting the M31 Satellite Plane. Astrophys. J. 2024, 975, 138. [Google Scholar] [CrossRef]
- Collins, M.L.M.; Karim, N.; Martinez-Delgado, D.; Monelli, M.; Tollerud, E.J.; Donatiello, G.; Navabi, M.; Charles, E.; Boschin, W. Pisces VII/Triangulum III—M33’s second dwarf satellite galaxy. Mon. Not. R. Astron. Soc. 2024, 528, 2614–2620. [Google Scholar] [CrossRef]
- Patel, E.; Carlin, J.L.; Tollerud, E.J.; Collins, M.L.M.; Dooley, G.A. ΛCDM predictions for the satellite population of M33. Mon. Not. R. Astron. Soc. 2018, 480, 1883–1897. [Google Scholar] [CrossRef]
- Makarova, L.N.; Makarov, D.I.; Karachentsev, I.D.; Tully, R.B.; Rizzi, L. Star formation history of And XVIII: A dwarf spheroidal galaxy in isolation. Mon. Not. R. Astron. Soc. 2017, 464, 2281–2289. [Google Scholar] [CrossRef]
- Tamm, A.; Tempel, E.; Tenjes, P.; Tihhonova, O.; Tuvikene, T. Stellar mass map and dark matter distribution in M 31. Astron. Astrophys. 2012, 546, A4. [Google Scholar] [CrossRef]
- Hayashi, K.; Chiba, M. The Prolate Dark Matter Halo of the Andromeda Galaxy. Astrophys. J. 2014, 789, 62. [Google Scholar] [CrossRef]
- Sofue, Y. Dark halos of M 31 and the Milky Way. Publ. Astron. Soc. Jpn. 2015, 67, 75. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, B.; Chen, P.; Sun, J.; Tian, Z. The rotation curve and mass distribution of M31. Mon. Not. R. Astron. Soc. 2024, 528, 2653–2666. [Google Scholar] [CrossRef]
- Fardal, M.A.; Weinberg, M.D.; Babul, A.; Irwin, M.J.; Guhathakurta, P.; Gilbert, K.M.; Ferguson, A.M.N.; Ibata, R.A.; Lewis, G.F.; Tanvir, N.R.; et al. Inferring the Andromeda Galaxy’s mass from its giant southern stream with Bayesian simulation sampling. Mon. Not. R. Astron. Soc. 2013, 434, 2779–2802. [Google Scholar] [CrossRef]
- Veljanoski, J.; Ferguson, A.M.N.; Mackey, A.D.; Huxor, A.P.; Irwin, M.J.; Côté, P.; Tanvir, N.R.; Bernard, E.J.; Chapman, S.C.; Ibata, R.A.; et al. Kinematics of Outer Halo Globular Clusters in M31. Astrophys. J. 2013, 768, L33. [Google Scholar] [CrossRef]
- Patel, E.; Besla, G.; Mandel, K. Orbits of massive satellite galaxies—II. Bayesian estimates of the Milky Way and Andromeda masses using high-precision astrometry and cosmological simulations. Mon. Not. R. Astron. Soc. 2017, 468, 3428–3449. [Google Scholar] [CrossRef]
- van der Marel, R.P.; Fardal, M.; Besla, G.; Beaton, R.L.; Sohn, S.T.; Anderson, J.; Brown, T.; Guhathakurta, P. The M31 Velocity Vector. II. Radial Orbit toward the Milky Way and Implied Local Group Mass. Astrophys. J. 2012, 753, 8. [Google Scholar] [CrossRef]
- Diaz, J.D.; Koposov, S.E.; Irwin, M.; Belokurov, V.; Evans, N.W. Balancing mass and momentum in the Local Group. Mon. Not. R. Astron. Soc. 2014, 443, 1688–1703. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Gómez, F.A.; Besla, G.; Erkal, D.; Ma, Y.Z. A timing constraint on the (total) mass of the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. 2016, 456, L54–L58. [Google Scholar] [CrossRef]
- Drlica-Wagner, A.; Bechtol, K.; Rykoff, E.S.; Luque, E.; Queiroz, A.; Mao, Y.Y.; Wechsler, R.H.; Simon, J.D.; Santiago, B.; Yanny, B.; et al. Eight Ultra-faint Galaxy Candidates Discovered in Year Two of the Dark Energy Survey. Astrophys. J. 2015, 813, 109. [Google Scholar] [CrossRef]
- Karachentsev, I.D.; Karachentseva, V.E.; Huchtmeier, W.K.; Makarov, D.I. A Catalog of Neighboring Galaxies. Astron. J. 2004, 127, 2031–2068. [Google Scholar] [CrossRef]
- Walker, M.G.; Mateo, M.; Olszewski, E.W.; Sen, B.; Woodroofe, M. Clean Kinematic Samples in Dwarf Spheroidals: An Algorithm for Evaluating Membership and Estimating Distribution Parameters When Contamination is Present. Astron. J. 2009, 137, 3109–3138. [Google Scholar] [CrossRef]
- Conn, B.C.; Jerjen, H.; Kim, D.; Schirmer, M. On the Nature of Ultra-faint Dwarf Galaxy Candidates. I. DES1, Eridanus III, and Tucana V. Astrophys. J. 2018, 852, 68. [Google Scholar] [CrossRef]
- Cerny, W.; Pace, A.B.; Drlica-Wagner, A.; Ferguson, P.S.; Mau, S.; Adamów, M.; Carlin, J.L.; Choi, Y.; Erkal, D.; Johnson, L.C.; et al. Discovery of an Ultra-faint Stellar System near the Magellanic Clouds with the DECam Local Volume Exploration Survey. Astrophys. J. 2021, 910, 18. [Google Scholar] [CrossRef]
- Carlin, J.L.; Sand, D.J.; Muñoz, R.R.; Spekkens, K.; Willman, B.; Crnojević, D.; Forbes, D.A.; Hargis, J.; Kirby, E.; Peter, A.H.G.; et al. Deep Subaru Hyper Suprime-Cam Observations of Milky Way Satellites Columba I and Triangulum II. Astron. J. 2017, 154, 267. [Google Scholar] [CrossRef]
- Luque, E.; Pieres, A.; Santiago, B.; Yanny, B.; Vivas, A.K.; Queiroz, A.; Drlica-Wagner, A.; Morganson, E.; Balbinot, E.; Marshall, J.L.; et al. The Dark Energy Survey view of the Sagittarius stream: Discovery of two faint stellar system candidates. Mon. Not. R. Astron. Soc. 2017, 468, 97–108. [Google Scholar] [CrossRef]
- Ferrarese, L.; Mould, J.R.; Kennicutt, R.C., Jr.; Huchra, J.; Ford, H.C.; Freedman, W.L.; Stetson, P.B.; Madore, B.F.; Sakai, S.; Gibson, B.K.; et al. The Hubble Space Telescope Key Project on the Extragalactic Distance Scale. XXVI. The Calibration of Population II Secondary Distance Indicators and the Value of the Hubble Constant. Astrophys. J. 2000, 529, 745–767. [Google Scholar] [CrossRef]
- Strauss, M.A.; Huchra, J.P.; Davis, M.; Yahil, A.; Fisher, K.B.; Tonry, J. A Redshift Survey of IRAS Galaxies. VII. The Infrared and Redshift Data for the 1.936 Jansky Sample. Astrophys. J. 1992, 83, 29. [Google Scholar] [CrossRef]
- Hargis, J.R.; Kimmig, B.; Willman, B.; Caldwell, N.; Walker, M.G.; Strader, J.; Sand, D.J.; Grillmair, C.J.; Yoon, J.H. Evidence That Hydra I is a Tidally Disrupting Milky Way Dwarf Galaxy. Astrophys. J. 2016, 818, 39. [Google Scholar] [CrossRef]
- Torrealba, G.; Belokurov, V.; Koposov, S.E.; Li, T.S.; Walker, M.G.; Sanders, J.L.; Geringer-Sameth, A.; Zucker, D.B.; Kuehn, K.; Evans, N.W.; et al. The hidden giant: Discovery of an enormous Galactic dwarf satellite in Gaia DR2. Mon. Not. R. Astron. Soc. 2019, 488, 2743–2766. [Google Scholar] [CrossRef]
- Ji, A.P.; Koposov, S.E.; Li, T.S.; Erkal, D.; Pace, A.B.; Simon, J.D.; Belokurov, V.; Cullinane, L.R.; Da Costa, G.S.; Kuehn, K.; et al. Kinematics of Antlia 2 and Crater 2 from the Southern Stellar Stream Spectroscopic Survey (S5). Astrophys. J. 2021, 921, 32. [Google Scholar] [CrossRef]
- McQuinn, K.B.W.; Mao, Y.Y.; Tollerud, E.J.; Cohen, R.E.; Shih, D.; Buckley, M.R.; Dolphin, A.E. Discovery and Characterization of Two Ultrafaint Dwarfs outside the Halo of the Milky Way: Leo M and Leo K. Astrophys. J. 2024, 967, 161. [Google Scholar] [CrossRef]
- Laevens, B.P.M.; Martin, N.F.; Sesar, B.; Bernard, E.J.; Rix, H.W.; Slater, C.T.; Bell, E.F.; Ferguson, A.M.N.; Schlafly, E.F.; Burgett, W.S.; et al. A New Distant Milky Way Globular Cluster in the Pan-STARRS1 3π Survey. Astrophys. J. 2014, 786, L3. [Google Scholar] [CrossRef]
- Kirby, E.N.; Simon, J.D.; Cohen, J.G. Spectroscopic Confirmation of the Dwarf Galaxies Hydra II and Pisces II and the Globular Cluster Laevens 1. Astrophys. J. 2015, 810, 56. [Google Scholar] [CrossRef]
- Mau, S.; Cerny, W.; Pace, A.B.; Choi, Y.; Drlica-Wagner, A.; Santana-Silva, L.; Riley, A.H.; Erkal, D.; Stringfellow, G.S.; Adamów, M.; et al. Two Ultra-faint Milky Way Stellar Systems Discovered in Early Data from the DECam Local Volume Exploration Survey. Astrophys. J. 2020, 890, 136. [Google Scholar] [CrossRef]
- Simon, J.D.; Geha, M. The Kinematics of the Ultra-faint Milky Way Satellites: Solving the Missing Satellite Problem. Astrophys. J. 2007, 670, 313–331. [Google Scholar] [CrossRef]
- Grillmair, C.J. Four New Stellar Debris Streams in the Galactic Halo. Astrophys. J. 2009, 693, 1118–1127. [Google Scholar] [CrossRef]
- Gregory, A.L.; Collins, M.L.M.; Erkal, D.; Tollerud, E.; Delorme, M.; Hill, L.; Sand, D.J.; Strader, J.; Willman, B. Uncovering the orbit of the hercules dwarf galaxy. Mon. Not. R. Astron. Soc. 2020, 496, 1092–1104. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Anugu, N.; Bauböck, M.; Benisty, M.; Berger, J.P.; Blind, N.; Bonnet, H.; Brandner, W.; et al. Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar] [CrossRef]
- Monaco, L.; Bellazzini, M.; Ferraro, F.R.; Pancino, E. The distance to the Sagittarius dwarf spheroidal galaxy from the red giant branch tip. Mon. Not. R. Astron. Soc. 2004, 353, 874–878. [Google Scholar] [CrossRef]
- Kirby, E.N.; Bullock, J.S.; Boylan-Kolchin, M.; Kaplinghat, M.; Cohen, J.G. The dynamics of isolated Local Group galaxies. Mon. Not. R. Astron. Soc. 2014, 439, 1015–1027. [Google Scholar] [CrossRef]
- Longeard, N.; Martin, N.; Ibata, R.A.; Starkenburg, E.; Jablonka, P.; Aguado, D.S.; Carlberg, R.G.; Côté, P.; González Hernández, J.I.; Lucchesi, R.; et al. The pristine dwarf-galaxy survey—III. Revealing the nature of the Milky Way globular cluster Sagittarius II. Mon. Not. R. Astron. Soc. 2021, 503, 2754–2762. [Google Scholar] [CrossRef]
- Fadely, R.; Willman, B.; Geha, M.; Walsh, S.; Muñoz, R.R.; Jerjen, H.; Vargas, L.C.; Da Costa, G.S. Segue 3: An Old, Extremely Low Luminosity Star Cluster in the Milky Way’s Halo. Astron. J. 2011, 142, 88. [Google Scholar] [CrossRef]
- Fritz, T.K.; Carrera, R.; Battaglia, G.; Taibi, S. Gaia DR 2 and VLT/FLAMES search for new satellites of the LMC. Astron. Astrophys. 2019, 623, A129. [Google Scholar] [CrossRef]
- Huxor, A.P.; Mackey, A.D.; Ferguson, A.M.N.; Irwin, M.J.; Martin, N.F.; Tanvir, N.R.; Veljanoski, J.; McConnachie, A.; Fishlock, C.K.; Ibata, R.; et al. The outer halo globular cluster system of M31—I. The final PAndAS catalogue. Mon. Not. R. Astron. Soc. 2014, 442, 2165–2187. [Google Scholar] [CrossRef]
- Weisz, D.R.; Dolphin, A.E.; Martin, N.F.; Albers, S.M.; Collins, M.L.M.; Ferguson, A.M.N.; Lewis, G.F.; Mackey, A.D.; McConnachie, A.; Rich, R.M.; et al. A rogues gallery of Andromeda’s dwarf galaxies—II. Precise distances to 17 faint satellites. Mon. Not. R. Astron. Soc. 2019, 489, 763–770. [Google Scholar] [CrossRef]
- Watkins, L.L.; Evans, N.W.; van de Ven, G. A census of orbital properties of the M31 satellites. Mon. Not. R. Astron. Soc. 2013, 430, 971–985. [Google Scholar] [CrossRef]
- Karachentsev, I.D.; Kaisina, E.I.; Makarov, D.I. Suites of Dwarfs around nearby Giant Galaxies. Astron. J. 2014, 147, 13. [Google Scholar] [CrossRef]
- Oh, S.H.; Hunter, D.A.; Brinks, E.; Elmegreen, B.G.; Schruba, A.; Walter, F.; Rupen, M.P.; Young, L.M.; Simpson, C.E.; Johnson, M.C.; et al. High-resolution Mass Models of Dwarf Galaxies from LITTLE THINGS. Astron. J. 2015, 149, 180. [Google Scholar] [CrossRef]
- Martin, N.F.; Chambers, K.C.; Collins, M.L.M.; Ibata, R.A.; Rich, R.M.; Bell, E.F.; Bernard, E.J.; Ferguson, A.M.N.; Flewelling, H.; Kaiser, N.; et al. Spectroscopy of the Three Distant Andromedan Satellites Cassiopeia III, Lacerta I, and Perseus I. Astrophys. J. 2014, 793, L14. [Google Scholar] [CrossRef]
- Richardson, J.C.; Irwin, M.J.; McConnachie, A.W.; Martin, N.F.; Dotter, A.L.; Ferguson, A.M.N.; Ibata, R.A.; Chapman, S.C.; Lewis, G.F.; Tanvir, N.R.; et al. PAndAS’ Progeny: Extending the M31 Dwarf Galaxy Cabal. Astrophys. J. 2011, 732, 76. [Google Scholar] [CrossRef]
- Martin, N.F.; Ibata, R.A.; Irwin, M.J.; Chapman, S.; Lewis, G.F.; Ferguson, A.M.N.; Tanvir, N.; McConnachie, A.W. Discovery and analysis of three faint dwarf galaxies and a globular cluster in the outer halo of the Andromeda galaxy. Mon. Not. R. Astron. Soc. 2006, 371, 1983–1991. [Google Scholar] [CrossRef]
- Sakari, C.M.; Wallerstein, G. The integrated calcium II triplet as a metallicity indicator: Comparisons with high-resolution [Fe/H] in M31 globular clusters. Mon. Not. R. Astron. Soc. 2016, 456, 831–843. [Google Scholar] [CrossRef]
- Mackey, A.D.; Huxor, A.P.; Martin, N.F.; Ferguson, A.M.N.; Dotter, A.; McConnachie, A.W.; Ibata, R.A.; Irwin, M.J.; Lewis, G.F.; Sakari, C.M.; et al. A Peculiar Faint Satellite in the Remote Outer Halo of M31. Astrophys. J. 2013, 770, L17. [Google Scholar] [CrossRef]
- Collins, M.L.M.; Chapman, S.C.; Rich, R.M.; Ibata, R.A.; Martin, N.F.; Irwin, M.J.; Bate, N.F.; Lewis, G.F.; Peñarrubia, J.; Arimoto, N.; et al. A Kinematic Study of the Andromeda Dwarf Spheroidal System. Astrophys. J. 2013, 768, 172. [Google Scholar] [CrossRef]
- Alam, S.; Albareti, F.D.; Allende Prieto, C.; Anders, F.; Anderson, S.F.; Anderton, T.; Andrews, B.H.; Armengaud, E.; Aubourg, É.; Bailey, S.; et al. The Eleventh and Twelfth Data Releases of the Sloan Digital Sky Survey: Final Data from SDSS-III. Astrophys. J. 2015, 219, 12. [Google Scholar] [CrossRef]
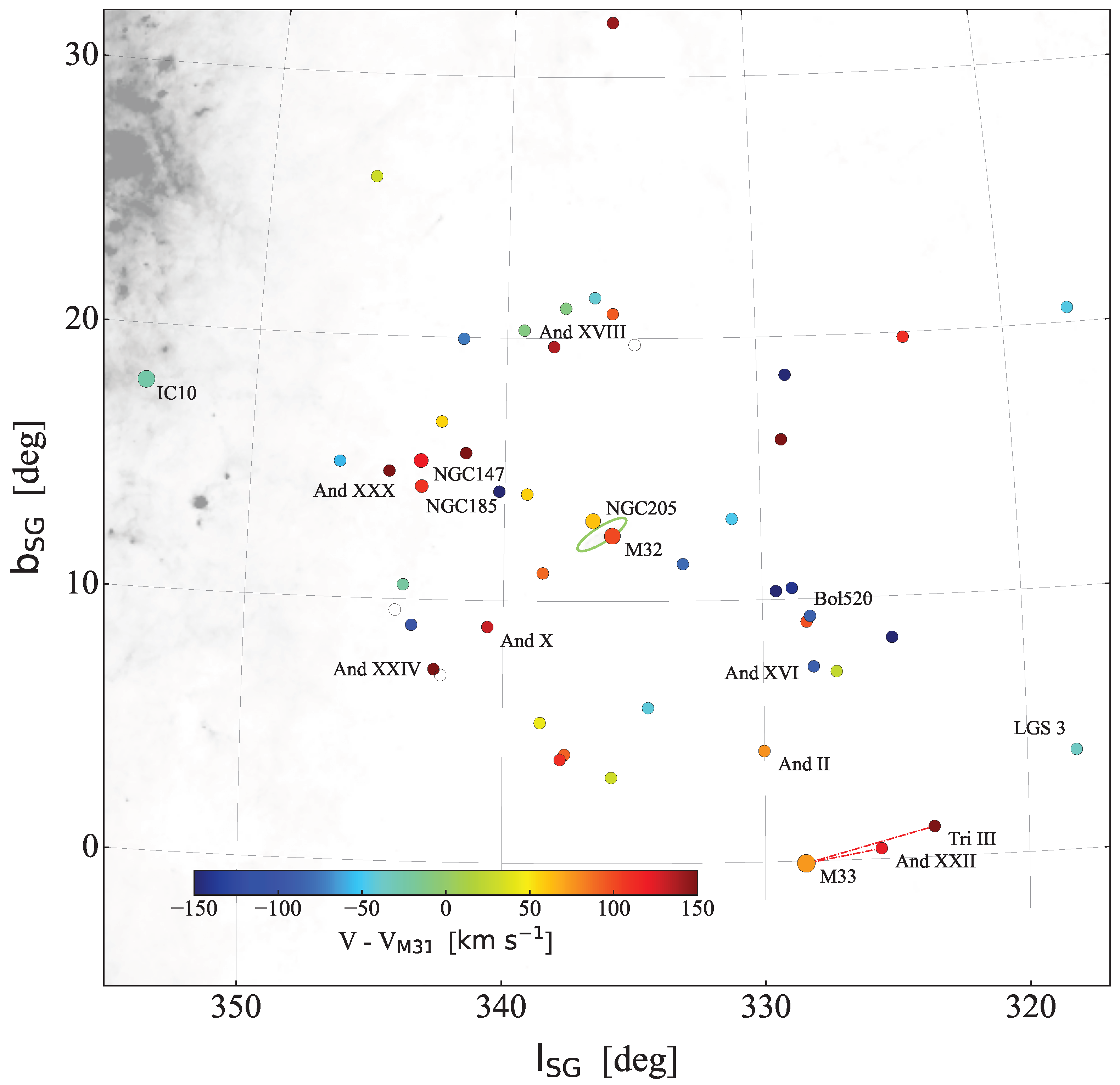
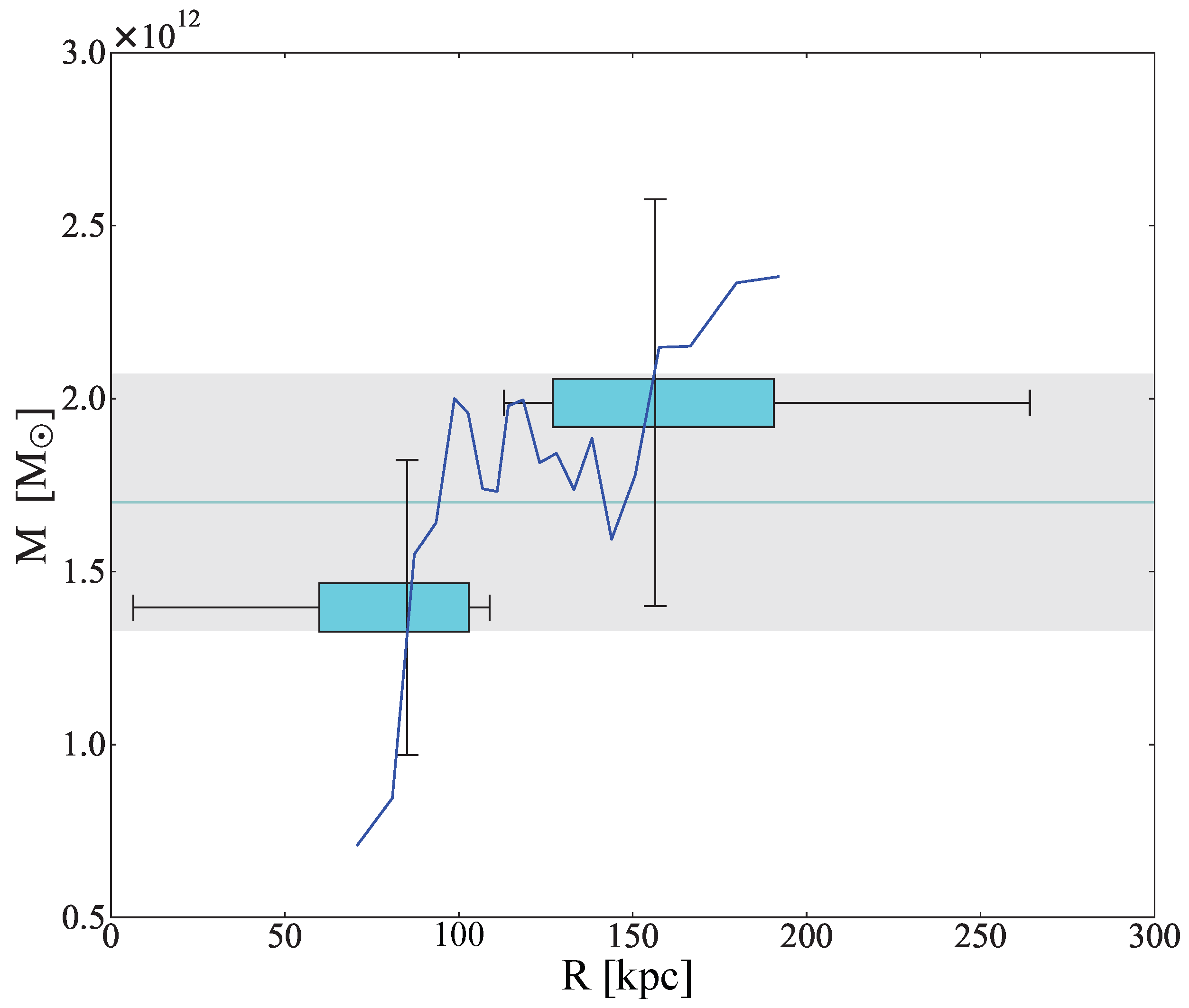
| Sample | Median | ||||
|---|---|---|---|---|---|
| Observations from the outside (the case of M 31) | |||||
| Heavy halos | 1.054 | 0.103 | 1.055 | ||
| Satellites | 0.858 | 0.384 | 0.848 | ||
| Observations from the inside (the case of MW) | |||||
| Heavy halos | 1.022 | 0.116 | 1.047 | ||
| Satellites | 0.704 | 0.315 | 0.625 | ||
| Sample | Range [kpc] | # | [ ] | |
|---|---|---|---|---|
| All | 23 | 257 | 49 | |
| w/o Leo I | 23 | 236 | 48 | |
| w/o 8 | 23 | 257 | 41 | |
| w/o 8 and Leo I | 23 | 236 | 40 | |
| kpc | 23 | 86 | 28 | |
| w/o 8 | 23 | 86 | 20 | |
| kpc | 89 | 257 | 21 | |
| w/o Leo I | 89 | 236 | 20 | |
| Sample | # | ||||
|---|---|---|---|---|---|
| km s−1 | |||||
| 47 | 121.1 | ||||
| D and | 33 | 114.1 | |||
| w/o 2 † | 31 | 113.6 | |||
| w/o 3 ‡ | 30 | 112.7 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makarov, D.; Makarov, D.; Kozyrev, K.; Libeskind, N. Line-of-Sight Mass Estimator and the Masses of the Milky Way and Andromeda Galaxy. Universe 2025, 11, 144. https://doi.org/10.3390/universe11050144
Makarov D, Makarov D, Kozyrev K, Libeskind N. Line-of-Sight Mass Estimator and the Masses of the Milky Way and Andromeda Galaxy. Universe. 2025; 11(5):144. https://doi.org/10.3390/universe11050144
Chicago/Turabian StyleMakarov, Danila, Dmitry Makarov, Kirill Kozyrev, and Noam Libeskind. 2025. "Line-of-Sight Mass Estimator and the Masses of the Milky Way and Andromeda Galaxy" Universe 11, no. 5: 144. https://doi.org/10.3390/universe11050144
APA StyleMakarov, D., Makarov, D., Kozyrev, K., & Libeskind, N. (2025). Line-of-Sight Mass Estimator and the Masses of the Milky Way and Andromeda Galaxy. Universe, 11(5), 144. https://doi.org/10.3390/universe11050144







