Gauge-Invariant Perturbation Theory on the Schwarzschild Background Spacetime Part I: Formulation and Odd-Mode Perturbations
Abstract
:1. Introduction
2. Review of Our General-Relativistic Gauge-Invariant Perturbation Theory
2.1. First Kind Gauge
2.2. Second Kind Gauge
2.3. The General-Relativistic Gauge-Invariant Linear Perturbation Theory
3. Linear Perturbations on Spherically Symmetric Background
3.1. Conventional Perturbation Decomposition and Its Inverse Relation
3.2. Treatments of the Kernel Modes
3.2.1.
3.2.2.
3.2.3.
3.2.4. Summary of the Mode Decomposition Including Modes
3.3. Explicit Form of the Mode Functions
3.3.1. Explicit Form of
3.3.2. Explicit Form of
3.4. Proposal of the Treatment of -Mode Perturbations
4. Construction of Gauge-Invariant Variables
4.1. Gauge-Transformation Rules
4.2. Gauge-Invariant and Gauge-Variant Variables
4.2.1. Odd Modes
4.2.2. Even Modes
4.2.3. Summary of Gauge-Invariant and Gauge-Dependent Variables
5. Einstein Equations
5.1. Odd Mode Perturbation Equations
5.2. Even Mode Perturbation Equations
6. Component Treatment for the Odd-Mode Perturbations of the Einstein Equations
6.1. Strategy to Solve Odd-Mode Perturbations
6.2. Odd-Mode Solutions
6.2.1. Odd Mode
6.2.2. Odd-Mode Vacuum Solution
6.3. Odd Mode Non-Vacuum Solution
7. Summary and Discussions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Explicit Form of Conventional Spherical Harmonics on S2
Appendix B. Covariant Derivatives in 2 + 2 Formulation and Background Curvatures
Appendix C. Summary of the 2 + 2 Representations of the Tensor , ,
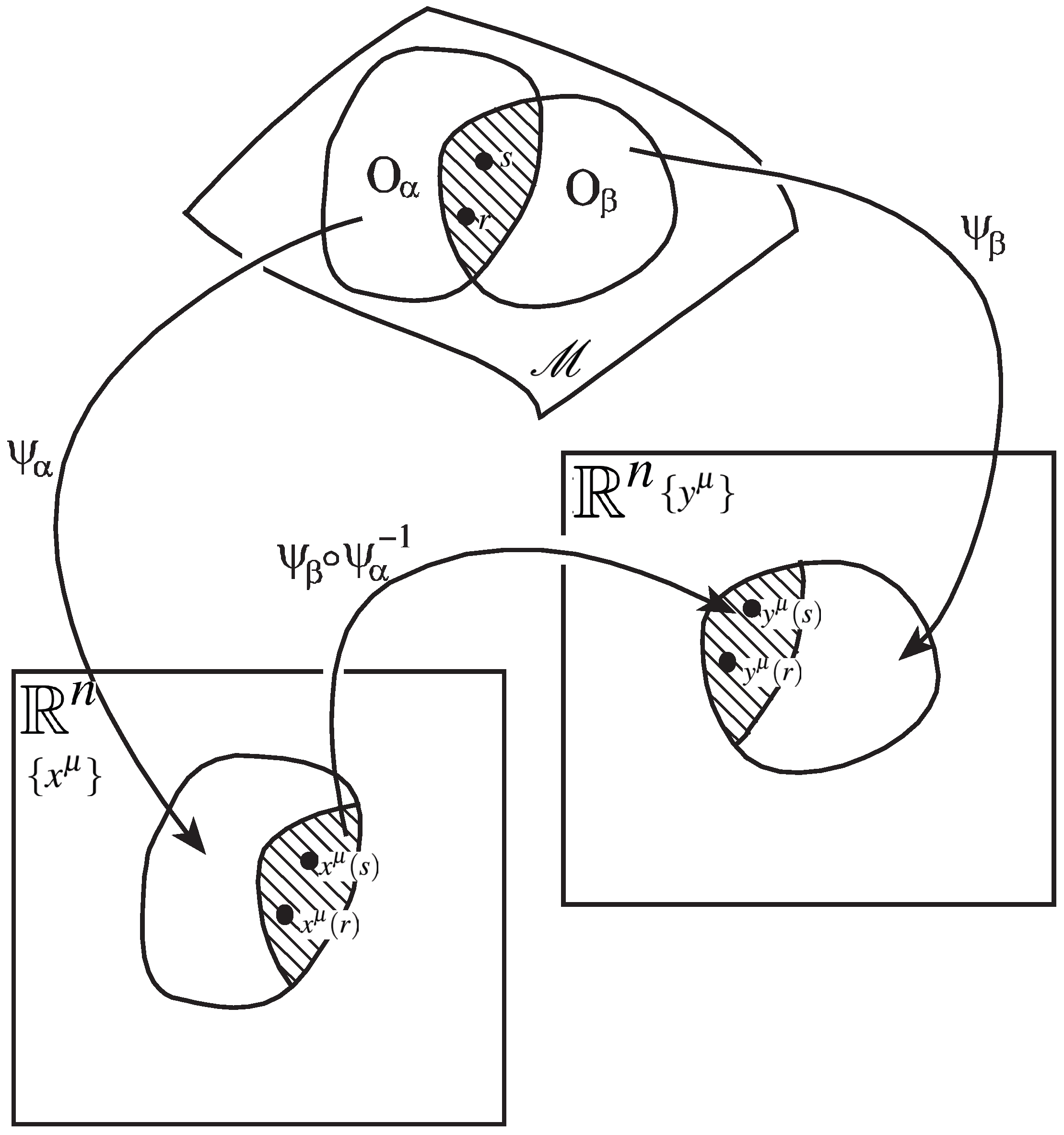
| 1 | In the derivation of the Lie derivative in § 94 of ref. [48], the coordinate transformation is performed, at first, and the comparison inverse matrices and at the “same coordinate value” is carried out. The comparison at the “same coordinate value” under the coordinate transformation means the comparison the inverse metrics at the “different points” on the same manifold as shown in Equation (3). |
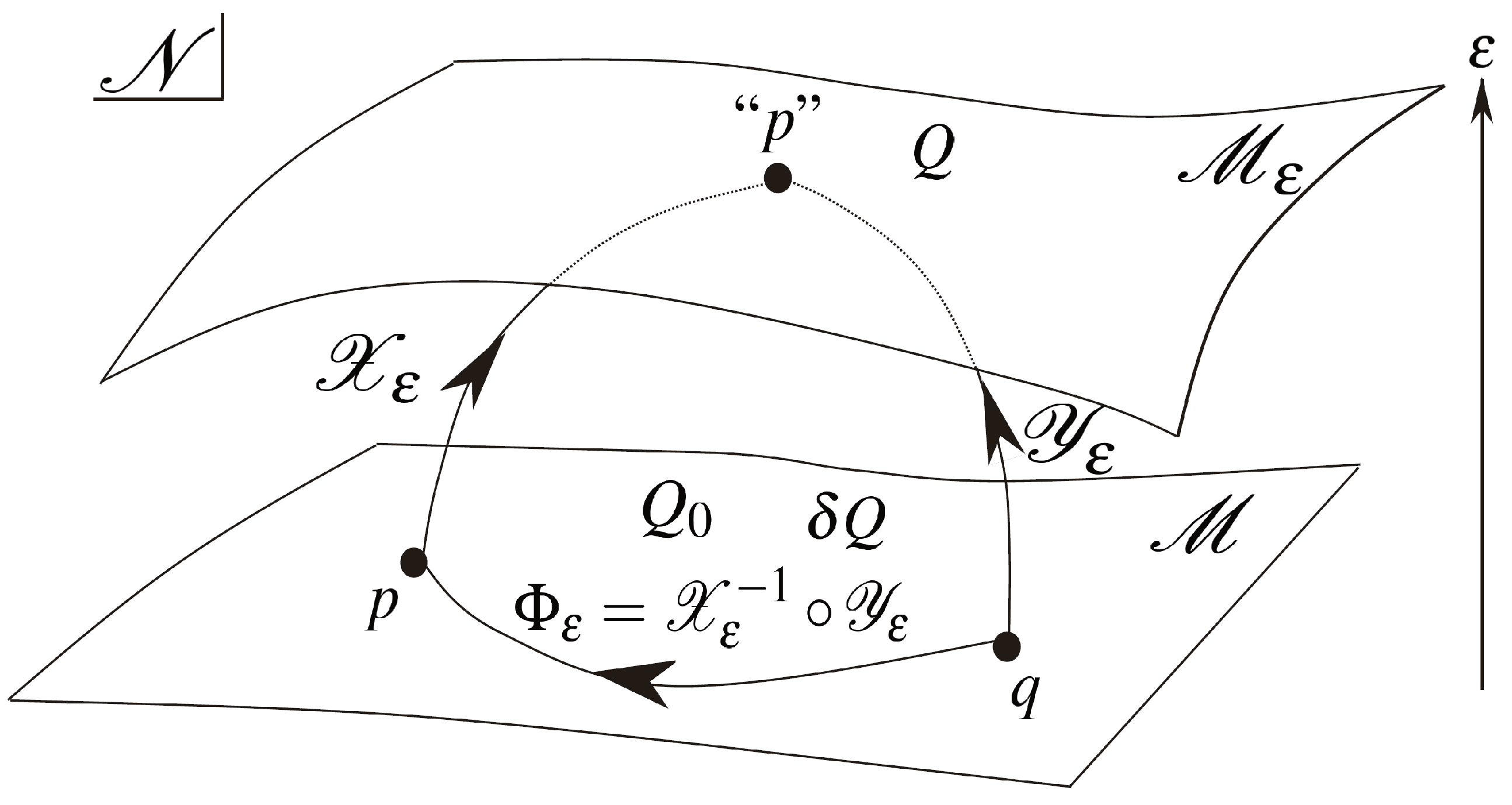
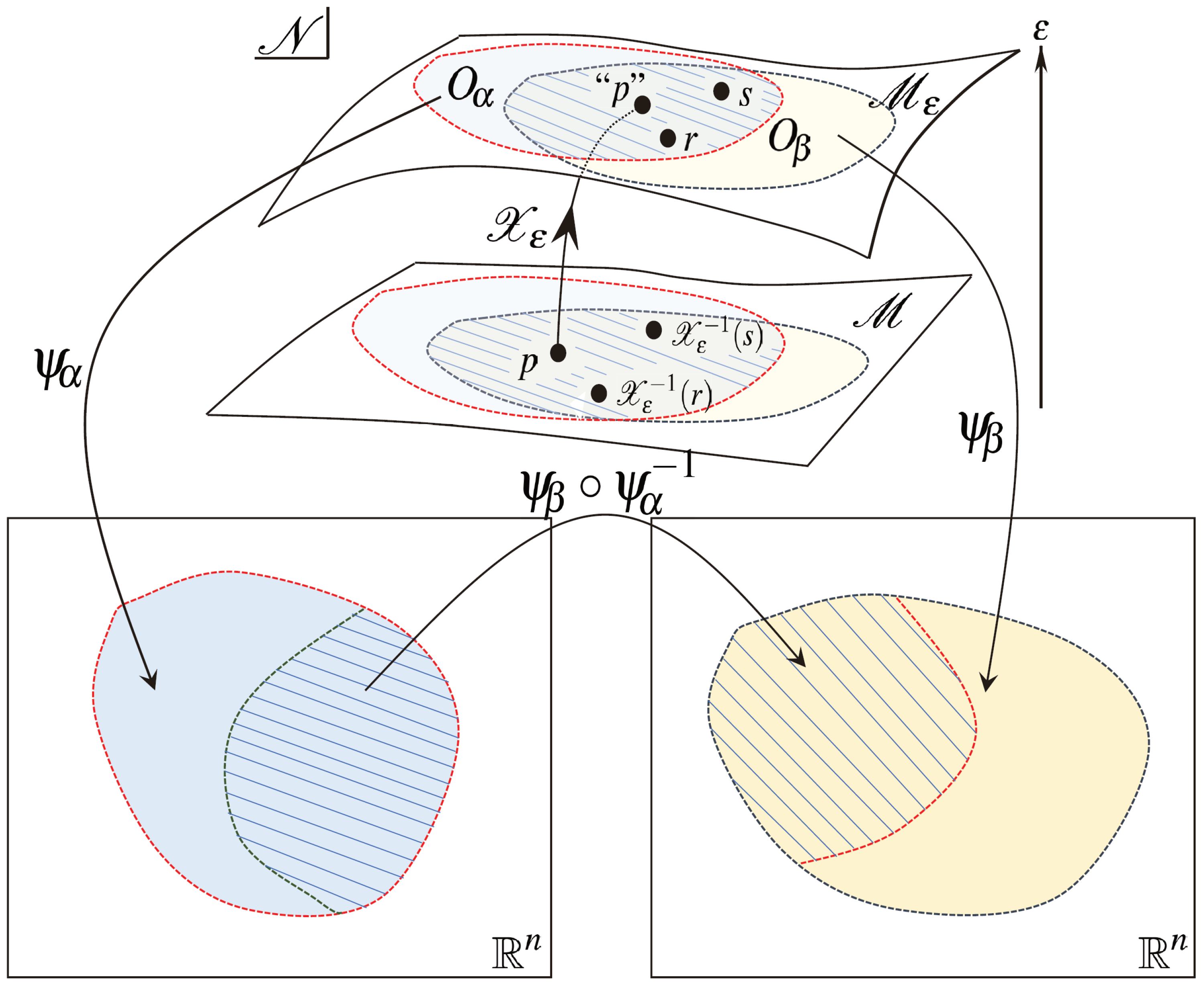
| 2 | As depicted in Figure 2, the action of the diffeomorphism is the replacement of =p. However, the evaluations of the both-side of Equation (9) are carried out at the same point on the background spacetime and Equation (11) is also evaluated at the same point on the background spacetime as the result, while Equation (6) represents the difference between the tensor field at different points on the same manifold. To explain this, we consider the points , (), and and the action of the diffeomorphisms , and so that and . Through this setup, Equation (9) derived as |
| 3 | This statement of the Proposal 1 actually indicates that at once we ignore the neighborhood of the region where the harmonic function diverges but we apply the analytic extension of the linearized solution to these regions when we choose . |
| 4 | From Equation (257) and the descriptions in ref. [61], readers might regard that the extension to mode case of the Cunningham-Price-Moncrief variable is the same variable as the gauge-invariant variable defined by Equation (185). Actually, if we can identify with , the extension to mode case of the Cunningham-Price-Moncrief variable coincides with the definition of and there is the description in ref. [61] which is similar to Equation (257). However, this identification is not appropriate, since is gauge-invariant in the sense of the second-kind but is not gauge-invariant. We actually take in the singular harmonic when we solve the mode-by-mode Einstein equations. However, this does not mean , nevertheless the term in the metric perturbation disappear since the singular harmonic function vanishes due to the choice . This difference also appears when we obtain the gauge-invariant relation between the components of and the extension to mode case of Cunningham-Price-Moncrief variable by integrating the linearized Einstein equations. In this integration, the integration constants appear in the relation between the components and . This integration “constants” are automatically gauge-invariant in the sense of second-kind. On the other hand, when we integrate to obtain the explicit relation with , there is no guarantee that the integration “constants” are gauge-invariant, because is not gauge-invariant. |
| 5 | Although the simple integration of Equation (258) yields the time-dependence of , this time-dependence is inconsistent with Equation (241). This inconsistency is due to the fact that we just use the constraint (241) in the form when we derive Equation (249). |
References
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration. 2025. Available online: https://ligo.org (accessed on 8 January 2025).
- Virgo. 2025. Available online: https://www.virgo-gw.eu (accessed on 8 January 2025).
- KAGRA. 2025. Available online: https://gwcenter.icrr.u-tokyo.ac.jp (accessed on 8 January 2025).
- LIGO INDIA. 2025. Available online: https://www.ligo-india.in (accessed on 8 January 2025).
- Einstein Telescope. 2025. Available online: https://www.et-gw.eu (accessed on 8 January 2025).
- Cosmic Explorer. 2025. Available online: https://cosmicexplorer.org/ (accessed on 8 January 2025).
- LISA. 2025. Available online: https://lisa.nasa.gov/ (accessed on 8 January 2025).
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. Prog. Theor. Exp. Phys. 2021, 2021, 05A105. [Google Scholar] [CrossRef]
- Mei, J.; Bai, Y.; Bao, J.; Barausse, E.; Cai, L.; Canuto, E.; Cao, B.; Chen, W.; Chen, Y.; Ding, Y.; et al. The TianQin project: Current progress on science and technology. Prog. Theor. Exp. Phys. 2020, 2020, 05A107. [Google Scholar]
- Luo, Z.; Wang, Y.; Wu, Y.; Hu, W.; Jin, G. The Taiji program:A concise overview. Prog. Theor. Exp. Phys. 2020, 2020, 05A108. [Google Scholar]
- Barack, L.; Pound, A. Self-force and radiation reaction in general relativity. Rep. Prog. Phys. 2019, 82, 016904. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433. [Google Scholar] [CrossRef]
- Kimura, M.; Harada, T.; Naruko, A.; Toma, K. Backreaction of mass and angular momentum accretion on black holes: General formulation of metric perturbations and application to the Blandford–Znajek process. Prog. Theor. Exp. Phys. 2021, 2021, 093E3. [Google Scholar] [CrossRef]
- Nakamura, K. Gauge Invariant Variables in Two-Parameter Nonlinear Perturbations. Prog. Theor. Phys. 2003, 110, 723. [Google Scholar] [CrossRef]
- Nakamura, K. Second-Order Gauge Invariant Perturbation Theory—Perturbative Curvatures in the Two-Parameter Case. Prog. Theor. Phys. 2005, 113, 481. [Google Scholar] [CrossRef]
- Regge, T.; Wheeler, J.A. Stability of a Schwarzschild Singularity. Phys. Rev. 1957, 108, 1063. [Google Scholar] [CrossRef]
- Zerilli, F. Effective potential for even-parity Regge-Wheeler gravitational perturbation equations. Phys. Rev. Lett. 1970, 24, 737. [Google Scholar] [CrossRef]
- Zerilli, F. Gravitational Field of a Particle Falling in a Schwarzschild Geometry Analyzed in Tensor Harmonics. Phys. Rev. D 1970, 2, 2141. [Google Scholar] [CrossRef]
- Moncrief, V. Gravitational Perturbations of Spherically Symmetric Systems. I. The Exterior Problem. Ann. Phys. 1974, 88, 323. [Google Scholar] [CrossRef]
- Moncrief, V. Gravitational Perturbations of Spherically Symmetric Systems. II. Perfect Fluid Interiors. Ann. Phys. 1974, 88, 343. [Google Scholar] [CrossRef]
- Cunningham, C.T.; Price, R.H.; Moncrief, V. Radiation from collapsing relativistic stars. I. linearized odd-parity radiation. Astrophys. J. 1978, 224, 643. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon Press: Oxford, UK, 1983. [Google Scholar]
- Gerlach, U.H.; Sengupta, U.K. Gauge-invariant perturbations on most general spherically symmetric space-times. Phys. Rev. D 1979, 19, 2268. [Google Scholar] [CrossRef]
- Gerlach, U.H.; Sengupta, U.K. Junction conditions for odd-parity perturbations on most general spherically symmetric space-times. Phys. Rev. D 1979, 20, 3009. [Google Scholar] [CrossRef]
- Gerlach, U.H.; Sengupta, U.K. Even parity junction conditions for perturbations on most general spherically symmetric space–times. J. Math. Phys. 1979, 20, 2540. [Google Scholar] [CrossRef]
- Gerlach, U.H.; Sengupta, U.K. Gauge-invariant coupled gravitational, acoustical, and electromagnetic modes on most general spherical space-times. Phys. Rev. D 1980, 22, 1300. [Google Scholar] [CrossRef]
- Nakamura, T.; Oohara, K.; Kojima, Y. General Relativistic Collapse to Black Holes and Gravitational Waves from Black Holes. Prog. Theor. Phys. Suppl. No. 1987, 90, 1. [Google Scholar] [CrossRef]
- Gundlach, C.; Martín-García, J.M. Gauge-invariant and coordinate-independent perturbations of stellar collapse: The interior. Phys. Rev. D 2000, 61, 084024. [Google Scholar] [CrossRef]
- Martín-García, J.M.; Gundlach, C. Gauge-invariant and coordinate-independent perturbations of stellar collapse. II. Matching to the exterior. Phys. Rev. D 2001, 64, 024012. [Google Scholar] [CrossRef]
- Nagar, A.; Rezzolla, L. Gauge-invariant non-spherical metric perturbations of Schwarzschild black-hole spacetimes. Class. Quantum Grav. 2005, 22, R167, Erratum in Class. Quantum Grav. 2006, 23, 4297. [Google Scholar] [CrossRef]
- Martel, K.; Poisson, E. Gravitational perturbations of the Schwarzschild spacetime: A practical covariant and gauge-invariant formalism. Phys. Rev. D 2005, 71, 104003. [Google Scholar] [CrossRef]
- Nakamura, K. General formulation of general-relativistic higher-order gauge-invariant perturbation theory. Class. Quantum Grav. 2011, 28, 122001. [Google Scholar] [CrossRef]
- Nakamura, K. Gauge-invariant variables in general-relativistic perturbations: Globalization and zero-mode problem. Int. J. Mod. Phys. D 2012, 21, 124004. [Google Scholar] [CrossRef]
- Nakamura, K. Construction of gauge-invariant variables of linear metric perturbations on an arbitrary background spacetime. Prog. Theor. Exp. Phys. 2013, 2013, 043E02. [Google Scholar] [CrossRef]
- Nakamura, K. Recursive structure in the definitions of gauge-invariant variables for any order perturbations. Class. Quantum Grav. 2014, 31, 135013. [Google Scholar] [CrossRef]
- Nakamura, K. Second-Order Gauge Invariant Cosmological Perturbation Theory—Einstein Equations in Terms of Gauge Invariant Variables. Prog. Theor. Phys. 2007, 117, 17. [Google Scholar] [CrossRef]
- Nakamura, K. Perturbations of matter fields in the second-order gauge-invariant cosmological perturbation theory. Phys. Rev. D 2009, 80, 124021. [Google Scholar] [CrossRef]
- Nakamura, K. Second-Order Gauge-Invariant Cosmological Perturbation Theory: Current Status. Adv. Astron. 2010, 2010, 576273. [Google Scholar] [CrossRef]
- Brizuela, D.; Martin Garcia, J.M.; Mena Marugan, G.A. High-order gauge-invariant perturbations of a spherical spacetime. Phys. Rev. D 2007, 79, 024004. [Google Scholar] [CrossRef]
- Nakamura, K. Proposal of a gauge-invariant treatment of l=0,1-mode perturbations on Schwarzschild background spacetime. Class. Quantum Grav. 2021, 38, 145010. [Google Scholar] [CrossRef]
- Nakamura, K. Formal Solutions of Any-Order Mass, Angular-Momentum, and Dipole Perturbations on the Schwarzschild Background Spacetime. Lett. High Energy Phys. 2021, 2021, 215. [Google Scholar] [CrossRef]
- Nakamura, K. Gauge-invariant perturbation theory on the Schwarzschild background spacetime Part II:— Even-mode perturbations. arXiv 2021, arXiv:2110.13512. [Google Scholar]
- Nakamura, K. Gauge-invariant perturbation theory on the Schwarzschild background spacetime Part III:— Realization of exact solutions. arXiv 2021, arXiv:2110.13519. [Google Scholar]
- Sachs, R.K. Gravitational Radiation. In Relativity, Groups and Topology; DeWitt, C., DeWitt, B., Eds.; Gordon and Breach: New York, NY, USA, 1964. [Google Scholar]
- Kobayashi, S.; Nomizu, K. Foundations of Differential Geometry; Wiley Classic Library Edition; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996; Volume I. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Landau, L.; Lifshitz, E. The Classical Theory of Fields; Addison-Wesley: Reading, MA, USA, 1962. [Google Scholar]
- Stewart, J.M.; Walker, M. Perturbations of Space-Times in General Relativity. Proc. R. Soc. Lond. A 1974, 341, 49. [Google Scholar]
- Stewart, J.M. Perturbations of Friedmann-Robertson-Walker cosmological models. Class. Quantum Grav. 1990, 7, 1169. [Google Scholar] [CrossRef]
- Stewart, J.M. Advanced General Relativity; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Bruni, M.; Matarrese, S.; Mollerach, S.; Sonego, S. Perturbations of spacetime: Gauge transformations and gauge invariance at second order and beyond. Class. Quantum Grav. 1997, 14, 2585. [Google Scholar] [CrossRef]
- Bruni, M.; Sonego, S. Observables and gauge invariance in the theory of nonlinear spacetime perturbations. Class. Quantum Grav. 1999, 16, L29. [Google Scholar] [CrossRef]
- Sonego, S.; Bruni, M. Gauge Dependence in the Theory of Non-Linear Spacetime Perturbations. Commun. Math. Phys. 1998, 193, 209. [Google Scholar] [CrossRef]
- York, J.W., Jr. Conformally invariant orthogonal decomposition of symmetric tensors on Riemannian manifolds and the initial-value problem of general relativity. J. Math. Phys. 1973, 14, 456. [Google Scholar] [CrossRef]
- York, J.W., Jr. Covariant decompositions of symmetric tensors in the theory of gravitation. Ann. Inst. H. Poincaré 1974, 21, 319. [Google Scholar]
- Deser, S. Covariant decomposition of symmetric tensors and the gravitational Cauchy problem. Ann. Inst. H. Poincaré 1967, 7, 149. [Google Scholar]
- Szmytkowski, R. Closed form of the generalized Green’s function for the Helmholtz operator on the two-dimensional unit sphere. J. Math. Phys. 2006, 47, 063506. [Google Scholar] [CrossRef]
- Szmytkowski, R. Closed forms of the Green’s function and the generalized Green’s function for the Helmholtz operator on the N-dimensional unit sphere. J. Phys. A Math. Theor. 2007, 40, 995–1009. [Google Scholar] [CrossRef]
- Sakurai, J.J. Modern Quantum Mechanics, Revised Edition; Tuan, S.F., Ed.; Addison-Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Kodama, H.; Ishihara, H.; Fujiwara, Y. Does a domain wall emit gravitational waves? General-relativistic perturbative analysis of a simple case. Phys. Rev. D 1994, 50, 7292. [Google Scholar] [CrossRef]
- Mano, S.; Suzuki, H.; Takasugi, E. Analytic Solutions of the Teukolsky Equation and Their Low Frequency Expansions. Prog. Theor. Phys. 1996, 95, 1079. [Google Scholar] [CrossRef]
- Mano, S.; Suzuki, H.; Takasugi, E. Analytic Solutions of the Regge-Wheeler Equation and the Post-Minkowskian Expansion. Prog. Theor. Phys. 1996, 96, 549. [Google Scholar] [CrossRef]
- Mano, S.; Takasugi, E. Analytic Solutions of the Teukolsky Equation and Their Properties. Prog. Theor. Phys. 1997, 97, 213. [Google Scholar]
- Tagoshi, H.; Mano, S.; Takasugi, E. Post-Newtonian Expansion of Gravitational Waves from a Particle in Circular Orbits around a Rotating Black Hole—Effects of Black Hole Absorption. Prog. Theor. Phys. 1997, 98, 829. [Google Scholar] [CrossRef]
- Boyer, R.H.; Lindquist, R.W. Maximal Analytic Extension of the Kerr Metric. J. Math. Phys. 1967, 8, 265. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Heusler, M. Black Hole Uniqueness Theorems; Cambridge University Press: New York, NY, USA, 1996; ISBN 978-0-511-66139-6. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large-Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, K. Gauge-Invariant Perturbation Theory on the Schwarzschild Background Spacetime Part I: Formulation and Odd-Mode Perturbations. Universe 2025, 11, 39. https://doi.org/10.3390/universe11020039
Nakamura K. Gauge-Invariant Perturbation Theory on the Schwarzschild Background Spacetime Part I: Formulation and Odd-Mode Perturbations. Universe. 2025; 11(2):39. https://doi.org/10.3390/universe11020039
Chicago/Turabian StyleNakamura, Kouji. 2025. "Gauge-Invariant Perturbation Theory on the Schwarzschild Background Spacetime Part I: Formulation and Odd-Mode Perturbations" Universe 11, no. 2: 39. https://doi.org/10.3390/universe11020039
APA StyleNakamura, K. (2025). Gauge-Invariant Perturbation Theory on the Schwarzschild Background Spacetime Part I: Formulation and Odd-Mode Perturbations. Universe, 11(2), 39. https://doi.org/10.3390/universe11020039






