Abstract
We investigate gravity, where R is the Ricci scalar and T the trace of the energy–momentum tensor, focusing on the subclass defined by . Instead of assuming a parametric form, we adopt a non-parametric reconstruction based on genetic algorithms (GA), a machine learning technique that does not rely on predefined models. Using Hubble parameter measurements from cosmic chronometers, baryon acoustic oscillations, and the Dark Energy Spectroscopic Instrument (DESI) data, we reconstruct in a model-independent way. This reconstruction allows us to derive both numerical and analytical forms of through the modified Friedmann equations. The analytic expression derived via GA provides an excellent fit to the numerical reconstruction. Furthermore, we compare the evolution of the Hubble parameter predicted by our model with that of the standard ΛCDM scenario (Planck), finding a good agreement for . These results highlight the robustness of GA-based reconstructions and suggest that the functional form of obtained here may serve as a promising tool for further applications in cosmology and astrophysics.
1. Introduction
In recent years, observations such as Type Ia supernovae [1,2,3], the cosmic microwave background [4,5,6], large-scale structure surveys [7,8,9], and baryon acoustic oscillations [10], in particular the recent DESI Data Release 2 results [11] have established that the observable Universe is undergoing an accelerated expansion. Moreover, studies of the ages of the oldest stellar populations and globular clusters showed that the dimensionless product differs significantly from the value expected for a flat, matter-dominated Friedmann–Lemaître–Robertson–Walker (FLRW) Universe without a cosmological constant [12,13]. This independent line of evidence, already apparent by the mid-1990s, provided an early indication that matter alone could not account for the observed expansion history. Although the component driving this acceleration is commonly denoted “dark energy” within the framework of General Relativity (GR), its fundamental origin remains unclear. This accelerated expansion can be modeled by a component with negative pressure. The cosmological constant is the simplest candidate, yet it faces severe theoretical challenges related to fine-tuning and the large discrepancy between the theoretical and observed vacuum energy density [14,15,16].
Although the ΛCDM model, which incorporates the cosmological constant and cold dark matter (CDM), successfully explains a wide range of observations, it faces a serious problem when calibrated with the Planck 2018 parameters [17], known as the Hubble tension, which refers to the discrepancy between late-time and early-Universe determinations of the Hubble constant [18]. In addition to the Hubble tension, the latest BAO measurements from DESI DR2 suggest a possible deviation from a cosmological constant, indicating a nontrivial evolution of dark energy when combined with CMB and supernova datasets [11]. This provides an important motivation for considering more complicated cosmological models than GR supplemented by a pure cosmological constant.
Consequently, significant efforts have been devoted to constructing dark energy phenomenologies by modifying the geometric sector of the Einstein–Hilbert action. Modified gravity approaches have been investigated as alternatives or complements to dark energy and dark matter, in certain regimes they have been applied to galactic rotation curves, cluster dynamics and various cosmological observations [19,20,21,22,23,24,25,26,27]. Notably, theories can naturally produce inflationary dynamics (e.g., Starobinsky inflation), account for the late-time acceleration, and, in some contexts, mimic effects usually attributed to dark matter. The compatibility of gravity with observational data is well established [28,29,30,31].
Beyond gravity, other extensions have been proposed to tackle open problems in cosmology. Examples include scalar Gauss–Bonnet, , gravity [32,33], gravity (where denotes the torsion scalar) [34,35], and gravity (where Q denotes the non-metricity scalar) [36,37,38,39,40,41]. These frameworks explore different geometric ingredients and offer complementary phenomenology; nevertheless, consistency with local tests and with the full set of cosmological observations must be established case by case.
Bertolami et al. [42] extended gravity by incorporating an explicit coupling between an arbitrary function of the Ricci scalar, R, and the matter Lagrangian density . This approach introduces a non-minimal interaction between matter and space-time geometry at the action level. Further generalization was explored in [43], where the gravitational field’s Lagrangian was proposed as a general function of both R and . In gravity, the intrinsic properties of matter are presumed to be encapsulated within the matter Lagrangian . Harko and Lobo [44] subsequently broadened this concept to encompass arbitrary couplings between matter and geometry. More recently, Harko et al. [45] introduced another extension of General Relativity, termed modified gravity. In this framework, the gravitational Lagrangian is an arbitrary function of the Ricci scalar, R, and the trace, T, of the energy–momentum tensor. This T-dependence may be interpreted phenomenologically as an effective description of imperfect fluids, particle production effects, or quantum contributions. However, it generically leads to nonconservation of the energy–momentum tensor and to an additional force that can modify the motion of test particles, as discussed in Ref. [45].
Several works have examined the cosmological and astrophysical implications of gravity [46,47,48,49,50,51,52,53,54,55], and some studies have investigated its weak-field and solar-system limits under specific assumptions [56]. Other investigations have discussed possible impacts on galactic dynamics [57], deviations from geodesic motion [58], and gravitational lensing phenomena [59]. These results are model dependent and should be interpreted with the appropriate caveats.
In many previous works, the common strategy is to assume a specific functional form for and then constrain its parameters with observational data [60]. While useful, this procedure may introduce model bias because the outcome depends strongly on the assumed parametrization. In this work, we pursue a different strategy based on machine-learning techniques, aiming to reconstruct the functional form of directly from observational data without assuming any predefined model.
For this purpose, we employ genetic algorithms, a heuristic optimization method that iteratively refines candidate solutions until a function that adequately matches the data is obtained. Alternative non-parametric techniques, such as Gaussian processes [61,62] and artificial neural networks [63,64], have also been used in cosmology. GA-based reconstructions present the advantage of being largely independent of a prior choice of functional form, for example, Gaussian process reconstructions can be sensitive to the kernel choice, while neural network results depend on the selection of hyperparameters and typically require large training sets.
Since the equations of motion in gravity can be rather complex, in this study we focus on the case originally proposed in [45]. In this formulation, the additional term modifies the effective coupling between matter and curvature, leading to a non-minimal interaction that can alter the dynamics of both matter and spacetime. Such a modification has been suggested as a possible mechanism for mimicking dark energy effects or for modeling effective matter interactions. To reconstruct in a model-independent way, we employ Hubble parameter measurements from cosmic chronometers (CC), baryon acoustic oscillations (BAO), and the DESI data release. Our procedure consists of first reconstructing using GA, which then serves as the basis for deriving the corresponding functional form of within the framework through the modified Friedmann equations.
2. Gravity
The theory of gravity is a well-known extension of General Relativity, initially proposed by Harko et al. [45]. In this framework, the gravitational action is assumed to depend on an arbitrary function of both the Ricci scalar, R, and the trace of the energy-momentum tensor, T. The corresponding action is given by
where g is the determinant of the metric, , and denotes the matter Lagrangian density. The energy–momentum tensor associated with the matter content is derived from the matter Lagrangian density and its trace is defined as
and , respectively. If the matter Lagrangian density depends explicitly on the metric tensor components, , but not on their derivatives, the energy–momentum tensor reduces to
By varying the action with respect to the metric tensor, one derives the field equations of the gravity theory, which take the following form
where and denote the partial derivatives of the function with respect to R and T, respectively. The symbol denotes the covariant derivative, and the operator corresponds to the d’Alembertian operator, while the tensor is defined as .
In this work, we consider that the matter content of the Universe can be modeled as a perfect fluid, whose energy-momentum tensor is given by
where and p denote the energy density and pressure of the fluid, respectively, and is the four-velocity of the fluid satisfying . The trace of the energy-momentum tensor is then given by
The equations of gravity are more complicated than those of General Relativity, even when adopting a spatially homogeneous and isotropic Friedmann–Lemaître–Robertson–Walker (FLRW) background. To address the resulting complexity, various functional forms of have been proposed in the literature to facilitate the resolution of the modified equations. Among the most commonly studied examples are models of the type , , where and are arbitrary functions of R and T, and and are real parameters [45,65,66,67,68,69], and [70], etc.
In the present work, we assume that , where is an arbitrary function of T. The dependence on T reflects a non-minimal coupling between matter and geometry. This assumption has been considered in several previous studies [53,68,71,72,73]. The gravitational field equations, Equation (4), become
with . The field equations then take the form
In the case of dust with , the gravitational field equations reduce to
The cosmological background is assumed to be spatially homogeneous and isotropic, described by a flat FLRW metric
where is the scale factor. Taking into account this metric, Equation (9) yields the modified Friedmann equations in gravity as follows:
where denotes the Hubble parameter, the dot stands for the derivative with respect to cosmic time t, and is the matter energy density.
3. Analysis and Results
3.1. Genetic Algorithms
In this work, we use genetic algorithms to reconstruct the functional form of gravity in a model-independent manner. To place this approach in a broader perspective, machine learning, a branch of artificial intelligence, provides a framework for extracting patterns from data and constructing predictive models. Within this framework, GA constitutes a stochastic symbolic regression technique aimed at identifying analytic functions that best reproduce observational data. Unlike supervised methods, which rely on labeled datasets, GAs perform regression without predefined models, making them well suited for cosmological applications where theoretical assumptions must be minimized.
The algorithm begins with a randomly generated population of candidate functions, each constructed from a predefined set of elementary operations (the “grammar”), including polynomials, rational functions, trigonometric and exponential terms, and the basic arithmetic operators (). The fitness of each candidate is evaluated using a statistic with respect to the observational data. The most successful candidates are retained through tournament selection [74] and refined using two stochastic operators: crossover, which combines elements of different candidates, and mutation, which introduces random modifications. This iterative procedure, carried out over many generations, progressively improves the accuracy of the candidate functions. Importantly, GA does not require complex initial expressions; more elaborate and accurate functional forms emerge dynamically through repeated applications of crossover and mutation. A schematic representation of the algorithmic flow adopted in our GA implementation is shown in Figure 1 of Ref. [75].
Our primary objective is to reconstruct gravity, which depends directly on the Hubble parameter, . The reconstruction is carried out in two steps. First, we reconstruct using the GA. The initial population of trial functions is generated under minimal physical priors, the Hubble parameter satisfies , all functions are continuous and differentiable, and no singularities are permitted within the redshift range of the data. These conditions exclude unphysical solutions and suppress overfitting while maintaining model independence, i.e., without adopting a specific dark energy parametrization or gravitational model. In the second step, the reconstructed is used to derive the function both numerically and analytically within the framework of .
Each candidate is then evaluated against the data, and the best-performing functions are refined through crossover and mutation over multiple generations. Independent runs with different random seeds are performed to ensure a thorough exploration of the functional space. The outcome of this stage is a smooth function that describes the reconstructed cosmic expansion history.
Uncertainties on the reconstructed function are estimated following the analytic prescription of Refs. [76,77], which computes errors through a path integral evaluation over the functional space explored by the GA. This approach has been validated against Fisher matrix estimates and the bootstrap Monte Carlo method, yielding consistent and robust results.
3.2. Reconstruction of Hubble Data
In this section, we make use of the Hubble parameter measurements, , obtained through two complementary techniques. The first one exploits the clustering of galaxies and quasars, where the position of the baryon acoustic oscillation peak along the line-of-sight direction provides a direct probe of the expansion rate [78]. The second one is the differential age method, commonly referred to as the cosmic chronometer approach. This method relies on the relation between the Hubble parameter and the time derivative of the redshift of passively evolving galaxies, expressed as [79]
which allows the estimation of by measuring relative age differences in massive early type galaxies at different redshifts.
For our analysis, we use 63 data points, including 32 measurements from the CC method and 33 from BAO observations. The BAO dataset consists of 26 previously published measurements together with five recent points from the Dark Energy Spectroscopic Instrument collaboration [80]. Since CC measurements are not independent of each other and some BAO measurements are correlated with one another, we incorporate the corresponding covariance matrices in our analysis in order to improve the robustness of the reconstruction. In particular, for CC measurements, the sources of uncertainty may arise from factors such as stellar metallicity and contamination by younger stellar populations, which are generally uncorrelated between objects at different redshifts. Nonetheless, additional systematic uncertainties can result from the use of a common stellar population synthesis model, particularly related to the choice of the initial mass function and stellar libraries. A more detailed discussion of the origin and modeling of these systematic errors can be found in Ref. [81]. In addition, some of the BAO data are correlated either because they originate from the same survey analysis or due to partial overlap between galaxy samples. The corresponding covariance matrices for these data points are publicly available in the cited references. A summary of the full dataset is provided in Table 1.

Table 1.
Compilation of measurements with their corresponding uncertainties , expressed in km s−1 Mpc−1, from CC, BAO, and DESI data, used in the present study.
To infer the cosmic expansion history from the measurements, we adopt a non-parametric reconstruction of the Hubble parameter using genetic algorithms. The likelihood function is evaluated through the Chi-squared statistic, which depends on whether datasets are correlated or uncorrelated. For correlated data, we use
while for uncorrelated points it simplifies to the standard form
where and are the observed values and uncertainties of the Hubble parameter at redshift , respectively, denotes the GA reconstruction, is the covariance matrix, and N is the number of data points considered. The total chi-squared is then
A key feature of the GA approach is that no prior assumptions are imposed on the underlying cosmological model, such as the dark energy parametrization or spatial flatness. This guarantees that the reconstruction is model-independent and minimizes theoretical bias. Moreover, the iterative nature of GA allows the algorithm to avoid premature convergence to local minima, enhancing the likelihood of identifying the global solution. For the dataset summarized in Table 1, GA yields the best-fit reconstruction of the form
with km s−1 Mpc−1. Figure 1 shows the reconstructed Hubble parameter compared to the ΛCDM model.
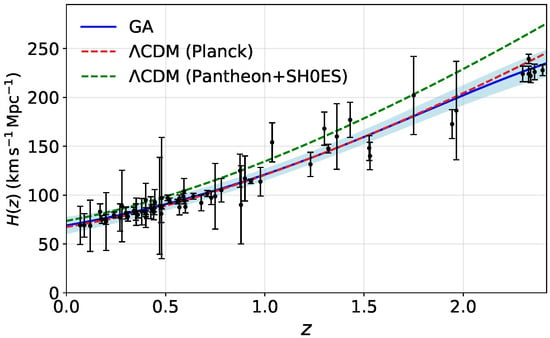
Figure 1.
Compilation of measurements with the GA best-fit (solid blue curve), the ΛCDM model from Planck 2018 (dashed red curve), and the ΛCDM model from Pantheon+SH0ES (dashed green curve). The light blue region represents the ( confidence level) for the GA model, while the black points with error bars represent the observational data.
3.3. Numerical and Analytical Reconstruction of Gravity
In this section, we reconstruct the functional form of within gravity using the Hubble parameter , previously obtained through the application of genetic algorithms to observational data. Within the framework of gravity, the dynamics of are governed by the Friedmann equation, Equation (11), which can be expressed in terms of the redshift. Considering a matter-dominated Universe with vanishing pressure (), we have . In this case, the framework behaves as a modified gravity theory with an effective cosmological constant that varies with redshift, determined by the Hubble parameter, .
By introducing
where the prime denotes the derivative with respect to z, and
The Friedmann equation, Equation (11), can be recast as
Substituting the equation of state for matter into this expression yields a differential equation for
To solve this equation numerically, we specify initial conditions by evaluating the Friedmann equation at , under the approximation . This assumption ensures that the effective gravitational coupling, [45], coincides with Newton’s constant at the present epoch, so that the model recovers General Relativity and remains consistent with local gravitational tests. This leads to
where we adopt from the Planck 2018 results [17]. Using the reconstructed , we numerically determine the corresponding , as shown in the left panel Figure 2, along with the associated confidence regions.
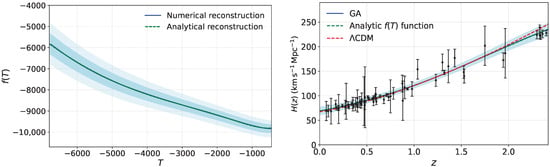
Figure 2.
(Left) Independent reconstruction of the function from observational data using GA. Numerical reconstruction (blue curve), best-fit analytical model (dashed green curve), (68%) and (95%) confidence levels (blue and light blue regions, respectively). (Right) Evolution of from GA (blue curve with region), analytical reconstruction (dashed green curve), and ΛCDM model (dashed red curve).
To gain deeper insight into the behavior of the reconstructed function, we next seek an analytical representation of . This serves both as a cross-validation of the numerical reconstruction and as a more practical expression for subsequent applications. To this end, we employ a second genetic algorithm directly on the numerical solution, in order to search for an analytic function that best describes the data. Unlike approaches in which a specific parametric form is postulated and then fitted to the data, our method allows GA to identify the analytic structure directly, thus avoiding potential bias from an incorrect model choice. This procedure takes advantage of the ability of genetic algorithms to converge towards the global optimum.
Our analysis indicates that the optimal analytic expression is given by
As illustrated in the left panel of Figure 2, this function (dashed green curve) provides an excellent approximation to the numerically reconstructed (blue curve).
As an additional consistency check, we compare the evolution of the Hubble parameter predicted by three models: (i) the direct GA reconstruction, (ii) the analytic function obtained from the second genetic algorithm, Equation (23), and (iii) the standard ΛCDM cosmology, using Planck 2018 data. The results are shown in the right panel of Figure 2. For redshifts , the three curves are in close agreement. At higher redshifts, deviations appear, although this may be attributed to the limited availability of direct measurements in that range. This comparison reinforces the robustness of our reconstruction and highlights the potential of the genetic algorithm approach for probing the functional structure of gravity.
4. Conclusions
In this work, we have applied genetic algorithms to the gravity framework, focusing on the reconstruction of the function within the model . Using measurements of the Hubble parameter from cosmic chronometers, baryon acoustic oscillations, and the DESI data release, we reconstructed both numerically and analytically. This formulation incorporates matter effects via the trace T, while simplifying the structure of the Friedmann equations and facilitating their use in cosmological applications.
Our methodology relied on genetic algorithms to reconstruct the Hubble parameter in a model-independent way, without assuming any predefined functional form. The resulting is consistent with the standard ΛCDM model using Planck 2018 data [17], and served as the basis for the subsequent numerical determination of through the Friedmann equation, Equation (11). To obtain an analytic expression, we applied a second genetic algorithm directly to the numerical reconstruction. The resulting function, Equation (23) was derived without assuming a specific model and provides an excellent fit to the numerical solution.
As a validation step, we compared the Hubble parameter, , evolution derived from three cases: (i) direct GA reconstruction, (ii) analytic model, and (iii) the standard ΛCDM cosmology. The three curves exhibit close agreement for , while differences at higher redshift may be attributed to the lack of direct measurements. This consistency check reinforces the robustness of our reconstruction and highlights the ability of GA-based methods to capture the essential cosmological dynamics in modified gravity frameworks.
Compared with other machine learning techniques such as Gaussian processes and artificial neural networks, the GA approach presents several advantages. In Gaussian processes, the choice of kernel can significantly influence the outcome of the reconstruction, while in neural networks the quality of the results strongly depends on hyperparameter selection and the availability of large training sets. By contrast, genetic algorithms operate without predefined assumptions on the form of the reconstructed functions and naturally provide analytic expressions that accurately describe the data.
In light of the ongoing Hubble tension, a recent study shows that when Type Ia supernovae and BAO data are treated as uncalibrated cosmic standards within a flat FLRW cosmology (that is, without an external distance calibration), using cosmic chronometers as the only probe of the absolute expansion timescale yields an value very close to the Planck value [101]. Complementary analyses combining DESI BAO measurements and Type Ia supernovae data have suggested that the Hubble tension may arise from a late-time dynamical behavior of dark energy. Using a non-parametric reconstruction of the dark energy equation of state , this study finds that decreases as a function of redshift, implying that a redshift-dependent may alleviate the discrepancy between local and early Universe determinations of the Hubble constant [102]. We note, however, that this conclusion can be sensitive to the reconstruction method and to the dataset used; therefore, the claim is still debated. Nonetheless, this possibility further motivates the exploration of modified gravity or dynamical dark energy models that allow for deviations from ΛCDM at low redshift.
The results of this work reveal that GA-based reconstructions constitute a promising tool for probing the functional structure of modified gravity theories. Future works will extend the present analysis by incorporating additional observational probes, including type Ia supernovae, large-scale structure, and CMB data, to impose tighter constraints on the viability of gravity.
The results of this work indicate that GA-based reconstructions provide a promising, model-independent framework for exploring the functional form of modified gravity theories such as . It is also important to mention that certain forms of gravity can substantially modify the evolution of matter perturbations, which may render some models inconsistent with the observed cosmic evolution [103]. In particular, in the sub-Hubble regime (), where k denotes the comoving wavenumber, the evolution of the matter density contrast reduces to a second-order differential equation, whose solution may deviate significantly from the ΛCDM prediction for well-motivated Lagrangians under the quasi-static approximation. This may lead to accelerated growth of structure on scales Mpc, which has been proposed as a solution to the Hubble and BAO tensions faced by ΛCDM while retaining a background Planck cosmology [104]. In this work, our reconstruction is limited to the background cosmological dynamics. Future studies will extend the present analysis by incorporating additional observational probes, such as Type Ia supernovae and large-scale structure data, in order to impose tighter constraints on the viability of gravity.
Author Contributions
Conceptualization, R.E.O.; Methodology, R.E.O.; Software, R.E.O.; Validation, R.E.O., D.M., A.B. and T.O.; Formal analysis, R.E.O. and A.B.; Resources, R.E.O.; Data curation, R.E.O. and A.B.; Writing—original draft preparation, R.E.O.; Writing—review and editing, D.M., A.B. and T.O.; Visualization, R.E.O.; Supervision, T.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
There are no new data associated with this article.
Acknowledgments
R.E.O. is grateful for support from the PhD-Associate Scholarship—PASS grant (number 29 UMP2023) provided by the National Center for Scientific and Technical Research in Morocco.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Riess, A.G. et al. [Supernova Search Team Collaboration]. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S. et al. [Supernova Cosmology Project Collaboration]. Measurements of Ω and Λ from 42 High Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Riess, A.G. et al. [Supernova Search Team collaboration]. Type Ia supernova discoveries at z > 1 from the Hubble Space Telescope: Evidence for past deceleration and constraints on dark energy evolution. Astrophys. J. 2004, 607, 665. [Google Scholar] [CrossRef]
- Bennett, C.L. et al. [WMAP Collaboration]. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Preliminary maps and basic results. Astrophys. J. Suppl. 2003, 148, 1. [Google Scholar] [CrossRef]
- Spergel, D.N. et al. [WMAP Collaboration]. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175. [Google Scholar] [CrossRef]
- Spergel, D.N. et al. [WMAP Collaboration]. Wilkinson Microwave Anisotropy Probe (WMAP) three year results: Implications for cosmology. Astrophys. J. Suppl. 2007, 170, 377. [Google Scholar] [CrossRef]
- Hawkins, E.; Maddox, S.; Cole, S.; Madgwick, D.; Norberg, P.; Peacock, J.; Baldry, I.; Baugh, C.; Bland-Hawthorn, J.; Bridges, T.; et al. The 2dF Galaxy Redshift Survey: Correlation functions, peculiar velocities and the matter density of the universe. Mon. Not. R. Astron. Soc. 2003, 346, 78. [Google Scholar] [CrossRef]
- Tegmark, M. et al. [SDSS Collaboration]. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 103501. [Google Scholar] [CrossRef]
- Cole, S. et al. [2dFGRS Collaboration]. The 2dF Galaxy Redshift Survey: Power-spectrum analysis of the final dataset and cosmological implications. Mon. Not. R. Astron. Soc. 2005, 362, 505. [Google Scholar] [CrossRef]
- Eisenstein, D.J. et al. [SDSS Collaboration]. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560. [Google Scholar] [CrossRef]
- Karim, M.A. et al. [DESI Collaboration]. DESI DR2 results. II. Measurements of baryon acoustic oscillations and cosmological constraints. Phys. Rev. D 2025, 112, 083515. [Google Scholar] [CrossRef]
- Jimenez, R.; Thejll, P.; Jørgensen, U.G.; MacDonald, J.; Pagel, B. Ages of globular clusters: A new approach. Mon. Not. R. Astron. Soc. 1996, 282, 926. [Google Scholar] [CrossRef]
- Bolte, M.; Hogan, C.J. Conflict over the age of the Universe. Nature 1995, 376, 399. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef]
- Tsujikawa, S. Modified gravity models of dark energy. Lect. Notes Phys. 2010, 800, 99. [Google Scholar]
- Aghanim, N. et al. [Planck Collaboration]. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Valentino, E.D., et al. [CosmoVerse Network]. The CosmoVerse White Paper: Addressing observational tensions in cosmology with systematics and fundamental physics. Phys. Dark Univ. 2025, 49, 101965. [Google Scholar] [CrossRef]
- Capozziello, S.; Lambiase, G. Higher-order corrections to the effective gravitational action from Noether symmetry approach. Gen. Relat. Grav. 2000, 32, 295. [Google Scholar] [CrossRef]
- Capozziello, S.; Nesseris, S.; Perivolaropoulos, L. Reconstruction of the Scalar-Tensor Lagrangian from a LCDM Background and Noether Symmetry. J. Cosmol. Astropart. Phys. 2007, 2007, 009. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity and its reconstruction from the universe expansion history. J. Phys. Conf. Ser. 2007, 66, 012005. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. A Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Capozziello, S.; Piedipalumbo, E.; Rubano, E.; Scudellaro, P. Noether symmetry approach in phantom quintessence cosmology. Phys. Rev. D 2009, 80, 104030. [Google Scholar] [CrossRef]
- Capozziello, S.; Martin-Moruno, P.; Rubano, C. Exact f (R)-cosmological model coming from the request of the existence of a Noether symmetry. AIP Conf. Proc. 2009, 1122, 213. [Google Scholar]
- De Felice, A.; Tsujikawa, S. f (R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Non-singular exponential gravity: A simple theory for early- and late-time accelerated expansion. Phys. Rev. D 2011, 83, 086006. [Google Scholar] [CrossRef]
- Jamil, M.; Mahomed, F.M.; Momeni, D. Noether symmetry approach in f (R)–tachyon model. Phys. Lett. B 2011, 702, 315. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f (R) gravity. J. Exp. Theor. Phys. Lett. 2007, 86, 157. [Google Scholar] [CrossRef]
- Bamba, K.; Nojiri, S.; Odintsov, S.D. The Universe future in modified gravity theories: Approaching the finite-time future singularity. J. Cosmol. Astropart. Phys. 2008, 2008, 045. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155. [Google Scholar] [CrossRef]
- Ladghami, Y.; Asfour, B.; Bouali, A.; Errahmani, A.; Ouali, T. 4D-EGB black holes in RPS thermodynamics. Phys. Dark Univ. 2023, 41, 101261. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Sami, M. Dark energy cosmology from higher-order, string-inspired gravity and its reconstruction. Phys. Rev. D 2006, 74, 046004. [Google Scholar] [CrossRef]
- Ouardi, R.E.; Bouali, A.; Bojaddaini, I.E.; Errahmani, A.; Ouali, T. Model-Independent Reconstruction of f (T) Gravity Using Genetic Algorithms. Chin. Phys. C 2025, 49, 115106. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without an inflaton. Phys. Rev. D 2007, 75, 084031. [Google Scholar] [CrossRef]
- Koussour, M.; Dahmani, S.; Bennai, M.; Ouali, T. Cosmic jerk parameter in symmetric teleparallel cosmology. Eur. Phys. J. Plus 2023, 138, 179. [Google Scholar] [CrossRef]
- Mhamdi, D.; Bouali, A.; Dahmani, S.; Errahmani, A.; Ouali, T. Cosmological constraints on f (Q) gravity with redshift space distortion data. Eur. Phys. J. C 2024, 84, 310. [Google Scholar] [CrossRef]
- Enkhili, O.; Dahmani, S.; Mhamdi, D.; Ouali, T.; Errahmani, A. Cosmological constraints on a dynamical dark energy model in F(Q) gravity. Eur. Phys. J. C 2024, 84, 806. [Google Scholar] [CrossRef]
- Mhamdi, D.; Bargach, F.; Dahmani, S.; Bouali, A.; Ouali, T. Constraints on power law and exponential models in f (Q) gravity. Phys. Lett. B 2024, 859, 139113. [Google Scholar] [CrossRef]
- Heisenberg, L. Review on f (Q) gravity. Phys. Rept. 2024, 1066, 1–78. [Google Scholar] [CrossRef]
- Ouardi, R.E.; Bouali, A.; Dahmani, S.; Errahmani, A.; Ouali, T. Exploring f (Q) gravity through model-independent reconstruction with genetic algorithms. Phys. Lett. B 2025, 863, 139374. [Google Scholar] [CrossRef]
- Bertolami, O.; Boehmer, C.G.; Harko, T.; Lobo, F.S.N. Extra force in f (R) modified theories of gravity. Phys. Rev. D 2007, 75, 104016. [Google Scholar] [CrossRef]
- Harko, T. Modified gravity with arbitrary coupling between matter and geometry. Phys. Lett. B 2008, 669, 376. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N. f (R,Lm) gravity. Eur. Phys. J. C 2010, 70, 373. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f (R, T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Harko, T. Thermodynamic interpretation of the generalized gravity models with geometry-matter coupling. Phys. Rev. D 2014, 90, 044067. [Google Scholar] [CrossRef]
- Baffou, E.H.; Houndjo, M.J.S.; Rodrigues, M.E.; Kpadonou, A.V.; Tossa, J. Cosmological evolution in f (R, T) theory with collisional matter. Phys. Rev. D 2015, 92, 084043. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Arbanil, J.D.V.; Malheiro, M. Stellar equilibrium configurations of compact stars in f (R, T) theory of gravity. J. Cosmol. Astropart. Phys. 2016, 2016, 005. [Google Scholar] [CrossRef]
- Yousaf, Z.; Bamba, K.; Zaeem-ul-Haq Bhatti, M. Causes of irregular energy density in f (R, T) gravity. Phys. Rev. D 2016, 93, 124048. [Google Scholar] [CrossRef]
- Alves, M.E.S.; Moraes, P.H.R.S.; de Araujo, J.C.N.; Malheiro, M. Gravitational waves in f (R, T) and f (R, Tϕ) theories of gravity. Phys. Rev. D 2016, 94, 024032. [Google Scholar] [CrossRef]
- Zubair, M.; Azmat, H.; Noureen, I. Dynamical analysis of cylindrically symmetric anisotropic sources in f (R, T) gravity. Eur. Phys. J. C 2017, 77, 169. [Google Scholar] [CrossRef]
- Sharif, M.; Nawazish, I. Cosmological analysis of scalar field models in f (R, T) gravity. Eur. Phys. J. C 2017, 77, 198. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. Modeling wormholes in f (R, T) gravity. Phys. Rev. D 2017, 96, 044038. [Google Scholar] [CrossRef]
- Bouali, A.; Chaudhary, H.; Harko, T.; Lobo, F.S.N.; Ouali, T.; Pinto, M.A.S. Observational constraints and cosmological implications of scalar–tensor f (R, T) gravity. Mon. Not. R. Astron. Soc. 2023, 526, 4192–4208. [Google Scholar] [CrossRef]
- Errahmani, A.; Bouali, A.; Dahmani, S.; Bojaddaini, I.E.; Ouali, T. Constraining dark energy equations of state in F(R, T) gravity. Phys. Dark Univ. 2024, 45, 101512. [Google Scholar] [CrossRef]
- Shabani, H.; Farhoudi, M. Cosmological and solar system consequences of f (R, T) gravity models. Phys. Rev. D 2014, 90, 044031. [Google Scholar] [CrossRef]
- Zaregonbadi, R.; Farhoudi, M.; Riazi, N. Dark matter from f (R, T) gravity. Phys. Rev. D 2016, 94, 084052. [Google Scholar] [CrossRef]
- Baffou, E.H.; Houndjo, M.J.S.; Rodrigues, M.E.; Kpadonou, A.V.; Tossa, J. Geodesic deviation equation in f (R, T) gravity. Chin. J. Phys. 2017, 55, 467–477. [Google Scholar] [CrossRef]
- Alhamzawi, A.; Alhamzawi, R. Gravitational lensing by f (R, T) gravity. Int. J. Mod. Phys. D 2016, 25, 1650020. [Google Scholar] [CrossRef]
- Rudra, P.; Giri, K. Observational constraint in f (R, T) gravity from the cosmic chronometers and some standard distance measurement parameters. Nucl. Phys. B 2021, 967, 115428. [Google Scholar] [CrossRef]
- Seikel, M.; Clarkson, C.; Smith, M. Reconstruction of dark energy and expansion dynamics using Gaussian processes. J. Cosmol. Astropart. Phys. 2012, 2012, 036. [Google Scholar] [CrossRef]
- Fortunato, J.A.S.; Moraes, P.H.R.S.; de Júnior, J.G.; Brito, E. Search for the f (R, T) gravity functional form via gaussian processes. Eur. Phys. J. C 2024, 84, 198. [Google Scholar] [CrossRef]
- de Dios Rojas Olvera, J.; Gómez-Vargas, I.; Vázquez, J.A. Observational cosmology with artificial neural networks. Universe 2022, 8, 120. [Google Scholar] [CrossRef]
- Chantada, A.T.; Landau, S.J.; Protopapas, P.; Scóccola, C.G.; Garraffo, C. Cosmology-informed neural networks to solve the background dynamics of the Universe. Phys. Rev. D 2023, 107, 063523. [Google Scholar] [CrossRef]
- Houndjo, M.J.S. Reconstruction of f (R, T) gravity describing matter dominated and accelerated phases. Int. J. Mod. Phys. D 2012, 21, 1250003. [Google Scholar] [CrossRef]
- Houndjo, M.J.S.; Piattella, O.F. Reconstructing f (R, T) gravity from holographic dark energy. Int. J. Mod. Phys. D 2012, 21, 1250024. [Google Scholar] [CrossRef]
- Houndjo, M.J.S.; Batista, C.E.M.; Campos, J.P.; Piattella, O.F. Finite-time singularities in f (R, T) gravity and the effect of conformal anomaly. Can. J. Phys. 2013, 91, 548. [Google Scholar] [CrossRef]
- Alvarenga, F.G.; Houndjo, M.J.S.; Monwanou, A.V.; Orou, J.B.C. Testing some f (R, T) gravity models from energy conditions. J. Mod. Phys. 2013, 4, 130–139. [Google Scholar] [CrossRef]
- Pasqua, A.; Chattopadhyay, S.; Khomenko, I. A reconstruction of modified holographic Ricci dark energy in f (R, T) gravity. Can. J. Phys. 2013, 91, 632. [Google Scholar] [CrossRef]
- Chakraborty, S. An alternative f (R, T) gravity theory and the dark energy problem. Gen. Relativ. Gravit. 2013, 45, 2039. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Correa, R.A.C.; Lobato, R.V. Analytical general solutions for static wormholes in f (R, T) gravity. J. Cosmol. Astropart. Phys. 2017, 2017, 029. [Google Scholar] [CrossRef]
- Velten, H.; Caramês, T.R.P. Cosmological inviability of f (R, T) gravity. Phys. Rev. D 2017, 95, 123536. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. Wormholes in exponential f (R, T) gravity. Eur. Phys. J. C 2019, 79, 677. [Google Scholar] [CrossRef]
- Bogdanos, C.; Nesseris, S. Genetic Algorithms and Supernovae Type Ia Analysis. J. Cosmol. Astropart. Phys. 2009, 2009, 006. [Google Scholar] [CrossRef]
- Kamerkar, A.; Nesseris, S.; Pinol, L. Machine learning cosmic inflation. Phys. Rev. D 2023, 108, 43509. [Google Scholar] [CrossRef]
- Nesseris, S.; García-Bellido, J. A new perspective on Dark Energy modeling via Genetic Algorithms. J. Cosmol. Astropart. Phys. 2012, 2012, 033. [Google Scholar] [CrossRef]
- Arjona, R.; Nesseris, S. Hints of dark energy anisotropic stress using machine learning. J. Cosmol. Astropart. Phys. 2020, 2020, 042. [Google Scholar] [CrossRef]
- Gaztanaga, E.; Cabre, A.; Hui, L. Clustering of luminous red galaxies—IV. Baryon acoustic peak in the line-of-sight direction and a direct measurement of H(z). Mon. Not. R. Astron. Soc. 2009, 399, 1663–1680. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining cosmological parameters based on relative galaxy ages. Astrophys. J. 2002, 573, 37. [Google Scholar] [CrossRef]
- Adame, A.G. et al. [DESI Collaboration]. DESI 2024 VI: Cosmological constraints from the measurements of baryon acoustic oscillations. J. Cosmol. Astropart. Phys. 2025, 2025, 021. [Google Scholar] [CrossRef]
- Moresco, M.; Jimenez, R.; Verde, L.; Cimatti, A.; Pozzetti, L. Setting the stage for cosmic chronometers. II. Impact of stellar population synthesis models systematics and full covariance matrix. Astrophys. J. 2020, 898, 82. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Yuan, S.; Liu, S.; Zhang, T.-J.; Sun, Y.-C. Four new observational H(z) data from luminous red galaxies in the Sloan Digital Sky Survey data release seven. Res. Astron. Astrophys. 2014, 14, 1221. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% Measurement of the Hubble Parameter at z ∼ 0.45: Direct Evidence of the Epoch of Cosmic Re-acceleration. J. Cosmol. Astropart. Phys. 2016, 2016, 014. [Google Scholar] [CrossRef]
- Jimenez, R.; Verde, L.; Treu, T.; Stern, D. Constraints on the equation of state of dark energy and the Hubble constant from stellar ages and the cosmic microwave background. Astrophys. J. 2003, 593, 622. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic chronometers: Constraining the equation of state of dark energy. I: H(z) measurements. J. Cosmol. Astropart. Phys. 2010, 2010, 008. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved Constraints on the Expansion Rate of the Universe up to z ∼ 1.1 from the Spectroscopic Evolution of Cosmic Chronometers. J. Cosmol. Astropart. Phys. 2012, 2012, 006. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Borghi, N.; Moresco, M.; Cimatti, A. Toward a Better Understanding of Cosmic Chronometers: A New Measurement of H(z) at z ∼ 0.7. Astrophys. J. Lett. 2022, 928, L4. [Google Scholar] [CrossRef]
- Moresco, M. Raising the Bar: New Constraints on the Hubble Parameter with Cosmic Chronometers at z ∼ 2. Mon. Not. R. Astron. Soc. 2015, 450, L16. [Google Scholar] [CrossRef]
- Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Väisänen, P. Age-dating luminous red galaxies observed with the Southern African Large Telescope. Mon. Not. R. Astron. Soc. 2017, 467, 3239–3254. [Google Scholar] [CrossRef]
- Anderson, L. et al. [BOSS Collaboration]. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 2014, 441, 24–62. [Google Scholar] [CrossRef]
- Oka, A.; Saito, S.; Nishimichi, T.; Taruya, A.; Yamamoto, K. Simultaneous constraints on the growth of structure and cosmic expansion from the multipole power spectra of the SDSS DR7 LRG sample. Mon. Not. R. Astron. Soc. 2014, 439, 2515–2530. [Google Scholar] [CrossRef]
- Wang, Y. et al. [BOSS Collaboration]. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Tomographic BAO analysis of DR12 combined sample in configuration space. Mon. Not. R. Astron. Soc. 2017, 469, 3762–3774. [Google Scholar] [CrossRef]
- Blake, C. et al. [WiggleZ Collaboration]. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z < 1. Mon. Not. R. Astron. Soc. 2012, 425, 405–414. [Google Scholar] [CrossRef]
- Alam, S. et al. [BOSS Collaboration]. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Chuang, C.H.; Wang, Y. Modelling the Anisotropic Two-Point Galaxy Correlation Function on Small Scales and Single-Probe Measurements of H(z), DA(z), and f (z)σ8(z) from the Sloan Digital Sky Survey DR7 Luminous Red Galaxies. Mon. Not. R. Astron. Soc. 2013, 435, 255–262. [Google Scholar] [CrossRef]
- Zhao, G.B. et al. [eBOSS Collaboration]. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: A tomographic measurement of cosmic structure growth and expansion rate based on optimal redshift weights. Mon. Not. R. Astron. Soc. 2019, 482, 3497–3513. [Google Scholar] [CrossRef]
- Busca, N.G. et al. [BOSS Collaboration]. Baryon acoustic oscillations in the Lyα forest of BOSS quasars. Astron. Astrophys. 2013, 552, A96. [Google Scholar] [CrossRef]
- Delubac, T. et al. [BOSS Collaboration]. Baryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
- Font-Ribera, A. et al. [BOSS Collaboration]. Quasar-Lyman α Forest Cross-Correlation from BOSS DR11: Baryon Acoustic Oscillations. J. Cosmol. Astropart. Phys. 2014, 2014, 027. [Google Scholar] [CrossRef]
- Guo, W.; Wang, Q.; Cao, S.; Biesiada, M.; Liu, T.; Lian, Y.; Jiang, X.; Mu, C.; Cheng, D. Newest measurements of Hubble constant from DESI 2024 baryon acoustic oscillation observations. Astrophys. J. Lett. 2025, 978, L33. [Google Scholar] [CrossRef]
- Jia, X.D.; Hu, J.P.; Gao, D.H.; Yi, S.X.; Wang, F.Y. The Hubble Tension resolved by the DESI Baryon Acoustic Oscillations Measurements. arXiv 2025, arXiv:2509.17454. [Google Scholar] [CrossRef]
- Alvarenga, F.G.; de la Cruz-Dombriz, A.; MHoundjo, J.S.; Rodrigues, M.E.; Saez-Gomez, D. Dynamics of scalar perturbations in f (R, T) gravity. Phys. Rev. D 2013, 87, 103526. [Google Scholar] [CrossRef]
- Banik, I.; Kalaitzidis, V. Testing the local void hypothesis using baryon acoustic oscillation measurements over the last 20 yr. Mon. Not. R. Astron. Soc. 2025, 540, 545–561. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).