Study of Singly Charmed Dibaryons in Quark Model
Abstract
1. Introduction
2. Quark Model and Resonating Group Method
2.1. The Chiral Quark Model
2.2. The Resonating Group Method
3. Results and Discussion
3.1. Wave Function Construction
3.2. The Effective Potential
3.3. Bound-State Calculation
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Urey, H.C.; Brickwedde, F.G.; Murphy, G.M. A Hydrogen Isotope of Mass 2. Phys. Rev. 1932, 39, 164–165. [Google Scholar] [CrossRef]
- Jaffe, R.L. Perhaps a Stable Dihyperon. Phys. Rev. Lett. 1977, 38, 617. [Google Scholar] [CrossRef]
- Kamae, T.; Fujita, T. Possible Existence of a Deeply Bound ΔΔ System. Phys. Rev. Lett. 1977, 38, 471–475. [Google Scholar] [CrossRef]
- Goldman, J.T.; Maltman, K.; Stephenson, G.J., Jr.; Schmidt, K.E.; Wang, F. An ’inevitable’ nonstrange dibaryon. Phys. Rev. C 1989, 51, 1889–1895. [Google Scholar] [CrossRef]
- Adlarson, P. et al. [WASA-at-COSY Collaboration] Isospin Decomposition of the Basic Double-Pionic Fusion in the Region of the ABC Effect. Phys. Lett. B 2013, 721, 229–236. [Google Scholar] [CrossRef]
- Goldman, J.T.; Maltman, K.; Stephenson, G.J., Jr.; Schmidt, K.E.; Wang, F. strangeness-3 dibaryon. Phys. Rev. Lett. 1987, 59, 627. [Google Scholar] [CrossRef] [PubMed]
- Oka, M. Flavor-octet dibaryons in the quark model. Phys. Rev. D 1988, 38, 298. [Google Scholar] [CrossRef] [PubMed]
- Silvestre-Brac, B.; Leandri, J. Systematics of q6 systems in a simple chromomagnetic model. Phys. Rev. D 1992, 45, 4221. [Google Scholar] [CrossRef]
- Dai, L.R.; Zhang, D.; Li, C.R.; Tong, L. Structures of NΩ and ΔΩ Dibaryons. Chin. Phys. Lett. 2007, 24, 389. [Google Scholar]
- Li, Q.B.; Shen, P.N. NΩ and ΔΩ dibaryons in SU(3) chiral quark model. Eur. Phys. J. A 2000, 8, 417–421. [Google Scholar] [CrossRef]
- Huang, H.X.; Ping, J.L.; Wang, F. Further study of the NΩ dibaryon within constituent quark models. Phys. Rev. C 2015, 92, 065202. [Google Scholar] [CrossRef]
- Chen, X.H.; Wang, Q.N.; Chen, W.; Chen, H.X. Mass spectra of NΩ dibaryons in the 3S1 and 5S1 channels. Phys. Rev. D 2021, 103, 094011. [Google Scholar] [CrossRef]
- Adam, J. et al. [STAR Collaboration] The Proton-Ω correlation function in Au + Au collisions at = 200 GeV. Phys. Lett. B 2019, 790, 490–497. [Google Scholar] [CrossRef]
- [ALICE Collaboration]. Unveiling the strong interaction among hadrons at the LHC. Nature 2020, 588, 232–238. [Google Scholar] [CrossRef]
- Yan, Y.; Huang, Q.; Yang, Y.; Huang, H.X.; Ping, J.L. Investigating the p-Ω interactions and correlation functions. Sci. China Phys. Mech. Astron. 2025, 68, 232012. [Google Scholar] [CrossRef]
- Aaij, R. et al. [LHCb Collaboration] Observation of the doubly charmed baryon Ξcc. Phys. Rev. Lett. 2017, 119, 112001. [Google Scholar]
- Lee, N.; Luo, Z.G.; Chen, X.L.; Zhu, S.L. Possible deuteron-like molecular states composed of heavy baryons. Phys. Rev. D 2011, 84, 014031. [Google Scholar] [CrossRef]
- Liu, Y.R.; Oka, M. ΛcΩ bound states revisited. Phys. Rev. D 2012, 85, 014015. [Google Scholar] [CrossRef]
- Meng, L.; Li, N.; Zhu, S.L. Deuteron-like states composed of two doubly charmed baryons. Phys. Rev. D 2017, 95, 114019. [Google Scholar] [CrossRef]
- Chen, R.; Wang, F.L.; Hosaka, A.; Liu, X. Exotic triple-charm deuteronlike hexaquarks. Phys. Rev. D 2018, 97, 114011. [Google Scholar] [CrossRef]
- Pan, Y.W.; Liu, M.Z. Triply charmed dibaryons in the one-boson exchange model. Phys. Rev. D 2020, 102, 054025. [Google Scholar] [CrossRef]
- Wang, Z.G. Triply-charmed dibaryon states or two-baryon scattering states from QCD sum rules. Phys. Rev. D 2020, 102, 034008. [Google Scholar] [CrossRef]
- Junnarkar, P.M.; Mathur, N. Study of three-flavored heavy dibaryons using lattice QCD. Phys. Rev. D 2022, 106, 054511. [Google Scholar] [CrossRef]
- Lyu, Y.; Tong, H.; Sugiura, T.; Aoki, S.; Doi, T.; Hatsuda, T.; Meng, J.; Miyamoto, T. Dibaryon with Highest Charm Number near Unitarity from Lattice QCD. Phys. Rev. Lett. 2021, 127, 072003. [Google Scholar] [CrossRef]
- Junnarkar, P.M.; Mathur, N. Spectrum of two-flavored spin-zero heavy dibaryons in lattice QCD. Phys. Rev. D 2025, 111, 014512. [Google Scholar] [CrossRef]
- Gal, A.; Garcilazo, H.; Valcarce, A.; Fernández-Caramés, T. Pion-assisted charmed dibaryon candidate. Phys. Rev. D 2014, 90, 014019. [Google Scholar] [CrossRef]
- Richard, J.M.; Valcarce, A.; Vijande, J. Very Heavy Flavored Dibaryons. Phys. Rev. Lett. 2020, 124, 212001. [Google Scholar] [CrossRef]
- Xia, Z.C.; Fan, S.J.; Zhu, X.M.; Huang, H.X.; Ping, J.L. Search for doubly heavy dibaryons in the quark delocalization color screening model. Phys. Rev. C 2022, 105, 025201. [Google Scholar] [CrossRef]
- Martín-Higueras, P.; Entem, D.R.; Ortega, P.G.; Segovia, J.; Fernández, F. Study of the ΩcccΩccc and ΩbbbΩbbb dibaryons in constituent quark model. arXiv 2024, arXiv:2406.19208. [Google Scholar] [CrossRef]
- Cui, Y.; Wu, Y.H.; Huang, H.X.; Ping, J.L.; Zhu, X.M. Search for singly charmed dibaryons in baryon-baryon scattering. Phys. Rev. D 2024, 110, 114055. [Google Scholar] [CrossRef]
- Valcarce, A.; Garcilazo, H.; Fernandez, F.; Gonzalez, P. Quark-model study of few-baryon systems. Rep. Prog. Phys. 2005, 68, 965–1042. [Google Scholar] [CrossRef]
- Vijande, J.; Fernandez, F.; Valcarce, A. Constituent quark model study of the meson spectra. J. Phys. G 2005, 31, 481. [Google Scholar] [CrossRef]
- Beringer, J. et al. [Particle Data Group] Review of Particle Physics. Phys. Rev. D 2012, 86, 010001. [Google Scholar] [CrossRef]
- Kamimura, M. Chapter V. A Coupled Channel Variational Method for Microscopic Study of Reactions between Complex Nuclei. Prog. Theor. Phys. Suppl. 1977, 62, 236–294. [Google Scholar] [CrossRef]
- Bali, G.S. QCD forces and heavy quark bound states. Phys. Rep. 2001, 343, 1–136. [Google Scholar] [CrossRef]
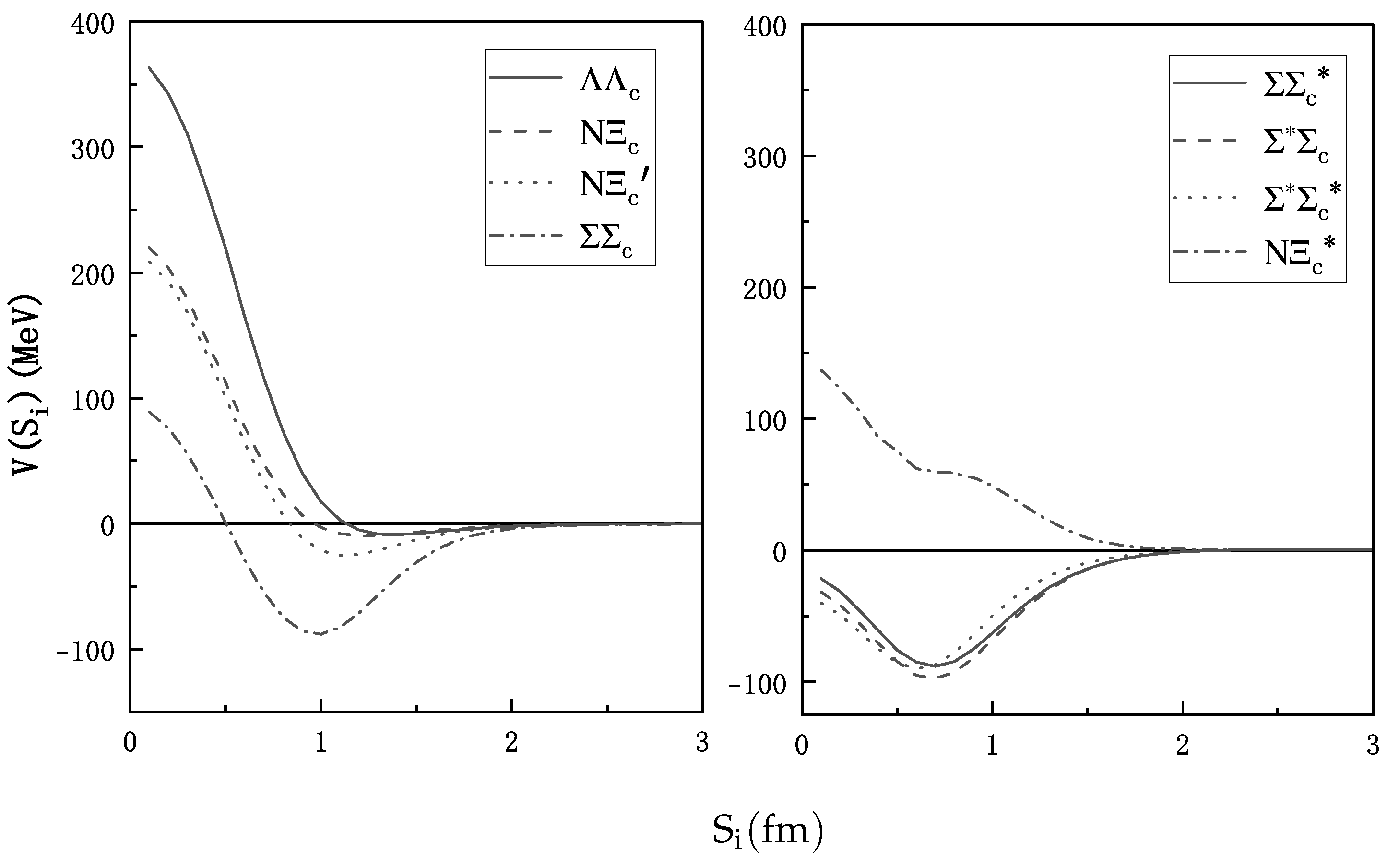
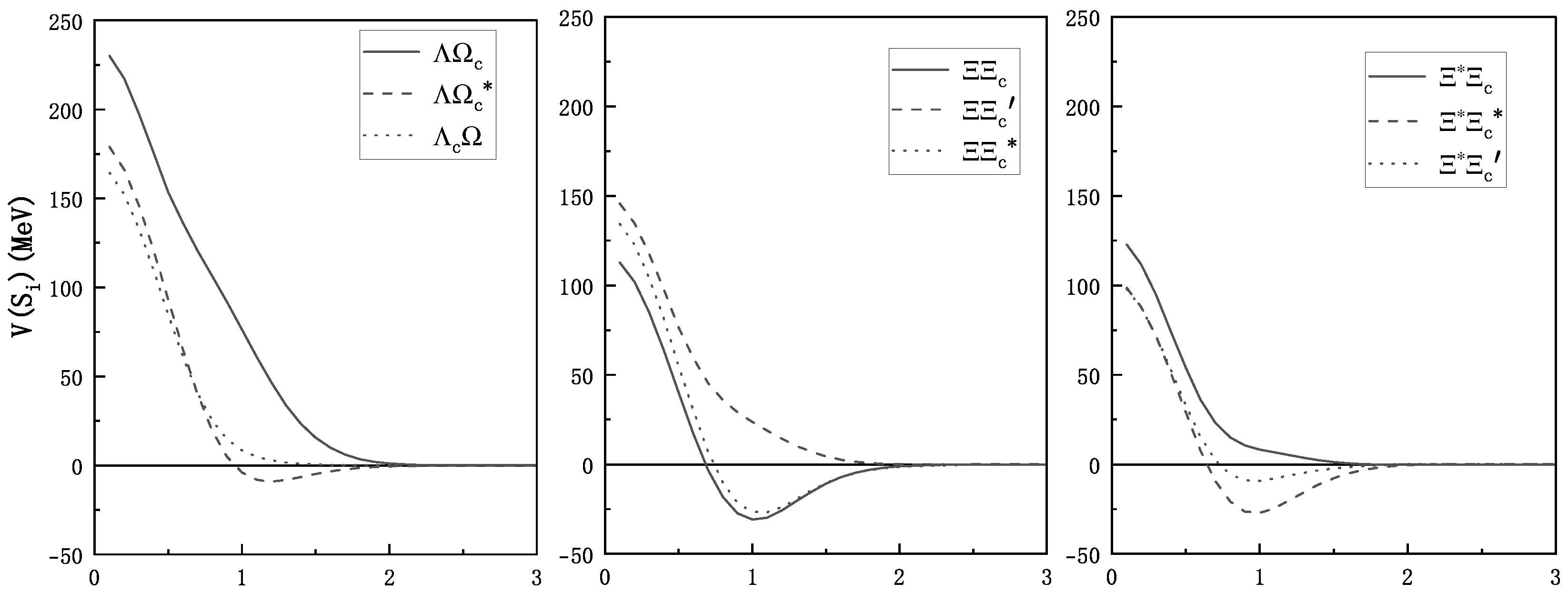
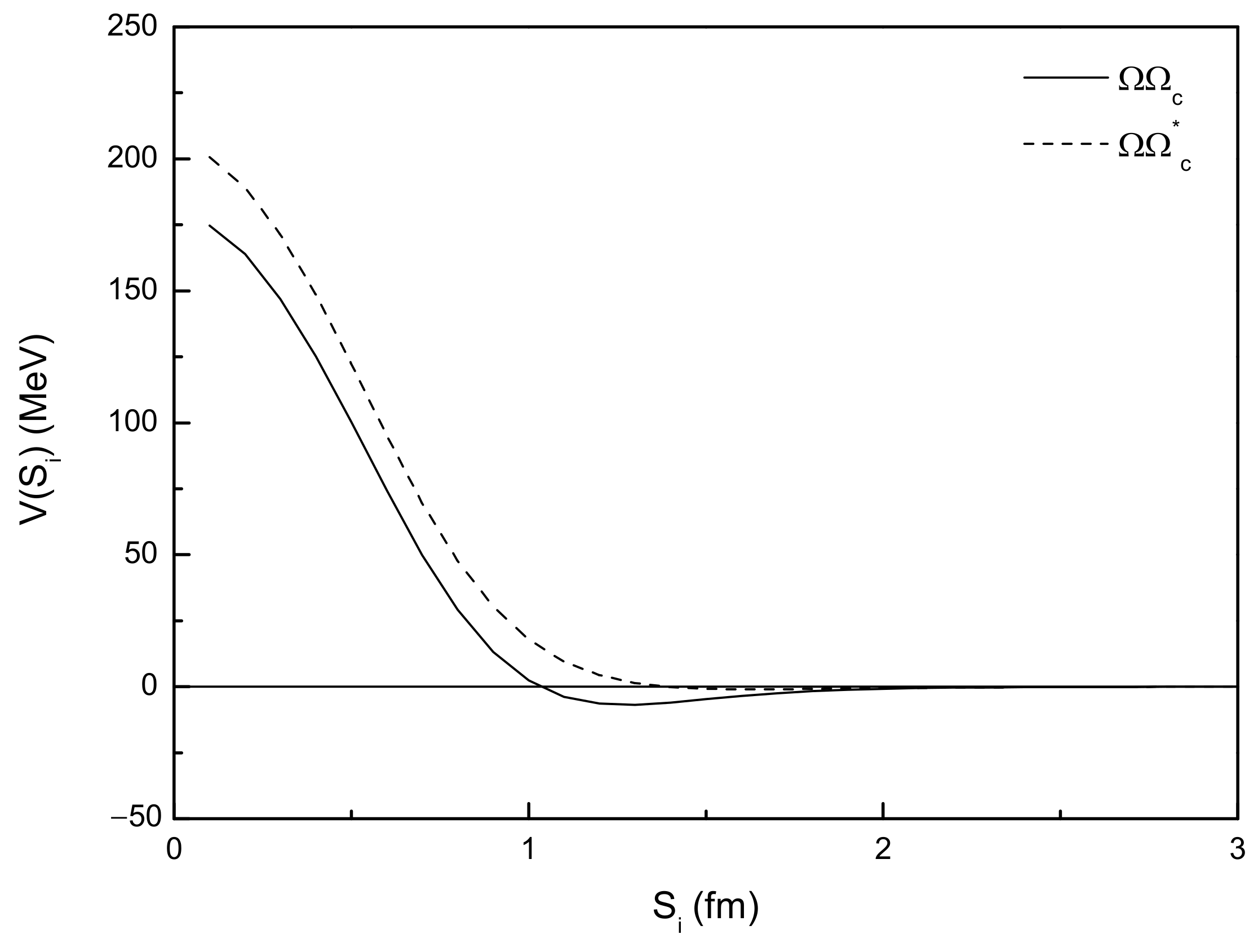
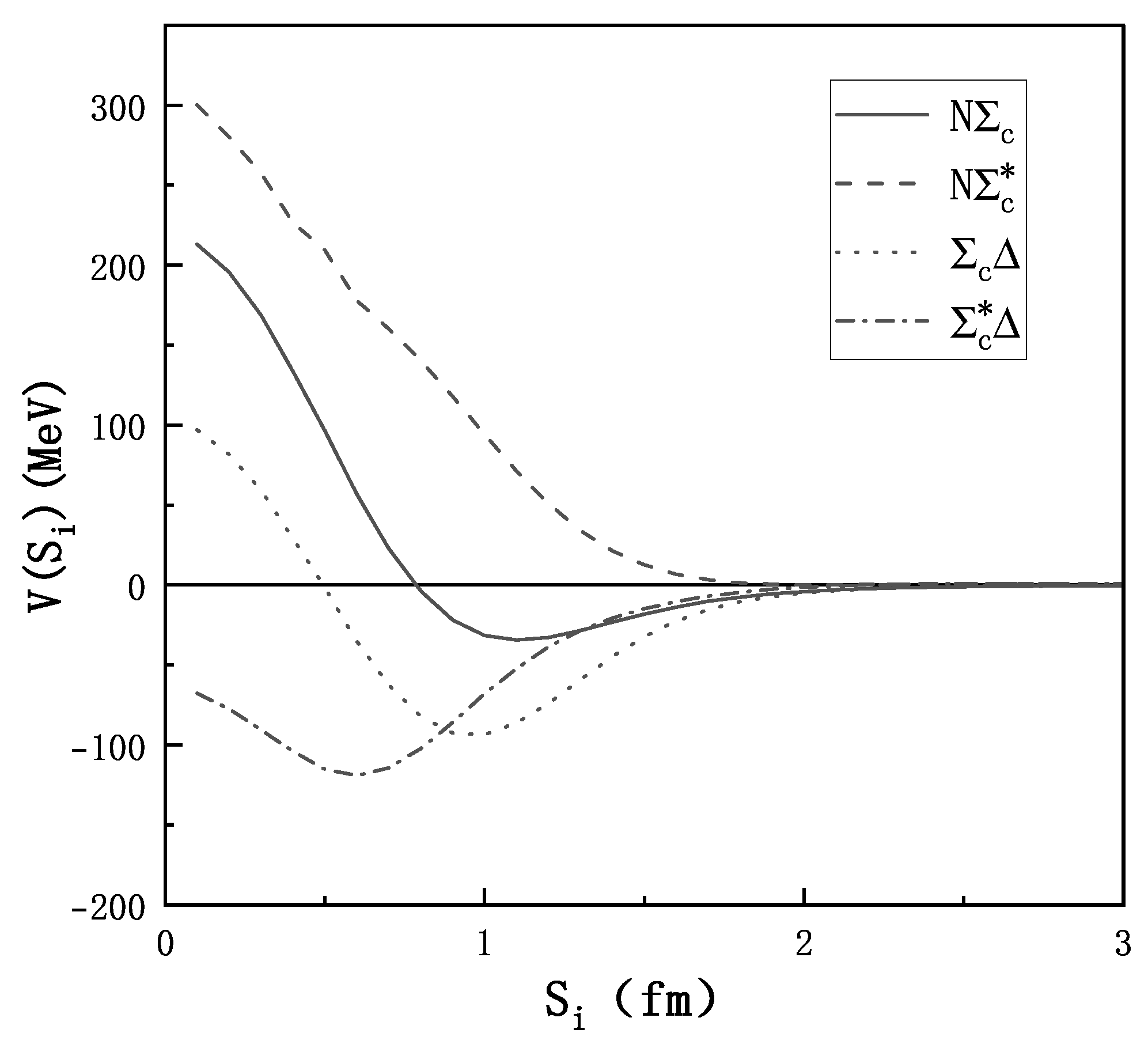
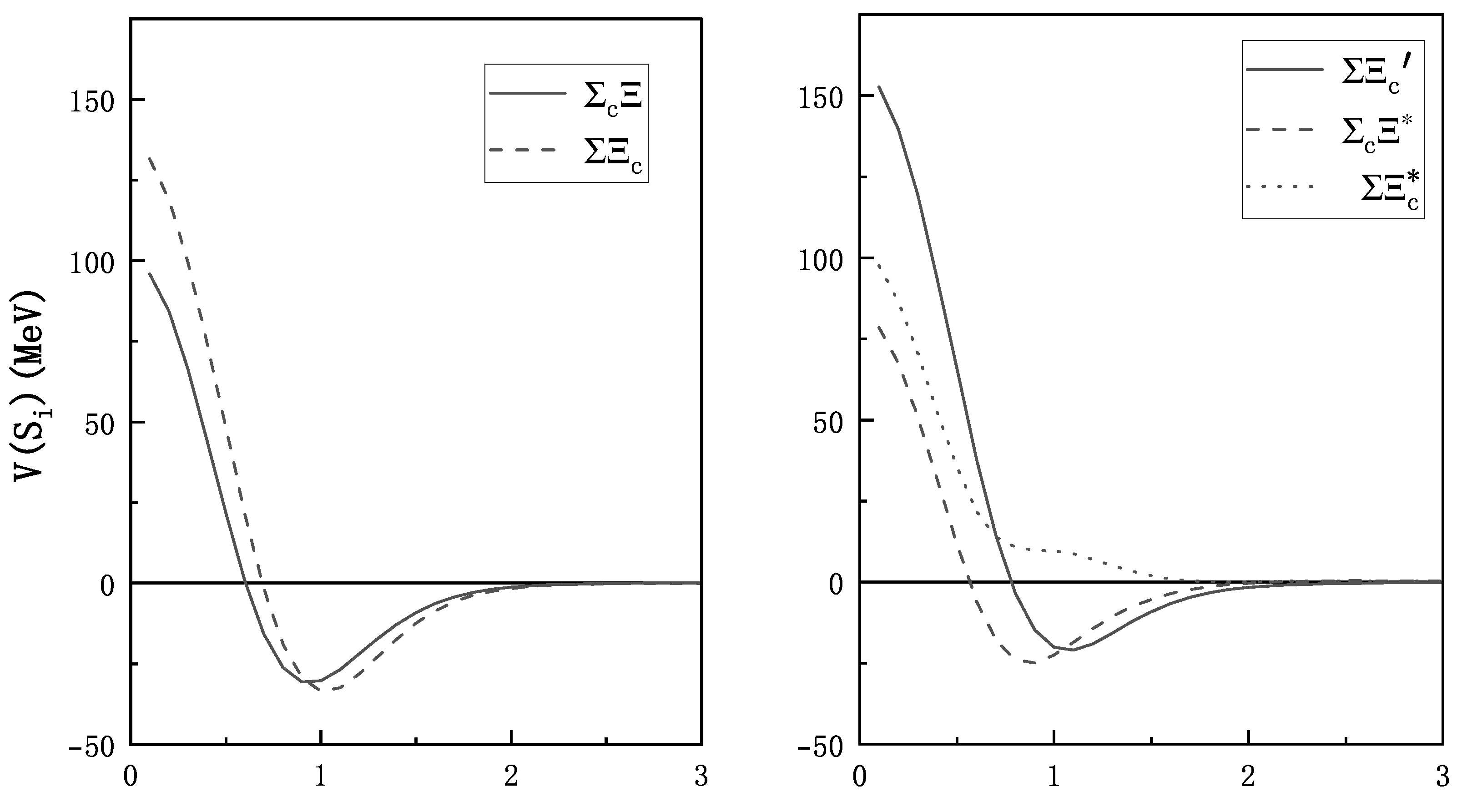
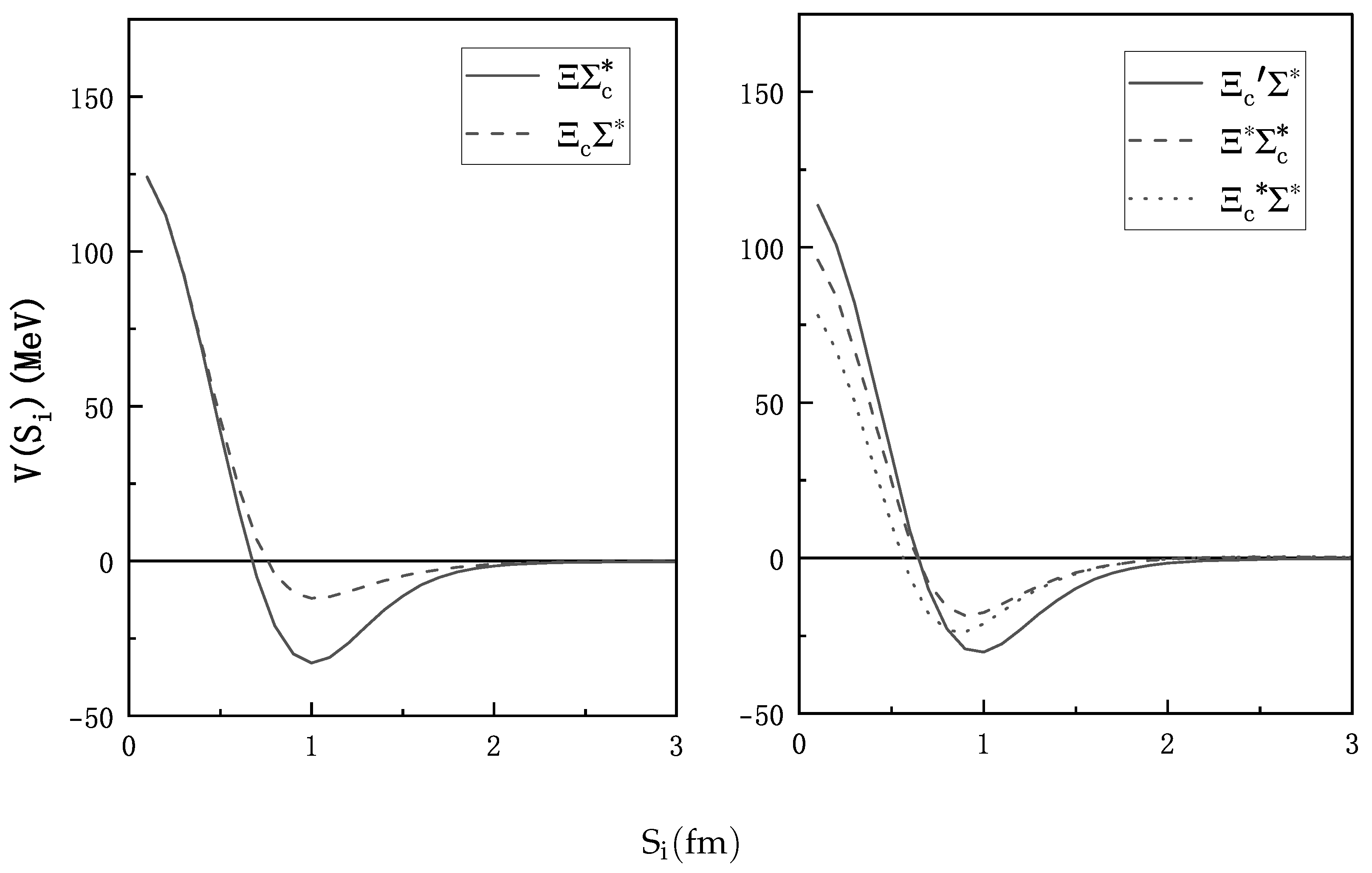
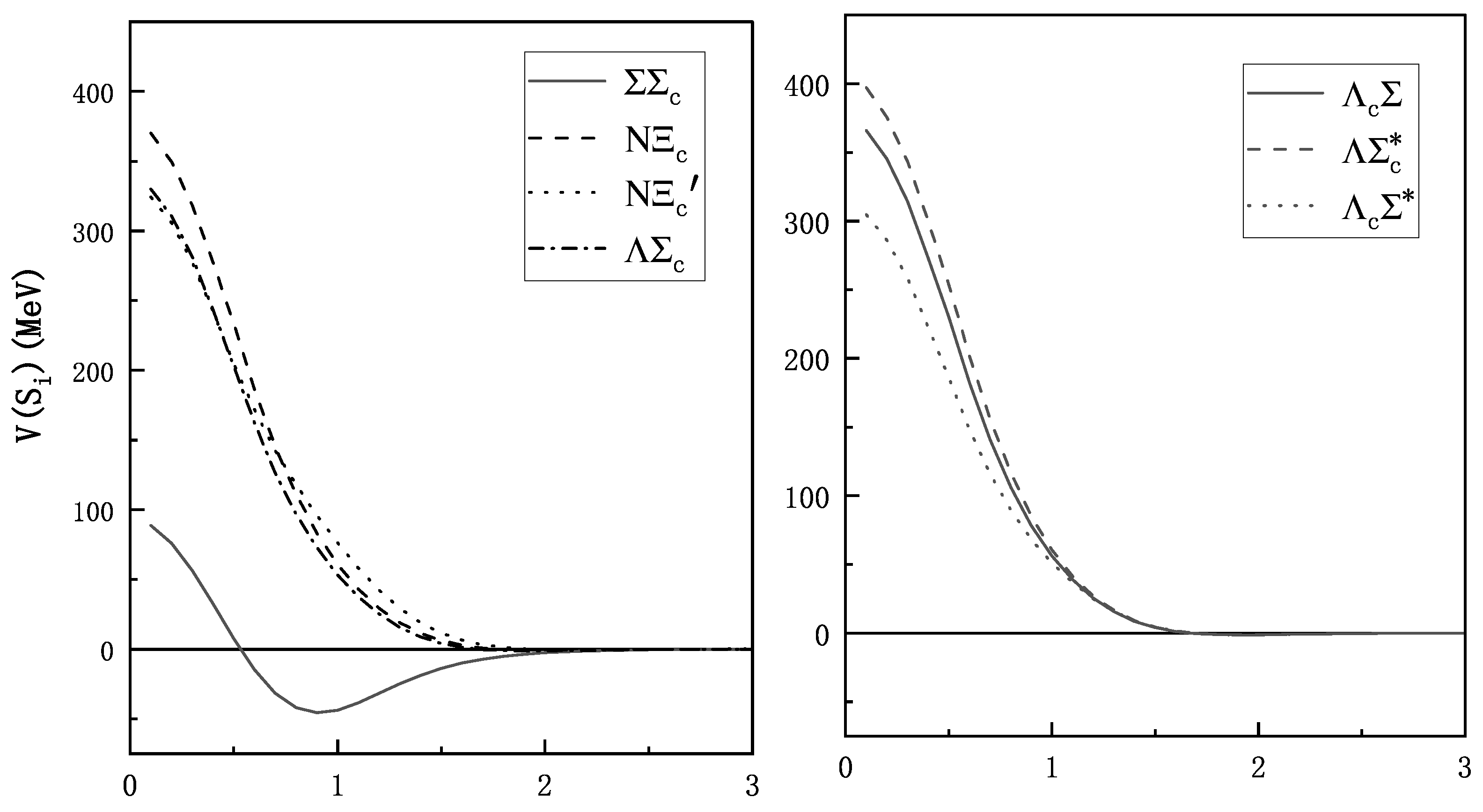

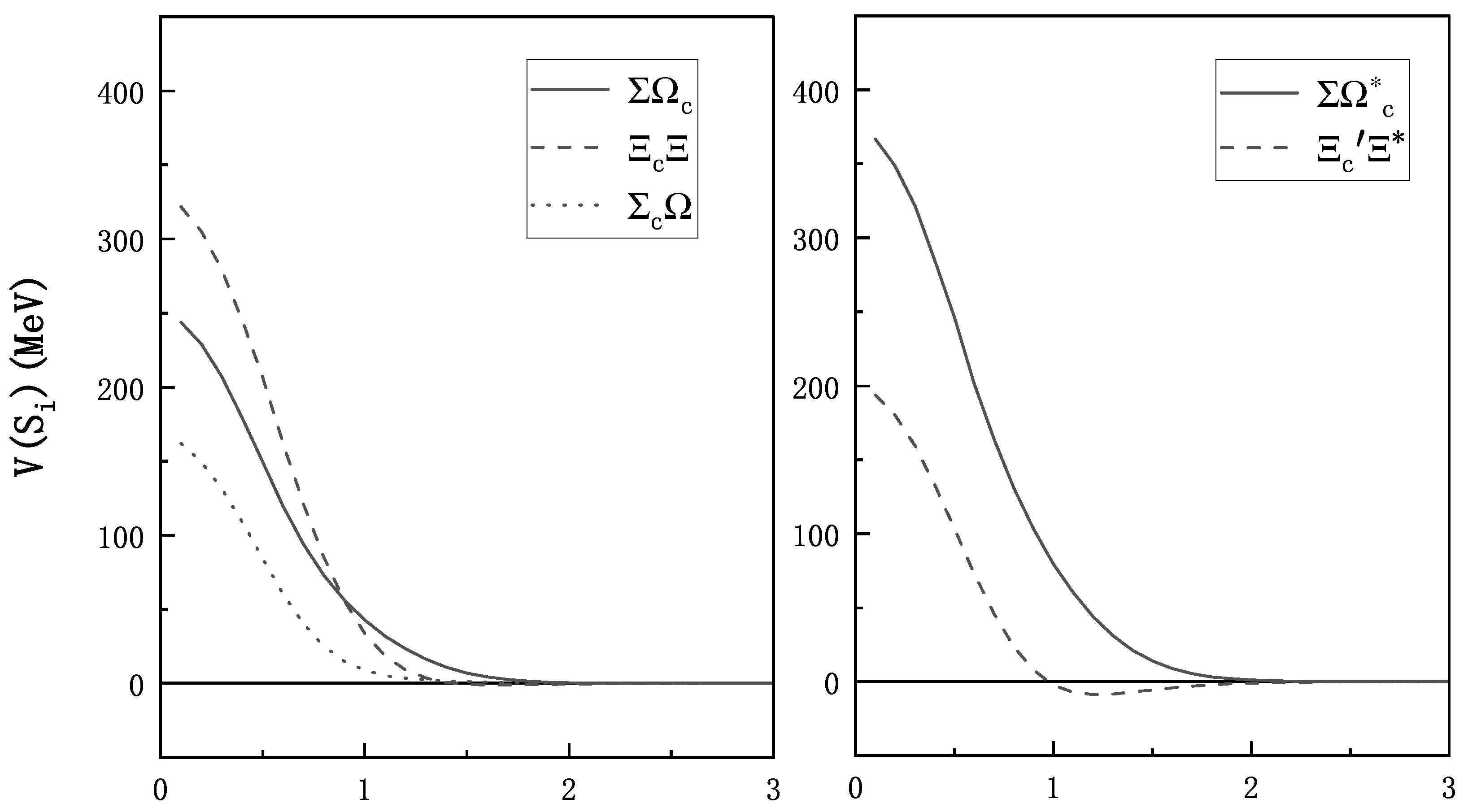
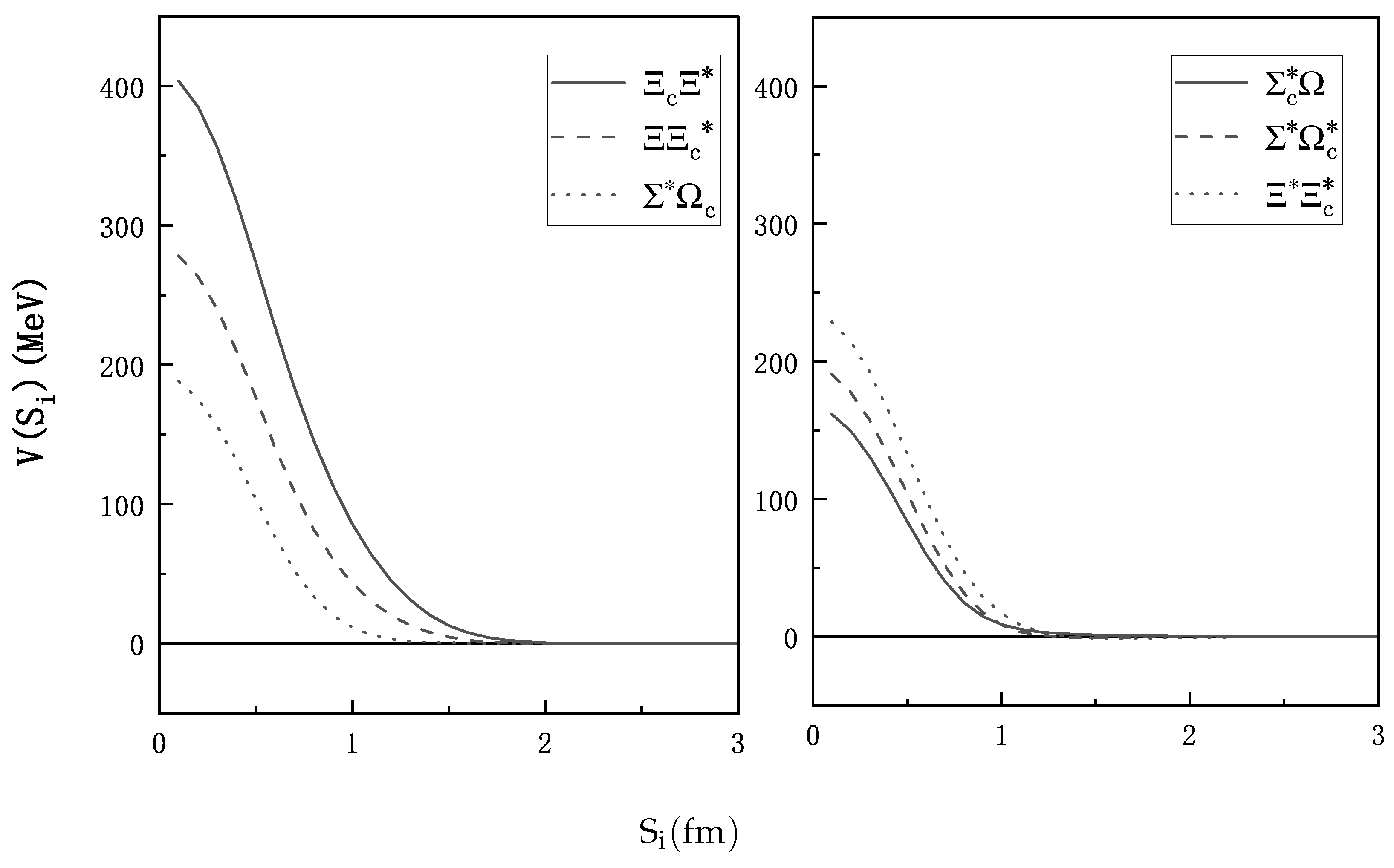
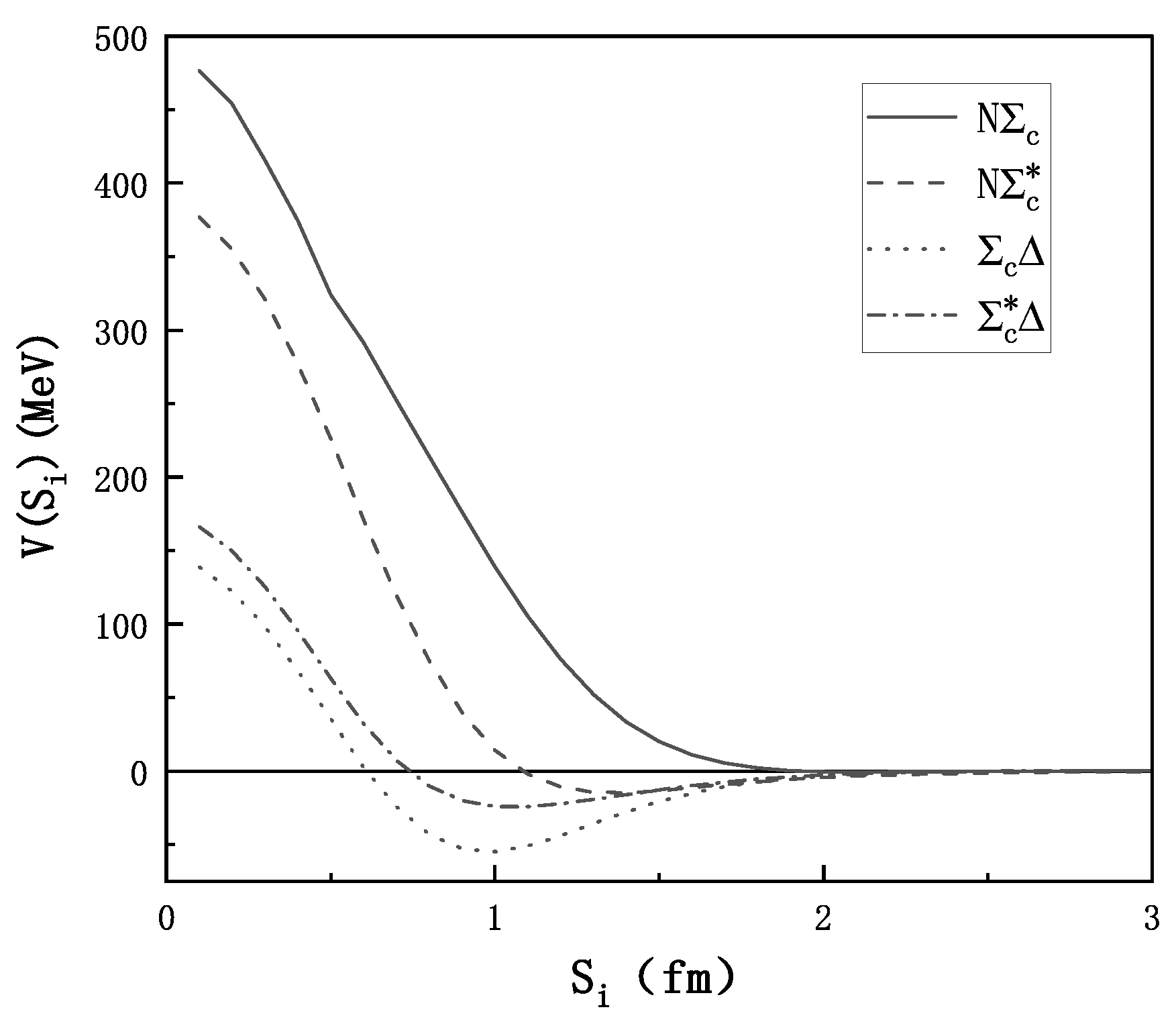
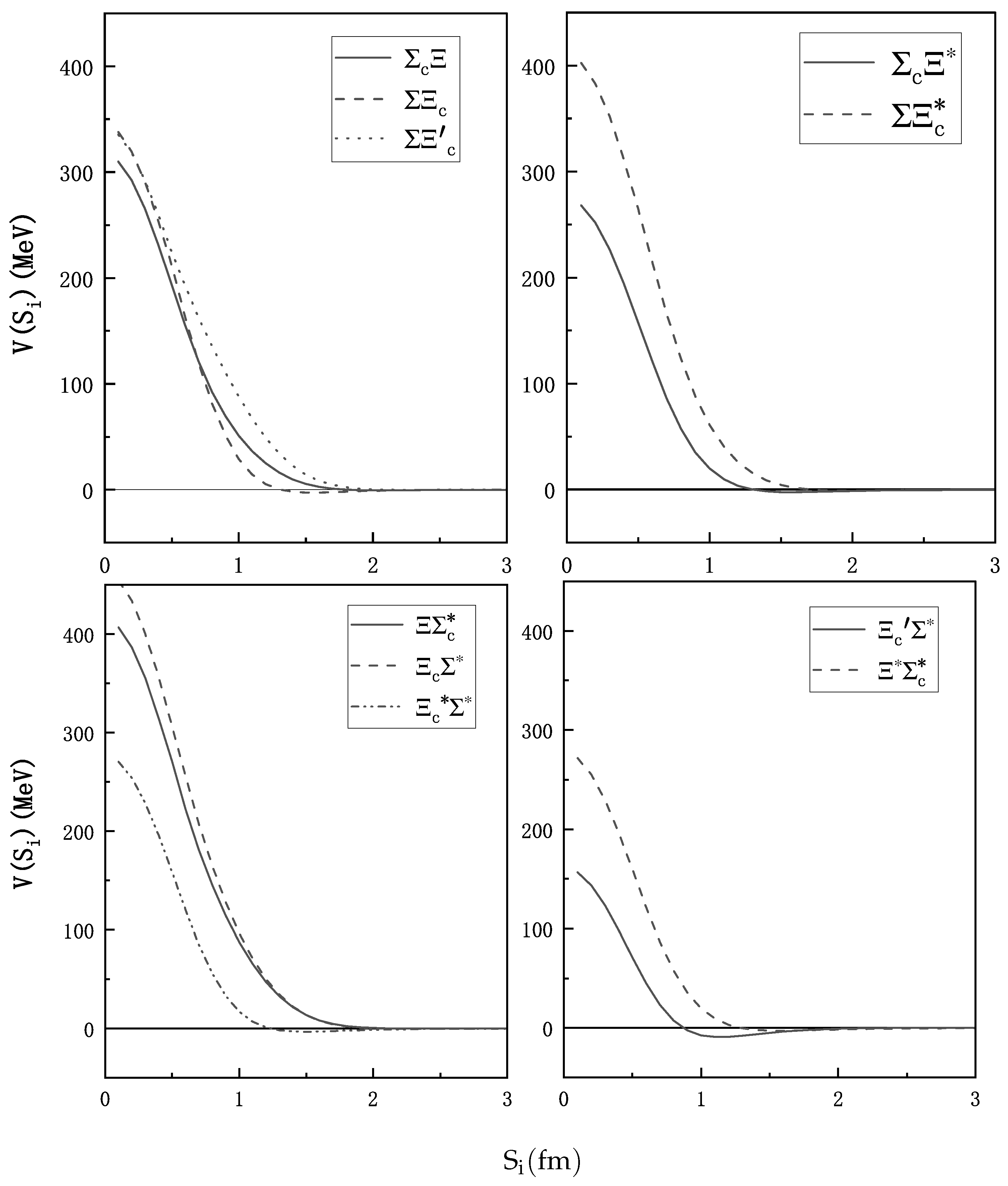
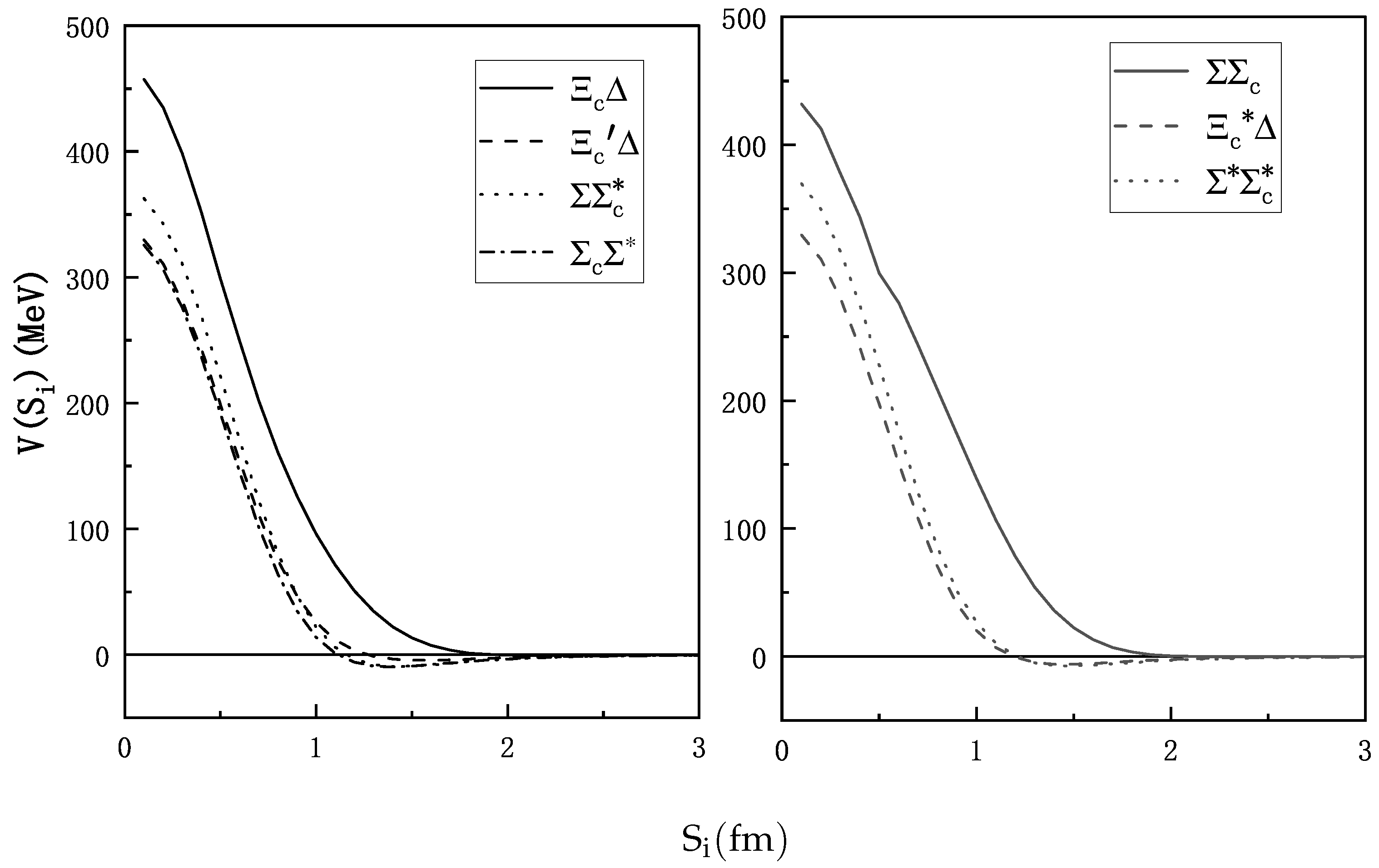

| (MeV) | (MeV) | ||
| ChQM | 0.52088 | 313 | 590 |
| MeV) | (MeV | ||
| ChQM | 1700 | 49.560 | −1.0778 |
| ChQM | 0.67249 | 0.83964 | 0.71678 |
| ChQM | 0.59298 | 0.60778 | 1.0810 |
| N | ||||
| ChQM | 932.7 | 1254.03 | 1104.85 | 1207.94 |
| Exp | 939 | 1233 | 1116 | 1189 |
| ChQM | 1374.63 | 1662.98 | 1344.26 | 1510.95 |
| Exp | 1385 | 1672 | 1315 | 1530 |
| ChQM | 2224.08 | 2416.80 | 2449.04 | 2453.80 |
| Exp | 2286 | 2455 | 2520 | 2470 |
| ChQM | 2548.35 | 2573.26 | 3492.87 | 2695.61 |
| Exp | 2578 | 2645 | 3519 | 2695 |
| ChQM | 2713.10 | |||
| Exp | 2700 |
| S | Channels | |
|---|---|---|
| 0 | −1 | |
| −3 | ||
| −5 | ||
| 0 | ||
| −2 | ||
| 1 | −1 | |
| −3 | ||
| 0 | ||
| −2 | ||
| 2 | −1 | |
| 0 |
| Channels | |||||
|---|---|---|---|---|---|
| 3328.93 | 3337.16 | ub | |||
| 3386.50 | 3394.06 | ub | |||
| 3481.05 | 3486.15 | ub | |||
| 3505.96 | 3515.29 | ub | 3335.76 | ub | |
| 3624.74 | 3602.88 | −21.86 | |||
| 3656.98 | 3632.82 | −24.16 | |||
| 3791.64 | 3759.45 | −32.19 | |||
| 3823.67 | 3798.47 | −25.20 |
| Channels | |||||
|---|---|---|---|---|---|
| 3800.46 | 3808.17 | ub | |||
| 3817.95 | 3857.99 | ub | |||
| 3887.06 | 3893.80 | ub | |||
| 3798.06 | 3801.09 | ub | 3801.09 | ub | |
| 3892.61 | 3899.32 | ub | |||
| 3917.52 | 3921.04 | ub | |||
| 3964.75 | 3971.04 | ub | |||
| 4084.21 | 4089.45 | ub | |||
| 4059.30 | 4061.86 | ub |
| Channels | |||||
|---|---|---|---|---|---|
| 4358.59 | 4364.18 | ub | 4362.77 | ub | |
| 4376.08 | 4381.11 | ub |
| Channels | |||||
|---|---|---|---|---|---|
| 3349.50 | 3353.24 | ub | |||
| 3381.74 | 3392.190.853 | ub | 3353.24 | ub | |
| 3670.83 | 3647.01 | −23.83 | |||
| 3703.07 | 3659.46 | −43.61 |
| Channels | |||||
|---|---|---|---|---|---|
| 3761.06 | 3763.79 | ub | |||
| 3661.74 | 3664.94 | ub | |||
| 3756.29 | 3760.88 | ub | |||
| 3927.75 | 3931.17 | ub | |||
| 3781.20 | 3788.38 | ub | 3663.83 | ub | |
| 3793.30 | 3796.45 | ub | |||
| 3828.43 | 3833.93 | ub | |||
| 3922.98 | 3925.13 | ub | |||
| 3959.99 | 3964.89 | ub | |||
| 3947.89 | 3951.90 | ub |
| Channels | |||||
|---|---|---|---|---|---|
| 3624.74 | 3623.86 | −0.88 | |||
| 3386.50 | 3395.74 | ub | |||
| 3481.05 | 3489.93 | ub | |||
| 3521.65 | 3529.89 | ub | |||
| 3432.02 | 3441.02 | ub | |||
| 3553.89 | 3562.78 | ub | |||
| 3598.71 | 3607.14 | ub | 3395.74 | ub | |
| 3505.96 | 3515.30 | ub | |||
| 3707.83 | 3710.28 | ub | |||
| 3802.38 | 3804.44 | ub | |||
| 3656.98 | 3661.94 | ub | |||
| 3791.64 | 3794.29 | ub | |||
| 3827.29 | 3829.58 | ub | |||
| 3823.67 | 3827.95 | ub |
| Channels | |||||
|---|---|---|---|---|---|
| 3903.55 | 3910.56 | ub | |||
| 3798.06 | 3805.30 | ub | |||
| 4079.78 | 4085.53 | ub | |||
| 3921.04 | 3928.33 | ub | |||
| 4059.30 | 4063.89 | ub | |||
| 3964.75 | 3972.15 | ub | 3805.26 | ub | |
| 3917.52 | 3924.83 | ub | |||
| 4070.24 | 4076.09 | ub | |||
| 4112.02 | 4118.34 | ub | |||
| 4087.73 | 4093.79 | ub | |||
| 4084.21 | 4090.34 | ub |
| Channels | |||||
|---|---|---|---|---|---|
| 3349.50 | 3359.29 | ub | |||
| 3381.74 | 3389.20 | ub | 3359.28 | ub | |
| 3670.83 | 3667.72 | −3.11 | |||
| 3703.07 | 3707.86 | ub |
| Channels | |||||
|---|---|---|---|---|---|
| 3761.06 | 3768.49 | ub | |||
| 3661.74 | 3669.34 | ub | |||
| 3756.29 | 3764.25 | ub | |||
| 3927.75 | 3933.88 | ub | |||
| 3781.20 | 3788.98 | ub | 3668.94 | ub | |
| 3793.30 | 3801.80 | ub | |||
| 3828.43 | 3836.46 | ub | |||
| 3922.98 | 3928.37 | ub | |||
| 3959.99 | 3954.42 | −5.57 | |||
| 3947.89 | 3966.57 | ub |
| Channels | |||||
|---|---|---|---|---|---|
| 3707.83 | 3716.40 | ub | |||
| 3802.38 | 3808.93 | ub | |||
| 3656.98 | 3664.12 | ub | |||
| 3791.43 | 3797.31 | ub | 3633.55 | ub | |
| 3624.74 | 3633.55 | ub | |||
| 3827.29 | 3834.01 | ub | |||
| 3823.67 | 3830.44 | ub |
| Channels | |||||
|---|---|---|---|---|---|
| 3670.83 | 3674.72 | ub | 3674.72 | ub | |
| 3703.07 | 3709.99 | ub |
| I | S | Quasi-Stable States | Decay Channels |
|---|---|---|---|
| 0 | −1 | ||
| 0 | |||
| 1 | −1 | ||
| 0 | |||
| −2 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; Cui, Y.; Tan, Z.; Tao, J.; Huang, H.; Ping, J. Study of Singly Charmed Dibaryons in Quark Model. Universe 2025, 11, 351. https://doi.org/10.3390/universe11100351
Du Y, Cui Y, Tan Z, Tao J, Huang H, Ping J. Study of Singly Charmed Dibaryons in Quark Model. Universe. 2025; 11(10):351. https://doi.org/10.3390/universe11100351
Chicago/Turabian StyleDu, Yuxuan, Yao Cui, Zhiyun Tan, Jin Tao, Hongxia Huang, and Jialun Ping. 2025. "Study of Singly Charmed Dibaryons in Quark Model" Universe 11, no. 10: 351. https://doi.org/10.3390/universe11100351
APA StyleDu, Y., Cui, Y., Tan, Z., Tao, J., Huang, H., & Ping, J. (2025). Study of Singly Charmed Dibaryons in Quark Model. Universe, 11(10), 351. https://doi.org/10.3390/universe11100351






