Abstract
We present a freeze-out approach for describing the formation of heavy elements in expanding nuclear matter. Applying concepts used in modeling heavy-ion collisions or ternary fission, we determine the abundances of heavy elements taking into account in-medium effects such as Pauli blocking and the Mott effect, which describes the dissolution of nuclei at high densities of nuclear matter. With this approach, we search for a universal initial distribution in a quasi-equilibrium state from which the coarse-grained pattern of the solar abundances of heavy elements freezes out and evolves by radioactive decay of the excited states. The universal initial state is characterized by the Lagrange parameters, which are related to temperature and chemical potentials of neutrons and protons. We show that such a state exists and determine a temperature of 5.266 MeV, a neutron chemical potential of 940.317 MeV and a proton chemical potential of 845.069 MeV, with a baryon number density of 0.013 fm−3 and a proton fraction of . Heavy neutron-rich nuclei such as the hypothetical double-magic nucleus 358Sn appear in the initial distribution and contribute to the observed abundances after fission. We discuss astrophysical scenarios for the realization of this universal initial distribution for heavy-element nucleosynthesis, including supernova explosions, neutron star mergers and the inhomogeneous Big Bang. The latter scenario may be of interest in the light of early massive objects observed with the James Webb Space Telescope and opens new perspectives on the universality of the observed r-process patterns and the lack of observations of population III stars.
1. Introduction
Explaining the cosmic inventory of nuclear species is one of the fundamental challenges for astrophysics and cosmology. Our knowledge of the isotopic abundances at various astrophysical sites has improved rapidly in recent decades thanks to a combination of advanced observational techniques and theoretical modeling. For the solar system, the isotopic abundances are well studied [1,2,3,4,5]. For other astrophysical sites, the measurements are usually restricted to elemental abundances. Particular efforts have been made to determine these abundances in metal-poor stars [6,7,8].
The solar abundances of isotopes (mass number A, charge number Z) are expressed in terms of mass fractions , where is the number density of the isotope, and the baryon number density. The mass fractions of isotopes in the solar system are not constant but change with time t due to nuclear reactions. For example, fusion processes convert H to heavier elements. In the Sun, H is burned into He, which, in the future will partially be converted into C and O. For stars significantly more massive than the Sun, the production of heavier elements reaches up to the iron group. On Earth, we observe the radioactive decay of some long-lived isotopes such as U and Th. The time-dependent distribution of elemental and isotopic abundances must have started with some initial state. This raises the question of the origin of the elements.
The current understanding of the origin of the isotopic distribution of the elements is the standard Big-Bang nucleosynthesis model [9,10,11,12]. The expanding Universe cools down, and at the end of the “first three minutes” after the Big Bang, the light elements 2H, 3He, 4He and 7Li are synthesized. A homogeneous Universe is assumed, in which the baryon density is constant in space. The primordial mass fractions at the baryonic density inferred from the cosmic microwave background are theoretically determined as [11]
We use the notation HBBN for the homogeneous Big-Bang nucleosynthesis considered here, as we also consider in this work the inhomogeneous Big-Bang nucleosynthesis (IBBN) as an alternative scenario. The mass fractions for heavier isotopes are very small, on the order of , and can be neglected. The mass fractions agree well with observational data [11]. One exception is , which is significantly higher (by a factor of ) than the primordial abundance derived from observations. This discrepancy is known to as the “cosmological lithium problem”.
The HBBN scenario has important implications. One of them is that there should be a first generation of stars—usually referred to as population III—that have formed from pristine HBBN material and contain virtually no metals, i.e., elements heavier than He. This lack of metals affects the formation, the evolution and, ultimately, the explosions of population III stars [13]. So far, no population III stars have been found observationally [7,14]. Even the recently observed stars with the lowest Fe abundance [15] contain a certain amount of elements beyond He. Moreover, neither pair-instability supernovae, which are supposed to result from population III stars, nor the associated nucleosynthetic imprints have yet been identified beyond doubt in observations.
In their seminal papers, Burbidge et al. [16] and Cameron [17] proposed that all elements heavier than those produced in HBBN are formed by nuclear reactions under favorable conditions in specific astrophysical sites. Over the past decades, substantial knowledge has been accumulated about the structure of nuclei and their reaction processes. The nuclear reactions responsible for the temporal evolution of are incorporated in nuclear reaction network (NRN) codes such as SkyNet [18] and WinNet [19]. Starting out from the primordial HBBN distribution , the formation of heavier elements in suitable astrophysical sites is modeled with these nuclear reaction networks [12,16]. The synthesis of the nuclear species in stars up to the iron–nickel region is well established [20]. Our work focuses on the origin of heavy elements () which remained elusive for a long time [21]. Heavy elements are nuclei beyond the iron peak that are almost not modified by stellar burning processes, but there is no sharp limit for the mass number. As discussed below in Section 3, we choose the value .
Burbidge et al. [16] invoked nucleosynthesis processes (now called the p-, s- and r-processes, and some variants thereof) for the production of heavy elements. For details, see the recent reviews by Arcones and Thielemann [12], Cowan et al. [22], Diehl et al. [23], Bandyopadhyay and Beers [24] and the references given there. It is assumed that the nucleosynthesis pathway of the r-process (rapid neutron-capture process) proceeds close to the neutron-drip line in the nuclear chart. The astrophysical objects and events that provide the required conditions for the r-process to operate, i.e., high neutron fluxes, turned out to be difficult to identify [12,22,25,26,27,28,29]. Most of the astrophysical sites proposed for the r-process involve the ejection of material from regions of high densities and contain neutron stars (NSs) or black holes (BHs). Potentially, conditions for the operation of the r-process are reached during core-collapse of massive stars or mergers in double-compact systems [22]. While for many years the occurrence of the r-process has been associated with supernovae (SNe), where the innermost ejecta close to the central neutron star were supposed to be neutron-rich, more recent studies have cast substantial doubts on this environment for heavy-isotope production. Recent core-collapse supernova simulations [30] indicate that the extreme conditions necessary for the r-process to operate are not reached, and it seems safe to conclude that neutrino-driven proto-neutron star winds are excluded as the major origin of heavy r-process elements [31]. Moreover, detailed spectroscopic observations even disfavor more extreme supernova events producing gamma-ray bursts as site for the production of r-process elements [32].
Mergers in double-compact systems containing neutron stars, black holes or white dwarfs have been investigated as alternative sites for heavy-element production [29,33,34]. Spectroscopic observations of kilonova AT2017gfo associated with the neutron star merger GW170817 confirmed the production of r-process elements in this event [35]. Postprocessing the nuclear reactions in simulations of binary neutron star mergers reveals details of the production of heavy elements in such neutron-rich and dense environments [27,36,37]. The impact of nuclear matter properties on the nucleosynthesis and the kilonova from binary neutron star merger ejecta was recently studied by Ricigliano et al. [38]—see also Just et al. [39]. Although the production of r-process elements in NS mergers is confirmed by observations, it remains unclear whether they merely contribute to the enrichment of the Universe with heavy elements or whether they can account for the total cosmic abundances of these heavy nuclei. In particular, r-process elements detected in metal-poor stars require a source in the very early Universe and the time scales of enrichment with r-process elements due to NS mergers may be too long [40]—see also Section 4.3.
An interesting finding from the observation of metal-poor stars is the similarity of the abundance pattern of heavy elements with mass numbers to that observed in the Sun [22,24,41,42,43,44,45]. This similarity initiated the notion of the “universality of the r-process”—at least for the heaviest stable and observable elements. The similarity of the abundances observed in extremely metal-poor stars and the Sun is one of the most important clues to the astrophysical origin of heavy elements [46,47,48,49]. It is assumed that at least one relatively common r-process source in the early Universe produced a consistent abundance pattern among some light elements spanning the first and second r-process peaks [50]. Deviations from universality were recently discussed by Ji et al. [51]. Any proposal about the site of nucleosynthesis of heavy elements is confronted with this universality feature.
Together with the non-detection of population III stars, this raises the question of whether there are alternatives to the Burbidge et al. [16] scenario, which assumes the formation of the heavy elements as a product of a build-up process from light nuclei in specific astrophysical sites. Such an alternative scenario is that of inhomogeneous Big-Bang Nucleosynthesis (IBBN), which posits that large dense objects form in the early Universe before nucleosynthesis takes place [52,53,54]. The baryonic matter expands in the space between these massive objects and forms nuclei when the density drops below the baryon saturation density1 . Compared with HBBN, baryonic matter in this case takes a different evolutionary path in the phase diagram, and heavy nuclei are created very early during the IBBN. In this scenario, the homogeneous low-density state with the primordial distribution , Equation (1), is not the only initial state for the formation of elements. Although the average baryon number density in HBBN is low (of the order of ), density fluctuations are assumed to occur, forming compact, dense objects; see Ref. [55].
A reaction pathway near the neutron drip-line to form the heavy elements is not absolutely necessary, and later events such as supernova explosions and neutron star mergers are not the only prerequisite for the formation of the heavy elements, although such events can still contribute and modify the isotopic distributions. The IBBN scenario opens new perspectives to explain universality of the observed r-process patterns and the lack of observations of population III stars.
In contrast to the nuclear reaction network calculations starting from the primordial distribution , as given in Equation (1), we explore another potential pathway to the formation of heavy elements: As a starting point, we aim to find in this work a universal initial state of baryonic matter in quasi-equilibrium, specified by the temperature T, the baryon number density , and the proton fraction , with a distribution of mass fractions of nuclei extending out to very large values of A. This state is chosen without referring to a specific astrophysical site it could be realized in. Given this initial quasi-equilibrium state, we determine whether the observed solar heavy-element pattern of mass fractions for isotopes with mass number A and charge number Z can be recovered from this state in a freeze-out scenario with a feed-down afterburner, i.e., a reaction network which describes in particular the decay of the excited, unstable nuclei.
The primary goal of our work is to describe expanding hot and dense nuclear matter using the freeze-out concept, which defines an initial distribution of nuclei described by few nonequilibrium parameters related to temperature and chemical potentials. We infer such an initial distribution for the solar abundances considering the heavy-element distribution and using approaches similar to those that have proved successful in describing heavy-ion collisions (HICs). We introduce the concept of heavy element freeze-out (HEFO), which considers the temporal evolution of the distribution of heavy elements to be a slow process when certain conditions (hot, neutron-rich dense matter) are not provided. We are concerned with the formation of nuclear clusters2 (nuclei, resonances) in high-density matter, which requires quantum statistical approaches to describe in-medium effects, in particular Pauli blocking and the Mott effect [56]. These effects are usually not accounted for in current approaches to nucleosynthesis. Our freeze-out concept is of general interest in the search for the astrophysical site of heavy-element creation.
The paper is organized as follows: We give a short review of the behavior of expanding nuclear matter in laboratory experiments in Section 2.1 and discuss the coarse-grained pattern of the solar mass fraction distribution in Section 2.2. In Section 2.3, we present our methods—the Zubarev method of the nonequilibrium statistical operator, that has the freeze-out concept and the nuclear reaction kinetics as special cases—and in Section 2.4 the method of Green’s functions, which describes clusters in dense matter. As results, we demonstrate in Section 3.1 the impact of in-medium corrections on the distribution of light elements, and in Section 3.3 we give an estimation for an initial distribution fitted to the solar abundances. Processes leading to the final distribution of heavy nuclei are considered in Section 3.2. In Section 4, we discuss our results and draw the conclusions in the final Section 5.
2. Methods
Common approaches to describe the temporal evolution of astrophysical systems involving nuclear reactions are based on a combination of the equations of fluid dynamics coupled to nuclear reaction networks. This method is well established at low densities, where the components of the system can be considered as particles that move almost freely and occasionally have reactive collisions. At high densities, this approach becomes invalid as in-medium effects change the properties of the components and of the reaction rates. Bound states are dissolved (Mott effect) and correlations in the continuum become important. Such effects break the assumption of an ideal fluid. We show that the freeze-out concept, which is able to incorporate the in-medium effects, can be embedded in a general approach to nonequilibrium, and we demonstrate this general approach to in-medium corrections using a thermodynamic Green’s function approach. This allows us to consistently treat matter at high densities, where the usual reaction–kinetic networks are no longer valid.
2.1. Analogies to Nuclear Cluster Formation in Laboratory Experiments
The expansion of hot and dense nuclear matter is studied in laboratory experiments. The yields of different isotopes are observed in heavy-ion collisions (HIC) at various energies. Here, we give only a few examples: At the highest energy densities presently reached in laboratory experiments, the formation of clusters up to 4He ( particle) and its antiparticle was measured at the Large Hadron Collider (LHC) at CERN [57]. A laboratory test of the nuclear matter equation of state has been performed at low collision energies in the range of the Fermi energy [58,59]. It has been shown that the simple nuclear statistical equilibrium is not able to describe the measured yields, and in-medium corrections must be taken into account. The production of light elements has been studied in ternary (spontaneous or induced) fission, where, for example, isotopes up to 24Mg were observed, formed in the low-density neck region at the scission point of fission of 242Pu [60].
At first glance, the distribution of observed yields of nuclei formed in HIC or ternary fission shows features very similar to that obtained from the mass action law (sometimes called the Saha equation), which describes chemical equilibrium. This concept is also widely used in nuclear astrophysics. A simple statistical model—that of nuclear statistical equilibrium (NSE), see, e.g., Ref. [61]—can be employed to infer the temperature and the density of a suggested freeze-out state.
For both modeling HIC and astrophysical processes, however, a more sophisticated version of the freeze-out approach has to account for the following problems:
- The observed yields are not identical with the initial (primordial) yields because of afterburner processes, in particular the decay of unstable states.
- The initial (primordial) distribution is not a mixture of non-interacting stable nuclei. We have to consider excited states and continuum correlations, but also in-medium effects such as self-energy shifts and Pauli blocking.
While the first problem is usually taken into account in astrophysical models, the second problem is often ignored.
A self-consistent determination of the primordial distribution of nuclear species from observed yields is a complex problem and the use of a simple NSE model to fit the thermodynamic parameters at freeze-out is insufficient. Since chemical evolution is a nonequilibrium process, a quantum statistical approach is required that can describe cluster formation and the influence of the surrounding medium when expanding dense matter is considered. The method of the nonequilibrium statistical operator (NSO) as discussed in detail by Zubarev et al. [62] represents a general approach to modeling such nonequilibrium processes; see Section 2.3. It combines the freeze-out scenario with nuclear reaction kinetics as described by NRN codes.
For instance, it has been found [63] that in ternary spontaneous fission of 252Cf, 17 % of the observed particles are produced primordially as 5He, which is surprising given the unstable nature of this isotope. In-medium effects have clearly been identified in HIC at low temperatures [59]. With the approach discussed above, it was possible to determine the parameters for the primordial distribution of nuclei at freeze-out. For HIC at ultrarelativistic energies [57], the inferred parameters at freeze-out are MeV and ; for HIC at energies in the Fermi energy range [59], temperatures of 5– and baryon number densities of – were reported, and for ternary fission of 242Pu the freeze-out values MeV, fm−3 and proton fraction have been found [64]. Together with an afterburner (decay) process, which leads to the feed-down of excited nuclei and unstable states, the improved freeze-out approach proved to be very successful in explaining the yields of isotopes from expanding hot and dense nuclear matter (i.e., a fireball). With this approach, it is possible to infer quasi-equilibrium parameters for a primordial distribution in a consistent way. More details are found in Appendix A.
In this work, we discuss the solar abundances of isotopes, in particular the heavy nuclei with mass numbers . We infer parameter values for the initial distribution at the heavy-element freeze-out—see Section 2.2— taking into account in-medium effects, in particular self-energy effects, Pauli blocking, screening, and continuum correlations. We discuss the conditions under which such nuclei are formed. Röpke [54] found parameter values of for the temperature and for the baryon number density. Regardless of the particular scenarios discussed above (supernova explosions, double-compact object mergers, IBBN), such conditions are of general relevance for the creation of heavy elements in the Universe.
2.2. Distribution of the Solar Accumulated Mass Fractions
For our study, we take the solar abundances reported by Lodders [1] as a reference. Instead of the usual detailed dependence of the abundances of isotopes on their mass number A and charge number Z, we use the average dependence on A as shown in Figure 1, introducing the accumulated mass fraction
and the -metallicity3
Here, denotes the baryon number density, and the number density of clusters with mass number A and charge number Z. The intrinsic quantum number gives the excitation state of the nucleus and characterizes the group of clusters; it can take values in . This coarse-grained representation of the abundance distribution of nuclear species shows neither the odd–even staggering nor the high abundances of light nuclei, which are averaged over. The only significant deviations from the general monotonic decrease of with increasing A as shown as blue “×” symbols in Figure 1 are the low abundance related to the weakly bound elements Li, Be and B, the large values in the maximally bound Fe–Ni region (iron peak), and enhanced abundances in the regions referred to as the first, second and third -process peak [12,65]. These peaks are discussed in reference to the nuclear shell model, which implies larger binding energies near the magic numbers of Z and .
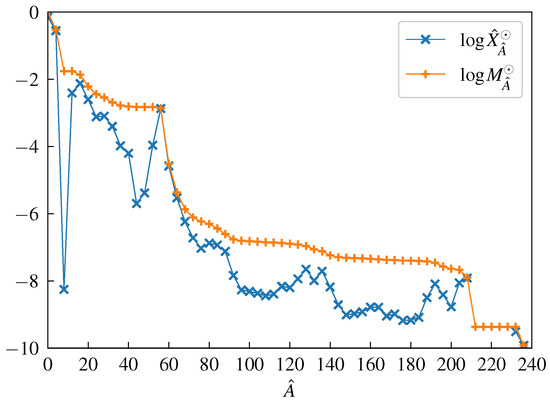
The -metallicity shown as orange “+” symbols in Figure 1 gives the sum of mass fractions of isotopes with mass number . It is monotonically decreasing with A. Due to normalization, . The -metallicity will be of importance for our considerations, in particular to determine the freeze-out conditions in Section 3.3.
Using the coarse-grained, accumulated mass fractions (as shown in Figure 1) in the discussion of the time evolution of the distribution instead of the non-averaged mass fractions has the advantage that they are invariant with respect to special processes such as , and reactions. Emission and absorption of neutrons or protons change the distribution only locally (), but leave the coarse-grained pattern nearly unaffected, which, however, is significantly modified by -decay, fission, and fusion processes. We suppose that this coarse-grained pattern of the cluster distribution function is formed already before the details like even–odd staggering are frozen out. Whereas the last stage of the chemical evolution of the expanding nuclear system is described by reaction kinetics, i.e., NRNs, which fix the composition but not the kinetic spectra, the coarse-grained distribution is more robust and contains information about the earlier state of matter.
Likewise, the -metallicity is invariant with respect to , and reactions. Whereas emission or absorption of single nucleons give rise to a diffusion process (with respect to the variable A) for the accumulated mass fractions, the metallicity provides an integral distribution, and as such it better reflects the global changes of the mass number distribution of clusters.
In this work, we focus on the heavy clusters and propose an initial distribution which can explain the coarse-grained pattern of the distribution of heavy-element abundances arising from expanding hot and dense matter. Initially, we assume a local thermodynamic equilibrium. As is generally accepted, the formation of heavy elements is associated with a hot, neutron-rich environment. Relaxation to thermodynamic equilibrium freezes out when the parameter values of the environment, for example the density, become subcritical.
Neither the light-element distribution nor the detailed isotopic distribution of the heavy elements will be considered here. Even–odd staggering and similar individual deviations from the coarse-grained pattern can be obtained via an NRN treatment from the distribution for the expanding and cooling matter after freeze-out. Our final coarse-grained distribution can be considered as an initial distribution for an NRN calculation, which describes the evolution of the distribution of nuclei after freeze-out and allows us to derive the details of the final elemental abundances.
2.3. The Method of the Nonequilibrium Statistical Operator
The nonequilibrium evolution of a system is described by the statistical operator , which is the solution of the Liouville–von Neumann equation,
with given initial conditions. In the Zubarev method of the nonequilibrium statistical operator (NSO) [62], the initial conditions are represented by the average values of a set of relevant observables in the past that characterize the state of the system. This information is used to construct the relevant statistical operator as the maximum of the information entropy under given boundary conditions, i.e., the self-consistency conditions
As known from equilibrium statistics, these self-consistency conditions are taken into account in the variational problem via Lagrange parameters , and we obtain the generalized Gibbs distribution
The Lagrange parameters must be eliminated using the self-consistency conditions (5), which represent the nonequilibrium generalizations of the equations of state.
The solution of the Liouville–von Neumann equation at given boundary conditions (5) is
in the limit .
The Zubarev–NSO method was also formulated for relativistic hydrodynamics by Zubarev et al. [66]. For various applications, see [67,68,69,70,71,72]. For reasons of mathematical convenience, a co-moving system is usually used, in which standard quantum statistical methods can be applied.
A special feature of the method of the NSO is the selection of the set of relevant observables . A minimum set of relevant observables are the conserved quantities energy H and the particle numbers , with , for neutrons and protons, respectively, in a volume V (neglecting weak interaction). The solution is the generalized Gibbs distribution
Note that the Lagrange multipliers , which generally depend on time, are not identical to the equilibrium parameters T and , but can be regarded as nonequilibrium generalizations of the temperature and the chemical potentials. The information entropy can only be unambiguously identified with the thermodynamic entropy if the system is in thermodynamic equilibrium, and then we can define the quantities T and with the known properties.
Further correlations in the nonequilibrium state that are not included in the set of relevant observables are generated dynamically and appear in by taking the limit . If each fluctuation within the relevant distribution relaxes to zero within the time , the limit in Equation (7) can be replaced by . For , the relevant statistical operator remains almost constant during the relaxation time, so that, according to Equation (7), can be approximated by . The memory of the system is short in this so-called Markov limit. All other observables are assumed to relax fast to this relevant state. Then, for instance, a Markov approximation to describe the nonequilibrium evolution is possible.
If special fluctuations do not fulfill this requirement, they should be included in the set of relevant observables. This new set , as well as the corresponding relevant statistical operator , includes the former set of relevant observables but adds new degrees of freedom. The temporal evolution is now described by an extended set of averages , for which so-called kinetic equations must be solved. The instant of time where the relaxation to the relevant state is no longer realized and new degrees of freedom appear marks the onset of freeze-out. It depends on the process which is considered, and which degrees of freedom become new relevant observables, because they describe long-lived fluctuations.
If, for example, the densities of the conserved quantities are considered to be relevant observables, a hydrodynamical description with Lagrange parameters as a function of time and position is obtained [62]. The relevant distribution freezes out if the relaxation of certain fluctuations becomes too slow, so that a temporal change in the conditions (5) can no longer relax to . Then, these particular fluctuations should be added to the set of relevant observables , so that a Markov approach remains possible.
To give an example of HIC, the state of nuclear matter is described by the density of energy and the particle density of the baryons if it is sufficiently hot and dense. Other degrees of freedom such as composition are governed by the corresponding Lagrange parameters T and . In a simple approximation, we obtain the Saha equation describing the state of NSE. Better approximations lead to virial expansions and the generalized Beth–Uhlenbeck equation [56,73]. When matter expands and cools, inelastic reactive collisions become rare and the composition freezes out—this is also referred to as “chemical freeze-out”. New degrees of freedom are the partial densities of the various components, i.e., the nuclei. An NRN code describes the subsequent evolution. Nevertheless, elastic collisions can be active for longer, so that each component approaches the equilibrium (Boltzmann) distribution as a function of the center-of-mass momentum. If the relaxation owing to elastic collisions also becomes too slow, the occupation numbers in momentum space become the new degrees of freedom. The corresponding kinetic freeze-out provides the spectrum for the various components in momentum space, and the subsequent evolution is described by the temporal evolution of the distribution function in momentum space.
We are interested in the reactions between the components of the expanding hot and dense nuclear matter. When the reaction rates become too slow, the composition of the system freezes out. The composition remains at the values of the relevant state described by the parameters at freeze-out if no further reactions are considered. For the sake of simplicity, we also use the terms T and for the nonequilibrium Lagrange parameters instead of and at the freeze-out time.
But even after freezing out, further reactions take place that change the abundances of the various components. This stage of the nonequilibrium evolution due to nuclear reactions is often referred to as the afterburner process. The method of NSO offers the possibility of extending the set of relevant observables . To derive kinetic equations, the occupation numbers of the quasiparticle states must be included in the set of relevant observables in order to achieve rapid convergence when calculating reaction rates [62]. Further Lagrange parameters then appear in the generalized Gibbs distribution, such as parameters related to the single-particle distribution function. The Boltzmann equations result when only the occupation numbers of the components in momentum space are considered as relevant observables. The equilibrium solution is the ideal quantum gas, without correlations and in violation of energy conservation. To improve this, we need to add the densities of the conserved quantities as relevant observables, as known from the hydrodynamical description. The NSO method includes the hydrodynamic freeze-out approach and the reaction–kinetic approach using NRN codes as special cases.
The freeze-out concept is related to the particular process for which the fast relaxation is disturbed. We consider expanding hot and dense matter, where the rapid neutron exchange leads to a quasi-equilibrium, which determines also the distribution of the heavy nuclei. If with decreasing density the absorption of neutrons by nuclei becomes slow, the initial distribution of heavy nuclei freezes out. After this heavy-element freeze-out (HEFO), fusion reactions between the light components can still remain frequent, so that the freeze-out of the composition of the light elements occurs at a later time. This subsequent evolution of after HEFO can be approximated by NRN calculations if in-medium effects are irrelevant—see Section 3.2.
We emphasize this staircase character of the freeze-out processes. The chemical freeze-out related to reactive collisions between the constituents and the subsequent kinetic freeze-out related to elastic collisions are known from HIC. If we start from hot and dense matter in local thermodynamic equilibrium, we consider HEFO solely in connection with processes that change the mass number A of the nuclei, before the chemical freeze-out occurs, related to all kinds of nuclear reactions. Even after freeze-out, the various processes continue, but they no longer lead to a generalized equilibrium (6). Instead, further degrees of freedom are established.
The aim of the present work is to infer the values of the Lagrange parameters T and for the generation of the solar abundances of elements, i.e., the initial distribution in a freeze-out scenario for expanding hot and dense matter. This distribution can serve as an initial condition for NRN calculations describing the evolution of the expanding hot and dense matter after freeze-out up to the observed composition. Before switching to the NRN approximation, however, the NSO method allows us to improve the reaction–kinetic approach by taking into account in-medium effects in a systematic quantum statistical approach to obtain a consistent description of expanding hot and dense nuclear matter, which also remains valid at high densities. In particular, the treatment of light clusters in hot and dense nuclear matter near the Mott point is a difficult task [56,74,75]. The contribution of light clusters to the equation of state, in particular the symmetry energy, is often neglected or treated in simple approximations such as the NSE [76] or the excluded volume [77] approaches, which are not valid near the saturation density. The need for a consistent description of nuclear matter including correlations and bound state formation in the subsaturation density range was discussed recently in the context of proto-neutron stars—see, e.g., Dinh Thi et al. [75], Gulminelli and Raduta [78], Pais et al. [79,80], Furusawa et al. [81], Furusawa and Nagakura [82], Dinh Thi et al. [83] and references given therein. One advantage of the NSO approach for nonequilibrium processes is that it enables the application of the many-body theory, since the relevant statistical operator (6) has the form of a Gibbs ensemble.
2.4. Green’s Function Method
A main challenge is the elimination of the Lagrange parameters T and according to Equations (5) and (8), i.e., the nonequilibrium forms of equations of state. Because as given in Equation (8) has an exponential form, this many-body problem can be solved using the method of thermodynamic Green’s functions [84]. For hot and dense nuclear matter, the cluster decomposition of the single-nucleon spectral function [56,85] leads to the equation of state for the total density of nucleons as the sum of the partial densities of the nucleus with mass number A, charge Z and intrinsic quantum number (e.g., spin)
with
The quasiparticle energy of the nucleus depends on the center-of-mass momentum . For , it is the solution of the in-medium Schrödinger equation
which contains the self-energy (SE) term and the Pauli blocking factors . The occupation number of the single-particle state, in momentum-spin–isospin representation, can be approximated by the Fermi function for the uncorrelated medium.
Various approximations are known for the self-energy shift. We use the DD2-RMF model [86] fitted to empirical data,
Expressions for and are given by Typel et al. [86] and expressions for the Pauli blocking shift are provided by Röpke [87,88,89,90].
The solution of the in-medium Schrödinger Equation (11) can have a bound part and a continuum part, which is denoted by the intrinsic quantum number . For , summing over (including continuum correlations) leads to the Beth–Uhlenbeck formula [73] for the second virial coefficient. In the non-degenerate case, we perform the integral over the center-of-mass momentum p in Equation (10) and obtain for the partial density of the nucleus in the channel the expression
where is the medium-modified ground state energy of the nucleus . The degeneracy factor and the sum over all excited states, including the continuum contributions, are absorbed in the prefactor , the intrinsic partition function. For the light elements, the excited states of the nuclei and their degeneracy are known [91] so that the summation can be performed within the intrinsic partition function and the continuum contribution to the virial form [64,92]. For the heavier nuclei, the summation over their excited states can be replaced by the integral over the density of states [93]
where we take and as the binding energy of the bound state . For a more detailed discussion of the intrinsic partition function, see Rauscher [94].
From the Beth–Uhlenbeck results for the virial coefficients for 2H, 4H, 5He and 8Be, the approximation
was suggested for the light clusters by [92], with the energy of the continuum edge of scattering states (for resonances, the negative value of the resonance energy). The Pauli blocking shifts for light elements were considered in Röpke [90]. For , the expression
was found. A more detailed treatment requires us to take into account not only the influence of T but also the dependence on the center-of-mass momentum of the nucleus. Both effects result in a decrease of the Pauli-blocking shift. A further effect is that the bound-state contribution to the partial densities (9) disappears if the binding energy becomes zero, but, according to the Levinson theorem, a contribution of the continuum appears, which can be interpreted as a relic of the merging bound state with the continuum [73]. We impose a Pauli blocking shift
for , which describes the effective suppression of the contribution of the nucleus to the partial density.
The solution of the in-medium Schrödinger Equation (11) for the ground state (and excited states) of nuclei is very complex and requires an expression for the interaction potential. Instead, the empirical data for the binding energies can be used, which are known for many isotopes ([91], see also [95]). Since we need values for the binding energies of isotopes far from stability, we estimate them using model calculations. Hartree–Fock–Bogoliubov calculations [96], microscopic mass formulas [97] and calculations with the Finite-Range Droplet Model [98] were proposed for this purpose. Since we are not dealing with the fine structure of element abundances, we use simple estimates for the general behavior of heavy nuclei. Here, we consider the liquid droplet model (LDM) for the ground-state bound state energies of Equation (13),
The parameters , , and are known for isolated clusters [99]. Further contributions to the LDM consider pairing (not of relevance for the averages ) and shell corrections [97,98,100,101], but see also Skyrme–Hartree-Fock–Bogoliubov (SHFB) calculations [96] and machine learning approaches [102]. We use the parametrization of the shell correction according to Dieperink and van Isacker [101]. The shell correction to the bound state energy is
where
with denoting the number of valence neutrons (protons) and the neutron (proton) valence shell, e.g., for the 50–82 shell. We use the magic numbers 2, 8, 14, 20, 28, 50, 82, 126, 184 and add the numbers 228 and 308 given by Koura and Chiba [103]. In general, the contributions of the shell corrections in Equation (14) depend on T—see Iljinov et al. [104]—which should be taken into account in a more sophisticated approach. There is increasing knowledge about the properties of nuclei far from stability, which is relevant for reaction-network calculations—see the recent publications by Storbacka and Qi [105] and Mollaebrahimi et al. [106]. In our work, we use the simple estimates of the Duflo–Zuker parametrization since we are far from stability, where no empirical data are available, and we consider only the averaged behavior of the distribution of mass fractions.
In addition to the self-energy and Pauli blocking associated with the strong interaction, another in-medium correction is the screening of the Coulomb interaction. Instead of more sophisticated approaches for the dielectric function of a charged particle system using Green’s function techniques [107], we use the simple Wigner–Seitz model, in which the Coulomb part of the binding energy, Equation (18), of a droplet cluster is reduced so that
with as the proton density of the matter and as the proton density in the cluster.
The method of Green’s functions offers a systematic approach to treat in-medium effects, in particular self-energy and Pauli blocking. At high densities, nuclear matter can no longer be considered as an ideal mixture of baryons and nuclei. A semiempirical approach to account for the effect of Pauli blocking is the concept of an excluded volume—see, e.g., Hempel and Schaffner-Bielich [77]. However, this concept is neither able to reproduce details of Pauli blocking such as its momentum and temperature dependence, nor the dissolution of bound states (Mott effect).
3. Results
To determine the Lagrange parameter values for the initial distribution at freeze-out from local thermodynamic equilibrium, we consider the heavier elements which are almost not influenced by stellar burning cycles. We discuss the coarse-grained heavy-element distribution , of the solar abundances, as shown in Figure 1 and listed in Appendix B.
When hot and dense matter expands and cools, the initial distribution of heavy elements evolves after freeze-out through decay processes such as particle emission, -decay and fission. The reverse reactions are increasingly suppressed with decreasing density. We demonstrate this freeze-out approach in Section 3.1, discuss the decay processes in Section 3.2 and present an estimate of the Lagrangian parameters T, and at heavy-element freeze-out (HEFO) in Section 3.3. We focus here on the expansion of hot and dense matter, regardless of how this state was reached.
3.1. Initial Distribution for the Light Elements H and He
We follow an approach similar to that taken in interpreting ternary fission and HIC experiments—see Appendix A. To move on to astrophysical conditions, we start out with calculations for a nuclear system with . Considering a final mass fraction of in the H–He system, which is close to the observed solar composition, we search for possible initial distributions characterised by T and , taking the proton fraction as a free parameter. We include all isotopes of H and He, as well as their excited states, in the initial distribution. Continuum correlations and in-medium modifications are taken into account. We assume that in the expansion phase after freeze-out, neutrons and all H isotopes decay to the stable nuclei 1H and 2H—they feed down to these stable isotopes. Similarly, all He isotopes decay to the stable nuclei 3He and 4He—they feed down to these stable He isotopes. The remaining neutrons feed the yield of 1H.
The results of the calculations for and are shown in Figure 2. For these different parameter values of the proton fraction , the parameter values are shown for which a mass fraction of 4He is recovered in the final distribution. The corresponding initial distributions also contain isotopes of H and He with higher mass numbers. In particular, in the neutron-rich case , the isotopes 5He and 6He will be abundant with increasing density and even exceed the initial yield of 4He. The mass fractions of the heavy helium isotopes 5He, 6He, etc., increase with higher densities. Note that the mass fraction 0.245 refers to the final 4He components given by . The emitted neutrons from the heavier He isotopes eventually contribute to the stable components of H.
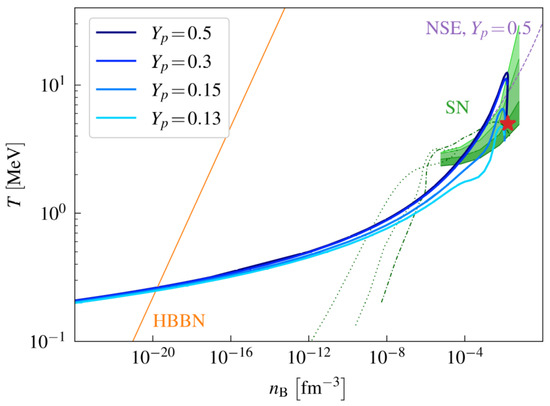
Figure 2.
Nuclear matter phase diagram. For given proton fraction and , the temperature is shown at which the final mass fraction of 4He takes the value 0.245, as a function of the baryon density (full lines). Only light elements are considered. For comparison, the ideal gas (NSE) approximation (dashed) for is also shown. The red star denotes the estimated freeze-out parameter values of Röpke [54]. The dashed line indicates the pathway of the homogeneous Big Bang path (HBBN) and the green shaded areas indicate typical conditions in matter during supernova explosions (SN) [108,109] ( profiles at time steps after 1, 2, 5, 10 s; from above). The dark green curves show the evolution of two tracer particles placed in the supernova simulation. The dash-dotted curve represents matter that ends up deep inside the forming NS, whereas the dotted curve follows the evolution of matter that get ejected in the explosion.
However, above a critical density of about , the helium clusters are dissolved due to Pauli blocking and the Mott effect—see Figure 3. For comparison, the corresponding curve at for the simple NSE considering the stable isotopes of H and He is also shown in the figure. The deviation at high densities is caused by taking into account the unstable states of helium isotopes. A similar behavior is encountered for the H isotopes. With increasing density, the abundance of heavier H isotopes increases, but it goes down at the Mott density, where the bound clusters are dissolved. However, the protons (1H) and the neutrons remain in the nuclear matter as quasiparticles. Pauli blocking, which lowers the binding energies and finally gives rise to the dissolution of bound states, is a dominant effect at subsaturation densities fm−3. We consider as a critical baryon density at which bound states are formed. This value depends only weakly on the proton fraction . It should be mentioned that a more detailed treatment of correlations in nuclear matter predicts a smoother dissolution of the bound states if the dependence on the center-of-mass momentum and the contribution of the continuum are taken into account rigorously.
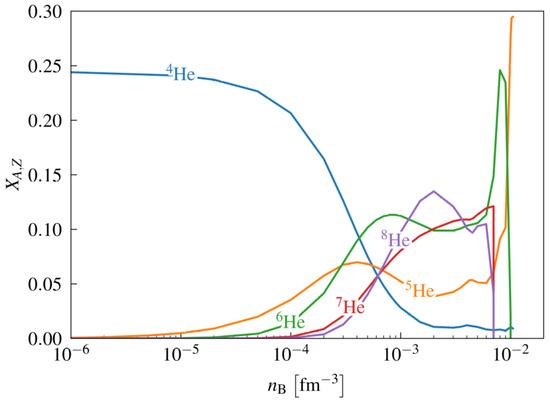
Figure 3.
Composition at freeze-out for the final distribution with , . Temperatures as a function of baryon density according Figure 2. The primary mass fractions of various He-isotopes 4He–8He are presented.
Comparing the two cases shown in Figure 2—the quantum-statistical calculation with in-medium corrections (solid line) and the NSE (dashed line)—one main difference is the suppression of cluster formation at increasing density. All bound states are dissolved near fm−3. The kink behavior near fm−3 is related to the disappearance of 9He and 10He. These isotopes are not shown here, because their abundances are small.
In-medium corrections, in particular Pauli blocking and the Mott effect, are important phenomena in the calculation of the initial distribution not only for HIC or ternary fission experiments, but also for astrophysical sites where hot and dense matter occurs. There are calculations of light clusters in supernova matter at subsaturation densities ( fm−3), based on the concept of NSE. An unexpectedly high concentration of light clusters, such as 4H and 8He and more neutron-rich isotopes, in the central part of collapsing stars was reported by Yudin et al. [110]. These results are unrealistic because in-medium corrections are not taken into account (in particular Pauli blocking and the Mott effect), as shown by Fischer et al. [111]. Since we expect the site of heavy-element formation to fall in a high-density region, we must also take these effects into account. A description in terms of NSE is not valid in this region.
3.2. Heavy-Element Chemical Freeze-Out and the Final Abundances of Isotopes
As discussed in Section 2.3, the freeze-out concept defines the initial distribution, which is the relevant distribution at the instant of time when the fluctuations no longer relax fast enough to restore this relevant state. The mass fractions of the various components remain in local thermodynamic equilibrium up to the heavy-element freeze-out (HEFO) where the initial distribution is obtained. The balance of emission and absorption of neutrons by nuclei necessary for the chemical equilibrium of heavy nuclei is not realised if the density of the neutron environment decreases. After HEFO, we treat the evolution of the distribution as an approximation similar to the case of HIC and ternary fission (see Appendix A) considering the decay of excited states as feed-down processes.
In this reaction–kinetic stage of evolution, and decays convert the excited nuclei to lower-energy states without changing their mass number A. Only processes that change the mass number A are of relevance for the evolution of . In the case of heavy nuclei, the transition to nuclei with a lower mass number takes place by emission of nucleons (e.g., the evaporation of neutrons), -decay and fission.
Excited neutron-rich nuclei emit neutrons. This evaporation process is well known, for instance at fission. There, daughter nuclei are formed, which emit the average number of neutrons with an energy distribution corresponding to a temperature of about . The average neutron multiplicity is nearly proportional to the excitation energy, , with , , and [112]. At temperature T, a nucleus with A nucleons has an excitation energy of with as obtained from the phenomenological Fermi gas approximation [113] and an empirical value of [114]. We estimate the neutron multiplicity evaporated from a nucleus A at temperature T as
with . The increase with A is also shown in the evaporated neutron distribution of spontaneous fission of 252Cf [113].
The emission of neutrons (22) from a nucleus with mass number A gives a nucleus with average mass number , with (for averages, we consider A as continuous variable, to be replaced by discrete values with corresponding probabilities at the end). This process of evaporation transforms the initial distribution to . The mass fraction of the interval is reduced by , but also the interval is changed by the same value so that the values at the new position remain, taking A as a variable. Since A is a discrete number, we have to redistribute the mass fraction over the intervals of in order to obtain the accumulated mass fraction after evaporation, but the height remains almost unchanged. The metallicity is shifted and reduced, taking A as variable.
The initial distribution is characterized by the parameters T, and , and it extends over arbitrary A, including values of the order of . The heaviest stable nucleus is 208Pb. Nuclei with will decay. They feed down lower values of A in the final distribution. The processes of main interest are -decay, binary fission, ternary fission and multifragmentation.
A comprehensive discussion of the decay of actinides and superheavy elements would go beyond the scope of this work. We only mention that the -decay daughter nucleus remains in the heavy element range, so that this reaction has only a minor influence on the total amount of matter bound in the heavy elements. We consider the fate of nuclei with obtained in the initial accumulated mass fraction after HEFO (see below). Some of these nuclei undergo alpha decay and feed down the nuclei found in the intervals with lower accumulated mass numbers . For example, actinides such as Po decay into nuclei in the lead range ( and 208 of the coarse-grained distribution) that are stable. A more detailed consideration of this afterburning process should take into account the half-lives for decay. Some isotopes such as 232Th, 235U, 238U and 244Pu have extremely long half-lives and are present in the solar abundances.
The role of fission for nucleosynthesis became of increasing interest during the last decade [113,115,116,117,118,119,120]. Since we are not concerned with the problem how fission becomes active starting from low-density matter, the initial distribution at HEFO contains all possible nuclei and resonances so that only the decay of them is of interest. Although nuclear fission is of great importance for the description of the abundances of the heavy elements, only limited experimental data are available. As described in [113], experimental data and the GEF (general description of fission observables) calculations tend to indicate symmetrical fission for large mass numbers A. Fission fragments populate the regions near and . Part of th mass fraction observed in that range can be attributed to a fission origin [14]. Fission has no effect on the total amount , , of matter bound in the heavy elements if the fission fragment nuclei remain in the heavy element range.
After HEFO, the evolution of the distribution can be approximated by NRN calculations as afterburner, based on detailed information about the isotopes, their excited states and reaction cross sections. This is not the aim of our present work. Instead, we are interested in determining the parameter values T, and for an initial distribution. Therefore, we consider only the coarse-grained pattern of the distribution function given by the accumulated mass fractions . For future work, NRN calculations would be of interest to determine the final distribution . It should be mentioned, however, that these calculations make approximations if HEFO appears at extreme conditions. The typical NRN approximation neglects in-medium corrections such as Pauli blocking and self-energy effects, which are included in the relevant statistical operator at freeze-out, as well as correlations in the continuum.
3.3. Initial Distribution from the Heavy-Element Abundances
To construct the initial distribution at heavy-element freeze-out (HEFO), the binding energies of nuclei are needed. As generally accepted, the formation of the heavy elements requires a neutron-rich, hot environment; see also Figure 2. Neutron-rich nuclei are formed, with binding energies not known from experiments.
Hartree–Fock–Bogoliubov or Finite-Range Droplet Model calculations are applied to determine the binding energies of nuclei far from stability, but one has to consider the effects of the medium which influence the properties of nuclei. For the light nuclei, where the binding energies are measured experimentally, the shifts of the binding energies due to self-energy and Pauli blocking are known. For the heavy nuclei, we use the Liquid Droplet Model (LDM) (18). Its parameter values , , and depend on the surrounding medium. Within the Wigner–Seitz approximation, the modification of the Coulomb term was already discussed in Section 2.4. Because of screening and a low proton fraction, the Coulomb term becomes very small at high densities. We assume that the asymmetry energy is not modified.
Self-energy shifts affect bound states as well as continuum states so that they effectively modify the chemical potentials. We use the DD2-RMF result [86] given in Section 2.4 for the nucleons in the nuclei, which leads to a renormalization of the chemical potentials and . Typical values for the self-energy of nucleons at , and are and . The Pauli blocking partially compensates the self-energy shift and leads to the dissolution of the bound states (Mott effect), as discussed in Section 2.4. According to Equation (17), we introduce the parameter as an average value of and add this to the bulk parameter . For and , we estimate .
For an estimate of the parameter value of the surface term , we consider the ratio as shown in Figure 4. Using the solar data (see Table A1) we expect a smooth average dependence on A. However, there are strong deviations related to the peaks in owing to the magic numbers and the iron peak (see Figure 1), which are not relevant for our present discussion of the LDM.
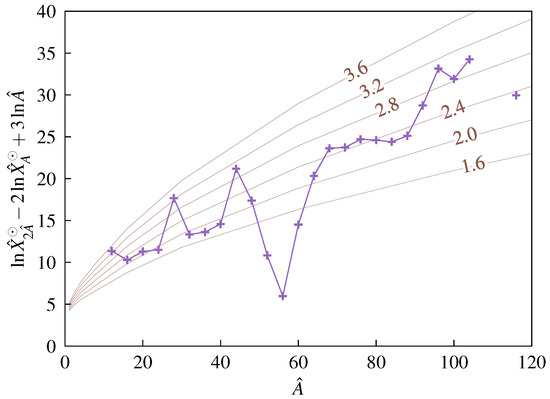
Figure 4.
Double ratio of accumulated mass fractions. Solar distribution (purple “+” symbols, lines to guide the eyes; values from Table A1) compared with liquid droplet model calculations, Equation (23), brown curves, for various parameter values as given in the line labels. Further parameter values are provided in the text.
We employ the LDM (18) to calculate the ratio . For a nucleus with mass number A, we assume an average charge number . From Equation (13) we obtain
The bulk term and the asymmetry term of the Bethe–Weizsäcker relation (18) cancel in the exponent.
We use this relation to infer values for and by comparison with the solar data listed in Table A1; see Figure 4. The strong deviations from a smooth behavior are due to the fact that magic numbers are not included in the Bethe–Weizsäcker relation (18). Relation (23) is shown in Figure 4 for various parameter values . The graph is not very sensitive to the first term on the right-hand side of (23) for which , and has been used. The least-mean-square-deviation fit to the data for , which are heavy nuclei not related to magic numbers, gives and . The small value of the Coulomb term in the LDM is an indication of a small value of the proton fraction and the strong screening in the dense, neutron-rich matter. Of interest is the result for the surface term . Assuming a temperature of about , the value follows, which is smaller than the free value given above. The corresponding free value is in conflict with the observed data; see Figure 4. Lattimer and Swesty [121] discuss a reduction of the surface term for nuclei embedded in hot and dense matter; see also Ravenhall et al. [122]. The simple LDM discussed here supposes a value of the surface term in the range .
In a next step, we construct the initial distribution at HEFO. With the in-medium modifications of the LDM and the nucleon self-energy shifts given above, we determine the parameter values T, and so that . The assumption that the observed distribution of the heavy elements is obtained from an initial distribution predominately by decay processes (neutron emission, -decay, fission) has the consequence that the initial -metallicity must have been larger than the presently observed -metallicity in the region . At , only the evaporation of neutrons from the heavy nuclei significantly changes the initial distribution to the final one. The flow of matter bound in heavy nuclei across due to -decay is small. It is determined by the number of nuclei which emit the particles. Fission gives almost no flow of matter across because the fission fragments remain with mass numbers . Evaporation of neutrons after fission has to be taken into account. The -metallicity in the range of is nearly conserved with respect to fission processes. We consider these conditions for in the region as a prerequisite to infer the initial distribution from the observed final abundances.
As an example, in Figure 5, we show a result for parameter values , and . The chemical potentials are and . Here, the model parameter values and have been used. The parameter values for T, and are obtained from the conditions that and in the range as shown in Figure 5d. The small deviation is self-consistently determined by the -decay of heavy nuclei which is discussed below.
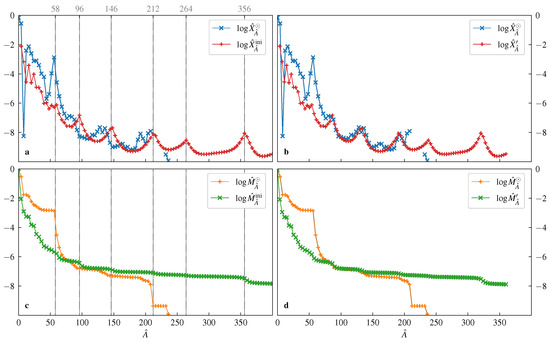
Figure 5.
Accumulated mass fraction (top row) compared with the solar accumulated mass fraction (blue “×” symbols) and -metallicity (bottom row) compared with the solar -metallicity (orange “+” symbols). Values are given in Table A1. Dotted lines mark the double magic numbers , , , , and (included in ). Panel (a): Initial accumulated mass fraction (red “+” symbols) for the parameter values , and . Panel (b): Accumulated mass fraction after evaporation of neutrons (red “+” symbols) for . Panel (c): Initial -metallicity (green “×” symbols) for the parameter values , and . Panel (d): -metallicity after evaporation of neutrons (green “×” symbols) for .
The inferred distribution at HEFO extends to very large numbers of A; the accumulated initial mass fraction drops down above . The initial -metallicity also has a long tail. As shown in Figure 5c, it crosses the solar near . The value of for agrees well with the observed values, implying that the gain of heavy nuclei matter by fission of light nuclei and neutron absorption is compensated by the loss of heavy nuclei matter due to evaporation of neutrons and -decay. We consider as the border between light and heavy nuclei. The accumulated solar mass fraction takes a minimum here. Burning processes will hardly extend much beyond the iron peak, and fission of superheavy elements and emission of clusters are also not expected to contribute to a flow across this value. Emission of neutrons is possible but will give only a small left-directed flow, which is compensated by the right-directed fusion flow. The metallicity can approximately be considered as conserved quantity. We expect only minor changes of its value after HEFO. Fusion will change the distribution of the light nuclei after HEFO, forming, for example, the iron peak. We do not discuss the light nuclei here.
For the heavy nuclei, we obtain three peaks at mass numbers near the observed maxima, but at slightly higher values of A, as shown in Figure 5a. These and further maxima are related to magic numbers of neutrons and protons, , , and . The proton fractions for these double-magic nuclei are close to the assumed proton fraction of the nuclear matter. The corresponding nuclei are bound but far from stability. The neutron separation energy is negative, but they nonetheless contribute to the composition of matter as correlations in the continuum. For example, as discussed in Appendix A, experiments find that the unstable nucleus 5He () contributes to the primordial distribution in ternary fission. The appearance of peaks at higher mass numbers and 356 is of interest.
De-excitation processes will modify the initial distribution. - and -decays do not change the distribution of mass fractions. The evaporation of neutrons concerns all heavy nuclei which are excited. Using Equation (22) with , the evaporation of neutrons results in the mass fraction distribution shown in Figure 5b. A corresponding plot of the accumulated mass fractions shows a good reproduction of the three peaks.
The accumulated mass fraction extends significantly beyond the limit of stability at . Nuclei with are unstable with respect to -decay, binary fission, ternary fission and multifragmentation. -decays shift the actinides toward the lead region. The overpopulation of accumulated mass fractions and accounts for part of the actinides. For an estimate, we calculate the mass fraction of the overpopulation . The amount of matter bound in nuclei with mass numbers to decay through fission or through -decay is . For the estimate, we assume a sharp separation between nuclei with smaller mass numbers A, which decay by emission of an particle, and superheavy nuclei with larger mass numbers, which decay by fission. Of course, the branching ratios for fission and -decay of superheavy nuclei do not jump sharply with A. In this simple estimate, since , the fraction of matter bound in nuclei with is required to account for the overpopulation at . The loss of matter bound in heavy nuclei due to -decay is estimated as over this interval. This determines the difference given above in the interval . The process of -decay is not completed yet; reduced values of the accumulated mass fractions of and 236 (Th, U, Pu) remain and are subject to chemochronology.
Fission is the fate of the remaining heavy nuclei, with a total mass fraction of according to our estimate. Of particular relevance is the peak at , which is related to the double magic nucleus 356Sn. After evaporation of neutrons, the maximum in the distribution appears near . Assuming symmetric fission [113], fragments near would appear, which can explain the enhanced observed mass fractions in that region.
The example of the freeze-out distribution considered here is determined by the Lagrange parameters T, and which yield the initial -metallicity shown in Figure 5c; see also Table A1. The inferred parameter values , and satisfy the requirements and for given at the beginning of this section. After evaporation of neutrons, coincides with in the range with the small gap , which accounts for the -decay. Taking into account -decay and fission, metallicity will change further, so it will approach . The material bound in heavy clusters, , and its change with A, , are nearly conserved. We investigated only the coarse-grained pattern of the final distribution of the mass fractions , which concerns the sum of the detailed mass fractions with four subsequent mass numbers A. In order to obtain the final distribution of the mass fractions , a more detailed description of the individual properties of nuclei is necessary, for example of the decay processes of the various excited isotopes far from the region of stability.
4. Discussion
Our work deals with the question of whether the shape of the heavy-element abundances can tell us something about the origin of these nuclei. In the framework of a nonequilibrium approach, we reconstruct the Lagrange parameter values of the heavy-element freeze-out (HEFO) in a region where in-medium corrections are essential. We considered the coarse-grained pattern of the mass fraction distribution and used the metallicity in the region to determine the value of the Lagrange parameters. We did not perform NRN simulations to calculate the isotopic abundances of the individual stable nuclei, but instead consider our final distribution as input for such calculations of the abundances of the elements. Current NRN calculations usually start when the temperature decreases to 0.7 MeV, with the initial composition being determined assuming nuclear statistical equilibrium (NSE); see, e.g., Ricigliano et al. [38], Fischer et al. [109]. There are several other issues that will be addressed in more detail in the following discussion.
4.1. HEFO and In-Medium Corrections
Our scenario describes expanding hot and dense matter in which relaxation to the generalized Gibbs state (8) takes place as long as the relaxation time for reactive collisions is sufficiently short. To describe nuclear matter at subsaturation densities, in-medium corrections must be taken into account, in particular self-energy shifts and Pauli blocking. Resonances, i.e., correlations in the continuum, must be considered. The Mott density determines the region in which bound states can exist.
If the density and/or the temperature decrease, the relaxation of the fluctuations can become so slow that the general local equilibrium is no longer maintained, but new degrees of freedom occur at this freeze-out point. In contrast to the NRNs, which consider all types of nuclear reactions, the accumulated mass fractions of the elements can only be changed by emission and absorption of particles, fission and fusion processes. The freeze-out for heavy elements (HEFO) occurs when the equilibrium of these processes is no longer maintained. The subsequent temporal evolution of the accumulated mass fraction distribution is then dominated by decay processes.
For the state of the nuclear system at HEFO, the Zubarev NSO approach provides a systematic quantum mechanical description, so that correlations in the system are taken into account in the distribution function . This is not possible for an NRN approach, which is based on single-particle properties and reaction rates in free space. In this approximation, the local thermodynamic equilibrium solution is an ideal gas composed of various components. It would be of interest to work out reaction kinetics including in-medium effects, based, e.g., on the spectral function, but this is presently out of reach. We consider decay processes in a summary approach to derive the final distribution—a method known from investigations in nuclear physics; see Appendix A.
After HEFO, the excited, unstable states of nuclei, which exist in the initial distribution, will decay and feed the abundances of nuclei with lower mass numbers A. The NRNs currently used to simulate the r-process are well established to describe chemical evolution in the low-density regime ( fm−3) where in-medium effects are less important. For subsaturation densities ( fm−3), however, Pauli blocking and the Mott effect must be taken into account. The concept of NSE [110] cannot be applied in this regime and leads to flawed results as shown by Fischer et al. [111].
It is also not expected that the formation of heavy elements would terminate in the neutron-rich superheavy region due to fission and rarely extend beyond the element [119]. If the trajectory of matter in the density–temperature plane passes through states characterized by the Lagrangian parameters given in this work (see Figure 3), nuclei with mass numbers as large as are formed in the initial distribution. Fission and -decay are a common side effects of nucleosynthesis. Hence, an interesting prediction of the HEFO scenario is the increased initial abundance of nuclei in the range around —see Figure 5a—which due to fission contributes significantly to the observed increased abundances in the range .
4.2. Phase Transition and Distribution of Lagrange Parameters
Within the framework of a nonequilibrium approach, which includes both the kinetic and the hydrodynamic approximation for the description of expanding dense matter, parameter values for the freeze-out of heavy-element formation () are inferred. Under our specific approximations, the values of the HEFO parameter (8) corresponding to , , and are estimated, which characterize a potential astrophysical site of heavy-element formation with the characteristic abundance pattern of the solar system. Regardless of the specific astrophysical event (supernova explosions, NS mergers or inhomogeneous Big Bang), these relevant parameter values are an important prerequisite for discussing the origin of the observed abundances.
It is of interest to look at the abundance patterns of objects beyond the solar system. We expect different values for the Lagrange parameters . Chemical compositions have been measured for many stars and galaxies. Information is also available for cosmic rays. The heavy-element distribution is quite robust, but a distribution of the Lagrange parameters is expected. For example, a higher freeze-out temperature is implied by the heavy-element abundances in cosmic rays.
The HEFO parameter values are located in the range of thermodynamic instability of the nuclear matter (liquid–gas) phase transition ([54], see also [123]), so that a rapid change in the parameter values—especially the baryon density—is to be expected during expansion. Pasta-like structures can appear as known from proto-neutron stars. The connection between freeze-out and the formation of bound states (Mott effect) in nuclear matter was recently discussed by Blaschke et al. [124]. The investigation of the dynamical evolution of hot and dense matter under these conditions (nucleation in a nuclear matter fog) is beyond the scope of this work but is the subject of future investigations. Nevertheless, we assume that our final coarse-grained distribution can serve as an initial condition for performing NRN calculations for the elemental abundances.
4.3. Inhomogeneous Big-Bang Nucleosynthesis
Simulations and observations indicate that violent astrophysical processes such as SN explosions and NS mergers give rise to conditions for heavy-element formation, so the pattern of the heavy-element mass-fraction distribution may change during these events. However, it is an open question whether these violent processes are the only places for the formation of heavy elements, or whether heavy elements were already formed very early in the Universe under other conditions. New observations of massive objects at large redshifts, e.g., with the James Webb Space Telescope (JWST) [125], suggest that massive objects already existed very early in the evolution of the Universe. Unusual nucleosynthesis has been detected for a massive star in the early Universe [51].
Open questions also arise in the context of galactic chemical evolution (GCE). It is beyond the scope of this article to review the research field of GCE, and we refer to Matteucci [126]. Here, we only mention the following special problem: stars with high r-process abundances ([Eu/Fe] = ) and extremely low metallicity () have been observed, and an astrophysical site for nucleosynthesis is under discussion in an environment with lower metallicity than binary NS mergers could have—see Farouqi et al. [47], Wehmeyer et al. [127,128], Thielemann et al. [129]. Upcoming measurements will provide an important constraint on the actual local NS-NS merger rate, and will help to decide whether or not compact binary mergers are the dominant source of r-process elements in the Universe [130].
An additional production site of heavy elements active in the early Universe would provide an alternative. Hydrodynamic simulations of this additional r-process source still need to ensure the conditions for a robust r-process pattern [131]. The values for the Lagrangian parameters and the corresponding distributions given in our work may be of interest here.
We briefly mention inhomogeneous Big-Bang nucleosynthesis (IBBN) as an alternative or complementary source of heavy elements. This scenario implies that heavy elements are formed very early in the Universe. According to the IBBN, large density fluctuations arise in the context of the quark–hadron phase transition [132,133,134] and are assumed to exist already at , when the primordial distribution, Equation (1), would freeze out in the HBBN model. Phase transitions and the formation of gravitationally bound clusters of matter are possible processes for the emergence of long-lived, dense objects already at high mean density and temperature. This stage of the early Universe is quite hypothetical. For a recent discussion of primordial density fluctuations in the context of primordial black hole formation and heavy element synthesis, see Gonin et al. [55], where further details and references can be found. The IBBN scenario, which avoids all matter passing through the compositional state (1), could explain the so-far unsuccessful search for population III stars and pair-instability supernovae. Moreover, the IBBN scenario coupled to our freeze-out model for the formation of heavy elements provides a natural explanation for the universal abundance pattern beyond the iron group found in various astrophysical objects. In this framework, only the three parameter values for T, and determine the initial distribution at heavy-element freeze-out, from which the observed abundance pattern evolves.
5. Conclusions
In the framework of a general nonequilibrium approach, we relate the observed coarse-grained distribution of the mass fractions of heavy elements to a hot and dense state of nuclear matter described by the Lagrangian parameters T and , the nonequilibrium generalizations of temperature and chemical potentials. Values inferred from the solar abundances are presented. After the freeze-out of the heavy-element mass fraction distribution, the evolution of the corresponding coarse-grained distribution function is determined by decay processes. At a later stage, further nuclear reactions freeze out, and nuclear reaction networks can be employed to follow the temporal evolution of the individual isotopic distributions that lead to the observed mass fractions.
The description of clusters in hot and dense nuclear matter requires a quantum statistical approach to account for in-medium effects. For conditions close to nuclear saturation density, self-energy and Pauli blocking must be taken into account. In this regime, the standard model of nuclear statistical equilibrium, which is based on the properties of free nuclei, is no longer valid, since bound states are dissolved by the Mott effect. Continuum correlations, in particular resonances, must be included. It is expected that large neutron-rich clusters form, for example the double magic nucleus 358Sn. However, nuclear physics needs to be further developed to explore the properties of nuclei in the range of subsaturation densities.
Our proposed scenario raises the question of the astrophysical sites of heavy-element production. Parameter values of density and temperature at heavy-element freeze-out are encountered in supernova explosions in the forming proto-neutron star where the pasta structures appear in the crust. Here we are confronted with the nuclear matter phase transition, and future work is needed to study the behavior of nuclear matter in this critical regime. Neutron star mergers are thought to be the site for the origin of heavy elements, but this might not be the only source of r-process elements. Additional, perhaps complementary production sites of heavy elements may exist in the early Universe. From the coarse-grained pattern of the element abundances, we derive the Lagrange parameters T, and for the heavy-element freeze-out, which can be instrumental for characterizing the state of such additional production sites.
Author Contributions
Conceptualization, data curation, writing—original draft preparation, G.R.; writing—review and editing, D.B. and F.K.R.; visualization, G.R. and F.K.R.; funding acquisition, G.R., D.B. and F.K.R. All authors have read and agreed to the published version of the manuscript.
Funding
G.R. acknowledges a stipend from the Foundation for Polish Science within the Alexander von Humboldt programme under grant No. DPN/JJL/402-4773/2022. D.B. was supported by NCN under grant No. 2021/43/P/ST2/03319. The work of F.K.R. is supported by the Klaus Tschira Foundation, by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—RO 3676/7-1, project number 537700965, and by the European Union (ERC, ExCEED, project number 101096243). Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.
Data Availability Statement
Data are available from https://doi.org/10.5281/zenodo.17418930.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been updated to include a Data Availability Statement. This change does not affect the scientific content of the article.
Appendix A. Freeze-Out Approach for Laboratory Experiments
We demonstrate the freeze-out concept and the afterburner approach for the formation of the light elements H and He in expanding hot and dense nuclear matter. To explain the evolution of the primordial (initial) distribution after freeze-out, we consider nuclear matter with only two elements, H and He, together with neutrons in the primordial distribution of isotopes. Can we derive the Lagrange parameters T and at freeze-out from observed yields of the stable isotopes 1H, 2H, 3He, 4He? This problem was investigated for HIC [58,59] and ternary fission [64,92]. The primordial distribution contains not only the stable isotopes but also all unstable isotopes, including their excited states and continuum contributions. The energies of the ground state and the excited states are modified by in-medium effects such as self-energy and Pauli blocking. A simple NSE description is invalid because it neglects these effects. For HIC at collision energies of per nucleon, Natowitz et al. [58] reported the freeze-out baryon density for and a proton fraction of .
In ternary fission, nuclei are formed during scission in the neck region, where the proton fraction is low, so that neutron-rich isotopes appear more abundantly. For instance, in addition to the stable nuclei 2H, 3H, 3He, 4He, the abundance of unstable nuclei such as 5He in the hot and dense primordial matter is calculated, which decay after freeze-out and feed the observed yields of 4He. Their contribution of about 17 % to all observed 4He events was determined by experiments [63], in which the correlations in the ternary spontaneous fission of 252Cf were measured. The same was observed for the unstable isotope 7He, which feeds the final yield of 6He. Also 4H is obtained in the primordial distribution, but it feeds the final yield of 3H. If all decay processes are taken into account (see [64,92]), the primordial distribution at freeze-out converts to the final distribution. This analysis allows us to infer the Lagrange parameters for the primordial distribution (13) from the observed elemental and isotopic abundances. Together with the observed yields of 2H and 3H, a freeze-out parametrisation for 241Pu of the neck region at fission was obtained with , baryon density fm−3 and proton fraction . For this purpose, a least-squares fit was performed between the observed yields and the calculated final distribution, which is determined by the Lagrange parameters T and .
Comparing the calculated yields of 6He and 8He with the observed yields, the suppression of weakly bound clusters due to Pauli blocking was discussed [92]. These in-medium effects are more evident in the suppression of the weakly bound isotopes 11Li and 19C [64]. Medium effects are also evident in HIC [59].
Appendix B. Coarse-Grained Pattern of Solar Abundances
In Table A1 we give values for the accumulated mass fraction , defined in Equation (2) and the -metallicity , defined in Equation (3) as plotted in Figure 1 and Figure 5. Solar mass fractions and -metallicity are obtained from Lodders et al. [3]. The initial mass fractions and -metallicity assume parameter values of , and .

Table A1.
Accumulated mass fractions and -metallicities .
Table A1.
Accumulated mass fractions and -metallicities .
| 0 | −0.1523 | 0.0000 | … | 0.0000 |
| 4 | −0.5555 | −0.5291 | −2.1068 | −2.0424 |
| 8 | −8.2524 | −1.7580 | −3.1644 | −2.9030 |
| 12 | −2.4070 | −1.7580 | −4.5508 | −3.2476 |
| 16 | −2.1284 | −1.8684 | −3.4172 | −3.2698 |
| 20 | −2.6028 | −2.2147 | −4.6030 | −3.8108 |
| 24 | −3.1198 | −2.4432 | −4.0245 | −3.8873 |
| 28 | −3.1011 | −2.5459 | −4.9128 | −4.4543 |
| 32 | −3.4024 | −2.6876 | −4.9323 | −4.6400 |
| 36 | −3.9822 | −2.7807 | −5.2269 | −4.9501 |
| 40 | −4.2017 | −2.8089 | −6.0153 | −5.2767 |
| 44 | −5.6959 | −2.8268 | −5.9716 | −5.3642 |
| 48 | −5.3849 | −2.8274 | −6.3886 | −5.4874 |
| 52 | −3.9617 | −2.8286 | −6.1494 | −5.5457 |
| 56 | −2.8715 | −2.8618 | −6.2884 | −5.6701 |
| 60 | −4.5829 | −4.5167 | −6.1171 | −5.7897 |
| 64 | −5.5298 | −5.3657 | −6.7205 | −6.0659 |
| 68 | −6.2388 | −5.8679 | −7.1405 | −6.1747 |
| 72 | −6.7211 | −6.1088 | −7.3338 | −6.2244 |
| 76 | −7.0309 | −6.2303 | −7.5739 | −6.2595 |
| 80 | −6.8766 | −6.3052 | −7.5629 | −6.2811 |
| 84 | −6.9336 | −6.4408 | −7.6142 | −6.3044 |
| 88 | −7.1233 | −6.6093 | −7.4308 | −6.3263 |
| 92 | −7.8379 | −6.7681 | −7.2421 | −6.3618 |
| 96 | −8.2692 | −6.8067 | −6.8260 | −6.4231 |
| 100 | −8.3142 | −6.8219 | −7.4362 | −6.6418 |
| 104 | −8.3692 | −6.8362 | −7.8646 | −6.7177 |
| 108 | −8.4435 | −6.8491 | −8.1783 | −6.7499 |
| 112 | −8.3928 | −6.8603 | −8.3965 | −6.7664 |
| 116 | −8.1629 | −6.8732 | −8.5154 | −6.7767 |
| 120 | −8.2007 | −6.8961 | −8.6020 | −6.7847 |
| 124 | −7.9386 | −6.9182 | −8.6037 | −6.7913 |
| 128 | −7.6523 | −6.9617 | −8.5831 | −6.7981 |
| 132 | −7.9881 | −7.0607 | −8.4733 | −6.8053 |
| 136 | −7.7132 | −7.1154 | −8.3179 | −6.8147 |
| 140 | −8.1821 | −7.2417 | −8.0678 | −6.8285 |
| 144 | −8.7119 | −7.2946 | −7.7928 | −6.8543 |
| 148 | −9.0105 | −7.3116 | −7.6929 | −6.9075 |
| 152 | −8.9770 | −7.3203 | −8.2115 | −6.9852 |
| 156 | −8.9190 | −7.3300 | −8.5854 | −7.0118 |
| 160 | −8.7799 | −7.3414 | −8.8581 | −7.0236 |
| 164 | −8.7875 | −7.3575 | −9.0451 | −7.0299 |
| 168 | −9.0449 | −7.3739 | −9.1690 | −7.0342 |
| 172 | −8.9853 | −7.3833 | −9.2471 | −7.0374 |
| 176 | −9.1763 | −7.3943 | −9.2859 | −7.0401 |
| 180 | −9.1656 | −7.4011 | −9.2979 | −7.0425 |
| 184 | −9.0851 | −7.4091 | −9.2786 | −7.0446 |
| 188 | −8.4962 | −7.4183 | −9.2322 | −7.0475 |
| 192 | −8.0903 | −7.4562 | −9.1452 | −7.0504 |
| 196 | −8.4125 | −7.5710 | −9.0142 | −7.0537 |
| 200 | −8.7710 | −7.6385 | −8.8327 | −7.0586 |
| 204 | −8.0595 | −7.6718 | −8.6202 | −7.0660 |
| 208 | −7.9157 | −7.9005 | −8.3788 | −7.0783 |
| 212 | … | −9.3651 | −8.0964 | −7.1006 |
| 216 | … | −9.3651 | −8.2286 | −7.1468 |
| 220 | … | −9.3651 | −8.6321 | −7.1844 |
| 224 | … | −9.3651 | −8.8996 | −7.2002 |
| 228 | … | −9.3651 | −9.0644 | −7.2089 |
| 232 | −9.5072 | −9.3651 | −9.1504 | −7.2150 |
| 236 | −9.9195 | −9.9195 | −9.1806 | −7.2201 |
| 240 | … | … | −9.1699 | −7.2249 |
| 244 | … | … | −9.1305 | −7.2299 |
| 248 | … | … | −9.0676 | −7.2353 |
| 252 | … | … | −8.9829 | −7.2418 |
| 256 | … | … | −8.8717 | −7.2497 |
| 260 | … | … | −8.7252 | −7.2602 |
| 264 | … | … | −8.5343 | −7.2754 |
| 268 | … | … | −8.7735 | −7.2999 |
| 272 | … | … | −9.0477 | −7.3148 |
| 276 | … | … | −9.2409 | −7.3229 |
| 280 | … | … | −9.3691 | −7.3282 |
| 284 | … | … | −9.4461 | −7.3322 |
| 288 | … | … | −9.4848 | −7.3356 |
| 292 | … | … | −9.4959 | −7.3387 |
| 296 | … | … | −9.4889 | −7.3417 |
| 300 | … | … | −9.4711 | −7.3448 |
| 304 | … | … | −9.4482 | −7.3481 |
| 308 | … | … | −9.4243 | −7.3515 |
| 312 | … | … | −9.4017 | −7.3552 |
| 316 | … | … | −9.3806 | −7.3591 |
| 320 | … | … | −9.3598 | −7.3633 |
| 324 | … | … | −9.3358 | −7.3677 |
| 328 | … | … | −9.3038 | −7.3724 |
| 332 | … | … | −9.2566 | −7.3775 |
| 336 | … | … | −9.1856 | −7.3833 |
| 340 | … | … | −9.0802 | −7.3902 |
| 344 | … | … | −8.9283 | −7.3991 |
| 348 | … | … | −8.7156 | −7.4122 |
| 352 | … | … | −8.4272 | −7.4343 |
| 356 | … | … | −8.0566 | −7.4809 |
| 360 | … | … | −8.2879 | −7.6149 |
| 364 | … | … | −8.7160 | −7.7186 |
| 368 | … | … | −9.0654 | −7.7646 |
| 372 | … | … | −9.3259 | −7.7869 |
| 376 | … | … | −9.4967 | −7.7997 |
| 380 | … | … | −9.5922 | −7.8085 |
| 384 | … | … | −9.6293 | −7.8157 |
| 388 | … | … | −9.6242 | −7.8224 |
| 392 | … | … | −9.5897 | −7.8293 |
| 396 | … | … | −9.5365 | −7.8369 |
| 400 | … | … | −9.4723 | −7.8457 |
Notes
| 1 | In nuclear physics, the baryon number density is given usually in fm−3. For conversion to the mass density use corresponding to . We consider also as energy which is usually measured in MeV, corresponds to the thermodynamic temperature . With we have . |
| 2 | We use the term “cluster” for referring to a nuclear particle correlation in high-density matter and not in the sense of clusters of astrophysical objects, such as stars or galaxies. |
| 3 | Usually, the astrophysical term “metals” (Z) refers to the set of all elements beyond He. In analogy, with the A-metallicity we denote the fraction of material found in nuclei with mass numbers . |
References
- Lodders, K. Solar System Abundances and Condensation Temperatures of the Elements. Astrophys. J. 2003, 591, 1220–1247. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef]
- Lodders, K.; Palme, H.; Gail, H.P. Abundances of the Elements in the Solar System. Landolt Börnstein 2009, 4B, 712. [Google Scholar] [CrossRef]
- Lodders, K. Relative Atomic Solar System Abundances, Mass Fractions, and Atomic Masses of the Elements and Their Isotopes, Composition of the Solar Photosphere, and Compositions of the Major Chondritic Meteorite Groups. Space Sci. Rev. 2021, 217, 44. [Google Scholar] [CrossRef]
- Magg, E.; Bergemann, M.; Serenelli, A.; Bautista, M.; Plez, B.; Heiter, U.; Gerber, J.M.; Ludwig, H.G.; Basu, S.; Ferguson, J.W.; et al. Observational constraints on the origin of the elements. IV. Standard composition of the Sun. Astron. Astrophys. 2022, 661, A140. [Google Scholar] [CrossRef]
- Frebel, A.; Norris, J.E. Near-Field Cosmology with Extremely Metal-Poor Stars. Annu. Rev. Astron. Astrophys. 2015, 53, 631–688. [Google Scholar] [CrossRef]
- Frebel, A. From Nuclei to the Cosmos: Tracing Heavy-Element Production with the Oldest Stars. Annu. Rev. Nucl. Part. Sci. 2018, 68, 237–269. [Google Scholar] [CrossRef]
- Roederer, I.U.; Lawler, J.E.; Den Hartog, E.A.; Placco, V.M.; Surman, R.; Beers, T.C.; Ezzeddine, R.; Frebel, A.; Hansen, T.T.; Hattori, K.; et al. The R-process Alliance: A Nearly Complete R-process Abundance Template Derived from Ultraviolet Spectroscopy of the R-process-enhanced Metal-poor Star HD 222925. Astrophys. J. Suppl. Ser. 2022, 260, 27. [Google Scholar] [CrossRef]
- Fields, B.D.; Molaro, P.; Sarkar, S. Big-Bang Nucleosynthesis. Chin. Phys. C 2014, 38, 339–344. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.H. Big bang nucleosynthesis: Present status. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- Coc, A.; Vangioni, E. Primordial nucleosynthesis. Int. J. Mod. Phys. E 2017, 26, 1741002. [Google Scholar] [CrossRef]
- Arcones, A.; Thielemann, F.K. Origin of the elements. Astron. Astrophys. Rev. 2023, 31, 1. [Google Scholar] [CrossRef]
- Heger, A.; Woosley, S.E. The Nucleosynthetic Signature of Population III. Astrophys. J. 2002, 567, 532–543. [Google Scholar] [CrossRef]
- Roederer, I.U.; Vassh, N.; Holmbeck, E.M.; Mumpower, M.R.; Surman, R.; Cowan, J.J.; Beers, T.C.; Ezzeddine, R.; Frebel, A.; Hansen, T.T.; et al. Element abundance patterns in stars indicate fission of nuclei heavier than uranium. Science 2023, 382, adf1341. [Google Scholar] [CrossRef]
- Keller, S.C.; Bessell, M.S.; Frebel, A.; Casey, A.R.; Asplund, M.; Jacobson, H.R.; Lind, K.; Norris, J.E.; Yong, D.; Heger, A.; et al. A single low-energy, iron-poor supernova as the source of metals in the star SMSS J031300.36-670839.3. Nature 2014, 506, 463–466. [Google Scholar] [CrossRef]
- Burbidge, M.E.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the elements in stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef]
- Cameron, A.G.W. Nuclear reactions in stars and nucleogenesis. Publ. Astron. Soc. Pac. 1957, 69, 201–222. [Google Scholar] [CrossRef]
- Lippuner, J.; Roberts, L.F. SkyNet: A modular nuclear reaction network library. Astrophys. J. Suppl. 2017, 233, 18. [Google Scholar] [CrossRef]
- Reichert, M.; Winteler, C.; Korobkin, O.; Arcones, A.; Bliss, J.; Eichler, M.; Frischknecht, U.; Fröhlich, C.; Hirschi, R.; Jacobi, M.; et al. The Nuclear Reaction Network WinNet. Astrophys. J. Suppl. Ser. 2023, 268, 66. [Google Scholar] [CrossRef]
- Iliadis, C. Nuclear Physics of Stars; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar] [CrossRef]
- National Research Council. Connecting Quarks with the Cosmos: Eleven Science Questions for the New Century; The National Academies Press: Washington, DC, USA, 2003. [Google Scholar] [CrossRef]
- Cowan, J.J.; Sneden, C.; Lawler, J.E.; Aprahamian, A.; Wiescher, M.; Langanke, K.; Martínez-Pinedo, G.; Thielemann, F.K. Origin of the heaviest elements: The rapid neutron-capture process. Rev. Mod. Phys. 2021, 93, 15002. [Google Scholar] [CrossRef]
- Diehl, R.; Korn, A.J.; Leibundgut, B.; Lugaro, M.; Wallner, A. Cosmic nucleosynthesis: A multi-messenger challenge. Prog. Part. Nucl. Phys. 2022, 127, 103983. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Beers, T.C. Recent Advances in Understanding R-Process Nucleosynthesis in Metal-Poor Stars and Stellar Systems. Universe 2025, 11, 229. [Google Scholar] [CrossRef]
- Wanajo, S.; Sekiguchi, Y.; Nishimura, N.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Nucleosynthesis in Neutron Star Mergers. JPS Conf. Proc. 2018, 23, 012033. [Google Scholar] [CrossRef]
- Siegel, D.M. r-Process nucleosynthesis in gravitational-wave and other explosive astrophysical events. Nat. Rev. Phys. 2022, 4, 306–318. [Google Scholar] [CrossRef]
- Fischer, T.; Guo, G.; Langanke, K.; Martinez-Pinedo, G.; Qian, Y.Z.; Wu, M.R. Neutrinos and nucleosynthesis of elements. Prog. Part. Nucl. Phys. 2024, 137, 104107. [Google Scholar] [CrossRef]
- Chen, H.Y.; Landry, P.; Read, J.S.; Siegel, D.M. Inference of multi-channel r-process element enrichment in the Milky Way using binary neutron star merger observations. arXiv 2024, arXiv:2402.03696. [Google Scholar] [CrossRef]
- Chen, M.H.; Li, L.X.; Chen, Q.H.; Hu, R.C.; Liang, E.W. Neutron star mergers as the dominant contributor to the production of heavy r-process elements. Mon. Not. R. Astron. Soc. 2024, 529, 1154–1160. [Google Scholar] [CrossRef]
- Arcones, A.; Thielemann, F.K. Neutrino-driven wind simulations and nucleosynthesis of heavy elements. J. Phys. G 2013, 40, 013201. [Google Scholar] [CrossRef]
- Wanajo, S. The r-process in proto-neutron-star wind revisited. Astrophys. J. Lett. 2013, 770, L22. [Google Scholar] [CrossRef]
- Blanchard, P.K.; Villar, V.A.; Chornock, R.; Laskar, T.; Li, Y.; Leja, J.; Pierel, J.; Berger, E.; Margutti, R.; Alexander, K.D.; et al. JWST detection of a supernova associated with GRB 221009A without an r-process signature. Nat. Astron. 2024, 8, 774–785. [Google Scholar] [CrossRef]
- Freiburghaus, C.; Rosswog, S.; Thielemann, F.K. R-Process in Neutron Star Mergers. Astrophys. J. 1999, 525, L121–L124. [Google Scholar] [CrossRef]
- Thielemann, F.K.; Eichler, M.; Panov, I.V.; Wehmeyer, B. Neutron Star Mergers and Nucleosynthesis of Heavy Elements. Annu. Rev. Nucl. Part. Sci. 2017, 67, 253–274. [Google Scholar] [CrossRef]
- Watson, D.; Hansen, C.J.; Selsing, J.; Koch, A.; Malesani, D.B.; Andersen, A.C.; Fynbo, J.P.U.; Arcones, A.; Bauswein, A.; Covino, S.; et al. Identification of strontium in the merger of two neutron stars. Nature 2019, 574, 497–500. [Google Scholar] [CrossRef] [PubMed]
- Janka, H.T.; Bauswein, A. Dynamics and Equation of State Dependencies of Relevance for Nucleosynthesis in Supernovae and Neutron Star Mergers. In Handbook of Nuclear Physics; Tanihata, I., Toki, H., Kajino, T., Eds.; Springer Nature: Singapore, 2020; pp. 1–98. [Google Scholar] [CrossRef]
- Goriely, S.; Kullmann, I. R-Process Nucleosynthesis in Neutron Star Merger Ejecta and Nuclear Dependences. In Handbook of Nuclear Physics; Tanihata, I., Toki, H., Kajino, T., Eds.; Springer Nature: Singapore, 2020; pp. 1–26. [Google Scholar] [CrossRef]
- Ricigliano, G.; Jacobi, M.; Arcones, A. Impact of nuclear matter properties on the nucleosynthesis and the kilonova from binary neutron star merger ejecta. Mon. Not. R. Astron. Soc. 2024, 533, 2096–2112. [Google Scholar] [CrossRef]
- Just, O.; Vijayan, V.; Xiong, Z.; Goriely, S.; Soultanis, T.; Bauswein, A.; Guilet, J.; Janka, H.T.; Martínez-Pinedo, G. End-to-end Kilonova Models of Neutron Star Mergers with Delayed Black Hole Formation. Astrophys. J. 2023, 951, L12. [Google Scholar] [CrossRef]
- Kobayashi, C.; Karakas, A.I.; Lugaro, M. The Origin of Elements from Carbon to Uranium. Astrophys. J. 2020, 900, 179. [Google Scholar] [CrossRef]
- Cowan, J.J.; Burris, D.L.; Sneden, C.; McWilliam, A.; Preston, G.W. Evidence of Heavy Element Nucleosynthesis Early in the History of the Galaxy: The Ultra–metal-poor Star CS 22892-052. Astrophys. J. 1995, 439, L51. [Google Scholar] [CrossRef]
- Sneden, C.; McWilliam, A.; Preston, G.W.; Cowan, J.J.; Burris, D.L.; Armosky, B.J. The Ultra–Metal-poor, Neutron-Capture–rich Giant Star CS 22892-052. Astrophys. J. 1996, 467, 819. [Google Scholar] [CrossRef]
- Hill, V.; Plez, B.; Cayrel, R.; Beers, T.C.; Nordström, B.; Andersen, J.; Spite, M.; Spite, F.; Barbuy, B.; Bonifacio, P.; et al. First stars. I. The extreme r-element rich, iron-poor halo giant CS 31082-001. Implications for the r-process site(s) and radioactive cosmochronology. Astron. Astrophys. 2002, 387, 560–579. [Google Scholar] [CrossRef]
- Roederer, I.U.; Kratz, K.L.; Frebel, A.; Christlieb, N.; Pfeiffer, B.; Cowan, J.J.; Sneden, C. The End of Nucleosynthesis: Production of Lead and Thorium in the Early Galaxy. Astrophys. J. 2009, 698, 1963–1980. [Google Scholar] [CrossRef]
- Ernandes, H.; Castro, M.J.; Barbuy, B.; Spite, M.; Hill, V.; Castilho, B.; Evans, C.J. Reanalysis of neutron-capture elements in the benchmark r-rich star CS 31082-001. Mon. Not. R. Astron. Soc. 2023, 524, 656–677. [Google Scholar] [CrossRef]
- Casey, A.R.; Schlaufman, K.C. The Universality of the Rapid Neutron-capture Process Revealed by a Possible Disrupted Dwarf Galaxy Star. Astrophys. J. 2017, 850, 179. [Google Scholar] [CrossRef]
- Farouqi, K.; Thielemann, F.K.; Rosswog, S.; Kratz, K.L. Correlations of r-process elements in very metal-poor stars as clues to their nucleosynthesis sites. Astron. Astrophys. 2022, 663, A70. [Google Scholar] [CrossRef]
- Orce, J.N.; Dey, B.; Ngwetsheni, C.; Bhattacharya, S.; Pandit, D.; Lesch, B.; Zulu, A. Enhanced symmetry energy may bear universality of r-process abundances. Mon. Not. R. Astron. Soc. 2023, 525, 6249–6256. [Google Scholar] [CrossRef]
- Holmbeck, E.M.; Surman, R.; Roederer, I.U.; McLaughlin, G.C.; Frebel, A. HD 222925: A New Opportunity to Explore the Astrophysical and Nuclear Conditions of r-process Sites. Astrophys. J. 2023, 951, 30. [Google Scholar] [CrossRef]
- Roederer, I.U.; Cowan, J.J.; Pignatari, M.; Beers, T.C.; Den Hartog, E.A.; Ezzeddine, R.; Frebel, A.; Hansen, T.T.; Holmbeck, E.M.; Mumpower, M.R.; et al. The R-Process Alliance: Abundance Universality among Some Elements at and between the First and Second R-Process Peaks. Astrophys. J. 2022, 936, 84. [Google Scholar] [CrossRef]
- Ji, A.P.; Curtis, S.; Storm, N.; Chandra, V.; Schlaufman, K.C.; Stassun, K.G.; Heger, A.; Pignatari, M.; Price-Whelan, A.M.; Bergemann, M.; et al. Spectacular Nucleosynthesis from Early Massive Stars. Astrophys. J. Lett. 2024, 961, L41. [Google Scholar] [CrossRef]
- Terasawa, N.; Sato, K. Production of 9Be and Heavy Elements in the Inhomogeneous Universe. Astrophys. J. 1990, 362, L47. [Google Scholar] [CrossRef]
- Nakamura, R.; Hashimoto, M.A.; Ichimasa, R.; Arai, K. Big-Bang nucleosynthesis: Constraints on nuclear reaction rates, neutrino degeneracy, inhomogeneous and Brans-Dicke models. Int. J. Mod. Phys. E 2017, 26, 1741003. [Google Scholar] [CrossRef]
- Röpke, G. Element abundances in hot nuclear matter. Phys. Lett. B 1987, 185, 281–286. [Google Scholar] [CrossRef]
- Gonin, M.; Hasinger, G.; Blaschke, D.; Ivanytskyi, O.; Röpke, G. Primordial black-hole formation and heavy r-process element synthesis from the cosmological QCD transition. Two aspects of an inhomogeneous early Universe. Eur. Phys. J. A 2025, 61, 170. [Google Scholar] [CrossRef]
- Röpke, G.; Münchow, L.; Schulz, H. Particle clustering and Mott transitions in nuclear matter at finite temperature (I). Method and general aspects. Nucl. Phys. A 1982, 379, 536–552. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef]
- Natowitz, J.B.; Ropke, G.; Typel, S.; Blaschke, D.; Bonasera, A.; Hagel, K.; Klahn, T.; Kowalski, S.; Qin, L.; Shlomo, S.; et al. Symmetry energy of dilute warm nuclear matter. Phys. Rev. Lett. 2010, 104, 202501. [Google Scholar] [CrossRef]
- Qin, L.; Hagel, K.; Wada, R.; Natowitz, J.B.; Schlomo, S.; Bonasera, A.; Roepke, G.; Typel, S.; Chen, Z.; Huang, M.; et al. Laboratory Tests of Low Density Astrophysical Equations of State. Phys. Rev. Lett. 2012, 108, 172701. [Google Scholar] [CrossRef] [PubMed]
- Köster, U.; Faust, H.; Fioni, G.; Friedrichs, T.; Groß, M.; Oberstedt, S. Ternary fission yields of 241Pu(nth, f). Nucl. Phys. A 1999, 652, 371–387. [Google Scholar] [CrossRef]
- Seitenzahl, I.R.; Townsley, D.M.; Peng, F.; Truran, J.W. Nuclear statistical equilibrium for Type Ia supernova simulations. At. Data Nucl. Data Tables 2009, 95, 96–114. [Google Scholar] [CrossRef]
- Zubarev, D.; Morozov, V.; Röpke, G. Statistical Mechanics of Non-equilibrium Processes I/II; Wiley: Hoboken, NJ, USA, 1996/1997. [Google Scholar]
- Kopatch, Y.N.; Mutterer, M.; Schwalm, D.; Thirolf, P.; Gonnenwein, F. 5He, 7He, and 8Li (E* = 2.26 MeV) intermediate ternary particles in the spontaneous fission of 252Cf. Phys. Rev. C 2002, 65, 044614. [Google Scholar] [CrossRef]
- Natowitz, J.B.; Pais, H.; Röpke, G. Employing ternary fission of 242Pu as a probe of very neutron-rich matter. Phys. Rev. C 2023, 107, 014618. [Google Scholar] [CrossRef]
- Asplund, M.; Amarsi, A.M.; Grevesse, N. The chemical make-up of the Sun: A 2020 vision. Astron. Astrophys. 2021, 653, A141. [Google Scholar] [CrossRef]
- Zubarev, D.N.; Prozorkevich, A.V.; Smolyanskii, S.A. Derivation of nonlinear generalized equations of quantum relativistic hydrodynamics. Theor. Math. Phys. 1979, 40, 821–831. [Google Scholar] [CrossRef]
- Höll, A.; Morozov, V.; Röpke, G. Covariant linear response theory of relativistic QED plasmas. Phys. A Stat. Mech. Its Appl. 2003, 319, 371–403. [Google Scholar] [CrossRef]
- Becattini, F.; Bucciantini, L.; Grossi, E.; Tinti, L. Local thermodynamical equilibrium and the beta frame for a quantum relativistic fluid. Eur. Phys. J. C 2015, 75, 191. [Google Scholar] [CrossRef]
- Becattini, F.; Buzzegoli, M.; Grossi, E. Reworking Zubarev’s Approach to Nonequilibrium Quantum Statistical Mechanics. Particles 2019, 2, 197–207. [Google Scholar] [CrossRef]
- Akkelin, S.V. Cosmological particle creation in the little bang. Phys. Rev. D 2021, 103, 116014. [Google Scholar] [CrossRef]
- Harutyunyan, A.; Sedrakian, A.; Rischke, D.H. Relativistic second-order dissipative hydrodynamics from Zubarev’s non-equilibrium statistical operator. Ann. Phys. 2022, 438, 168755. [Google Scholar] [CrossRef]
- Adzhymambetov, M.D.; Akkelin, S.V.; Sinyukov, Y.M. Quantum local-equilibrium state with fixed multiplicity constraint and Bose-Einstein momentum correlations. Phys. Rev. D 2023, 108, 096030. [Google Scholar] [CrossRef]
- Schmidt, M.; Röpke, G.; Schulz, H. Generalized beth-uhlenbeck approach for hot nuclear matter. Ann. Phys. 1990, 202, 57–99. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Röpke, G. Appearance of light clusters in post-bounce evolution of core-collapse supernovae. Phys. Rev. C 2008, 77, 055804. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Fantina, A.F.; Gulminelli, F. Light clusters in the liquid proto-neutron star inner crust. Eur. Phys. J. A 2023, 59, 292. [Google Scholar] [CrossRef]
- Hillebrandt, W.; Nomoto, K.; Wolff, R.G. Supernova explosions of massive stars - The mass range 8 to 10 solar masses. Astron. Astrophys. 1984, 133, 175–184. [Google Scholar]
- Hempel, M.; Schaffner-Bielich, J. Statistical Model for a Complete Supernova Equation of State. Nucl. Phys. A 2010, 837, 210–254. [Google Scholar] [CrossRef]
- Gulminelli, F.; Raduta, A.R. Unified treatment of subsaturation stellar matter at zero and finite temperature. Phys. Rev. C 2015, 92, 055803. [Google Scholar] [CrossRef]
- Pais, H.; Chiacchiera, S.; Providência, C. Light clusters, pasta phases and phase transitions in core-collapse supernova matter. Phys. Rev. C 2015, 91, 055801. [Google Scholar] [CrossRef]
- Pais, H.; Gulminelli, F.; Providência, C.; Röpke, G. Full distribution of clusters with universal couplings and in-medium effects. Phys. Rev. C 2019, 99, 055806. [Google Scholar] [CrossRef]
- Furusawa, S.; Togashi, H.; Nagakura, H.; Sumiyoshi, K.; Yamada, S.; Suzuki, H.; Takano, M. A new equation of state for core-collapse supernovae based on realistic nuclear forces and including a full nuclear ensemble. J. Phys. G 2017, 44, 094001. [Google Scholar] [CrossRef]
- Furusawa, S.; Nagakura, H. Nuclei in core-collapse supernovae engine. Prog. Part. Nucl. Phys. 2023, 129, 104018. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Fantina, A.F.; Gulminelli, F. The proto-neutron star inner crust in the liquid phase. Astron. Astrophys. 2023, 672, A160. [Google Scholar] [CrossRef]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; McGraw-Hill: San Francisco, CA, USA, 1971. [Google Scholar]
- Röpke, G.; Schmidt, M.; Münchow, L.; Schulz, H. Particle clustering and Mott transition in nuclear matter at finite temperature (II). Nucl. Phys. A 1983, 399, 587–602. [Google Scholar] [CrossRef]
- Typel, S.; Röpke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Röpke, G. Light nuclei quasiparticle energy shifts in hot and dense nuclear matter. Phys. Rev. C 2009, 79, 014002. [Google Scholar] [CrossRef]
- Röpke, G. Parametrization of light nuclei quasiparticle energy shifts and composition of warm and dense nuclear matter. Nucl. Phys. A 2011, 867, 66–80. [Google Scholar] [CrossRef]
- Röpke, G. Nuclear matter equation of state including two-, three-, and four-nucleon correlations. Phys. Rev. C 2015, 92, 054001. [Google Scholar] [CrossRef]
- Röpke, G. Light p-shell nuclei with cluster structures (4 ≤ A ≤ 16) in nuclear matter. Phys. Rev. C 2020, 101, 064310. [Google Scholar] [CrossRef]
- National Nuclear Data Center. NuDat 3.0. 2024. Available online: https://www.nndc.bnl.gov/nudat/ (accessed on 28 July 2024).
- Röpke, G.; Natowitz, J.B.; Pais, H. Nonequilibrium information entropy approach to ternary fission of actinides. Phys. Rev. C 2021, 103, 061601. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B. Nuclear Structure; W.A. Benjamin, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Rauscher, T. Nuclear partition functions at temperatures exceeding 1010 K. Astrophys. J. Suppl. 2003, 147, 403. [Google Scholar] [CrossRef]
- Wang, M.; Huang, W.J.; Kondev, F.G.; Audi, G.; Naimi, S. The AME 2020 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2021, 45, 030003. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Skyrme-Hartree-Fock-Bogoliubov Nuclear Mass Formulas: Crossing the 0.6 MeV Accuracy Threshold with Microscopically Deduced Pairing. Phys. Rev. Lett. 2009, 102, 152503. [Google Scholar] [CrossRef] [PubMed]
- Duflo, J.; Zuker, A.P. Microscopic mass formulas. Phys. Rev. C 1995, 52, R23–R27. [Google Scholar] [CrossRef]
- Möller, P.; Sierk, A.J.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations: FRDM(2012). At. Data Nucl. Data Tables 2016, 109, 1–204. [Google Scholar] [CrossRef]
- Rohlf, J.W. Modern Physics from α to Z°; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Royer, G. On the coefficients of the liquid drop model mass formulae and nuclear radii. Nucl. Phys. A 2008, 807, 105–118. [Google Scholar] [CrossRef]
- Dieperink, A.E.L.; van Isacker, P. Shell corrections to a liquid-drop description of nuclear masses and radii. Eur. Phys. J. A 2009, 42, 269–279. [Google Scholar] [CrossRef]
- Munoz, J.M.; Udrescu, S.M.; Garcia Ruiz, R.F. Discovering Nuclear Models from Symbolic Machine Learning. arXiv 2024, arXiv:2404.11477. [Google Scholar] [CrossRef]
- Koura, H.; Chiba, S. Single-Particle Levels of Spherical Nuclei in the Superheavy and Extremely Superheavy Mass Region. J. Phys. Soc. Jpn. 2013, 82, 014201. [Google Scholar] [CrossRef]
- Iljinov, A.S.; Mebel, M.V.; Bianchi, N.; De Sanctis, E.; Guaraldo, C.; Lucherini, V.; Muccifora, V.; Polli, E.; Reolon, A.R.; Rossi, P. Phenomenological statistical analysis of level densities, decay widths and lifetimes of excited nuclei. Nucl. Phys. A 1992, 543, 517–557. [Google Scholar] [CrossRef]
- Storbacka, M.; Qi, C. Location of the neutron drip line for Sn and its impact on r-process abundances. Phys. Lett. B 2024, 855, 138822. [Google Scholar] [CrossRef]
- Mollaebrahimi, A.; Walls, C.; Dickel, T.; Miyagi, T.; Sieverding, A.; Andreoiu, C.; Ash, J.; Ashrafkhani, B.; Belosevic, I.; Bergman, J.; et al. Precision Mass Measurements Reveal Low Neutron Pairing in Tin beyond N = 82 and Its Impact on Stellar Nucleosynthesis. Phys. Rev. Lett. 2025, 134, 232701. [Google Scholar] [CrossRef] [PubMed]
- Kraeft, W.D.; Kremp, D.; Ebeling, W.; Röpke, G. Quantum Statistics of Charged Particle Systems; Akademie-Verlag: Berlin, Germany, 1986. [Google Scholar] [CrossRef]
- Fischer, T.; Hempel, M.; Sagert, I.; Suwa, Y.; Schaffner-Bielich, J. Symmetry energy impact in simulations of core-collapse supernovae. Eur. Phys. J. A 2014, 50, 46. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.; Blaschke, D.; Cierniak, M.; Hempel, M.; Klähn, T.; Martínez-Pinedo, G.; Newton, W.G.; Röpke, G.; Typel, S. The State of Matter in Simulations of Core-Collapse supernovae—Reflections and Recent Developments. Publ. Astron. Soc. Aust. 2017, 34, e067. [Google Scholar] [CrossRef]
- Yudin, A.; Hempel, M.; Blinnikov, S.; Nadyozhin, D.; Panov, I. Asymmetric Nuclear Light Clusters In Supernova Matter. Mon. Not. Roy. Astron. Soc. 2019, 483, 5426–5433. [Google Scholar] [CrossRef]
- Fischer, T.; Typel, S.; Röpke, G.; Bastian, N.U.F.; Martínez-Pinedo, G. Medium modifications for light and heavy nuclear clusters in simulations of core collapse supernovae—Impact on equation of state and weak interactions. Phys. Rev. C 2020, 102, 055807. [Google Scholar] [CrossRef]
- Fraisse, B.; Bélier, G.; Méot, V.; Gaudefroy, L.; Francheteau, A.; Roig, O. Complete neutron-multiplicity distributions in fast-neutron-induced fission. Phys. Rev. C 2023, 108, 014610. [Google Scholar] [CrossRef]
- Lemaître, J.F.; Goriely, S.; Bauswein, A.; Janka, H.T. Fission fragment distributions and their impact on the r-process nucleosynthesis in neutron star mergers. Phys. Rev. C 2021, 103, 025806. [Google Scholar] [CrossRef]
- Pochodzalla, J.; Mohlenkamp, T.; Rubehn, T.; Schuttauf, A.; Worner, A.; Zude, E.; Begemann-Blaich, M.; Blaich, T.; Emling, H.; Ferrero, A.; et al. Probing the nuclear liquid–gas phase transition. Phys. Rev. Lett. 1995, 75, 1040–1043. [Google Scholar] [CrossRef] [PubMed]
- Beun, J.; McLaughlin, G.C.; Surman, R.; Hix, W.R. Fission cycling in a supernova r process. Phys. Rev. C 2008, 77, 035804. [Google Scholar] [CrossRef]
- Eichler, M.; Arcones, A.; Kelic, A.; Korobkin, O.; Langanke, K.; Marketin, T.; Martinez-Pinedo, G.; Panov, I.V.; Rauscher, T.; Rosswog, S.; et al. The Role of Fission in Neutron Star Mergers and its Impact on the r-Process Peaks. Astrophys. J. 2015, 808, 30. [Google Scholar] [CrossRef]
- Panov, I.V.; Glazyrin, S.I.; Röpke, F.K.; Blinnikov, S.I. Nucleosynthesis during a Thermonuclear Supernova Explosion. Astron. Lett. 2018, 44, 309–314. [Google Scholar] [CrossRef]
- Panov, I.V. Fission-Fragment Mass Distribution and Heavy Nuclei Nucleosynthesis. Phys. Part. Nucl. 2023, 54, 542–546. [Google Scholar] [CrossRef]
- Chen, J.; Pei, J.; Qiang, Y.; Chi, J. Fission Properties of Neutron-Rich Nuclei around the End Point of r-Process. Chin. Phys. Lett. 2023, 40, 012401. [Google Scholar] [CrossRef]
- Xylakis-Dornbusch, T.; Hansen, T.T.; Beers, T.C.; Christlieb, N.; Ezzeddine, R.; Frebel, A.; Holmbeck, E.; Placco, V.M.; Roederer, I.U.; Sakari, C.M.; et al. The R-Process Alliance: Analysis of limited-r stars. Astron. Astrophys. 2024, 688, A123. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, D.F. A generalized equation of state for hot, dense matter. Nucl. Phys. A 1991, 535, 331–376. [Google Scholar] [CrossRef]
- Ravenhall, D.G.; Pethick, C.J.; Lattimer, J.M. Nuclear interface energy at finite temperatures. Nucl. Phys. A 1983, 407, 571–591. [Google Scholar] [CrossRef]
- Ishizuka, C.; Ohnishi, A.; Sumiyoshi, K. Liquid-gas phase transition of supernova matter and its relation to nucleosynthesis. Nucl. Phys. A 2003, 723, 517–543. [Google Scholar] [CrossRef]
- Blaschke, D.; Liebing, S.; Röpke, G.; Dönigus, B. Cluster production and the chemical freeze-out in expanding hot dense matter. Phys. Lett. B 2025, 860, 139206. [Google Scholar] [CrossRef]
- Morishita, T.; Roberts-Borsani, G.; Treu, T.; Brammer, G.; Mason, C.A.; Trenti, M.; Vulcani, B.; Wang, X.; Acebron, A.; Bahé, Y.; et al. Early Results from GLASS-JWST. XIV. A Spectroscopically Confirmed Protocluster 650 Million Years after the Big Bang. Astrophys. J. 2023, 947, L24. [Google Scholar] [CrossRef]
- Matteucci, F. Chemical Evolution of Galaxies; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wehmeyer, B.; Pignatari, M.; Thielemann, F.K. Galactic evolution of rapid neutron capture process abundances: The inhomogeneous approach. Mon. Not. R. Astron. Soc. 2015, 452, 1970–1981. [Google Scholar] [CrossRef]
- Wehmeyer, B.; Frohlich, C.; Côté, B.; Pignatari, M.; Thielemann, F.K. Using failed supernovae to constrain the Galactic r-process element production. Mon. Not. R. Astron. Soc. 2019, 487, 1745–1753. [Google Scholar] [CrossRef]
- Thielemann, F.K.; Farouqi, K.; Rosswog, S.; Kratz, K.L. r-Process Contributions to Low-Metallicity Stars. Eur. Phys. J. Web Conf. 2022, 260, 09002. [Google Scholar] [CrossRef]
- Côté, B.; Belczynski, K.; Fryer, C.L.; Ritter, C.; Paul, A.; Wehmeyer, B.; O’Shea, B.W. Advanced LIGO Constraints on Neutron Star Mergers and R-Process Sites. Astrophys. J. 2017, 836, 230. [Google Scholar] [CrossRef]
- Côté, B.; Eichler, M.; Arcones, A.; Hansen, C.J.; Simonetti, P.; Frebel, A.; Fryer, C.L.; Pignatari, M.; Reichert, M.; Belczynski, K.; et al. Neutron Star Mergers Might not be the Only Source of r-Process Elements in the Milky Way. Astrophys. J. 2019, 875, 106. [Google Scholar] [CrossRef]
- Kajantie, K.; Kurki-Suonio, H. Bubble Growth and Droplet Decay in the Quark Hadron Phase Transition in the Early Universe. Phys. Rev. D 1986, 34, 1719–1738. [Google Scholar] [CrossRef] [PubMed]
- Ignatius, J.; Kajantie, K.; Kurki-Suonio, H.; Laine, M. The growth of bubbles in cosmological phase transitions. Phys. Rev. D 1994, 49, 3854–3868. [Google Scholar] [CrossRef] [PubMed]
- Ignatius, J.; Kajantie, K.; Kurki-Suonio, H.; Laine, M. Large scale inhomogeneities from the QCD phase transition. Phys. Rev. D 1994, 50, 3738–3745. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).