Sgr A* Shadow Study with KTN Space Time and Investigation of NUT Charge Existence

Abstract

In this paper, I investigate the existence of the NUT charge through the KTN spacetime using shadow observations of Sgr A*. I report that the range of my constraint for the NUT charge is between −0.5 and 0.5 for Schwarzschild-like and very slowly rotating KTN black holes. This range extends to 1.5 for spins up to −2 and −1.5 for spins up to 2 based on Keck observations for both 40° and 10° viewing angles. For VLTI observations, Schwarzschild-like and very slowly rotating KTN black holes are excluded for a 40° viewing angle, and the NUT charge is constrained to a very narrow range for a 10° viewing angle. I report that the possibility of having KTN naked singularities in Sgr A* is small, considering the uncertainties in the shadow size.

1. Introduction

General Relativity predicts that the final product of gravitational collapse is Kerr black holes. These black holes are characterized by mass and spin [1,2]. The Kerr paradigm has been successfully tested in weak regimes. However, precise measurements in strong gravity regimes are still lacking.

A test of General Relativity in the strong gravity regime can be executed by different methods such as Gravitational Waves [3,4], X-ray reflection spectroscopy [5], the Continuum fitting method [6] and the black hole shadow [7,8,9]. Methods such as X-ray reflection spectroscopy and the continuum fitting method are parametrically degenerate in measuring spin and deviation from General Relativity. All deformation parameters should vanish to verify the Kerr black holes scenario.

One way to test the Kerr black holes paradigm is to consider deviations from Kerr spacetime by introducing extra parameters and trying to constrain the parameters. In this work, I consider the shadow of black holes.

The shadow of a black hole is a dark area in the observer plane. This dark area appears over a bright background region. The boundary of the shadow depends on the background metric and the observer viewing angle in the case of a geometrically thick and optically thin accretion disk structure. So far, there are two observations from the Event Horizon Telescope group of the shadow of a compact object. One is the shadow of M87* [7,8] and the other is the shadow of Sgr A* [9].

In paper [10], my collaborators and I studied the shadow of M87* for the Kerr-Taub-NUT (KTN) spacetime [11]. KTN spacetime has a Newman-Unti-Tamburino (NUT) [12] charge in addition to Kerr parameters. In the case of a vanishing NUT charge, the metric reduces to the Kerr metric, and in the case of a vanishing spin parameter, the metric is the Taub-NUT spacetime with mass and NUT charge. There are reports in [13] and also [14,15,16] about the existence of the effect of a gravitomagnetic monopole, also known as NUT charge, in the spectra of quasars, supernovae, or active galactic nuclei. Based on X-ray observations of GRO J1655-40, it has been reported that this is more consistent with KTN spacetime rather than Kerr spacetime [17].

I investigate the possibility of the existence of a gravitomagnetic monopole, that is, the NUT charge, in the shadow of M87*. In this paper, I consider the KTN spacetime again, but my simulation is for the case of the shadow of Sgr A*. In the M87* case, I found that a non-zero NUT charge is still compatible with the EHT result of M87*. I show that in prograde rotation ($a_{*}>0$), $n_{*}$ cannot be greater than 1.1, and in retrograde rotation ($a_{*}<0$), $n_{*}$ cannot be less than −1.1 for the shadow of M87*. Here, $a_{*}=a/M$ is the spin parameter, and $n_{*}=n/M$ is the NUT charge with mass M. In addition, the results show that there can be a shadow for both cases of the KTN black hole and the KTN naked singularity. In this paper on the Sgr A* shadow, the allowed range for the KTN naked singularity is narrow, so I conclude that the possibility of having KTN naked singularities in Sgr A* is small, considering the uncertainties in the shadow size. The range for the KTN black hole is between −0.5 and 0.5 for spin zero and up to 1.5 for spin −2 and −1.5 for spin two.

As for the shadow of naked singularities, due to the presence of a strong gravitational field, naked singularities can still cast a shadow. Depending on the geometry, there is a region where light cannot escape. Also, the light can be deflected and create a shadow-like region. The bending or trapping can occur in a specific way. However, the nature and specifically the shape and size of the shadow can be different from those of a standard black hole. The difference in these distortions or asymmetry effects can lead to potential signatures in observations to distinguish a naked singularity from a standard black hole. Even in the absence of a photon sphere, due to the strong gravitational field resulting in light bending, photons can reach the observer plane. There are a number of references that calculate the shadow of naked singularities. I cite some of them as [18,19,20,21,22,23].

The significance of this study is in probing deviations from Kerr spacetime, quantifying the NUT charge or gravitomagnetic monopole, testing the cosmic censorship conjecture, linking observations with theory through the mathematically interesting theory of KTN spacetime and introducing new and exotic physics.

The structure of this paper is as follows. I present the KTN spacetime in Section 2. The shadow description is presented in Section 3. Section 4 is devoted to constraining the NUT charge and the results of this paper. The conclusion is written in Section 5.

2. Theoretical Framework of Kerr-Taub-NUT Space Time

In this section, I describe the KTN space time as follows. The metric of KTN space time can be written as [11]

$$\begin{array}{ccc}\hfill d{s}^2& =& -{\displaystyle \frac{\mathrm{\Delta }}{p^2}}{(dt-Ad\varphi )}^2+{\displaystyle \frac{p^2}{\mathrm{\Delta }}}d{r}^2+p^{2}d{\theta }^2\hfill \\ & +& {\displaystyle \frac{1}{p^2}}{sin}^2\theta {(adt-Bd\varphi )}^2\hfill \end{array}$$

(1)

with

$$\begin{array}{ccc}\hfill \mathrm{\Delta }& =& r^2-2Mr+a^2-n^2,p^2=r^2+{(n+acos\theta )}^2,\hfill \\ \hfill A& =& a{sin}^2\theta -2ncos\theta ,B=r^2+a^2+n^2\hfill \end{array}$$

(2)

where M is the mass, $a_{*}=a/M$ is spin parameter and $n_{*}=n/M$ is NUT charge. The NUT parameter is known as the gravitomagnetic monopole of a compact object as well. The outer horizon is expressed as

$$\begin{array}{ccc}\hfill r_h& =& M(1+\sqrt{1+n_{*}^2-a_{*}^2}).\hfill \end{array}$$

(3)

There is indication of location of singularity in KTN space time when $p^2$ vanishes [24],

$$\begin{array}{c}\hfill r=0\mathrm{and}{\theta }_s={cos}^{-1}(-n_{*}/a_{*}).\end{array}$$

(4)

Expression (4) shows that singularity does not arise for $|n_{*}|>|a_{*}|$. Singularity is covered by horizon at ${\theta }_s=\pi$. Depending on the numerical value of $a_{*}$ and $n_{*}$ for the KTN black hole or KTN naked singularity, singularity always arises for $|n_{*}|\le |a_{*}|$. The horizon, Equation (3), vanishes for $|a_{*}|>\sqrt{1+n_{*}^2}$. This leads to KTN naked singularity. Meanwhile, for $|n_{*}|\le |a_{*}|\le \sqrt{1+n_{*}^2}$, the KTN black hole with (covered) singularity is obtained. One can refer to paper [10] for more information about the metric of space time.

3. Methods and Description of Shadow Boundary of a Compact Object

The image of a black hole, also called the black hole shadow, is a dark area over a brighter region. Capture, scatter to infinity, and the critical curve are the trajectories of photons approaching the black hole from distant radii around the black hole. The critical curve is the separation between capture and scatter to infinity trajectories. In the case of a nearly tangential to circular orbit, the 3-momentum of the light ray is unstable and orbits around the black hole several times, which creates a brighter area around the darker region. The 2D dark region in the observer’s sky plane is the shadow of the black hole. To obtain the shadow for a specific spacetime geometry, one should solve the geodesic equations. In this paper, I solve these equations numerically using the ray tracing technique. Solving the equations is achieved with a class of the Runge–Kutta–Nystrom method with adaptive step size and error control [25]. Ray tracing images the observer’s perception of a distant object or portion of the sky. Each observed light ray is traced back to the object. Ray tracing studies the distortion or appearance of a background distant star by local gravitational fields.

The Runge–Kutta–Nystrom method is a numerical technique for second-order ordinary differential equations. There is no need to convert them into a system of first-order equations. I start from equations like

$$\begin{array}{c}\hfill {\displaystyle \frac{{\mathrm{d}}^{2}y}{\mathrm{d}{\tau }^2}}=f(\tau ,y,{\displaystyle \frac{\mathrm{d}y}{\mathrm{d}\tau }}).\end{array}$$

(5)

As geodesic equations are second-order differential equations, I can use the Runge–Kutta–Nystrom method to solve them numerically. In the case of geodesic equations

$$\begin{array}{c}\hfill {\displaystyle \frac{{\mathrm{d}}^2{x}^{\mu }}{\mathrm{d}{\tau }^2}}+{\mathsf{\Gamma }}_{\alpha \beta }^{\mu }{\displaystyle \frac{\mathrm{d}{x}^{\alpha }}{\mathrm{d}\tau }}{\displaystyle \frac{\mathrm{d}{x}^{\beta }}{\mathrm{d}\tau }}=0,\end{array}$$

(6)

I have $y=x^{\mu }\left(\tau \right)$. The Runge–Kutta–Nystrom method updates the position of $x^{\mu }$ and ${\displaystyle \frac{\mathrm{d}{x}^{\mu }}{\mathrm{d}\tau }}$. It uses a specific iterative scheme to perform this update. As for adaptive step sizes, I have control over errors in each step, ensuring the solution remains accurate by controlling the errors dynamically and computing with high precision.

I start from the observer plane. The observer’s sky plane in my setup is located at the Cartesian coordinate $\left(x^{\prime },y^{\prime },z^{\prime }\right)$ and the compact object is at $\left(x,y,z\right)$. The distance of the observer is D and the viewing angle is i. $k_0=(k_0^t,k_0^r,k_0^{\theta },k_0^{\varphi })$ is the photon 4-momentum perpendicular to the observer plane from which I fire the photon. This observer plane is a grid of fired photons and the ray is traced back. The initial conditions are as follows.

The transformation from image plane $x^{\prime },y^{\prime },z^{\prime }$ to compact object $x,y,z$ is

$$\begin{array}{ccc}\hfill x& =& Dsin\left(i\right)-y^{\prime }cos\left(i\right)+z^{\prime }sin\left(i\right),\hfill \\ \hfill y& =& x^{\prime },\hfill \\ \hfill z& =& Dcos\left(i\right)+y^{\prime }sin\left(i\right)+z^{\prime }cos\left(i\right).\hfill \end{array}$$

(7)

The coordinate system reduces to a spherical coordinate far from the compact object with transformation.

$$\begin{array}{ccc}\hfill r& =& \sqrt{x^2+y^2+z^2},\hfill \\ \hfill \theta & =& arccos\left({\displaystyle \frac{z}{r}}\right),\hfill \\ \hfill \varphi & =& arctan\left({\displaystyle \frac{y}{x}}\right).\hfill \end{array}$$

(8)

Considering photon initial position at $\left(x_0^{\prime },y_0^{\prime },0\right)$ with 3-momentum $k_0=-k_0{z}^{\prime }$ perpendicular to the image plane, the photon initial conditions are obtained by substituting Equation (7) into Equation (8) at $\left(x_0^{\prime },y_0^{\prime },0\right)$,

$$\begin{array}{ccc}\hfill t_0& =& 0,\hfill \\ \hfill r_0& =& \sqrt{x_0^{\prime 2}+y_0^{\prime 2}+D^2},\hfill \\ \hfill {\theta }_0& =& arccos{\displaystyle \frac{y_0^{\prime }sini+Dcosi}{\sqrt{x_0^{\prime 2}+y_0^{\prime 2}+D^2}}},\hfill \\ \hfill {\varphi }_0& =& arctan{\displaystyle \frac{x_0^{\prime }}{Dsini-y_0^{\prime }cosi}}.\hfill \end{array}$$

(9)

The initial condition of the 4-momentum is

$$\begin{array}{ccc}\hfill k_0^r& =& -{\displaystyle \frac{D}{\sqrt{x_0^{\prime 2}+y_0^{\prime 2}+D^2}}}\left|k_0\right|,\hfill \\ \hfill k_0^{\theta }& =& {\displaystyle \frac{cosi-D\frac{y_0^{\prime }sini+Dcosi}{x_0^{\prime 2}+y_0^{\prime 2}+D^2}}{\sqrt{x_0^{\prime 2}+{(Dsini-y_0^{\prime }cosi)}^2}}}\left|k_0\right|,\hfill \\ \hfill k_0^{\varphi }& =& {\displaystyle \frac{x_0^{\prime }sini}{x_0^{\prime 2}+{(Dsini-y_0^{\prime }cosi)}^2}}\left|k_0\right|,\hfill \\ \hfill k_0^t& =& \sqrt{{\left(k_0^r\right)}^2+r_0^2{\left(k_0^{\theta }\right)}^2+r_0^2{sin}^2{\theta }_0{\left(k_0^{\varphi }\right)}^2}\hfill \end{array}$$

(10)

where $g_{\mu \nu }{k}^{\mu }{k}^{\nu }=0$ is used to calculate $k_0^t$.

To define the boundary of the shadow, I use the following definition: $\rho (x^{\prime },y^{\prime })=1$ for inside the shadow and $\rho (x^{\prime },y^{\prime })=0$ for outside the shadow.

$$\begin{array}{ccc}\hfill x_{\mathrm{center}}^{\prime }& =& {\displaystyle \frac{\int \int \rho (x^{\prime },y^{\prime })x^{\prime }d{x}^{\prime }d{y}^{\prime }}{\int \int \rho (x^{\prime },y^{\prime })d{x}^{\prime }d{y}^{\prime }}}\hfill \\ \hfill y_{\mathrm{center}}^{\prime }& =& {\displaystyle \frac{\int \int \rho (x^{\prime },y^{\prime })y^{\prime }d{x}^{\prime }d{y}^{\prime }}{\int \int \rho (x^{\prime },y^{\prime })d{x}^{\prime }d{y}^{\prime }}},\hfill \end{array}$$

(11)

$\varphi =0$ is the shorter segment of the symmetry axis of the shadow, which is $x^{\prime }$. Starting from $\varphi =0$, $R\left(\varphi \right)$ defines each point of the boundary of the shadow from the center of the shadow. Please see Figure 1 for shadow boundary definitions. Also refer to [26,27] for shadow description.

4. Constraining the NUT Charges in Sgr A*

EHT collaborations [9] characterize the deviation from the shadow size of the Schwarzschild black hole of Sgr A* as

$$\begin{array}{c}\hfill {\delta }_{\mathrm{metric}}={\displaystyle \frac{{\tilde{d}}_{\mathrm{metric}}}{6\sqrt{3}}}-1\end{array}$$

(12)

where ${\tilde{d}}_{\mathrm{metric}}$ is the shadow size, that is, the diameter between two points of the boundary of the shadow along the $x^{\prime }$ axis. The size of the Schwarzschild shadow is $6\sqrt{3}$; it is circular. The authors report that the $\delta$ values for Sgr A* are as follows [9]:

$$\begin{array}{ccc}\hfill \mathrm{Keck}:& & \delta =-0.{04}_{-0.10}^{+0.09}\hfill \\ \hfill \mathrm{VLTI}:& & \delta =-0.{08}_{-0.09}^{+0.09}\hfill \end{array}$$

(13)

In this paper, I use these values to constrain the NUT charge.

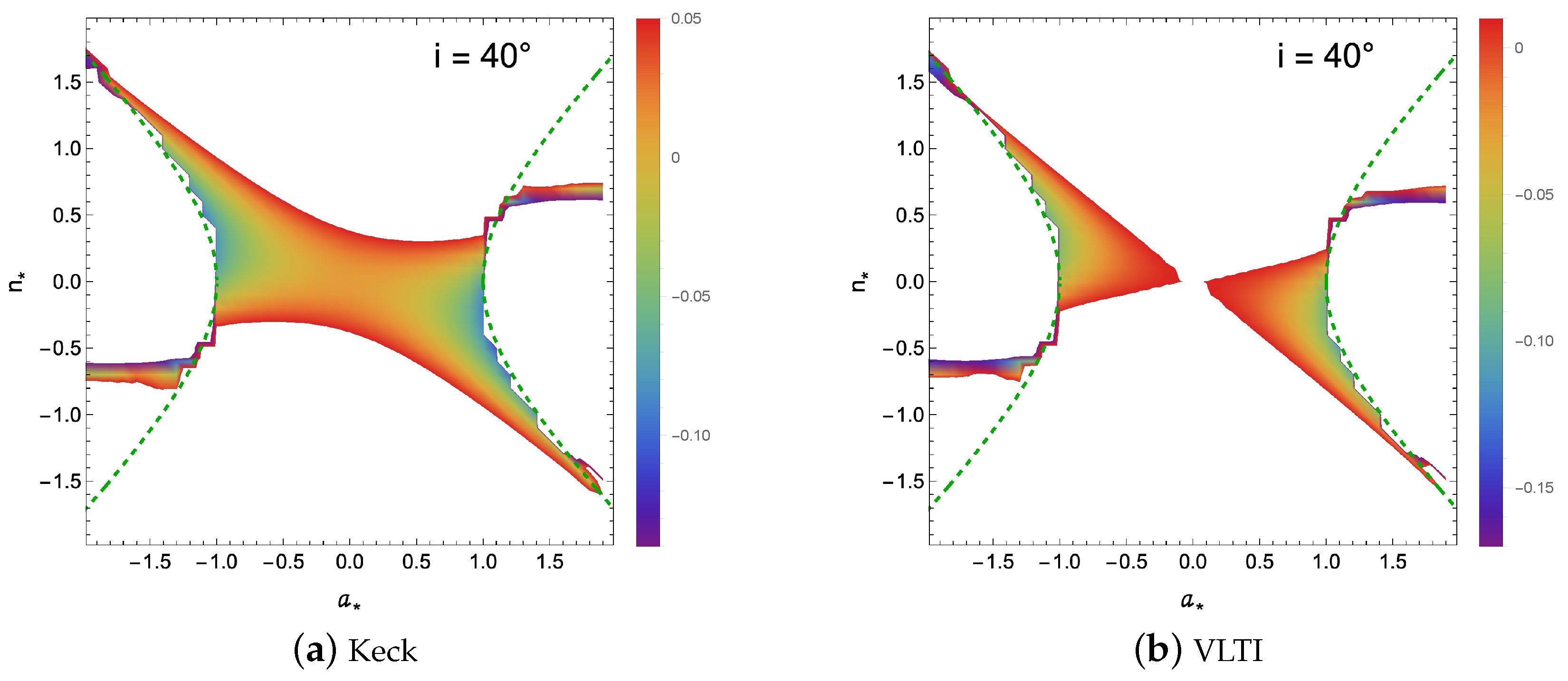
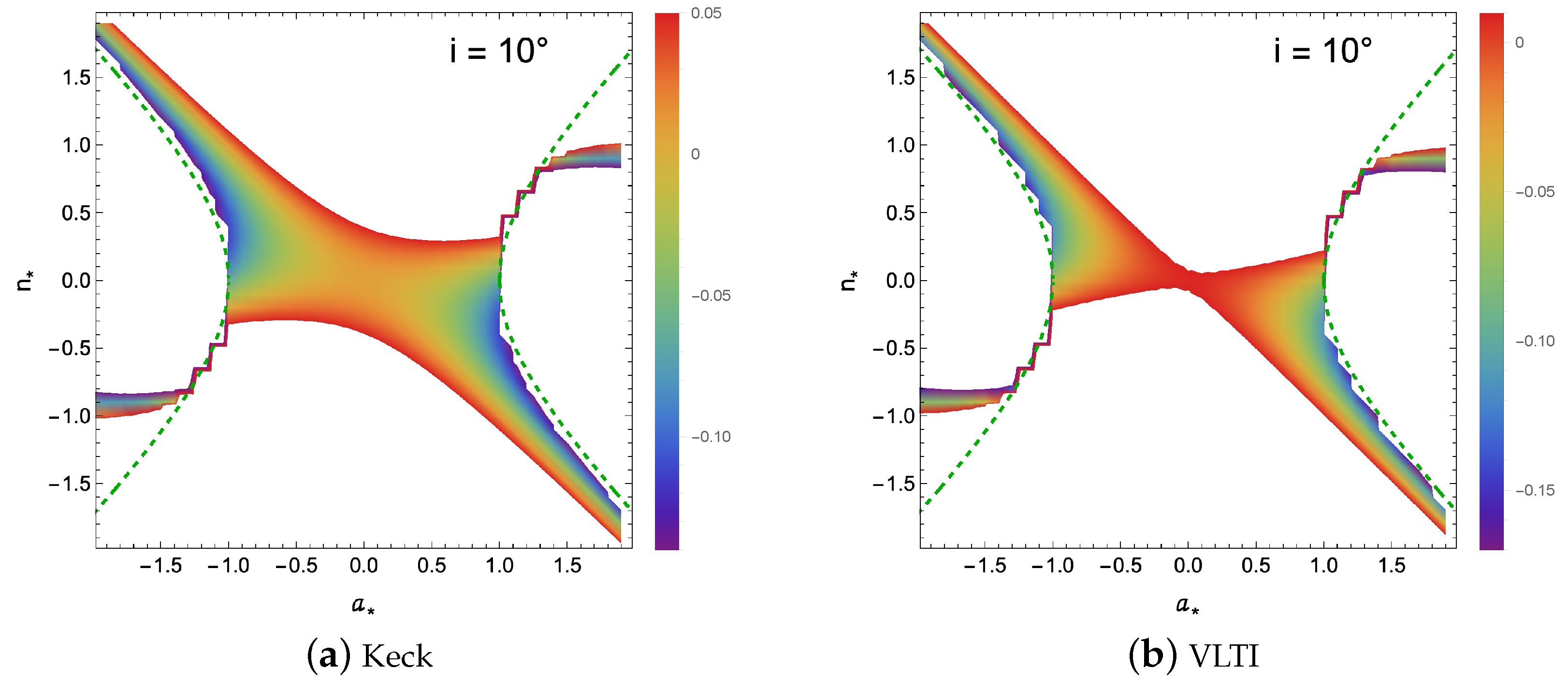
I calculate ${\delta }_{\mathrm{metric}}$ of Equation (12) for each $a_{*}$ and $n_{*}$. I consider a viewing angle of 40° and 10°. I plot both values of the reported $\delta$ of Keck and VLTI observations. Figure 2 and Figure 3 show my results. I limit the color region to the value reported in Equation (13) as the EHT collaboration stated [9].

As can be seen in plots Figure 2a and Figure 3a for Keck observations, the NUT charge can vary from about −0.5 to about 0.5 for the central region, that is, Schwarzschild and very slowly rotating KTN black holes. The colored region is extended to a NUT charge of 1.5 for a negative spin up to −2 and −1.5 for a positive spin up to 2 for KTN black holes.

As can be seen in plot Figure 2b for VLTI observations, the central region, that is, for Schwarzschild-like and very slowly rotating KTN black holes, is excluded. However, for plot Figure 3b for VLTI observations, the middle part is not excluded, but the constrained range for the NUT charge is narrow and close to the zero value. The colored region is extended to a NUT charge of 1.5 for a negative spin up to −2 and −1.5 for a positive spin up to 2 for KTN black holes.

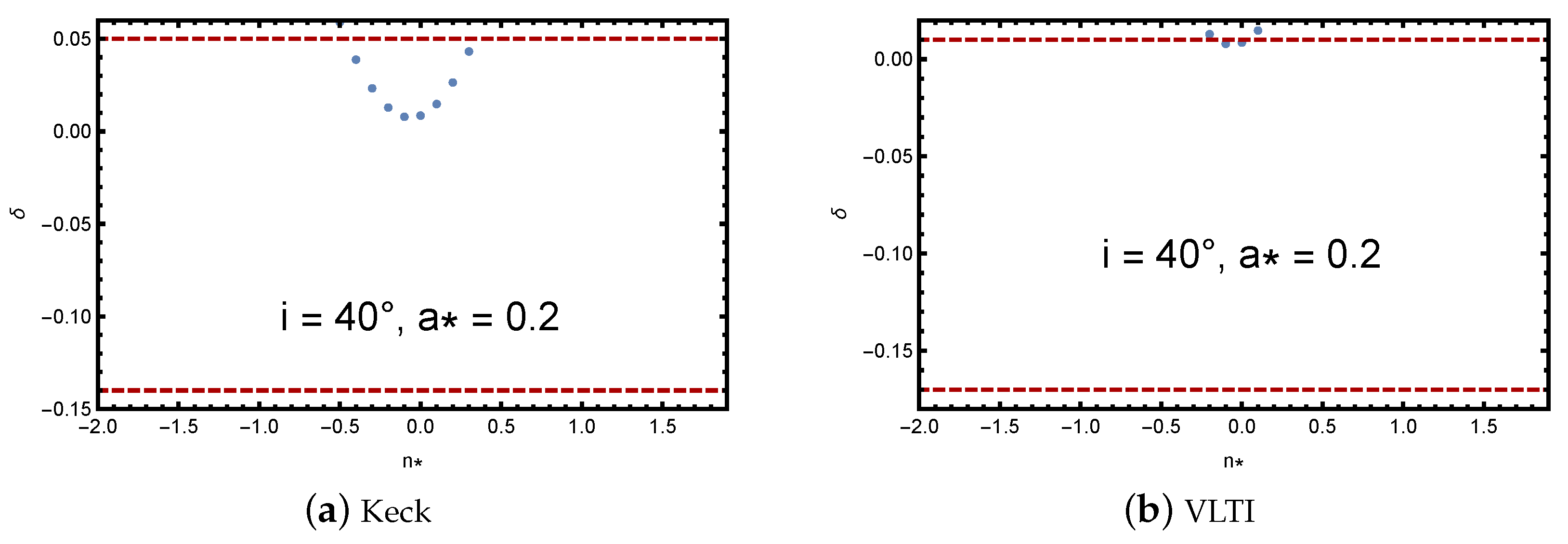
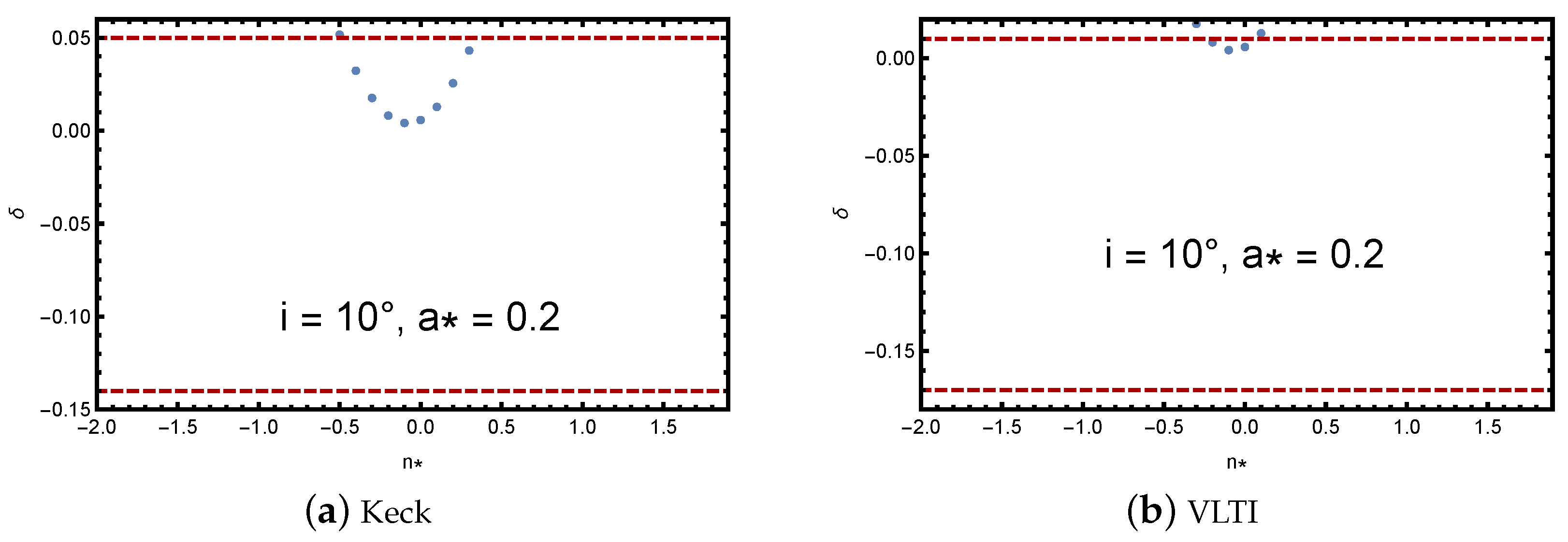
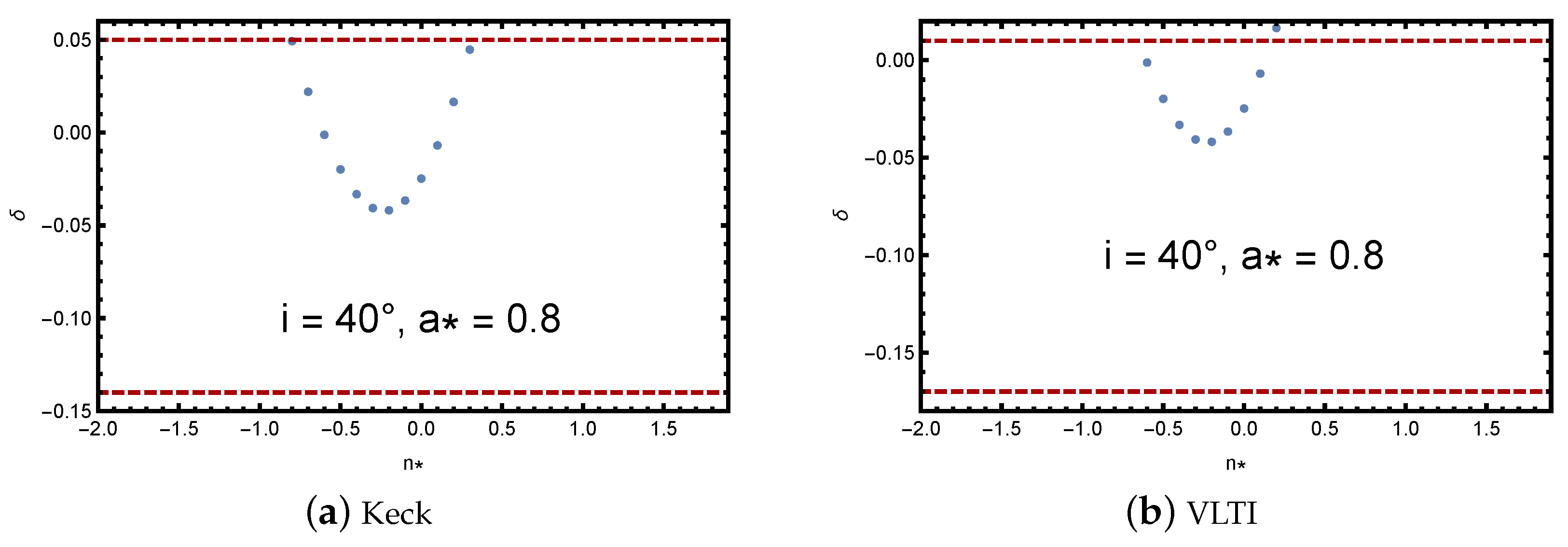
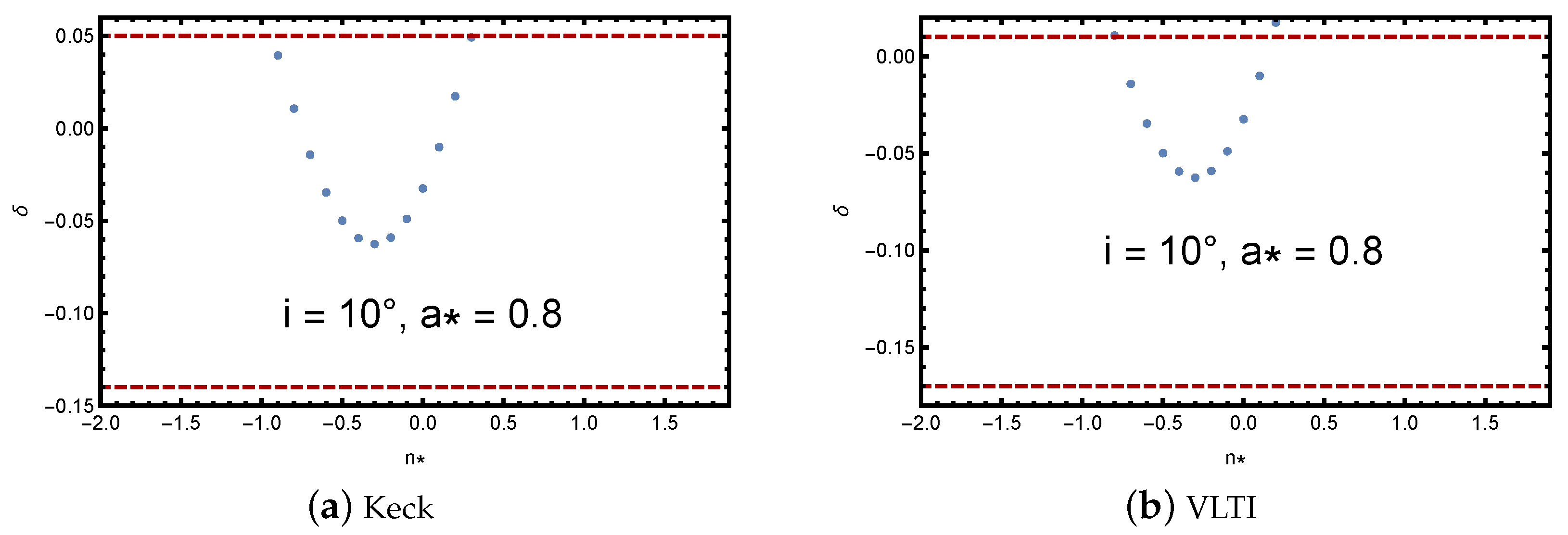
In Figure 4, Figure 5, Figure 6 and Figure 7, I fix some spin values as examples in order to see better ranges for the NUT charge. The red dashed lines in all plots show the limits from the EHT observation of Sgr A*, reported in Equation (13) for $\delta$. As discussed above, for slowly rotating KTN black holes, such as the plots in Figure 4 and Figure 5 with a spin of 0.2, the constraints are narrower and for VLTI observations are nearly zero. For larger spin values, such as 0.8 in Figure 6 and Figure 7, it spans a larger range as shown in the plots. All plots include a zero value for he NUT charge. A slowly rotating KTN black hole in the sample plots, Figure 4 and Figure 5, does not contain negative values for $\delta$, but a stronger gravitational field with larger spin values in the plots, Figure 6 and Figure 7, introduces negative values for $\delta$, causing the shape to become distorted compared with the shape of Schwarzschild black holes.

As the colored region for KTN naked singularities is narrow and considering uncertainties, I conclude that the possibility for Sgr A* as a KTN naked singularities is small for both cases of Keck and VLTI for both 40° and 10° viewing angles. Qualitatively speaking, according to Figure 3, for a fixed spin value within the naked singularity region, the color distribution is symmetric, with the middle part showing a more bluish or greenish hue, while moving towards higher or lower NUT charges shifts the color towards red. This indicates that the middle part corresponds to more negative $\delta$ values, transitioning to positive values as the color becomes redder. This implies that the shadow shape is becoming oblate as it transitions to a reddish color. However, when the viewing angle is increased to 40° in Figure 2, the colors become mixed, and no specific trend is observed. Nevertheless, qualitatively speaking, the dominant color in the Keck observation is red, and possibly yellow (positive values), with a smaller blue region. For VLTI, the blue color (negative values) is more prominent. In all cases depicted in Figure 2 and Figure 3, the NUT charge appears constant with increasing spin values ($|a_{*}|$) in the naked singularity region.

5. Conclusions and Discussion

The KTN space time is generalization of the Kerr space time as a rotating black hole in General Relativity. The KTN space time introduces additional parameter, the NUT charge. As key features of the KTN space time, it is rotating like the Kerr case with mass and angular momentum. The additional parameter, the NUT charge or a related gravitomagnetic monopole, provides a non-trivial topology and alters the causal structure. Like the Kerr case, the off-diagonal component in the metric leads to a frame-dragging signature, but the KTN case is more complex because of the presence of the NUT charge. As for limitations, the physical interpretation of the NUT charge is not clear in nature. It is kind of a dual mass or a gravitational analog to a magnetic monopole that there is no direct observational evidence for its existence so far. The KTN space time is mathematically interesting, but it physical implications and relevance to astrophysics is an open question.

In this paper, I investigate the existence of the NUT charge in the shadow of Sgr A* reported by the EHT collaborations. I consider the metric of KTN spacetime in this study. I calculate the shadow of Sgr A* with KTN spacetime, including the NUT charge. Then, I constrain my results with the reported values of deviations from the Schwarzschild shadow size from the EHT collaborations. In a previous paper, we calculated, the shadow of the same spacetime for M87*. We show that M87* can be both a KTN black hole and a KTN naked singularity. We report that the upper limit for the NUT charge is not greater than 1.1 for a positive spin. The lower limit reports that the NUT charge cannot be less than −1.1 for negative spin values. Also, a KTN naked singularity can still be compatible with M87* observations.

In this work, the ranges for constraining the NUT charge from the Keck observation of Sgr A* can be a maximum of 0.5 for Schwarzschild-like and very slowly rotating KTN black holes, and extended to 1.5 for negative spin values up to −2. The minimum value for the NUT charge for Keck observations can be −0.5 for Schwarzschild-like and very slowly rotating KTN black holes, and extended to −1.5 for positive spin values up to 2. I consider two values of 40° and 10° for viewing angles. For VLTI observations, the Schwarzschild-like and very slowly rotating KTN black holes are excluded for 40° and the range is very narrow in the NUT charge for 10°. The colored region is extended to 1.5 for the NUT charge for negative spin values up to −2 and −1.5 for positive spin values up to 2. For all four plots I report, there is a small possibility of indications of KTN naked singularities considering uncertainties.

The main significance of the result is testing General Relativity and exploring alternative gravity theories, deviations from the Kerr solution, and exploring the possibility of exotic physics. Constraining the NUT charge, which would be interpreted as the gravitational analog of a magnetic monopole through observations, could lead to certain extensions and modifications of standard General Relativity. Confirming the existence of the NUT charge has implications for the type of objects that can exist, the end state of gravitational collapse and black hole formationand Galactic dynamics.

In addition to the possible constraining of exotic solutions and the implications of a gravitational monopole, my work supports the cosmic censorship conjecture (singularities should be hidden within the event horizon) by reducing the possibility of the existence of naked singularities in the shadow of Sgr A*. Naked singularities are a theoretical challenge in General Relativity.

In general, the possibility of singularities with other observations is reduced. As one example, one can study X-ray data through the iron line method to probe strong gravity regimes. X-ray reflection spectroscopy, also known as the iron line method, studies the prominent feature of the iron $K\alpha$ line in X-ray reflection spectra. In the inner region of the accretion disk, close to the compact object in the presence of a strong gravitational field, the line is broadened and asymmetric. Currently, this method is used for measuring black hole spin considering the Kerr spacetime. It is also used to test deviations from the Kerr case. In paper [28], the authors show that the iron line of naked singularities is different from that of a black hole. For instance, the line introduces three peaks instead of two peaks. One can also simulate the KTN naked singularity iron line and see the differences.

Regarding the test of General Relativity and black holes through X-ray observations, there are some problems as well. These observations suffer from parametric degeneracy problems with current facilities. That means that the same observations can be fitted by considering a spacetime deviated from the Kerr case. Shadow observations and the narrow range of the NUT charge in this study can help to better understand alternatives to the Kerr paradigm.

Moreover, in another recent manuscript [29], the authors consider some naked singular spacetimes and study them using the shadow of Sgr A* and M87*. They show that a broad class of naked singularities is excluded.

Regarding the viewing angle, one can consider different angles as there are no strong constraints from observation on the viewing angle. The EHT group only report values below 50°, so I consider 40° and 10° as examples. There is also some reported range from infrared, radio, and other observations; it is mostly between 30° and 60°. One can also consider higher values, but as they are not reported by observations, do not consider them here.

A crucial point is understanding the impact of plasma on the shadow; for example, blob of plasma can affect it as a Doppler shift on the shadow image due to the plasma’s high velocity and the resulting relativistic Doppler effect. Additionally, it can distort the appearance of the black hole. Observationally, the brightness of the photon ring caused by moving/orbiting plasma causes variability in time for the shadow image. GRMHD simulations can model the plasma and its behavior. The Doppler shift and beaming signature can be studied. The brightness and spectrum of the accretion disk and jet can lead to an asymmetric structure in these studies, and the resulting photon ring appearance would be asymmetric as well.