A Study of Spin 1 Unruh–De Witt Detectors
Abstract
1. Introduction
Preliminaries
2. Evaluation of the Qutrit Density Matrix in the Case of the Dephasing Coupling Detectors
3. Tomita–Takesaki Modular Theory and the von Neumann Algebra of the Weyl Operators
- i.
- ;
- ii.
- is dense in .
4. The Bell–CHSH Inequality
- When the quantum field is removed, i.e., , and therefore, , we recover the Bell–CHSH inequality of Quantum Mechanics for qutrits, whose maximum value is [14,15]One notices that this value is lower than Tsirelson’s bound, as we are dealing with a spin 1 system.
- The contributions arising from the scalar field are encoded in the exponential terms and . It is worth remembering here that the parameter is related to the norm of the test function , Equation (62); that is, this parameter reflects the freedom one has in defining the test function through the operator s. As pointed out in [19,25], is a free parameter which appears in the Quantum Field Theory formulation of the Bell–CHSH inequality in terms of Weyl operators, playing a similar role of the free Bell’s angles and it can bee chosen in the most suitable way. This feature can be understood as follows. Looking at the Bell’s operators , Equation (63), one realizes that they are dichotomic for arbitrary values of the parameters . As such, they are completely free and, in fact, are chosen to be the most convenient in the final expression of the Bell–CHSH inequality. The same pattern is encountered in the case of the parameter . One has to notice that the Weyl operatoris unitary for any value of the parameter .
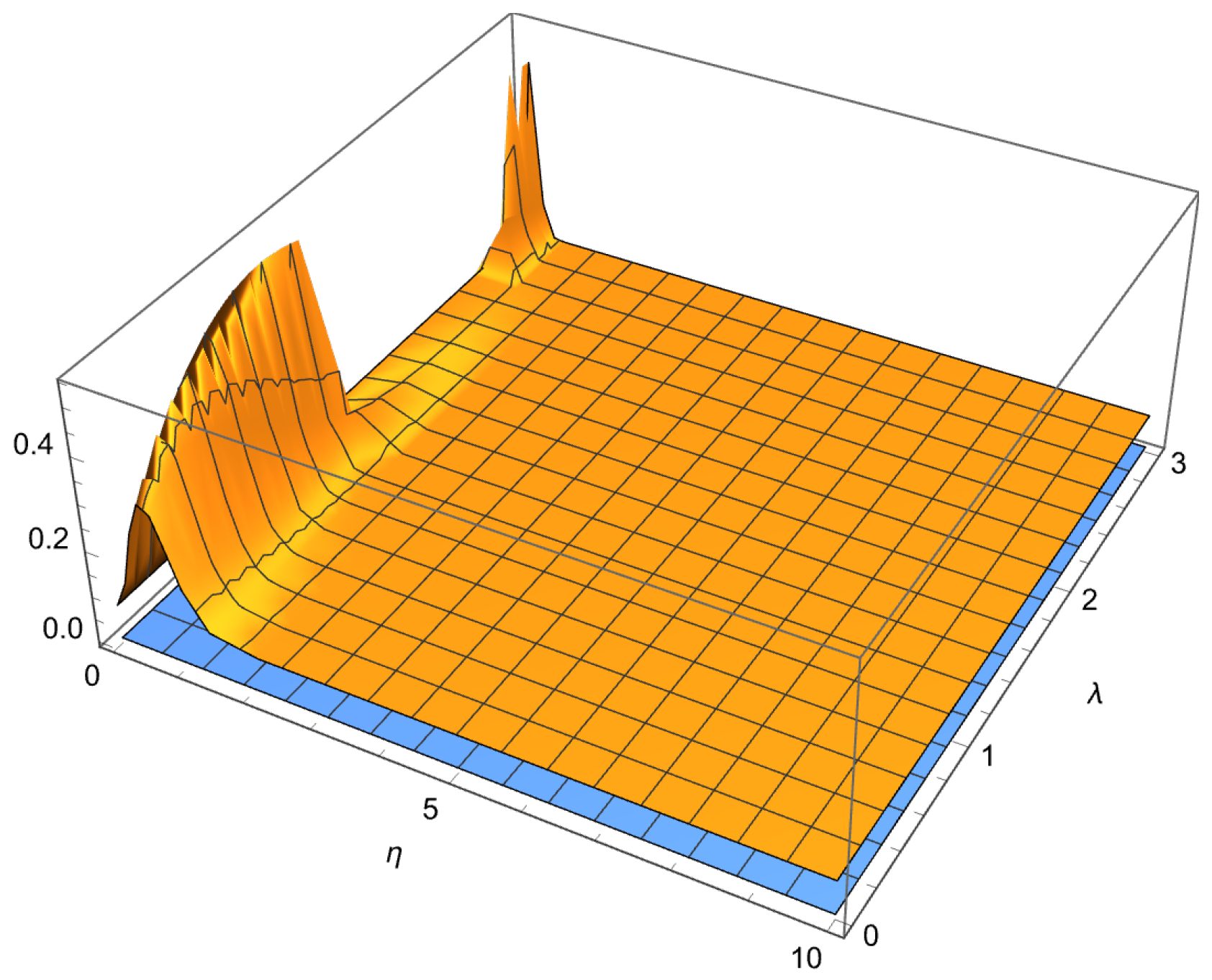
- We now have to face the choice of the spectral subspace of the modular operator . This is a not an easy task due to the fact that has a continuous spectrum given by the positive real line . For a better illustration of this point, we remind here the expression found in [12] for the violation of the Bell–CHSH in the vacuum state of a quantum scalar field2, namelyfrom which the choice of the spectral subspace follows. The maximum violation is attained for . The important point here is that this choice can be made, as belongs to the continuous spectrum of .In our case, we proceed as follows. From , we obtain the roots . We can distinguish two possibilities. The first one is when . In this case, the quantum field produces a damping, resulting in a decrease in the violation of the Bell–CHSH inequality, as compared to the pure Quantum Mechanical case. The second possibility takes place when , resulting in an improvement of the size of the violation. In other words, we pick up the spectral subspace . This spectral subspace has been identified through a numerical analysis. Again, it is a possible choice.
- Let us also check that the Tsirelson bound is fulfilled for arbitrary values of the parameter . Observing that the maximum value of the angular part of Equation (65) is , attained for the following values of the Bell’s angles:it follows that
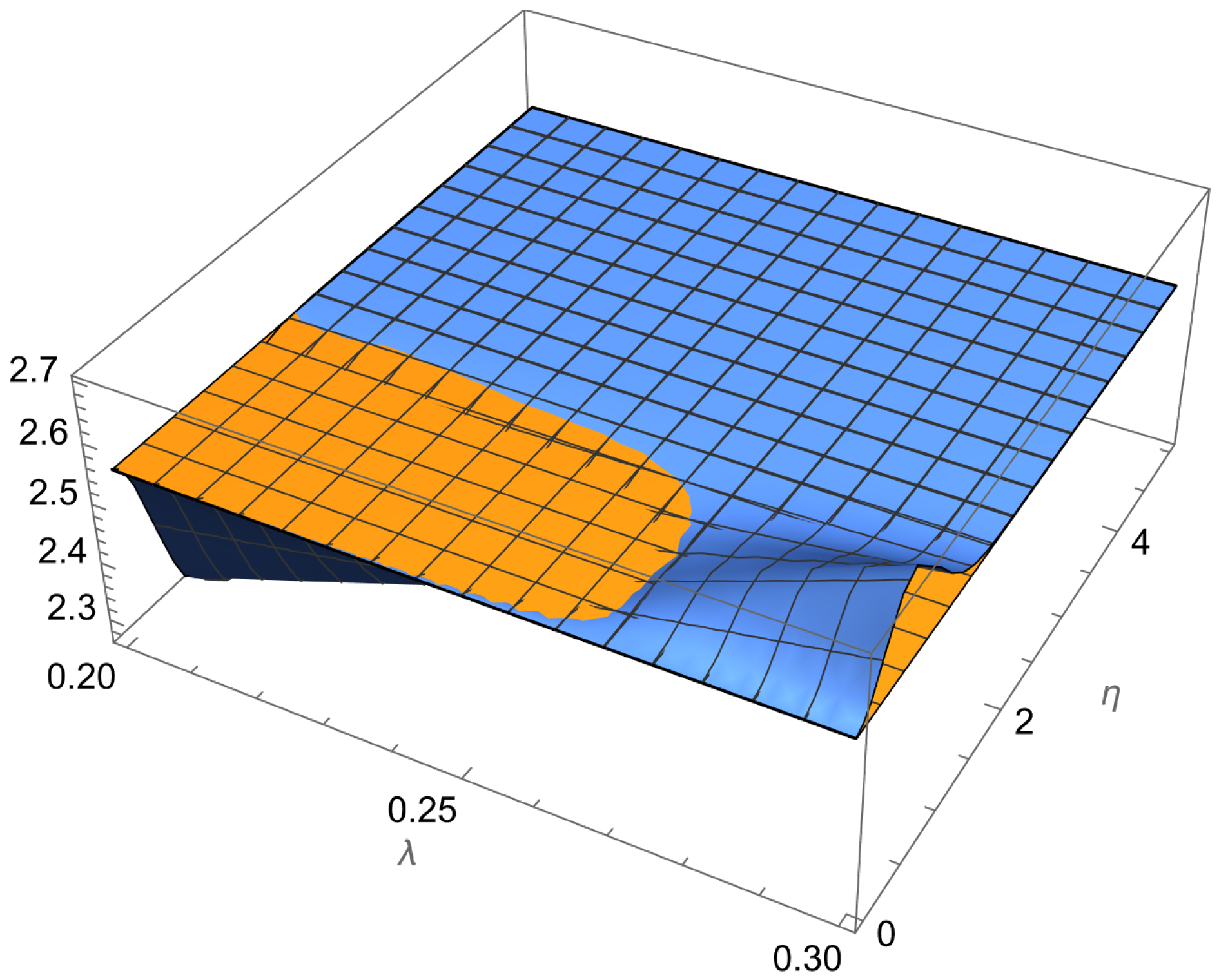
- The whole effects produced by the quantum field can be seen in Figure 2. The orange surface represents the maximum value of without the presence of , i.e., . One notices the existence of a small region in blue, above the orange surface. This region corresponds to values of for which the size of the violation is improved, almost till approximately . This phenomenon occurs when .
Comparison with the Spin Case
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | A smooth function f with compact support is a continuous infinitely differentiable function which vanishes outside the region . |
| 2 | See Section III, just before Corollary 3.2. |
| 3 | Since the function depends only from , we can always take to be non-negative. |
References
- Reznik, B. Entanglement from the vacuum. Found. Phys. 2003, 33, 167. [Google Scholar] [CrossRef]
- Tjoa, E. Quantum teleportation with relativistic communication from first principles. Phys. Rev. A 2022, 106, 032432. [Google Scholar] [CrossRef]
- Tjoa, E. Nonperturbative simple-generated interactions with a quantum field for arbitrary Gaussian states. Phys. Rev. D 2023, 108, 045003. [Google Scholar] [CrossRef]
- Lima, C.; Patterson, E.; Tjoa, E.; Mann, R.B. Unruh phenomena and thermalization for qudit detectors. Phys. Rev. D 2023, 108, 105020. [Google Scholar] [CrossRef]
- Barbado, L.C.; Castro-Ruiz, E.; Apadula, L.; Brukner, Č. Unruh effect for detectors in superposition of accelerations. Phys. Rev. D 2020, 102, 045002. [Google Scholar] [CrossRef]
- Foo, J.; Onoe, S.; Zych, M. Unruh-deWitt detectors in quantum superpositions of trajectories. Phys. Rev. D 2020, 102, 085013. [Google Scholar] [CrossRef]
- Verdon-Akzam, G.; Martin-Martinez, E.; Kempf, A. Asymptotically limitless quantum energy teleportation via qudit probes. Phys. Rev. A 2016, 93, 022308. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195. [Google Scholar] [CrossRef]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed Experiment to Test Local Hidden-Variable Theories. Phys. Rev. Lett. 1969, 23, 880. [Google Scholar] [CrossRef]
- Guedes, F.M.; Guimaraes, M.S.; Roditi, I.; Sorella, S.P. Unruh-De Witt detectors, Bell-CHSH inequality and Tomita-Takesaki theory. J. High Energy Phys. 2024, 2024, 31. [Google Scholar] [CrossRef]
- Summers, S.J.; Werner, R. Bell’s Inequalities and Quantum Field Theory. I. General Setting. J. Math. Phys. 1987, 28, 2440. [Google Scholar] [CrossRef]
- Summers, S.J.; Werner, R. Bell’s inequalities and quantum field theory. II. Bell’s inequalities are maximally violated in the vacuum. J. Math. Phys. 1987, 28, 2448. [Google Scholar] [CrossRef]
- Tsirelson, B.S. Quantum analogues of the Bell inequalities. The case of two spatially separated domains. J. Math. Sci. 1987, 36, 557. [Google Scholar] [CrossRef]
- Gisin, N.; Peres, A. Maximal violation of Bell’s inequality for arbitrarily large spin. Phys. Lett. A 1992, 162, 15. [Google Scholar] [CrossRef]
- Peruzzo, G.; Sorella, S.P. Entanglement and maximal violation of the CHSH inequality in a system of two spins j: A novel construction and further observations. Phys. Lett. A 2023, 474, 128847. [Google Scholar] [CrossRef]
- Lin, S.Y.; Chou, C.H.; Hu, B.L. Disentanglement of two harmonic oscillators in relativistic motion. Phys. Rev. D 2008, 78, 125025. [Google Scholar] [CrossRef]
- Witten, E. APS Medal for Exceptional Achievement in Research: Invited article on entanglement properties of quantum field theory. Rev. Mod. Phys. 2018, 90, 045003. [Google Scholar] [CrossRef]
- Bratteli, O.; Robinson, D.W. Operator Algebras and Quantum Statistical Mechanics 1. C*- and W*-Algebras. Symmetry Groups. Decomposition of States. In Theoretical and Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Fabritiis, P.D.; Guedes, F.M.; Guimaraes, M.S.; Peruzzo, G.; Roditi, I.; Sorella, S.P. Weyl operators, Tomita-Takesaki theory, and Bell-Clauser-Horne-Shimony-Holt inequality violations. Phys. Rev. D 2023, 108, 085026. [Google Scholar] [CrossRef]
- Haag, R. Local Quantum Physics: Fields, Particles, Algebras; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Guido, D. Modular theory for the von Neumann algebras of Local Quantum Physics. Contemp. Math. 2011, 534, 97. [Google Scholar]
- Rieffel, M.A.; Van Daele, A. A bounded operator approach to Tomita-Takesaki theory. Pac. J. Math. 1977, 69, 187. [Google Scholar] [CrossRef]
- Eckmann, J.-P.; Osterwalder, K. An application of Tomita’s theory of modular Hilbert algebras: Duality for free Bose fields. J. Funct. Anal. 1973, 13, 1. [Google Scholar] [CrossRef]
- Bisognano, J.J.; Wichmann, E.H. On the duality condition for a Hermitian scalar field. J. Math. Phys. 1975, 16, 985. [Google Scholar] [CrossRef]
- Guimaraes, M.S.; Roditi, I.; Sorella, S.P. Bell-CHSH inequality and unitary operators. arXiv 2024, arXiv:2403.15276. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guedes, F.M.; Guimaraes, M.S.; Roditi, I.; Sorella, S.P. A Study of Spin 1 Unruh–De Witt Detectors. Universe 2024, 10, 307. https://doi.org/10.3390/universe10080307
Guedes FM, Guimaraes MS, Roditi I, Sorella SP. A Study of Spin 1 Unruh–De Witt Detectors. Universe. 2024; 10(8):307. https://doi.org/10.3390/universe10080307
Chicago/Turabian StyleGuedes, F. M., M. S. Guimaraes, I. Roditi, and S. P. Sorella. 2024. "A Study of Spin 1 Unruh–De Witt Detectors" Universe 10, no. 8: 307. https://doi.org/10.3390/universe10080307
APA StyleGuedes, F. M., Guimaraes, M. S., Roditi, I., & Sorella, S. P. (2024). A Study of Spin 1 Unruh–De Witt Detectors. Universe, 10(8), 307. https://doi.org/10.3390/universe10080307





