Abstract
QCD with the isospin chemical potential is a useful laboratory to delineate the microphysics in dense QCD. To study the quark–hadron continuity, we use a quark–meson model that interpolates hadronic and quark matter physics at microscopic level. The equation of state is dominated by mesons at low density but taken over by quarks at high density. We extend our previous studies with two flavors to the three-flavor case to study the impact of the strangeness, which may be brought by kaons and the UA(1) anomaly. In the normal phase, the excitation energies of kaons are reduced by in the same way as hyperons in nuclear matter at the finite baryon chemical potential. Once pions condense, kaon excitation energies increase as does. Moreover, strange quarks become more massive through the UA(1) coupling to the condensed pions. Hence, at zero and low temperature, the strange hadrons and quarks are highly suppressed. The previous findings in two-flavor models, sound speed peak, negative trace anomaly, gaps insensitive to , persist in our three-flavor model and remain consistent with the lattice results to 1 GeV. We discuss the non-perturbative power corrections and quark saturation effects as important ingredients to understand the crossover equations of state measured on the lattice.
1. Introduction
Recently there has been increasing attention paid to two-color QCD (QC2D) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19], or QCD at finite isospin but zero baryon densities (isospin QCD, QCDI in short) [20,21,22,23,24,25,26,27,28,29,30,31]. In these theories, lattice simulations are viable without the sign problem. Confronting theories with lattice results should provide us with useful insights into QCD matter at high baryon density (); see, for example, reviews [32,33,34,35,36].
Equations of state (EOSs) of dense matter have a one-to-one correspondence with the mass-radius (M-R) relations of neutron stars. One of the important indications from neutron star observations and nuclear constraints is that QCD matter is soft around nuclear saturation density , but rapidly becomes stiff around – [37,38]. The density for this radical stiffening is smaller than the density where baryons of the radius – fm spatially overlap. Meanwhile nuclear many-body calculations become problematic for –. Observationally, rapid stiffening is supported by a small variation (or even increase) in radii from to neutron stars. If EOSs stiffen only gently as in typical hadronic EOS with many-body forces, the radii of ≃ neutron stars would be substantially smaller than neutron stars by ∼1 km [39]. Such contrast in to radii may be also studied by gravitational waves from binary neutron star mergers; see, for example, Refs. [40,41,42,43].
To study the interplay between hadronic and quark matter, it is crucial to understand rapid stiffening at the microscopic level. Several theoretical studies [44,45,46,47] suggest that such rapid stiffening around 2– is triggered by quark degrees of freedom, whether or not quarks are confined or deconfined. Assuming a model in which quarks remain confined in baryons, quarks can still occupy states with a certain probability and eventually affect baryons through the quark Pauli blocking [46,47]. Such quark constraint becomes substantial even before baryons overlap. After quark states at low momentum are saturated (“quark saturation” [46]), the quark Fermi sea begins to form with the diffused Fermi surface whose thickness is ≃200–300 MeV. The quark saturation forces matter of non-relativistic baryons to change into that of relativistic baryons or quarks, driving the rapid growth in pressure but modest change in the energy density [46]. The quark momentum distribution at finite density has been manifestly computed for two-dimensional QCD [48].
The quark saturation and the associated stiffening may occur also in QC2D and QCDI, although baryons are replaced with diquark baryons and mesons, respectively. In these theories, the Bose–Einstein Condensation of diquarks or mesons occurs at the onset of matter; (composite) bosons occupy the zero momentum state. At a finite chemical potential exceeding the mass threshold, the amplitude of condensates would grow indefinitely unless some sort of repulsive forces temper the growth of the amplitude. For theories of elementary bosons, we do not have definite rationals why such repulsion should exist, while, for theories of bosons made of fermions, the indefinite growth in boson amplitudes would violate the Pauli exclusion principle. Hence, irrespective to the details of interactions, effective repulsions among bosons must emerge.
For isospin QCD, there have been many studies; see Ref. [49] for a recent good summary to 2019. Recently, isospin QCD has attracted renewed attention as a laboratory to study concepts proposed for neutron star physics [50,51,52] or to derive some constraints on neutron star EOS [53,54,55,56]. In Refs. [50,51], we used a two-flavor quark–meson model to discuss the rapid stiffening and related microphysics. This model is renormalizable and includes mesons and quarks [57,58]. At low density, the EOS is dominated by mesons while, at high density, quarks dominate. In quark matter, region mesonic degrees of freedom as condensates remain near the quark Fermi surface.
In this paper, after adding some supplements to our previous two-flavor studies, we then extend the analyses to three flavors. Although a strange quark does not have isospin, hadronic strange particles, such as kaons, , and so on, contain u,d-quarks and can be affected by the isospin density. Indeed, the excitation energies of decrease with increasing and would eventually condense unless other particles in the system repel such kaons. Another effect of interest is the impact of the UA(1) anomaly that affects the strangeness in the Dirac sea [59,60]. At finite density, the reduction in the effective u,d quark masses softens the chiral symmetry breaking in the strange quark sector, while the appearance of the pion condensates can enhance the strange quark mass by a few hundred MeV. This continues until the medium screening cuts off such effects. A similar coupling, diquark-to-chiral order parameters, has been discussed in the context of quark–hadron crossover [61,62,63,64]. Thus, the strange particles are useful probes to diagnose various medium effects in dense matter.
In this paper, we use a quark–meson model to discuss a quark–hadron crossover [65,66,67,68,69,70]. In Section 2, we first discuss a picture behind this model to inform readers of what physics we try to describe. We will use the expansion to classify the effects caused by different degrees of freedom [71,72]. In Section 3, we present a quark–meson model including the strangeness and the UA(1) anomaly effects. In Section 4, we study the effective potential and meson spectra at the tree level. In Section 5, we include quarks to change the structure of the theory and discuss how it leads to the trend consistent with the lattice results. In Section 6, we mention our parameter fixing through meson poles in vacuum with quark-loop corrections. In Section 7, we examine EOS at zero temperature and its relationship with the microphysics. Section 8 is devoted to the summary.
2. A Quark–Meson Model at Finite Density: Outline
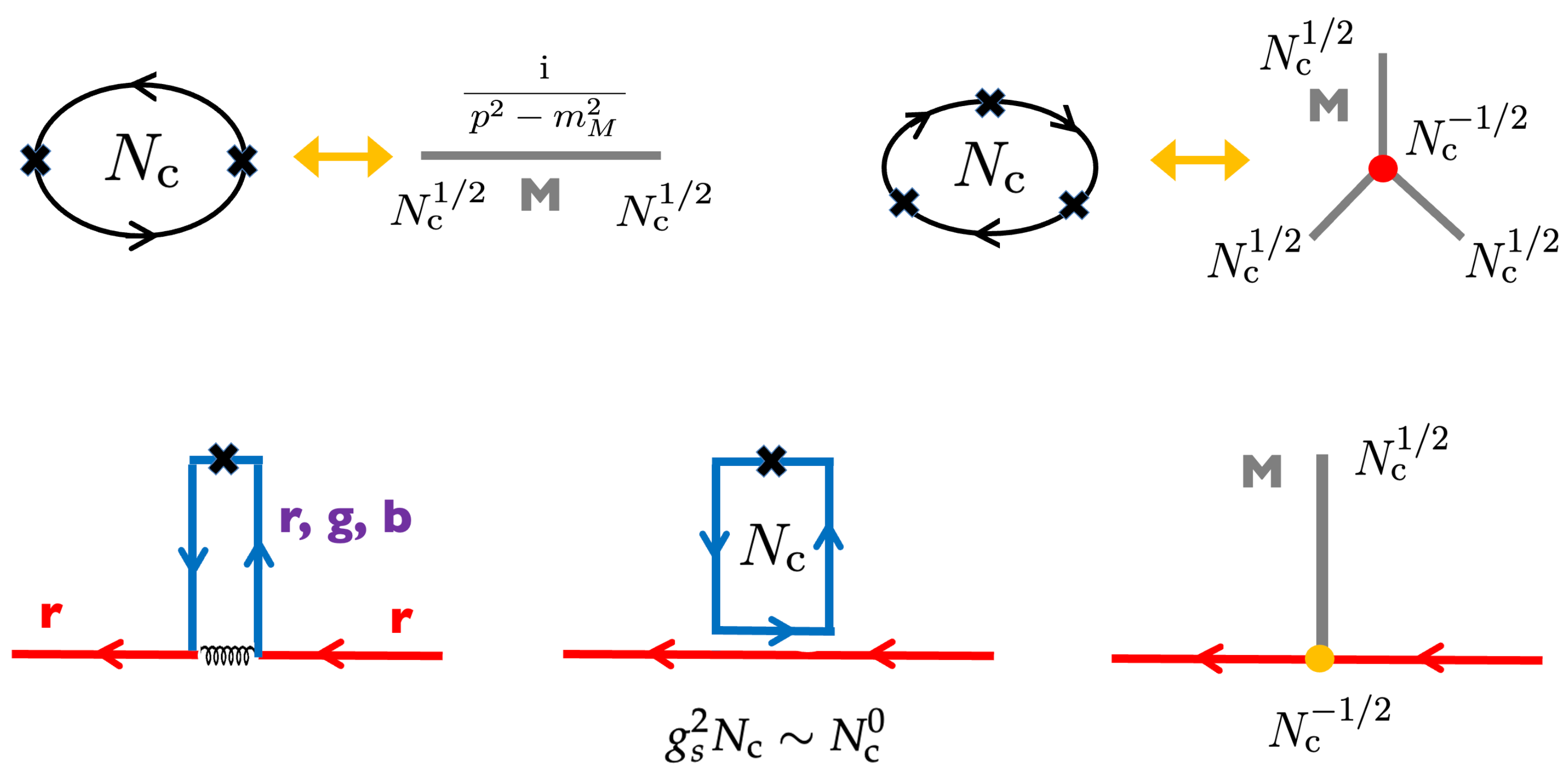
We begin with the counting of a quark–meson coupling. A diagrammatic representation is given in Figure 1. To derive the counting of hadronic parameters, we match the counting in a color line graph and a hadronic graph. For instance, from a mesonic correlator with the magnitude of , one can conclude that a quark bilinear operator couples to a mesonic state with the strength . Using this estimate and repeating the similar matching, one can deduce that the meson–meson interaction is ∼ for three-meson vertices and ∼ for four-meson vertices, and so on. Similarly, for a quark–meson coupling graph with the amplitude of ∼∼, one can conclude that the quark–meson coupling is . While we consider only a single gluon exchange, including more gluons introduces ∼ 1 so that the counting is not affected.
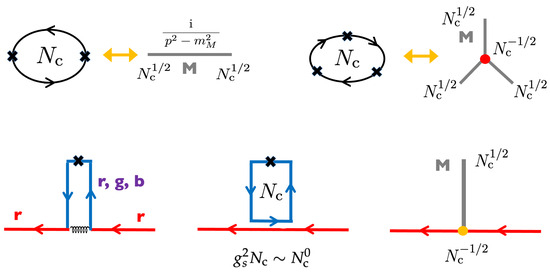
Figure 1.
(upper) Some examples of the correspondence between quark–gluon, color line graphs, and hadronic graphs. The coupling between quark bilinear operators and mesonic state must be ∼ for the consistency with the color line graphs. Meson three-point vertices must be ∼. (lower) The quark–meson vertices in quark–gluon, color line, and quark–meson representations. The quark–meson coupling must be ∼ to be consistent with the color line representation.
Below, we assume that this quark–meson coupling g is dominated by soft gluons for which the quark–gluon coupling is large and characterizes the size of the quark–meson coupling. The soft gluon exchanges occur indefinitely within the produced mesons. This sort of process cannot be represented by perturbative treatments at the finite order. The purpose of manifestly including mesonic degrees of freedom is to replace or parametrize these processes in a book keeping manner.
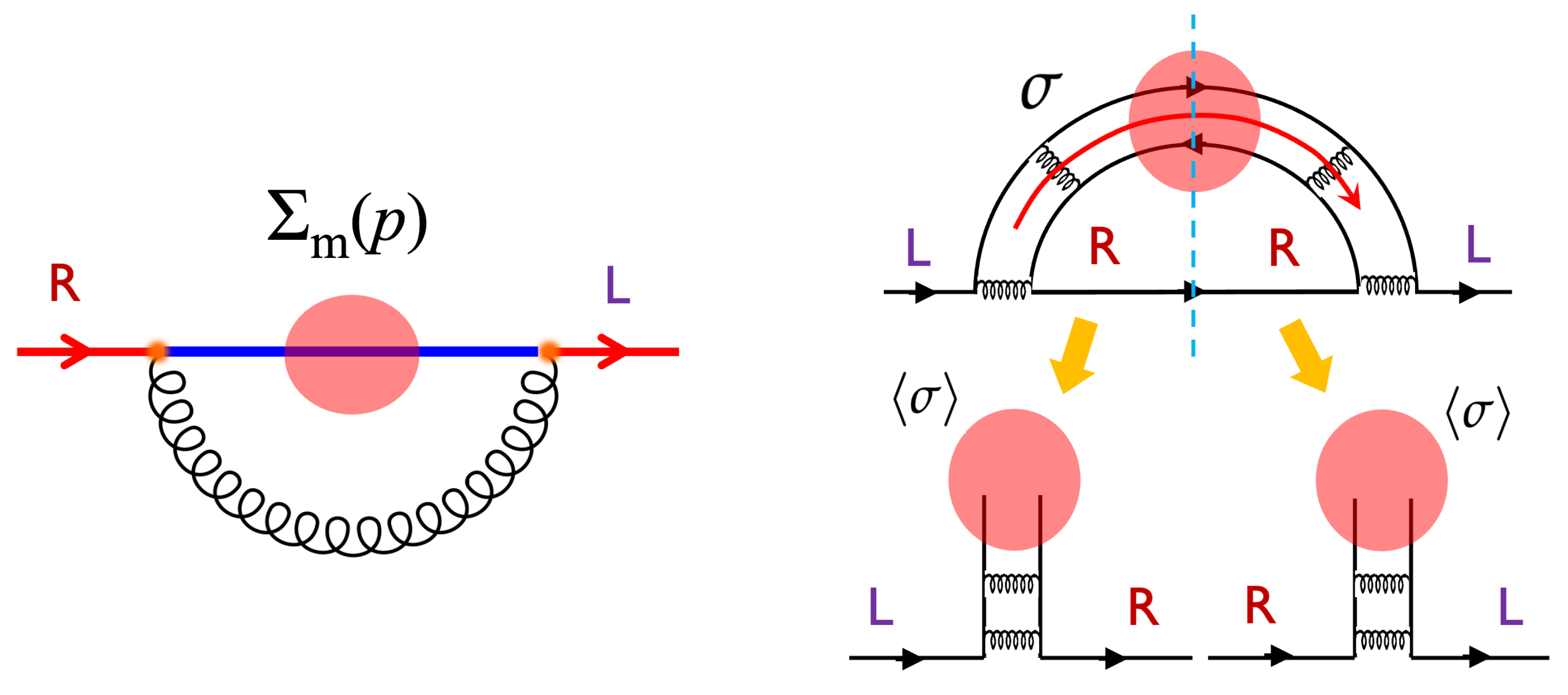
The quark self-energy with gluon loops (leftmost panel, Figure 2) are ∼ yielding the mass of ∼. The factor amplification occurs, as there is a color loop in the color line representations. In contrast, the self-energy with mesonic loops is ∼∼ and suppressed (rightmost panel, Figure 2). There is an exception, however. When mesons form condensates, the self-energies originating from meson loops can be amplified to . The condensate contains indefinite numbers of pairs. In the case of chiral condensates, condensed or pairs transform into , generating the mass self-energies. If we neglect changes in the number of pairs in the condensate, a quark propagator with meson loops can be factorized into a product of quark propagators with a background meson condensate. Since quark propagators with the meson background already contain graphs with many soft gluons, to avoid double counting, we do not manifestly include the quark self-energy graphs with soft gluon loops. Meanwhile, graphs with hard gluons may be added separately for more complete exploration of the phase space in the intermediate states.
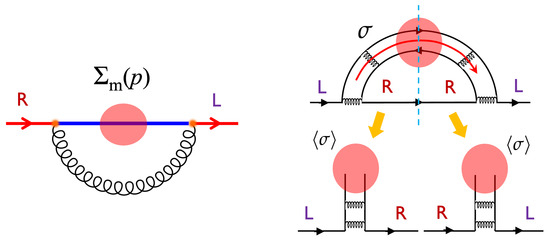
Figure 2.
The mass self-energy graphs with (left) gluon and (right) meson loops. The gluon loop graph is ∼∼. The meson loop graph is ∼∼∼, except when the meson condenses. With meson condensates of ∼∼, the graphs with condensate can represent (some part of) the gluon loop graphs in the leftmost panel.
The reduction in meson masses can be important even before mesons condense. Such precursory effects are important near the phase boundaries and have been studied in the context of color superconductivity [73,74,75].
We include “mesons” as a representative of the propagating graph with an indefinite numbers of soft gluon exchanges. Using meson degrees of freedom at high density might look unnatural, but models manifestly including mesons can be dynamical reduced to pure quark descriptions; the dissociation and structural changes of these mesons into quarks can be described by inserting quark loops in the meson propagators. Thus, unwanted contributions can be canceled by including quark loops [76].
At high density, quarks typically have large momenta, but the excitation energies can be small, ∼ (: chemical potential) near the Fermi surface. These soft quarks and soft gluons may keep quark–meson couplings as strong as in vacuum unless screening processes cut off soft gluons. For S-wave condensates, a quark with and an antiquark with make a pair in which soft gluons are exchanged. For a pion-condensed phase in isospin QCD, these soft gluons should be largely unscreened because the condensate is a color singlet and colored excitations are gapped. These unscreened gluon propagators are supported by lattice simulations for two-color QCD [11,77,78,79,80,81].
With soft gluons being unscreened, the size of the gap is ∼ or can be even larger. To see this, we parametrize the soft gluon exchange forces as
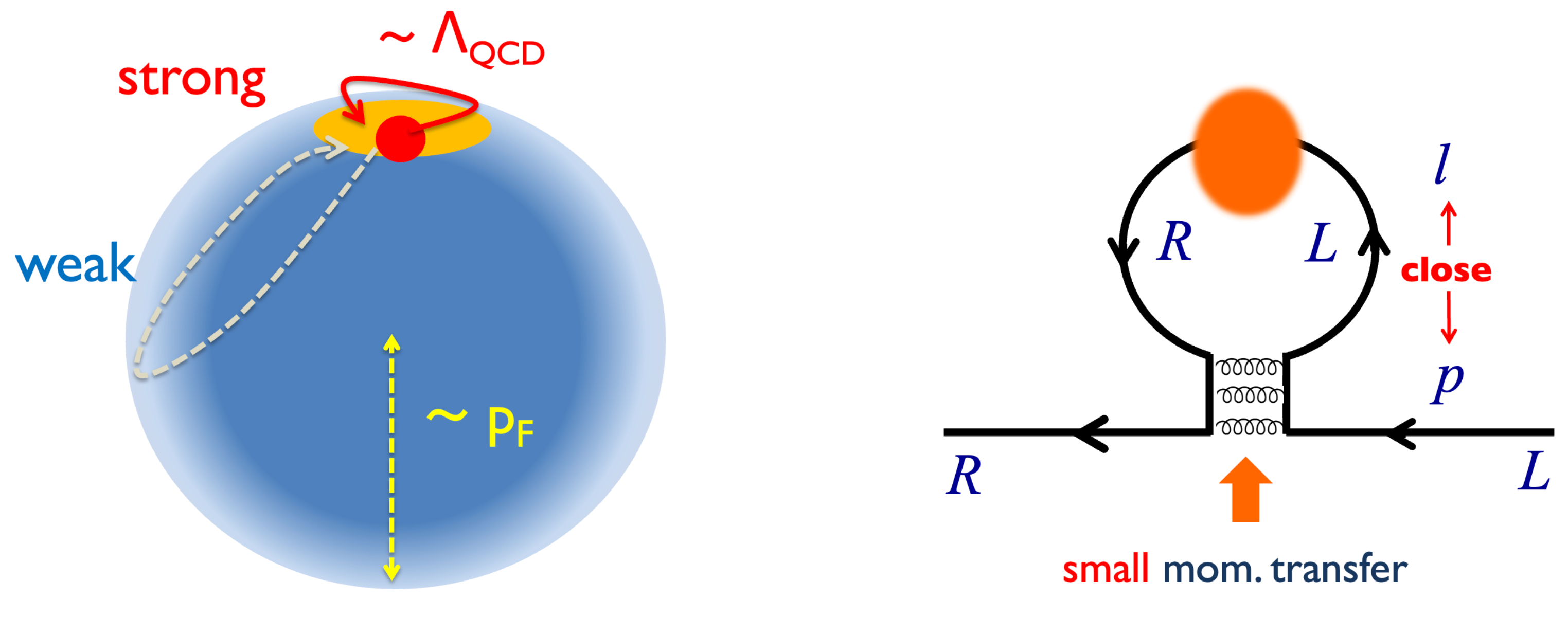
where is the typical strength for a soft momentum transfer . This model has been used for quarkyonic chiral spirals [82,83,84] and QCD in a magnetic field [85,86,87] to yield the gap equation local in momentum space (Figure 3). The resultant gap is ∼, and we expect the same happens for the soft gluonic part in isospin QCD.
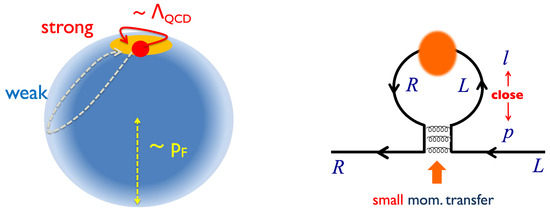
Figure 3.
The gap created by soft gluons. The self-energies caused by soft gluons are not very sensitive to the size of the Fermi surface because quarks fluctuate only within small domain. The produced gap is characterized by soft gluons and is supposed to be ∼, until hard gluon processes dominate over soft gluon processes.
Now, the gap equation reads
Decomposing the loop momentum as with , the conservative estimate for the range is and . Then, one can simplify the gap equation into (: Fermi velocity)
If and hold, we can omit the term in the range of integral to factorize the integral. The condition will be checked a posteriori. At this stage, the equation loses the -dependence and so does the solution. Further calculation reads
Thus, the gap is . For a stronger coupling, the gap grows to , and the condition is satisfied.
The present arguments show that, even at large or large quark Fermi momenta, non-perturbative phenomena characterized by are still possible. This continues until screening effects set in. When is sufficiently large, we should also add hard gluon contributions, which can be treated within the weak coupling method; this hard contributions are sensitive to the phase space around the Fermi surface and hence to . As we see later, the gap (which is insensitive to ) adds the power corrections, ∼, to the pressure . These power corrections, not capable within perturbative computations, have played important roles in QCD phenomenology [88,89,90] and also seem essential to describe the lattice simulation data at large density [50,51].
3. A Quark–Meson Model: Mean Field Treatments
Now, we consider a practical description of a three-flavor quark–meson model. The Lagrangian is
The quark with the Yukawa interaction takes the form
where . We have scalar and pseudoscalar flavor nonets. In our notation, the isospin chemical potential is , coupled to rather than the isospin density operator in the conventional sense.
The mesonic Lagrangian with the isospin chemical potential is
where isotriplet and two isodoublets couple to the isospin chemical potential. The field normalization for isospin-charged fields are , and so on. Since commutes with the isospin rotation operator around the -axis, the symmetry is preserved at the level of the Lagrangian. This symmetry is broken when pions condense.
The mesonic potential consists of three pieces
with a U(3) symmetric potential
and a symmetry-breaking term associating the current quark masses,
and the Kobayashi–Maskawa–’t Hooft (KMT) interaction
which is responsible for the UA breaking.
Increasing , the excitation energies of mesons including u or are reduced, i.e., the excitation energies of decrease linearly as a function of . As we see shortly, the tree level analyses show that the lightest pion condenses first, and then the reduction in energies for the other mesons is stopped; no other mesons condense. At the tree level, this is interpreted as the effective repulsion between condensed pions and the other mesons. We assume this holds even after including loop corrections. Thus, we take the mean field as
Here, we could choose fields for condensed fields without loss of generality since the Lagrangian has the symmetry. The mean-field Yukawa term now takes the form
where we write , , and . Substituting the mean fields into the potentials, one finds
and ()
Below, we first examine the effective potential at the tree level which includes only the mesonic degrees of freedom. The quark dynamics manifestly enters only after including the quark loops. As we see later, the quark loops change the structure of theories and impose important constraints on the meson mean fields.
4. Purely Hadronic Descriptions: Tree Level Analyses
4.1. Gap Equations at Tree Level
We first study the tree level potential, including only meson degrees of freedom. Combining the potentials with the terms, including the chemical potential in , the effective potential at the tree level is
The gap equations are
We can show that . We combine the first and third equations to derive a simple relation,
The curvature with respect to is positive for small so that is favored. Then, the gap equation is the same as in the vacuum case; in this domain and holds. The curvature becomes negative for , leading to the scaling . This in turn leads to from the condition . The strange quark is affected by the isospin density only through the anomaly term.
4.2. Meson Kinetic and Mass Matrices at Tree Level
We now quickly review the properties of mesons in a medium of condensed pions. We first take a look at the excitation energies of charged mesons in the low-density domain. Then, the Lagrangian has the following structure ():
where for the isotriplet and for the isodoublet. The spectra are found to be
Mesons with positive isospins have energy reduction. This continues until one of those mesons condenses. The pions are the lightest and have the largest isospin , so they condense first, at .
Before the pion condensation, a pair of positive- and negative-charged mesons maintains the -independence of the thermodynamics. The thermodynamic potential from a (non-interacting) meson for is
after the terms cancel. The resulting energy is the same zero point energy as in the vacuum. The expression is valid until reaches the meson mass.
After the pions condense, mesons with an energy reduction in the normal phase are now subject to effective repulsions, and hence the gap remains in the excitation energies. In addition, condensed pions supply isospin and parity violating sources so that various mesons mix. At the tree level, the mixing is caused through the quartic and the KMT interaction. We read off the meson mass matrices masses by looking at the quadratic order of the potential
where we evaluate the second derivative at the mean field values, and also use the fact that is real. The mass matrices for and are
and the parity-breaking – couplings induced by the pion condensate are
The pion condensate induces the conversion and , and also causes the conversion between the and sectors. For light flavors, all channels but mix. The exceptional and are protected from the mixing because of the G-parity [91] type symmetries as we discuss shortly. All kaons are mixed with one another. But the isodoublets do not mix with the isoscalar nor the isovector since the condensed supply integer isospins.
To understand the decoupling of and from the others, we consider the unitary transformations induced by
where P and C are parity and charge conjugation, respectively. We define and so that the G-parity is for all pions. In this definition, and .
The symmetry holds in our symmetric Lagrangian for any . The question is whether this symmetry is spontaneously broken or not. The condensate under this symmetry transforms to
which in general is the mixture of and . But setting and writing , we conclude that . Thus, the parity is conserved in the presence of the condensates. We also note that parity is also not violated by and condensates. Thus, can be used to classify various mesons. Under the transformation, the isoscalar and isovectors transform as
Next, we consider . First, we note that the isospin density is invariant for ,
where we used . The Lagrangian is also invariant. The condensates , , and are also invariant. Under the transformation, the isoscalar and isovectors transform as
Combining these symmetries, the isoscalar and isovector sectors can be decomposed into
Meanwhile, for the isodoublet sectors,
are all mixed.
4.2.1. The Spectra of , , and
Here, we display some analytic expressions for , , and . The and decouple from the other modes, and the mass matrices are
where for , we use the gap equation. For these neutral modes, the excitation energies directly coincide with the mass .
Next, we look into the charged sector. The pion mass matrices are
and the neutral sector has the mass matrices
The mixing is induced by
The coupling between the and sectors is induced through the convolution of the anomaly and the pion condensate. Meanwhile, the mixing between and is due to the explicit SU(3) breaking, which appears through and the meson condensates existing only in the sector.
The isospin chemical potentials in the kinetic terms and mass terms together yield the massless modes. For a simple illustration, we consider the case where K is small. In this approximation, and decouple. Now, the quadratic terms in are
We use the expression of and . The determinant of the matrix becomes zero at , reflecting that there is a massless mode associated with the spontaneous breakdown of the symmetry.
4.2.2. The Spectra of
Next, we discuss the isodoublet (kaon) sector. The diagonal part is
where we use the gap equation for the pion sector. The difference in the mass matrices between the pion and kaon sectors comes from the effective quark mass. The mixing matrices are
These form a matrix and need numerical analyses for the determination of the spectra.
To obtain analytic insights, we consider the case where for which the mixing is neglected compared to the diagonal part. Combining the mass matrices with the kinetic term, (we write )
For kaons being the isodoublet, the energy reduction associated with the chemical potential is weaker than in the pion, and hence the terms do not cancel. The excitation energies manifestly depend on ,
The same also holds for the scalar meson .
5. Quark Descriptions
Now, we include loops made of mean-field quark propagators. We keep only one loop with the leading contributions; quark loops for the vertex corrections are neglected. In the counting of loops, the quark contributions appear as radiative “corrections” to the tree level, but in fact the quark contributions should be regarded as leading-order contributions at finite density [50]; indeed, as increases, the quark contributions dominate over hadronic contributions and change the structure of gap equations and EOS.
5.1. The Structure of the Effective Potential
Beyond tree calculations, the parameters in the effective potential must be also reinterpreted as bare parameters which are split into the renormalized parameters and counter terms. First, we attach an index B to fields , q, , and so on, and factor out the renormalized parameters and fields [50],
We also use with , and so on. The represents the radiative corrections without those for the external lines. The loop corrections to the quark self-energies and quark–meson vertices appear only through meson loops and hence
Meanwhile, the meson self-energies and tadpole contain quark loops of which are combined with vertices to yield
and hence one must keep these corrections. It is useful to note that the relation
in the large limit. With the first relation, the dynamically generated quark mass and gap are RG invariant. The second relation tells that the running of can be studied by examining the meson propagators.
The effective potential up to one-loop consists of three type of terms
The takes the same form as in the tree level, but the parameters are to be interpreted as renormalized ones. The includes the counter terms originating from the splitting, e.g., ,
The quark contribution is
where and , and
In the -quark sector, quarks have the energy dispersion of the BCS type.
For small , the pion condensate is absent. Then, the chemical potential disappears from the ,
reflecting the Sliver Blaze property that the isospin density begins to change only when either or are satisfied. In the present case, is the driving force.
The is UV divergent. This divergence is canceled by the counter terms from the masses, couplings, and field normalization factor from the mesonic Lagrangian. We isolate the divergences as [92]
where the twice-subtracted energy density, including only -quark contributions, is
The is UV finite and vanishing when and . At a large density, the subtracted energy scales as , dominating the thermodynamic potential.
To understand the physical meaning of the subtracted potential at large , it is instructive to consider the limit and decompose the integral into the and domains. For ,
and for ,
Thus, at is nothing but the standard quasi-particle contributions to the thermodynamic potential.
The divergent piece in is evaluated in the scheme,
where is the renormalization scale. In the scheme, the counter terms are used to absorb only the terms. Then, the counter terms are fixed as
In our previous studies, we further discussed the on-mass-shell renormalization to tune the pole positions of and . We do this when we fix parameters of our model.
Putting everything together, the effective potential is reorganized as
where the contributions from -quarks are
and from s-quarks
and the -s quark mixing induced by the KMT interaction,
We note that, the strange quark sector shows the substantial dependence because of the (1)-induced coupling, ∼; the increases as does. The similar effects have been studied in the context of color superconductivity [61,62,63,64].
The expression of is the renormalization group (RG) invariant for a given field values, provided that the renormalized masses, couplings, etc., follow the RG evolution. We have set the renormalization scale to be the vacuum light quark mass, , and then the couplings, etc., should be interpreted as those evaluated at .
Finally, we mention that the expression is invalid for very large [93]. As is well known, the one-loop effective potential is unbound for large field limits; there, we need higher orders in loops.
5.2. The Structure of the Gap Equations
The quark loops have added the logarithmic terms, which change the structure of the effective potential, especially at large . Let us see this assuming . At the tree level, the effective potential behaves as
The gap equation for balances the first and second terms, so inevitably follows. Substituting back the solution into the , we find
The hadronic parameter entirely fixes the coefficient of the term.
This trend changes after including quark contributions. We assume that the gap equation leads to , and then check the consistency of this assumption (Figure 4). The large behavior of is
where the tree level terms, except term, are suppressed compared to and terms. We note that the logarithmic contribution changes the sign at ; it becomes attractive contributions for but repulsive for . At large density, the latter stops the growth of induced by the tree contribution before terms are activated.
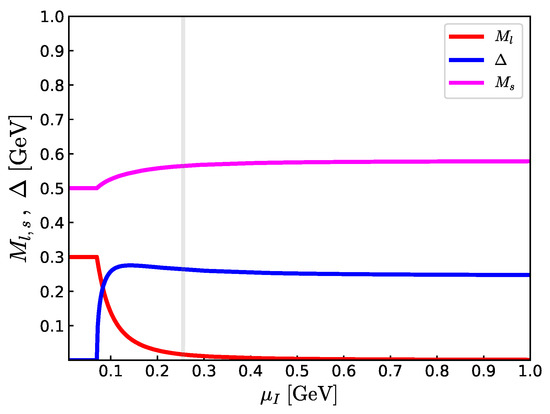
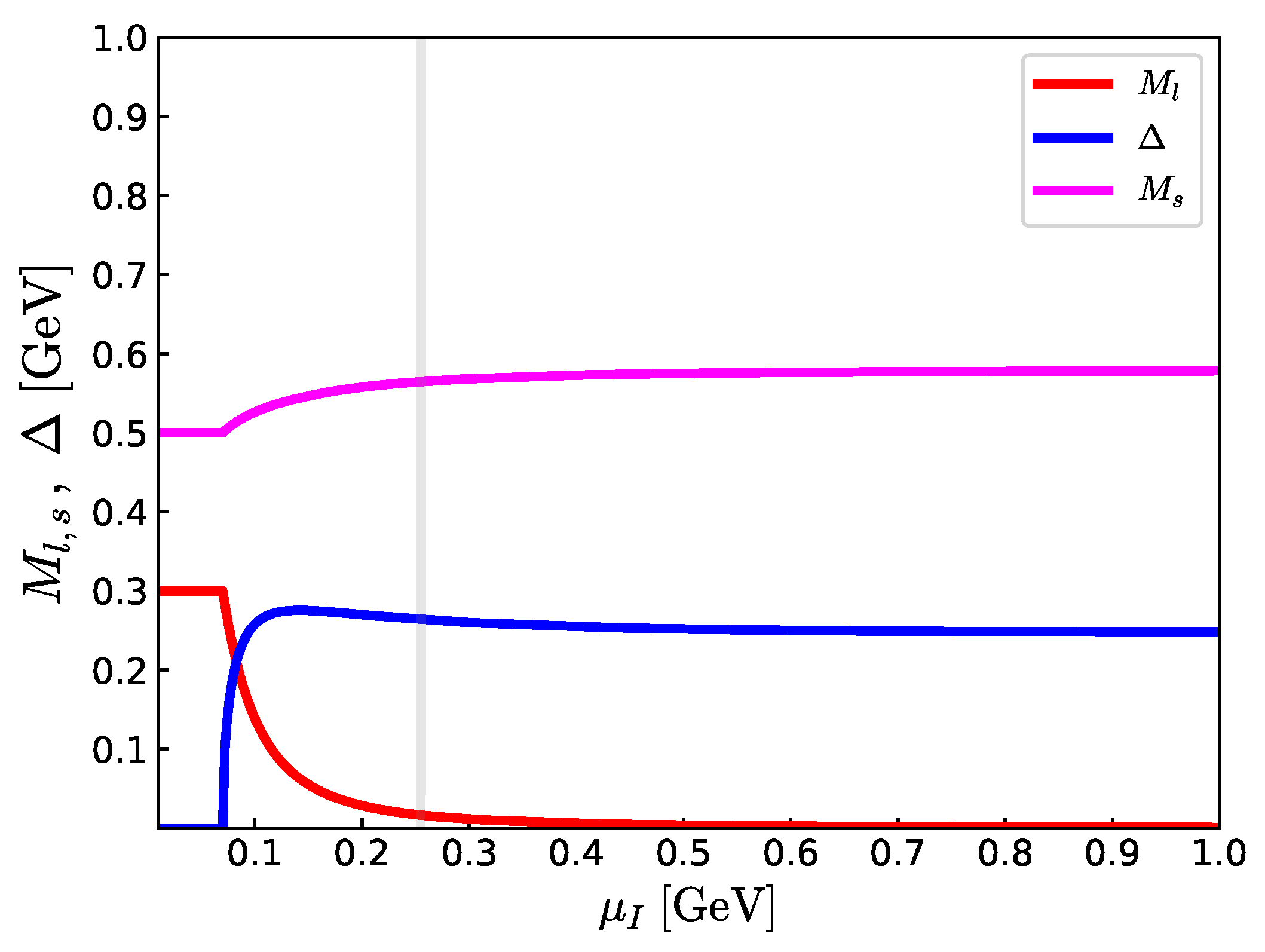
Figure 4.
The effective quark masses and the BCS gap as functions of in the quark–meson model with the set B in Table 1. The growth in the strange quark mass comes from the (1) anomaly through which strange quarks couple to the pion condensate.
It turns out that is well saturated by terms and weakly depends on . Then, the gap equation is dominated by the coefficients of term as
This form with the logarithm is typical for low-dimensional systems; in the present case, the Fermi surface plays the role for the dimensional reduction. Unlike the tree level solution, at , the gap does not manifestly contain the dependence,
The g dependence is a bit puzzling; the usual BCS-type calculations have the form of with a coupling constant G, meaning that a stronger G increases the size of the gap. In contrast, a large g reduces the gap in our model. Our interpretation is the following: the condensed mesons at the tree level, where quarks inside are neglected, overreact to the increase in and become overpopulated as one can see from the scaling . In particular, the quark Pauli blocking is neglected. In light of this viewpoint, the explicit inclusion of quarks with the coupling to mesons should cancel the unwanted contributions and should temper the growth of . This effect is stronger for a larger g. For a very small g, apparently blows up, but then terms become dominant and the situation goes back to the tree-level model or purely mesonic models. The philosophy here is in line with ref. [94] that introduced ghosts to cancel double counted contributions.
Substituting back the into , the thermodynamic potential at very large scales as
Note that, in at large , the mesonic parameters and no longer play important roles, while the Yukawa coupling g is now hidden into the gap parameter .
6. Meson Poles at One-Loop: Parameter Fixing
Now we have all expressions needed to discuss EOS, but still the parameters in our model remain to be fixed. We use meson nonets in vacuum to fix our parameters. Here, the meson self-energies induced by quark loops must be taken into account for the consistency with the gap equations, Meanwhile, in this work, we do not address in-medium self-energies to meson masses.
6.1. Meson Poles
As we have constructed the effective potential at one loop, we need to upgrade the tree-level expressions of meson masses. This is essential to reproduce the masses of the Goldstone bosons which arise at the minima of the effective potential at a given order of approximation. The analyses go as in the Nambu–Jona–Lasinio model [95].
An inverse of the meson propagator with loops takes the form
where comes from quark loops, while from the counter terms. In the case of pions, we have
We obtained the counter terms from the tree-level bare parameters.
It is convenient to define
with a function including the Feynman parameter,
This logarithm in the integral can be negative for and . (Actually, the latter regime does not occur for .) In such a case, the imaginary part appears as . The imaginary part describes the decay of mesons into constituent quarks, but this is supposed to be an artifact of not taking account the quark confinement. Realistically, a meson decays into mesons, and the width is typically smaller than the mass, except for some scalar mesons. For simplicity, in this work, we estimate a meson mass as the location where the real part becomes zero. Also, we discuss the mixing between the flavor singlet and octet using the real part only.
Remember that we chose for the effective potential, so we do the same in the following. For the pseudoscalar channels,
Moreover, to obtain similar expressions for the scalar channel, we can simply replace with .
Let us see some examples. For pions
Combining this expression with the counter term , the UV divergence proportional to is canceled by the previously determined . The divergence coupled to can be canceled by choosing
Below, we write for the renormalized self-energy. The pole condition for pions is with
For kaons, the above chosen counter terms cancel the divergence in the kaon self-energy, leaving the condition with
We do the same for 00, 88, and 08 channels, which are to be diagonalized to yield the and spectra. The and masses are found by searching satisfying
The mixing is induced by the flavor breaking associated with . It is worth mentioning that the mixing angle depends on the energy, not a constant [95].
6.2. Parameter Fixing
We have for our parameters. We treat and as our input parameters, and set
Next, we fix and so that the minima of the effective potential in vacuum are found at and ,
The leftover parameters are . We have four meson spectra GeV, so the four parameters can be fixed. Here, we use the pseudo-scalar mesons for the parameter fixing instead of using mesons since the nature of mesons is more uncertain than the pseudo-scalar mesons. The results are summarized in Table 1 and Table 2. The and masses are sensitive to the value of K; is reduced, while is enhanced by the anomaly. Here, we include the spectra of scalar mesons just because we can compute them. As is well known, however, scalar mesons are not well described by simple valence quark states and indeed the agreement between our model and experimental results is not good especially for mesons which, together with the isosinglet , are often regarded as molecules.

Table 1.
The parameters in the quark–meson model ( are given in GeV units). The parameters are chosen to reproduce the masses of the pseudo scalar nonet. We use the set B unless otherwise stated.

Table 2.
The masses of the pseudo scalar and scalar nonets with the experimental masses indicated in the parenthesis (experimentally, the and have the width of ∼500 MeV).
7. Equations of State at Zero Temperature
We examine equations of state. Substituting the solutions of gap equations into , the thermodynamic potential is . The isospin density is
As we mentioned before, we define in an unconventional way to simplify the notation. For physical interpretation, we should use , rather than , which is directly derivable from the derivative of P. The energy density is .
At low density, the condensate is driven by pions with ; as far as isospin density is saturated by those pions, one can interpret the isospin density as the pion density . A good measure to estimate the density where pions overlap is
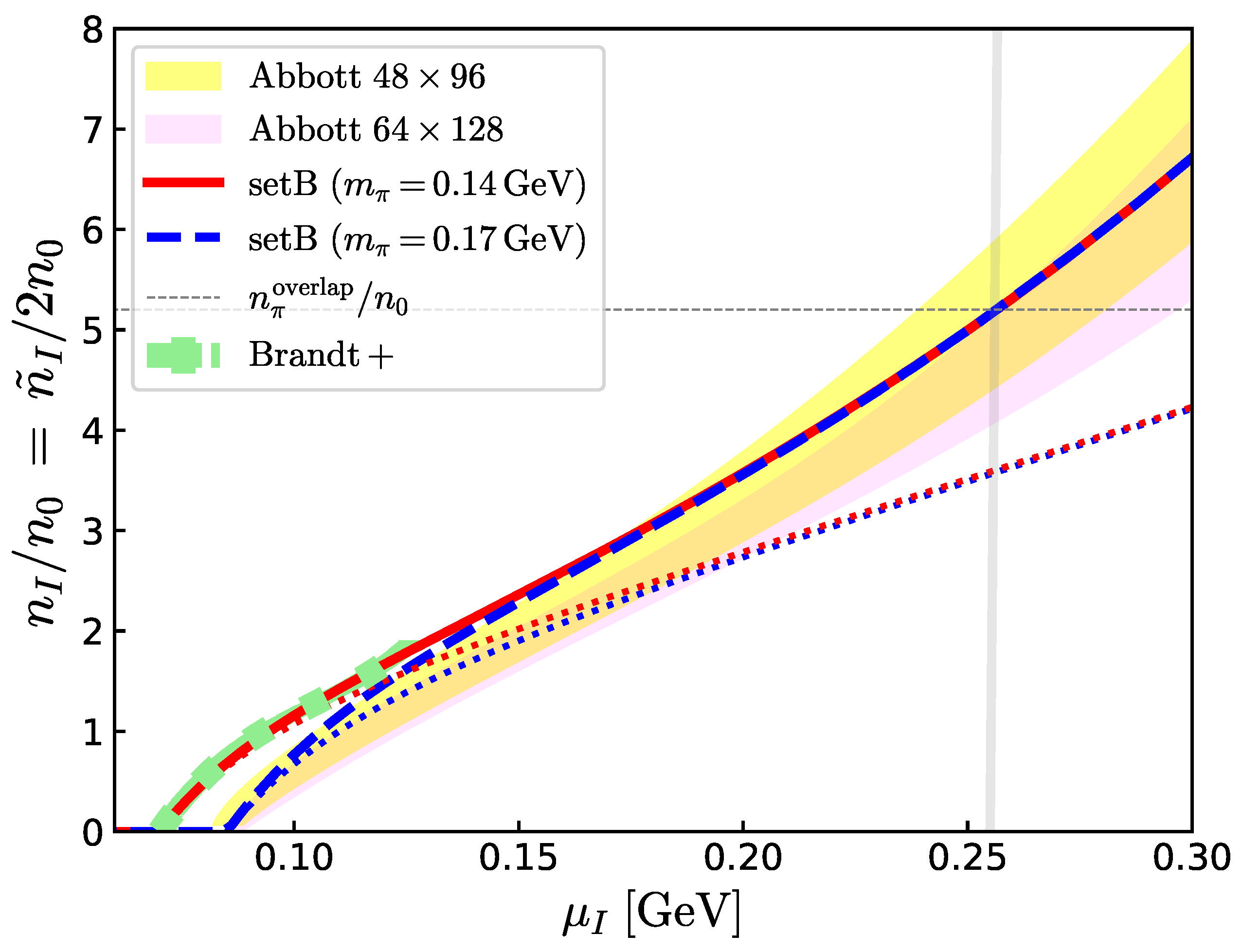
where we introduced as a unit frequently used in nuclear physics. The estimate utilizes the root-mean-square radius of a pion, fm, in vacuum [96,97,98,99]. The size of a pion is comparable to that of a nucleon; the nucleon charge root-mean-square radius is ≃0.84 fm, while its mass radius based on the gravitational form factor [100] is ≃0.55 fm [101], or the “valence quark core radius” is ≃0.5 fm [102]. The relation between and is shown in Figure 5. The overlap density is reached at a low chemical potential GeV.
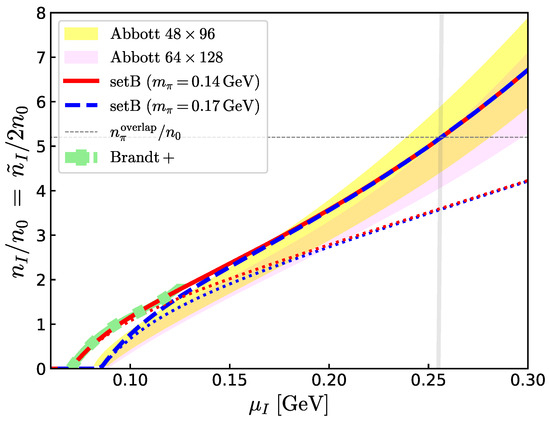
Figure 5.
The isospin density as a function of . The results of the quark–meson model for GeV and GeV are compared with the lattice data by Brandt et al. [22] and Abbott et al. [21], respectively. The overlap density which is achieved at GeV is shown as a guide. The red and blue dotted curves are from the leader order ChPT for and GeV, respectively.
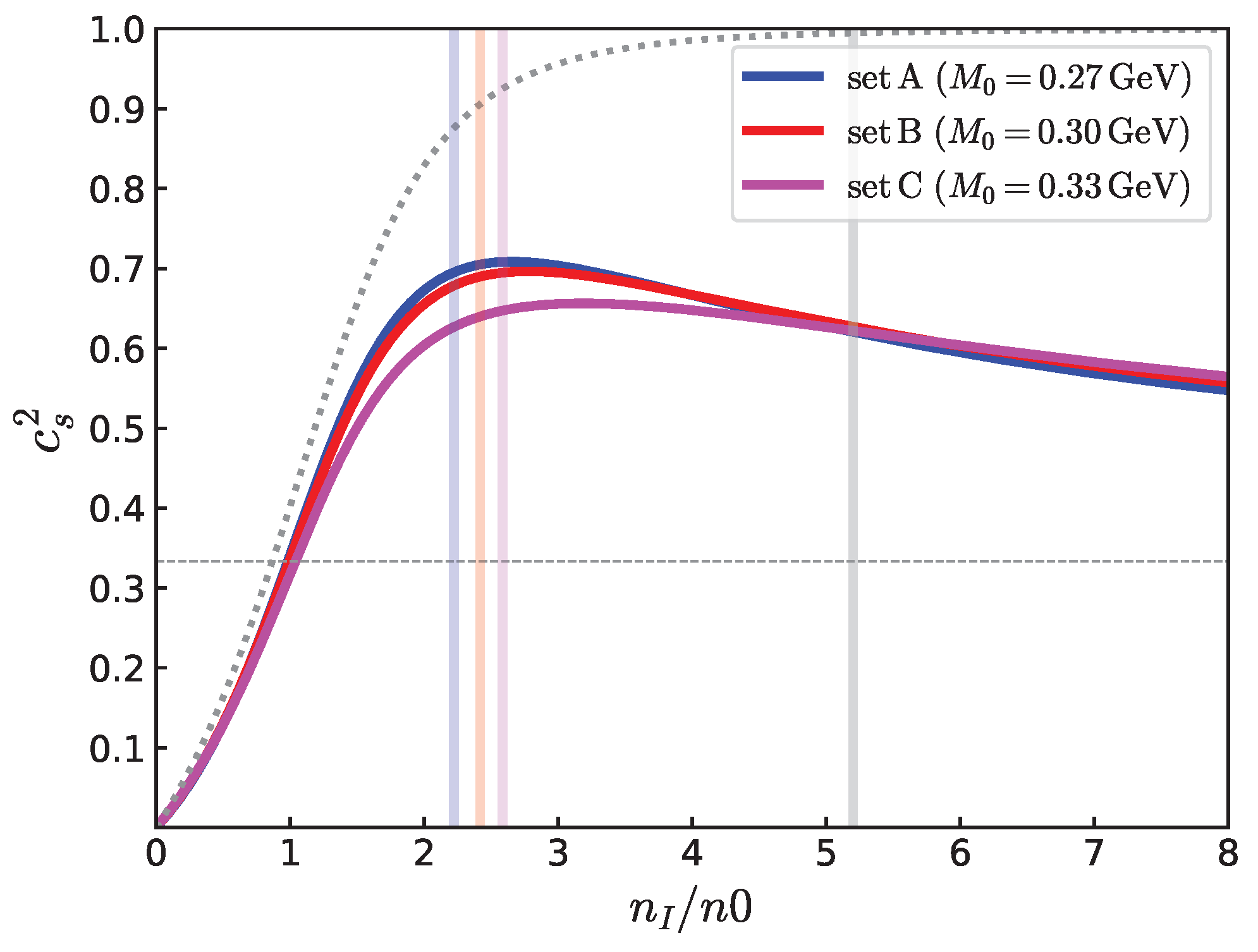
A useful quantity characterizing the rapid stiffening is the sound speed. A matter is called stiff (soft), i.e., P is large (small) at a given , and its variation is reflected in . Writing the susceptibility as , the sound speed is given by
The result of the quark–meson model is shown in Figure 6. The grows quickly just after the onset of the pion condensation, makes a peak before reaching , and slowly relaxes to the conformal limit . The result is compared with the lattice results of Brandt et al. [22] which have more focus on low density and those of Abbott et al. [21], which study the global structure for a wider range of . The results are consistent. Later, we delineate the behavior of at low and high densities from the microphysics viewpoint.

Figure 6.
The sound speed as a function of . The results of the quark–meson model for GeV and GeV are compared with the lattice data by Brandt et al. [22] and Abbott et al. [21], respectively. The conformal value and the ChPT results (dotted curves) are also shown as guides.
Recently, the trace anomaly of EOS has attracted attention [70,103,104,105]. It is one of hot topics for forthcoming electron ion collider experiments which will explore the nucleon structure in great detail. The trace anomaly normalized by [103],
is a useful measure for the deviation from the conformal limit. The result is shown in Figure 7. In the non-relativistic limit, , the . In the conformal limit, . When , there should be strong correlation effects. Below, we discuss the power corrections as candidates to drive to the negative value.
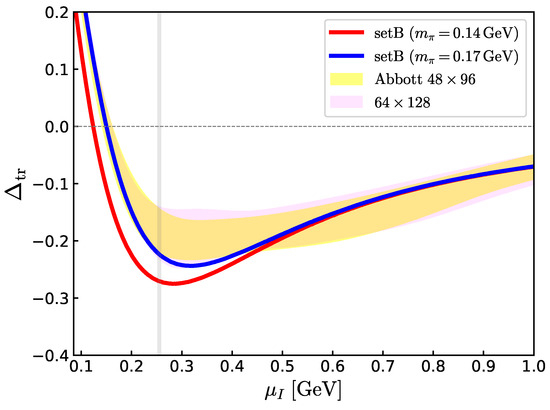
Figure 7.
The trace anomaly for the same setup as Figure 6. The conformal limit is .
As a guide for the low-density behaviors, it is useful to quote the results from the chiral perturbation theory (ChPT),
which leads to
At large density, the sound speed asymptotically approaches . Here, the scaling holds; the system is as if it is dominated by repulsive two-body forces.
7.1. High-Density Regime: Conformal Behaviors
Let us first consider the high-density regime in our model and the effective degrees of freedom. In the conformal limit with no mass scale other than , the dimensional analyses lead to
This relation is approximately satisfied in the high-density limit, where the kinetic energy dominates over mass and interaction energies. (Strictly speaking, there are self-energies that do not necessarily die out at high energy; in QCD, the asymptotic freedom guarantees the self-energies become weaker at high energy.)
The conformal limit by itself does not tell which degrees of freedom are relevant. Indeed, supposing , the conformal limit is obtained for whatever value of a; we have to specify a to tell which degrees of freedom dominate. As we saw, the tree-level pressure includes only mesonic degrees of freedom, and the one-loop pressure (dominated by quark degrees of freedom) scales as
where and we should substitute . In order for the former to reproduce the latter, we need , which is unacceptably large. For , the plays an essential role for the conformal scaling, and its magnitude is determined by details of interactions. In stark contrast, the conformal scaling of is determined by the number of quark degrees of freedom and is robust to the interactions.
7.2. High-Density Regime: Perturbative and Power Corrections
Next, we consider corrections to the conformal limit. The most frequently and rigorously discussed is the perturbative corrections at the weak coupling regime. The perturbative corrections modify the coefficient of term by adding series of , where is the renormalization scale to be set to the natural scale for a given problem. At large density, is the natural choice. The intrinsic scale of QCD, –300 MeV, appearing only through , shows up in the form of ∼. To the one-loop -function,
This reduces P, , and from the conformal value. At asymptotic density, the approaches the conformal limit from below.
In addition, in QCD, there are power corrections in powers of . This sort of term cannot be expressed by powers of series of ,
and hence is non-perturbative. For the momentum transfer of ∼, quarks are supposed to strongly interact.
Actually, whether such soft interactions are important or not depends on the presence of the color screening. If the screening is strong in the infrared, soft interactions are cut off. In the case of the pion-condensed phase, the condensate is a color-singlet and produces a gap for a quark–hole excitation. This suppresses the Debye and Meissner screening. Hence the electric and magnetic color interactions can be as strong as in the vacuum until the phase space factor ∼ overwhelms the suppression factor by the gap.
Adding the power corrections can change the qualitative behavior of [50,106,107,108,109,110]. In particular, the power corrections adding positive contributions to the pressure favors the trend opposite to those from perturbative corrections, and hence can be thought of a clear indicator for non-perturbative physics in the high-density domain. For a simple parametrization [50]
with being dimensionless constants and B included for normalization, we find
with which
varying between 1/3 and 1. In our quark–meson model , , and –0.3 GeV [50]. The power corrections of to the pressure occurs when
where the corrections increase as for GeV. The non-perturbative effects would survive at a relatively high density of GeV. These analyses, although still crude, indicate that the convergence of expansion at high density, which seems to be universal, may not be sufficient to judge the relevance/irrelevance of the non-perturbative physics.
The lattice results for EOS by Abbott et al. [21] to GeV ( defined in our work is a half of theirs) show qualitative deviation from perturbative QCD predictions. One of the plausible sources is the power corrections from the ∼ terms, where is non-analytic in the strong coupling constant . This indicates that non-perturbative physics can survive to a very high density, even where is reasonably small [50]. Recently, ref. [21] used the deviation between the perturbative EOS and lattice results to estimate the size of the BCS gap in the weak coupling region GeV [20]. The expression used for the EOS is [52]
The lattice results show that increases toward the low-density region. Meanwhile, the gap estimated by the weak coupling method is
which is sensitive to the choice of the running . The estimates with and cover the range consistent with those estimated from the lattice results and Equation (92). On the other hand, the dependence looks the opposite; the gap of Equation (93) decreases toward the low-density region. We conjecture that the physics of soft gluons and quarks enhances the gap and cures the discrepancy.
The power corrections also play important roles in the trace anomaly. In the parametrization Equation (88), the energy density is
so that
Remarkably, the power corrections yield negative contributions. Meanwhile, the normalization (bag) constant measures the energy difference between the conformal and non-perturbative vacuum and should be ∼ and positive. Perturbative corrections not written here also give positive contributions [50]. Hence, the negative trace anomaly can be regarded as a good indicator for the importance of the non-perturbative physics in dense matter.
7.3. Quark Saturation
Finally, we try to characterize EOS through quarks inside of pions. At sufficiently low density, quarks should show up only as constituents of pions. Pion condensation generates BCS gaps for quarks with which quark contributions can become finite even for ; see the structure of Equation (49). In the pion-condensed phase, the occupation probability of quark states can be written as
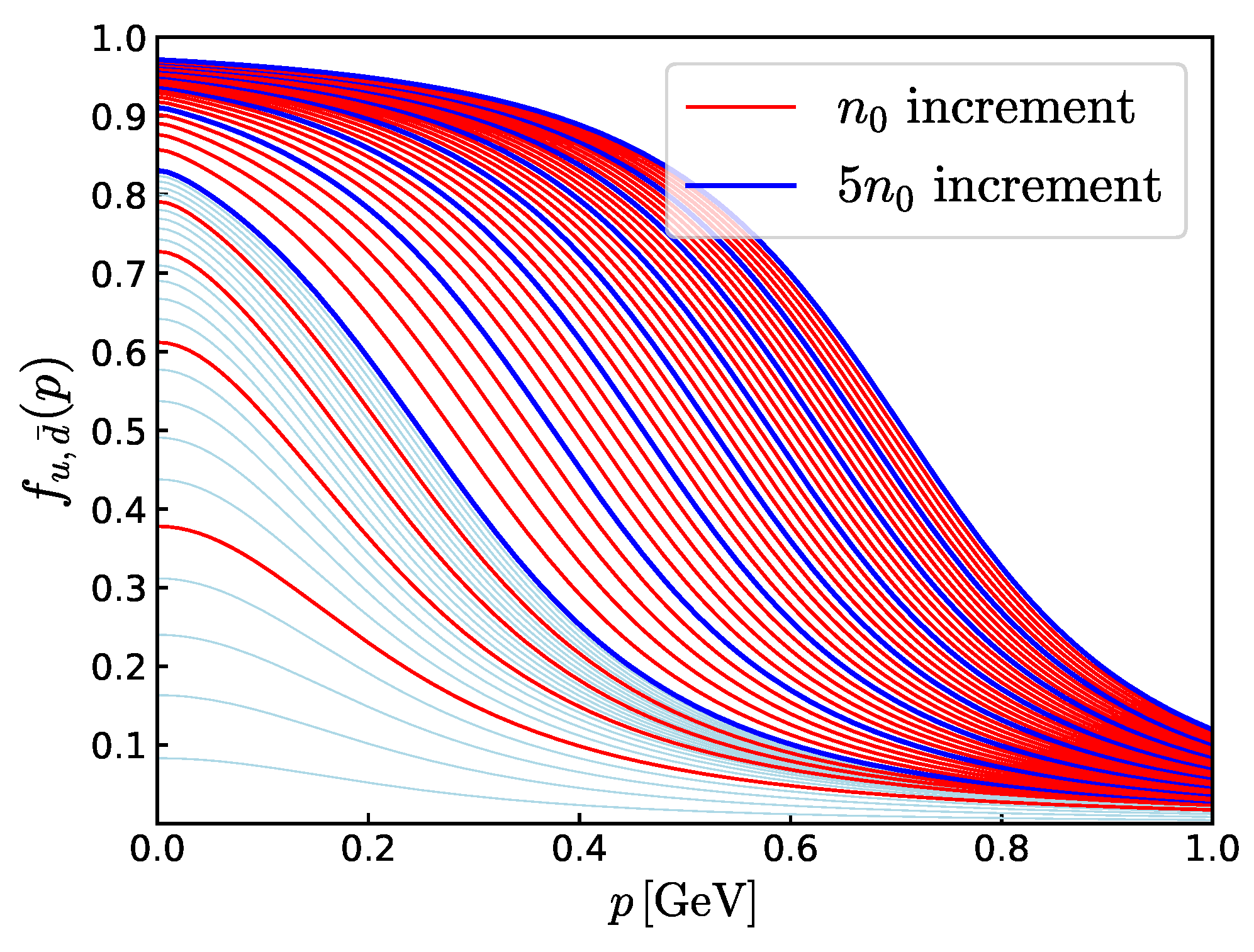
which becomes for . The behavior of as a function of p for various is shown in Figure 8 for the parameter set B.
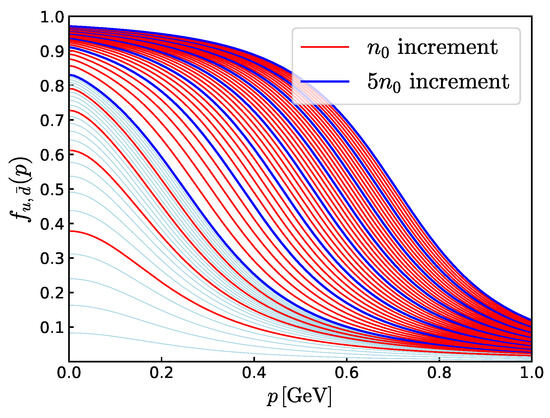
Figure 8.
The occupation probability as a function of p for the parameter set B in Table 1. Red curves represent curves for increments, while blue curves represent those for increments. To , we also show thin light blue curves for increments. The figure covers up to .
As quarks are bound to a compact object, the quark momentum distribution is broad in momentum. In particular, the occupation probability at is substantially smaller than 1. As the density increases, the magnitude of becomes larger. If we neglect the interactions and the structural changes of pions, we would find the scaling
where pions condense into the zero momentum state; each pion gives the same quark contribution and hence simply scale as ∼. Obviously, extrapolating this expression would violate the Pauli exclusion principle for quarks, for any p. We define the “(pseudo-)quark-saturation” density as
and use as the characteristic measure, where either pion interactions or quark saturation constraints become important.
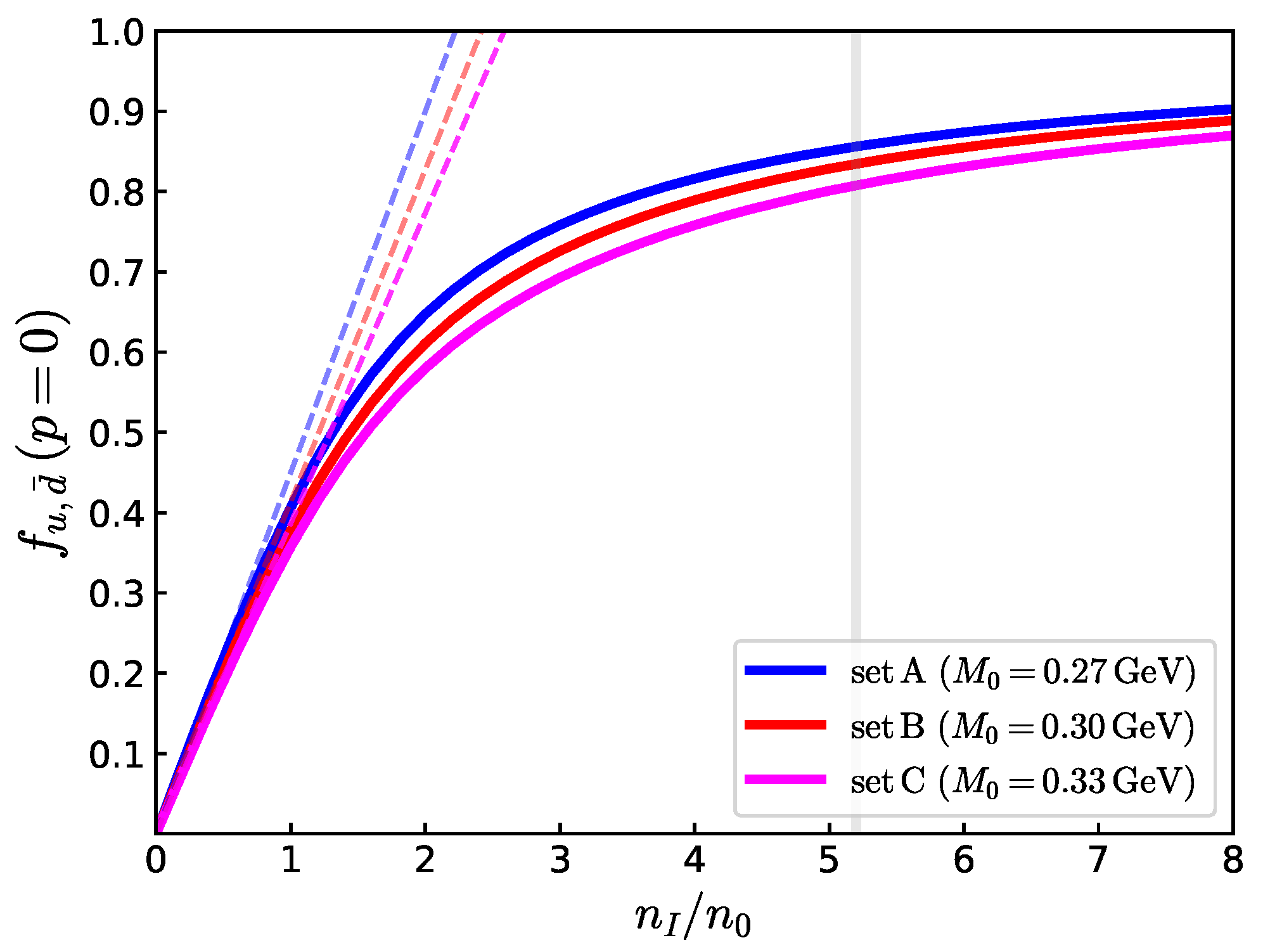
Figure 9 shows as a measure of the quark saturation. We also show the with dashed lines to examine . To examine how depends on the compactness, we vary to change the binding energy of a pion, , while maintaining the spectra of pseudo-scalar nonets within a reasonable range. Concretely, we compare the set A-C in Table 1. With a larger , the is larger, as the pion is spatially more compact and has a broader quark momentum distribution. For GeV, we find , respectively. These densities are substantially smaller than the .

Figure 9.
The occupation probability at zero momentum, at various . With the parameter sets A–C, we vary to change the “binding energies” for quarks to form pions; a larger has the stronger binding ∼ and leads to a more spatially compact state. The dashed curves are a linear extrapolation of the low-density behavior , which characterizes the for non-interacting pions. We also show as a guide.
In principle, by specifying and gaps at a given , one can reconstruct the corresponding EOS as
and hence, the evolution of (and for antiparticles) contains sufficient information to study the EOS.
Shown in Figure 10 are the behaviors of and at several densities and . For a greater , the gap is naturally larger. As guides, we display using several vertical lines. The general tendency is that, beyond , the gap becomes insensitive to , reflecting that the gap equations are dominated by soft gluon and soft quark contributions. The parameter set A-C leads to the gap of ∼– GeV around GeV. Hard gluon contributions, which are omitted in this work, should further enhance the size of the gap and introduce the stronger dependence, as it is sensitive to the phase space around the Fermi surface.
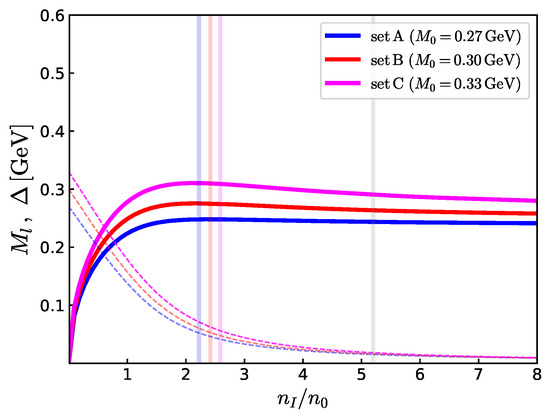
Finally, in Figure 11 we examine the sound speed for varying . For smaller , the rising of occurs at a lower density. This is natural, as pions are less compact objects. Increasing delays the rising of . The structure of a hadron, its valence core size, and quantum fluctuations around it [111] have direct relevance to the stiffening of matter. The relation between the baryon structure and nuclear matter has been discussed in refs. [112,113,114,115].
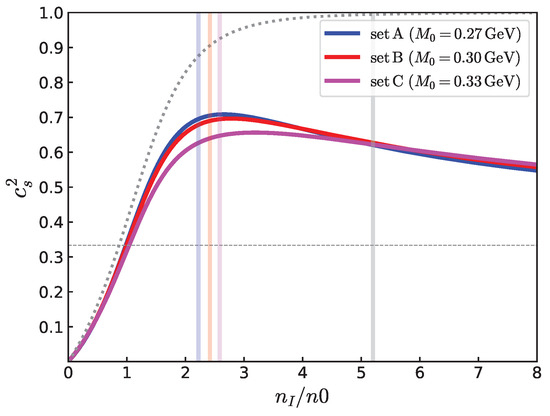
Figure 11.
The sound speed as a function of for the same parameter set as Figure 9. When pions are more spatially compact ( is larger), the repulsion among pions or quark saturation effects set in at larger densities.
8. Summary
In this paper, we study the EOS of isospin QCD and its relationship to the microphysics. We used a quark–meson model that interpolates the hadronic and quark sector at microscopic level. While it is difficult for such model studies to avoid model dependence to some degree, instead they can clarify the microphysics which is manifestly taken into account by studies based on the interpolation of ChPT and perturbative computations supplemented by astrophysical constraints. Among several effective models such as Nambu–Jona–Lasinio-type models, the quark–meson model is more useful, as it is renormalizable so that it can be used to cover from low to high densities, at least formally. Although the model does not cover the aspects of QCD caused by hard gluons, it captures some aspects of the physics caused by soft gluons in a parametrized manner.
One of the important issues in dense QCD is how non-perturbative effects relevant in hadron physics die out. Recent lattice results for EOS [21] to GeV ( defined in our work is a half of theirs) indicate the importance of the power corrections from the ∼ terms with being non-analytic in the QCD coupling constant , even at high density, where is reasonably small [50]. Concerning the size of the gap, there are several questions to be answered. The first question is at which density the evaluation of the gap is closed within the weak coupling regime; in the weak coupling estimates, we assume that hard momentum transfer processes dominate the gap equation because of the large phase space. This mechanism is sensitive to the density, and at low density, soft gluons should become important. How the transition between these two regimes occurs is directly related to the reliability of various estimates. The second question is to what extent the extrapolation from isospin QCD to QCD at finite baryon density can be valid. The mechanism for the emergence of the BCS gap is the diquark condensates in the color superconductivity. The typical estimate for the gap, mostly based on the weak coupling picture, is MeV; the coefficient of in the weak coupling expression of gap is larger than in the isospin QCD so that the gap is smaller. Analyses predicting a greater gap are mostly based on effective models constrained by hadron physics. It is important to fill the gap between the two regimes.
The quarks in pions seem important before reaching the overlap density for pions, , which is inferred from the size of a pion in vacuum. Even if we neglect the structural change of pions such as swelling or dissociation, we cannot go much beyond ∼ neglecting constraints from the quark Pauli blocking. The sound speed peak is also found around ∼. If the quark exchange interactions (or meson exchange) among pions effectively increase the size of pions, quark states at low momenta become saturated more quickly, inducing the Pauli blocking effects even earlier. The quark Pauli blocking near hadronic matter should also give insights on many-body forces among hadrons. In the context of neutron star EOS, it is typical to utilize two- and three-body repulsion to satisfy the two-solar mass constraints. But in such descriptions, there always remains a question of how to handle the convergence of many-body forces. We need an organizing principle. We guess that the quark saturation effects do the job.
Analyses in this paper left several important problems. In the methodology, we should improve the one-loop results. Another important topic is the meson spectra at finite density, including quark loops. We have computed the meson spectra in vacuum for the parameter fixing but have not performed analyses at finite density. The latter is necessary to answer to interesting questions such as how mesons dissociate and change the structure. How mesons or quarks in medium contribute to the entropy is also important to understand the color confinement at finite density, a question originally posed in the quarkyonic matter hypothesis [116]. The analyses toward this issue are in progress.
Author Contributions
Conceptualization, T.K., D.S. and R.C.; formal analysis, T.K. and R.C.; writing—original draft preparation, T.K.; writing—review and editing, T.K. and D.S. All authors have read and agreed to the published version of the manuscript.
Funding
T.K. was supported by JSPS KAKENHI Grant No. 23K03377 and No. 18H05407, and by the Graduate Program on Physics for the Universe (GPPU) at Tohoku university; D.S. by JSPS KAKENHI Grant No. 23H05439.
Data Availability Statement
The data is provided upon request.
Acknowledgments
We thank Bastian B. Brandt and Gergely Endrődi for kindly providing us with their lattice data in Ref. [22], and Ryan Abbott and his collaborators for their kindness of sending the lattice data in Ref. [21]. T.K. thanks Yuki Fujimoto and Larry McLerran for discussions on the quark saturation effects. The authors thank the Yukawa Institute for Theoretical Physics at Kyoto University and RIKEN iTHEMS. Discussions during the workshop (YITP-T-23-05) on “Condensed Matter Physics of QCD 2024” were useful to complete this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QC2D | two-color quantum chromodynamics |
| QCDI | isospin QCD |
| EOS | equations of state |
| –300 MeV | non-perturbative scale in QCD |
| nuclear saturation density | |
| ChPT | Chiral perturbation theory |
References
- Kogut, J.B.; Stephanov, M.A.; Toublan, D. On two color QCD with baryon chemical potential. Phys. Lett. B 1999, 464, 183–191. [Google Scholar] [CrossRef]
- Kogut, J.B.; Stephanov, M.A.; Toublan, D.; Verbaarschot, J.J.M.; Zhitnitsky, A. QCD-like theories at finite baryon density. Nucl. Phys. B 2000, 582, 477–513. [Google Scholar] [CrossRef]
- Iida, K.; Itou, E.; Murakami, K.; Suenaga, D. Lattice study on finite density QC2D towards zero temperature. arXiv 2024, arXiv:2405.20566. [Google Scholar]
- Iida, K.; Itou, E.; Lee, T.G. Two-colour QCD phases and the topology at low temperature and high density. J. High Energy Phys. 2020, 1, 181. [Google Scholar] [CrossRef]
- Iida, K.; Itou, E.; Lee, T.G. Relative scale setting for two-color QCD with Nf = 2 Wilson fermions. Prog. Theor. Exp. Phys. 2021, 2021, 013B05. [Google Scholar] [CrossRef]
- Boz, T.; Giudice, P.; Hands, S.; Skullerud, J.I. Dense two-color QCD towards continuum and chiral limits. Phys. Rev. D 2020, 101, 074506. [Google Scholar] [CrossRef]
- Boz, T.; Cotter, S.; Fister, L.; Mehta, D.; Skullerud, J.I. Phase transitions and gluodynamics in 2-colour matter at high density. Eur. Phys. J. A 2013, 49, 87. [Google Scholar] [CrossRef]
- Cotter, S.; Giudice, P.; Hands, S.; Skullerud, J.I. Towards the phase diagram of dense two-color matter. Phys. Rev. D 2013, 87, 034507. [Google Scholar] [CrossRef]
- Hands, S.; Kenny, P.; Kim, S.; Skullerud, J.I. Lattice Study of Dense Matter with Two Colors and Four Flavors. Eur. Phys. J. A 2011, 47, 60. [Google Scholar] [CrossRef][Green Version]
- Astrakhantsev, N.; Braguta, V.; Ilgenfritz, E.; Kotov, A.; Nikolaev, A. Lattice study of thermodynamic properties of dense QC2D. Phys. Rev. D 2020, 102, 074507. [Google Scholar] [CrossRef]
- Bornyakov, V.G.; Braguta, V.V.; Nikolaev, A.A.; Rogalyov, R.N. Effects of Dense Quark Matter on Gluon Propagators in Lattice QC2D. Phys. Rev. D 2020, 102, 114511. [Google Scholar] [CrossRef]
- Muroya, S.; Nakamura, A.; Nonaka, C. Behavior of hadrons at finite density: Lattice study of color SU(2) QCD. Phys. Lett. B 2003, 551, 305–310. [Google Scholar] [CrossRef]
- Suenaga, D.; Murakami, K.; Itou, E.; Iida, K. Probing the hadron mass spectrum in dense two-color QCD with the linear sigma model. Phys. Rev. D 2023, 107, 054001. [Google Scholar] [CrossRef]
- Suenaga, D.; Murakami, K.; Itou, E.; Iida, K. Mass spectrum of spin-one hadrons in dense two-color QCD: Novel predictions by extended linear sigma model. arXiv 2023, arXiv:2312.17017. [Google Scholar] [CrossRef]
- Kawaguchi, M.; Suenaga, D. Sound velocity peak induced by the chiral partner in dense two-color QCD. arXiv 2024, arXiv:2402.00430. [Google Scholar] [CrossRef]
- Sun, G.f.; He, L.; Zhuang, P. BEC-BCS crossover in the Nambu-Jona-Lasinio model of QCD. Phys. Rev. D 2007, 75, 096004. [Google Scholar] [CrossRef]
- Brauner, T.; Fukushima, K.; Hidaka, Y. Two-color quark matter: U(1)(A) restoration, superfluidity, and quarkyonic phase. Phys. Rev. D 2009, 80, 074035, Erratum in Phys. Rev. D 2010, 81, 119904. [Google Scholar] [CrossRef]
- Strodthoff, N.; von Smekal, L. Polyakov-Quark-Meson-Diquark Model for two-color QCD. Phys. Lett. B 2014, 731, 350–357. [Google Scholar] [CrossRef]
- Strodthoff, N.; Schaefer, B.J.; von Smekal, L. Quark-meson-diquark model for two-color QCD. Phys. Rev. D 2012, 85, 074007. [Google Scholar] [CrossRef]
- Abbott, R.; Detmold, W.; Illa, M.; Parreño, A.; Perry, R.J.; Romero-López, F.; Shanahan, P.E.; Wagman, M.L. QCD constraints on isospin-dense matter and the nuclear equation of state. arXiv 2024, arXiv:2406.09273. [Google Scholar]
- Abbott, R.; Detmold, W.; Romero-López, F.; Davoudi, Z.; Illa, M.; Parreño, A.; Perry, R.J.; Shanahan, P.E.; Wagman, M.L. Lattice quantum chromodynamics at large isospin density: 6144 pions in a box. arXiv 2023, arXiv:2307.15014. [Google Scholar]
- Brandt, B.B.; Cuteri, F.; Endrodi, G. Equation of state and speed of sound of isospin-asymmetric QCD on the lattice. J. High Energy Phys. 2023, 7, 55. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. QCD at finite isospin density. Phys. Rev. Lett. 2001, 86, 592–595. [Google Scholar] [CrossRef]
- Son, D.T.; Stephanov, M.A. QCD at finite isospin density: From pion to quark-antiquark condensation. Phys. Atom. Nucl. 2001, 64, 834–842. [Google Scholar] [CrossRef]
- Splittorff, K.; Son, D.T.; Stephanov, M.A. QCD-like theories at finite baryon and isospin density. Phys. Rev. D 2001, 64, 016003. [Google Scholar] [CrossRef]
- Gómez Nicola, A.; Vioque-Rodríguez, A. Effective Lagrangian at nonzero isospin chemical potential. Phys. Rev. D 2022, 106, 114017. [Google Scholar] [CrossRef]
- Lu, Z.Y.; Xia, C.J.; Ruggieri, M. Thermodynamics and susceptibilities of isospin imbalanced QCD matter. Eur. Phys. J. C 2020, 80, 46. [Google Scholar] [CrossRef]
- Fraga, E.S.; Palhares, L.F.; Villavicencio, C. Quark mass and isospin dependence of the deconfining critical temperature. Phys. Rev. D 2009, 79, 014021. [Google Scholar] [CrossRef]
- Stiele, R.; Fraga, E.S.; Schaffner-Bielich, J. Thermodynamics of (2+1)-flavor strongly interacting matter at nonzero isospin. Phys. Lett. B 2014, 729, 72–78. [Google Scholar] [CrossRef]
- Graf, T.; Schaffner-Bielich, J.; Fraga, E.S. Perturbative thermodynamics at nonzero isospin density for cold QCD. Phys. Rev. D 2016, 93, 085030. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G.; Fraga, E.S.; Hippert, M.; Schaffner-Bielich, J.; Schmalzbauer, S. New class of compact stars: Pion stars. Phys. Rev. D 2018, 98, 094510. [Google Scholar] [CrossRef]
- Fukushima, K.; Hatsuda, T. The phase diagram of dense QCD. Rep. Prog. Phys. 2011, 74, 014001. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Kojo, T. QCD equations of state and speed of sound in neutron stars. AAPPS Bull. 2021, 31, 11. [Google Scholar] [CrossRef]
- Vuorinen, A. Particle-theory Input for Neutron-star Physics. Acta Phys. Polon. B 2024, 55, 4-A4. [Google Scholar] [CrossRef]
- Drischler, C.; Han, S.; Lattimer, J.M.; Prakash, M.; Reddy, S.; Zhao, T. Limiting masses and radii of neutron stars and their implications. Phys. Rev. C 2021, 103, 045808. [Google Scholar] [CrossRef]
- Han, M.Z.; Huang, Y.J.; Tang, S.P.; Fan, Y.Z. Plausible presence of new state in neutron stars with masses above 0.98MTOV. Sci. Bull. 2023, 68, 913–919. [Google Scholar] [CrossRef]
- Kojo, T.; Baym, G.; Hatsuda, T. Implications of NICER for Neutron Star Matter: The QHC21 Equation of State. Astrophys. J. 2022, 934, 46. [Google Scholar] [CrossRef]
- Huang, Y.J.; Baiotti, L.; Kojo, T.; Takami, K.; Sotani, H.; Togashi, H.; Hatsuda, T.; Nagataki, S.; Fan, Y.Z. Merger and Postmerger of Binary Neutron Stars with a Quark-Hadron Crossover Equation of State. Phys. Rev. Lett. 2022, 129, 181101. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, Y.; Fukushima, K.; Hotokezaka, K.; Kyutoku, K. Gravitational Wave Signal for Quark Matter with Realistic Phase Transition. Phys. Rev. Lett. 2023, 130, 091404. [Google Scholar] [CrossRef] [PubMed]
- Kedia, A.; Kim, H.I.; Suh, I.S.; Mathews, G.J. Binary neutron star mergers as a probe of quark-hadron crossover equations of state. Phys. Rev. D 2022, 106, 103027. [Google Scholar] [CrossRef]
- Bauswein, A.; Bastian, N.U.F.; Blaschke, D.B.; Chatziioannou, K.; Clark, J.A.; Fischer, T.; Oertel, M. Identifying a first-order phase transition in neutron star mergers through gravitational waves. Phys. Rev. Lett. 2019, 122, 061102. [Google Scholar] [CrossRef] [PubMed]
- McLerran, L.; Reddy, S. Quarkyonic Matter and Neutron Stars. Phys. Rev. Lett. 2019, 122, 122701. [Google Scholar] [CrossRef] [PubMed]
- Jeong, K.S.; McLerran, L.; Sen, S. Dynamically generated momentum space shell structure of quarkyonic matter via an excluded volume model. Phys. Rev. C 2020, 101, 035201. [Google Scholar] [CrossRef]
- Kojo, T. Stiffening of matter in quark-hadron continuity. Phys. Rev. D 2021, 104, 074005. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Kojo, T.; McLerran, L.D. Momentum Shell in Quarkyonic Matter from Explicit Duality: A Dual Model for Cold, Dense QCD. Phys. Rev. Lett. 2024, 132, 112701. [Google Scholar] [CrossRef]
- Hayata, T.; Hidaka, Y.; Nishimura, K. Dense QCD2 with matrix product states. arXiv 2023, arXiv:2311.11643. [Google Scholar] [CrossRef]
- Mannarelli, M. Meson condensation. Particles 2019, 2, 411–443. [Google Scholar] [CrossRef]
- Chiba, R.; Kojo, T. Sound velocity peak and conformality in isospin QCD. Phys. Rev. D 2024, 109, 076006. [Google Scholar] [CrossRef]
- Chiba, R.; Kojo, T.; Suenaga, D. Thermal effects on sound velocity peak and conformality in isospin QCD. arXiv 2024, arXiv:2403.02538. [Google Scholar]
- Fujimoto, Y. Enhanced contribution of the pairing gap to the QCD equation of state at large isospin chemical potential. Phys. Rev. D 2024, 109, 054035. [Google Scholar] [CrossRef]
- Cohen, T.D. QCD inequalities for the nucleon mass and the free energy of baryonic matter. Phys. Rev. Lett. 2003, 91, 032002. [Google Scholar] [CrossRef]
- Navarrete, P.; Paatelainen, R.; Seppänen, K. Perturbative QCD meets phase quenching: The pressure of cold Quark Matter. arXiv 2024, arXiv:2403.02180. [Google Scholar]
- Fujimoto, Y.; Reddy, S. Bounds on the equation of state from QCD inequalities and lattice QCD. Phys. Rev. D 2024, 109, 014020. [Google Scholar] [CrossRef]
- Moore, G.D.; Gorda, T. Bounding the QCD Equation of State with the Lattice. J. High Energy Phys. 2023, 12, 133. [Google Scholar] [CrossRef]
- Adhikari, P.; Andersen, J.O.; Kneschke, P. On-shell parameter fixing in the quark-meson model. Phys. Rev. D 2017, 95, 036017. [Google Scholar] [CrossRef]
- Ayala, A.; Bandyopadhyay, A.; Farias, R.L.S.; Hernández, L.A.; Hernández, J.L. QCD equation of state at finite isospin density from the linear sigma model with quarks: The cold case. arXiv 2023, arXiv:2301.13633. [Google Scholar] [CrossRef]
- Gao, B.; Minamikawa, T.; Kojo, T.; Harada, M. Impacts of the U(1)A anomaly on nuclear and neutron star equation of state based on a parity doublet model. Phys. Rev. C 2022, 106, 065205. [Google Scholar] [CrossRef]
- Minamikawa, T.; Gao, B.; Kojo, T.; Harada, M. Chiral restoration of nucleons in neutron star matter: Studies based on a parity doublet model. arXiv 2023, arXiv:2302.00825. [Google Scholar]
- Hatsuda, T.; Tachibana, M.; Yamamoto, N.; Baym, G. New critical point induced by the axial anomaly in dense QCD. Phys. Rev. Lett. 2006, 97, 122001. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, N.; Tachibana, M.; Hatsuda, T.; Baym, G. Phase structure, collective modes, and the axial anomaly in dense QCD. Phys. Rev. D 2007, 76, 074001. [Google Scholar] [CrossRef]
- Hatsuda, T.; Tachibana, M.; Yamamoto, N. Spectral Continuity in Dense QCD. Phys. Rev. D 2008, 78, 011501. [Google Scholar] [CrossRef]
- Zhang, Z.; Fukushima, K.; Kunihiro, T. Number of the QCD critical points with neutral color superconductivity. Phys. Rev. D 2009, 79, 014004. [Google Scholar] [CrossRef]
- Schäfer, T.; Wilczek, F. Continuity of quark and hadron matter. Phys. Rev. Lett. 1999, 82, 3956–3959. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hadron-Quark Crossover and Massive Hybrid Stars with Strangeness. Astrophys. J. 2013, 764, 12. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hadron–quark crossover and massive hybrid stars. Prog. Theor. Exp. Phys. 2013, 2013, 073D01. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hyperon Puzzle, Hadron-Quark Crossover and Massive Neutron Stars. Eur. Phys. J. A 2016, 52, 65. [Google Scholar] [CrossRef]
- Tajima, H.; Tsutsui, S.; Doi, T.M.; Iida, K. Density-Induced Hadron–Quark Crossover via the Formation of Cooper Triples. Symmetry 2023, 15, 333. [Google Scholar] [CrossRef]
- Ma, Y.L.; Rho, M. Towards the hadron–quark continuity via a topology change in compact stars. Prog. Part. Nucl. Phys. 2020, 113, 103791. [Google Scholar] [CrossRef]
- ’t Hooft, G. A Planar Diagram Theory for Strong Interactions. Nucl. Phys. B 1974, 72, 461. [Google Scholar] [CrossRef]
- Witten, E. Baryons in the 1/n Expansion. Nucl. Phys. B 1979, 160, 57–115. [Google Scholar] [CrossRef]
- Nishimura, T.; Kitazawa, M.; Kunihiro, T. Anomalous enhancement of dilepton production as a precursor of color superconductivity. Prog. Theor. Exp. Phys. 2022, 2022, 093D02. [Google Scholar] [CrossRef]
- Kitazawa, M.; Koide, T.; Kunihiro, T.; Nemoto, Y. Pre-critical phenomena of two-flavor color superconductivity in heated quark matter: Diquark-pair fluctuations and non-Fermi liquid behavior. Prog. Theor. Phys. 2005, 114, 117–155. [Google Scholar] [CrossRef]
- Kitazawa, M.; Koide, T.; Kunihiro, T.; Nemoto, Y. Precursor of color superconductivity in hot quark matter. Phys. Rev. D 2002, 65, 091504. [Google Scholar] [CrossRef]
- Blaschke, D.; Buballa, M.; Dubinin, A.; Roepke, G.; Zablocki, D. Generalized Beth–Uhlenbeck approach to mesons and diquarks in hot, dense quark matter. Ann. Phys. 2014, 348, 228–255. [Google Scholar] [CrossRef]
- Boz, T.; Hajizadeh, O.; Maas, A.; Skullerud, J.I. Finite-density gauge correlation functions in QC2D. Phys. Rev. D 2019, 99, 074514. [Google Scholar] [CrossRef]
- Kojo, T.; Baym, G. Color screening in cold quark matter. Phys. Rev. D 2014, 89, 125008. [Google Scholar] [CrossRef]
- Suenaga, D.; Kojo, T. Gluon propagator in two-color dense QCD: Massive Yang-Mills approach at one-loop. Phys. Rev. D 2019, 100, 076017. [Google Scholar] [CrossRef]
- Kojo, T.; Suenaga, D. Thermal quarks and gluon propagators in two-color dense QCD. Phys. Rev. D 2021, 103, 094008. [Google Scholar] [CrossRef]
- Contant, R.; Huber, M.Q. Dense two-color QCD from Dyson-Schwinger equations. Phys. Rev. D 2020, 101, 014016. [Google Scholar] [CrossRef]
- Kojo, T.; Hidaka, Y.; McLerran, L.; Pisarski, R.D. Quarkyonic Chiral Spirals. Nucl. Phys. A 2010, 843, 37–58. [Google Scholar] [CrossRef]
- Kojo, T.; Pisarski, R.D.; Tsvelik, A.M. Covering the Fermi Surface with Patches of Quarkyonic Chiral Spirals. Phys. Rev. D 2010, 82, 074015. [Google Scholar] [CrossRef]
- Kojo, T.; Hidaka, Y.; Fukushima, K.; McLerran, L.D.; Pisarski, R.D. Interweaving Chiral Spirals. Nucl. Phys. A 2012, 875, 94–138. [Google Scholar] [CrossRef]
- Kojo, T.; Su, N. The quark mass gap in a magnetic field. Phys. Lett. B 2013, 720, 192–197. [Google Scholar] [CrossRef]
- Kojo, T.; Su, N. The quark mass gap in strong magnetic fields. Nucl. Phys. A 2014, 931, 763–768. [Google Scholar] [CrossRef]
- Hattori, K.; Kojo, T.; Su, N. Mesons in strong magnetic fields: (I) General analyses. Nucl. Phys. A 2016, 951, 1–30. [Google Scholar] [CrossRef]
- Novikov, V.A.; Okun, L.B.; Shifman, M.A.; Vainshtein, A.I.; Voloshin, M.B.; Zakharov, V.I. Charmonium and Gluons: Basic Experimental Facts and Theoretical Introduction. Phys. Rep. 1978, 41, 1–133. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and Resonance Physics. Theoretical Foundations. Nucl. Phys. B 1979, 147, 385–447. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and Resonance Physics: Applications. Nucl. Phys. B 1979, 147, 448–518. [Google Scholar] [CrossRef]
- Lee, T.D.; Yang, C.N. Charge Conjugation, a New Quantum Number G, and Selection Rules Concerning a Nucleon Anti-nucleon System. Nuovo Cim. 1956, 10, 749–753. [Google Scholar] [CrossRef]
- Andersen, J.O.; Adhikari, P.; Kneschke, P. Pion condensation and QCD phase diagram at finite isospin density. Proc. Sci. 2019, 336, 197. [Google Scholar] [CrossRef]
- Coleman, S.R.; Weinberg, E.J. Radiative Corrections as the Origin of Spontaneous Symmetry Breaking. Phys. Rev. D 1973, 7, 1888–1910. [Google Scholar] [CrossRef]
- Duarte, D.C.; Hernandez-Ortiz, S.; Jeong, K.S.; McLerran, L.D. Quarkyonic effective field theory, quark-nucleon duality, and ghosts. Phys. Rev. D 2021, 104, L091901. [Google Scholar] [CrossRef]
- Hatsuda, T.; Kunihiro, T. QCD phenomenology based on a chiral effective Lagrangian. Phys. Rep. 1994, 247, 221–367. [Google Scholar] [CrossRef]
- Tanabashi, M. et al. [Particle Data Group] Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Ananthanarayan, B.; Caprini, I.; Das, D. Electromagnetic charge radius of the pion at high precision. Phys. Rev. Lett. 2017, 119, 132002. [Google Scholar] [CrossRef]
- Koponen, J.; Bursa, F.; Davies, C.T.H.; Dowdall, R.J.; Lepage, G.P. Size of the pion from full lattice QCD with physical u, d, s and c quarks. Phys. Rev. D 2016, 93, 054503. [Google Scholar] [CrossRef]
- Wang, G.; Liang, J.; Draper, T.; Liu, K.F.; Yang, Y.B. Lattice Calculation of Pion Form Factor with Overlap Fermions. Phys. Rev. D 2021, 104, 074502. [Google Scholar] [CrossRef]
- Polyakov, M.V. Generalized parton distributions and strong forces inside nucleons and nuclei. Phys. Lett. B 2003, 555, 57–62. [Google Scholar] [CrossRef]
- Kharzeev, D.E. Mass radius of the proton. Phys. Rev. D 2021, 104, 054015. [Google Scholar] [CrossRef]
- Kaiser, N.; Weise, W. Sizes of the Nucleon. arXiv 2024, arXiv:2404.11292. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Fukushima, K.; McLerran, L.D.; Praszalowicz, M. Trace Anomaly as Signature of Conformality in Neutron Stars. Phys. Rev. Lett. 2022, 129, 252702. [Google Scholar] [CrossRef]
- Marczenko, M.; McLerran, L.; Redlich, K.; Sasaki, C. Reaching percolation and conformal limits in neutron stars. arXiv 2022, arXiv:2207.13059. [Google Scholar] [CrossRef]
- Tajima, H.; Iida, K.; Liang, H. Nonrelativistic trace anomaly and equation of state in dense fermionic matter. Phys. Rev. C 2024, 109, 055203. [Google Scholar] [CrossRef]
- Kojo, T.; Powell, P.D.; Song, Y.; Baym, G. Phenomenological QCD equation of state for massive neutron stars. Phys. Rev. D 2015, 91, 045003. [Google Scholar] [CrossRef]
- Kojo, T.; Suenaga, D. Peaks of sound velocity in two color dense QCD: Quark saturation effects and semishort range correlations. Phys. Rev. D 2022, 105, 076001. [Google Scholar] [CrossRef]
- Geißel, A.; Gorda, T.; Braun, J. Pressure and speed of sound in two-flavor color-superconducting quark matter at next-to-leading order. arXiv 2024, arXiv:2403.18010. [Google Scholar]
- Braun, J.; Geißel, A.; Schallmo, B. Speed of sound in dense strong-interaction matter. SciPost Phys. Core 2024, 7, 015. [Google Scholar] [CrossRef]
- Leonhardt, M.; Pospiech, M.; Schallmo, B.; Braun, J.; Drischler, C.; Hebeler, K.; Schwenk, A. Symmetric nuclear matter from the strong interaction. Phys. Rev. Lett. 2020, 125, 142502. [Google Scholar] [CrossRef]
- Fukushima, K.; Kojo, T.; Weise, W. Hard-core deconfinement and soft-surface delocalization from nuclear to quark matter. Phys. Rev. D 2020, 102, 096017. [Google Scholar] [CrossRef]
- Saito, K.; Tsushima, K.; Thomas, A.W. Nucleon and hadron structure changes in the nuclear medium and impact on observables. Prog. Part. Nucl. Phys. 2007, 58, 1–167. [Google Scholar] [CrossRef]
- Geesaman, D.F.; Saito, K.; Thomas, A.W. The nuclear EMC effect. Ann. Rev. Nucl. Part. Sci. 1995, 45, 337–390. [Google Scholar] [CrossRef]
- Koch, V.; McLerran, L.; Miller, G.A.; Vovchenko, V. Might Normal Nuclear Matter be Quarkyonic? arXiv 2024, arXiv:2403.15375. [Google Scholar]
- McLerran, L.; Miller, G.A. The Quark Pauli Principle and the Transmutation of Nuclear Matter. arXiv 2024, arXiv:2405.11074. [Google Scholar]
- McLerran, L.; Pisarski, R.D. Phases of cold, dense quarks at large N(c). Nucl. Phys. A 2007, 796, 83–100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).