Wormhole Restrictions from Quantum Energy Inequalities
Abstract
1. Introduction
Conventions
2. Pointwise Energy Conditions
2.1. Brief Overview
2.2. Example: The Klein–Gordon Field
3. Quantum Energy Inequalities
3.1. Algebraic Quantization
- In the algebraic approach, the fields are smeared with a smooth function and are elements of an algebra obeying properties that include the field equation and canonical commutation relations.
- The states are linear maps from the algebra to the field of complex numbers, while the two-point function is a bilinear map between the space of two functions and the field of complex numbers.
- In quantum field theory, products of fields—for example, the two-point function—are divergent when one tries to naively compute their expectation values. But an important aspect of the process is the choice of states: Hadamard states have a known singularity structure. Thus, it is sufficient to subtract these singularities from the two-point function to the correct order. The Hadamard parametrix is a bidistribution that includes all the singularities up to order k.
- The renormalization proceeds using point spliting: the classical stress tensor is written as an operator acting on two different points . After we have subtracted the singularities, we act on the two-point function with the point split operator , and we have a smooth object at coincident limit:
- This, up to renormalization ambiguities, corresponds to the —the object used instead of the classical stress tensor in QEIs.
- LinearityThe map is complex linear;
- Hermiticity;
- Field Equation;
- Canonical Commutation Relations.
3.2. Overview of Quantum Energy Inequalities
3.3. Null Quantum Energy Inequalities
3.4. ANEC
- Violations of the ANEC on chronal null geodesics.
- Violations of the non-self consistent ANEC, meaning that it does not satisfy the (classical or semiclassical) Einstein equation.
- Violations of the order of Planck scale.
4. Wormhole Basics
4.1. Description and History
4.2. Violations of Energy Conditions
5. Restrictions to ‘Short’ Wormholes
5.1. A Wormhole as a Time Machine
5.2. Timelike QEI Constraints
5.3. Causality Violations and the Achronal ANEC
6. Restrictions to Long Wormholes
6.1. The Wormhole of Maldacena, Milekhin, and Popov
6.2. SNEC
6.3. DSNEC
6.4. Two-Dimensional Bound
7. Discussion
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | A ‘short’ wormhole can be modified to act as a time machine, as discussed in Section 5.1. |
| 2 | In the sense that only terms of first order in curvature were considered. |
| 3 | This argument is possible to be extendable to asymptotically AdS manifolds, but this point requires further consideration. |
| 4 | The expression differs slightly from Ref. [48] due to the different definition of the Gaussian. |
References
- Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett. 1965, 14, 57–59. [Google Scholar] [CrossRef]
- Hawking, S.W. The Occurrence of singularities in cosmology. Proc. R. Soc. Lond. 1966, A294, 511–521. [Google Scholar] [CrossRef]
- Epstein, H.; Glaser, V.; Jaffe, A. Nonpositivity of energy density in Quantized field theories. Nuovo C. 1965, 36, 1016. [Google Scholar] [CrossRef]
- Ford, L.H. Quantum Coherence Effects and the Second Law of Thermodynamics. Proc. R. Soc. Lond. 1978, A364, 227–236. [Google Scholar] [CrossRef]
- Fewster, C.J.; Roman, T.A. Null energy conditions in quantum field theory. Phys. Rev. D 2003, D67, 044003, Erratum in Phys. Rev. D 2009, D80, 069903. [Google Scholar] [CrossRef]
- Graham, N.; Olum, K.D. Achronal averaged null energy condition. Phys. Rev. D 2007, 76, 064001. [Google Scholar] [CrossRef]
- Freivogel, B.; Krommydas, D. The Smeared Null Energy Condition. J. High Energy Phys. 2018, 12, 067. [Google Scholar] [CrossRef]
- Fliss, J.R.; Freivogel, B.; Kontou, E.A. The double smeared null energy condition. SciPost Phys. 2023, 14, 024. [Google Scholar] [CrossRef]
- Maldacena, J.; Milekhin, A.; Popov, F. Traversable wormholes in four dimensions. Class. Quantum Gravity 2023, 40, 155016. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.; Wheeler, J. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Curiel, E. A Primer on Energy Conditions. Einstein Stud. 2017, 13, 43–104. [Google Scholar] [CrossRef]
- Barcelo, C.; Visser, M. Twilight for the energy conditions? Int. J. Mod. Phys. D 2002, 11, 1553–1560. [Google Scholar] [CrossRef]
- Brown, P.J.; Fewster, C.J.; Kontou, E.A. A singularity theorem for Einstein–Klein–Gordon theory. Gen. Relativ. Gravit. 2018, 50, 121. [Google Scholar] [CrossRef]
- Pirani, F.A.E. On the Physical significance of the Riemann tensor. Acta Phys. Polon. 1956, 15, 389–405. [Google Scholar] [CrossRef]
- Hawking, S.W. Black holes in general relativity. Commun. Math. Phys. 1972, 25, 152–166. [Google Scholar] [CrossRef]
- Barcelo, C.; Visser, M. Scalar fields, energy conditions, and traversable wormholes. Class. Quantum Gravity 2000, 17, 3843–3864. [Google Scholar] [CrossRef]
- Fliss, J.R.; Freivogel, B.; Kontou, E.A.; Santos, D.P. Non-minimal coupling, negative null energy, and effective field theory. arXiv 2023, arXiv:2309.10848. [Google Scholar] [CrossRef]
- Khavkine, I.; Moretti, V. Algebraic QFT in curved spacetime and quasifree Hadamard states: An introduction. In Advances in Algebraic Quantum Field Theory; Mathematical Physics Studies; Springer: New York, NY, USA, 2015; pp. 191–251. [Google Scholar]
- Moretti, V. On the global Hadamard condition in QFT and the signed squared geodesic distance defined in domains larger than convex normal neighborhoods. arXiv 2021, arXiv:2107.04903. [Google Scholar] [CrossRef]
- Radzikowski, M.J. Micro-local approach to the Hadamard condition in quantum field theory on curved space-time. Commun. Math. Phys. 1996, 179, 529–553. [Google Scholar] [CrossRef]
- Hollands, S.; Wald, R.M. Local Wick polynomials and time ordered products of quantum fields in curved space-time. Commun. Math. Phys. 2001, 223, 289–326. [Google Scholar] [CrossRef]
- Hollands, S.; Wald, R.M. Conservation of the stress tensor in interacting quantum field theory in curved spacetimes. Rev. Math. Phys. 2005, 17, 227–312. [Google Scholar] [CrossRef]
- Decanini, Y.; Folacci, A. Hadamard renormalization of the stress-energy tensor for a quantized scalar field in a general spacetime of arbitrary dimension. Phys. Rev. D 2008, 78, 044025. [Google Scholar] [CrossRef]
- Wald, R.M. Trace Anomaly of a Conformally Invariant Quantum Field in Curved Space-Time. Phys. Rev. D 1978, 17, 1477–1484. [Google Scholar] [CrossRef]
- Ford, L.H.; Roman, T.A. Averaged energy conditions and quantum inequalities. Phys. Rev. D 1995, 51, 4277–4286. [Google Scholar] [CrossRef] [PubMed]
- Fewster, C.J.; Eveson, S.P. Bounds on negative energy densities in flat space-time. Phys. Rev. D 1998, 58, 084010. [Google Scholar] [CrossRef]
- Fewster, C.J. A General worldline quantum inequality. Class. Quantum Gravity 2000, 17, 1897–1911. [Google Scholar] [CrossRef]
- Fewster, C.J.; Smith, C.J. Absolute quantum energy inequalities in curved spacetime. Ann. Henri Poincare 2008, 9, 425–455. [Google Scholar] [CrossRef]
- Fewster, C.J.; Kontou, E.A. Quantum strong energy inequalities. Phys. Rev. D 2019, 99, 045001. [Google Scholar] [CrossRef]
- Fewster, C.J.; Osterbrink, L.W. Quantum Energy Inequalities for the Non-Minimally Coupled Scalar Field. J. Phys. A 2008, 41, 025402. [Google Scholar] [CrossRef]
- Kontou, E.A.; Olum, K.D. Quantum inequality in spacetimes with small curvature. Phys. Rev. D 2015, 91, 104005. [Google Scholar] [CrossRef]
- Kontou, E.A.; Olum, K.D. Multi-step Fermi normal coordinates. Class. Quantum Gravity 2013, 30, 175018. [Google Scholar] [CrossRef][Green Version]
- Kontou, E.A.; Olum, K.D. Averaged null energy condition in a classical curved background. Phys. Rev. D 2013, 87, 064009. [Google Scholar] [CrossRef]
- Kontou, E.A.; Sanders, K. Energy conditions in general relativity and quantum field theory. Class. Quantum Gravity 2020, 37, 193001. [Google Scholar] [CrossRef]
- Fewster, C.J. Quantum Energy Inequalities. In Wormholes, Warp Drives and Energy Conditions; Lobo, F.S.N., Ed.; Springer International Publishing: Berlin, Germany, 2017; pp. 215–254. [Google Scholar] [CrossRef]
- Fewster, C.J.; Pfenning, M.J. A Quantum weak energy inequality for spin one fields in curved space-time. J. Math. Phys. 2003, 44, 4480–4513. [Google Scholar] [CrossRef]
- Pfenning, M.J. Quantum inequalities for the electromagnetic field. Phys. Rev. D 2002, 65, 024009. [Google Scholar] [CrossRef]
- Fewster, C.J.; Mistry, B. Quantum weak energy inequalities for the Dirac field in flat space-time. Phys. Rev. D 2003, 68, 105010. [Google Scholar] [CrossRef]
- Dawson, S.P.; Fewster, C.J. An Explicit quantum weak energy inequality for Dirac fields in curved spacetimes. Class. Quantum Gravity 2006, 23, 6659–6681. [Google Scholar] [CrossRef]
- Smith, C.J. An Absolute quantum energy inequality for the Dirac field in curved spacetime. Class. Quantum Gravity 2007, 24, 4733–4750. [Google Scholar] [CrossRef][Green Version]
- Fewster, C.J.; Hollands, S. Quantum energy inequalities in two-dimensional conformal field theory. Rev. Math. Phys. 2005, 17, 577. [Google Scholar] [CrossRef]
- Bostelmann, H.; Cadamuro, D.; Fewster, C.J. Quantum Energy Inequality for the Massive Ising Model. Phys. Rev. D 2013, 88, 025019. [Google Scholar] [CrossRef]
- Fröb, M.B.; Cadamuro, D. A quantum energy inequality in the Sine–Gordon model. arXiv 2022, arXiv:2212.07377. [Google Scholar] [CrossRef]
- Bostelmann, H.; Cadamuro, D.; Mandrysch, J. Quantum energy inequalities in integrable models with several particle species and bound states. arXiv 2023, arXiv:2302.00063. [Google Scholar] [CrossRef]
- Cadamuro, D.; Fröb, M.B.; Ferrera, C.M. The Sine-Gordon QFT in de Sitter spacetime. arXiv 2024, arXiv:2404.12324. [Google Scholar]
- Flanagan, E.E. Quantum inequalities in two-dimensional Minkowski space-time. Phys. Rev. D 1997, 56, 4922–4926. [Google Scholar] [CrossRef]
- Flanagan, E.E. Quantum inequalities in two-dimensional curved space-times. Phys. Rev. D 2002, 66, 104007, Erratum in Phys. Rev. D 2020, 102, 129901. [Google Scholar] [CrossRef]
- Freivogel, B.; Kontou, E.A.; Krommydas, D. The Return of the Singularities: Applications of the Smeared Null Energy Condition. SciPost Phys. 2022, 13, 001. [Google Scholar] [CrossRef]
- Fliss, J.R.; Freivogel, B. Semi-local Bounds on Null Energy in QFT. SciPost Phys. 2022, 12, 084. [Google Scholar] [CrossRef]
- Leichenauer, S.; Levine, A. Upper and Lower Bounds on the Integrated Null Energy in Gravity. J. High Energy Phys. 2019, 01, 133. [Google Scholar] [CrossRef]
- Yurtsever, U. Does quantum field theory enforce the averaged weak energy condition? Class. Quantum Gravity 1990, 7, L251–L258. [Google Scholar] [CrossRef]
- Wald, R.M.; Yurtsever, U. General proof of the averaged null energy condition for a massless scalar field in two-dimensional curved space-time. Phys. Rev. D 1991, 44, 403–416. [Google Scholar] [CrossRef]
- Flanagan, E.E.; Wald, R.M. Does back reaction enforce the averaged null energy condition in semiclassical gravity? Phys. Rev. D 1996, 54, 6233–6283. [Google Scholar] [CrossRef]
- Verch, R. The Averaged Null energy condition for general quantum field theories in two-dimensions. J. Math. Phys. 2000, 41, 206–217. [Google Scholar] [CrossRef]
- Kelly, W.R.; Wall, A.C. Holographic proof of the averaged null energy condition. Phys. Rev. D 2014, 90, 106003, Erratum in Phys. Rev. D 2015, 91, 069902. [Google Scholar] [CrossRef]
- Bousso, R.; Fisher, Z.; Koeller, J.; Leichenauer, S.; Wall, A.C. Proof of the Quantum Null Energy Condition. Phys. Rev. D 2016, 93, 024017. [Google Scholar] [CrossRef]
- Faulkner, T.; Leigh, R.G.; Parrikar, O.; Wang, H. Modular Hamiltonians for Deformed Half-Spaces and the Averaged Null Energy Condition. J. High Energy Phys. 2016, 09, 038. [Google Scholar] [CrossRef]
- Fewster, C.J.; Olum, K.D.; Pfenning, M.J. Averaged null energy condition in spacetimes with boundaries. Phys. Rev. D 2007, 75, 025007. [Google Scholar] [CrossRef]
- Kontou, E.A.; Olum, K.D. Proof of the averaged null energy condition in a classical curved spacetime using a null-projected quantum inequality. Phys. Rev. D 2015, 92, 124009. [Google Scholar] [CrossRef]
- Visser, M. Gravitational vacuum polarization. 2: Energy conditions in the Boulware vacuum. Phys. Rev. D 1996, 54, 5116–5122. [Google Scholar] [CrossRef] [PubMed]
- Levi, A.; Ori, A. Versatile method for renormalized stress-energy computation in black-hole spacetimes. Phys. Rev. Lett. 2016, 117, 231101. [Google Scholar] [CrossRef] [PubMed]
- Klinkhammer, G. Averaged energy conditions for free scalar fields in flat space-times. Phys. Rev. D 1991, 43, 2542–2548. [Google Scholar] [CrossRef]
- Visser, M. Scale anomalies imply violation of the averaged null energy condition. Phys. Lett. B 1995, 349, 443–447. [Google Scholar] [CrossRef]
- Page, D.N. Thermal Stress Tensors in Static Einstein Spaces. Phys. Rev. D 1982, 25, 1499. [Google Scholar] [CrossRef]
- Meda, P.; Pinamonti, N.; Siemssen, D. Existence and Uniqueness of Solutions of the Semiclassical Einstein Equation in Cosmological Models. Annales Henri Poincare 2021, 22, 3965–4015. [Google Scholar] [CrossRef]
- Gottschalk, H.; Siemssen, D. The Cosmological Semiclassical Einstein Equation as an Infinite-Dimensional Dynamical System. Annales Henri Poincare 2021, 22, 3915–3964. [Google Scholar] [CrossRef]
- Sanders, K. Static symmetric solutions of the semi-classical Einstein-Klein-Gordon system. Ann. Henri Poincaré 2021, arXiv:2007.14311. [Google Scholar] [CrossRef]
- Visser, M. Lorentzian Wormholes: From Einstein to Hawking; American Inst. of Physics: Melville, NY, USA, 1995. [Google Scholar]
- Flamm, L. Beiträge zur Einsteinschen Gravitationstheorie. Phys. Z. 1916, 17, 448–454. [Google Scholar]
- Flamm, L. Republication of: Contributions to Einstein’s theory of gravitation. Gen. Relativ. Gravit. 2015, 47, 72. [Google Scholar] [CrossRef]
- Einstein, A.; Rosen, N. The Particle Problem in the General Theory of Relativity. Phys. Rev. 1935, 48, 73–77. [Google Scholar] [CrossRef]
- Wheeler, J.A. Geons. Phys. Rev. 1955, 97, 511–536. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, Time Machines, and the Weak Energy Condition. Phys. Rev. Lett. 1988, 61, 1446–1449. [Google Scholar] [CrossRef]
- Sen, N. Über die grenzbedingungen des schwerefeldes an unstetigkeitsflächen. Ann. Phys. 1924, 378, 365–396. [Google Scholar] [CrossRef]
- Lanczos, K. Flächenhafte verteilung der materie in der einsteinschen gravitationstheorie. Ann. Phys. 1924, 379, 518–540. [Google Scholar] [CrossRef]
- Barrabes, C.; Israel, W. Thin shells in general relativity and cosmology: The Lightlike limit. Phys. Rev. D 1991, 43, 1129–1142. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Jafferis, D.L.; Wall, A.C. Traversable Wormholes via a Double Trace Deformation. J. High Energy Phys. 2017, 12, 151. [Google Scholar] [CrossRef]
- Freivogel, B.; Galante, D.A.; Nikolakopoulou, D.; Rotundo, A. Traversable wormholes in AdS and bounds on information transfer. J. High Energy Phys. 2020, 01, 050. [Google Scholar] [CrossRef]
- Giddings, S.B.; Strominger, A. Axion Induced Topology Change in Quantum Gravity and String Theory. Nucl. Phys. B 1988, 306, 890–907. [Google Scholar] [CrossRef]
- Coleman, S.R. Why There Is Nothing Rather Than Something: A Theory of the Cosmological Constant. Nucl. Phys. B 1988, 310, 643–668. [Google Scholar] [CrossRef]
- Tipler, F.J. Singularities and Causality Violation. Ann. Phys. 1977, 108, 1–36. [Google Scholar] [CrossRef]
- Geroch, R.P. Topology in general relativity. J. Math. Phys. 1967, 8, 782–786. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Friedman, J.L.; Schleich, K.; Witt, D.M. Topological censorship. Phys. Rev. Lett. 1993, 71, 1486–1489, Erratum in Phys. Rev. Lett. 1995, 75, 1872. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S. Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
- Ford, L.H.; Roman, T.A. Quantum field theory constrains traversable wormhole geometries. Phys. Rev. D 1996, 53, 5496–5507. [Google Scholar] [CrossRef] [PubMed]
- Fewster, C.J.; Roman, T.A. On wormholes with arbitrarily small quantities of exotic matter. Phys. Rev. D 2005, 72, 044023. [Google Scholar] [CrossRef]
- Fewster, C.J.; Teo, E. Quantum inequalities and ‘quantum interest’ as eigenvalue problems. Phys. Rev. D 2000, 61, 084012. [Google Scholar] [CrossRef]
- Fewster, C.J.; Pfenning, M.J. Quantum energy inequalities and local covariance. I. Globally hyperbolic spacetimes. J. Math. Phys. 2006, 47, 082303. [Google Scholar] [CrossRef]
- Hochberg, D.; Popov, A.; Sushkov, S.V. Selfconsistent wormhole solutions of semiclassical gravity. Phys. Rev. Lett. 1997, 78, 2050–2053. [Google Scholar] [CrossRef]
- Tipler, F.J. Causality violation in asymptotically flat space-times. Phys. Rev. Lett. 1976, 37, 879–882. [Google Scholar] [CrossRef]
- Hawking, S.W. The Chronology protection conjecture. Phys. Rev. D 1992, 46, 603–611. [Google Scholar] [CrossRef] [PubMed]
- Mallett, R.L. The gravitational field of a circulating light beam. Found. Phys. 2003, 33, 1307–1314. [Google Scholar] [CrossRef]
- Lobo, F.S.N. From the Flamm–Einstein–Rosen bridge to the modern renaissance of traversable wormholes. Int. J. Mod. Phys. D 2016, 25, 1630017. [Google Scholar] [CrossRef]

| Condition | Physical Form | Geometric Form | Perfect Fluid |
|---|---|---|---|
| WEC | and | ||
| SEC | and | ||
| NEC |
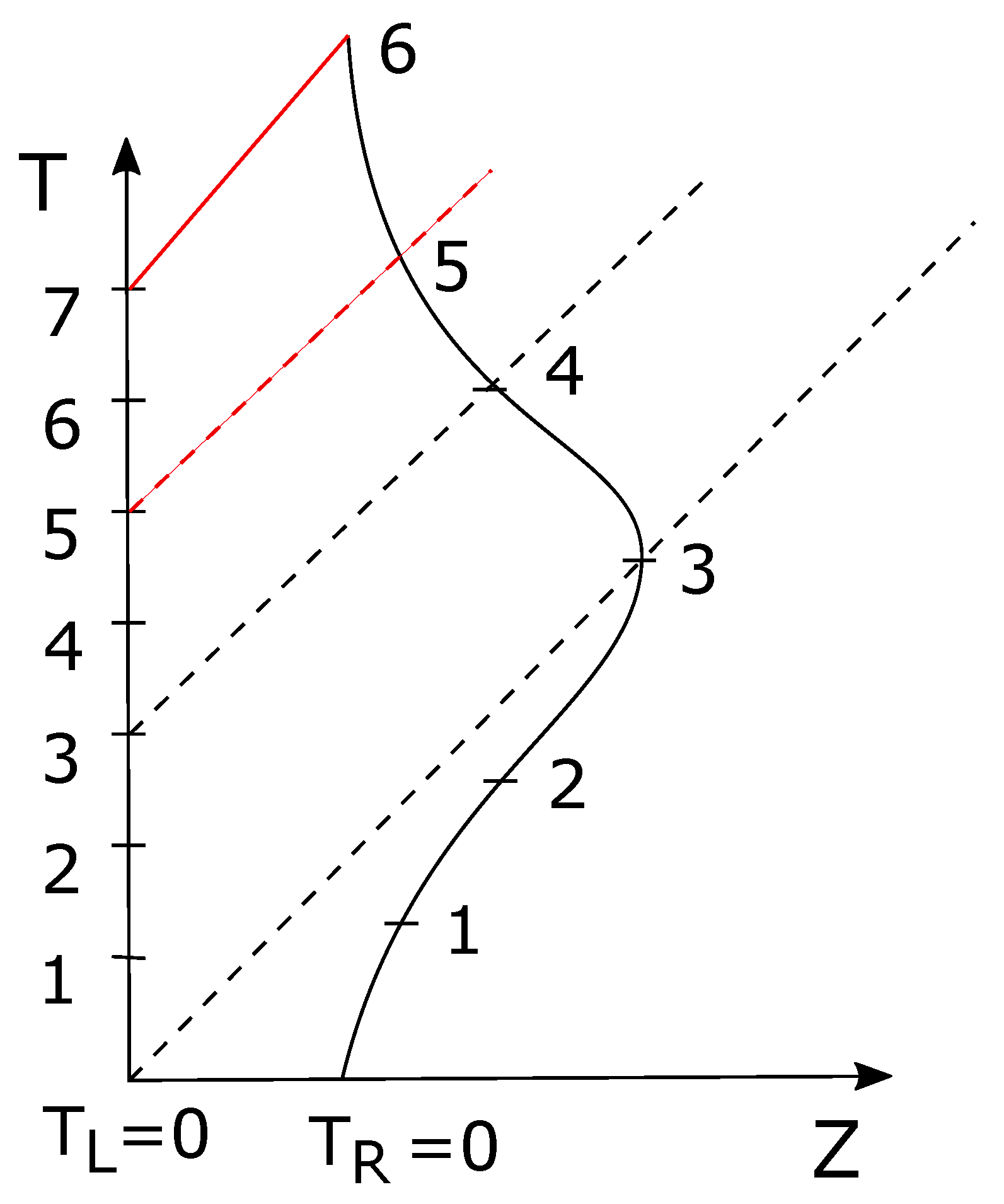
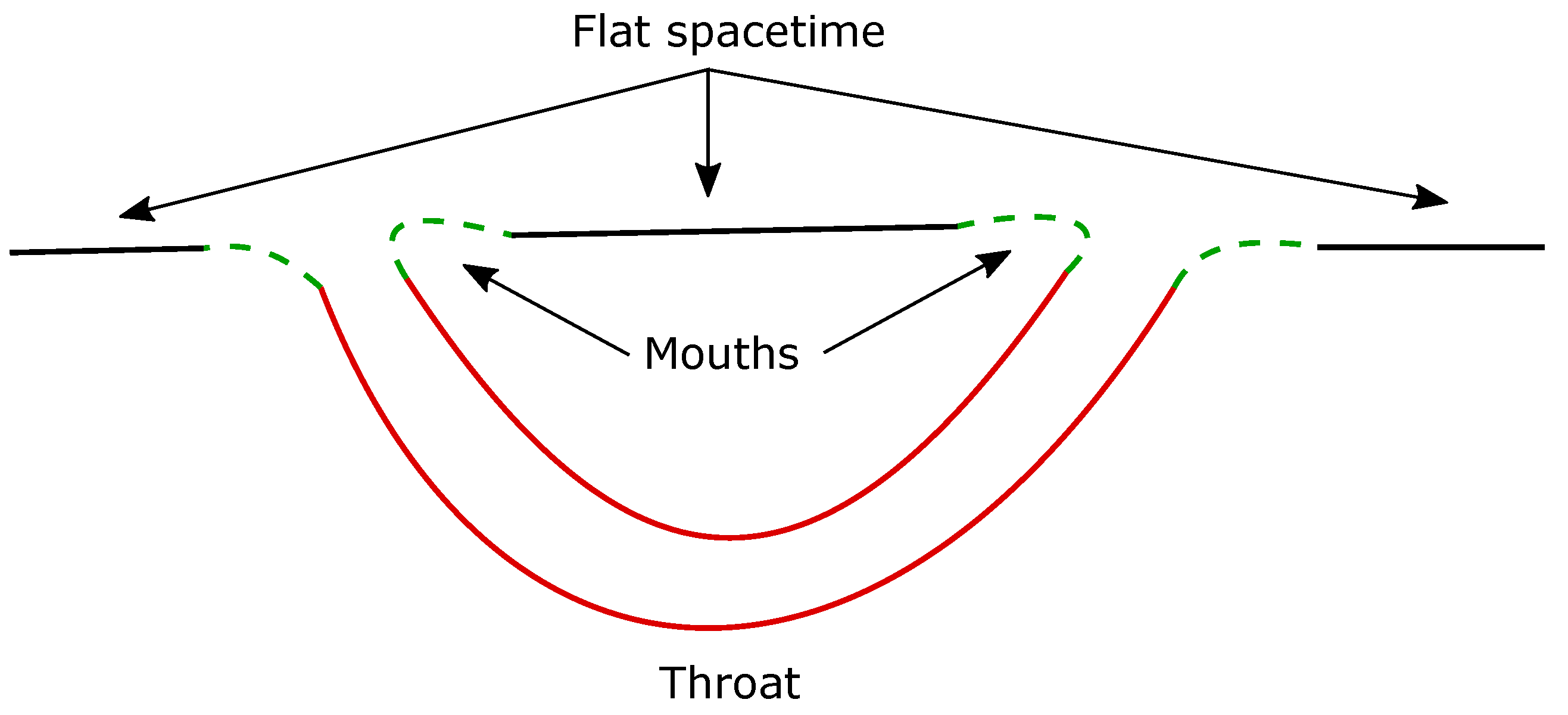
| Right Mouth | Left Mouth |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontou, E.-A. Wormhole Restrictions from Quantum Energy Inequalities. Universe 2024, 10, 291. https://doi.org/10.3390/universe10070291
Kontou E-A. Wormhole Restrictions from Quantum Energy Inequalities. Universe. 2024; 10(7):291. https://doi.org/10.3390/universe10070291
Chicago/Turabian StyleKontou, Eleni-Alexandra. 2024. "Wormhole Restrictions from Quantum Energy Inequalities" Universe 10, no. 7: 291. https://doi.org/10.3390/universe10070291
APA StyleKontou, E.-A. (2024). Wormhole Restrictions from Quantum Energy Inequalities. Universe, 10(7), 291. https://doi.org/10.3390/universe10070291







