The High Mass Accretion in the Innermost Regions of a Viscously Evolved Protoplanetary Disk
Abstract
1. Introduction
2. The Protoplanetary Disk Model
2.1. The Molecular Cloud Core’s Properties
2.2. The Disk Model
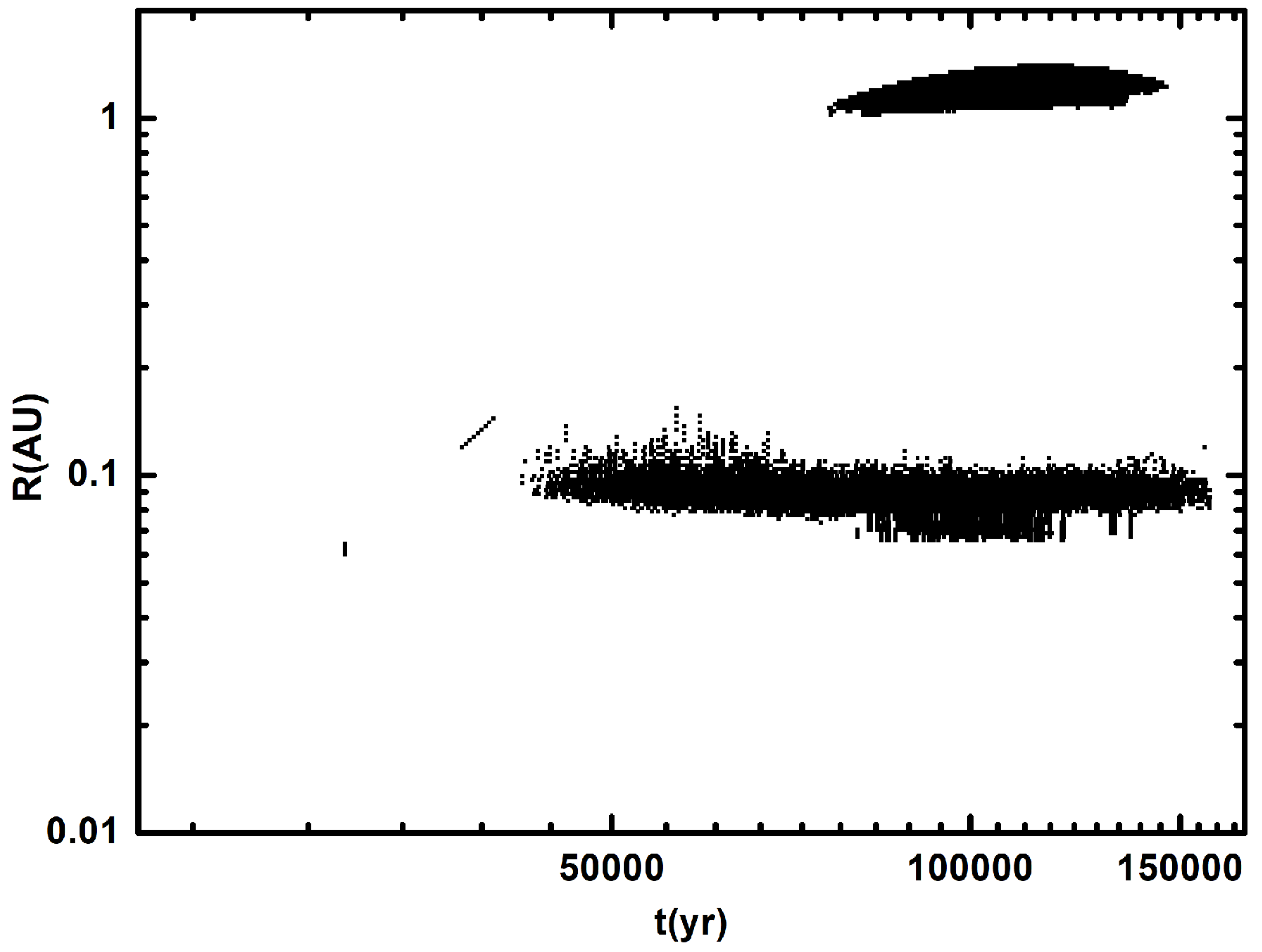
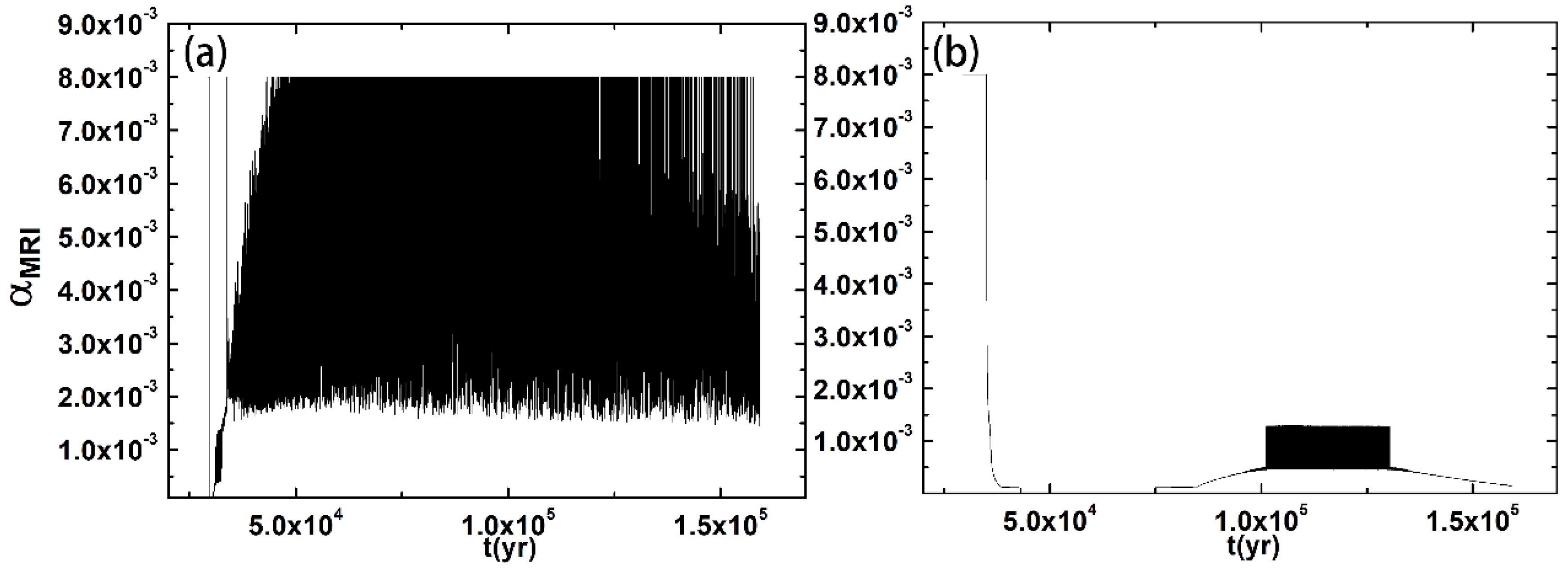
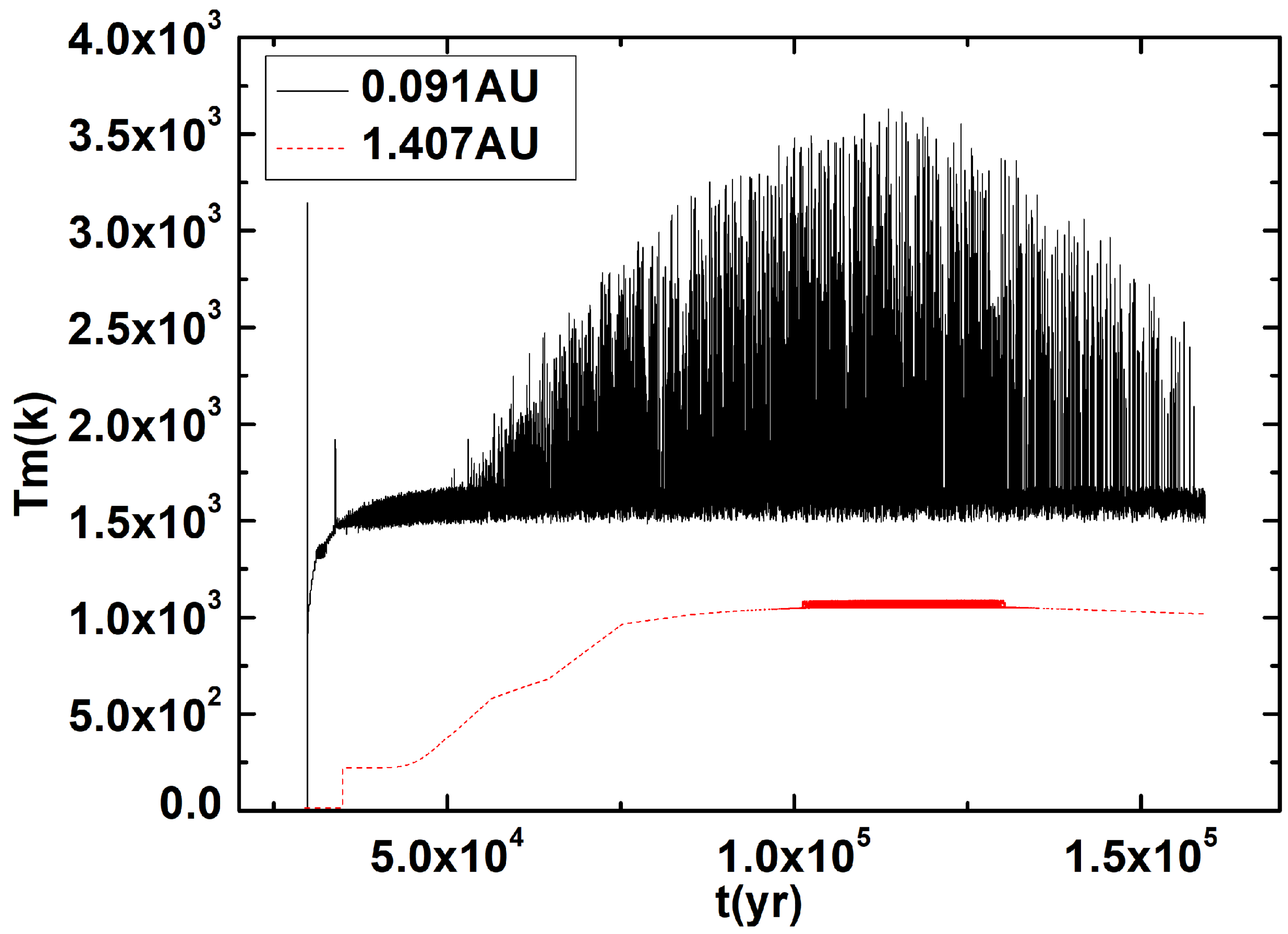
3. The High Mass Accretion Properties in the Innermost Regions
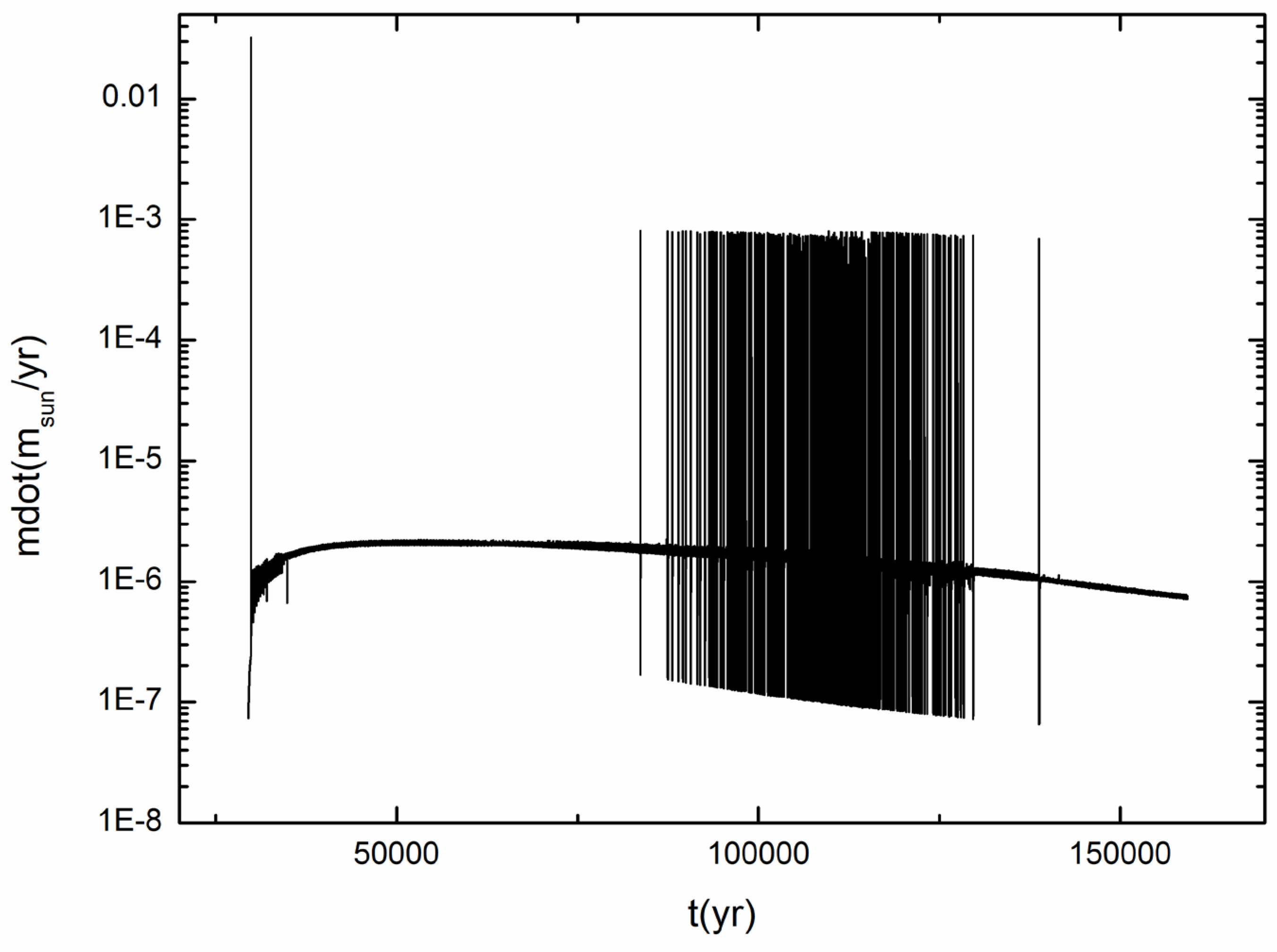
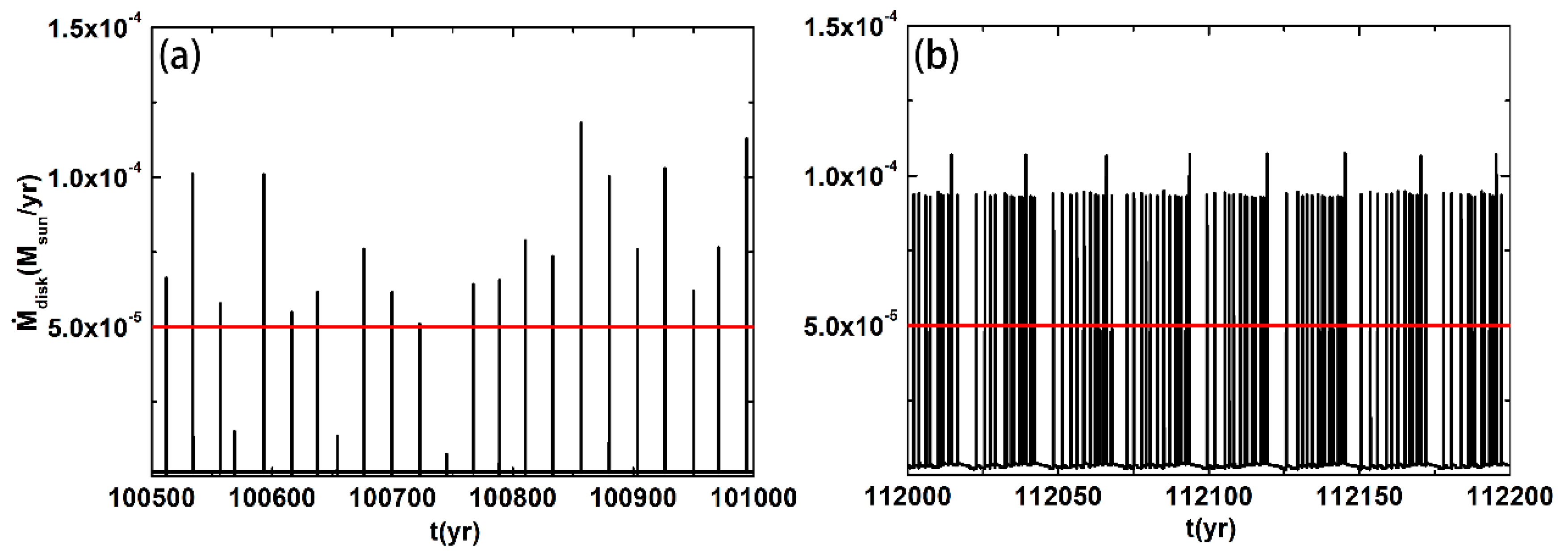
3.1. The Typical Model
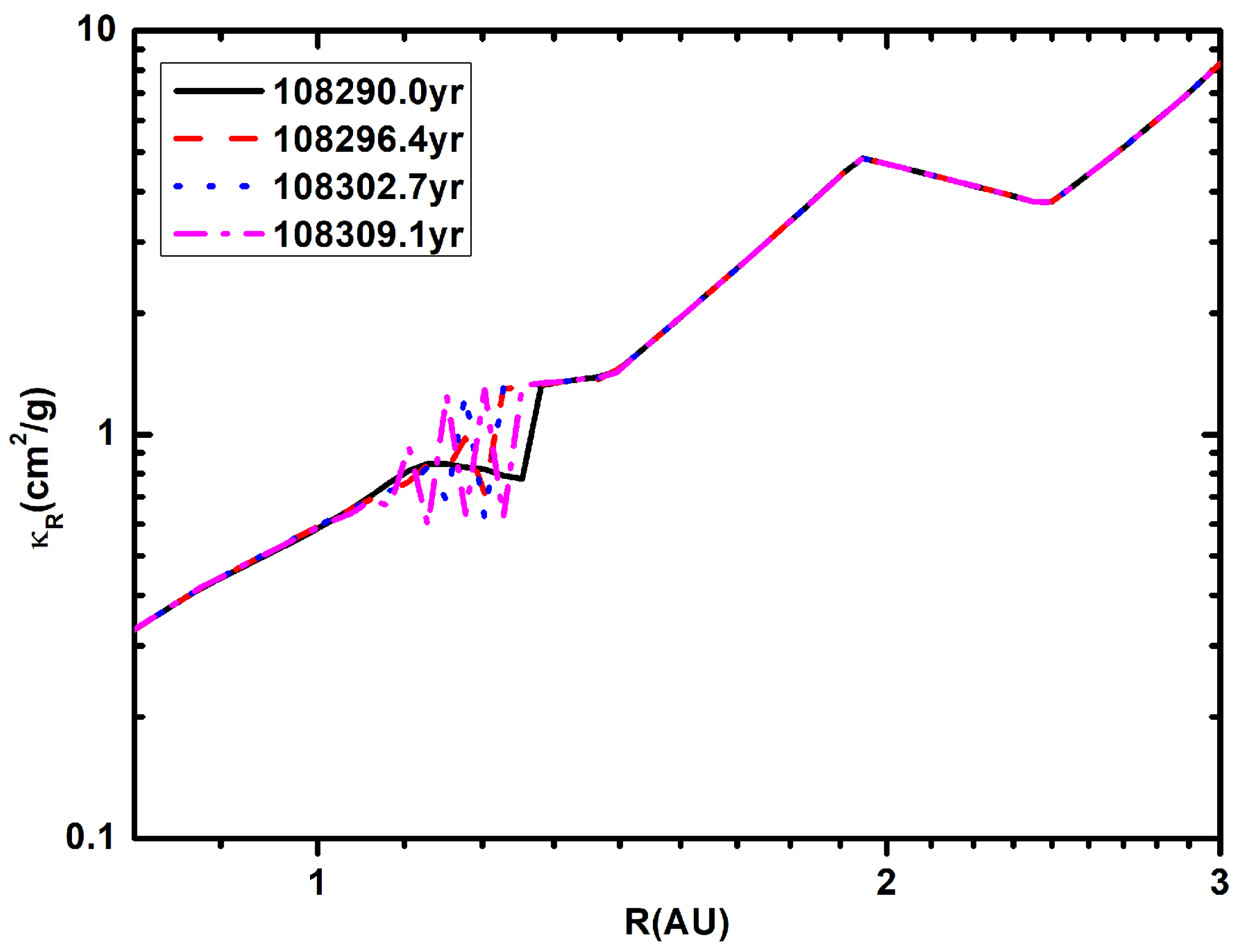
3.2. The Physical Reason for the Two Regions
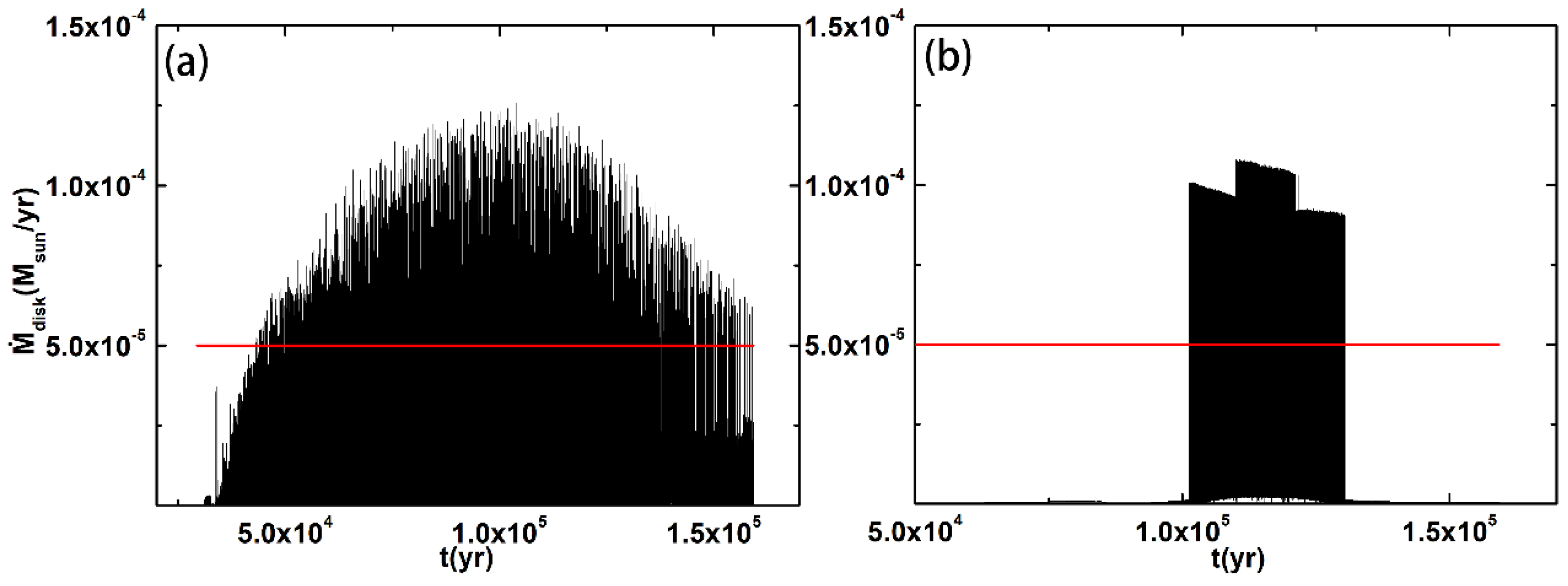
3.3. The Varying Parameters Model
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bell, K.R.; Lin, D.N.C. Using FU Orionis Outbursts to Constrain Self-Regulated Protostellar Disk Models. Astrophys. J. 1994, 427, 987–1004. [Google Scholar] [CrossRef]
- Vorobyov, E.I.; Basu, S. The Burst Mode of Accretion and Disk Fragmentation in the Early Embedded Stages of Star Formation. Astrophys. J. 2010, 719, 1896–1911. [Google Scholar] [CrossRef]
- Fleming, T.; Stone, J.M. Local Magnetohydrodynamic Models of Layered Accretion Disks. Astrophys. J. 2003, 585, 908–920. [Google Scholar] [CrossRef]
- Chambers, J.E. Planet Formation with Migration. Astrophys. J. 2006, 652, L133–L136. [Google Scholar] [CrossRef][Green Version]
- Bae, J.; Hartmann, L.; Zhu, Z.; Nelson, R.P. Accretion Outbursts in Self-Gravitating Protoplanetary Disks. Astrophys. J. 2014, 795, 61–75. [Google Scholar] [CrossRef]
- Kadam, K.; Vorobyov, E.; Regály, Z.; Kóspál, Á.; Ábrahám, P. Outbursts in Global Protoplanetary Disk Simulations. Astrophys. J. 2020, 895, 41–56. [Google Scholar] [CrossRef]
- Forgan, D.; Rice, K. Stellar Encounters in the context of Outburst Phenomena. Mon. Not. R. Astron. Soc. 2010, 402, 1349–1356. [Google Scholar] [CrossRef]
- Bonnell, I.; Bastien, P. A Binary Origin for FU Orionis Stars. Astrophys. J. 1992, 401, L31. [Google Scholar] [CrossRef]
- Lodato, G.; Clarke, C.J. Massive Planets in FU Orionis Discs: Implications for Thermal Instability Models. Mon. Not. R. Astron. Soc. 2004, 353, 841–854. [Google Scholar] [CrossRef]
- Liu, C.J.; Yao, Z.; Li, H.N.; Wang, H.S. The Evolution of the Protoplanetary Disk with Mass Influx from a Molecular Cloud core and the Photoevaporation Winds. New Astron. 2018, 58, 72–83. [Google Scholar] [CrossRef]
- Jin, L.; Li, M. Diversity of Extrasolar Planets and Diversity of molecular cloud cores. I. Semimajor Axes. Astrophys. J. 2014, 783, 37–55. [Google Scholar] [CrossRef]
- Nakamoto, T.; Nakagawa, Y. Formation, Early Evolution, and Gravitational Stability of Protoplanetary Disks. Astrophys. J. 1994, 421, 640. [Google Scholar]
- Alexander, R.D.; Clarke, C.J.; Pringle, J.E. Photoevaporation of Protoplanetary Discs.-I. Hydrodynamic Models. Mon. Not. R. Astron. Soc. 2006, 369, 216. [Google Scholar] [CrossRef]
- Alexander, R.D.; Clarke, C.J.; Pringle, J.E. Photoevaporation of Protoplanetary Discs.-II. Evolutionary Models and Observable Properties. Mon. Not. R. Astron. Soc. 2006, 369, 229. [Google Scholar] [CrossRef]
- Kratter, K.M.; Matzner, C.D.; Krumholz, M.R. Global Models for the Evolution of Embedded, Accreting Protostellar Disks. Astrophys. J. 2008, 681, 375. [Google Scholar] [CrossRef]
- Laughlin, G.; Bodenheimer, P. Nonaxisymmetric Evolution in Protostellar Disks. Astrophys. J. 1994, 436, 335. [Google Scholar] [CrossRef]
- Laughlin, G.; Rozyczka, M. The Effect of Gravitational Instabilities on Protostellar Disks. Astrophys. J. 1996, 456, 279. [Google Scholar] [CrossRef]
- Umebayashi, T. The Densities of Charged particles in very dense Interstellar Clouds. Prog. Theor. Phys. 1983, 69, 480. [Google Scholar] [CrossRef]
- Zhu, Z.; Hartmann, L.; Nelson, R.P.; Gammie, C.F. Challenges in Forming Planets by Gravitational Instability: Disk Irradiation and Clump Migration, Accretion, and Tidal Destruction. Astrophys. J. 2012, 746, 110. [Google Scholar] [CrossRef]
- McKee, C.F.; Ostriker, E.C. Theory of Star Formation. Annu. Rev. Astron. Astrophys. 2007, 45, 565. [Google Scholar] [CrossRef]
- Goodman, A.A.; Benson, P.J.; Fuller, G.A.; Myers, P.C. Dense Cores in Dark Clouds. VIII. Velocity Gradients. Astrophys. J. 1993, 406, 528. [Google Scholar]
- Caselli, P.; Benson, P.J.; Myers, P.C.; Tafalla, M. Dense Cores in Dark Clouds. XIV. N2H+ (1-0) Maps of Dense cloud Cores. Astrophys. J. 2002, 572, 238. [Google Scholar] [CrossRef]
- Shu, F.H. Self-similar collapse of Isothermal spheres and Star Formation. Astrophys. J. 1977, 214, 488. [Google Scholar] [CrossRef]
- Jijina, J.; Myers, P.C.; Adams, F.C. Dense Cores Mapped in Ammonia: A Database. Astrophys. J. Suppl. Ser. 1999, 125, 161. [Google Scholar] [CrossRef]
- Motte, F.; Andre, P.; Neri, R. The Initial Conditions of Star Formation in the rho Ophiuchi Main Cloud: Wild-field millimeter continuum mapping. Astron. Astrophys. 1998, 336, 150. [Google Scholar]
- Shakura, N.I.; Sunyaev, R.A. Black Holes in Binary Systems. Observational Appearance. Astron. Astrophys. 1973, 24, 337. [Google Scholar]
- Jin, L.; Sui, N. The Evolution of the Solar Nebula. I. Evolution of the Global Properties and Planet Masses. Astrophys. J. 2010, 710, 1179. [Google Scholar] [CrossRef]
- Fukue, J. Radiative Transfer in Protoplanetary Disks under Irradiation by the Protostar. Prog. Theor. Exp. Phys. 2013, 5, 053E02. [Google Scholar] [CrossRef][Green Version]
- Balbus, S.A.; Hawley, J.F. A Powerful Local Shear Instability in Weakly Magnetized Disks. I. Linear Analysis. Astrophys. J. 1991, 376, 214. [Google Scholar] [CrossRef]
- Gammie, C.F. Layered Accretion in T Tauri Disks. Astrophys. J. 1996, 457, 355. [Google Scholar] [CrossRef]
- Lodato, G.; Rice, W.K.M. Testing the Locality of Transport in Self-Gravitating Discs -II. The Massive Disc Case. Mon. Not. R. Astron. Soc. 2005, 358, 1489. [Google Scholar] [CrossRef]
- Forgan, D.; Rice, K.; Cossins, P.; Lodato, G. The Nature of Angular Momentum Transport in Radiative Self-Gravitating Protostellar Discs. Mon. Not. R. Astron. Soc. 2011, 410, 994. [Google Scholar] [CrossRef]
- Toomre, A. On the Gravitational Instability of a Disk of Stars. Astrophys. J. 1964, 139, 1217. [Google Scholar] [CrossRef]
- Dubrulle, B. Differential Rotation as a Source of Angular Momentum Transfer in the solar nebula. Icarus 1993, 106, 59. [Google Scholar] [CrossRef]
- Klahr, H.H.; Bodenheimer, P. Turbulence in Accretion Disks: Vorticity Generation and Angular Momentum Transport via the Global Baroclinic Instability. Astrophys. J. 2003, 582, 869. [Google Scholar] [CrossRef]
- Richard, D. On non-linear hydrodynamic instability and enhanced transport in differentially rotating flows. Astron. Astrophys. 2003, 408, 409. [Google Scholar] [CrossRef][Green Version]
- Dubrulle, B.; Marié, L.; Normand, C.; Richard, D.; Hersant, F.; Zahn, J.P. An hydrodynamic shear instability in stratified disks. Astron. Astrophys. 2005, 429, 1. [Google Scholar]
- Clarke, C.J.; Lin DN, C. Pre-conditions for disc generated FU Orionis outbursts. Mon. Not. R. Astron. Soc. 1990, 242, 439. [Google Scholar] [CrossRef]
- Scholz, A.; Froebrich, D.; Wood, K. A systematic survey for eruptive young stellar objects using mid-infrared photometry. Mon. Not. R. Astron. Soc. 2013, 430, 2910. [Google Scholar] [CrossRef]
- Audard, M.; Ábrahám, P.; Dunham, M.M.; Green, J.D.; Grosso, N.; Hamaguchi, K.; Kastner, J.H.; Kóspál, A.; Lodato, G.; Romanova, M.M.; et al. Epesodic Accretion in Young Stars. In Protostars and Planets VI; Beuther, H., Klessen, R.S., Dullemond, C.P., Henning, T.K., Eds.; University of Arizona Press: Tucson, AZ, USA, 2014; p. 387. [Google Scholar]



| 10 | 0.0007 | 0.00016 |
| 100 | 0.0013 | 0.00019 |
| 1000 | 0.006 | 0.0019 |
| ≥20,000 | 0.012 | 0.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Yao, Z.; Quan, Y. The High Mass Accretion in the Innermost Regions of a Viscously Evolved Protoplanetary Disk. Universe 2024, 10, 185. https://doi.org/10.3390/universe10040185
Liu C, Yao Z, Quan Y. The High Mass Accretion in the Innermost Regions of a Viscously Evolved Protoplanetary Disk. Universe. 2024; 10(4):185. https://doi.org/10.3390/universe10040185
Chicago/Turabian StyleLiu, Chunjian, Zhen Yao, and Yue Quan. 2024. "The High Mass Accretion in the Innermost Regions of a Viscously Evolved Protoplanetary Disk" Universe 10, no. 4: 185. https://doi.org/10.3390/universe10040185
APA StyleLiu, C., Yao, Z., & Quan, Y. (2024). The High Mass Accretion in the Innermost Regions of a Viscously Evolved Protoplanetary Disk. Universe, 10(4), 185. https://doi.org/10.3390/universe10040185






