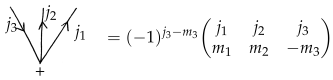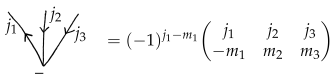Causal Structure in Spin Foams
Abstract
1. Introduction
2. Discrete Causal Structure
2.1. Bare Causality
2.2. Time Orientability
2.3. Discrete Bare Causality
2.4. Discrete Time Orientability
3. Causality on the Dual Skeleton
- An arrow from past to future on time-like edges,
- No arrow on space-like edges.
3.1. Dual Causal Set
- Reflexivity: (by convention).
- Anti-symmetry: and imply .
- Transitivity: and imply .
3.2. Causal Wedges
4. Lorentzian Regge Calculus
4.1. Lorentzian Regge Action
4.2. First-Order Regge Calculus
4.3. Causal Structure from Dynamics
5. Causal Path Integral
5.1. General Boundary Formulation
5.2. Regge Path Integral
5.3. Causal Structure of the Boundary
5.4. Causal Amplitude
6. BF Theory
6.1. Discrete BF Theory
- 1.
- a distinguished edge to each face that serves as a starting point in the product;
- 2.
- an orientation to each face that tells the order of the following edges.
- 3.
- a distinguished face to each edge that serves as a starting point in the tensor product;
- 4.
- an orientation of the faces around each edge, which can be thought of as an arrow on the edge (with the right-hand convention to turn around for instance).
6.2. Ponzano–Regge Model
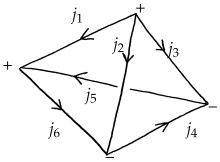
- To each link l, associate a variable that will be summed over;
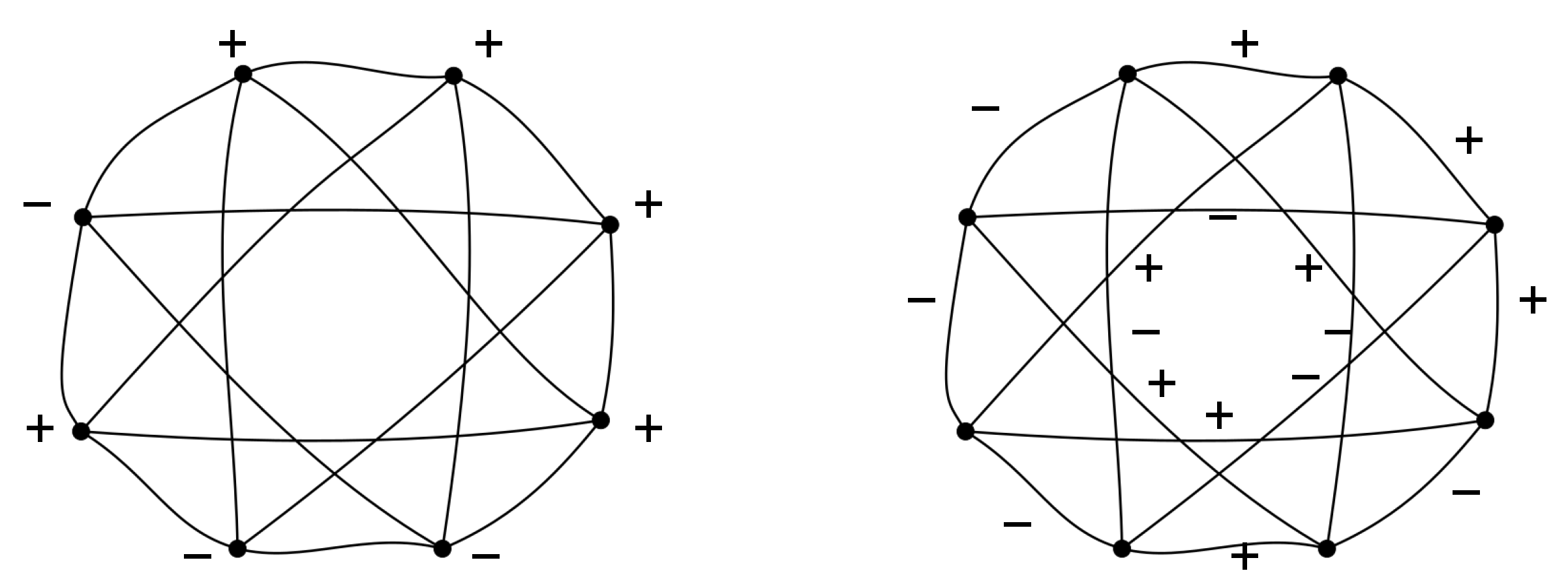
- The 3jm-Wigner symbol8 is associated with the following nodes:The sign on the node indicates the sense in which the attached links shall be read.
- If an arrow is reversed, replace in the formula above with and multiply by , likeorA positive (resp. negative) node with an incoming (resp. outgoing) link corresponds to a counter-alignment of the face and the edge.
- Multiply all factors and sum over all from to (integer steps).
- A flip of a link orientation brings a global factor if the two endpoints carry opposite signs, none otherwise.
- A flip of a node orientation brings an overall factor .
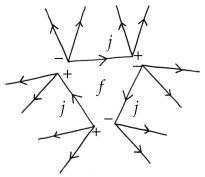
6.3. Causal Ponzano–Regge Model
6.4. BF Theory
- 5.
- at each edge, the surrounding faces are partitioned into two sets of two (there exist three such partitions);
- 6.
- these two sets are ordered (e.g., called left and right).
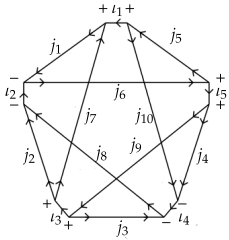
7. EPRL Model and Its Causal Structure
7.1. Lorentzian EPRL Model
- a starting wedge per each face;
- an orientation per each face;
- an orientation to each wedge, i.e., each wedge w has a source edge and a target edge ;
- a distinguished edge per each vertex v.
7.2. Causal Structures in the EPRL Model
8. Relation to Earlier Proposals
8.1. Livine–Oriti Barrett–Crane Causal Model
8.2. Divergence and Spikes
8.3. Engle’s Proper Vertex
9. Conclusions
- −
- The notion of causality in general relativity encompasses two related but conceptually different notions: bare causality and time orientability.
- −
- There is a natural way to translate these notions to a simplicial complex.
- −
- The causal structure can be implemented on the dual 1-skeleton (edges). It can be seen as the combination of a causal set with a neighborhood relation.
- −
- It can also be encoded on the dual 2-skeleton (wedges) with a degeneracy of 2 that corresponds to a global time-reversal symmetry.
- −
- Starting from the set of all possible wedge orientations, the Lorentzian Regge action determines equations of motion whose solutions fix a proper causal structure.
- −
- The metric propagator can be written as a sum over all possible wedge orientations. By fixing the causal structure from the beginning, one defines a causal metric propagator, similar to the Feynman propagator.
- −
- Discrete BF theory naturally carries an orientation structure on the edges and faces, although it is blind to it in the bulk.
- −
- Discrete BF theory is sensitive to the orientation on the boundary. There are simple rules of crossing symmetry to go from one orientation to another.
- −
- There is a simple way to break the orientation invariance in the bulk, which provides a toy model to study causality in spin foam models (70).
- −
- The EPRL amplitude can be regarded as a sum over all possible configurations of wedge orientations , which provide additional dynamical variables encoding the causal structure. Only a subset of it corresponds to properly causal configurations.
- −
- The causal EPRL vertex shares common traits with the Livine–Oriti causal version of the Barrett–Crane model and with Engle’s proper vertex.
- −
- Whether one should use the causal or the full EPRL amplitude depends on what one wants to compute: a projector on the physical Hilbert space or a causal propagator.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Orientation Invariance of the Ponzano–Regge Model
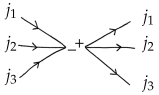
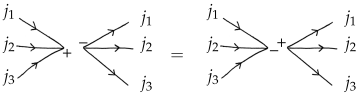
- Reversing the arrow of a link in-between two positive or two negative nodes amounts to multiplying by .
- Reversing the arrow of a link in-between a positive and a negative link does not change the vertex amplitude.
Appendix B. Causal Barrett–Crane Model
Appendix B.1. Lorentzian Barrett–Crane
Appendix B.2. Livine–Oriti Causal Model
| 1 | The denomination is ours. Surprisingly, it seems that this notion does not carry a specific name in the literature. It is usually simply called “causality”, but here we need a specific name to be accurate. |
| 2 | |
| 3 | We deliberately ignore the null case, which does not seem to shed much light on our investigation. |
| 4 | A directed graph is given by a set of vertices and a set of ordered pairs of vertices (arrows). It is considered simple if there are no arrows from a vertex to itself. It is considered oriented if there is at most one arrow between any two vertices. |
| 5 | A directed graph is acyclic if it has no directed cycles, which means, in causal language, no closed time-like curves. If we do assume the presence of directed cycles, then the construction of the poset is still possible but subtler because the anti-symmetry implies the contraction of such cycles, so that more combinatorial information is lost. |
| 6 | We denote indifferently or when the vertex v is an endpoint of the edge e. |
| 7 | Given a vertex, the vertex graph associates a node to each edge and a link to each wedge in-between. In graph theory, the word “edge” is usually used instead of “link”. But, we stick to a common convention in loop quantum gravity (see [7]) where “edge” is reserved to the bulk of 2-complexes and “link” is used for the boundary. |
| 8 | We refer to [51] for an introduction to the mathematical material used in this section. |
| 9 | More abstractly, it can be regarded as a section of the Hopf bundle. |
| 10 | Note that, a priori, it is not clear that the restrictions introduced in the two proposals match away from the semi-classical limit. In fact, Engle’s proper vertex introduces a step-function on each wedge, which depends on data on the full 4-simplex, while the step function in (70) is local on the wedge but includes the wedge orientations as additional dynamical variables. |
| 11 | Note that in [16], the expressions are directly on the triangulation instead of the dual picture. |
References
- Malament, D.B. The Class of Continuous Timelike Curves Determines the Topology of Spacetime. J. Math. Phys. 1977, 18, 1399–1404. [Google Scholar] [CrossRef]
- Hawking, S.W.; King, A.R.; Mccarthy, P.J. A New Topology for Curved Space-Time Which Incorporates the Causal, Differential, and Conformal Structures. J. Math. Phys. 1976, 17, 174–181. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Perez, A. The Spin Foam Approach to Quantum Gravity. Living Rev. Rel. 2013, 16, 3. [Google Scholar] [CrossRef]
- Bianchi, E. Spinfoam Gravity. In Loop Quantum Gravity: The First 30 Years; Ashtekar, A., Pullin, J., Eds.; WSP: Montreal, QC, Canada, 2017; pp. 97–124. [Google Scholar] [CrossRef]
- Livine, E.R. Spinfoam Models for Quantum Gravity: Overview. arXiv 2024, arXiv:2403.09364. [Google Scholar]
- Rovelli, C.; Vidotto, F. Covariant Loop Quantum Gravity; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Thiemann, T. Modern Canonical Quantum General Relativity; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bianchi, E. A short review of loop quantum gravity. Rept. Prog. Phys. 2021, 84, 042001. [Google Scholar] [CrossRef] [PubMed]
- Reisenberger, M.P.; Rovelli, C. ‘Sum over surfaces’ form of loop quantum gravity. Phys. Rev. D 1997, 56, 3490–3508. [Google Scholar] [CrossRef]
- Markopoulou, F.; Smolin, L. Causal evolution of spin networks. Nucl. Phys. B 1997, 508, 409–430. [Google Scholar] [CrossRef]
- Barrett, J.W.; Crane, L. A Lorentzian signature model for quantum general relativity. Class. Quant. Grav. 2000, 17, 3101–3118. [Google Scholar] [CrossRef]
- Markopoulou, F.; Smolin, L. Quantum geometry with intrinsic local causality. Phys. Rev. D 1998, 58, 084032. [Google Scholar] [CrossRef]
- Markopoulou, F. Quantum causal histories. Class. Quant. Grav. 2000, 17, 2059–2072. [Google Scholar] [CrossRef]
- Gupta, S. Causality in spin foam models. Phys. Rev. D 2000, 61, 064014. [Google Scholar] [CrossRef]
- Livine, E.R.; Oriti, D. Implementing causality in the spin foam quantum geometry. Nucl. Phys. B 2003, 663, 231–279. [Google Scholar] [CrossRef][Green Version]
- Pfeiffer, H. On the causal Barrett-Crane model: Measure, coupling constant, Wick rotation, symmetries and observables. Phys. Rev. D 2003, 67, 064022. [Google Scholar] [CrossRef]
- Hawkins, E.; Markopoulou, F.; Sahlmann, H. Evolution in quantum causal histories. Class. Quant. Grav. 2003, 20, 3839. [Google Scholar] [CrossRef]
- Oriti, D. The Feynman propagator for spin foam quantum gravity. Phys. Rev. Lett. 2005, 94, 111301. [Google Scholar] [CrossRef] [PubMed]
- Freidel, L.; Livine, E.R. Ponzano-Regge model revisited III: Feynman diagrams and effective field theory. Class. Quant. Grav. 2006, 23, 2021–2062. [Google Scholar] [CrossRef]
- Oriti, D. Generalised group field theories and quantum gravity transition amplitudes. Phys. Rev. D 2006, 73, 061502. [Google Scholar] [CrossRef]
- Oriti, D.; Tlas, T. Causality and matter propagation in 3-D spin foam quantum gravity. Phys. Rev. D 2006, 74, 104021. [Google Scholar] [CrossRef]
- Livine, E.R.; Terno, D.R. Quantum causal histories in the light of quantum information. Phys. Rev. D 2007, 75, 084001. [Google Scholar] [CrossRef]
- Bianchi, E.; Ding, Y. Lorentzian spinfoam propagator. Phys. Rev. D 2012, 86, 104040. [Google Scholar] [CrossRef]
- Rovelli, C.; Wilson-Ewing, E. Discrete Symmetries in Covariant LQG. Phys. Rev. D 2012, 86, 064002. [Google Scholar] [CrossRef]
- Bianchi, E.; Hellmann, F. The Construction of Spin Foam Vertex Amplitudes. SIGMA 2013, 9, 008. [Google Scholar] [CrossRef][Green Version]
- Oriti, D. Group field theory as the 2nd quantization of Loop Quantum Gravity. Class. Quant. Grav. 2016, 33, 085005. [Google Scholar] [CrossRef]
- Immirzi, G. A note on the spinor construction of Spin Foam amplitudes. Class. Quant. Grav. 2014, 31, 095016. [Google Scholar] [CrossRef][Green Version]
- Cortês, M.; Smolin, L. Spin foam models as energetic causal sets. Phys. Rev. D 2016, 93, 084039. [Google Scholar] [CrossRef]
- Immirzi, G. Causal spin foams. arXiv 2016, arXiv:1610.04462. [Google Scholar]
- Finocchiaro, M.; Oriti, D. Spin foam models and the Duflo map. Class. Quant. Grav. 2020, 37, 015010. [Google Scholar] [CrossRef]
- Dona, P.; Speziale, S. Asymptotics of lowest unitary SL(2,C) invariants on graphs. Phys. Rev. D 2020, 102, 086016. [Google Scholar] [CrossRef]
- Jercher, A.F.; Oriti, D.; Pithis, A.G.A. Complete Barrett-Crane model and its causal structure. Phys. Rev. D 2022, 106, 066019. [Google Scholar] [CrossRef]
- Regge, T. General Relativity Without Coordinates. Nuovo Cim. 1961, 19, 558–571. [Google Scholar] [CrossRef]
- Engle, J.; Livine, E.; Pereira, R.; Rovelli, C. LQG vertex with finite Immirzi parameter. Nucl. Phys. B 2008, 799, 136–149. [Google Scholar] [CrossRef]
- Engle, J. Proposed proper Engle-Pereira-Rovelli-Livine vertex amplitude. Phys. Rev. D 2013, 87, 084048. [Google Scholar] [CrossRef]
- Engle, J.; Zipfel, A. Lorentzian proper vertex amplitude: Classical analysis and quantum derivation. Phys. Rev. D 2016, 94, 064024. [Google Scholar] [CrossRef]
- Freidel, L.; Speziale, S. Twisted geometries: A geometric parametrisation of SU(2) phase space. Phys. Rev. D 2010, 82, 084040. [Google Scholar] [CrossRef]
- Bombelli, L.; Lee, J.; Meyer, D.; Sorkin, R. Space-Time as a Causal Set. Phys. Rev. Lett. 1987, 59, 521–524. [Google Scholar] [CrossRef]
- Surya, S. The causal set approach to quantum gravity. Living Rev. Rel. 2019, 22, 5. [Google Scholar] [CrossRef]
- Wieland, W.M. A new action for simplicial gravity in four dimensions. Class. Quant. Grav. 2015, 32, 015016. [Google Scholar] [CrossRef]
- Barrett, J.W.; Foxon, T.J. Semiclassical limits of simplicial quantum gravity. Class. Quant. Grav. 1994, 11, 543–556. [Google Scholar] [CrossRef]
- Barrett, J.W. First order Regge calculus. Class. Quant. Grav. 1994, 11, 2723–2730. [Google Scholar] [CrossRef]
- Misner, C.W. Feynman quantization of general relativity. Rev. Mod. Phys. 1957, 29, 497–509. [Google Scholar] [CrossRef]
- Wheeler, J.A. Geometrodynamics and the issue of final state. In Proceedings of the Les Houches Summer School of Theoretical Physics: Relativity, Groups and Topology; DeWitt, C., DeWitt, B., Eds.; Gordon and Breach Science Publishers: New York, NY, USA, 1964; pp. 317–522. [Google Scholar]
- Hawking, S.W. Quantum Gravity and Path Integrals. Phys. Rev. D 1978, 18, 1747–1753. [Google Scholar] [CrossRef]
- Oeckl, R. General boundary quantum field theory: Foundations and probability interpretation. Adv. Theor. Math. Phys. 2008, 12, 319–352. [Google Scholar] [CrossRef]
- Teitelboim, C. Quantum Mechanics of the Gravitational Field. Phys. Rev. D 1982, 25, 3159. [Google Scholar] [CrossRef]
- Baez, J.C. An Introduction to Spin Foam Models of BF Theory and Quantum Gravity. Lect. Notes Phys. 2000, 543, 25–93. [Google Scholar] [CrossRef]
- Ponzano, G.; Regge, T. Semiclassical Limit of Racah Coefficients. In Proceedings of the Spectroscopy and Group Theoretical Methods in Physics; Bloch, F., Ed.; North-Holland Publ. Co.: Amsterdam, The Netherlands, 1968. [Google Scholar]
- Martin-Dussaud, P. A Primer of Group Theory for Loop Quantum Gravity and Spin-foams. Gen. Rel. Grav. 2019, 51, 110. [Google Scholar] [CrossRef]
- Roberts, J. Classical 6j-symbols and the tetrahedron. Geom. Topol. 1999, 3, 21–66. [Google Scholar] [CrossRef]
- Rovelli, C. Zakopane lectures on loop gravity. PoS 2011, QGQGS 2011, 003. [Google Scholar] [CrossRef]
- Barrett, J.W.; Dowdall, R.J.; Fairbairn, W.J.; Hellmann, F.; Pereira, R. Lorentzian spin foam amplitudes: Graphical calculus and asymptotics. Class. Quant. Grav. 2010, 27, 165009. [Google Scholar] [CrossRef]
- Barrett, J.W.; Dowdall, R.J.; Fairbairn, W.J.; Gomes, H.; Hellmann, F. Asymptotic analysis of the EPRL four-simplex amplitude. J. Math. Phys. 2009, 50, 112504. [Google Scholar] [CrossRef]
- Ashtekar, A.; Campiglia, M.; Henderson, A. Casting Loop Quantum Cosmology in the Spin Foam Paradigm. Class. Quant. Grav. 2010, 27, 135020. [Google Scholar] [CrossRef]
- Henderson, A.; Rovelli, C.; Vidotto, F.; Wilson-Ewing, E. Local spinfoam expansion in loop quantum cosmology. Class. Quant. Grav. 2011, 28, 025003. [Google Scholar] [CrossRef]
- Christodoulou, M.; Langvik, M.; Riello, A.; Roken, C.; Rovelli, C. Divergences and Orientation in Spinfoams. Class. Quant. Grav. 2013, 30, 055009. [Google Scholar] [CrossRef]
- Halliwell, J.J.; Hartle, J.B. Wave functions constructed from an invariant sum over histories satisfy constraints. Phys. Rev. D 1991, 43, 1170–1194. [Google Scholar] [CrossRef] [PubMed]
- Engle, J. A spin-foam vertex amplitude with the correct semiclassical limit. Phys. Lett. B 2013, 724, 333–337. [Google Scholar] [CrossRef][Green Version]
- Vojinović, M. Cosine problem in EPRL/FK spinfoam model. Gen. Rel. Grav. 2014, 46, 1616. [Google Scholar] [CrossRef][Green Version]
- Bianchi, E.; Satz, A. Semiclassical regime of Regge calculus and spin foams. Nucl. Phys. B 2009, 808, 546–568. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchi, E.; Martin-Dussaud, P. Causal Structure in Spin Foams. Universe 2024, 10, 181. https://doi.org/10.3390/universe10040181
Bianchi E, Martin-Dussaud P. Causal Structure in Spin Foams. Universe. 2024; 10(4):181. https://doi.org/10.3390/universe10040181
Chicago/Turabian StyleBianchi, Eugenio, and Pierre Martin-Dussaud. 2024. "Causal Structure in Spin Foams" Universe 10, no. 4: 181. https://doi.org/10.3390/universe10040181
APA StyleBianchi, E., & Martin-Dussaud, P. (2024). Causal Structure in Spin Foams. Universe, 10(4), 181. https://doi.org/10.3390/universe10040181