Checking the ⁸Be Anomaly with a Two-Arm Electron Positron Pair Spectrometer

Abstract

We have repeated the experiment performed recently by ATOMKI Laboratory (Debrecen, Hungary), which may indicate a new particle called X17 in the literature. In order to obtain a reliable and independent result, we used a different structure of the electron–positron pair spectrometer at the VNU University of Science. The spectrometer has two arms and simpler acceptance and efficiency as a function of the correlation angle, but the other conditions of the experiment were very similar to the published ones. We could confirm the presence of the anomaly measured at E_p = 1225 keV, which is above the E_p = 1040 keV resonance.

1. Introduction

An experiment was conducted at the ATOMKI Laboratory (Debrecen, Hungary) [1] in 2016, studying the ⁷Li(p,e⁺e⁻)⁸Be nuclear reaction. The target nucleus was excited through proton capture, with the experiment set up to detect e⁺e⁻ pairs produced in the Internal Pair Creation (IPC) during the transition from the excited to the ground state of ⁸Be. The experimental setup used a set of multiwire proportional counters placed in front of $\Delta$E and E detectors, so as to determine the e⁺e⁻ opening angle, $\theta \left(e^{+}{e}^{-}\right)$. The very thin $\Delta$E detectors were made of plastic scintillators and chosen to provide excellent gamma suppression, while the much thicker E detectors were used to measure the total energy of the electron and positron. A detailed description of the experimental setup can be found in [2]. The ATOMKI collaboration observed a deviation in the $\theta \left(e^{+}{e}^{-}\right)$ distribution with respect to the expected Rose theory distribution [3], at around 140 degrees.

Zhang and Miller [4] studied the protophobic vector boson explanation in ⁸Be, by deriving an isospin relation between the coupling of photons and X17 to nucleons. They are expected to have contributions from M1 multipolarity transitions coming from the resonant proton capture (17.6 and 18.15 MeV $J^{\pi }=1^{+}$ states) as well as from the E1 multipolarity transitions resulting from the direct proton-capture process.

After 2016, the ATOMKI collaboration repeated the measurements, while improving the experimental setup in many different ways [5,6]. The anomaly kept appearing in the follow-up experiments, with no nuclear physics model being able to explain it. This led to the explanation of a new particle, beyond the Standard Model of particle physics, created and decaying to e⁺e⁻ pairs, being detected in these experiments. The hypothetical particle is now commonly referred to as X17, because of the invariant mass calculated from the e⁺e⁻ anomalies.

In addition to the ⁷Li(p,e⁺e⁻)⁸Be nuclear reaction, since 2019, the same collaboration has also studied the ³H(p,e⁺e⁻)⁴He [5] and ¹¹B(p,e⁺e⁻)¹²C [6] reactions. Different proton energies were used, leading to anomalies appearing in the $\theta \left(e^{+}{e}^{-}\right)$ distributions at different angles. All were consistent with the assumption of an $m_X\approx$ 17 MeV particle being created with different kinetic energies, leading to different opening angles between the electron–positron pairs.

The ATOMKI anomaly, being a genuine physics effect, is supported by a number of arguments as follows:

• The anomaly has been observed in ⁸Be with experimental setups using different geometries, with five and six-arm spectrometers [7].
• The anomaly has been observed using fundamentally different position-sensitive detectors: multi-wire chambers and silicon strip detectors [1,7].
• The anomaly has been observed in three different nuclei by now (⁹Be, ⁴He and ¹²C), showing up at e⁺e⁻ opening angles consistent with a single particle [1,5,6].
• The anomaly has been observed at different proton beam energies at varying e⁺e⁻ opening angles, which were also consistent with a single particle [1,5,6].
• All observed anomalies have a very high statistical significance such as 6.8$\sigma$ [1], $6.6-8.9\sigma$ [5], and $3-8\sigma$ [6].

Despite the consistency of the numerous observations at ATOMKI, more experimental data are needed to understand the nature of this anomaly. Many experiments around the world started looking for such a particle in different channels, or are planning to do so. Many of these experiments [8,9,10,11] already put constraints on the coupling of such a hypothetical particle with ordinary matter. Others are still in an R&D phase, soon to contribute to a deeper understanding of this phenomenon as concluded by the community report of the Frascati conference [8]. The report also presents a nice overview of the possible theoretical interpretation of the observed anomalies in ⁸Be, ⁴He, and ¹²C [8].

At the VNU University of Science (HUS), we have a 5SDH-2 Pelletron accelerator, of a 1.7 MV tandem electrostatic type. It can provide a proton beam with energy from 0.35 to 3.4 MeV or 0.7–5.1 MeV for the alpha beam. The accelerator was installed and operated in 2011 [12], and some initial work for the research in nuclear reaction cross-sections has been carried out [13]. This article aims to look for the ⁸Be anomaly at the VNU University of Science (HUS) with a two-arm electron–positron spectrometer specifically designed and built for this purpose.

2. Experimental Methods

In order to make our experimental results easier to reproduce, in the first part of this paper, we give a more precise description of our $e^{+}{e}^{-}$ pair spectrometer with the setup of the detectors and the electronics connected to them. This will be followed by a brief description of the data-acquisition system and the results of testing and calibrating the detectors.

2.1. The e⁺e⁻ Spectrometer

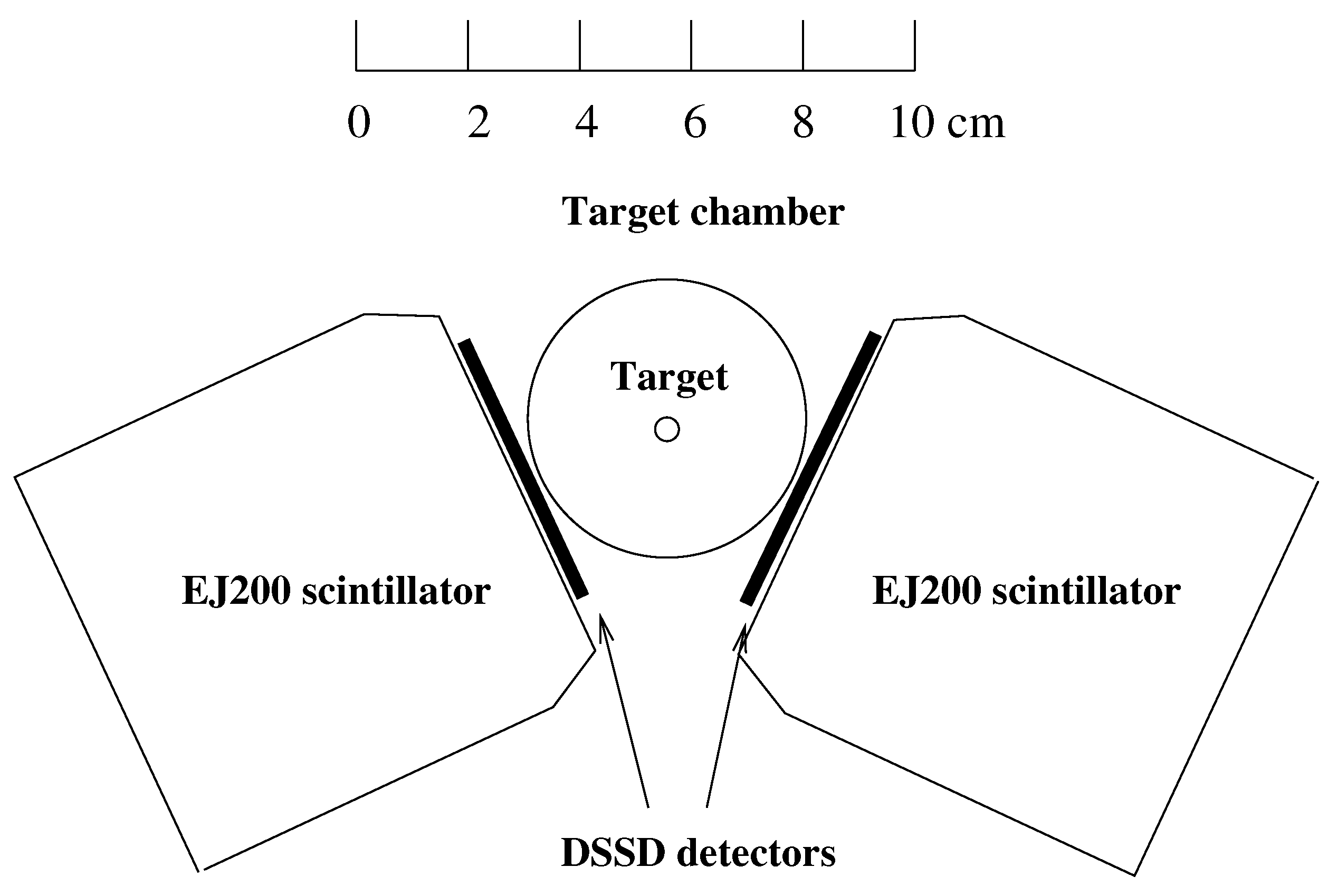
In the present experiment, two detector telescopes, including Double Silicon Strip Detectors (DSSD) and plastic scintillators, were used, placed at an angle of 140° with respect to each other. The diameter of the carbon-fiber tube of the target chamber has been reduced from 70 mm (used in ATOMKI) to 48 mm to allow a closer placement of the telescopes to the target. In this way, we could cover a solid angle at 140° similar to the one used in the ATOMKI experiment, as shown in Figure 1.

In this setup, the efficiency function has only one maximum as a function of the $e^{+}{e}^{-}$ opening angle. This angular dependence can be simulated and calibrated more robustly than for more complicated configurations. Another advantage of the setup that we used is that its sensitivity to background noise from cosmic radiation is significantly lower.

The two detector telescopes were placed at the azimuthal angles −20° and −160° with respect to the horizontal plain. This meant that cosmic rays, predominantly arriving vertically, would have a very low chance of hitting both telescopes at the same time.

For the detection of 1–20 MeV e⁺ and e⁻ particles, which are considered high-energy in nuclear physics, Geant4 (Release 10.6.3) [14] calculations were performed for different detector materials. This included plastic scintillators, Ge semiconductor detectors (Ortec, CA, USA) and LaBr₃ scintillators. A much better energy resolution could be achieved with the latter two types of detectors than with a plastic scintillator. An FWHM below 20 keV can be achieved at 17.6 MeV for the Ge detector and 150 keV for the LaBr₃ detector. However, our simulations also showed that in the case of high-density and high Z detectors, the efficiency of the total energy detection in the energy response function is greatly reduced compared to the integral of the response function. The ratio between the numbers of full energy events and total recorded events is smaller than 1.5% at an electron energy of 18 MeV for a 3 × 3 inch² LaBr₃ detector (Canberra, CT, USA). In materials with higher atomic numbers, the e⁺ and e⁻ particles slow down faster, and thus the probability of generating bremsstrahlung radiation is higher. However, there is a high probability that these radiations will escape the detector. This is why the probability of detecting e⁺ and e⁻ particles at full energy is reduced in these high-Z materials. Therefore, we used special plastic scintillators for this task. The dimensions of the EJ200 plastic scintillators were chosen (82 × 82 × 80 mm³ each) in such a way that these high-energy particles would be completely stopped in them.

To collect the light generated by the e⁺e⁻ particles slowing down in the detector from all corners with the same efficiency, the SCIONIX company provided the detector with specially shaped light guides. The surfaces of both the detectors and the light guides were diamond-polished. The collected light was converted to an electronic signal by Hamamatsu photomultiplier tube (PMT)-type R594 assemblies.

The time resolution of the detector turned out to be adequate despite the large size of the detector and multiple light reflections inside. It was measured with a ⁶⁰Co source between the two detectors, and found to be less than 1 ns, as shown in Figure 2.

In the absence of a high-energy electron source, the energy resolution of the detector could only be determined with the help of e⁺e⁻ pairs from internal pair creation. We will come back to this in Section 2.4 in connection with the energy calibration of the detectors.

Double-sided Silicon Strip Detectors (DSSD), W1(DS)-500 from Micron, West Sussex, UK, were used to measure the energy loss of the $e^{+}{e}^{-}$ particles and their directions. The DSSDs were purchased from Micron Semiconductor. They consist of 16 sensitive strips on the junction side and 16 orthogonal strips on the ohmic side. Their element pitch is 3.01 mm for a total coverage of 49.5 × 49.5 mm². They are mounted on a printed circuit board (PCB), with 34 pins on one edge for their readout. These are connected via 34-conductor flat cables to the pre-amp boxes.

Mesytec MUX32-type 32-channel preamplifiers, linear amplifiers, timing filter amplifiers, timing discriminators, and multiplexers were used. The full width of the fifth order-shaped energy signals is 1.5 μs, and the full rate capability of the MUX32 unit is 800 kHz. The energy resolution of the channels is 5.5 keV Si + 0.064 keV/pF. The timing filter amplifier signals are shaped with a 20 ns integration time and a 100 ns differentiation time, followed by leading edge discriminators. It is a very fast multiplexed preamplifier, shaper, and discriminator combination with very good energy and timing resolutions. The MUX-32 consists of two MUX-16s; each MUX-16 manages 16 inputs, up to two simultaneous responding channels are identified, and two amplitudes plus the two corresponding amplitude-coded addresses (position signals) are sent to the outputs. Therefore, it can manage double-hit events with full energy and position information in the x and y directions. These modules are especially well-suited for DSSD detectors.

By properly shielding and grounding the detectors, using 10 μm thick Al foils mounted on PCBs both at the front and the back side of the detectors, and shielding the flat cables and connectors, we managed to reduce their electronic noise and could lower the levels of the discriminators below 50 keV. For simplicity, the detectors are operated in air without dedicated cooling. The first test and calibration of the detectors were performed with a mixed $\alpha$-source containing ²³⁹Pu, ²⁴⁴Cm, and ²⁴¹Am. The experimental configuration was used in Geant4 simulation code [14]. All materials used to construct the experiment have been included in the simulation geometry. Therefore, the energy loss in the Al foil and in the air (5 mm) were taken into account.

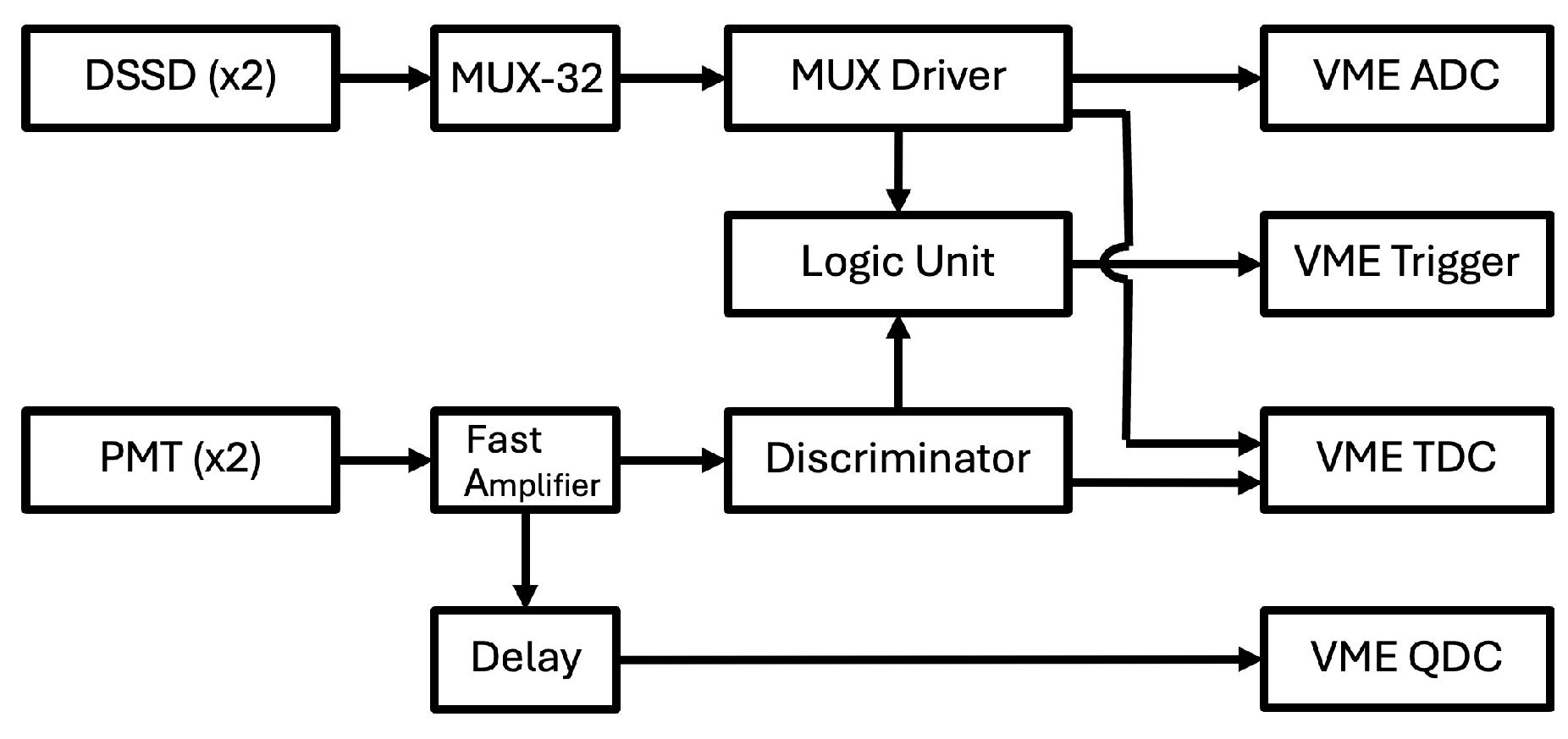
2.2. Data-Acquisition System

The data-acquisition system uses Versa Module Eurocard (VME), Analog-to-Digital Converter (ADC), Time-to-Digital Converter (TDC), and Charge-to-Digital Converter (QDC) units, which were read out with the help of a commodity desktop PC. The software used for configuring the VME devices and recording the data collected can be found in [15,16].

Constant Fraction Discriminators (CFDs) and TDC units were used to determine the arrival time of the signals coming from the plastic scintillators, and QDCs were used to digitize their energy signals. The block diagram of the electronics connected to the detectors is shown in Figure 3. The signals received from the MUX32 multiplexer were digitized with the help of ADC and TDC units.

2.3. Calibration of the DSSD Detectors

The energy measured by the DSSD was calibrated using information from the e⁺e⁻ particles, which were produced by the ⁷Li(p,$\gamma$)⁸Be nuclear reaction. The energy of the bombarding protons was set to the E_p = 441 keV resonance. When creating the spectrum, we required a real coincidence between the DSSD detector and the plastic scintillator located behind it by requiring a time difference smaller than 400 ns. The two plastics measured the total energy of the e⁺e⁻ particles. We also required this energy to be in the 6–20 MeV range. The experimental configuration was used in Geant4 simulation code [14]. Figure 4 shows the energy loss distribution of electrons and positrons passing through one of the DSSD detectors. The histograms show reasonably good agreement between the experimental and simulated distributions; however, we obtained some differences around 100 keV and 350 keV. The former can be caused by some electronic noise, while the latter is caused by the events when both the e⁺ and e⁻ created during the internal pair production passed through the same DSSD detector. The detection efficiency with a CFD threshold of 50 keV was greater than 97% for electrons and positrons. The 120 keV lower limit on the electron/positron energy was applied in the event selection.

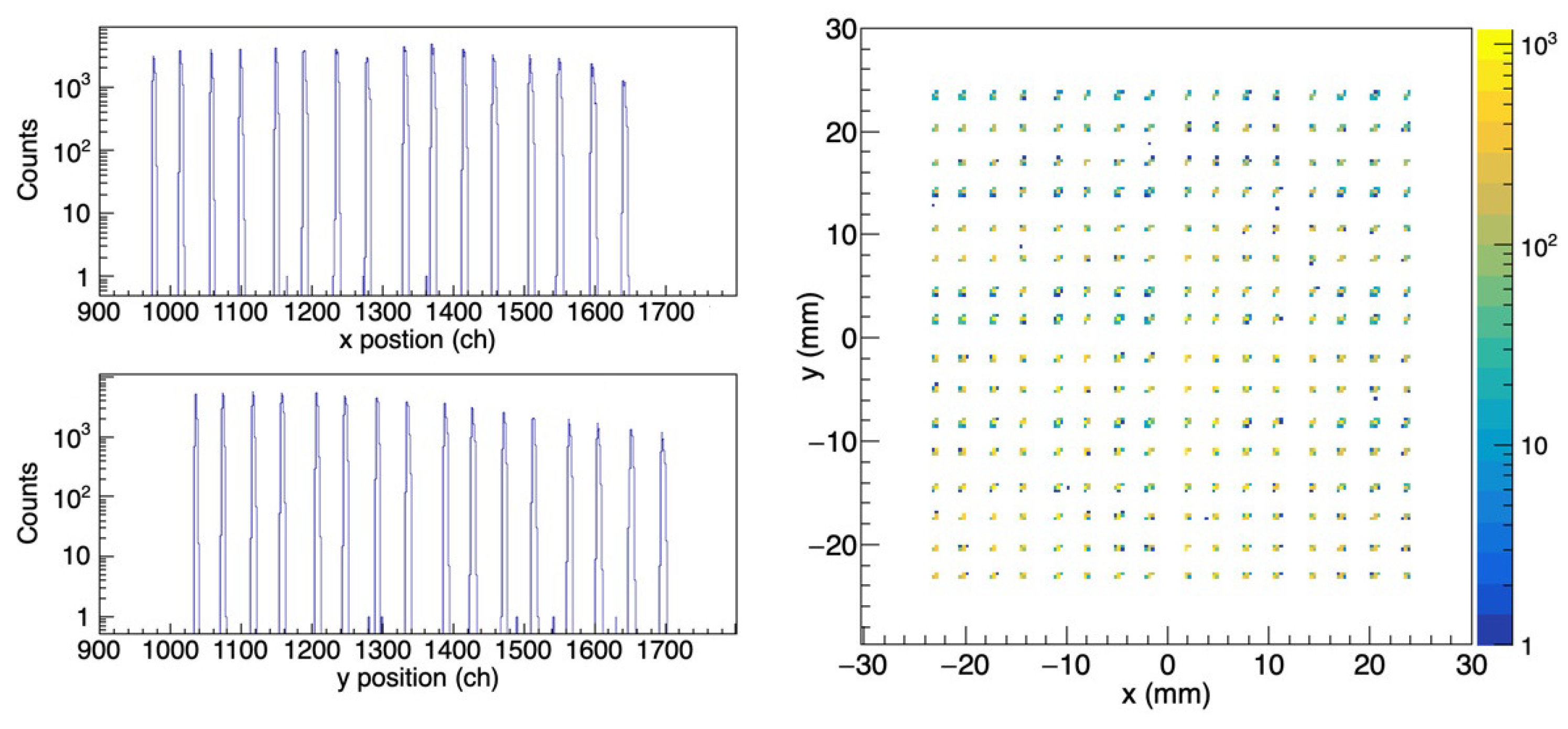
The histograms in Figure 5 show the (non-calibrated) distribution of the x and y coordinates of the impact points of the e⁺/e⁻ particles that hit the DSSD detector. The peaks of the fence spectrum correspond to the coordinates of particles passing through the individual silicon strips. As shown, the assignment of the recorded data to the x and y strips is very clear. The width of the DSSD was used to convert the recorded data to positions on the cm scale with thew origin at the center (the two-dimensional plot in Figure 5). Of the 70,000 events recorded for these distributions, only around 3% of events had to be excluded due to missing information in either the x or y directions.

2.4. Calibration of the Scintillation Detectors

The energy distribution of the electrons and positrons in the individual internal pair creation is contiguous. However, if the electron and positron lose their energy in the same detector, the energy distribution of such events will show peaks at the transition energies–$2m_e{c}^2$. The scintillator detectors were calibrated using such events. If the detectors are close enough to the target, there is a high probability of the above internal energy summing. The energy spectrum measured by the scintillators for events selected by gating on double hits in the DSSD detector can be found in Figure 6.

3. Experimental Results

The experiments were performed in Hanoi (Vietnam) at the 1.7 MV Tandem accelerator of HUS, with different proton beam energies between 0.4 $\le E_p\le 1.3$ MeV. The typical beam currents for these experiments were from 1 to 1.5 μA.

LiF targets with thicknesses of ≈30 μg/cm² evaporated onto 10 μm thick Al foils, as well as Li₂O targets with thicknesses of ≈0.3 mg/cm², were used on 1 μm thick Ni foils in order to maximize the yield of the $e^{+}{e}^{-}$pairs. The LiF is a more stable target, and it easily evaporates. For that reason, we used it at a low bombarding energy (E_p = 441 keV, E_x = 17.6 MeV) to calibrate the spectrometer. However, if we would increase the beam energy from 441 keV (E_x = 17.6 MeV) to 1.04 MeV (E_x = 18.15 MeV), the cross-section of the ¹⁹F(p,$\alpha$)¹⁶O reaction would increase very fast and the created e⁺e⁻ pairs coming from the decay of the 6.05 MeV E₀ transition would overload our electronics and data-acquisition equipment, and observing e⁺e⁻ pairs from the 18.15 MeV transition would not be feasible.

$\gamma$ radiations were detected by a 3″ × 3″ NaI(Tl) detector also monitoring any potential target losses. The detector was placed at a distance of 25 cm from the target at an angle of 90 degrees to the beam direction.

A single energy spectrum measured by the scintillators and gated by “multiplicity = 2” events in the DSSD detector, which means that both the electron and positron coming from the internal pair creation were detected by the same telescope, is shown in Figure 6 for telescope 1. Figure 6 clearly shows the transitions from the decay of the 17.6 MeV resonance state to the ground and first excited states in ⁸Be. The cosmic ray background was already subtracted from that. The energy resolution of the plastic scintillator at 17.6 MeV was extremely good (5.2% FWHM), proving the very good light collection from the whole detector. The “background” below the peak comes mostly from the wide (1.5 MeV) transition going to the first excited state of ⁸Be and from the tail of the 17.6 MeV transition. The energy resolution of the 6.05 MeV (¹⁶O) peak is also good.

In order to check the effective thickness of the Li₂O targets, we measured the excitation function of ⁸Be via the ⁷Li(p,$\gamma$)⁸Be reaction by scanning the proton beam energies from 441 keV to 1300 keV. The events with multiplicity-2 in the DSSD and measured energies in the plastic scintillator larger than 10 MeV were counted, and their rate is plotted in Figure 7. Two resonance peaks were observed at the proton beam energies of around 441 and 1040 keV [17,18]. The width of the resonance shows the effect of the target thickness. For the 441 keV resonance, it was found to be approximate 150 keV, which means a target thickness of about 0.44 mg/cm², since the energy loss of the protons is 340 keV/mg/cm².

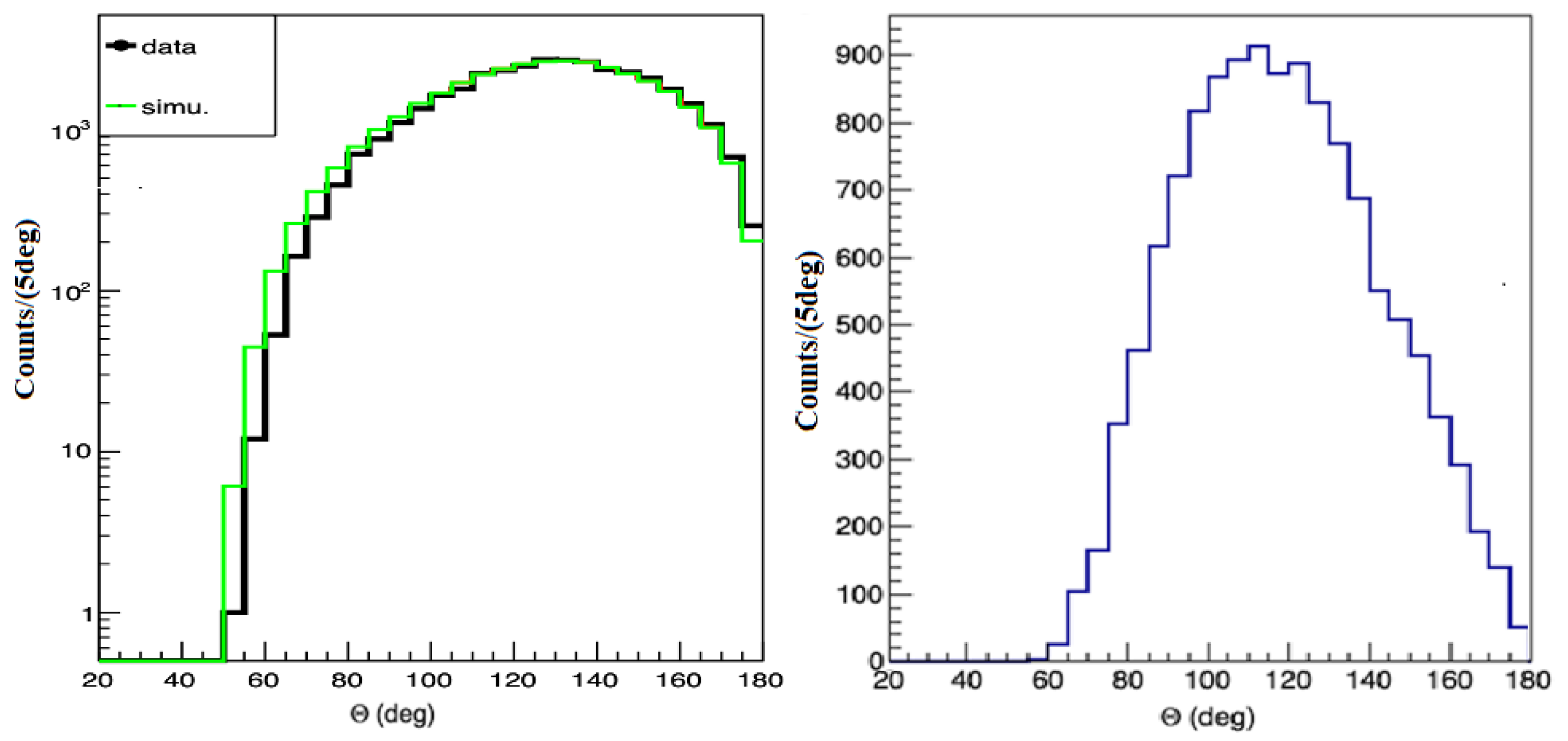
The efficiency (acceptance) as a function of the correlation angle in comparison to isotropic emission was determined from the same data set by using uncorrelated e⁺e⁻ pairs formed out of separate, single events [2]. To do this, uncorrelated e⁺e⁻ pairs were recorded during the experiment. The analysis selected event pairs with uncorrelated electrons/positrons hitting different telescopes in the events. The opening angle distribution of electron/positron pairs from such events is shown by the black line in Figure 8 (left). The green line is a simulation curve produced using Geant4. They show quite a good agreement between the estimated experimental and simulation efficiencies.

Coincidence events, with both arms of the spectrometer detecting e⁺/e⁻ particles, were also recorded. The opening angle distribution of e⁺e⁻ pairs from such events is shown in Figure 8 (right). The cosmic background data were collected and analyzed similarly to the experimental data and subtracted. The total time collection of both data sets has been normalized.

In the first experiment, we used a proton beam energy of 411 keV to bombard the LiF target. Through this, the ⁸Be nucleus would be created in the 17.6 MeV excited state. Figure 9 shows the angular correlations of e⁺e⁻ pairs originating from the transition of this 17.6 MeV excited state of ⁸Be to its ground state. The Monte Carlo detector simulations of the experiment were performed using Geant4 and are shown as histograms in Figure 9 for M1 (dash-dotted line) and E1 (dotted line) multipolarity transitions. The simulation included the geometries of the target chamber, target backing, and detector arm assemblies. The interaction of the generated electrons, positrons, and gamma rays was then simulated with the experimental setup. Internal Pair Creation (IPC) events, generated from both the possible E1 and M1 transitions, were simulated in this way. The combination of the E1+M1 distributions shows a good agreement with the experimental data when the contributing fractions are fitted. The dominant M1 part (87.4%) is clearly understood since it is a 1⁺ –> 0⁺ transition. The 12.8% E1 mixing can also be understood, since the energy loss in the target was about 150 keV, which is about 14 times larger than the width of the resonance ($\Gamma$ = 10.7 keV) [17], and we integrated a reasonable amount from the proton direct-capture part of the excitation function [18] as well, which has a multipolarity of E1.

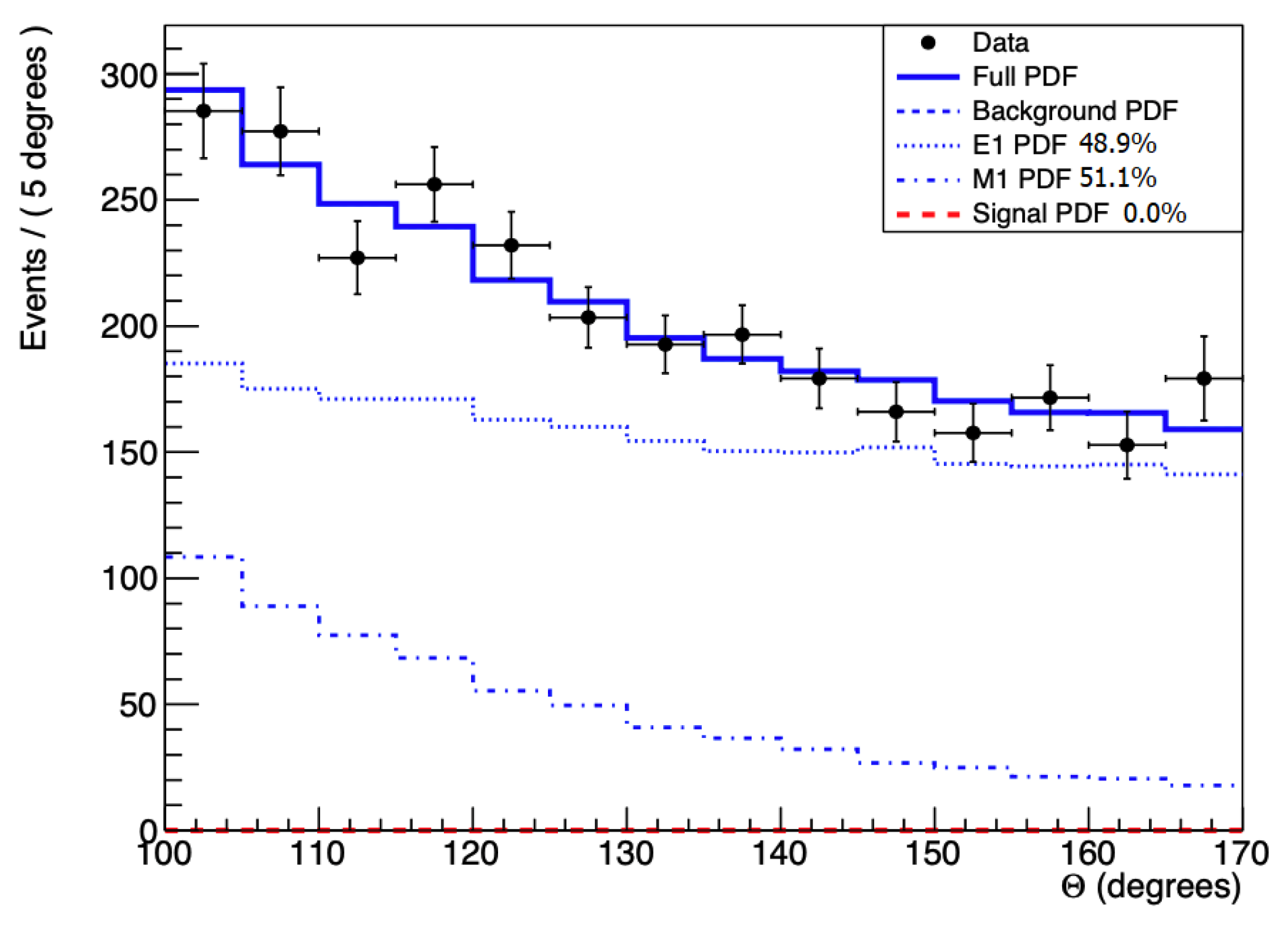
In the second experiment, we changed the proton beam energy to 800 keV at the off-resonance energies. With the same method used to build the total simulation curve and show the experimental data in Figure 10, we can see the simulated curve go through the middle of data points. There is no systematic deviation of the experimental points from the IPC simulation curve. As can be seen in the insert of Figure 10, the background could be described well with 48.9% E1 and 51.1% M1 components. The E1 component comes from the direct proton capture, while the 51.1% M1 component comes from the tails of the E_p = 441 keV and 1040 keV resonances. We did not observe any contribution from the X17 decay as Sas, et al. [19] observed before. Since during this experiment the target was burned out (punctured) many times, the effective energy of the protons was changing and may have washed out the anomaly caused by the X17 to e⁺e⁻ decay.

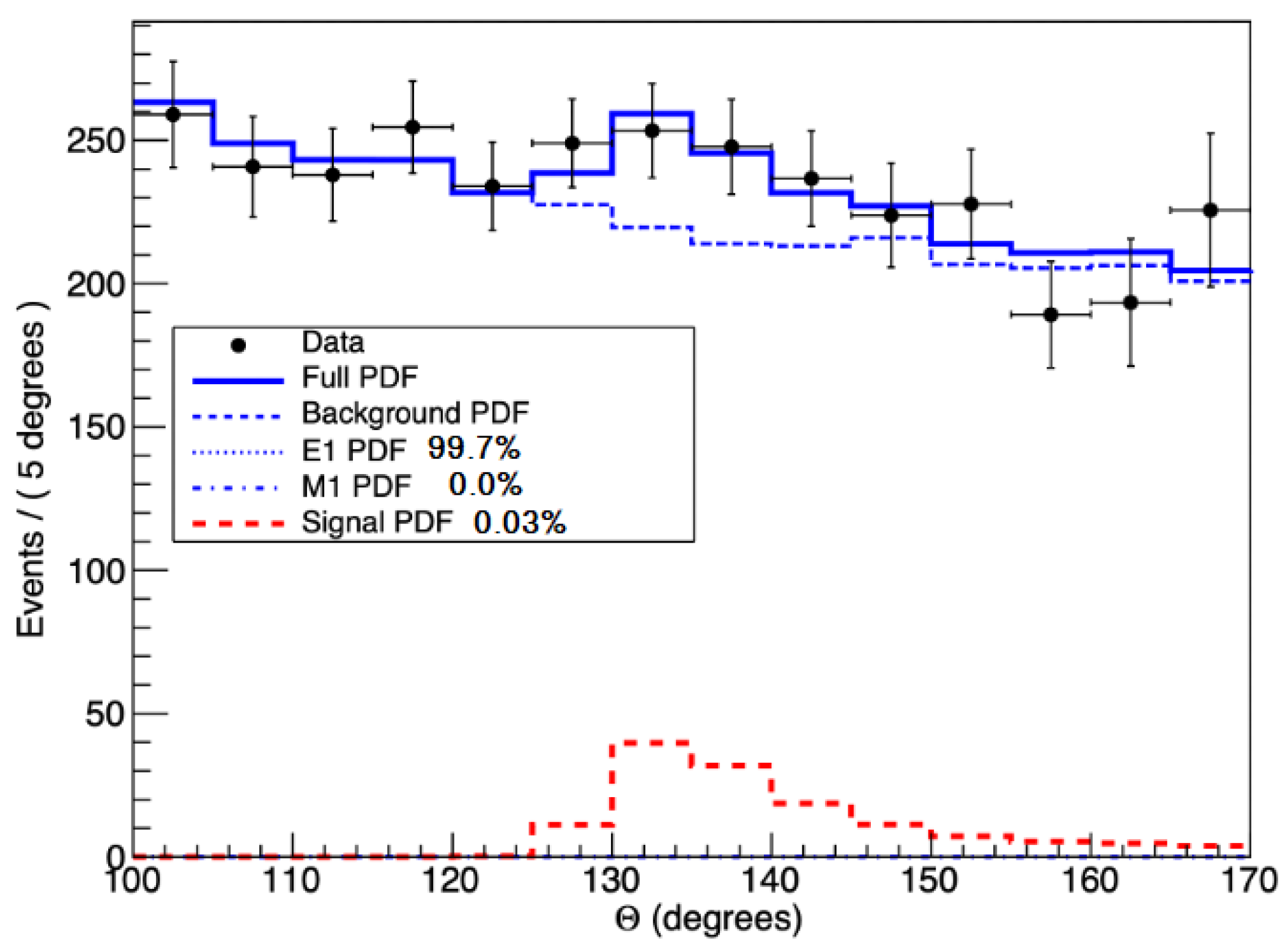
Finally, we changed the proton beam energy to 1225 keV, which is higher than the 1040 keV resonance, to check the off-resonance region. The combined IPC simulation curve and experimental data for this transition are shown in Figure 11. It clearly shows a deviation in the e⁺e⁻ opening angle distribution between the data and the simulation around ${135}^{\circ }$. This deviation is in agreement with the result published by the ATOMKI collaboration in [1]. By assuming that the deviation is coming from the creation and immediate decay of an intermediate particle to an e⁺e⁻ pair [3], we can calculate a mass of $m_X{c}^2=16.66\pm 0.47$ (stat.) MeV for this particle with a confidence above 4$\sigma$. As can be seen in the insert of Figure 11, we could describe the background with pure E1 distribution, which shows that we are indeed in the off-resonance region.

The systematic uncertainty on the calculated particle mass from the beam spot’s position was estimated using a series of simulations using different beam spot positions. This resulted in a $\Delta m_X{c}^2$(systematic)= $\pm 0.35$ MeV uncertainty. The additional potential systematic uncertainty caused by e⁺e⁻ pairs induced by external pairing in the DSSD detectors by gamma radiation was evaluated in the simulation.

Based on the best-fit results shown in Figure 11, it can be concluded that X17-boson particles were created simultaneously with the IPC due to the E1 transition in this experiment. The branching ratio of the e⁺e⁻ decay of such bosons to IPC and the $\gamma$ decay of the 18.15 MeV level is found to be 2.8 × 10⁻³ and 1.1 × 10⁻⁵, respectively. It seems that the X17 particle is created in the E1 transition and not in the M1 one. In Ref. [1], they obtained a branching ratio of 5.8 × 10⁻⁶, which is about half of the value we obtained here. They performed the experiment on the 1040 keV resonance, and in this way the M1 contribution of the resonance may not produced any X17 particles.

4. Summary

We successfully built a two-arm e⁺e⁻ spectrometer in Hanoi. The spectrometer was tested and calibrated using the 17.6 MeV M1 transition excited in the ⁷Li(p,e⁺e⁻)⁸Be reaction. We have obtained a nice agreement between the experimentally determined acceptance of the spectrometer and the one coming from our simulation. The angular correlation of the e⁺e⁻ pairs measured for the 17.6 MeV transition (E_p = 441 keV) agrees well with the simulated one dominated by the M1 transition, and no anomaly was observed for this. However, a significant anomaly (>4σ) was observed for E_p = 1225 keV, which is the off-resonance region above the E_p = 1040 keV resonance, at around 135°, in agreement with the ATOMKI results published in 2016 [1]. The mass of the hypothetical particle from this result was obtained to be $16.66\pm 0.47$ (statistical) $\pm 0.35$ (systematic) MeV. In the future, we plan to upgrade the spectrometer to obtain a wider angular acceptance.