Jet Precession in Gamma-Ray Bursts
Abstract
1. Introduction
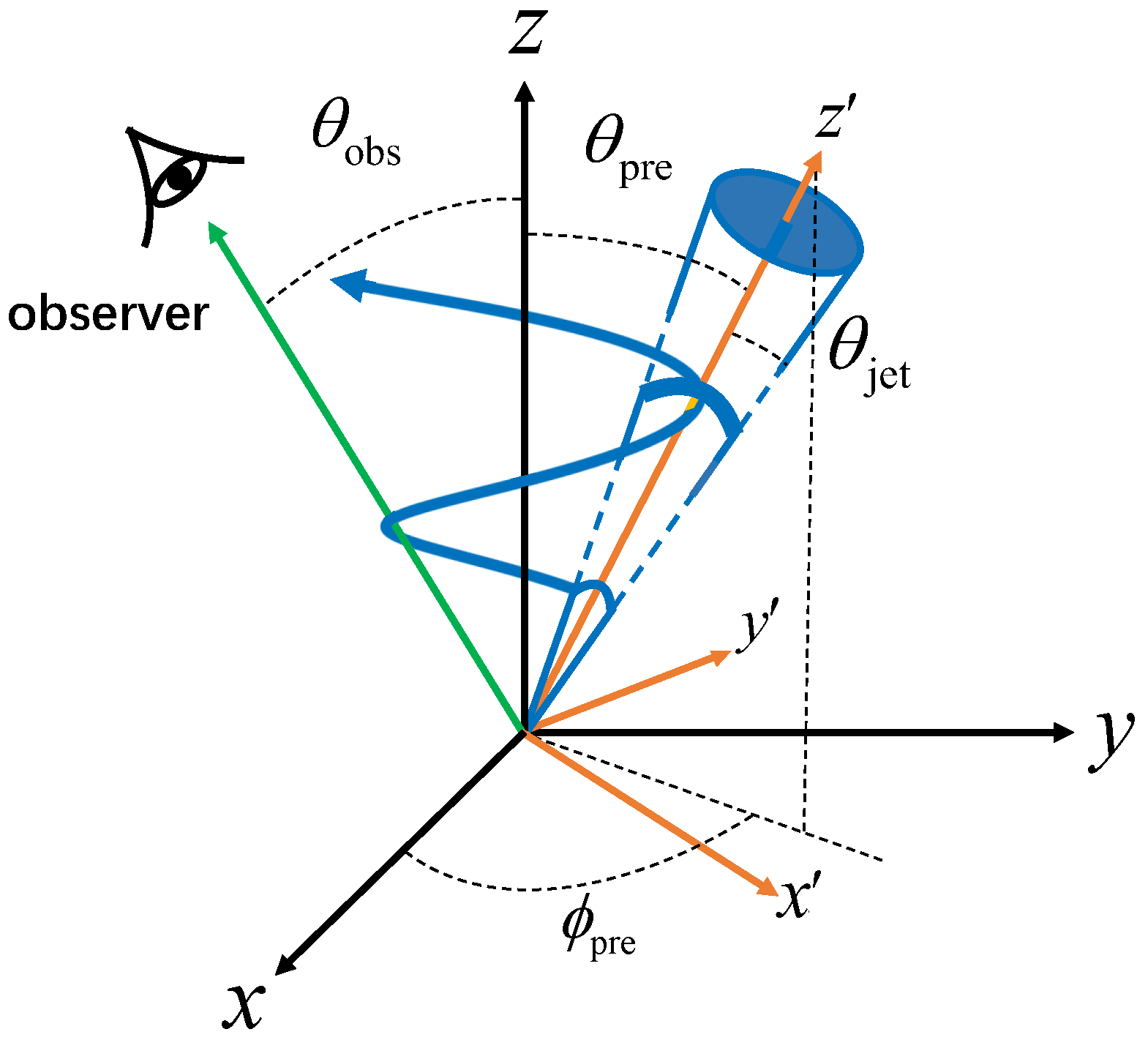
2. Light Curves with Jet Precession in GRBs
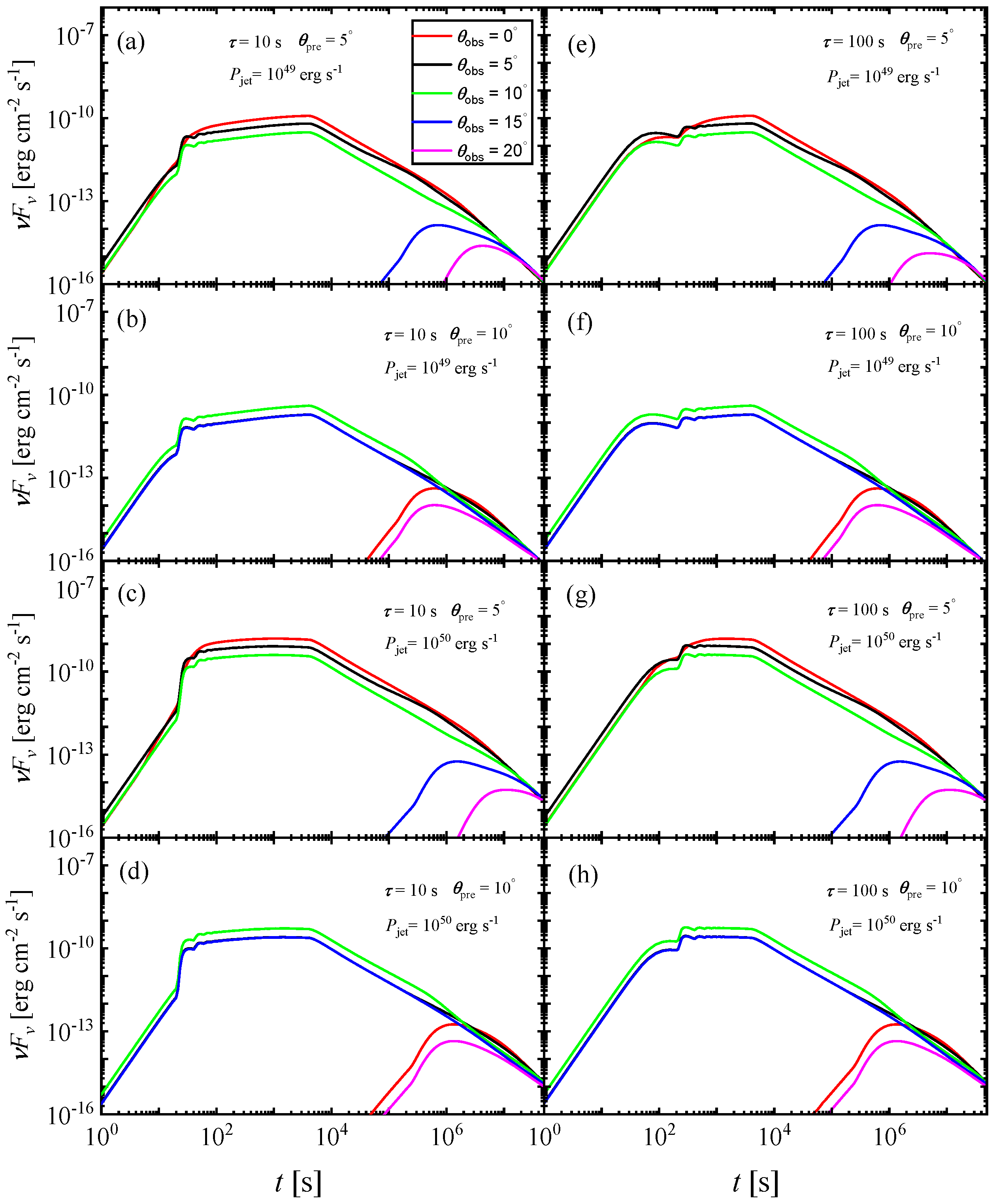
2.1. Prompt Light Curves with Jet Precession
2.2. Afterglow Light Curves with Jet Precession
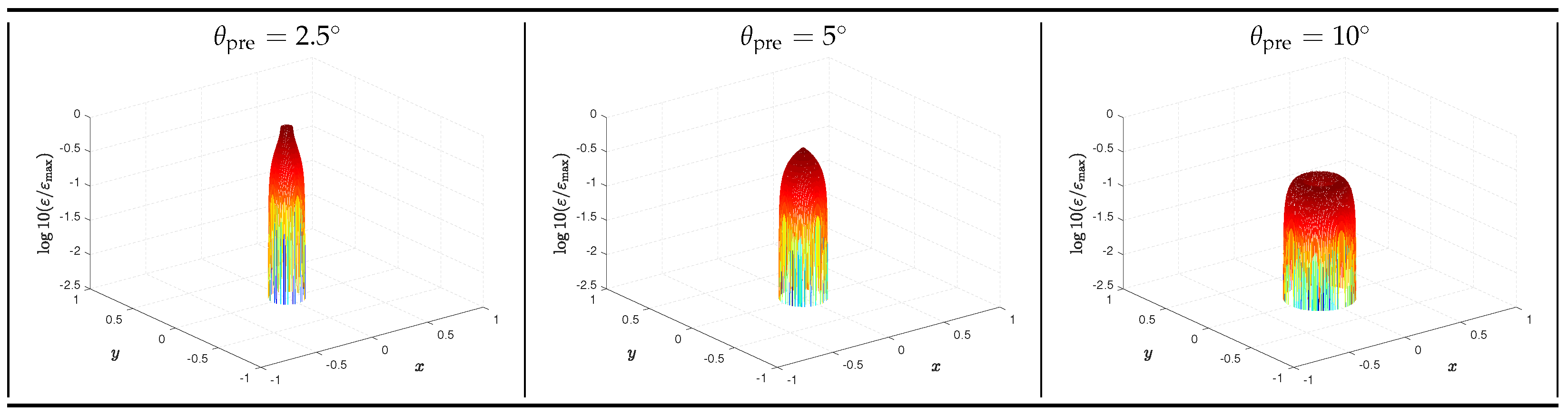
3. Ejecta Structures with Jet Precession in GRBs
4. Polarization Signal with Jet Precession in GRBs
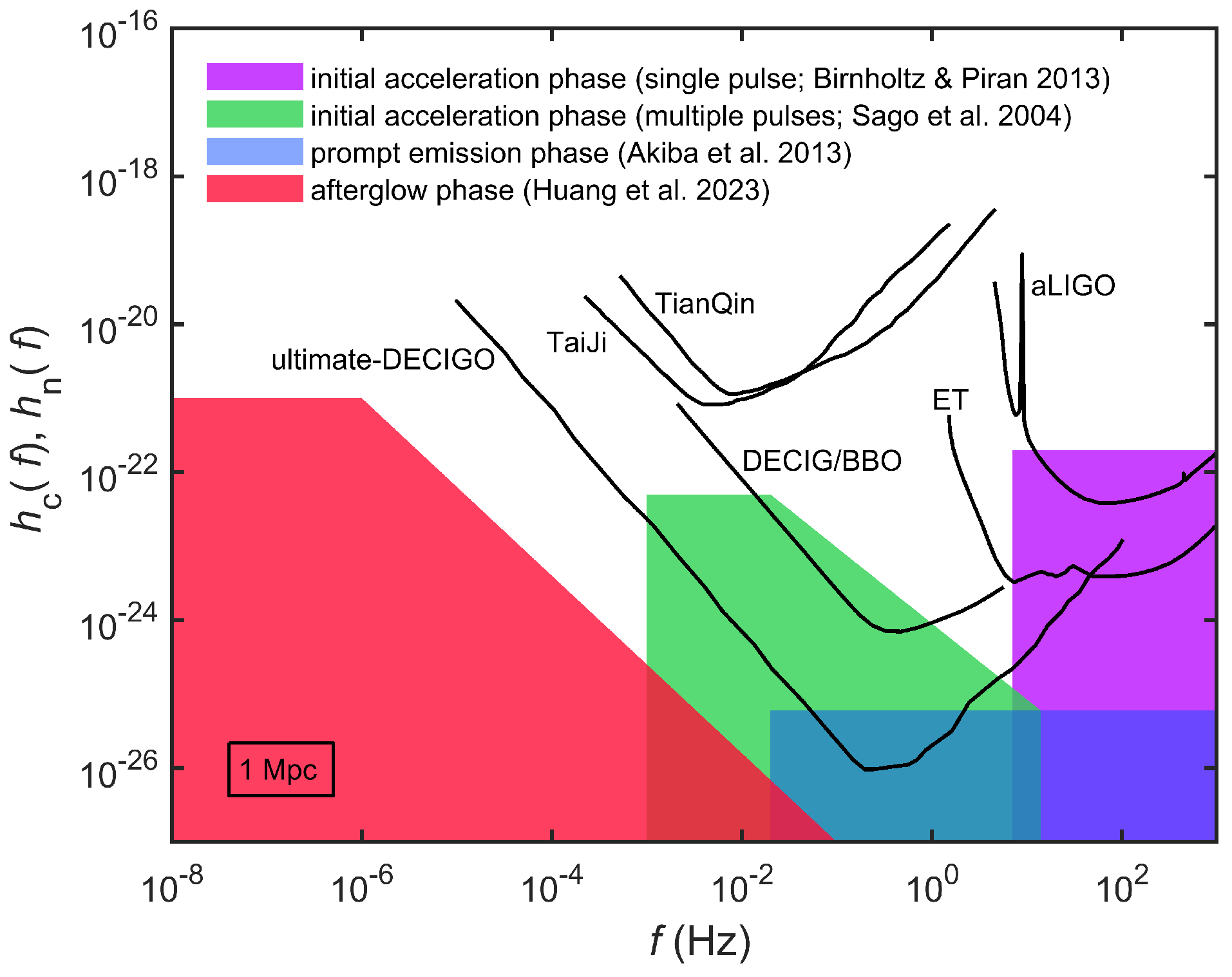
5. GW Signal with Jet Precession in GRBs
6. Summary
Funding
Conflicts of Interest
References
- Caproni, A.; Abraham, Z.; Monteiro, H. Parsec-scale jet precession in BL Lacertae (2200+420). Mon. Not. R. Astron. Soc. 2013, 428, 280–290. [Google Scholar] [CrossRef]
- Qian, S.-J.; Britzen, S.; Witzel, A.; Krichbaum, T.P.; Gan, H.-Q.; Gao, L. A possible precessing nozzle and the Lense-Thirring effect in blazar 3C 454.3. Res. Astron. Astrophys. 2014, 14, 249–274. [Google Scholar] [CrossRef]
- Caproni, A.; Abraham, Z.; Motter, J.C.; Monteiro, H. Jet precession driven by a supermassive black hole binary system in the BL Lac object PG 1553+113. Astrophys. J. Lett. 2017, 851, L39. [Google Scholar] [CrossRef]
- Britzen, S.; Fendt, C.; Witzel, G.; Qian, S.-J.; Pashchenko, I.N.; Kurtanidze, O.; Zajacek, M.; Martinez, G.; Karas, V.; Aller, M.; et al. OJ287: Deciphering the ‘Rosetta stone’ of blazars. Mon. Not. R. Astron. Soc. 2018, 478, 3199–3219. [Google Scholar] [CrossRef]
- Qian, S.J.; Britzen, S.; Witzel, A.; Krichbaum, T.P.; Kun, E. Model simulation of jet precession in quasar PG 1302–102. Astron. Astrophys. 2018, 615, A123. [Google Scholar] [CrossRef]
- Britzen, S.; Zajaček, M.; Gopal-Krishna; Fendt, C.; Kun, E.; Jaron, F.; Sillanpää, A.; Eckart, A. Precession-induced Variability in AGN Jets and OJ 287. Astrophys. J. 2023, 951, 106. [Google Scholar] [CrossRef]
- Caproni, A.; Mosquera Cuesta, H.J.; Abraham, Z. Observational Evidence of Spin-induced Precession in Active Galactic Nuclei. Astrophys. J. Lett. 2004, 616, L99–L102. [Google Scholar] [CrossRef]
- Kudryavtseva, N.A.; Britzen, S.; Witzel, A.; Ros, E.; Karouzos, M.; Aller, M.F.; Aller, H.D.; Teräsranta, H.; Eckart, A.; Zensus, J.A. A possible jet precession in the periodic quasar B0605-085. Astron. Astrophys. 2011, 526, A51. [Google Scholar] [CrossRef]
- Qian, S.J.; Britzen, S.; Witzel, A.; Krichbaum, T.P.; Gan, H.Q. Possible quasi-periodic ejections in quasar B1308+326. Astron. Astrophys. 2017, 604, A90. [Google Scholar] [CrossRef]
- Britzen, S.; Fendt, C.; Zajaček, M.; Jaron, F.; Pashchenko, I.; Aller, M.F.; Aller, H.D. 3C 84: Observational Evidence for Precession and a Possible Relation to TeV Emission. Galaxies 2019, 7, 72. [Google Scholar] [CrossRef]
- Nandi, S.; Caproni, A.; Kharb, P.; Sebastian, B.; Roy, R. Double-peaked Lines, Dual VLBI Components, and Precessing Jets in J1328+2752. Astrophys. J. 2021, 908, 178. [Google Scholar] [CrossRef]
- Lobanov, A.P.; Roland, J. A supermassive binary black hole in the quasar 3C 345. Astron. Astrophys. 2005, 431, 831–846. [Google Scholar] [CrossRef]
- Lu, J.-F.; Zhou, B.-Y. Observational Evidence of Jet Precession in Galactic Nuclei Caused by Accretion Disks. Astrophys. J. Lett. 2005, 635, L17–L20. [Google Scholar] [CrossRef]
- Brown, R.L. Precessing jets in Sagittarius A: Gas dynamics in the central parsec of the galaxy. Astrophys. J. 1982, 262, 110–119. [Google Scholar] [CrossRef]
- Romero, G.E.; Chajet, L.; Abraham, Z.; Fan, J.H. Beaming and precession in the inner jet of 3C 273—II. The central engine. Astron. Astrophys. 2000, 360, 57–64. [Google Scholar]
- Caproni, A.; Abraham, Z. Can long-term periodic variability and jet helicity in 3C 120 be explained by jet precession? Mon. Not. R. Astron. Soc. 2004, 349, 1218–1226. [Google Scholar] [CrossRef]
- Caproni, A.; Abraham, Z. Precession in the Inner Jet of 3C 345. Astrophys. J. 2004, 602, 625–634. [Google Scholar] [CrossRef]
- Martí-Vidal, I.; Marcaide, J.M.; Alberdi, A.; Pérez-Torres, M.A.; Ros, E.; Guirado, J.C. Detection of jet precession in the active nucleus of M 81. Astron. Astrophys. 2011, 533, A111. [Google Scholar] [CrossRef]
- Gower, A.C.; Gregory, P.C.; Unruh, W.G.; Hutchings, J.B. Relativistic precessing jets in quasars and radio galaxies: Models to fit high resolution data. Astrophys. J. 1982, 262, 478–496. [Google Scholar] [CrossRef]
- Ekers, R.D.; Fanti, R.; Lari, C.; Parma, P. NGC 326: A radio galaxy with a precessing beam. Nature 1978, 276, 588–590. [Google Scholar] [CrossRef]
- Florido, E.; Battaner, E.; Sanchez-Saavedra, M.L. Spatial Distribution of Antisymmetrically Curved Extragalactic Radio Jets. Astrophys. Space Sci. 1990, 164, 131–137. [Google Scholar] [CrossRef]
- Proctor, D.D. Morphological Annotations for Groups in the First Database. Astrophys. J. Suppl. Ser. 2011, 194, 31. [Google Scholar] [CrossRef]
- Sethi, S.; Kuźmicz, A.; Jamrozy, M.; Slavcheva-Mihova, L. Discovery of a 100 kpc Narrow Curved Twin Jet in the S-shaped Giant Radio Galaxy J0644+1043. Astrophys. J. 2024, 969, 156. [Google Scholar] [CrossRef]
- Pajdosz-Śmierciak, U.; Śmierciak, B.; Jamrozy, M. Possible jet reorientation in low-frequency radio structures of blazars. Mon. Not. R. Astron. Soc. 2022, 514, 2122–2134. [Google Scholar] [CrossRef]
- Lense, J.; Thirring, H. Über den Einfluß der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Phys. Z. 1918, 19, 156. [Google Scholar]
- Bardeen, J.M.; Petterson, J.A. The Lense-Thirring Effect and Accretion Disks around Kerr Black Holes. Astrophys. J. Lett. 1975, 195, L65. [Google Scholar] [CrossRef]
- Nealon, R.; Price, D.J.; Nixon, C.J. On the Bardeen-Petterson effect in black hole accretion discs. Mon. Not. R. Astron. Soc. 2015, 448, 1526–1540. [Google Scholar] [CrossRef]
- Sarazin, C.L.; Begelman, M.C.; Hatchett, S.P. Disk-driven precession in SS 433. Astrophys. J. Lett. 1980, 238, L129–L132. [Google Scholar] [CrossRef]
- Lu, J.F. Accretion disk-driven jet precession in active galactic nuclei. Astron. Astrophys. 1990, 229, 424–426. [Google Scholar]
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Massive black hole binaries in active galactic nuclei. Nature 1980, 287, 307–309. [Google Scholar] [CrossRef]
- Roos, N.; Kaastra, J.S.; Hummel, C.A. A massive binary black hole in 1928+738? Astrophys. J. 1993, 409, 130. [Google Scholar] [CrossRef]
- Katz, J.I. A precessing disk in OJ 287? Astrophys. J. 1997, 478, 527. [Google Scholar] [CrossRef]
- Britzen, S.; Roland, J.; Laskar, J.; Kokkotas, K.; Campbell, R.M.; Witzel, A. On the origin of compact radio sources. The binary black hole model applied to the gamma-bright quasar PKS 0420-014. Astron. Astrophys. 2001, 374, 784. [Google Scholar] [CrossRef]
- Crampton, D.; Hutchings, J.B. The SS 433 binary system. Astrophys. J. 1981, 251, 604. [Google Scholar] [CrossRef]
- Margon, B. Observations of SS 433. Ann. Rev. Astron. Astrophys. 1984, 22, 507. [Google Scholar] [CrossRef]
- Fabrika, S. The jets and supercritical accretion disk in SS433. Astrophys. Space Phys. Rev. 2004, 12, 1. [Google Scholar] [CrossRef]
- Veledina, A.; Poutanen, J.; Ingram, A. A unified Lense-Thirring precession model for optical and X-ray quasi-periodic oscillations in black hole binaries. Astrophys. J. 2013, 778, 165. [Google Scholar] [CrossRef]
- de Ruiter, I.; van den Eijnden, J.; Ingram, A.; Uttley, P. A systematic study of the phase difference between QPO harmonics in black hole X-ray binaries. Mon. Not. R. Astron. Soc. 2019, 485, 3834–3844. [Google Scholar] [CrossRef]
- Ma, X.; Tao, L.; Zhang, S.-N.; Zhang, L.; Bu, Q.-C.; Ge, M.-Y.; Chen, Y.-P.; Qu, J.-L.; Zhang, S.; Lu, F.-J.; et al. Discovery of oscillations above 200 keV in a black hole X-ray binary with Insight-HXMT. Nat. Astron. 2021, 5, 94–102. [Google Scholar] [CrossRef]
- Meszaros, P. Gamma-ray bursts. Rep. Prog. Phys. 2006, 69, 2259–2321. [Google Scholar] [CrossRef]
- Zhang, B. Gamma-Ray Bursts in the Swift Era. Chin. J. Astron. Astrophys. 2007, 7, 1–50. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of Two Classes of Gamma-Ray Bursts. Astrophys. J. Lett. 1993, 413, L101. [Google Scholar] [CrossRef]
- Paciesas, W.S.; Meegan, C.A.; Pendleton, G.N.; Briggs, M.S.; Kouveliotou, C.; Koshut, T.M.; Lestrade, J.P.; McCollough, M.L.; Brainerd, J.J.; Hakkila, J.; et al. The Fourth BATSE Gamma-Ray Burst Catalog (Revised). Astrophys. J. Suppl. Ser. 1999, 122, 465–495. [Google Scholar] [CrossRef]
- Stern, B.E.; Tikhomirova, Y.; Kompaneets, D.; Svensson, R.; Poutanen, J. An Off-Line Scan of the BATSE Daily Records and a Large Uniform Sample of Gamma-Ray Bursts. Astrophys. J. 2001, 563, 80–94. [Google Scholar] [CrossRef]
- Zhang, B. Astrophysics: A burst of new ideas. Nature 2006, 444, 1010–1011. [Google Scholar] [CrossRef]
- Nakar, E. Short-hard gamma-ray bursts. Phys. Rep. 2007, 442, 166–236. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-Ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Woosley, S.E. Gamma-Ray Bursts from Stellar Mass Accretion Disks around Black Holes. Astrophys. J. 1993, 405, 273. [Google Scholar] [CrossRef]
- Usov, V.V. Millisecond pulsars with extremely strong magnetic fields as a cosmological source of γ-ray bursts. Nature 1992, 357, 472–474. [Google Scholar] [CrossRef]
- Dai, Z.G.; Lu, T. Gamma-ray burst afterglows and evolution of postburst fireballs with energy injection from strongly magnetic millisecond pulsars. Astron. Astrophys. 1998, 333, L87–L90. [Google Scholar] [CrossRef]
- Zhang, B.; Mészáros, P. Gamma-Ray Burst Afterglow with Continuous Energy Injection: Signature of a Highly Magnetized Millisecond Pulsar. Astrophys. J. Lett. 2001, 552, L35–L38. [Google Scholar] [CrossRef]
- Liu, T.; Gu, W.-M.; Zhang, B. Neutrino-dominated accretion flows as the central engine of gamma-ray bursts. New Astron. Rev. 2017, 79, 1–25. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Relativistic fireballs—Energy conversion and time-scales. Mon. Not. R. Astron. Soc. 1992, 258, 41. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J. Relativistic Fireballs and Their Impact on External Matter: Models for Cosmological Gamma-Ray Bursts. Astrophys. J. 1993, 405, 278. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Unsteady Outflow Models for Cosmological Gamma-Ray Bursts. Astrophys. J. Lett. 1994, 430, L93. [Google Scholar] [CrossRef]
- Giannios, D. Prompt GRB emission from gradual energy dissipation. Astron. Astrophys. 2008, 480, 305–312. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Collisional mechanism for gamma-ray burst emission. Mon. Not. R. Astron. Soc. 2010, 407, 1033–1047. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, H. The Internal-collision-induced Magnetic Reconnection and Turbulence (ICMART) Model of Gamma-ray Bursts. Astrophys. J. 2011, 726, 90. [Google Scholar] [CrossRef]
- Deng, M.; Schaefer, B.E. Search for millisecond periodic pulsations in BATSE gamma-ray bursts. Astrophys. J. 1997, 491, 720–724. [Google Scholar] [CrossRef]
- Kruger, A.T.; Loredo, T.J.; Wasserman, I. Search for high-frequency periodicities in time-tagged event data from gamma-ray bursts and soft gamma repeaters. Astrophys. J. 2002, 576, 932–941. [Google Scholar] [CrossRef][Green Version]
- Dichiara, S.; Guidorzi, C.; Frontera, F.; Amati, L. A search for pulsations in short gamma-ray bursts to constrain their progenitors. Astrophys. J. 2013, 777, 132. [Google Scholar] [CrossRef]
- Tarnopolski, M.; Marchenko, V. A comprehensive power spectral density analysis of astronomical time series. II. The Swift/BAT long gamma-ray bursts. Astrophys. J. 2021, 911, 20. [Google Scholar] [CrossRef]
- Xiao, S.; Peng, W.-X.; Zhang, S.-N.; Xiong, S.-L.; Li, X.-B.; Tuo, Y.-L.; Gao, H.; Wang, Y.; Zheng, C.; Li, T.-P.; et al. Search for quasiperiodic oscillations in precursors of short and long gamma-ray bursts. Astrophys. J. 2022, 941, 166. [Google Scholar] [CrossRef]
- Zhou, Z.-M.; Wang, X.-G.; Liang, E.-W.; Cao, J.-X.; Liu, H.-Y.; Li, C.-K.; Li, B.; Lin, D.-B.; Zheng, T.-C.; Lu, R.-J.; et al. A comprehensive analysis of Insight-HXMT gamma-ray burst data. I. Power density spectrum. Astrophys. J. 2024, 972, 190. [Google Scholar] [CrossRef]
- Liu, D.-J.; Zou, Y.-C. Searching for QPOs in BATSE short gamma-ray bursts based on narrowband and broadband features. J. Cosmol. Astropart. Phys. 2024, 2024, 070. [Google Scholar] [CrossRef]
- Chirenti, C.; Dichiara, S.; Lien, A.; Miller, M.C.; Preece, R. Kilohertz quasiperiodic oscillations in short gamma-ray bursts. Nature 2023, 613, 253–256. [Google Scholar] [CrossRef]
- Xiao, S.; Zhang, Y.-Q.; Zhu, Z.-P.; Xiong, S.-L.; Gao, H. The peculiar precursor of a gamma-ray burst from a binary merger involving a magnetar. Astrophys. J. 2024, 970, 6. [Google Scholar] [CrossRef]
- Chirenti, C.; Dichiara, S.; Lien, A.; Miller, M.C. Evidence of a strong 19.5 Hz flux oscillation in Swift BAT and Fermi GBM gamma-ray data from GRB 211211A. Astrophys. J. 2024, 967, 26. [Google Scholar] [CrossRef]
- Blackman, E.G.; Yi, I.; Field, G.B. Relativistic precessing jets and cosmological gamma-ray bursts. Astrophys. J. Lett. 1996, 473, L79. [Google Scholar] [CrossRef]
- Portegies Zwart, S.F.; Lee, C.-H.; Lee, H.K. Can precessing jets explain the light curves of gamma-ray bursts? Astrophys. J. 1999, 520, 666–679. [Google Scholar] [CrossRef]
- Portegies Zwart, S.F.; Lee, C.-H.; Lee, H.K. Explaining the light curves of gamma-ray bursts with a precessing jet. Astron. Astrophys. Suppl. Ser. 1999, 138, 503–504. [Google Scholar] [CrossRef]
- Portegies Zwart, S.F.; Totani, T. Precessing jets interacting with interstellar material as the origin for the light curves of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2001, 328, 951–957. [Google Scholar] [CrossRef]
- Stone, N.; Loeb, A.; Berger, E. Pulsations in short gamma ray bursts from black hole-neutron star mergers. Phys. Rev. D 2013, 87, 084053. [Google Scholar] [CrossRef]
- Li, Y.; Shen, R.-F.; Zhang, B.-B. Quasiperiodic oscillation in short gamma-ray bursts from black hole-neutron star mergers. Astrophys. J. 2023, 955, 98. [Google Scholar] [CrossRef]
- Reynoso, M.M.; Romero, G.E.; Sampayo, O.A. Precession of neutrino-cooled accretion disks in gamma-ray burst engines. Astron. Astrophys. 2006, 454, 11–16. [Google Scholar] [CrossRef]
- Lei, W.H.; Wang, D.X.; Gong, B.P.; Huang, C.Y. A model of the light curves of gamma-ray bursts. Astron. Astrophys. 2007, 468, 563–569. [Google Scholar] [CrossRef]
- Liu, T.; Liang, E.-W.; Gu, W.-M.; Zhao, X.-H.; Dai, Z.-G.; Lu, J.-F. Jet precession driven by neutrino-cooled disk for gamma-ray bursts. Astron. Astrophys. 2010, 516, A16. [Google Scholar] [CrossRef]
- Wang, X.I.I.; Zhang, B.B.; Lei, W.H. GRB 200826A: A precursor of a long gamma-ray burst with missing main emission. Astrophys. J. Lett. 2022, 931, L2. [Google Scholar] [CrossRef]
- Gao, H.; Li, A.; Lei, W.-H.; You, Z.-Q. Repeating emission episodes in gamma-ray bursts: Millilensing or jet precession? Astrophys. J. 2023, 945, 17. [Google Scholar] [CrossRef]
- Zhang, Z.; Yin, Y.-H.; Wang, C.; Wang, X.; Yang, J.; Meng, Y.-Z.; Liu, Z.-K.; Chen, G.-Y.; Fu, X.; Gao, H.; et al. GRB 220408B: A three-episode burst from a precessing jet. Res. Astron. Astrophys. 2023, 23, 115023. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Optical and long-wavelength afterglow from gamma-ray bursts. Astrophys. J. 1997, 476, 232–237. [Google Scholar] [CrossRef]
- LHAASO Collaboration; Cao, Z.; Aharonian, F.; An, Q.; Axikegu, A.; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; et al. A tera-electron volt afterglow from a narrow jet in an extremely bright gamma-ray burst. Science 2023, 380, 1390–1396. [Google Scholar] [CrossRef]
- Costa, E.; Frontera, F.; Heise, J.; Feroci, M.; in’t Zand, J.; Fiore, F.; Cinti, M.N.; Dal Fiume, D.; Nicastro, L.; Orlandini, M.; et al. Discovery of an X-ray afterglow associated with the γ-ray burst of 28 February 1997. Nature 1997, 387, 783–785. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and light curves of gamma-ray burst afterglows. Astrophys. J. Lett. 1998, 497, L17–L20. [Google Scholar] [CrossRef]
- Zhang, B.; Fan, Y.Z.; Dyks, J.; Kobayashi, S.; Mészáros, P.; Burrows, D.N.; Nousek, J.A.; Gehrels, N. Physical processes shaping gamma-ray burst X-ray afterglow light curves: Theoretical implications from the Swift X-ray telescope observations. Astrophys. J. 2006, 642, 354–370. [Google Scholar] [CrossRef]
- Yi, S.-X.; Du, M.; Liu, T. Statistical analyses of the energies of X-ray plateaus and flares in gamma-ray bursts. Astrophys. J. 2022, 924, 69. [Google Scholar] [CrossRef]
- Suvorov, A.G.; Kokkotas, K.D. Evidence for magnetar precession in X-ray afterglows of gamma-ray bursts. Astrophys. J. Lett. 2020, 892, L34. [Google Scholar] [CrossRef]
- Suvorov, A.G.; Kokkotas, K.D. Precessing magnetars as central engines in short gamma-ray bursts. Mon. Not. R. Astron. Soc. 2021, 502, 2482–2494. [Google Scholar] [CrossRef]
- Zou, L.; Zheng, T.-C.; Yang, X.; Zhang, H.-m.; Li, X.-Y.; Ren, J.; Lin, D.-B.; Liang, E.-W. GRB 101225A as orphan dipole radiation of a newborn magnetar with precession rotation in an off-axis gamma-ray burst. Astrophys. J. Lett. 2021, 921, L1. [Google Scholar] [CrossRef]
- Zou, L.; Liang, E.-W. Early evolution of a newborn magnetar with strong precession motion in GRB 180620A. Mon. Not. R. Astron. Soc. 2022, 513, L89–L93. [Google Scholar] [CrossRef]
- Zou, L.; Cheng, J.-G. Quasiperiodic oscillations in GRB 210514A: A case of a newborn supramassive precessing magnetar collapsing into a black hole? Astrophys. J. 2024, 973, 126. [Google Scholar] [CrossRef]
- Zheng, T.-C.; Wei, D.-M.; Wang, Y.; Zhou, H.; Li, L. Black hole activity imprints on the internal plateau and the subsequent sharp decay. Astrophys. J. 2024, 964, 169. [Google Scholar] [CrossRef]
- Hou, S.-J.; Liu, T.; Gu, W.-M.; Lin, D.-B.; Sun, M.-Y.; Wu, X.-F.; Lu, J.-F. Time evolution of flares in GRB 130925A: Jet precession in a black hole accretion system. Astrophys. J. 2014, 781, L19. [Google Scholar] [CrossRef]
- Hou, S.-J.; Gao, H.; Liu, T.; Gu, W.-M.; Lin, D.-B.; Li, Y.-P.; Men, Y.-P.; Wu, X.-F.; Lei, W.-H.; Lu, J.-F. Variability of the giant X-ray bump in GRB 121027A and its possible origin. Mon. Not. R. Astron. Soc. 2014, 441, 2375–2379. [Google Scholar] [CrossRef][Green Version]
- Li, J.-D.; Gao, H.; Ai, S.; Lei, W.-H. Characteristics of gamma-ray burst afterglows in the context of non-axisymmetric structured jets. Mon. Not. R. Astron. Soc. 2023, 525, 6285–6294. [Google Scholar] [CrossRef]
- Huang, B.-Q.; Liu, T. Energy injection driven by precessing jets in gamma-ray burst afterglows. Astrophys. J. 2021, 916, 71. [Google Scholar] [CrossRef]
- Zhang, B. The Physics of Gamma-Ray Bursts, 1st ed.; Cambridge University Press: Cambridge, UK, 2018; pp. 663–664. [Google Scholar] [CrossRef]
- Rhoads, J.E. How to tell a jet from a balloon: A proposed test for beaming in gamma-ray bursts. Astrophys. J. Lett. 1997, 487, L1–L4. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J.; Wijers, R.A.M.J. Viewing angle and environment effects in gamma-ray bursts: Sources of afterglow diversity. Astrophys. J. 1998, 499, 301–308. [Google Scholar] [CrossRef]
- Lipunov, V.M.; Postnov, K.A.; Prokhorov, M.E. Gamma-ray bursts as standard-energy explosions. Astron. Rep. 2001, 45, 236–240. [Google Scholar] [CrossRef]
- Rossi, E.; Lazzati, D.; Rees, M.J. Afterglow light curves, viewing angle and the jet structure of γ-ray bursts. Mon. Not. R. Astron. Soc. 2002, 332, 945–950. [Google Scholar] [CrossRef]
- Zhang, B.; Mészáros, P. Gamma-Ray Burst Beaming: A Universal Configuration with a Standard Energy Reservoir? Astrophys. J. 2002, 571, 876–879. [Google Scholar] [CrossRef]
- Zhang, B.; Dai, X.; Lloyd-Ronning, N.M.; Mészáros, P. Quasi-universal Gaussian Jets: A Unified Picture for Gamma-Ray Bursts and X-Ray Flashes. Astrophys. J. Lett. 2004, 601, L119–L122. [Google Scholar] [CrossRef]
- Dai, X.; Zhang, B. A Global Test of a Quasi-universal Gamma-Ray Burst Jet Model through Monte Carlo Simulations. Astrophys. J. 2005, 621, 875–883. [Google Scholar] [CrossRef][Green Version]
- Frail, D.A.; Berger, E.; Galama, T.; Kulkarni, S.R.; Moriarty-Schieven, G.H.; Pooley, G.G.; Sari, R.; Shepherd, D.S.; Taylor, G.B.; Walter, F. The Enigmatic Radio Afterglow of GRB 991216. Astrophys. J. Lett. 2000, 538, L129–L132. [Google Scholar] [CrossRef]
- Berger, E.; Kulkarni, S.R.; Pooley, G.; Frail, D.A.; McIntyre, V.; Wark, R.M.; Sari, R.; Soderberg, A.M.; Fox, D.W.; Yost, S.; et al. A common origin for cosmic explosions inferred from calorimetry of GRB030329. Nature 2003, 426, 154–157. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Troja, E.; Piro, L.; van Eerten, H.; Wollaeger, R.T.; Im, M.; Fox, O.D.; Butler, N.R.; Cenko, S.B.; Sakamoto, T.; Fryer, C.L.; et al. The X-ray counterpart to the gravitational-wave event GW170817. Nature 2017, 551, 71–74. [Google Scholar] [CrossRef]
- Troja, E.; Piro, L.; Ryan, G.; van Eerten, H.; Ricci, R.; Wieringa, M.H.; Lotti, S.; Sakamoto, T.; Cenko, S.B. The outflow structure of GW170817 from late-time broad-band observations. Mon. Not. R. Astron. Soc. 2018, 478, L18–L23. [Google Scholar] [CrossRef]
- Urrutia, G.; De Colle, F.; Murguia-Berthier, A.; Ramirez-Ruiz, E. What determines the structure of short gamma-ray burst jets? Mon. Not. R. Astron. Soc. 2021, 503, 4363–4371. [Google Scholar] [CrossRef]
- Nativi, L.; Lamb, G.P.; Rosswog, S.; Lundman, C.; Kowal, G. Are interactions with neutron star merger winds shaping the jets? Mon. Not. R. Astron. Soc. 2022, 509, 903–913. [Google Scholar] [CrossRef]
- Urrutia, G.; De Colle, F.; López-Cámara, D. Three-dimensional numerical simulations of structured gamma-ray burst jets. Mon. Not. R. Astron. Soc. 2023, 518, 5145–5153. [Google Scholar] [CrossRef]
- Zhang, W.; Woosley, S.E.; MacFadyen, A.I. Relativistic jets in collapsars. Astrophys. J. 2003, 586, 356–371. [Google Scholar] [CrossRef]
- Huang, B.-Q.; Lin, D.-B.; Liu, T.; Ren, J.; Wang, X.-G.; Liu, H.-B.; Liang, E.-W. Jet structure in the afterglow phase for gamma-ray bursts with a precessing jet. Mon. Not. R. Astron. Soc. 2019, 487, 3214–3220. [Google Scholar] [CrossRef]
- Birnholtz, O.; Piran, T. Gravitational wave memory from gamma ray bursts’ jets. Phys. Rev. D 2013, 87, 123007. [Google Scholar] [CrossRef]
- Sago, N.; Ioka, K.; Nakamura, T.; Yamazaki, R. Gravitational wave memory of gamma-ray burst jets. Phys. Rev. D 2004, 70, 104012. [Google Scholar] [CrossRef]
- Akiba, S.; Nakada, M.; Yamaguchi, C.; Iwamoto, K. Gravitational-Wave Memory from the Relativistic Jet of Gamma-Ray Bursts. Publ. Astron. Soc. Jpn. 2013, 65, 59. [Google Scholar] [CrossRef]
- Huang, B.-Q.; Liu, T.; Xue, L.; Qi, Y.-Q. Low-frequency Gravitational-wave Memories from Gamma-Ray Burst Afterglows with Energy Injections. Astrophys. J. 2023, 944, 189. [Google Scholar] [CrossRef]
- Willis, D.R.; Barlow, E.J.; Bird, A.J.; Clark, D.J.; Dean, A.J.; McConnell, M.L.; Moran, L.; Shaw, S.E.; Sguera, V. Evidence of polarisation in the prompt gamma-ray emission from GRB 930131 and GRB 960924. Astron. Astrophys. 2005, 439, 245–253. [Google Scholar] [CrossRef]
- McGlynn, S.; Clark, D.J.; Dean, A.J.; Hanlon, L.; McBreen, S.; Willis, D.R.; McBreen, B.; Bird, A.J.; Foley, S. Polarisation studies of the prompt gamma-ray emission from GRB 041219a using the spectrometer aboard INTEGRAL. Astron. Astrophys. 2007, 466, 895–904. [Google Scholar] [CrossRef]
- Sharma, V.; Iyyani, S.; Bhattacharya, D.; Chattopadhyay, T.; Rao, A.R.; Aarthy, E.; Vadawale, S.V.; Mithun, N.P.S.; Bhalerao, V.B.; Ryde, F.; et al. Time-varying Polarized Gamma-Rays from GRB 160821A: Evidence for Ordered Magnetic Fields. Astrophys. J. Lett. 2019, 882, L10. [Google Scholar] [CrossRef]
- Gupta, R.; Gupta, S.; Chattopadhyay, T.; Lipunov, V.; Castro-Tirado, A.J.; Bhattacharya, D.; Pandey, S.B.; Oates, S.R.; Kumar, A.; Hu, Y.D.; et al. Probing into emission mechanisms of GRB 190530A using time-resolved spectra and polarization studies: Synchrotron origin? Mon. Not. R. Astron. Soc. 2022, 511, 1694–1713. [Google Scholar] [CrossRef]
- Zhang, S.-N.; Kole, M.; Bao, T.-W.; Batsch, T.; Bernasconi, T.; Cadoux, F.; Chai, J.-Y.; Dai, Z.-G.; Dong, Y.-W.; Gauvin, N.; et al. Detailed polarization measurements of the prompt emission of five gamma-ray bursts. Nat. Astron. 2019, 3, 258–264. [Google Scholar] [CrossRef]
- Mundell, C.G.; Steele, I.A.; Smith, R.J.; Kobayashi, S.; Melandri, A.; Guidorzi, C.; Gomboc, A.; Mottram, C.J.; Clarke, D.; Monfardini, A.; et al. Early optical polarization of a gamma-ray burst afterglow. Science 2007, 315, 1822. [Google Scholar] [CrossRef]
- Steele, I.A.; Mundell, C.G.; Smith, R.J.; Kobayashi, S.; Guidorzi, C. Ten per cent polarized optical emission from GRB090102. Nature 2009, 462, 767–769. [Google Scholar] [CrossRef]
- Uehara, T.; Toma, K.; Kawabata, K.S.; Chiyonobu, S.; Fukazawa, Y.; Ikejiri, Y.; Inoue, T.; Itoh, R.; Komatsu, T.; Miyamoto, H.; et al. GRB 091208B: First detection of the optical polarization in early forward shock emission of a gamma-ray burst afterglow. Astrophys. J. Lett. 2012, 752, L6. [Google Scholar] [CrossRef]
- Mundell, C.G.; Kopač, D.; Arnold, D.M.; Steele, I.A.; Gomboc, A.; Kobayashi, S.; Harrison, R.M.; Smith, R.J.; Guidorzi, C.; Virgili, F.J.; et al. Highly polarized light from stable ordered magnetic fields in GRB 120308A. Nature 2013, 504, 119–121. [Google Scholar] [CrossRef]
- Kopač, D.; Mundell, C.G.; Japelj, J.; Arnold, D.M.; Steele, I.A.; Guidorzi, C.; Dichiara, S.; Kobayashi, S.; Gomboc, A.; Harrison, R.M.; et al. Limits on optical polarization during the prompt phase of GRB 140430A. Astrophys. J. 2015, 813, 1. [Google Scholar] [CrossRef]
- Steele, I.A.; Kopač, D.; Arnold, D.M.; Smith, R.J.; Kobayashi, S.; Jermak, H.E.; Mundell, C.G.; Gomboc, A.; Guidorzi, C.; Melandri, A.; et al. Polarimetry and photometry of gamma-ray bursts with RINGO2. Astrophys. J. 2017, 843, 143. [Google Scholar] [CrossRef]
- Jordana-Mitjans, N.; Mundell, C.G.; Smith, R.J.; Guidorzi, C.; Marongiu, M.; Kobayashi, S.; Gomboc, A.; Shrestha, M.; Steele, I.A. Coherence scale of magnetic fields generated in early-time forward shocks of GRBs. Mon. Not. R. Astron. Soc. 2021, 505, 2662–2674. [Google Scholar] [CrossRef]
- Shrestha, M.; Steele, I.A.; Kobayashi, S.; Smith, R.J.; Guidorzi, C.; Jordana-Mitjans, N.; Jermak, H.; Arnold, D.; Mundell, C.G.; Gomboc, A. Polarimetry and photometry of gamma-ray bursts afterglows with RINGO3. Mon. Not. R. Astron. Soc. 2022, 516, 1584–1600. [Google Scholar] [CrossRef]
- Wijers, R.A.M.J.; Vreeswijk, P.M.; Galama, T.J.; Rol, E.; van Paradijs, J.; Kouveliotou, C.; Giblin, T.; Masetti, N.; Palazzi, E.; Pian, E.; et al. Detection of Polarization in the Afterglow of GRB 990510 with the ESO Very Large Telescope. Astrophys. J. 1999, 523, L33–L36. [Google Scholar] [CrossRef]
- Hjorth, J.; Bjornsson, G.; Andersen, M.I.; Caon, N.; Cairos, L.M.; Castro-Tirado, A.J.; Zapatero Osorio, M.R.; Pedersen, H.; Costa, E. Polarimetric constraints on the optical afterglow emission from GRB 990123. Science 1999, 283, 2073. [Google Scholar] [CrossRef]
- Rol, E.; Wijers, R.A.M.J.; Vreeswijk, P.M.; Kaper, L.; Galama, T.J.; van Paradijs, J.; Kouveliotou, C.; Masetti, N.; Pian, E.; Palazzi, E.; et al. GRB 990712: First indication of polarization variability in a gamma-ray burst afterglow. Astrophys. J. 2000, 544, 707. [Google Scholar] [CrossRef]
- Masetti, N.; Palazzi, E.; Pian, E.; Simoncelli, A.; Hunt, L.K.; Maiorano, E.; Levan, A.; Christensen, L.; Rol, E.; Savaglio, S.; et al. Optical and near-infrared observations of the GRB020405 afterglow. Astron. Astrophys. 2003, 404, 465–481. [Google Scholar] [CrossRef]
- Barth, A.J.; Sari, R.; Cohen, M.H.; Goodrich, R.W.; Price, P.A.; Fox, D.W.; Bloom, J.S.; Soderberg, A.M.; Kulkarni, S.R. Optical spectropolarimetry of the GRB 020813 afterglow. Astrophys. J. Lett. 2003, 584, L47. [Google Scholar] [CrossRef]
- Rol, E.; Wijers, R.A.M.J.; Fynbo, J.P.U.; Hjorth, J.; Gorosabel, J.; Egholm, M.P.; Castro Cerón, J.M.; Castro-Tirado, A.J.; Kaper, L.; Masetti, N.; et al. Variable polarization in the optical afterglow of GRB 021004. Astron. Astrophys. 2003, 405, L23–L27. [Google Scholar] [CrossRef]
- Maiorano, E.; Masetti, N.; Palazzi, E.; Savaglio, S.; Rol, E.; Vreeswijk, P.M.; Pian, E.; Price, P.A.; Peterson, B.A.; Jelínek, M.; et al. Physics of the GRB 030328 afterglow and its environment. Astron. Astrophys. 2006, 455, 423–431. [Google Scholar] [CrossRef]
- Wiersema, K.; Curran, P.A.; Krühler, T.; Melandri, A.; Rol, E.; Starling, R.L.C.; Tanvir, N.R.; van der Horst, A.J.; Covino, S.; Fynbo, J.P.U.; et al. Detailed optical and near-infrared polarimetry, spectroscopy and broad-band photometry of the afterglow of GRB 091018: Polarization evolution. Mon. Not. R. Astron. Soc. 2012, 426, 2–22. [Google Scholar] [CrossRef]
- Granot, J.; Königl, A. Linear polarization in gamma-ray bursts: The case for an ordered magnetic field. Astrophys. J. Lett. 2003, 594, L83–L87. [Google Scholar] [CrossRef]
- Lan, M.-X.; Xue, R.; Xiong, D.; Lei, W.-H.; Wu, X.-F.; Dai, Z.-G. Polarization of astrophysical events with precessing jets. Astrophys. J. 2019, 878, 140. [Google Scholar] [CrossRef]
- Huang, B.-Q.; Liu, T. Polarization in early optical afterglows of gamma-ray bursts driven by precessing jets. Astrophys. J. 2022, 933, 103. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Properties of the Binary Black Hole Merger GW150914. Phys. Rev. Lett. 2016, 116, 241102. [Google Scholar] [CrossRef]
- Segalis, E.B.; Ori, A. Emission of gravitational radiation from ultrarelativistic sources. Phys. Rev. D 2001, 64, 064018. [Google Scholar] [CrossRef]
- Yu, Y.-W. Gravitational-wave Memory from a Propagating Relativistic Jet: A Probe of the Interior of Gamma-Ray Burst Progenitors. Astrophys. J. 2020, 897, 19. [Google Scholar] [CrossRef]
- Romero, G.E.; Reynoso, M.M.; Christiansen, H.R. Gravitational radiation from precessing accretion disks in gamma-ray bursts. Astron. Astrophys. 2010, 524, A4. [Google Scholar] [CrossRef]
- Sun, M.-Y.; Liu, T.; Gu, W.-M.; Lu, J.-F. Gravitational Waves of Jet Precession in Gamma-Ray Bursts. Astrophys. J. 2012, 752, 31. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, B.-Q.; Liu, T. Jet Precession in Gamma-Ray Bursts. Universe 2024, 10, 438. https://doi.org/10.3390/universe10120438
Huang B-Q, Liu T. Jet Precession in Gamma-Ray Bursts. Universe. 2024; 10(12):438. https://doi.org/10.3390/universe10120438
Chicago/Turabian StyleHuang, Bao-Quan, and Tong Liu. 2024. "Jet Precession in Gamma-Ray Bursts" Universe 10, no. 12: 438. https://doi.org/10.3390/universe10120438
APA StyleHuang, B.-Q., & Liu, T. (2024). Jet Precession in Gamma-Ray Bursts. Universe, 10(12), 438. https://doi.org/10.3390/universe10120438






