Modeling the Spread and Control of COVID-19
Abstract
1. Introduction
- Social distancing is more important than personal hygiene (Section 4.3).
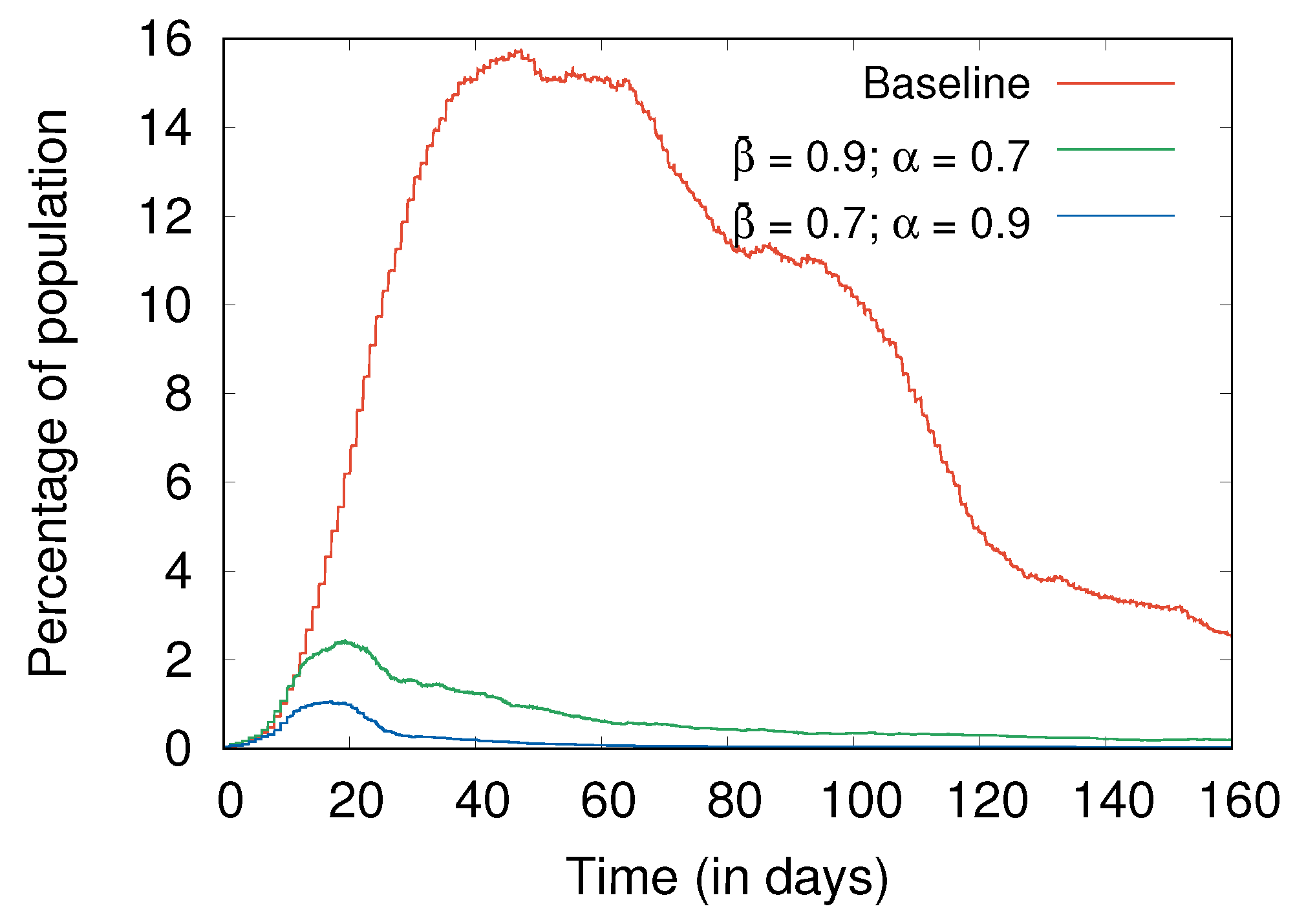
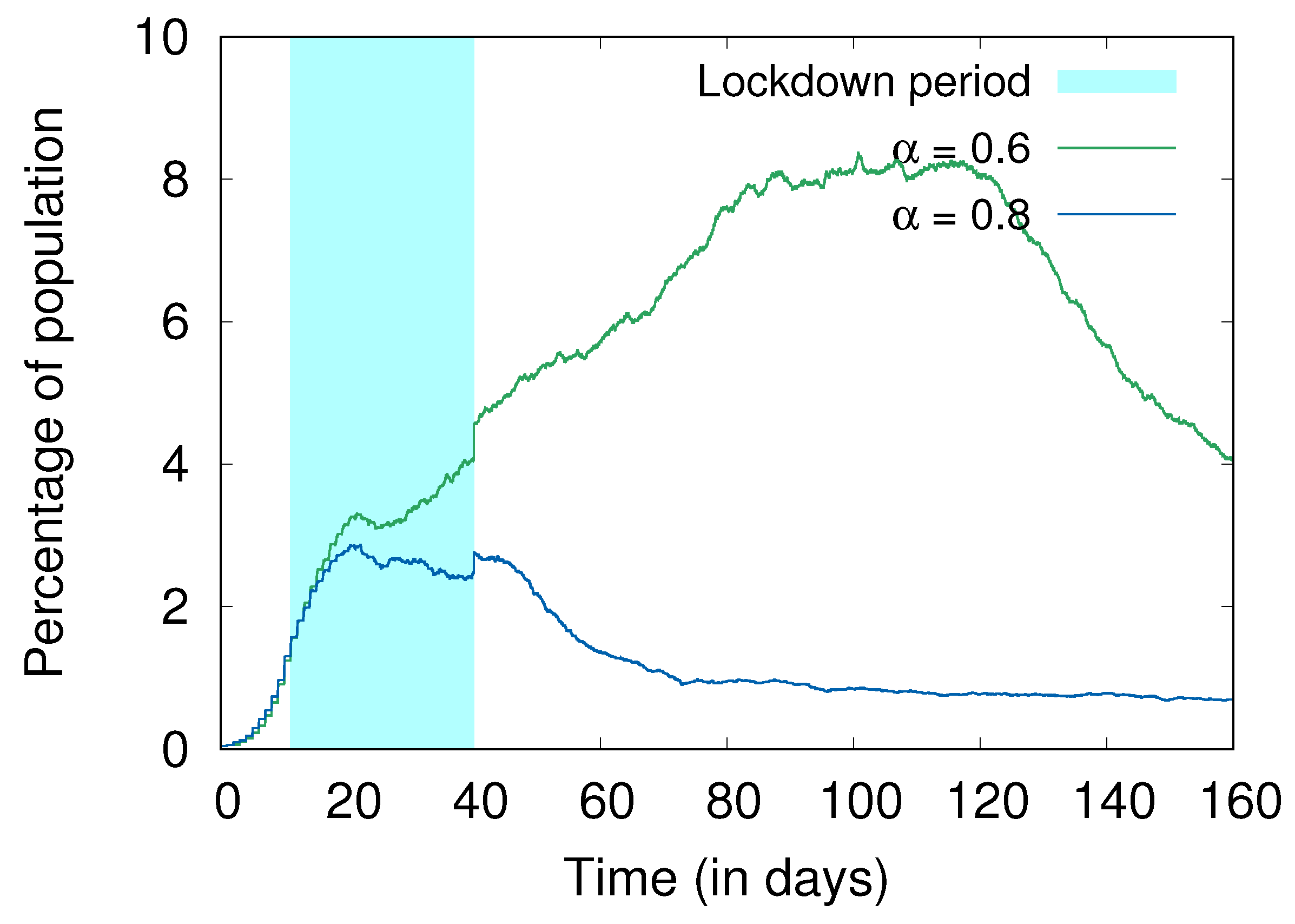
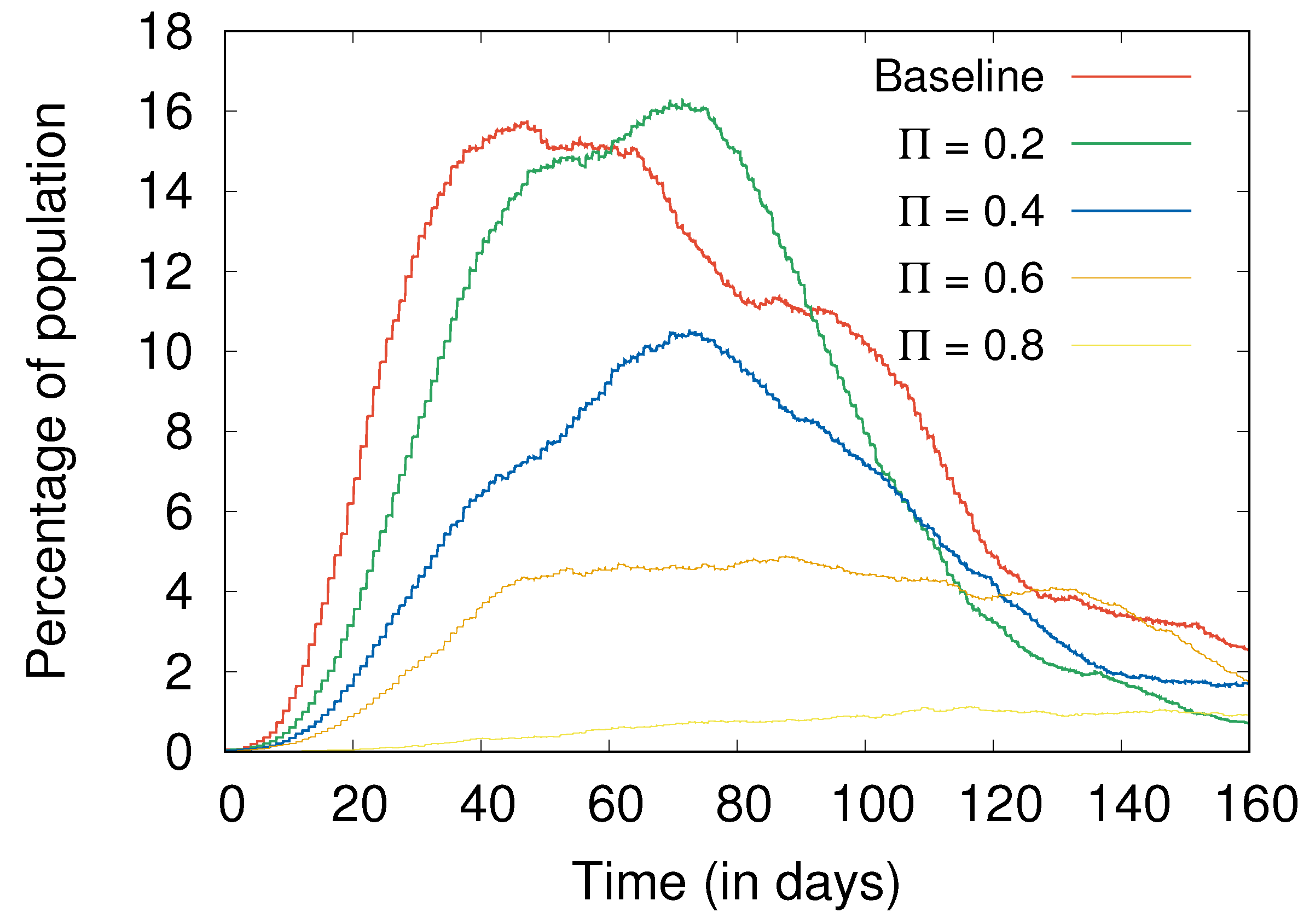
- Social distancing and hygiene together are more important than lockdowns for controlling the spread of disease (Section 4.4). In fact, in their absence, a lockdown can do more harm than good; without social distancing and hygiene, a post-lockdown peak of cases can be higher than without the lockdown, with a similar effect also observed with more stringent lockdowns as compared to more relaxed ones (Figure 7).
- When the fraction of the population that is immune to the disease (either by vaccination or by previous exposure or recovery) is small, e.g., 20%, the peak of infectious cases can be nearly as high, in the absence of social distancing and personal hygiene, as when there is no immunity at all in the population (Section 4.5). Even in the case in which approximately 40% of the population is immune, there can be a large number of infections in the absence of social distancing and hygiene (Figure 12b).
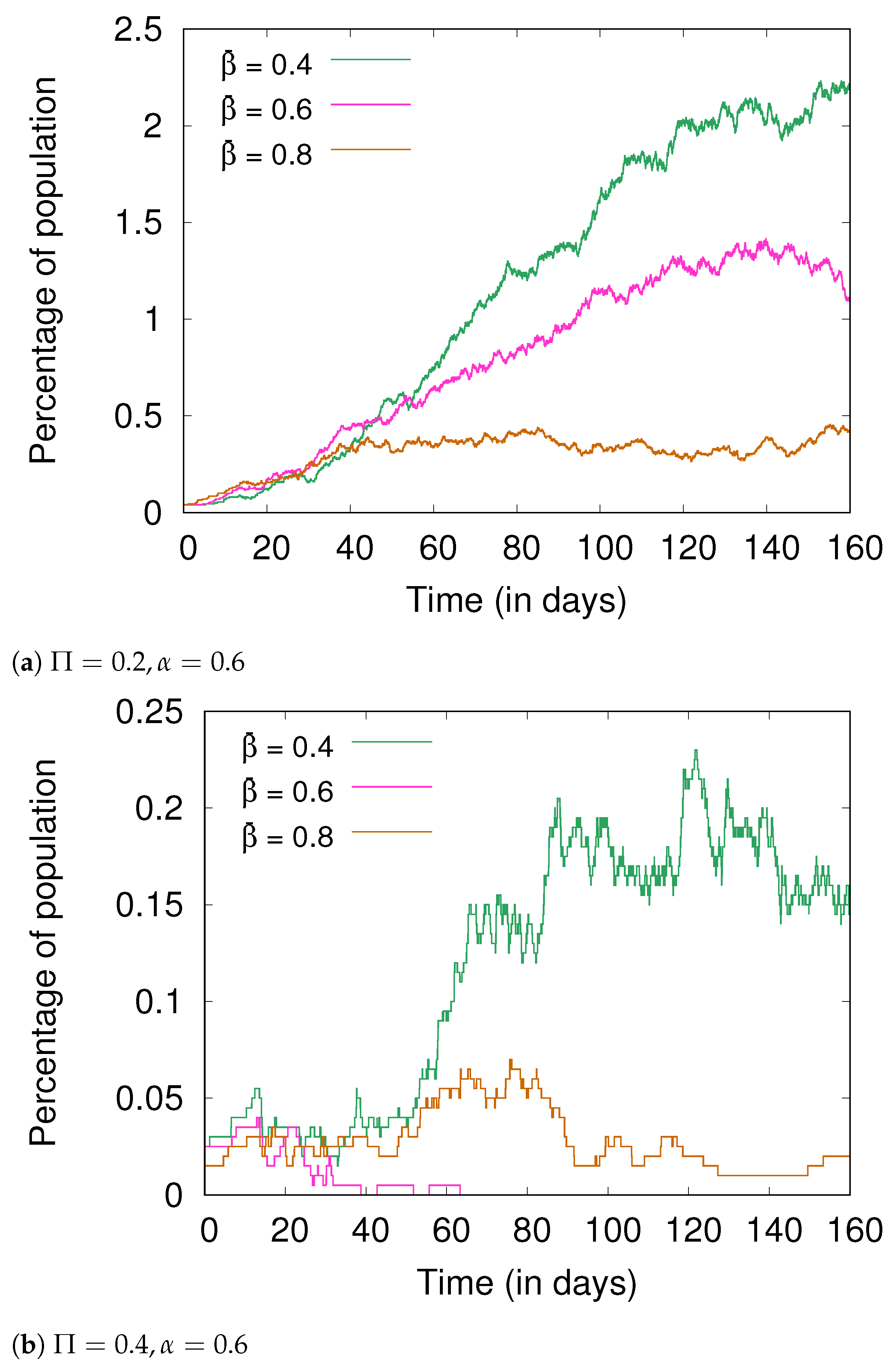
- Proper herd immunity in the classical sense is said to occur (in the total absence of social distancing and hygiene) only when a large fraction of the population becomes immune [22]. However, when the smaller fraction of 40% of the population is immune (i.e., the fractional immunity of the population is 0.4), this can be achieved with some observance of social distancing and hygiene; the same effect is also possible with an even smaller fraction of 20% of the population being immune, with a rigorous observance of social distancing and hygiene (Section 4.5).
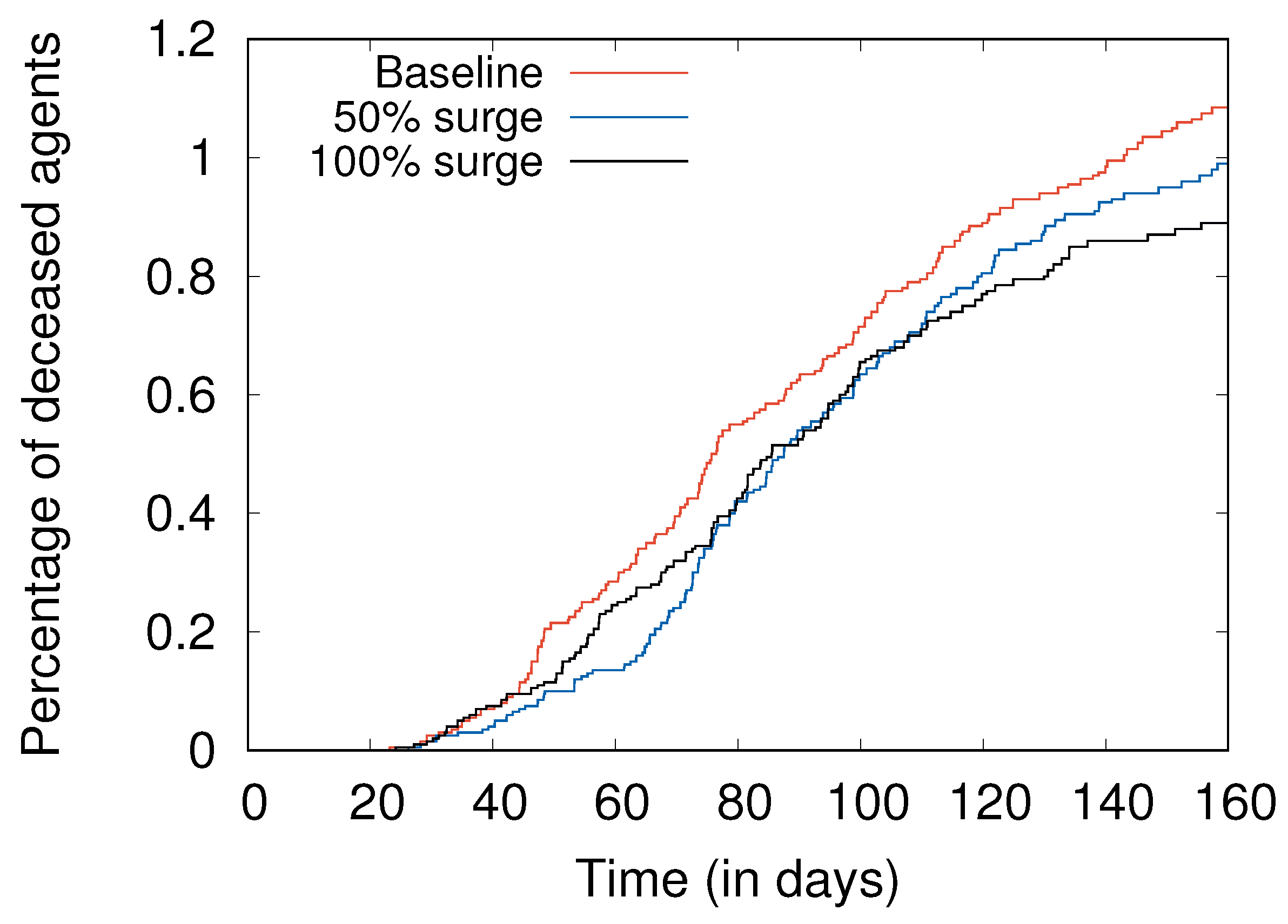
- Surges in hospital capacity (including critical care capacity) help reduce the number of severely ill people dying due to a lack of access to medical care, but do not directly affect the overall number of cases to a significant extent (Section 4.6).
2. Disease Model
2.1. Modified SEIR
- This is the infectious asymptomatic state, where an individual does not show signs of the disease at all, but can transmit it to others. It is presently believed that a large number of infected people recover directly from this state, and that coming into proximity with such asymptomatic individuals is responsible for a large fraction of the COVID-19 spread [25].
- This is the infectious symptomatic state, where an individual shows signs of the disease, but is not (yet) hospitalized, either because the symptoms are considered mild enough, or because hospital care is unavailable.
- This is the infectious hospitalized state, where an individual shows signs of the disease and receives hospital care.
- This is the infectious critical care state, where the individual is severely afflicted and receives critical care in an ICU or similar unit, including with specialized devices, such as ventilators.
2.2. State Transitions
- The state transition from susceptible to exposed happens when a susceptible individual comes into close contact with an infectious individual (someone in any of the states , , , or ). Each infectious individual has an infection range, and if another individual comes within their infection range, they are said to be in close contact. The state transition from S to E is considered instantaneous (see Section 3.3.1).
- The state transition from exposed to infectious asymptomatic happens upon the completion of the latent period of the disease, starting from the instant of exposure (see Section 3.3.2).
- The state transition from infectious asymptomatic to symptomatic happens upon the completion of the incubation period of the disease, starting from the instant of exposure. In many individuals, this transition may not happen at all, and the individual may instead transition to R (recovered) directly (see Section 3.3.2).
- The state transition from infectious symptomatic to hospitalized happens in some infected individuals when the symptoms worsen to the point of requiring hospital care (see Section 3.3.3).
- The state transition from hospitalized to critical care happens in some individuals whose aggravated conditions require ICU and similar critical care (see Section 3.3.4).
- The state transitions from , , and to D (deceased) happen in some individuals. Individuals who are in and and in need of more advanced care (in and , respectively) are at increased risk of transition to D when such care is unavailable. Individuals in are at increased risk of transitioning to D with increasing time spent in that state (see Section 3.3.5).
3. Agent Model
3.1. Black-Box and Glass-Box Views
3.2. Individual and Social Attributes
3.2.1. Agent Characteristics
- a is the age, .
- denotes the level of hygiene, .
- h denotes the level of overall health, .
- c denotes comorbidity level, .
- denotes the immunity, .
3.2.2. System Parameters
- denotes the efficacy of social distancing, .
- denotes the lockdown efficacy, .
- L denotes the lockdown duration, in days, .
- b denotes the number of beds per 1000 agents, .
- denotes the fractional immunity in the system, .
3.3. State Transitions
3.3.1. Transition from S, the Susceptible State
3.3.2. Transitions from E, the Exposed State, and , the Asymptomatic State
3.3.3. Transitions from , the Symptomatic State
3.3.4. Transitions from , the Hospitalized State
3.3.5. Transitions from , the Critical State
4. Experiments and Results
4.1. Simulation Environment
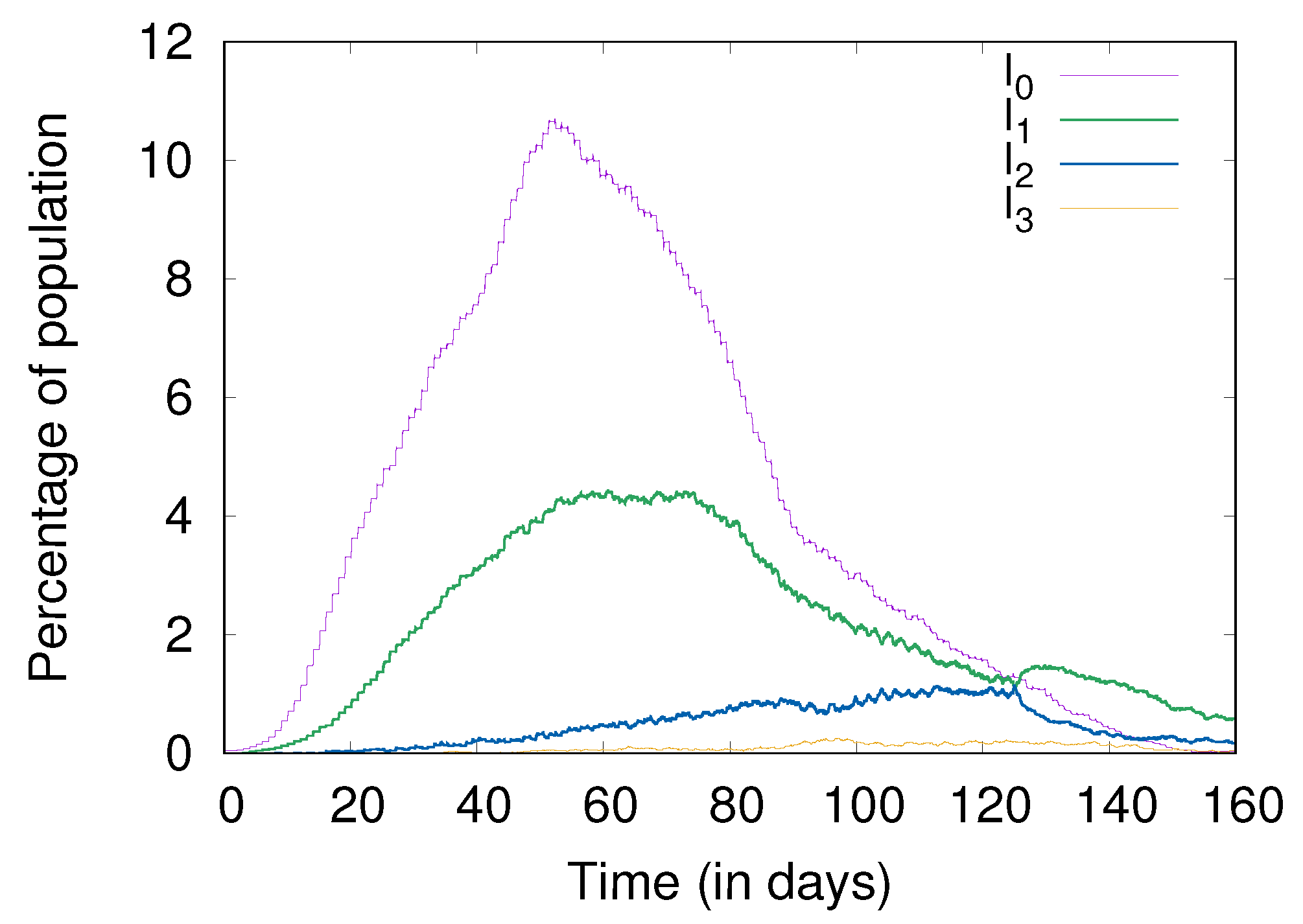
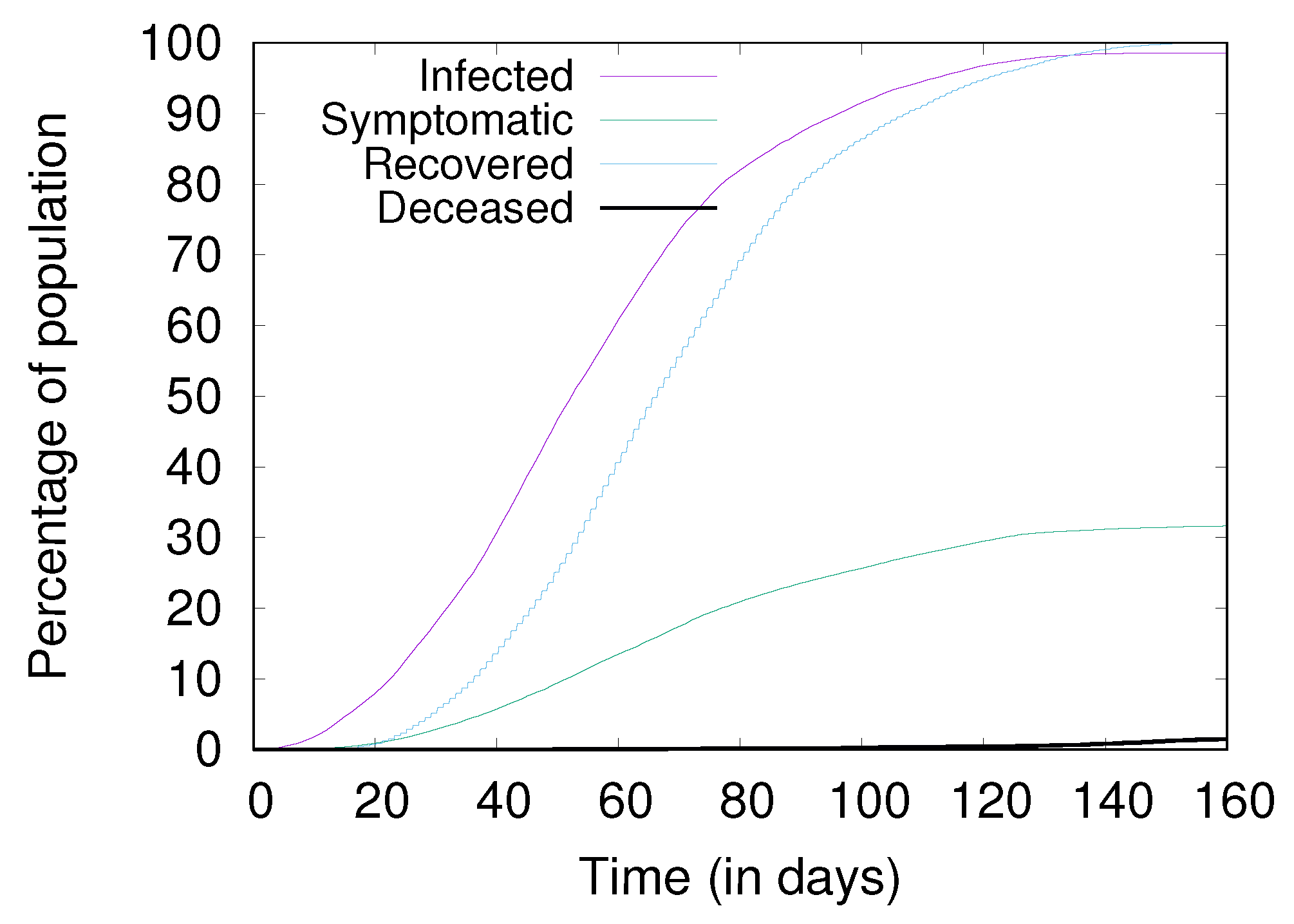
4.2. The Base Case
4.3. Hygiene and Social Distancing
4.4. Lockdowns
4.5. Fractional Immunity
4.6. Surges in Hospital Beds and ICUs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vynnycky, E.; White, R. An Introduction to Infectious Disease Modelling; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Texts in Applied Mathematics (Book 69); Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Arino, J.; Brauer, F.; van den Driessche, P.; Watmough, J.; Wu, J. Simple models for containment of a pandemic. J. R. Soc. Interface 2006, 3, 453–457. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Jung, E. Mathematical model of transmission dynamics and optimal control strategies for 2009 A/H1N1 influenza in the Republic of Korea. J. Theor. Biol. 2017, 412, 74–85. [Google Scholar] [CrossRef]
- Arino, J.; Portet, S. A simple model of COVID-19. Infect. Dis. Model. 2020, 5, 309–315. [Google Scholar] [CrossRef]
- Abdo, M.S.; Shah, K.; Wahash, H.A.; Panchal, S.K. On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative. Chaos Solitons Fractals 2020, 135, 109867. [Google Scholar] [CrossRef]
- Gu, Y. COVID-19 Projections Using Machine Learning. Available online: https://covid19-projections.com/ (accessed on 16 October 2020).
- New America. Pandemic Response Repository; New America: New York, NY, USA, 2020. [Google Scholar]
- Perez, L.; Dragicevic, S. An agent-based approach for modeling dynamics of contagious disease spread. Int. J. Health Geogr. 2009, 8, 50. [Google Scholar] [CrossRef] [PubMed]
- Miksch, F.; Urach, C.; Einzinger, P.; Zauner, G. A Flexible Agent-Based Framework for Infectious Disease Modeling. In Information and Communication Technology—EurAsia Conference (ICT-EurAsia 2014); Linawati, Mahendra, M.S., Neuhold, E.J., Tjoa, A.M., You, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 36–45. [Google Scholar] [CrossRef]
- Hunter, E.; Mac Namee, B.; Kelleher, J. An open-data-driven agent-based model to simulate infectious disease outbreaks. PLoS ONE 2018, 13, e0208775. [Google Scholar] [CrossRef] [PubMed]
- Tracy, M.; Cerdá, M.; Keyes, K.M. Agent-Based Modeling in Public Health: Current Applications and Future Directions. Annu. Rev. Public Health 2018, 39, 77–94. [Google Scholar] [CrossRef]
- Jindal, A.; Rao, S. Agent-Based Modeling and Simulation of Mosquito-Borne Disease Transmission. In Proceedings of the Sixteenth International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2017), São Paulo, Brazil, 8–12 May 2017; pp. 426–435. [Google Scholar]
- Khalil, K.M.; Abdel-Aziz, M.; Nazmy, T.T.; Salem, A.B.M. An agent-based modeling for pandemic influenza in Egypt. In Proceedings of the 7th International Conference on Informatics and Systems (INFOS 2010), Cairo, Egypt, 28–30 March 2010. [Google Scholar] [CrossRef]
- Hunter, E.; Mac Namee, B.; Kelleher, J. A Comparison of Agent-Based Models and Equation Based Models for Infectious Disease Epidemiology. In Proceedings of the 26th AIAI Irish Conference on Artificial Intelligence and Cognitive Science (AICS 2018), Dublin, Ireland, 6–7 December 2018; pp. 33–44. Available online: http://ceur-ws.org/Vol-2259/aics_5.pdf (accessed on 16 October 2020).
- Cuevas, E. An agent-based model to evaluate the COVID-19 transmission risks in facilities. Comput. Biol. Med. 2020, 121, 103827. [Google Scholar] [CrossRef]
- Silva, P.C.L.; Batista, P.V.C.; Lima, H.S.; Alves, M.A.; Guimarāes, F.G.; Silva, R.C.P. COVID-ABS: An Agent-Based Model of COVID-19 Epidemic to Simulate Health and Economic Effects of Social Distancing Interventions. Chaos Solitons Fractals 2020, 139, 110088. [Google Scholar] [CrossRef] [PubMed]
- del Rio, C.; Malani, P.N. COVID-19—New Insights on a Rapidly Changing Epidemic. JAMA 2020, 323, 1339–1340. [Google Scholar] [CrossRef]
- Arabi, Y.M.; Murthy, S.; Webb, S. COVID-19: A novel coronavirus and a novel challenge for critical care. Intensive Care Med. 2020, 46, 833–836, Corrected in Intensive Care Med. 2020, 46, 1087–1088. [Google Scholar] [CrossRef]
- Schueller, E.; Klein, E.; Tseng, K.; Kapoor, G.; Joshi, J.; Sriram, A.; Nandi, A.; Laxminarayan, R. COVID-19 in India: Potential Impact of the Lockdown and Other Longer-Term Policies; Center for Disease Dynamics, Economics & Policy (CDDEP): Washington, DC, USA, 2020. [Google Scholar]
- Randolph, H.E.; Barreiro, L.B. Herd Immunity: Understanding COVID-19. Immunity 2020, 52, 737–741. [Google Scholar] [CrossRef]
- Sun, C.; Hsieh, Y.H. Global analysis of an SEIR model with varying population size and vaccination. Appl. Math. Model. 2010, 34, 2685–2697. [Google Scholar] [CrossRef]
- Feng, Z. Final and peak epidemic sizes for SEIR models with quarantine and isolation. Math. Biosci. Eng. 2007, 4, 675–686. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Yao, L.; Wei, T.; Tian, F.; Jin, D.Y.; Chen, L.; Wang, M. Presumed Asymptomatic Carrier Transmission of COVID-19. JAMA 2020, 323, 1406–1407. [Google Scholar] [CrossRef]
- Last, J.M. (Ed.) A Dictionary of Public Heath; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Erren, T.C. Shift work, cancer and “white-box” epidemiology: Association and causation. Epidemiol. Perspect. Innov. 2010, 7, 11. [Google Scholar] [CrossRef] [PubMed][Green Version]
- van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef]
- Delamater, P.L.; Street, E.J.; Leslie, T.F.; Yang, Y.T.; Jacobsen, K.H. Complexity of the Basic Reproduction Number (R0). Emerg. Infect. Dis. 2019, 25, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Blakeley, D.; Smith, R.J. The Failure of R0. Comput. Math. Model. Med. 2011, 2011, 527610. [Google Scholar] [CrossRef]
- Davies, N.G.; Klepac, P.; Liu, Y.; Prem, K.; Jit, M.; CMMID COVID-19 Working Group; Eggo, R.M. Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat. Med. 2020, 26, 1205–1211. [Google Scholar] [CrossRef] [PubMed]
- Sanyaolu, A.; Okorie, C.; Marinkovic, A.; Patidar, R.; Younis, K.; Desai, P.; Hosein, Z.; Padda, I.; Mangat, J.; Altaf, M. Comorbidity and its Impact on Patients with COVID-19. SN Compr. Clin. Med. 2020, 2, 1069–1076. [Google Scholar] [CrossRef]
- Hermesh, T.; Moltedo, B.; López, C.B.; Moran, T.M. Buying time—The immune system determinants of the incubation period to respiratory viruses. Viruses 2010, 2, 2541–2558. [Google Scholar] [CrossRef] [PubMed]
- Gardner, I.D. The Effect of Aging on Susceptibility to Infection. Rev. Infect. Dis. 1980, 2, 801–810. [Google Scholar] [CrossRef]
- Ashby, B.; Bruns, E. The evolution of juvenile susceptibility to infectious disease. Proc. R. Soc. B 2018, 285, 20180844. [Google Scholar] [CrossRef] [PubMed]
- Prakash, B.; Adamic, L.; Iwashyna, T.; Tong, H.; Faloutsos, C. Fractional immunization in networks. In Proceedings of the SIAM International Conference on Data Mining 2013 (SMD 2013), Austin, TX, USA, 2–4 May 2013; Society for Industrial and Applied Mathematics Publications: Philadelphia, PA, USA, 2013; pp. 659–667. [Google Scholar] [CrossRef]
- Hanley, B. An object simulation model for modeling hypothetical disease epidemics—EpiFlex. Theor. Biol. Med. Model. 2006, 3, 32. [Google Scholar] [CrossRef] [PubMed]
- Kirkeby, C.; Halasa, T.; Gussmann, M.; Toft, N.; Græsbøll, K. Methods for estimating disease transmission rates: Evaluating the precision of Poisson regression and two novel methods. Sci. Rep. 2017, 7, 9496. [Google Scholar] [CrossRef]
- Stehlé, J.; Voirin, N.; Barrat, A.; Cattuto, C.; Colizza, V.; Isella, L.; Régis, C.; Pinton, J.F.; Khanafer, N.; den Broeck, W.V.; et al. Simulation of an SEIR infectious disease model on the dynamic contact network of conference attendees. BMC Med. 2011, 9, 87. [Google Scholar] [CrossRef]
- Liu, Y.; Gayle, A.A.; Wilder-Smith, A.; Rocklöv, J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Travel Med. 2020. [Google Scholar] [CrossRef]
- Virlogeux, V.; Fang, V.J.; Wu, J.T.; Ho, L.M.; Peiris, J.S.M.; Leung, G.M.; Cowling, B.J. Brief Report: Incubation Period Duration and Severity of Clinical Disease Following Severe Acute Respiratory Syndrome Coronavirus Infection. Epidemiology 2015, 26, 666. [Google Scholar] [CrossRef]
- CDC. Symptoms of Coronavirus. 2020. Available online: https://www.cdc.gov/coronavirus/2019-ncov/symptoms-testing/symptoms.html (accessed on 16 October 2020).
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.; Lau, E.H.; Wong, J.Y.; et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Sakurai, A.; Sasaki, T.; Kato, S.; Hayashi, M.; Tsuzuki, S.I.; Ishihara, T.; Iwata, M.; Morise, Z.; Doi, Y. Natural History of Asymptomatic SARS-CoV-2 Infection. N. Engl. J. Med. 2020, 383, 885–886. [Google Scholar] [CrossRef]
- CDC. Duration of Isolation and Precautions for Adults with COVID-19. 2020. Available online: https://www.cdc.gov/coronavirus/2019-ncov/hcp/duration-isolation.html (accessed on 16 October 2020).
- Marfil-Garza, B.A.; Belaunzarán-Zamudio, P.F.; Gulias-Herrero, A.; Zuñiga, A.C.; Caro-Vega, Y.; Kershenobich-Stalnikowitz, D.; Sifuentes-Osornio, J. Risk factors associated with prolonged hospital length-of-stay: 18-year retrospective study of hospitalizations in a tertiary healthcare center in Mexico. PLoS ONE 2018, 13, e0207203. [Google Scholar] [CrossRef] [PubMed]
- WHO. European Health Information Gateway. 2020. Available online: https://gateway.euro.who.int/en/indicators/hfa_478-5060-acute-care-hospital-beds-per-100-000/ (accessed on 16 October 2020).
- Johansson, A.; Helbing, D.; Al-Abideen, H.Z.; Al-Bosta, S. From crowd dynamics to crowd safety: A video-based analysis. Adv. Complex Syst. 2008, 11, 497–527. [Google Scholar] [CrossRef]
- Romanczuk, P.; Couzin, I.D.; Schimansky-Geier, L. Collective motion due to individual escape and pursuit response. Phys. Rev. Lett. 2009, 102, 010602. [Google Scholar] [CrossRef]
- Luke, S.; Cioffi-Revilla, C.; Panait, L.; Sullivan, K.; Balan, G. MASON: A Multiagent Simulation Environment. Simulation 2005, 81, 517–527. [Google Scholar] [CrossRef]
- Harpaz, R.; Dahl, R.M.; Dooling, K.L. Prevalence of Immunosuppression Among US Adults, 2013. JAMA 2016, 316, 2547–2548. [Google Scholar] [CrossRef]
- Poletti, P.; Tirani, M.; Cereda, D.; Trentini, F.; Guzzetta, G.; Sabatino, G.; Marziano, V.; Castrofino, A.; Grosso, F.; Del Castillo, G.; et al. Probability of symptoms and critical disease after SARS-CoV-2 infection. arXiv 2020, arXiv:2006.08471. [Google Scholar]
- Siegenfeld, A.F.; Taleb, N.N.; Bar-Yam, Y. Opinion: What models can and cannot tell us about COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 16092–16095. [Google Scholar] [CrossRef]






| Variable | Symbol | Range |
|---|---|---|
| Hygiene | [0, 1] | |
| Hygiene population mean | [0, 1] | |
| Age | a | [0, 90] |
| Health | h | {0, 1, 2, 3} |
| Comorbidity | c | {−2, −1, 0} |
| Immunity | {0, 1} | |
| Social distancing | [0, 1] | |
| Fractional immunity | [0, 1] | |
| Lockdown efficacy | [0, 1] | |
| Transmission constant | 0.25 | |
| Incubation period | [1, 14] | |
| Latent period | [1, 14] | |
| Recovery score | r | |
| Bed capacity | b | |
| Duration in | — | |
| Scaling constants | — |
| Peak Values (%) | Median Peak Day | D (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.40 | 0.40 | 3.12 | 0.97 | 0.24 | 76 | 148 | 138 | 0.53 |
| 0.40 | 0.60 | 1.73 | 0.60 | 0.12 | 119 | 157 | 152 | 0.18 |
| 0.40 | 0.80 | 0.02 | 0.01 | 0.01 | 25 | 43 | 27 | 0.00 |
| 0.40 | 0.90 | 0.01 | 0.00 | 0.00 | 14 | – | – | 0.00 |
| 0.60 | 0.40 | 2.60 | 0.88 | 0.21 | 83 | 157 | 146 | 0.46 |
| 0.60 | 0.60 | 1.14 | 0.41 | 0.10 | 135 | 158 | 148 | 0.13 |
| 0.60 | 0.80 | 0.02 | 0.01 | 0.00 | 20 | 18 | – | 0.00 |
| 0.60 | 0.90 | 0.01 | 0.00 | 0.00 | 14 | – | – | 0.00 |
| 0.80 | 0.40 | 2.33 | 0.76 | 0.17 | 107 | 158 | 149 | 0.29 |
| 0.80 | 0.60 | 0.56 | 0.18 | 0.05 | 158 | 155 | 152 | 0.06 |
| 0.80 | 0.80 | 0.01 | 0.00 | 0.00 | 16 | 3 | – | 0.00 |
| 0.80 | 0.90 | 0.01 | 0.00 | 0.00 | 10 | 4 | – | 0.00 |
| 0.90 | 0.40 | 2.39 | 0.76 | 0.15 | 118 | 158 | 149 | 0.25 |
| 0.90 | 0.60 | 0.51 | 0.16 | 0.04 | 153 | 152 | 154 | 0.04 |
| 0.90 | 0.80 | 0.02 | 0.00 | 0.00 | 13 | 6 | – | 0.00 |
| 0.90 | 0.90 | 0.01 | 0.00 | 0.00 | 11 | 3 | – | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trivedi, A.; Sreenivas, N.K.; Rao, S. Modeling the Spread and Control of COVID-19. Systems 2021, 9, 53. https://doi.org/10.3390/systems9030053
Trivedi A, Sreenivas NK, Rao S. Modeling the Spread and Control of COVID-19. Systems. 2021; 9(3):53. https://doi.org/10.3390/systems9030053
Chicago/Turabian StyleTrivedi, Ashutosh, Nanda Kishore Sreenivas, and Shrisha Rao. 2021. "Modeling the Spread and Control of COVID-19" Systems 9, no. 3: 53. https://doi.org/10.3390/systems9030053
APA StyleTrivedi, A., Sreenivas, N. K., & Rao, S. (2021). Modeling the Spread and Control of COVID-19. Systems, 9(3), 53. https://doi.org/10.3390/systems9030053






