Systemic States of Spreading Activation in Describing Associative Knowledge Networks II: Generalisations with Fractional Graph Laplacians and q-Adjacency Kernels
Abstract
1. Introduction
2. Materials and Methods
2.1. The Associative Knowledge Network to Be Explored
2.2. Diffusion Models and Generalised Systemic States
2.3. Activity Centrality Based on Systemic States
3. Results
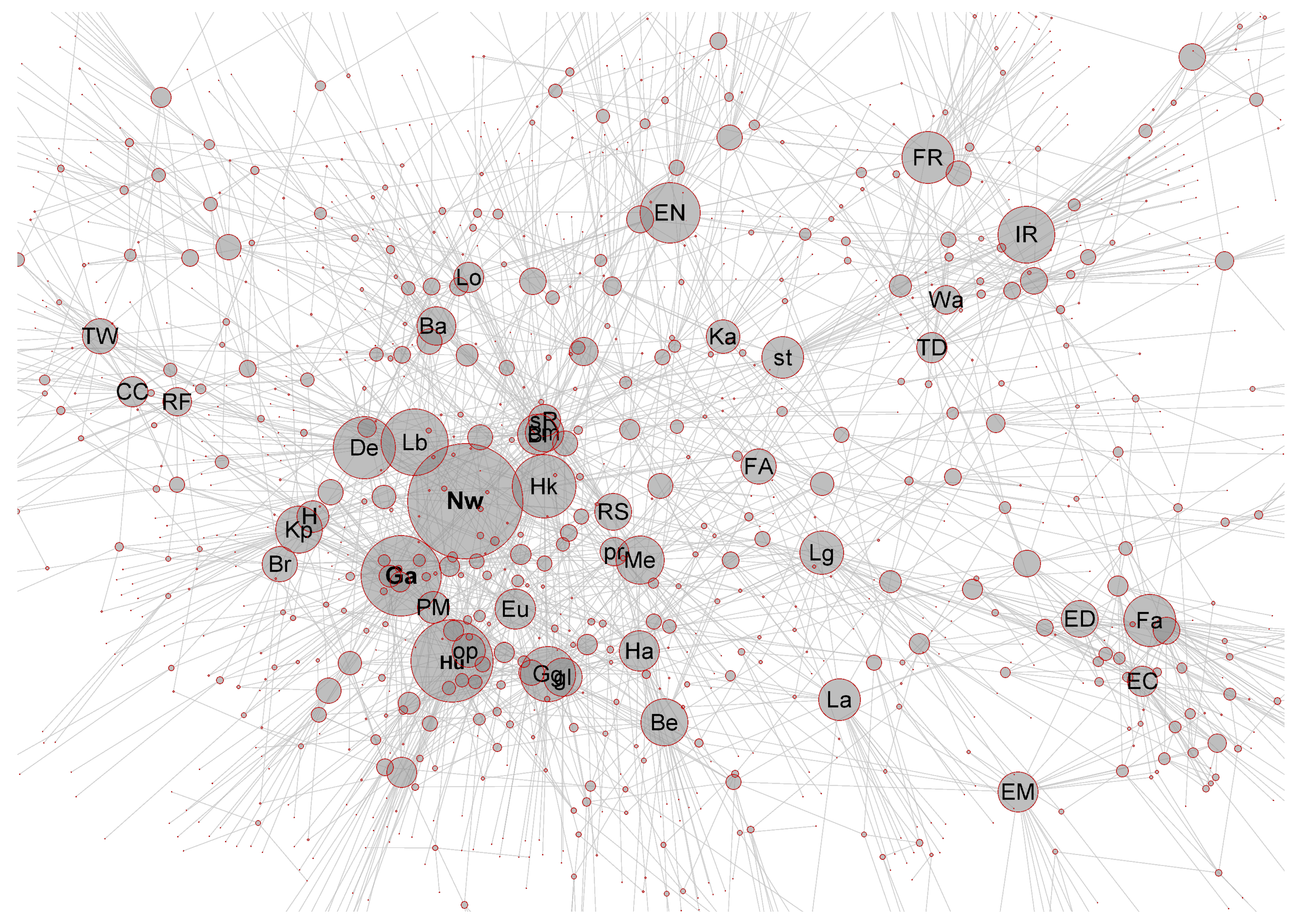
3.1. An Example: An Agglomerated Associative Knowledge Network
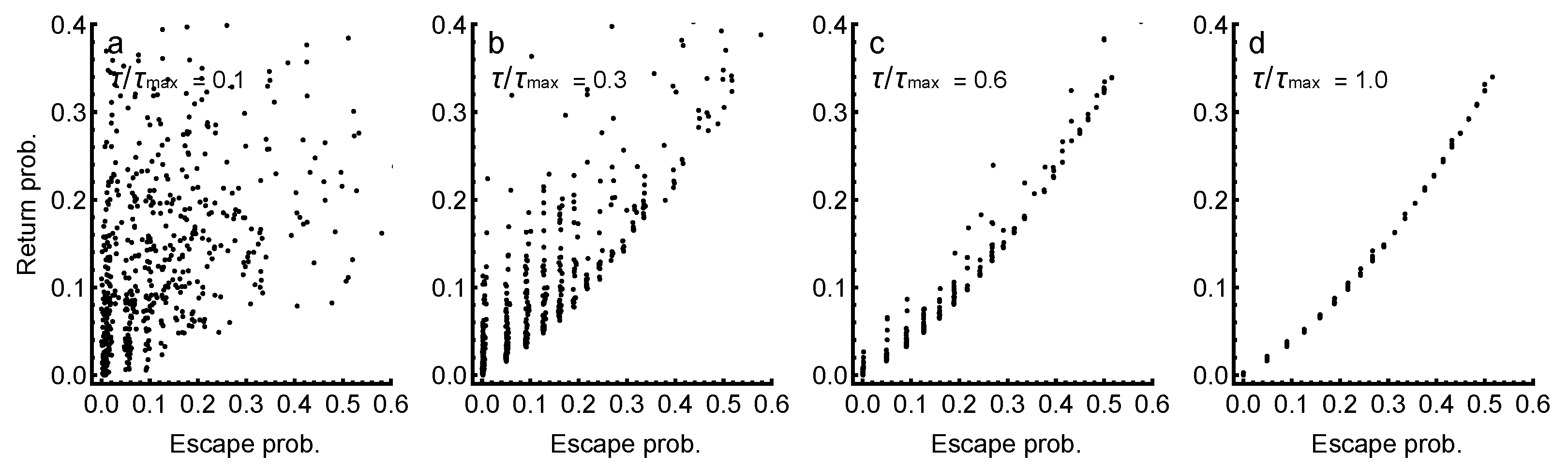
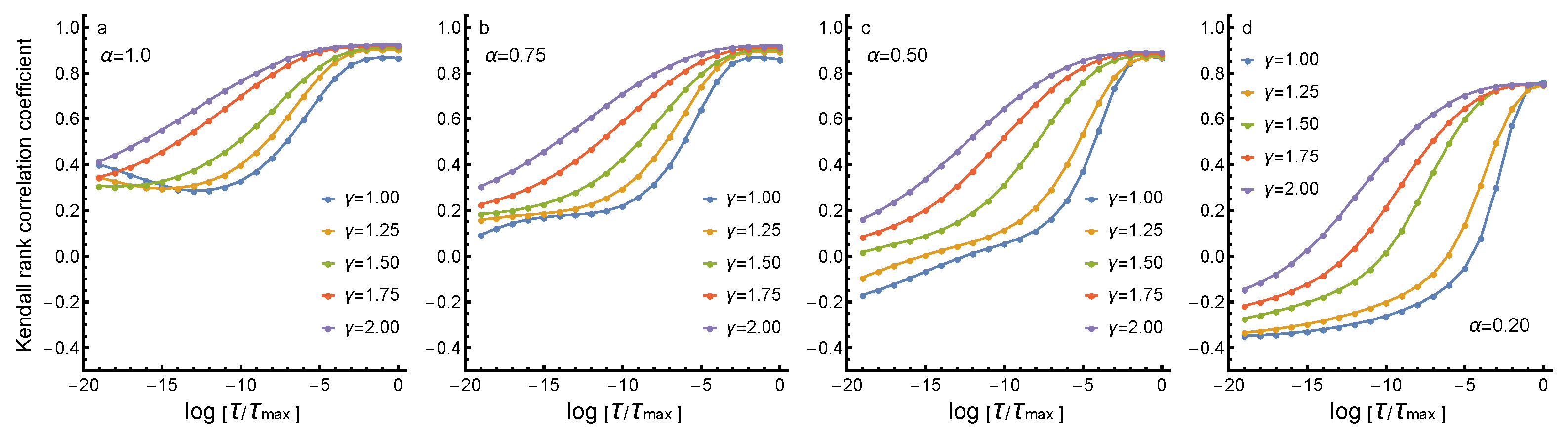
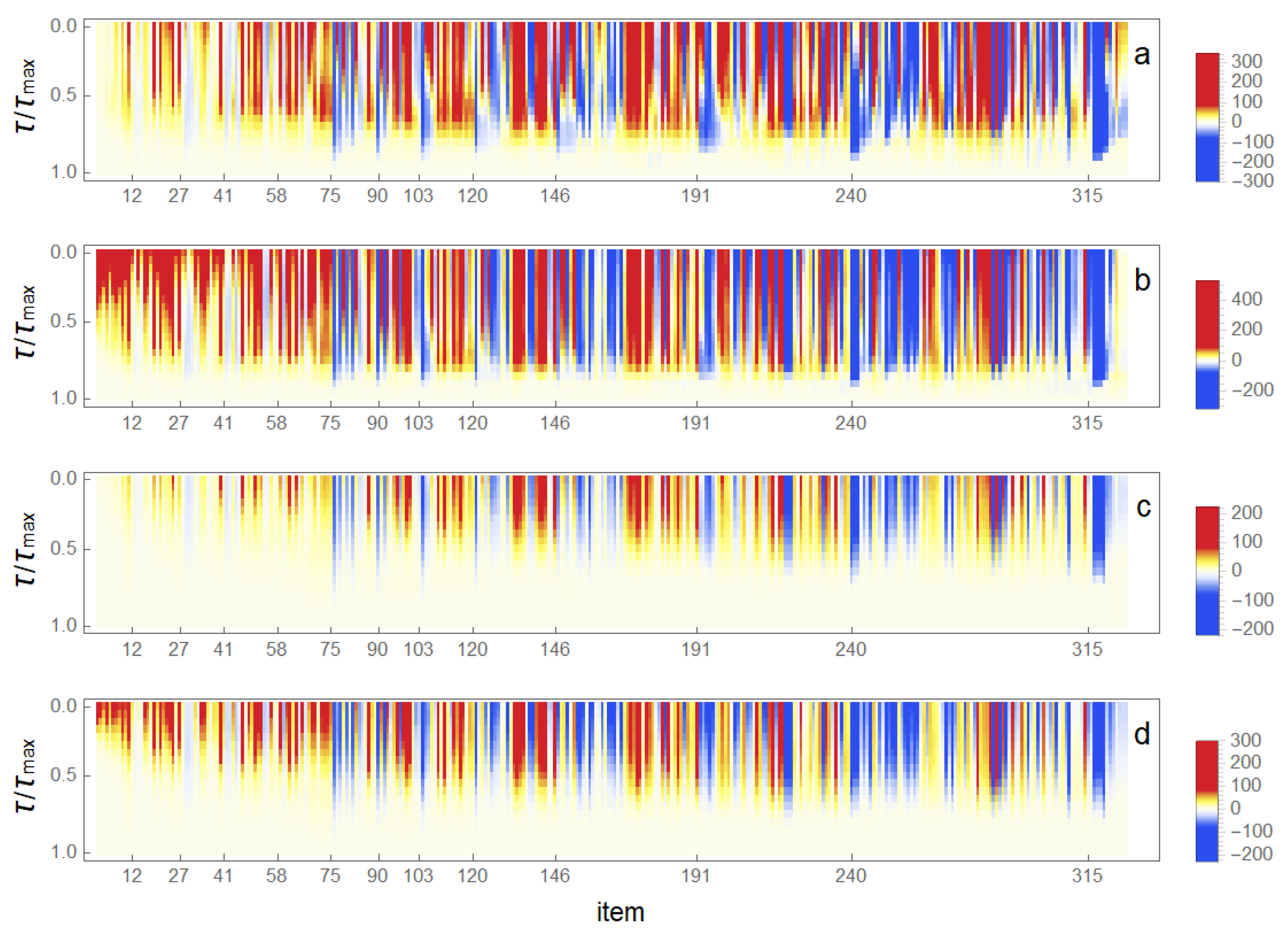
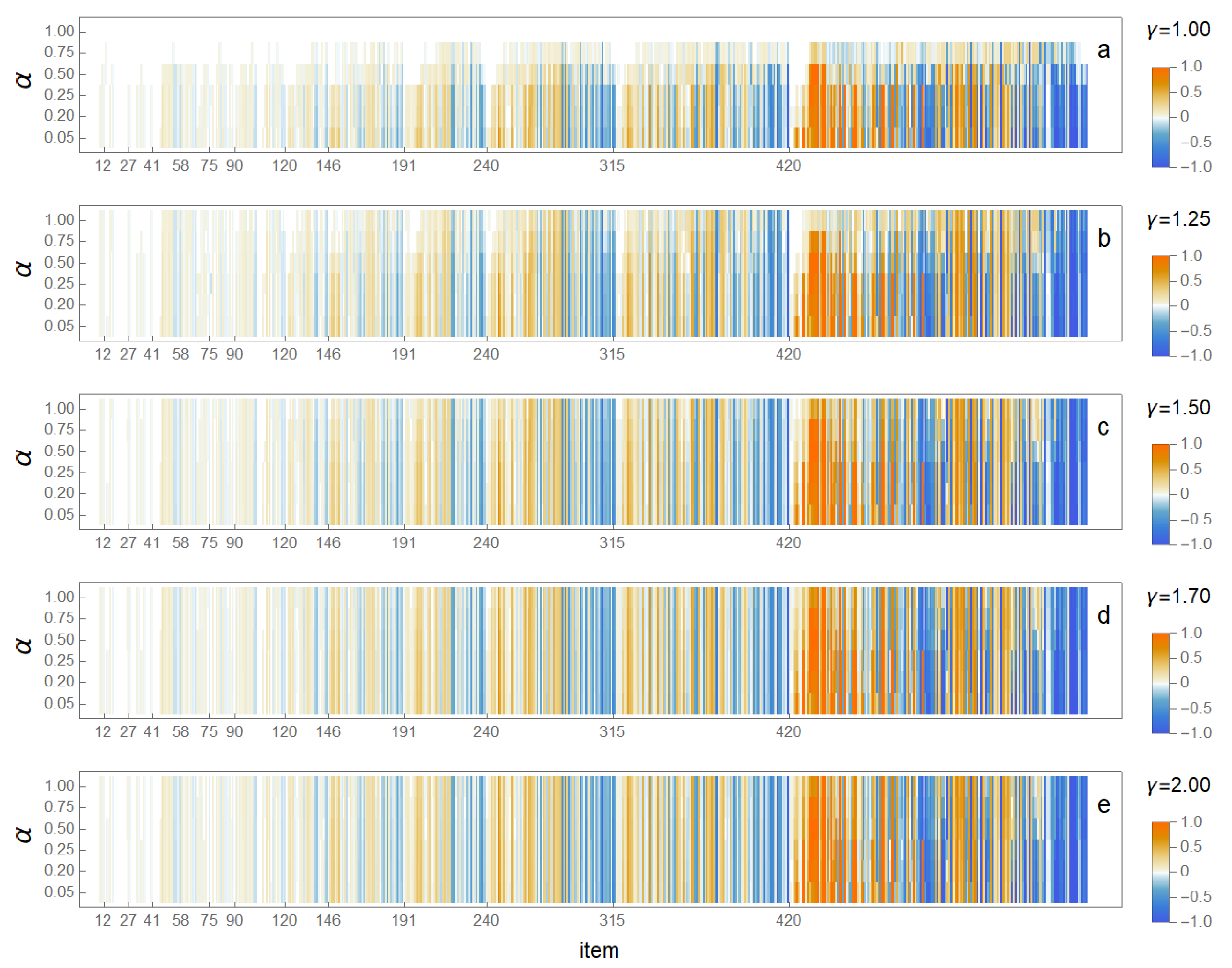
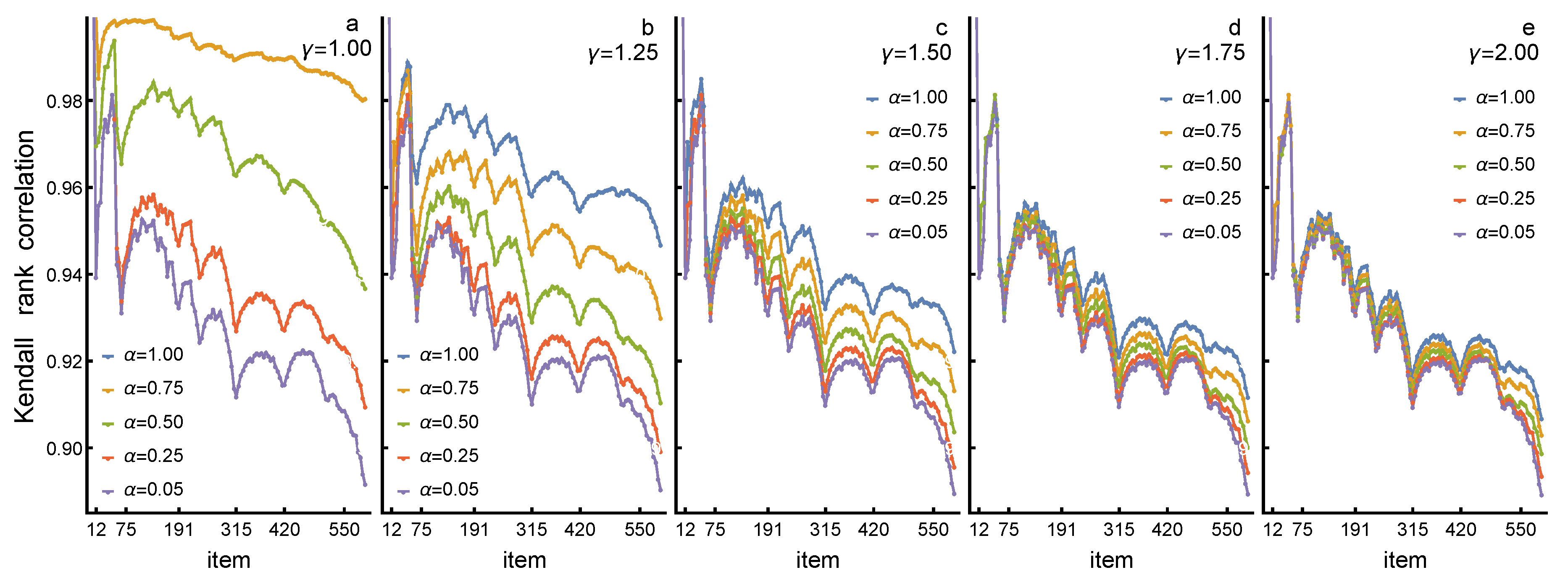
3.2. Changes in Rankings
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sowa, J.F. Semantic networks. In Encyclopedia of Cognitive Science; Nadel, L., Ed.; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Hartley, R.T.; Barnden, J.A. Semantic networks: Visualizations of knowledge. Trends Cogn. Sci. 1997, 1, 169–175. [Google Scholar] [CrossRef]
- Lehmann, F. Semantic networks. Comput. Math. Appl. 1992, 23, 1–50. [Google Scholar] [CrossRef]
- Siew, C.S.Q.; Wulff, D.U.; Beckage, N.M.; Kenett, Y.N. Cognitive Network Science: A Review of Research on Cognition through the Lens of Network Representations, Processes, and Dynamics. Complexity 2019, 2019, 2108423. [Google Scholar] [CrossRef]
- Siew, C.S.Q. Applications of Network Science to Education Research: Quantifying Knowledge and the Development of Expertise through Network Analysis. Educ. Sci. 2020, 10, 101. [Google Scholar] [CrossRef]
- Kenett, Y.N.; Beckage, N.M.; Siew, C.S.Q.; Wulff, D.U. Editorial: Cognitive Network Science: A New Frontier. Complexity 2020, 2020, 6870278. [Google Scholar] [CrossRef]
- Koponen, I.T.; Mäntylä, T. Editorial: Networks Applied in Science Education Research. Educ. Sci. 2020, 10, 142. [Google Scholar] [CrossRef]
- De Deyne, S.; Kenett, Y.N.; Anaki, D.; Faust, M.; Navarro, D. Large-scale network representations of semantics in the mental lexicon. In Frontiers of Cognitive Psychology. Big Data in Cognitive Science; Jones, M.N., Ed.; Routledge/Taylor & Francis Group: Abingdon, UK, 2017; pp. 174–202. [Google Scholar]
- Steyvers, M.; Tenenbaum, J.B. The Large-Scale Structure of Semantic Networks: Statistical Analyses and a Model of Semantic Growth. Cogn. Sci. 2005, 29, 41–78. [Google Scholar] [CrossRef]
- Collins, A.M.; Loftus, E.F. A spreading-activation theory of semantic processing. Psychol. Rev. 1975, 82, 407–428. [Google Scholar] [CrossRef]
- Lerner, I.; Bentin, S.; Shriki, O. Spreading Activation in an Attractor Network With Latching Dynamics: Automatic Semantic Priming Revisited. Cogn. Sci. 2012, 36, 1339–1382. [Google Scholar] [CrossRef]
- Hills, T.T.; Jones, M.N.; Todd, P.M. Optimal Foraging in Semantic Memory. Psychol. Rev. 2012, 119, 431–440. [Google Scholar] [CrossRef]
- Abbott, J.T.; Austerweil, J.L.; Griffiths, T.L. Random Walks on Semantic Networks Can Resemble Optimal Foraging. Psychol. Rev. 2015, 122, 558–569. [Google Scholar] [CrossRef] [PubMed]
- Kenett, Y.N.; Levi, E.; Anaki, D.; Faust, M. The Semantic Distance Task: Quantifying Semantic Distance With Semantic Network Path Length. J. Exp. Psychol. 2017, 43, 1470–1489. [Google Scholar] [CrossRef]
- Siew, C.S.Q. Spreadr: An R package to simulate spreading activation in a network. Behav. Res. Meth. 2019, 51, 910–929. [Google Scholar] [CrossRef]
- Griffiths, T.L.; Steyvers, M.; Firl, A. Google and the Mind: Predicting Fluency With PageRank. Psychol. Sci. 2007, 18, 1069–1076. [Google Scholar] [CrossRef]
- Koponen, I.T. Systemic States of Spreading Activation in Describing Associative Knowledge Networks: From Key Items to Relative Entropy Based Comparisons. Systems 2021, 9, 1. [Google Scholar] [CrossRef]
- Koponen, I.; Nousiainen, M. University students’ associative knowledge of history of science: Matthew effect in action? Eur. J. Sci. Math. Educ. 2018, 6, 69–81. [Google Scholar] [CrossRef]
- Biamonte, J.; Faccin, M.; De Domenico, M. Complex networks from classic to quantum. Commum. Phys. 2019, 2, 53. [Google Scholar] [CrossRef]
- Faccin, M.; Johnson, T.; Biamonte, J.; Kais, S.; Migdał, P. Degree Distribution in Quantum Walks on Complex Networks. Phys. Rev. X 2013, 3, 041007. [Google Scholar] [CrossRef]
- Paparo, D.P.; Müller, M.; Comellas, F.; Martin-Delgado, M.A. Quantum Google in a Complex Network. Sci. Rep. 2013, 3, 2773. [Google Scholar] [CrossRef]
- Garnerone, S. Thermodynamic formalism for dissipative quantum walks. Phys. Rev. A 2012, 86, 032342. [Google Scholar] [CrossRef]
- De Domenico, M.; Biamonte, J. Spectral Entropies as Information-Theoretic Tools for Complex Network Comparison. Phys. Rev. X 2016, 6, 041062. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef]
- Riascos, A.P.; Mateos, J.L. Fractional dynamics on networks: Emergence of anomalous diffusion and Lévy flights. Phys. Rev. E 2014, 90, 032809. [Google Scholar] [CrossRef] [PubMed]
- Riascos, A.P.; Mateos, J.L. Long-range navigation on complex networks using Lévy random walks. Phys. Rev. E 2012, 86, 056110. [Google Scholar] [CrossRef]
- Benzi, M.; Bertaccini, D.; Durastante, F.; Simunec, I. Non-local network dynamics via fractional graph Laplacians. J. Complex Netw. 2020, 8, cnaa017. [Google Scholar] [CrossRef]
- Estrada, E.; Hameed, E.; Hatano, N.; Langer, M. Path Laplacian operators and superdiffusive processes on graphs. I. One-dimensional case. Linear Algebra Appl. 2017, 523, 307–334. [Google Scholar] [CrossRef]
- Estrada, E.; Hameed, E.; Langer, M.; Puchalska, A. Path Laplacian operators and superdiffusive processes on graphs. II. Two-dimensional lattice. Linear Algebra Appl. 2018, 555, 373–397. [Google Scholar] [CrossRef]
- de Pablo, A.; Quirós, F.; Rodríguez, A.; Vázquez, J.L. A fractional porous medium equation. Adv. Math. 2011, 226, 1378–1409. [Google Scholar] [CrossRef]
- Vázquez, J.L. Recent progressin the theory of nonlinear diffusion with fractional Laplacian operators. Discret. Cont. Dyn. Syst. Ser. S 2014, 7, 857–885. [Google Scholar]
- Bologna, M.; Tsallis, C.; Grigolini, P. Anomalous diffusion associated with nonlinear fractional derivative Fokker–Planck-like equation: Exact time-dependent solutions. Phys. Rev. E 2000, 62, 2213–2218. [Google Scholar] [CrossRef]
- Koponen, I.T.; Palmgren, E.; Keski-Vakkuri, E. Characterising heavy-tailed networks using q-generalised entropy and q-adjacency kernels. Physica A 2021, 566, 125666. [Google Scholar] [CrossRef]
- Estrada, E. The Structure of Complex Networks: Theory and Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Newman, M.E.J. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Tsallis, C. Economics and Finance: Q-Statistical Stylized Features Galore. Entropy 2017, 19, 457. [Google Scholar] [CrossRef]
- Borges, E.P. On a q-generalization of circular and hyperbolic functions. J. Phys. A Math. Gen. 1998, 31, 5281–5288. [Google Scholar] [CrossRef]
- Yamano, T. Some properties of q-logarithm and q-exponential functions in Tsallis statistics. Physica A 2002, 305, 486–496. [Google Scholar] [CrossRef]
- Ferri, G.L.; Martinez, S.; Plastino, A. Equivalence of the four versions of Tsallis’s statistics. J. Stat. Mech. 2005, 2005, P04009. [Google Scholar] [CrossRef]
- Kunegis, J.; Fay, D.; Bauckhage, C. Spectral evolution in dynamic networks. Knowl. Inf. Syst. 2013, 37, 1–36. [Google Scholar] [CrossRef]
- Benzi, M.; Klymko, C. On the Limiting Behavior of Parameter-Dependent Network Centrality Measures. SIAM J. Matrix Anal. Appl. 2015, 36, 686–706. [Google Scholar] [CrossRef]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Sanchez-Burillo, E.; Duch, J.; Gomez-Gardenes, J.; Zueco, D. Quantum Navigation and Ranking in Complex Networks. Sci. Rep. 2012, 2, 605. [Google Scholar] [CrossRef]
- Martínez-García, M.; Gordon, T.; Shu, L. Extended Crossover Model for Human-Control of Fractional Order Plants. IEEE Access 2017, 5, 27622–27635. [Google Scholar] [CrossRef]
- Martínez-García, M.; Zhang, Y.; Gordon, T. Memory Pattern Identification for Feedback Tracking Control in Human–Machine Systems. Hum. Factors 2021, 63, 210–226. [Google Scholar] [CrossRef]
- Ifenthaler, D.; Hanewald, R. Digital Knowledge Maps in Education:Technology-Enhanced Support for Teachers and Learners; Springer: New York, NY, USA, 2014. [Google Scholar]
- Nesbit, J.C.; Adesope, O.O. Learning with Concept and Knowledge Maps: A Meta-Analysis. Rev. Educ. Res. 2006, 76, 413–448. [Google Scholar] [CrossRef]
- Kubsch, M.; Touitou, I.; Nordine, J.; Fortus, D.; Neumann, K.; Krajcik, J. Transferring Knowledge in a Knowledge-in-Use Task -Investigating the Role of Knowledge Organization. Educ. Sci. 2020, 10, 20. [Google Scholar] [CrossRef]
- Thurn, M.; Hänger, B.; Kokkonen, T. Concept Mapping in Magnetism and Electrostatics: Core Concepts and Development over Time. Educ. Sci. 2020, 10, 129. [Google Scholar] [CrossRef]
- Koponen, I.T.; Nousiainen, M. Concept networks of students’ knowledge of relationships between physics concepts: Finding key concepts and their epistemic support. Appl. Netw. Sci. 2018, 3, 14. [Google Scholar] [CrossRef]
- Koponen, I.T.; Nousiainen, M. Pre-service physics teachers’ understanding of the relational structure of physics concepts: Organising subject contents for purposes of teaching. Int. J. Sci. Math. Educ. 2013, 11, 325–357. [Google Scholar] [CrossRef]
- Derman, A.; Eilks, I. Using a word association test for the assessment of high school students’ cognitive structures on dissolution. Chem. Educ. Res. Pract. 2016, 17, 902–913. [Google Scholar] [CrossRef]
- Vukic, D.; Martincic-Ipsic, S.; Mestrovic, A. Structural Analysis of Factual, Conceptual, Procedural, and Metacognitive Knowledge in a Multidimensional Knowledge Network. Complexity 2020, 2020, 9407162. [Google Scholar] [CrossRef]
- Kapuza, A. How Concept Maps with and without a List of Concepts Differ: The Case of Statistics. Educ. Sci. 2020, 10, 91. [Google Scholar] [CrossRef]
- Siew, C.S.Q. Using network science to analyze concept maps of psychology undergraduates. Appl. Cogn. Psychol. 2019, 33, 662–668. [Google Scholar] [CrossRef]
- Koponen, M.; Asikainen, M.; Viholainen, A.; Hirvonen, P. Using network analysis methods to investigate how future teachers conceptualize the links between the domains of teacher knowledge. Teach. Teach. Educ. 2019, 79, 137–152. [Google Scholar] [CrossRef]
- Lommi, H.; Koponen, I.T. Network cartography of university students’ knowledge landscapes about the history of science: Landmarks and thematic communities. Appl. Netw. Sci. 2019, 4, 6. [Google Scholar] [CrossRef]
- Alcantara, M.C.; Braga, M.; van den Heuvel, C. Historical Networks in Science Education: A Case Study of an Experiment with Network Analysis by High School Students. Sci. Educ. 2020, 29, 101–121. [Google Scholar] [CrossRef]
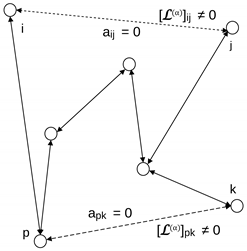
| Scheme of Long Jumps | Description | Symbol |
|---|---|---|
 | Adjacency matrix | |
| Elements of | ||
| Degree matrix | ||
| Graph Laplacian | ||
| F. g. Laplacian | ||
| Elements of | ||
| Systemic state | ||
| Elements of |
| Item | d | Ac | Item | d | Ac | Item | d | Ac |
|---|---|---|---|---|---|---|---|---|
| 1. Newton | 64 | Nw | 12. Bernoulli | 23 | Be | 23. Optics | 20 | op |
| 2. Galilei | 44 | Ga | 13. Faraday | 22 | Fa | 24. Bacon | 20 | Ba |
| 3. Huygens | 41 | Hu | 14. Electrodynamics | 22 | EM | 25. Scientific revol. | 20 | sR |
| 4.Hooke | 36 | Hk | 15. Industrial revol. | 22 | IR | 26. Brahe | 19 | Br |
| 5. Leibniz | 32 | Lb | 16. Kepler | 22 | Kp | 27. Planet motion | 19 | PM |
| 6. Descartes | 31 | De | 17. Gravitation law | 22 | gl | 28. Euler | 19 | Eu |
| 7. Gravitation | 30 | Gg | 18. Steam engine | 22 | st | 29. Electric current | 18 | EC |
| 8. Enlightenment | 29 | EN | 19. Royal Society | 22 | RS | 30. Electricity | 18 | ED |
| 9. Mechanics | 27 | Me | 20. French revol. | 21 | FR | 31. Thermodynamics | 18 | TD |
| 10. Empiricism | 23 | em | 21. French Academy | 21 | FA | 32. Reformation | 17 | RF |
| 11. Boyle | 23 | Bo | 22. Heliocentricity | 20 | H | 33. Locke | 17 | Lo |
| Key Items in Item Bands I–V | ||||
|---|---|---|---|---|
| I 33–46 (13/13) | II 47–60 (13/13) | III 61–100 (20/25) | IV 101–140 (18/25) | V 141–200 (16/25) |
| Locke (Lo) | Thermometer | Beeckman | Finnish War | Thought experim. |
| Halley (Ha) | Volta | Wave thr. light | Electric potential | Chatelet |
| Watt (Wa) | Earth magn field | Atmsph. pressure | Kirchhoff | Medical science |
| Cath. church (CC) | Stevin | Telescope | Hydrost. pressure | Gauss |
| Pressure (pr) | Ludvig XIV | Fire of London | Gay-Lussac law | Mozart |
| Laplace (LP) | Refraction law | Oersted | Spinoza | Electric charge |
| Lagrange (Lg) | Theory of light | d’Alambert | Speed of light | Electric motor |
| Scientific method | Pendulum | Liberalism | Magnetic field | Carnot’s engine |
| Napoleon | Mathematics | Pascal | Pendulum clock | Locomotive |
| Gilbert | Newton’s laws | Differential calc. | Maupertuis | Year 1848 |
| Kant (Ka) | Gravity | Hobbes | Cavendish | Swedish empire |
| 30 Y. War (TW) | Copernicus | Rationalism | Spectrum of light | Carnot’s process |
| Magnetism | Wren | Marx | Elizabeth I | Galvani |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koponen, I.T. Systemic States of Spreading Activation in Describing Associative Knowledge Networks II: Generalisations with Fractional Graph Laplacians and q-Adjacency Kernels. Systems 2021, 9, 22. https://doi.org/10.3390/systems9020022
Koponen IT. Systemic States of Spreading Activation in Describing Associative Knowledge Networks II: Generalisations with Fractional Graph Laplacians and q-Adjacency Kernels. Systems. 2021; 9(2):22. https://doi.org/10.3390/systems9020022
Chicago/Turabian StyleKoponen, Ismo T. 2021. "Systemic States of Spreading Activation in Describing Associative Knowledge Networks II: Generalisations with Fractional Graph Laplacians and q-Adjacency Kernels" Systems 9, no. 2: 22. https://doi.org/10.3390/systems9020022
APA StyleKoponen, I. T. (2021). Systemic States of Spreading Activation in Describing Associative Knowledge Networks II: Generalisations with Fractional Graph Laplacians and q-Adjacency Kernels. Systems, 9(2), 22. https://doi.org/10.3390/systems9020022






