Abstract
Macro-level trends and patterns are commonly used in business, science, finance, and engineering to provide insights and estimates to assist decision-makers. In this research effort, macro-level trends and patterns were explored on the diffusion rates of technological innovations, a component of a sorely under-studied question in technology assessment: When should a technological innovation be abandoned? A quantitative exploratory data analysis (EDA)-based approach was employed to examine diffusion market data of 42 U.S. consumer technological innovations from the early 1900s to the 2010s to extract general macro-level knowledge on technological innovation diffusion rates. A goal of this effort is to grow diffusion rate knowledge to enable the development of general macro-based forecasting tools. Such tools would aid decision-makers in making informed and proactive decisions on when to abandon a technological innovation. This research offers several significant contributions to the macro-level understanding of the boundaries and likelihood of achieving a range of technological innovation diffusion rates. These contributions include the determination that the frequency of diffusion rates are positively skewed when ordered from slowest to fastest, and the identification and ranking of probability density functions that best represent the rates of technological innovation diffusion.
1. Introduction
This research explores the likelihoods and probability boundaries of U.S. technological innovation diffusion rates and initiates a research thrust to build macro-based knowledge towards developing technological innovation abandonment intelligence. The initiatives drive is to support resource decision-makers in making informed and proactive decisions on when to abandon a technological innovation at a macro level. Specifically, the overall research program strives to address: what is the optimal point of abandonment of a technological innovation, and what is the economic impact of the speed at which the abandonment decision is made? This effort begins this exploration by focusing on examining a common factor required to address each of these questions, the diffusion rates of technological innovation, and is the primary focus of this endeavor.
This study employed diffusion market data from 42 U.S. technological innovations (products and processes) spanning more than 100 years to gain insight into the macro-perspective patterns on diffusion rates of technological innovation. These insights were gained by exploring and enriching the knowledge on boundaries and likelihoods on the diffusion rates of technological innovations via bulk trends and patterns. The resulting observations provide a means for structuring probabilistic-based forecast models on the diffusion rates of technological innovations via the best-fit probability density functions determined herein.
We will first establish an operational definition of the term technological innovation(s), since researchers of different disciplines use the term in various ways. For our purposes, we use the noun-based definition rather than the process-based definition of technological innovation, because our focus is not the process of technological innovation, but rather exploration of the product and process innovation life cycle. A technological innovation may be a new or (minor or major) improved product, process, or device that results in the societal distribution (commercialization) of new or improved goods (products or services) or a new or improved (products or services) production process [1,2,3]. Commercialized products and processes such as the microwave oven and chlorine-free paper production are examples of technological innovations. Thus, the diffusion of technological innovation, per the operational definition, is measurable and trackable via market diffusion sales data, allowing the study of product and process innovation diffusion from a generalized perspective. For this research, the term technological innovation may cover what some researchers consider inventions, technologies, innovations, products, or processes. For this reason, the terms technological innovation and innovation are used interchangeably in this paper, based on the above-established definition.
How is it done today, and what are the limits of the current practice? Technological innovation forecasting knowledge is often used to determine whether an innovation is worthy of pursuing, but not often as a means to signal when it has reached maturity or when it should be abandoned [4]. Such forecasting tools commonly require resource-intensive micro-based investigations of factors affecting a technological innovation’s diffusion rate and are often narrowly focused on a specific technological innovation. Accordingly, it is comprehensible that these micro-based forecasting tools are complex and involved (e.g., factors can be time-consuming and challenging to develop, measure, and track accurately or at all). The inherent complexity of micro-based forecasting tools is a disadvantage; it has been shown that, as task complexity goes up, cognitive demand goes up, and as cognitive demand goes up, a decision-maker is increasingly likely not to justify the use of a complex decision-making strategy, especially when time is a factor [5,6]. As a simplified analogy, it is easy to determine whether a cup of coffee is hot (macro level), but it requires more effort to determine its exact temperature (micro level). In practice, it requires significant effort to determine whether and to what extent potential adopters are satisfied with their existing solution (a micro-based factor identified by Choffray and Lilien [7] to gauge the diffusion rate of a technological innovation).
What is new in this approach? Decision-makers have a macro-level blind spot regarding the general assessment of patterns and trends of technological innovation diffusion rates. Macro-level bulk trends and patterns are commonly used in business, science, finance, and engineering to provide insights and estimates that enable decision-makers to make informed decisions expeditiously. In this effort, leveraging macro-level bulk trends and patterns, insights are gain on the boundaries and likelihoods on the diffusion rates of technological innovations. Knowledge of the boundaries and likelihoods of the diffusion rates of technological innovations via macro bulk trends and patterns has value in speeding and simplifying decision-making when appropriate. The development of macro-based forecasting knowledge could provide decision-makers with tools to assess and manage the economic impact of technological innovation abandonment in relation to time, which translates to a competitive advantage when it comes to growth and advancement [8,9,10].
What value would be created by this approach? A knowledge gap exists, in the forecasting and management research literature, for modeling the speeds (via probability density function) at which technological innovations spread at the macro level (bulk trends and patterns). This research initiative aims to reduce this knowledge gap, to better position decision-makers with intelligence on diffusion rates to make informed abandonment choices. As a consequence, the endeavor to study the diffusion rates of technological innovations has economic significance and adds value to any organization engaged in technological innovation, technology, and resource management [11]. Any organization that can be affected by technological change unavoidably engages in the forecasting and management of technology and technological innovation [12]. Accordingly, organizations are continuously striving to improve the management of limited resources (i.e., labor, equipment, materials, time, and capital) to maximize gains and to minimize losses. A key component of effectively directing resources is the understanding and continuous improvement of knowledge in forecasting and managing technological innovation. This knowledge includes improving the insights on factors (e.g., diffusion rates) that can impact resource and abandonment optimization, which is the objective of this research.
Insights and knowledge of the boundaries and likelihoods on the diffusion rates of technological innovation provide meaningful value for decision-makers. Without information, management, and decision-making of any kind is no more than guesswork [13]. As an example, if a resource management decision-maker has general assessment knowledge indicating that attaining a 12% per year innovation diffusion rate has a low likelihood of occurrence, he or she now has useful information that will help direct how to utilize resource investments. New macro-level understanding of the diffusion rates of technological innovations has prospective implications on improving a decision-maker’s ability to make proactive, knowledge-based decisions in a timely manner.
How is this endeavor to be accomplished? To examine the relationships between the diffusion rate of a technological innovation and its likelihood of occurrence, a quantitative exploratory data analysis (EDA)-based approach was be used due to the limited scholarly works in this area as well as for its ability to summarize and characterize data and patterns. Specifically, this paper aims to address and expand the following research questions, reveal data patterns in the process, and generate new exploratory hypotheses for future research, thereby giving management practitioners and researchers macro-based insights and knowledge on trends and patterns for assessing the diffusion rates of technological innovation.
- Principal question: What bulk trends and patterns regarding diffusion rates can be extracted from the market sales diffusion data of U.S. technological innovations?
- Sub-question #1: What are the probabilistic characteristics of the rates of diffusion of U.S. technological innovations?
- Sub-question #2: What distributions best fit the diffusion rates of U.S. technological innovations?
2. Background
The amount of relevant work examining the diffusion rates of technological innovations directly from bulk trends and patterns (a macro-based perspective) in the research literature is underwhelming. There are many research articles examining factors affecting diffusion rates of technological innovation from a micro-based perspective. In a significant number of these articles, indirect macro-based inferences are present. Two such works addressing or acknowledging the need for probabilistic boundaries and likelihoods of diffusion rates of technological innovations are Van den Bulte [14] and Choffray and Lilien [7]. Van den Bulte’s [14] research focused on determining whether, how much, and why diffusion speeds have changed for technological innovations from 1923 to 1996 within the United States. In this work, Van den Bulte reported the need and importance of considering the probability and time of technological innovation diffusion rates, but acknowledged that such probabilistic data were lacking or nonexistent. Additionally, Choffray and Lilien [7] examined the development of a decision system for new products as well as forecasting methods (via external factors such as customer satisfaction and competition) to determine the likelihood of attaining initial rates of penetration and speeds of diffusion of new products. Choffray and Lilien [7] utilized micro-based information that could only be gathered reactively during a technological innovation’s life cycle.
Although useful, these and other micro-based bodies of research leave a gap in understanding the boundaries and the probabilistic likelihoods of achieving a range of technological innovation diffusion rates from a macro-based perspective. At present, there is no direct body of work examining the boundaries and the probabilistic likelihoods of achieving a range of diffusion rates directly from bulk trends and patterns through a historical examination of the diffusion lifecycle of technological innovations. To establish a framework to explore these areas, there must be some agreement or a minimum acknowledgment of elemental definitions, terms, and concepts. Five critical terms and relationships are described in the following paragraphs to clarify concepts used by the authors.
2.1. Diffusion Versus Adoption
Diffusion and adoption, in relation to innovation, are closely linked concepts and processes [15]. For this reason, they are often confused and warrant a review. The focus of this research is on innovation diffusion and not adoption; thus, it is important to examine and review the distinction. Diffusion is a macro process describing the cumulative spread of an innovation from its origins to the group (i.e., public, community, country, organization), whereas adoption is a micro process that focuses on individual discrete acceptance or rejection of an innovation [16]. Put simply, adoption is a binary decision (accept or reject) in time, and diffusion is the change of the cumulative adoption decisions over time.
2.2. Diffusion of Innovation and Innovation Diffusion
Along with context, word combinations can change the meaning of a phrase. Innovation diffusion and diffusion of innovation, although using the same root words, can each mean something entirely different. For example, in Roger’s pivotal and highly cited book “The Diffusion of Innovation,” he examines the diffusion of innovation as the process (how and why) of innovation spread [15]. In this research, innovation diffusion is defined as the cumulative spread of an innovation (how much and how fast) from its origins through a group (public, community, country, organization, etc.). Although how and why an innovation spreads is an important area of study, it is not the focus of this effort. For clarity, this research examines and addresses the diffusion rates of technological innovation (i.e., the how fast).
2.3. Rate of Innovation and Innovation Diffusion Rate
A distinction between rate of innovation and innovation diffusion rate warrants an examination to frame the context of this research endeavor and avoid misinterpretations of its purpose, results, and conclusions. The use of the phrase rate of innovation in the literature commonly means the number of innovations over time. As an example, Huebner’s [17] macro-perspective examination of diffusion of innovation concluded that there is a declining trend for worldwide innovations over the last century. Huebner does not claim that innovation diffusion rates are increasing or decreasing, only that the total number of innovations year by year has declined. In contrast, the phrase innovation diffusion rate commonly means (in the research literature) and is defined for this research as the speed at which an innovation spreads into a market or industry.
2.4. The Study of Innovation Diffusion
The study of innovation diffusion can be grouped into two perspectives: micro and macro. The micro-perspective group focuses on understanding the factors affecting innovation diffusion, whereas the macro-perspective group focuses on understanding bulk trends and patterns. Contemporary analysis of innovation diffusion has principally focused on determining and understanding the factors driving the process of diffusion and its effects (a micro-perspective understanding of innovation diffusion). As a foundational example, Mansfield [18] explored differences among innovations and their rate of imitation (diffusion). His research examined why one innovation rate of diffusion is different from another within an organization. Mansfield demonstrated that there appeared to be a link between profitability and investment cost with an innovation’s or technology’s diffusion rate in an organization, but he admitted that his dataset was limited and his results were tentative at best, barring the addition of more diffusion (imitation) data. Other researchers contributing to a micro-perspective understanding of innovation and technology diffusion include Silverberg et al. [19], Grübler [20], Jovanovic and Lach [21], Caselli and Coleman [22], Manuelli and Seshadri [23], Comin and Hobijn [24], and Comin and Mestieri [25].
No direct macro-based contemporary research targeting the development of knowledge on the likelihoods and probability boundaries of technological innovation diffusion rates was discovered when this effort was conducted. The focus of existing macro-based research has been on determining if diffusion rates of innovations have increased over time; that is, technological innovations are diffusing faster now than in the past. For example, Grübler’s [20] work on transportation diffusion growth cluster factors analyzed two groups of innovation data over the past two centuries and concluded that there were little conclusive data on diffusion rate acceleration. Conversely, Olshavshy’s [26] study of diffusion factors of 25 consumer products indicated that diffusion rates are increasing. Other researchers contributing to the macro-perspective study of innovation diffusion rate acceleration include Mansfield [18], Fisher and Pry [27], Qualls et al. [28], Clark et al. [29], Bayus [9], and Kohli et al. [30]. Although an investigation of the inconsistencies present in these results is worthy of pursuit, it is out of the scope of this current effort.
2.5. Diffusion Models
The theory of the rate of innovation adoption suggests that the diffusion of innovation grows slowly and gradually in the beginning, followed by a period of rapid growth that slows and becomes stable to the point of saturation. This theory is best represented by an S-curve [15]. It should be noted that a bell curve is commonly used to represent the rate of growth of a system within a time span, and the cumulative number of “units” in a bell curve at any given point in time follows an S-curve, representing cumulative growth [31]. The S-curve accordingly demonstrates that the rate of growth is proportional to both the amount of growth already achieved and the amount of attainable growth remaining, a reason forecasting tools use the S-curve [31]. The S-curve began as a mathematical model and was later applied to various fields and applications—including but not limited to physics, biology, and anthropology—for projecting the performance of technologies, to foresee population changes, for market penetration analyses, for micro- and macro-economic studies, for diffusion mechanisms of technological and social inventions, for ecological modeling, and for innovation diffusion [31,32].
Observed and empirical research has shown and supported that innovation diffusion characteristically follows an S-curve [33,34,35,36,37,38,39]. Frequently used S-curve models for the innovation diffusion are the Logistic, Gompertz, and Bass models [39,40,41,42]. Numerous researchers have compared these and other innovation diffusion models, samples of which are presented in Table 1 [43]. Comparative studies suggest that there is no substantial evidence that one diffusion model is consistently superior to the others [44,45,46]. Selection of the best model to accurately forecast an innovation’s diffusion is dependent on multiple conditions (specific triggers and factors related to the innovation as well as market conditions). A comparison of the micro accuracy of these models, although informative, is not the focus of this endeavor. For the selection of a model to use in this endeavor, one must remember that, at their best, models are informative but not exact. Nevertheless, each of the models discussed (Logistic, Gompertz, and Bass) can be a good approximate when studying general (macro-based) diffusion trends and patterns [47,48].

Table 1.
Research examining innovation diffusion models.
For this research endeavor, the Logistic model will be used to extract diffusion rate data from the dataset under study; as such, its selection justification is warranted and provided herein. As mentioned, several diffusion models exist. However, the Logistic model is widely used to analyze innovation diffusion and is the cornerstone of many models in the research literature [18,48,54,55,56,57,58]. In addition, the Bass and Gompertz models can be derived from or be reduced to special forms of the Logistic model [14,59,60,61,62]. While the advantages and disadvantages of each diffusion model are well studied, the adaptability, simplicity (in estimating parameters and extracting patterns from observed data), and informative nature of the Logistic model make it foundational to macro-based diffusion examination [63,64]. Additionally, in the case of mature technological innovations, such as ones with an extensive set of historical adoption market data throughout their lifecycles, the diffusion parameter differences between models tend to be good fits and yield similar results [65]. Thus, the Logistic model provides a firm foundation for evaluating technological innovation diffusion.
The mathematical formulation of the Logistic model, used for innovation and technology growth, is shown in Equation (1) [66].
where C (Carrying Capacity) is the limit to growth or the maximum diffusion ceiling, a (Initial Condition Constant) is a constant determined by an appropriate initial condition, r (Diffusion Rate Constant) is the growth rate constant, and t (Time variable) represents time.
3. Research Methodology
To address the research questions posed by this endeavor, a quantitative EDA approach was selected and executed in three steps to determine the boundaries and likelihoods of the diffusion rates of technological innovations via bulk trends and patterns. In the first step, market technological innovation diffusion data were collected, sorted, fit, and validated against the Logistic model. To bound this research scope, only U.S. market data from commercialized technological innovations over the last 100 years were examined. The defining bounds were additionally driven by the data available to the researchers; the approach could be expanded in the future to include other regions and time spans. Next, diffusion rate data were extracted from the collected dataset of technological innovations. The last step was to reduce the data and analyze them to determine the dataset’s statistical descriptions, trends over time, and best-fit probability density function for the range of technological innovation diffusion rates extracted.
3.1. Data Collection
As a whole, technological innovation market diffusion data are laborious to attain because they often reside within private organizations’ sales and marketing data, much of which is not published or is considered proprietary. Several researchers have, however, taken up the difficult task of collecting this type of data in an effort to study areas such as the innovation lifecycle, three of which are cited in Table 2. As with many research endeavors, the work reported here sought to leverage and extract new knowledge (macro patterns and trends) from previously gathered and validated datasets in the areas of technological innovation diffusion.

Table 2.
Principal dataset sources.
We applied the following criteria to data sources sought in order to center this research effort: (1) technological innovation data with annual frequency, as the focus of this endeavor was long-run (macro) diffusion rather than short-run fluctuations; (2) mature U.S. technological innovations; (3) validated and frequently cited sources, to ensure that the results gathered can be reproduced with confidence; (4) sources that focused on intensive measures of technological innovation diffusion, such as market sales data, rather than extensive measures that require identification of the potential adopters of a technological innovation via time-consuming and challenging-to-acquire micro-based data [67]; and (5) no restrictions on the type or category of the innovation, for the purpose of this effort is to generate, as a starting point for resource management practitioners, generalized macro patterns and trends on technological innovation diffusion rates. The three principal data sources identified based on these criteria are cited in Table 2. It must be acknowledged that, although three validated data sources were used for this endeavor, their data were collected from various published sources. These data sources are acknowledged and cited within each of the principal sources shown in the table. Collectively, these sources have been referenced over 650 times (according to Google Scholar, retrieved 18 August 2020).
3.2. Data Extraction
The data extracted from the sources referenced in Table 2 were reviewed for accuracy, completeness, and root sources verified. Redundancies (same technological innovation data from multiple sources) were eliminated, and inconsistencies (differing technological innovation data from multiple sources) were resolved. Incomplete and inconsistent data that were not resolvable were discarded from the analysis. In cases where a technological innovation’s diffusion data were available from multiple sources, and when the data were inconsistent between sources, the data were remediated by examining the root source. All told, market sales diffusion data of 42 U.S. consumer technological innovations were identified and collected. The data consisted of annual market diffusion percentages of each technological innovation over its recorded life cycle. The dataset spanned technological innovations released to the U.S. market from the early 1900s to the 2010s.
Raw datasets become, in practical terms, unmanageable and useless unless there are efficient, consistent, and reliable methods to reduce and extract meaningful data for practitioners and researchers. For this exploratory endeavor, we reduced and extracted data by fitting the Logistic model to the raw diffusion data of the technological innovations gathered. Using Microsoft Excel Solver, the Logistic model was fitted to the diffusion data of each technological innovation in the collected dataset.
The Logistic model carrying capacity parameters for each technological innovation were selected as the highest recorded diffusion percentages achieved, for carrying capacity values become dynamic and decrease upon the obsolescence of a technological innovation [72]. By choosing the highest recorded diffusion percentage to represent the carrying capacity parameter, it is assured that the maximum diffusion rate could be no lower than the rate extracted mathematically via the Logistic model. In addition, the model used a time variable interval of one year, as the diffusion data were collected yearly. The growth rate constant (noted as r) and initial condition constant (noted as a) were resolved by fitting each innovation’s diffusion data to the Logistic model. The fit was accomplished by using Microsoft Excel Solver’s Generalized Reduced Gradient (GRG) nonlinear solver algorithm by minimizing the root mean square error (RMSE) of the collected data to the Logistic model. The results of these fits are shown in Table 3.

Table 3.
Logistic model fit resultant parameters.
3.2.1. Logistic Model Fit Check
To determine whether the fitted Logistic models were representative of the technological innovation diffusion rate dataset collected, we applied RMSE analysis. RMSE is one of the most widely used criteria for model fit in data regression analysis [73,74]. It is the square root of the variance of the residuals and indicates the absolute fit of the model to the data. Although there is no absolute criterion for a good value of RMSE, in general, the lower the RMSE value, the better the model fits the dataset [75]. For this research, if the RMSE value was less than three (3) standard deviations (a common method for outlier identification [76]) from the mean value of the fitted data, we accepted the Logistic model fit and used the model data.
3.2.2. Extraction of Diffusion Rate and Trends
Using calculus principles, we extracted the Logistic model derivatives, as shown in Table 4. The first derivative of the base function gives us the diffusion rate (slope of resultant tangent line) at any instant in the Logistic curve. The second derivative provides us with the rate of change of the diffusion rate at any instant on the Logistic curve. The maximum diffusion rate was solved by determining the root of the models’ second derivative (representing when an innovation’s diffusion rate has peaked), as illustrated in Figure 1. It is interesting to note that the point of maximum diffusion rate is also an inflection point of the Logistic model. To examine bulk trends, a simple linear regression analysis using linear trend estimation was conducted on the dataset’s extracted diffusion rates. Linear trend estimation is a well-established statistical technique to aid in the interpretation and behavior identification (patterns and trends) of the observed data [77,78].

Table 4.
Logistic equation derivatives.
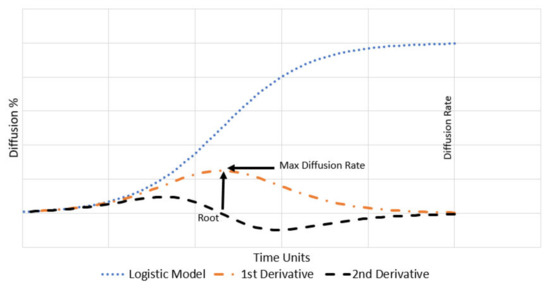
Figure 1.
Logistic model with derivatives.
3.2.3. Determination of Distribution Fit and Dataset Trends
To determine which probability density function best fits the resultant diffusion data (presented in Section 4.2), we performed a distribution fit analysis of the dataset. The diffusion rate data were used for the distribution fit analysis against 13 continuous distributions. The distributions selected were Exponential, Exponential—Two Parameter, Gamma, Gamma—Three Parameter, Largest Extreme Value, Logistic, LogLogistic, LogLogistic—Three Parameter, LogNormal, LogNormal—Three Parameter, Normal, Smallest Extreme Value, Weibull, and Weibull—Three Parameter. These distributions have been identified as some of the most widely used continuous distributions for data analysis [79]. Only continuous distributions were examined, since the outcome probability density function of a diffusion rate can assume an infinite number of different values.
We extracted the dataset’s descriptive statistics (including count, mean, and standard deviation) and evaluated which probability density function best fit the resultant diffusion data with Microsoft Excel with SPC™ (Statistical Analysis add-on). To make statistical inferences and to identify and extract appropriate statistical parameters of each distribution under examination, we employed the method of maximum likelihood estimation (MLE). We also used the MLE method to ascertain the most plausible probability distributions that would describe the collected set of observations. MLE is one of the most widely used methods employed to gain statistical inferences of data [80,81].
Using the MLE method, each distribution’s location, shape, scale, threshold, Log-Likelihood, Anderson–Darling, p-value, Likelihood Ratio Test (LRT), and Akaike Information Criterion (AIC) values were extracted, if applicable. The resultant MLE analysis helped us determine the rank order of the best-fit distribution model via goodness-of-fit examination, with the AIC estimator as the ranking factor. The AIC score rewards models that achieve a high goodness-of-fit score and penalizes them if they become overly complex. By itself, the AIC score is not much use unless it is compared with the AIC score of competing models, as was the case here.
To determine whether the general technological innovation population was likely to be skewed based on the sample set of this endeavor, a critical value statistical test adopted from Cramer [82], Equation (2), was applied. In general, the amount of sample skewness indicates how skewed a sample dataset is, whereas the skewness critical value statistical test ( shows whether the whole population is probably skewed, but not by how much (e.g., the higher the , the higher the probability of skewness) [82,83,84]. Population inferences for critical values adopted from Cramer [82] for a significance level of 0.05 are provided below and were used to make inferences about the general technological innovation population.
- If < −2, the population is very likely skewed negatively.
- If is between −2 and +2, no conclusion about the population skewness could be concluded.
- If > 2, the population is very likely skewed positively.where is the Sample Skewness and n is the sample size.
4. Results
4.1. Logistic Model Fit Results
To support the notion that the fitted Logistic models were representative of the innovation diffusion dataset, RMSE analysis was used to determine if the Logistic model was an acceptable fit. The resultant dataset RMSE descriptive statistics for the diffusion dataset under study are shown in Table 5. If the fitted technological innovation RMSE value was less than 1.22 (three standard deviations from the mean value), the Logistic model fit was accepted. As shown in Table 5, the maximum RSME value of the dataset was 1.086. Therefore, each Logistic Model fit was accepted, resulting in the utilization of 42 technological innovations for this research analysis.

Table 5.
Dataset RMSE values descriptive statistics.
4.2. Extraction of Diffusion Rate and Trend Results
The resultant maximum diffusion rate for each technological innovation was resolved by determining the model’s second derivatives root and then applying that point to the model’s first derivative. Table 6 lists the resultant maximum diffusion rates of each innovation under study. The outcome of the simple linear regression analysis conducted on the extracted maximum diffusion rate dataset (ordered in ascending year) resulted in a linear regressed slope of 0.09 with an intercept coefficient of −163.8 with a p-value of 0.005 and 0.003, respectively, Figure 2. The raw diffusion data, fitted Logistic model, and derivative curves from the datasets of three technological innovations, pulled from the 42 collected, are illustrated in Figure 3, Figure 4 and Figure 5 respectively, as a condensed reference of the entire dataset. To test the likelihood of skewness of the general technological innovation population set, a critical value statistical test was applied. The calculated for the dataset was resolved to be 5.45.

Table 6.
Resultant maximum diffusion rates of each technological innovation, ordered from slowest to fastest.
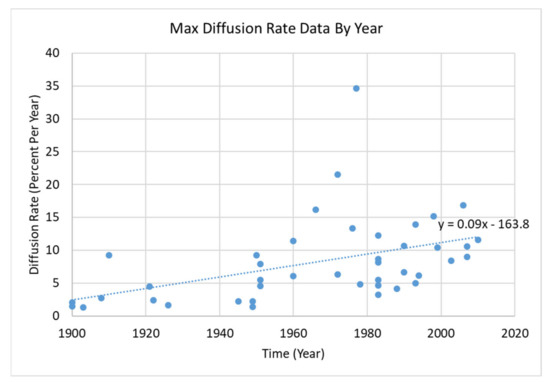
Figure 2.
Maximum diffusion rate by year.
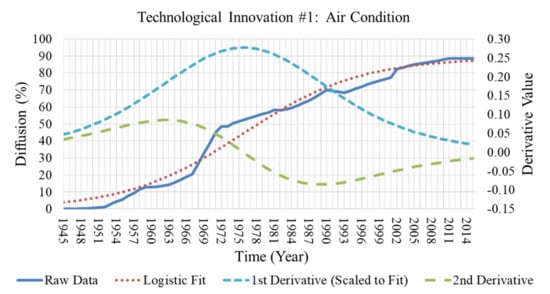
Figure 3.
Technological innovation sample 1.
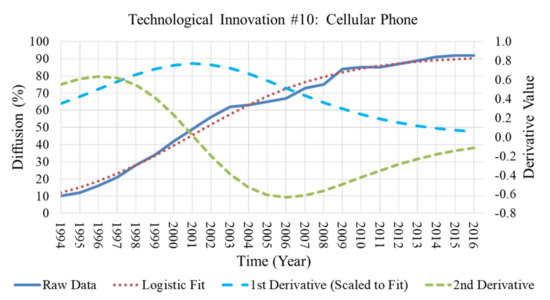
Figure 4.
Technological innovation sample 2.
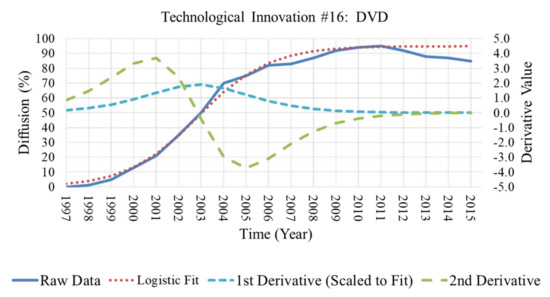
Figure 5.
Technological innovation sample 3.
4.3. Diffusion Rate Distribution Fit Results
The maximum diffusion rate dataset descriptive statistics (listed in Table 6) were determined in Microsoft Excel with SPC™ and are shown in Table 7. The resultant MLE analysis determined the rank order of the best-fit distribution model via goodness-of-fit examination using the AIC estimator as the primary ranking factor. The ranked results of the goodness-of-fit examination are shown in Table 8. Other descriptive (distribution density function and Q-Q plot) and ranking tool values (log-likelihood, Anderson–Darling, p-value) are provided as reference, in the spirit of this EDA approach, to aid the readers of this article in the identification of patterns and trends.

Table 7.
Maximum diffusion rate dataset descriptive statistics.

Table 8.
Maximum diffusion rate dataset MLE analysis results, ranked by ascending AIC.
5. Discussion
The principal objective of this research was to enrich the knowledge on the boundaries and likelihoods of the diffusion rates of technological innovations through an exploration of bulk trends and patterns. Building and developing macro-based forecasting knowledge will aid resource decision-makers as they consider proactive decisions on when to abandon a technological innovation. Through our research, we have taken the first steps at outlining a density function that models the probability distribution of achieving a given diffusion rate, accomplished by analyzing the diffusion characteristics of 42 U.S. technological innovations spanning 100+ years. Section 5.1, Section 5.2, Section 5.3 and Section 5.4 examine the results for trends and patterns and provide discussions of their implications framed against the driving questions of this effort.
5.1. Characteristics of Technological Innovation Diffusion Rates
Forty-two U.S. technological innovations, dating from the early 1900s to the 2010s, were identified and accepted, based on our acceptance criteria, into the dataset under study (see Table 3). The Logistic model was determined to be a good representation of each technological innovations’ diffusion. This warrants acknowledgment, for there is still much discourse on what model best represents the diffusion of technological innovation. To gauge the general shape of the maximum diffusion rate dataset distribution (Table 6), ordered from slowest to fastest diffusion rate, the dataset distribution’s descriptive statistics skewness value was examined. The resultant skewness value of 1.99 indicates that the distribution is highly skewed [85]. By definition, skewness is a measure of the asymmetry of a distribution; therefore, this result indicates that the distribution’s Mode < Median < Mean for unimodal densities [86,87,88]. This interpretation is only valid for the technological innovation dataset under study and cannot, with certainty, be applied to the whole population [82]. However, by testing the normality of the dataset using a critical value statistical test ( population skewness properties can be inferred and thus were examined next [82,89]. The resultant for the sample technological innovation maximum diffusion rate dataset distribution was determined to be 5.45. As a result, inferences can be made that there is a high likelihood that the general population of technological innovations is positively skewed from lowest to highest diffusion rate (population inferences critical values adopted from Cramer [82]).
The skewness value of the diffusion rate frequency occurrence for the dataset under study, ordered from past to present, is positive, indicating that the tail on the right side of the distribution is longer than on the left side and the bulk of the values lies to the left of the mean. The implication for resource management practitioners is that there is a high probability that the diffusion rate distribution of the general population of innovations is skewed positively and is not Normal. Thus, the distribution representing the maximum diffusion rates of technological innovation has a Mode < Median < Mean. If technological innovation diffusion rates can be probabilistically characterized, even to a reasonable level of confidence, macro-level likelihood knowledge on diffusion rates can be gained.
The simple linear regression analysis using linear trend estimation conducted on the extracted diffusion rate dataset determined that the linear regressed slope is a positive slope at 0.09 percent per year, indicating a trend that technological innovation diffusion rates are increasing. This was an unexpected result, not that the slope was positive, but that the magnitude was not higher, for it is commonly perceived that the rate of technological innovation diffusion rates is increasing rapidly. We speculate that this perception may be attributable to the fact that information regarding rapidly developing technological innovation tends to appear in the commercial tech news. As a check, to verify that older technological innovations were not overly biasing the results, we re-ran the regression analysis for this sample’s dataset, excluding any pre-1980s technological innovation data. This modified regression resulted in a slightly increased linear regressed slope of 0.21 percent per year. Although no definite conclusion can be made on how much technological innovation diffusion rates are increasing per year, inferences can be made. From a macro-based perspective, the data generally support the idea that technological innovation diffusion rates are increasing.
5.2. Diffusion Rate Distribution
As a means to reveal the boundaries and likelihoods of diffusion rates of technological innovations via exploration of bulk trends and patterns, we conducted a distribution fit analysis on the maximum diffusion rate dataset distribution (Table 6). The MLE was used to ascertain the most plausible probability density function that would describe the collected set of maximum diffusion rates [90,91]. MLE analysis results (Table 8), using goodness-of-fit examination, showed that the best-fit model of the population sample set was an Exponential—Two Parameter distribution, having the lowest AIC and largest p-value. The smaller the AIC and the larger the p-value, the stronger fit to the plausible distribution [92]. Conversely, the analysis can also determine if a distribution model is not a good fit, as a Normal distribution is for the population sample data set, ranked 12th out of the 13 distributions examined. In addition, the Normal distribution p-value was less than 0.05, indicating strong evidence that technological innovation diffusion rates, since the early 1900s to present, are not normally distributed.
It should be noted that an MLE analysis can determine that a distribution is a good fit, but not if it is the best model to represent reality. For example, as an innovation’s diffusion rate approaches zero, an Exponential—Two Parameter distribution would forecast a higher likelihood of occurrence, but this may not model reality. A distribution that may better model reality may be one in which the likelihood of occurrence peaks at a point between zero and the distribution Mean, such as a Gamma-, LogNormal-, or Weibull-based distribution. Thus, a study of the resultant top-ranked distributions warrants future examination to determine the impact variances of their selection.
5.3. Population Inferences, Assumptions, and Limitations
In terms of sample size and population inference, as previously mentioned, technological innovation diffusion data are difficult to gather; large sample size collection is problematic. A larger sample size would of course provide a more rigorous test of the validity and reliability of the herein-identified relationships between the boundaries and likelihoods of technological innovation diffusion rates. It is worth noting that much of the research examining technological innovation diffusion relies on sample sizes as small as 7 to as much as 37; this includes research by Mansfield [18], Fisher and Pry [27], Bass [93], Olshavsky [26], Qualls, Olshavsky, and Michaels [28], Clark, Freeman, and Hanssens [29], Takada and Jain [94], Rao and Yamada [95], Bayus [9], Kohli, Lehmann, and Pae [30], Agarwal and Bayus [96], Goldenberg et al. [97], Bass [98], Golder and Tellis [99], and [100]. The modest sample size of this endeavor (N = 42) can at a minimum provide macro-based associations on the likelihood trends and directional patterns of innovation diffusion rates. As more diffusion rate data are collected and added to this body of work, the confidence level and confidence interval of the model representing the population relationships will increase.
Given the macro nature of this endeavor, some assumptions and limitations must be acknowledged to provide context to the study boundaries. First, models (including diffusion models as used herein) are simplified representations of the real world. Care must always be taken when using any model, and sound judgment must be used in determining if results provided from a model are valid. Raw diffusion data rarely perfectly fit a diffusion model, for diffusion data are rarely homogenous and fully connected. The power of a diffusion model, assuming the raw data fit within defined limits, lies in its proven ability to aid and enable the quick and easy generation of representative information to allow decision-makers and researchers to easily interpret data and identify patterns [33,34,35,36,37,38,39]. Second, the data collected and studied for this effort are accurate and valid. Details of the sources used are provided in Table 2. for reference and to enable reproduction of this effort. Third, the technological innovation diffusion data used are U.S. market-derived; results may differ for other markets and regions. (It has been demonstrated that innovation diffusion can be affected by region [101]). Fourth, our results are macro-based and thus are not meant to be definitive, but rather associative and directional in nature.
5.4. Practitioner Implications and Significance
Knowledge that can change the way practitioners think, make decisions, or behave, as a consequence of insights gained, has managerial implications and significance [102]. As such, the insights and findings produced by this exploratory endeavor have significant and practical managerial implications in the area of technological innovation abandonment. Three potential areas are abandonment optimization of technological innovation, reducing the complexity of abandonment decisions, and providing a means for enabling proactive decisions through the use of the macro-based knowledge on diffusion rates gained herein.
5.4.1. Abandonment Optimization
A robust body of research exists on technological innovation and technology adoption in engineering management, but the areas of technological innovation and abandonment are significantly less well-developed and pose a common problem for practitioners [103,104]. As discussed previously, an observable skewness of the distribution model implies an increased likelihood in the direction of the skew. For this reason, knowledge of the skewness direction of the maximum diffusion rate distribution of technological innovations gives practitioners a greater understanding of a diffusion rate’s potential occurrence relative to the observable range and the derived historic-based Mean (see Table 7). Accordingly, knowledge of the skewness direction of the distribution of technological innovation diffusion rates is relevant to, but not limited to, resource management in terms of abandonment decisions and resource alignment.
Abandonment optimization of a technological innovation can be directly impacted by knowing the best-fit distribution of U.S. innovation diffusion rates, or at a minimum, knowing the skewness direction of the distribution. Leveraging this knowledge can help decision-makers make informed abandonment decisions, as explored in the following example. When should an incumbent technological innovation be abandoned and resources transferred toward reinvesting in a new candidate technological innovation to maximize gains and minimize losses? This challenge is difficult and resource-intensive when framed against micro-based factors, such as quantifying if an innovation’s potential adopters are not satisfied with their existing solution. However, information on making an informed decision can be obtained by leveraging the macro-based understanding of diffusion rate distributions developed herein.
For example, if a decision-maker knows that the incumbent technological innovation diffusion rate is 10%per year, meaningful information can be inferred without knowing anything about the potential candidate innovation. Information such as the chance that the candidate technological innovation will achieve a 10% per year diffusion rate is about 28%, as forecasted by the Exponential—Two Parameter distribution model identified in this research as the best-fit maximum diffusion rate distribution. Accordingly, if a decision-maker has insights into the boundaries and the likelihoods of innovation diffusion rates, a decision to delay or hasten abandonment may be made on the likelihood of diffusion rate attainment (or alternatively, risk tolerance). This includes assessing the impact of delaying or hastening abandonment, directly related to the speed at which abandonment decisions are made. Such information can be used to develop an abandonment optimization framework for decision-makers and will be examined in future research endeavors.
5.4.2. Complexity Reduction
Without a doubt, deciding when to abandon a technological innovation to maximize gains and minimize losses is a complex problem. An effective problem-solving tool for decision-makers in all disciplines is the simplification of complex problems to manageable forms. The complexity of forecasting a technological innovation’s diffusion rate is reduced by the macro-based perspective knowledge gained herein. By proxy, this knowledge also reduces the complexity of determining a technological innovation’s optimal point of abandonment; for which its diffusion rate is a factor. This reduction in complexity is accomplished by reducing the need for specific micro-based factors (often complex and challenging to acquire) to determine a technological innovation’s diffusion rate. To re-emphasize the analogy highlighted in the introduction, it is much easier to determine if a cup of coffee is hot (macro level) than it is to determine its exact temperature (micro level). Analysis via modeling and visualization of bulk trends and patterns of complex problems is a powerful tool for decision-makers [105]. The macro-based perspective knowledge of diffusion rates described herein lays a foundation for the development of general system-level rules for technological innovation abandonment.
Simplified abandonment information is also gained based on the skewness direction of the diffusion rate distribution, including the knowledge that diffusion rates are not normally distributed. Probabilistically, a technological innovation will have a high likelihood of achieving only a low rate of diffusion. Such knowledge can be used to curtail, or at a minimum simplify, heuristics and cognitive biases on technological innovation investments. If a practitioner has a macro understanding of the distribution model of technological innovation diffusion rates, a decision to delay or hasten abandonment may be made on the likelihood of diffusion rate attainment in order to maximize the potential for profit or minimize losses.
5.4.3. Proactive Abandonment Decisions
In a proactive environment, an organization strives to, and has a higher potential to, maximize gains and minimize losses, because proactive organizations have a higher potential to outpace those of reactive organizations [11,106,107,108]. The results of this research give practitioners impactful, proactive knowledge with which to make informed choices on how to best maximize their resources. Decision-makers may decide about their own technological innovation variant based on the general field of technological innovations: A fast diffusion rate in the general field of incumbent technological innovations may stimulate a decision-maker to adopt interventions and strategies that lengthen the life cycle for their technological innovation variant, while a slow diffusion rate may inspire the decision-maker to aim for another technological innovation or reconsider the marketing mix or the design of their own innovation variant. As noted, innovation and technology obsolescence is traditionally a reactive event, occurring when a new innovation or technology displaces an older one [109]. Conversely, optimization of innovation management (e.g., when a technological innovation is purposefully abandoned (phased-out) to shift resources to new investment areas) is a proactive occurrence, enabled through an understanding of diffusion rate characteristics.
The inference that U.S. technological innovation diffusion rates have increased over time suggests a contraction of the technological innovation life cycle. Consequently, this denotes the potential shortening of the time an organization has to make decisions concerning technological innovation investments. This alone is relevant to resource management and abandonment optimization. As an example, if innovation diffusion rates are increasing, an organization would be at a disadvantage if its decision speeds do not change [4]. Practitioners must strive to increase decision speeds or be at an increased disadvantage. Proactive organizations have an advantage over reactive organizations because they are positioned to make informed decisions quicker [106,107,110]. In addition, the advancement of this directional inference could challenge, or at the very least, adjust the understanding of innovation adoption models. If technological innovation diffusion rates are increasing, the notion of traditional consumer adoption decision processes (innovator, early adopter, early majority, late majority, and laggards, Rogers [15]) may warrant reexamination [26].
6. Conclusions
In an effort to aid decision-makers in making informed and proactive decisions on when to abandon a technological innovation, this research endeavors to add macro-based insights to the limited knowledge area of modeling the speeds at which technological innovation diffuses. Forecasting does not imply certainty but implies understanding and reducing uncertainties [111]. Accordingly, if uncertainties are reduced by understanding the boundaries and the likelihood of achieving a range of technological innovation diffusion rates, value has been created for practitioners and decision-makers. For this study, diffusion rate data from 42 U.S. technological innovations spanning over 100 years were used to determine directional and associative insights into diffusion rate likelihoods for the technological innovation population as a whole. At present, no such macro-based distribution characterization insights exist in the management or diffusion research literature. As the dataset expands, the model can be refined and improved. This research offers several important contributions to understanding the boundaries and likelihood of achieving a range of innovation diffusion rates: the determination that diffusion rates are positively skewed when ordered from slowest to fastest, the identification and ranking of probability density functions that best represent the rates of diffusion, and the conclusion that they have statistically increased over time. These contributions have prospective practical managerial implications for practitioners for simplifying, optimizing, and enabling the proactive assessment of abandonment decisions. As with all science-based disciplines, a foundational problem-solving tool for practitioners is the simplification of complex and involved problems, such as the problem of diffusion rate assessment, into manageable forms. The macro-level knowledge gain in this endeavor on diffusion rates provides a means of reducing the complexity of forecasting a technological innovation’s diffusion rate for proactive abandonment optimization, as outlined in Section 5.4.
One of the primary outcomes of an EDA is the development and forwarding of new exploratory hypothesis in a research area through the examination of patterns and trends. As such, this endeavor forwards three exploratory hypotheses to be considered in the future for this research area. First, the data analysis supported inferences that, as technological innovation diffusion rates increase, their likelihood of occurrence is positively skewed, forwarding the hypothesis (H1) that the frequency occurrence of U.S. technological innovation diffusion rates over the past 100+ years is positively skewed when ordered from slowest to fastest. Next, the data collected and analysis conducted in this EDA effort advances hypothesis (H2), that U.S. technological innovation diffusion rates, since the early 1900s to present, have statistically increased over time. Lastly, based on the results of the distribution fit analysis of this effort, a third new exploratory hypothesis was developed, (H3), that U.S. technological innovation diffusion rates, since the early 1900s to present, have followed a right-skewed single modal distribution.
Although this exploratory analysis study makes significant contributions to forwarding the knowledge of this topic area, one direction for future research is to extend this work to expand the dataset with additional technological innovations to further refine and strengthen inferences to the general population. This goes hand in hand with testing the exploratory hypotheses put forth in this effort. In addition, the expansion of the data beyond the United States warrants examination, to investigate whether these results are universal to other regions. Another future direction for research is the investigation of the impact of delaying or hastening abandonment, given that technological innovation diffusion rates can be grouped probabilistically (e.g., slow versus fast diffusion rates). Investigations into such areas would further provide knowledge to aid practitioners as to where to assign or remove resources in order to create value for an organization. A categorization of technological innovations was out of the scope of this exploratory analysis on the macro-perspective study of technological innovation diffusion rates, but it warrants future examination since it appears that technological innovation categories are potentially linked to different patterns of development [112,113]. Another future exploration area is the identification and examination of factors that affect diffusion rate patterns at the macro level. For example, how do major global events affect diffusion rate patterns, and are they lasting or temporary? In closing, the macro-based study of diffusion rates has prospective implications for building and developing forecasting knowledge to aid resource decision-makers in making informed and proactive decisions on when to abandon a technological innovation.
Author Contributions
Conceptualization, A.J.P.J. and M.G.B.; methodology, A.J.P.J. and M.G.B.; software, A.J.P.J.; validation, A.J.P.J. and M.G.B.; formal analysis, A.J.P.J.; investigation, A.J.P.J.; resources, A.J.P.J. and M.G.B.; data curation, A.J.P.J.; writing—original draft preparation, A.J.P.J.; writing—review and editing, A.J.P.J. and M.G.B.; visualization, A.J.P.J.; supervision, M.G.B.; project administration, A.J.P.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in FigShare at https://figshare.com/s/552c03578ea2622b8f62 (accessed on 18 February 2021).
Acknowledgments
In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sharlin, H.I.; Kelly, P.; Kranzberg, M. Technological Innovation: A Critical Review of Current Knowledge. Technol. Cult. 1981, 22, 349. [Google Scholar] [CrossRef][Green Version]
- Diaconu, M. Technological Innovation: Concept, Process, Typology and Implications in the Economy. Theor. Appl. Econ. 2011, 18, 10. [Google Scholar]
- OECD. The Measurement of Scientific and Technological Activities Oslo Manual Guidelines for Collecting and Interpreting Innovation Data, 3rd ed.; OECD Publishing: Paris, France, 2005. [Google Scholar]
- Parvin, A.J., Jr.; Beruvides, M.G. Technology abandonment and the time value of diffusion. In Proceedings of the 2019 IISE Annual Conference, Orlando, FL, USA, 18–21 May 2021; p. 10. [Google Scholar]
- Kahneman, D. Thinking, Fast and Slow; Farrar, Straus and Giroux: New York, NY, USA, 2011. [Google Scholar]
- Onken, J.; Hastie, R.; Revelle, W. Individual Differences in the Use of Simplification Strategies in a Complex Deci-sion-Making Task. J. Exp. Psychol. Hum. Percept. Perform. 1985, 11, 14. [Google Scholar] [CrossRef]
- Choffray, J.M.; Lilien, G.L. A decision-support system for evaluating sales prospects and launch strategies for new products. Ind. Mark. Manag. 1986, 15, 75–85. [Google Scholar] [CrossRef]
- Stalk, G., Jr.; Hout, T.M. Competing Against Time. Res. Technol. Manag. 1990, 33, 19–24. [Google Scholar] [CrossRef]
- Bayus, B.L. Have diffusion rates been accelerating over time? Mark. Lett. 1992, 3, 215–226. [Google Scholar] [CrossRef]
- Parvin, A.J., Jr.; Beruvides, M.G. Product and technology (innovation) diffusion economics’ time relation to abandon-ment. In Proceedings of the International Annual Conference of the American Society for Engineering Management, Philadelphia, PA, USA, 23–26 October 2019; p. 10. [Google Scholar]
- Parvin, A.J., Jr.; Beruvides, M.G. The relationship between a technology’s diffusion rate (time) and its economical impact (money). In Proceedings of the International Annual Conference of the American Society for Engineering Management, Coeur d’Alene, ID, USA, 17–20 October 2018; p. 8. [Google Scholar]
- Martino, J.P. Technological Forecasting for Decision Making, 2nd ed.; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Morlidge, S. Future Ready: How to Master Business Forecasting; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bulte, C.V.D. New Product Diffusion Acceleration: Measurement and Analysis. Mark. Sci. 2000, 19, 366–380. [Google Scholar] [CrossRef]
- Rogers, E.M. Diffusion of Innovations, 4th ed.; The Free Press: New York, NY, USA, 2010. [Google Scholar]
- Tyagi, C.; Kumar, A. Consumer Behaviour; Atlantic Publishers & Distributors: New Delhi, NY, USA, 2004. [Google Scholar]
- Huebner, J. A possible declining trend for worldwide innovation. Technol. Forecast. Soc. Chang. 2005, 72, 980–986. [Google Scholar] [CrossRef]
- Mansfield, E. Technical Change and the Rate of Imitation. Econometrica 1961, 29, 741. [Google Scholar] [CrossRef]
- Silverberg, G.; Dosi, G.; Orsenigo, L. Innovation, Diversity and Diffusion: A Self-Organisation Model. Econ. J. 1988, 98, 1032. [Google Scholar] [CrossRef]
- Grübler, A. Time for a Change: On the Patterns of Diffusion of Innovation. Daedalus 1996, 125, 19–42. [Google Scholar]
- Jovanovic, B.; Lach, S. Product Innovation and the Business Cycle. Int. Econ. Rev. 1997, 38, 3–22. [Google Scholar] [CrossRef]
- Caselli, F.; Coleman, W.J. Cross-Country Technology Diffusion: The Case of Computers. Am. Econ. Rev. 2001, 91, 328–335. [Google Scholar] [CrossRef]
- Manuelli, R.; Seshadri, A. Frictionless Technology Diffusion: The Case of Tractors. Am. Econ. Rev. 2014, 104, 1368–1391. [Google Scholar] [CrossRef]
- Comin, D.; Hobijn, B. An Exploration of Technology Diffusion. Am. Econ. Rev. 2010, 100, 2031–2059. [Google Scholar] [CrossRef]
- Comin, D.; Mestieri, M. Technology diffusion: Measurement, causes, and consequences. In Handbook of Economic Growth; Elsevier: Amsterdam, The Netherlands, 2014; Volume 2, pp. 565–622. [Google Scholar]
- Olshavsky, R.W. Time and the Rate of Adoption of Innovations. J. Consum. Res. 1980, 6, 425–428. [Google Scholar] [CrossRef]
- Fisher, J.; Pry, R. A simple substitution model of technological change. Technol. Forecast. Soc. Chang. 1971, 3, 75–88. [Google Scholar] [CrossRef]
- Qualls, W.; Olshavsky, R.W.; Michaels, R.E. Shortening of the PLC: An Empirical Test. J. Mark. 1981, 45, 76. [Google Scholar] [CrossRef]
- Clark, W.A.; Freeman, H.E.; Hanssens, D.M. Opportunities for revitalizing stagnant markets: An analysis of household appliances. J. Prod. Innov. Manag. 1984, 1, 242–254. [Google Scholar] [CrossRef]
- Kohli, R.; Lehmann, D.R.; Pae, J. Extent and Impact of Incubation Time in New Product Diffusion. J. Prod. Innov. Manag. 1999, 16, 134–144. [Google Scholar] [CrossRef]
- Kucharavy, D.; De Guio, R. Application of S-shaped curves. Procedia Eng. 2011, 9, 559–572. [Google Scholar] [CrossRef]
- Intepe, G.; Koc, T. The Use of S Curves in Technology Forecasting and its Application On 3D TV Technology. Int. J. Ind. Manuf. Eng. 2012, 6, 2491–2495. [Google Scholar] [CrossRef]
- Geroski, A.P. Models of technology diffusion. Res. Policy 2000, 29, 603–625. [Google Scholar] [CrossRef]
- Griliches, Z. Hybrid Corn: An Exploration in the Economics of Technological Change. Econometrica 1957, 25, 501. [Google Scholar] [CrossRef]
- Kemp, R.; Volpi, M. The diffusion of clean technologies: A review with suggestions for future diffusion analysis. J. Clean. Prod. 2008, 16, S14–S21. [Google Scholar] [CrossRef]
- Gort, M.; Klepper, S. Time Paths in the Diffusion of Product Innovations. Econ. J. 1982, 92, 630. [Google Scholar] [CrossRef]
- Grubler, A.; Nakićenović, N. Growth to Limits: Long Waves and the Dynamics of Technology; Review (Fernand Braudel Center); Research Foundation of State University of New York: New York, NY, USA, 1991; Volume 14, pp. 313–343. [Google Scholar]
- Bengisu, M.; Nekhili, R. Forecasting emerging technologies with the aid of science and technology databases. Technol. Forecast. Soc. Chang. 2006, 73, 835–844. [Google Scholar] [CrossRef]
- Adamuthe, A.C.; Thampi, G.T. Technology forecasting: A case study of computational technologies. Technol. Forecast. Soc. Chang. 2019, 143, 181–189. [Google Scholar] [CrossRef]
- Meade, N.; Islam, T. Technological Forecasting—Model Selection, Model Stability, and Combining Models. Manag. Sci. 1998, 44, 1115–1130. [Google Scholar] [CrossRef]
- Teng, J.; Grover, V.; Guttler, W. Information technology innovations: General diffusion patterns and its relationships to innovation characteristics. IEEE Trans. Eng. Manag. 2002, 49, 13–27. [Google Scholar] [CrossRef][Green Version]
- Michalakelis, C.; DeDe, G.; Varoutas, D.; Sphicopoulos, T. Impact of cross-national diffusion process in telecommunications demand forecasting. Telecommun. Syst. 2008, 39, 51–60. [Google Scholar] [CrossRef]
- Yu, J.R.; Dong, Y.W.; Chang, Y.H.; Tseng, F.-M. Comparison of innovation diffusion models: A case study on the DRAM industry. In Proceedings of the 2012 IEEE International Conference on Fuzzy Systems, Brisbane, Australia, 10–15 June 2012; pp. 1–7. [Google Scholar]
- Naseri, M.B.; Elliott, G. The diffusion of online shopping in Australia: Comparing the Bass, Logistic and Gompertz growth models. J. Mark. Anal. 2013, 1, 49–60. [Google Scholar] [CrossRef]
- Jha, A.; Saha, D. Forecasting and analysing the characteristics of 3G and 4G mobile broadband diffusion in India: A comparative evaluation of Bass, Norton-Bass, Gompertz, and logistic growth models. Technol. Forecast. Soc. Chang. 2020, 152, 119885. [Google Scholar] [CrossRef]
- Wu, F.-S.; Chu, W.-L. Diffusion models of mobile telephony. J. Bus. Res. 2010, 63, 497–501. [Google Scholar] [CrossRef]
- Meade, N.; Islam, T. Modelling and forecasting the diffusion of innovation—A 25-year review. Int. J. Forecast. 2006, 22, 519–545. [Google Scholar] [CrossRef]
- Ostojic, I. Bass Innovation Diffusion Model and Its Application in Policy Analysis for Adoption of Renewable Energy Technologies; Swiss Federal Institute of Technology: Zürich, Switzerland, 2010. [Google Scholar]
- Grubler, A. The Rise and Fall of Infrastructures: Dynamics of Evolution and Technological Change in Transport; Physica-Verlag: Heidelberg, Germany, 1990. [Google Scholar]
- Meade, N.; Islam, T. Forecasting with growth curves: An empirical comparison. Int. J. Forecast. 1995, 11, 199–215. [Google Scholar] [CrossRef]
- Kim, N.; Chang, D.R.; Shocker, A.D. Modeling Intercategory and Generational Dynamics for A Growing Information Technology Industry. Manag. Sci. 2000, 46, 496–512. [Google Scholar] [CrossRef]
- Kim, M.-S.; Kim, H. Innovation diffusion of telecommunications: General patterns, diffusion clusters and differences by technological attribute. Int. J. Innov. Manag. 2004, 8, 223–241. [Google Scholar] [CrossRef]
- Botelho, A.; Pinto, L.g.C. The Diffusion of Cellular Phones in Portugal. Telecommun. Policy 2004, 28, 427–437. [Google Scholar] [CrossRef]
- Suriñac, J.; Autant-Bernard, C.; Manca, F.; Massard, N.; Moreno, R. The Diffusion/Adoption of Innovation in the Internal Market; European Commission: Directorate General Economic and Financial Affairs (DG ECFIN), European Commission: Brussels, Belgium, 2009. [Google Scholar]
- Kijek, A.; Kijek, T. Modelling of Innovation Diffusion. Oper. Res. Decis. 2010, 20, 53–68. [Google Scholar]
- Devore, J.L.; Berk, K.N. Modern Mathematical Statistics with Applications; Brooks/Cole: Belmont, CA, USA, 2007. [Google Scholar]
- Kenneth, D.; Ronald, K. Advances in Business and Management Forecasting; Emerald Books: Bingley, UK, 1982. [Google Scholar]
- Kros, J.F. Forecasting New Products with a Non-Cumulative Logistic Growth Model: A Case Study of Modem Technology. J. Bus. Forecast. 2005, 1, 23–32. [Google Scholar]
- Chandrasekaran, D.; Tellis, G.J. A Critical Review of Marketing Research on Diffusion of New Products. Rev. Mark. Res. 2007, 3, 39–80. [Google Scholar] [CrossRef]
- Bass, F.M. A New Product Growth for Model Consumer Durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Norton, J.A.; Bass, F.M. A Diffusion Theory Model of Adoption and Substitution for Successive Generations of High-Technology Products. Manag. Sci. 1987, 33, 1069–1086. [Google Scholar] [CrossRef]
- Tsoularis, A.; Wallace, J. Analysis of logistic growth models. Math. Biosci. 2002, 179, 21–55. [Google Scholar] [CrossRef]
- Islam, R. Transfer, Adoption and Diffusion of Technology for Small and Cottage Industries; International Labour Organization: Geneva, Switzerland, 1992. [Google Scholar]
- Kucharavy, D.; De Guio, R. Logistic substitution model and technological forecasting. Procedia Eng. 2011, 9, 402–416. [Google Scholar] [CrossRef]
- Sokele, M. Growth Models for the Forecasting of New Product Market Adoption. Telektronikk 2008, 104, 144–154. [Google Scholar]
- Meyer, P.S.; Yung, J.W.; Ausubel, J.H. A Primer on Logistic Growth And Substitution: The Mathematics of the Loglet Lab Software. Technol. Forecast. Soc. Chang. 1999, 61, 247–271. [Google Scholar] [CrossRef]
- Comin, D.A.; Hobijn, B. The CHAT Dataset. SSRN Electron. J. 2009. [Google Scholar] [CrossRef]
- Dediu, H. Diffusion Data; Clayton Christensen Institute: Lexington, MA, USA, 2017; Available online: Horace.dediu@asymco.com (accessed on 15 January 2018).
- Comin, D.; Hobijn, B. Cross-Country Technology Adoption: Making the Theories Face the Facts. J. Monet. Econ. 2004, 51, 39–83. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M. Technology Diffusion & Adoption; Our World in Data (OurWorldInData.org): Oxford, UK, 2017. [Google Scholar]
- Cox, W.M.; Alm, R. Time Well Spent: The Declining Real Cost of Living in America. Annu. Rep. Fed. Reserve Bank Dallas 1997, 1, 2–24. [Google Scholar]
- Watanabe, C. Managing Innovation in Japan: The Role Institutions Play in Helping or Hindering How Companies Develop Technology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Salkind, N.J. Encyclopedia of Research Design; SAGE Publication Inc.: London, UK, 2010. [Google Scholar] [CrossRef]
- Kelley, K.; Lai, K. Accuracy in Parameter Estimation for the Root Mean Square Error of Approximation: Sample Size Planning for Narrow Confidence Intervals. Multivar. Behav. Res. 2011, 46, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Khemlani, S.; Trafton, G. Percentile Analysis for Goodness-Of-Fit Comparisons of Models to Data. In Proceedings of the Annual Meeting of the Cognitive Science Society, Quebec, QC, Canada, 23–26 July 2014. [Google Scholar]
- Bain, L.J.; Engelhardt, M. Introduction to Probability and Mathematical Statistics; Brooks/Cole: Belmont, CA, USA, 1987. [Google Scholar]
- Seltman, H.J. Experimental Design and Analysis; Carnegie Mellon University: Pittsburgh, PA, USA, 2012. [Google Scholar]
- Lane, D.M.; Scott, D.; Hebl, M.; Guerra, R.; Osherson, D.; Zimmer, H. An Introduction to Statistics; Rice University: Houston, TX, USA, 2017. [Google Scholar]
- Meeker, W.Q.; Escobar, L.A. Stastical Methods for Reliability Data; John Wiley & Sons Inc.: Hoboken NJ, USA, 1998. [Google Scholar]
- Hendry, D.F.; Nielsen, B. Econometric Modeling: A Likelihood Approach; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Chambers, R.L.; Steel, D.G.; Wang, S.; Welsh, A. Maximum Likelihood Estimation for Sample Surveys; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Cramer, D. Basic Statistics for Social Research: Step-by-Step Calculations & Computer Techniques Using Minitab; Routledge: Boca Raton, FL, USA, 2002. [Google Scholar]
- Oliveira, A.; Oliveira, T.A.; Seijas-Macias, A. The influence of ratios and combined ratios on the distribution of the product of two independent gaussian random variables. In Proceedings of the 59th World Statistics Congress of the International Statistical Institute, Hong Kong, China, 25–30 August 2013. [Google Scholar]
- Brown, S. Measures of Shape: Skewness and Kurtosis. Available online: https://brownmath.com/stat/shape.htm#Skew_Infer (accessed on 6 November 2018).
- Wegner, T. Applied Business Statistics: Methods and Excel-Based Applications; Juta and Company Ltd.: Johannesburg, South Africa, 2010. [Google Scholar]
- Von Hippel, P.T. Mean, Median, and Skew: Correcting a Textbook Rule. J. Stat. Educ. 2005, 13. [Google Scholar] [CrossRef]
- Kim, H.-Y. Statistical notes for clinical researchers: Assessing normal distribution (2) using skewness and kurtosis. Restor. Dent. Endod. 2013, 38, 52–54. [Google Scholar] [CrossRef] [PubMed]
- Doane, D.P.; Seward, L.E. Measuring Skewness: A Forgotten Statistic? J. Stat. Educ. 2011, 19, 1–18. [Google Scholar] [CrossRef]
- Joanes, D.N.; Gill, C.A. Comparing measures of sample skewness and kurtosis. J. R. Stat. Soc. Ser. D 1998, 47, 183–189. [Google Scholar] [CrossRef]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. Lond. Ser. A 1922, 222, 309–368. [Google Scholar] [CrossRef]
- White, H. Maximum Likelihood Estimation of Misspecified Models. Econometrica 1982, 50, 1–25. [Google Scholar] [CrossRef]
- Shanmugam, B.; Nielson, B.G.; Prevatt, D.O. Statistical and analytical models for roof components in existing light-framed wood structures. Eng. Struct. 2009, 31, 2607–2616. [Google Scholar] [CrossRef]
- Bass, F.M. The Relationship between Diffusion Rates, Experience Curves, and Demand Elasticities for Consumer Durable Technological Innovations. J. Bus. 1980, 53, S51–S67. [Google Scholar] [CrossRef]
- Takada, H.; Jain, D. Cross-National Analysis of Diffusion of Consumer Durables. J. Mark. 1991, 55. [Google Scholar] [CrossRef]
- Rao, A.G.; Yamada, M. Forecasting with a Repeat Purchase Diffusion Model. Manag. Sci. 1988, 34, 734–752. [Google Scholar] [CrossRef]
- Agarwal, R.; Bayus, B.L. The Market Evolution and Sales Takeoff of Product Innovations. Manag. Sci. 2002, 48, 1024–1041. [Google Scholar] [CrossRef]
- Goldenberg, J.; Libai, B.; Muller, E. Riding the Saddle: How Cross-Market Communications Can Create a Major Slump in Sales. J. Mark. 2002, 66, 1–16. [Google Scholar] [CrossRef]
- Bass, F.M. Comments on a New Product Growth for Model Consumer Durables. Manag. Sci. 2004, 50, 1833–1840. [Google Scholar] [CrossRef]
- Golder, P.N.; Tellis, G.J. Growing, Growing, Gone: Cascades, Diffusion, and Turning Points in the Product Life Cycle. Mark. Sci. 2004, 23, 207–218. [Google Scholar] [CrossRef]
- McDade, S.; Oliva, T.A.; Thomas, E. Forecasting Organizational Adoption of High-Technology Product Innovations Sep-arated by Impact: Are Traditional Macro-Level Diffusion Models Appropriate? Ind. Mark. Manag. 2010, 39, 298–307. [Google Scholar] [CrossRef]
- Sundqvist, S.; Frank, L.; Puumalainen, K. The effects of country characteristics, cultural similarity and adoption timing on the diffusion of wireless communications. J. Bus. Res. 2005, 58, 107–110. [Google Scholar] [CrossRef]
- Kohli, A.K. From the Editor: Reflections on the Review Process. J. Market. 2011, 75, 1–4. [Google Scholar] [CrossRef]
- Greenwood, B.N.; Agarwal, R.; Agarwal, R.; Gopal, A. The When and Why of Abandonment: The Role of Organizational Differences in medical technology life cycles. Manag. Sci. 2016, 63, 2948–2966. [Google Scholar] [CrossRef][Green Version]
- Parvin, A.J., Jr.; Beruvides, M.G. Forecasting technology obsolescence: Assessing the existing literature, a systematic review. In Proceedings of the International Annual Conference of the American Society for Engineering Management, Huntsville, AL, USA, 18–21 October 2017; pp. 1–13. [Google Scholar]
- Snyder, S. The Simple, the Complicated, and the Complex: Educational Reform through the Lens of Complexity Theory; OECD Education Working Paper; OCED: Paris, France, 2013. [Google Scholar] [CrossRef]
- LaPorte, T.R.; Consolini, P.M. Working in Practice but Not in Theory: Theoretical Challenges of “High-Reliability Organizations”. Crisis Manag. 1991, 1, 57. [Google Scholar]
- Pauchant, T.C.; Mitroff, I.I.; Weldon, D.N.; Ventolo, G.F. The ever-expanding scope of industrial crises: A systemic study of the Hinsdale telecommunications outage. Ind. Crisis Q. 1990, 4, 243–261. [Google Scholar] [CrossRef]
- Lin, Z.; Carley, K.M. Proactive or Reactive: An Analysis of the Effect of Agent Style on Organizational Decision-making Performance. Intell. Syst. Account. Financ. Manag. 1993, 2, 271–287. [Google Scholar] [CrossRef]
- Barreca, S.L. Technology Life-Cycles and Technological Obsolescence; BCRI Inc.: Birmingham, UK, 2000. [Google Scholar]
- Ulusoy, G.; Özgür, A.; Bilgiç, T.; Kaylan, A.R.; Payzın, E. A Study on Technology Management Process: The Parts and Components Suppliers in the Turkish Automotive Industry. Technol. Manag. 2001, 5, 245–260. [Google Scholar]
- Deming, W.E. The New Economics for Industry, Government, Education; The MIT Press: Cabridge, MA, USA, 2018. [Google Scholar]
- Abernathy, W.J.; Clark, K.B. Innovation: Mapping the winds of creative destruction. Res. Policy 1985, 14, 3–22. [Google Scholar] [CrossRef]
- Ortt, J.R.; Egyedi, T.M. The Effect of Pre-Existing Standards and Regulations on the Development and Diffusion of Radically New Innovations. Int. J. IT Stand. Stand. Res. 2014, 12, 17–37. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).