Abstract
Geometric-Zeno behaviour is a highly challenging problem in the analysis (including simulation) of hybrid systems. Geometric-Zeno can be defined as an infinite number of discrete mode switches in a finite time interval. Typically, for hybrid models exhibiting geometric-Zeno, the numerical simulation either halts or produces false results, because an infinite number of discrete events occur in a given simulation time-step. In this paper, we provide formal methods for regularization of geometric-Zeno behaviour by using a non-standard analysis. In particular, we provide formal conditions for the existence of geometric-Zeno in hybrid systems, and we propose methods to allow geometric-Zeno executions to be continued beyond geometric-Zeno limit points. The concepts are illustrated with a case study throughout the paper.
1. Introduction
Hybrid Systems are complex dynamical systems that combine both physical (plant, process, network) and control (decision making algorithm, computation) components. Hybrid systems exist in a wide variety of technological applications in which continuous physical behaviour is combined with discrete control actions [1,2,3,4,5,6]. The correct functioning of such systems is often safety-critical, thus their formal modelling and analysis is of utmost importance. Formally, hybrid automata modelling framework, with mixed discrete-continuous behaviour can be used to model the interactions between the logic decision making actions (i.e., discrete dynamics) and the continuous physical processes (i.e., continuous dynamics) of hybrid systems [2,4,7]. The behaviour of hybrid automata is characterized by a finite set of discrete states (or locations). In each discrete state, the evolution of the system’s continuous state over time is specified by differential equations (or inclusions), and the discrete state changes are modelled by instantaneous discrete transitions [2,8,9,10,11]. The reachability problem poses the question, whether a state from a given unsafe set is reachable from a given set of initial states. Since the reachability problem for hybrid systems is undecidable [10,12,13], different techniques were proposed to observe and analyse the behaviour of hybrid systems approximatively. One of these techniques, which is frequently used both in academia and industry, is simulation. Usually, simulation techniques for hybrid systems use some numerical methods to compute the dynamical evolution of the systems from a given initial state over time. Additionally, the discrete switches between the different control modes need to be detected and simulated [2,3,14]. However, geometric-Zeno behaviour is a highly challenging problem in the analysis (including simulation) of hybrid systems. Geometric-Zeno behaviour can be defined as an infinite number of discrete mode switches in a finite time interval [2,15,16]. Geometric-Zeno results from modelling abstraction (or over-approximation). The presence of geometric-Zeno behaviour indicates that the abstraction mechanism imperfectly describes the complex interaction between the continuous and discrete dynamics of the modelled hybrid system [2]. All kinds of iterative forward techniques for reachability computation used in almost all existing hybrid modelling and simulation tools have troubles to deal with geometric-Zeno behaviour, because the computations at the time instant of geometric-Zeno limit point either halt or produce faulty results.
Geometric-Zeno behaviour has been investigated in different ways. In [17,18,19], authors proposed methods to obtain non-Zeno solutions by perturbing geometric-Zeno hybrid models. However, their method results in stiff models for which the simulation performance might collapse. Other authors proposed sufficient conditions for the existence geometric-Zeno in particular classes of hybrid systems, such as linear complementarity systems [20,21,22], Lagrangian hybrid systems [15,16,23,24], quadrant hybrid systems [25,26]. However, the majority of the proposed methods are conservative and apply to particular classes of hybrid systems. Thus, there is a need to provide a computational framework that can be used as a general framework for regularization of geometric-Zeno behaviour in all classes of hybrid systems.
In this paper, we provide formal methods for regularization of geometric-Zeno behaviour by using a non-standard analysis of hybrid automaton execution. Non-standard analysis allows the continuous dynamics—represented by differential equations—to be modelled by recurrence equations, where the system’s continuous state changes within infinitesimal time steps, and therefore, the evolution of hybrid systems can be described only on discrete fashion, while at the same time the completeness in the state space is guaranteed. Through the non-standard analysis, we provide formal conditions for detecting geometric-Zeno, and we propose methods to allow geometric-Zeno execution to be continued beyond the geometric-Zeno limit point. This paper extends several results presented in [27]. The first version investigated sufficient conditions for geometric-Zeno based on the convergence of hybrid solution trajectory to a geometric-Zeno limit point as a non-standard Cauchy sequence. This paper investigates sufficient conditions for geometric-Zeno behaviour based on the convergence of hybrid automaton execution to a geometric-Zeno limit point through a contractive geometric simulation relation between hybrid states.
The paper is organized as follows: Section 2 introduces hybrid automata as modelling formalism for hybrid systems, and then provides the non-standard execution semantics for hybrid automata. Section 3 presents a realistic example of a hybrid model exhibiting geometric-Zeno behaviour and discusses the simulation of geometric-Zeno behaviour. Section 4 provides a non-standard analysis of geometric-Zeno, as well as non-standard formal conditions for the existence of geometric-Zeno and methods for geometric-Zeno elimination. Finally, Section 5 and Section 6 present simulation results and conclusions, respectively.
2. Non-Standard Hybrid Automata
Hybrid automata is a widely used modelling formalism for hybrid systems. A hybrid automaton is an extension of finite automaton, and consists of discrete states, discrete transitions, continuous invariants, guard conditions, reset maps, and -dimensional continuous functions [28]. A non-standard hybrid automaton is a hybrid automaton whose execution is defined using the theory of non-standard real numbers . That is, the non-standard execution of hybrid automata is based on using the non-standard time domain (a subset of ) as an execution time domain.
The field of non-standard real numbers has been used by several authors to define operational semantics of continuous and hybrid systems [28,29].
Definition 1.
(Infinitesimal and Closeness) An infinitesimal is a non-zero number whose absolute value is smaller than any positive real number [27,28,30]. That is, for all there exists an infinitesimal number such that . A Closeness ≈ is a binary relation which implies that if and only if is infinitesimal, where are both non-standard numbers.
Definition 2.
(Non-Standard Time Domain) A non-standard time domain is a time set with infinitesimal time steps [27,28].
Definition 3.
(Non-Standard Hybrid Automata) A non-standard hybrid automaton is a tuple where
- , , is a set of discrete states,
- is the non-standard continuous state space,
- is a set of non-standard initial states,
- : is a set of non-standard vector fields,
- : is a set of non-standard continuous invariants,
- , , is a set of discrete transitions,
- : is a set of non-standard guard conditions,
- : is a set of non-standard reset maps.
Definition 4.
(Non-Standard Execution of ) Given a time base , , , a time index set , and Boolean lattice . A non-standard execution of a hybrid automaton is a tuple [27] defined as a finite or infinite sequence of infinitesimal iterations of states such that the following conditions are satisfied:
- 1.
- and when ,
- 2.
- for all such that : , , , ,
- 3.
- for all such that : , , , and ,
where as the mode selector function that returns a discrete state in Q for any time instant t, that is, for all t.
3. Geometric-Zeno: Case Study
In the following, we give an example of a hybrid system whose model exhibits geometric-Zeno behaviour, and we discuss the challenges of simulating its model.
Example (Collision of Three Masses)
Consider a mechanical system consisting of three point masses, , , and , on a table, as shown in Figure 1. We assume that the friction force between the table and the three masses be neglected. Let , , and denote the displacement, velocity, and acceleration of mass in the x direction, respectively, and , , and denote the displacement, velocity, and acceleration of mass in the y direction, respectively, with . It is assumed that both masses and are at rest, while mass is moving to the right with initial velocity and collides with mass , which moves towards mass and collides with it. As a result, mass falls and starts bouncing on the ground, and the two masses , may either fall and start bouncing or eventually stop on the table. When a collision occurs between masses and , the velocities after collision can be derived from Newton’s rule and the law of conversion of momentum as
where and () are the velocities of mass i just after and just before the collision, respectively, and is a restitution coefficient. The same applies when a collision occurs between masses and .
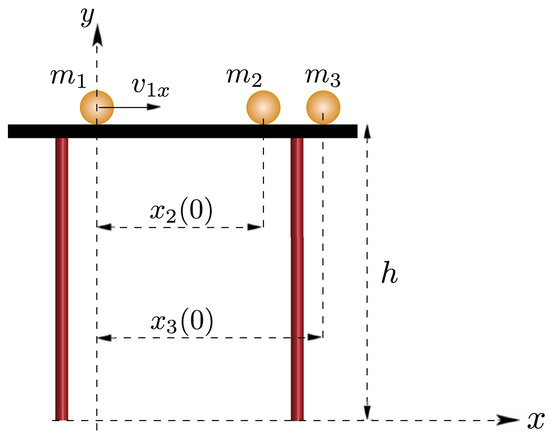
Figure 1.
The three masses system.
Figure 2 shows the hybrid automaton model of the three masses system with all possible collisions and/or bouncing scenarios. In all discrete states, the system’s dynamics are given by , , , . Table 1 gives the guard conditions together with the resets for the transitions , . In this example, three discrete events occur simultaneously if mass is positioned at the extreme edge of the table, that is, both masses and fall and start bouncing simultaneously, which results in a non-deterministic behaviour. In addition, at least mass will fall from the table and starts bouncing; the restitution coefficient models the loss of energy that happens when inelastic collisions with the ground occur during bouncing.
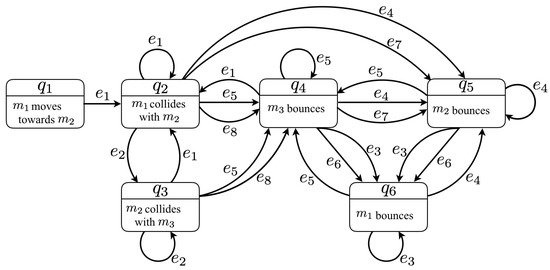
Figure 2.
The hybrid automaton model of the three masses system.

Table 1.
Guard conditions and resets for the transitions in Figure 2.
Consider the case when mass bounces on the ground (see Figure 3). One can easily calculate the time instants of discrete events by
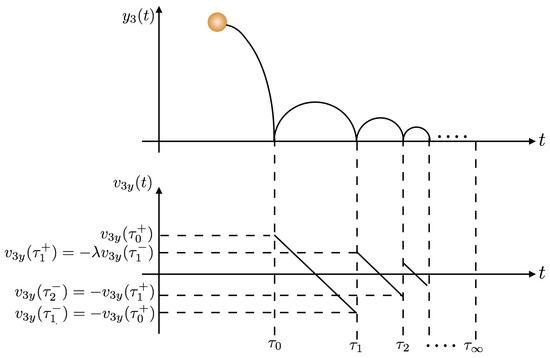
Figure 3.
Bouncing of mass ; the event times and refer to the times immediately before and after the collision j, respectively.
The series has a finite limit . The same applies when masses and bounce. When either of the three masses bounces, it becomes at rest with zero position and velocity in finite time, but after going through an infinite number of bounces.
The numerical simulation of the bouncing behaviour is highly challenging. In fact, the simulation either halts or produces faulty results. Figure 4a shows the simulation in Simulink [31] of the bouncing behaviour with . The simulation halts and terminates with a simulation error; see Figure 4b. This is because, near the geometric-Zeno limit point , the simulation exceeds the default number of consecutive zero crossings allowed in Simulink. With , the simulation in Simulink generates faulty results, where the simulated mass falls under the surface on which it is bouncing and then goes into a free-fall in the space below; see Figure 4c. This is because some discrete events are missed during simulation due to the accumulation of infinite number of discrete transitions. When simulating the bouncing behaviour in Openmodelica [32] with , the simulation produces faulty results due to numerical errors encountered by the Modelica discrete events detector; see Figure 4d. Many other simulation tools, such as HyVisual [33], Scicos [34], Acumen [35], Zélus [36], produce the same faulty results when simulating the bouncing behaviour.
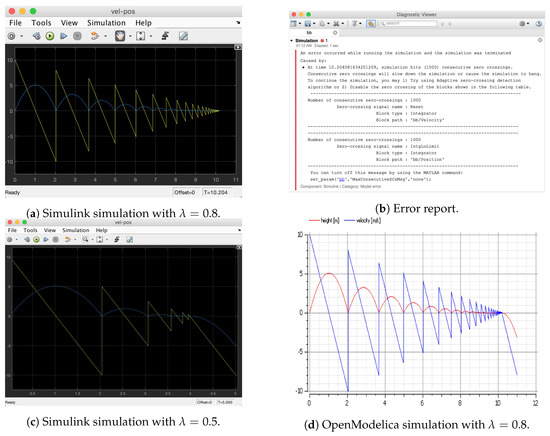
Figure 4.
The simulation of the bouncing behaviour in Simulink and OpenModelica.
4. Non-Standard Regularization of Geometric-Zeno
In the following, we use non-standard analysis to develop sufficient conditions for the existence of geometric-Zeno behaviour, and we propose methods to allow hybrid automaton execution to be carried beyond the geometric-Zeno limit point, thus avoiding simulation halt or faulty results when simulating models exhibiting geometric-Zeno.
The idea we propose is based on using non-standard simulation relation analysis through cyclic executions of hybrid automata. We show that the execution of a given hybrid automaton converges to a geometric-Zeno limit point if all the cycles detected during the execution converge according to a non-standard geometric contractive simulation relation.
Definition 5.
(Finite Cyclic Path) Given a directed graph , . A Finite cyclic path is an alternating sequence of discrete states and edges of the form such that for all i. It is called a finite cyclic path if the starting state is the same as the ending state (i.e., ). Furthermore, a portion of a finite path can be a finite cyclic path such as with , or with , etc.
Cycles are compared by using a non-standard simulation relationship. In order to derive sufficient conditions for the hybrid automaton execution to be convergent to a geometric-Zeno limit point, we firstly study the non-standard simulation relation between hybrid states, and then we introduce conditions for such simulation relation to be geometric, and geometric contractive.
Definition 6.
(Non-Standard Simulation Relation) Given a hybrid automaton , and two non-standard hybrid states of : and , where , and . We call the relation a non-standard simulation relation between and , denoted by , if and only if and for every successor state of after a non-standard micro-step there exists a successor state of after a non-standard micro-step such that .
The hybrid system’s continuous state is usually described by a finite set of continuous state variables. So in Definition 6, the continuous states and are given by and .
Definition 7.
(Non-Standard Geometric Simulation Relation) Given two non-standard hybrid states and and a non-standard simulation relation between them, as defined in Definition 6. The non-standard simulation relation ρ is geometric if and only if there exists , , and a diagonal matrix of elements such that the following property is satisfied:
with and as defined in Definition 6.
Definition 8.
(Non-Standard Contractive Simulation Relation) Given two non-standard hybrid states and and a non-standard geometric simulation relation between them, as defined in Definition 7. The non-standard geometric simulation relation ρ is contractive if and only if and for all .
If for every non-standard hybrid state —during the execution of the hybrid automaton —there exists a non-standard hybrid state such that with being geometric contractive, then the execution of the hybrid automaton converges asymptotically to a geometric-Zeno limit point.
Lemma 1.
(Sufficient Condition for Geometric-Zeno behaviour) An execution of a hybrid automaton is geometric-Zeno if the following conditions are satisfied:
- 1.
- The directed graph of contains a finite cyclic path.
- 2.
- For every non-standard hybrid state there exists a non-standard hybrid state such that with ρ being a geometric contractive simulation relation.
A continuation beyond the geometric-Zeno limit point is done by triggering an urgent transition immediately when the continuous state vectors and become infinitesimally close to each other, that is, when for all and , . In the interval where the transition from pre-Zeno to post-Zeno is taken, the hybrid automaton switches its dynamics to 0, which allows sliding on the switching surface on which geometric-Zeno occurs, and thus allows the hybrid model solution to be continued beyond the geometric-Zeno limit point.
Example (Collision of Three Masses) Revisited
Consider the scenario when a mass , , bounces on the ground. Figure 5 shows the bouncing hybrid trajectory on the -plane, where all bouncing cycles simulate each other according to a non-standard geometric contractive simulation relation. Denote to the non-standard state space of the bouncing hybrid trajectory. For each state in cycle there exists a state in cycle , with , such that , , , , and , where is the successor state of after a micro-step and is the successor state of after a micro-step . That is, the following property is satisfied for :
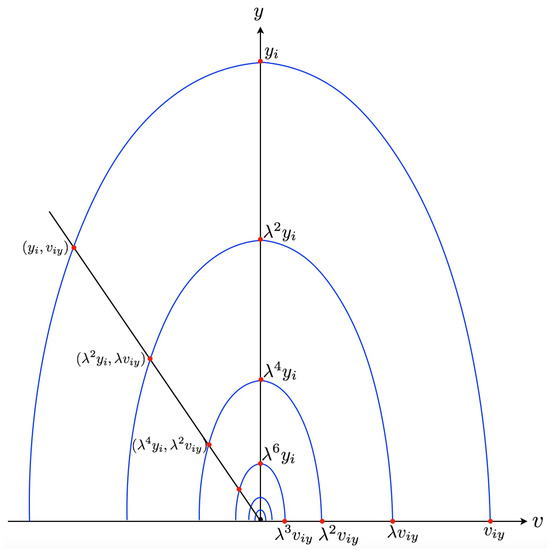
Figure 5.
The bouncing hybrid trajectory on ()-plane.
In our example, the non-standard geometric simulation relation is contractive because .
5. Simulation Results
The methods proposed in this paper were validated through two prototype implementations [37,38] developed in both Matlab and Simulink simulation tools. The first revision of these two prototype implementations was presented in [27]. This paper presents the second revision which implements the methods presented in Section 4.
Figure 6 and Figure 7 show the Zeno-free simulation of the bouncing behaviour in the case study presented in Section 3, with parameters: , , and initial conditions: , . The simulation time is set to 2[s]. During the simulation, the velocity of the bouncing mass decreases due to the energy loss through impact. As a result, more and more collisions are triggered and the time interval between two consecutive collisions keeps shrinking. The first bouncing cycle was detected at time . A geometric contractive simulation relation with coefficients (for the state variable ) and (for the state variable ) was observed for every pair of two consecutive cycles. The convergence of solution to a geometric-Zeno point took place at time 1.3549[s]. The dense points near the time 1.3549[s] indicates that more and more computation steps are taken near the geometric-Zeno limit point, so that discrete events are not missed during simulation. When the simulation closely approaches the geometric-Zeno point, the hybrid automaton automatically switches to integrate the dynamics such that a sliding occurs on the switching surface to which belong the geometric-Zeno state . Therefore, the simulation does not halt, and the solution trajectory of the hybrid model moves beyond the geometric-Zeno limit point. This reflects the real dynamics of the bouncing behaviour, where at the end of the bouncing the mass becomes at rest.
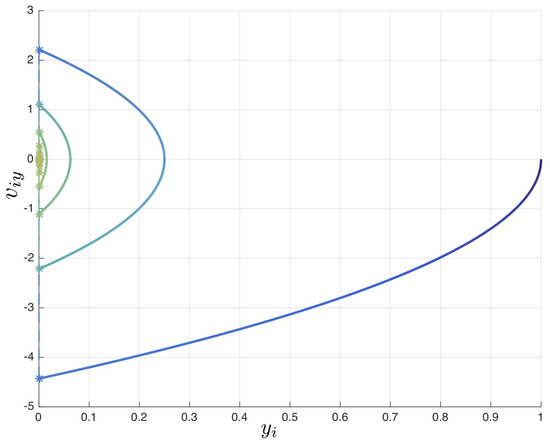
Figure 6.
Zeno-free simulation of the bouncing behaviour: versus .
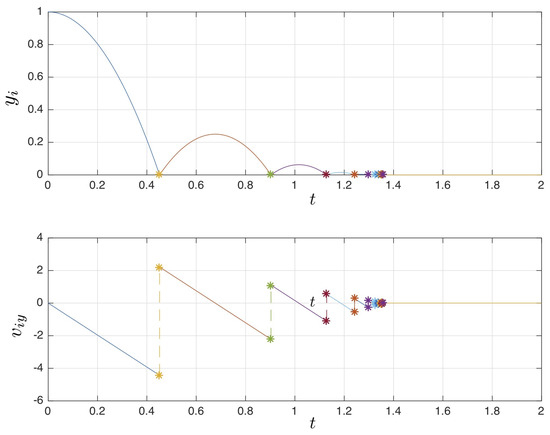
Figure 7.
Zeno-free simulation of the bouncing behaviour. Up: The time evolution of . Down: The time evolution of .
6. Conclusions and Perspectives
Geometric-Zeno behaviour is one of the most challenging problems in the analysis of hybrid systems. Such behaviour never occurs in real physical systems, but results from modelling abstraction (or over-approximation) when abstraction mechanisms fail to model the complex interaction between the continuous and discrete dynamics of hybrid systems. In this paper, we discussed—through a realistic case study—the challenges of simulating geometric-Zeno models of hybrid systems, and we provided a non-standard analysis of hybrid automata executions in densely ordered hybrid time domain. Through the non-standard analysis, we developed formal sufficient conditions for the existence geometric-Zeno based on the existence of a geometric contractive simulation relation between hybrid states in different execution cycles. The advantages of using non-standard semantics in the analysis of geometric-Zeno behavior is that the completeness in the space of the continuous dynamics and discrete dynamics is naturally introduced, so that it allows representing geometric-Zeno behaviour in a concrete way, while at the same time preserving the original semantics of the hybrid model. We also provided methods for carrying solution beyond geometric-Zeno limit point. The proposed methods for geometric-Zeno detection and elimination were validated through prototype implementations and simulation results.
The work presented in this paper can be continued in many different directions. In the future we want to explore the applicability of our methods for experimental case studies of complex hybrid systems having a large number of state variables (and thus a large space dimension), and whose models exhibit geometric-Zeno behaviour. Furthermore, we want to explore techniques for estimating geometric-Zeno time and geometric-Zeno state from given initial states, and the usage of such estimation to transition hybrid automaton execution beyond the geometric-Zeno limit point.
Author Contributions
Conceptualization, A.A., M.F., and M.S.Q.; methodology, formal methods, and analysis, A.A.; software and validation, A.A.; writing—draft preparation, review, and editing, A.A., M.F., and M.S.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Campbell, S.; Chancelier, J.P.; Nikoukhah, R. Modeling and Simulation in Scilab/Scicos with ScicosLab 4.4, 2nd ed.; Springer: New York, NY, USA, 2010; ISBN 978-1-4419-5526-5. [Google Scholar] [CrossRef]
- Lunze, J.; Lamnabhi-Lagarrigue, F. Handbook of Hybrid Systems Control: Theory, Tools, Applications; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Lee, E.A.; Seshia, S.A. Introduction to Embedded Systems, A Cyber-Physical Systems Approach, 2nd ed.; MIT Press: Cambridge, MA, USA, 2017; ISBN 978-0-262-53381-2. [Google Scholar]
- Betsuno, K.; Matsumoto, S.; Ueda, K. Symbolic Analysis of Hybrid Systems Involving Numerous Discrete Changes Using Loop Detection. In Cyber Physical Systems. Design, Modeling, and Evaluation; Lecture Notes in Computer Science; Berger, C., Mousavi, M., Wisniewski, R., Eds.; Springer: Cham, Switzerland, 2017; Volume 10107. [Google Scholar] [CrossRef]
- Antsaklis, P.J. Special issue on hybrid systems: Theory and applications a brief introduction to the theory and applications of hybrid systems. Proc. IEEE 2000, 88, 879–887. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Caillaudr, B. Chattering-free simulation of hybrid dynamical systems with the functional mock-up interface 2.0. In Proceedings of the First Japanese Modelica Conferences, Linkoping Electronic Conference Proceedings, Tokyo, Japan, 23–24 May 2016; Volume 124, pp. 95–105. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Zeng, Y.; Duracz, A.; Caillaud, B.; Taha, W. Chattering-free simulation for hybrid dynamical systems semantics and prototype implementation. In Proceedings of the 19th IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC) and 15th International Symposium on Distributed Computing and Applications for Business Engineering (DCABES), Paris, France, 24–26 August 2016; pp. 412–422. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Caillaud, B. On the Regularization of Chattering Executions in Real Time Simulation of Hybrid Systems. In Baltic Young Scientists Conference, The 11th Baltic Young Scientists Conference; Cap, C., Ed.; Universität Rostock: Tallinn, Estonia, 2015; p. 49. Available online: https://hal.archives-ouvertes.fr/hal-01246853 (accessed on 14 January 2020).
- Lygeros, J.; Tomlin, C.; Sastry, S. Hybrid Systems: Modeling, Analysis and Control, Lecture Notes on Hybrid Systems. Available online: http://www-inst.cs.berkeley.edu/~ee291e/sp09/handouts/book.pdf (accessed on 16 January 2020).
- Raskin, J.-F. Reachability Problems for Hybrid Automata; Springer: Berlin/Heidelberg, Germany, 2011; pp. 28–30. [Google Scholar]
- Henzinger, T.A. The theory of hybrid automata. In Proceedings of the 11th Annual IEEE Symposium on Logic in Computer Science, New Brunswick, NJ, USA, 27–30 July 1996; pp. 278–292. [Google Scholar] [CrossRef]
- Brihaye, T.; Doyen, L.; Geeraerts, G.; Ouaknine, J.; Raskin, J.F.; Worrell, J. On Reachability for Hybrid Automata over Bounded Time. In Automata, Languages and Programming. ICALP 2011, Zurich, Switzerland, July 4–8, 2011; Lecture Notes in Computer Science; Aceto, L., Henzinger, M., Sgall, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6756. [Google Scholar]
- Frehse, G.; Le Guernic, C.; Donze, A.; Cotton, S.; Ray, R.; Lebeltel, O.; Ripado, R.; Girard, A.; Dang, T.; Maler, O. Spaceex: Scalable verification of hybrid systems. In Computer Aided Verification; Springer: Berlin/Heidelberg, Germany, 2011; pp. 379–395. [Google Scholar]
- Aljarbouh, A.; Caillaudr, B. Simulation for hybrid systems: Chattering path avoidance. In Proceedings of the 56th Conference on Simulation and Modelling (SIMS 56), Linkoping Electronic Conference Proceedings, Linkoping, Sweden, 7–9 October 2015; Volume 119, pp. 175–185. [Google Scholar] [CrossRef]
- Goebel, R.; Teel, A.R. Lyapunov characterization of zeno behavior in hybrid systems. In Proceedings of the 47th IEEE Conference on Decision and Control (CDC 2008), Cancun, Mexico, 9–11 December 2008; pp. 2752–2757. [Google Scholar] [CrossRef]
- Lamperski, A.; Ames, A.D. Lyapunov theory for zeno stability. IEEE Trans. Autom. Control 2013, 58, 100–112. [Google Scholar] [CrossRef]
- Egerstedt, M.; Johansson, K.H.; Sastry, S.; Lygeros, J. On the regularization of Zeno hybrid automata. Syst. Control Lett. 1999, 38, 141–150. [Google Scholar]
- Johansson, K.H.; Lygeros, J.; Sastry, S.; Egerstedt, M. Simulation of zeno hybrid automata. In Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 7–10 December 1999; Volume 4, pp. 3538–3543. [Google Scholar] [CrossRef]
- Ames, A.D.; Sastry, S. Blowing up affine hybrid systems. In Proceedings of the 43rd IEEE Conference on Decision and Control (CDC), Atlantis, Bahamas, 14–17 December 2004; Volume 1, pp. 473–478. [Google Scholar] [CrossRef]
- Camlibel, M.K.; Schumacher, J.M. On the zeno behavior of linear complementarity systems. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; Volume 124, pp. 346–351. [Google Scholar] [CrossRef]
- Shen, J.; Pang, J.S. Linear complementarity systems: Zeno states. SIAM J. Control Opt. 2005, 44, 1040–1066. [Google Scholar] [CrossRef]
- Thuan, L.Q. Non-zenoness of piecewise affine dynamical systems and affine complementarity systems with inputs. Control Theory Technol. 2014, 12, 35–47. [Google Scholar] [CrossRef]
- Ames, A.D.; Zheng, H.; Gregg, R.D.; Sastry, S. Is there life after zeno? Taking executions past the breaking (zeno) point. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 6. [Google Scholar] [CrossRef]
- Lamperski, A.; Ames, A.D. Lyapunov-like conditions for the existence of zeno behavior in hybrid and lagrangian hybrid systems. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 115–120. [Google Scholar] [CrossRef]
- Ames, A.D.; Abate, A.; Sastry, S. Sufficient conditions for the existence of zeno behavior. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 696–701. [Google Scholar] [CrossRef]
- Lamperski, A.; Ames, A.D. On the existence of zeno behavior in hybrid systems with non-isolated zeno equilibria. In Proceedings of the 47th IEEE Conference on Decision and Control (CDC 2008), Cancun, Mexico, 9–11 December 2008; pp. 2776–2781. [Google Scholar] [CrossRef]
- Aljarbouh, A. Non-standard zeno-free simulation semantics for hybrid dynamical systems. In Verification and Evaluation of Computer and Communication Systems; Ganty, P., Kaâniche, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 16–31. [Google Scholar]
- Benveniste, A.; Bourke, T.; Caillaud, B.; Pouzet, M. Non-standard semantics of hybrid systems modelers. J. Comput. Syst. Sci. 2012, 78, 877–910. [Google Scholar] [CrossRef]
- Saghe, A. A new approach to nonstandard analysis. Sahand Commun. Math. Anal. 2018, 12. [Google Scholar] [CrossRef]
- Chen, L. Do simple infinitesimal parts solve Zeno’s paradox of measure? Synthese 2019. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/products/simulink.html (accessed on 11 December 2019).
- Available online: https://openmodelica.org/ (accessed on 11 December 2019).
- Available online: https://ptolemy.berkeley.edu/hyvisual/ (accessed on 13 December 2019).
- Available online: http://www.scicos.org/ (accessed on 4 January 2020).
- Available online: http://www.acumen-language.org/ (accessed on 11 January 2020).
- Available online: http://zelus.di.ens.fr/ (accessed on 6 January 2020).
- Sevama: A Simulink Toolbox and Simulator for Zeno-Free Simulation of Hybrid Dynamical Systems, with Zeno Detection and Avoidance in Run-Time. Available online: https://bil.inria.fr/fr/software/view/2679/tab (accessed on 23 January 2020).
- Domna: A Lite Matlab Simulator for Zeno-Free Simulation of Hybrid Dynamical Systems, with Zeno Detection and Avoidance in Run-Time. Available online: https://bil.inria.fr/fr/software/view/2691/tab (accessed on 23 January 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
