Abstract
The realization of large-scale complex engineered systems is contingent upon satisfaction of the preferences of the stakeholder. With numerous decisions being involved in all the aspects of the system lifecycle, from conception to disposal, it is critical to have an explicit and rigorous representation of stakeholder preferences to be communicated to key personnel in the organizational hierarchy. Past work on stakeholder preference representation and communication in systems engineering has been primarily requirement-driven. More recent value-based approaches still do not offer a rigorous framework on how to represent stakeholder preferences but assume that an overarching value function that can precisely capture stakeholder preferences exists. This article provides a formalism based on modal preference logic to aid in rigorous representation and communication of stakeholder preferences. Formal definitions for the different types of stakeholder preferences encountered in a systems engineering context are provided in addition to multiple theorems that improve the understanding of the relationship between stakeholder preferences and the solution space.
1. Introduction
Tremendous cost growths associated with Major Defense Acquisition Programs (MDAPs) is a crucial problem posed to the Department of Defense (DoD). Although as of 2016, cost growth is significantly lower than historical levels, there is still a significant cost growth associated with research, development, test, and evaluation (RDT&E) [1]. Multiple agencies have recognized the concerns in this growth, as evident by NSF, NASA, and DARPA launching a series of workshops that address the challenges and opportunities associated with the field of Systems Engineering and Design [2,3,4,5,6]. All of these workshops identified a need for underlying scientific foundations in systems engineering. One of the critical topics discussed in the workshops and past research is elicitation, representation, and communication of preferences associated with stakeholders who claim ownership of the large-scale complex engineered system (LSCES) under development. According to [7,8] good quality decision depends on key fundamental aspects like preferences, beliefs, alternatives, etc. Preference is a critical aspect in a decision-making process. Without an accurate elicitation and explicit representation of preferences, consistent decisions are difficult, if not impossible in a multi-agent organization.
In current Systems Engineering (SE) practices, large-scale systems are developed using requirements-based approaches. In the requirements-based approach, the needs (preferences) of key stakeholders are first elicited in the form of the “voice of the customer” [9]. This is followed by the generation of a concept of operations (ConOps) and identification of operational scenarios for the system of interest, based on the stakeholder preferences [10]. The ConOps and operational scenarios enable the identification of operational requirements for the system, which are then translated to system level requirements using requirements analysis methods such as House of Quality, N2 matrices, functional flow diagrams, and modeling and simulations [9]. The system level requirements are decomposed into subsystem and component level requirements which are flowed down the organizational hierarchy to aid in decision-making [11,12]. These requirements only serve as constraints in the solution space, not informing about the differences between feasible solutions. Multiple US National Defense Industry Association (NDIA) reports have identified the requirements definition, development and management processes currently being practiced, as one of the top five issues in systems and software engineering [13,14]. Value-based approaches communicate preferences through special-case objective functions but assume that a preference is understood in order to form the value models [15,16,17,18,19,20,21,22,23].
Preferences and their challenges are not a uniquely engineering problem. In Economics, preferences are typically represented numerically as in engineering, most commonly via utility functions [24]. Preferences have been studied extensively in the field of Philosophy using formal tools [25,26,27,28,29,30,31,32,33]. Two most common approaches of dealing with preferences include a syntactic approach [25,26,31,34], wherein preferences are expressed as binary relations between propositions or states of affairs, and a semantic approach where betterness models and Kripke structures are used to provide meaning to preference [30,35,36,37,38]. Researchers in Artificial Intelligence have extended multiple logics of preferences from philosophy to enable qualitative representation and reasoning of preferences using propositions [39], with the most prevalent qualitative formalism being CP-nets (Conditional Preference networks) [40,41,42].
In this paper, we will extend the existing logics of preference, specifically in [43] that is based on the classic possible-worlds approach [44,45,46], to provide theoretical foundations for Systems Engineering, specifically to improve understanding of the relationships between stakeholder preferences and the solution space that represents all potential alternatives that define the complex system. The purpose of the mathematical formalism proposed in this paper is as follows:
- To provide formal definitions for the different types of stakeholder preferences that may be encountered in a systems engineering context.
- To prove theorems that improve understanding of how stakeholder preferences affect the solution space:
- To formally define inconsistencies in stakeholder preferences and study the effect of inconsistent preferences on the solution space;
- To understand the effect of changes in stakeholder preferences on the solution space.
The paper is organized as follows. Section 2 provides the necessary background for the stakeholder preference problem and a summary of past work. In Section 3, the proposed formalism is presented. Descriptive examples are used in Section 3 to demonstrate the use of the proposed theoretical foundations in an industrial context. Section 4 provides a discussion of the contributions of the paper, and Section 5 discusses the conclusions and future work.
2. Background
The development of large-scale complex engineered systems involves hundreds to thousands of individuals making decisions across the organizational hierarchy. For decades, the development and design of LSCES has been requirement-driven, where the stakeholder’s preferences are represented and communicated in the form of requirements. Although considerably simpler to implement, requirements only communicate the boundaries of the solution space and do not provide a way to distinguish between feasible alternatives and tend to constrain design space exploration.
Recently, researchers have proposed a value-based alternative to requirement-driven approaches in systems engineering. The central idea in value-based approaches, a concept borrowed from Decision Analysis [8,47,48], is mathematically capturing stakeholder preferences using a value function, which is a special case of an objective function, and optimizing for maximum value. Value functions are formed as a function of system characteristics known as attributes and are typically singular in unit (such as money or probability of mission success) that directly correlate to the stakeholder’s preference. This formulation of a value function allows for a direct comparison of design alternatives from a wide range of systems that share the same set of attributes. The Decision Analysis community and some of the researchers in systems engineering and design take preferences as a primitive notion [8,48]. It is axiomatically established that preferences are precise and certain in the mind of a decision-maker and do not change. In other words, it is assumed that an accurate preference function explicitly representing the preferences of the decision-maker exists. In order to facilitate system design, one needs to map the decisions to system attributes, and then to value [49]. Considering the complexity involved in the development of large-scale complex engineered systems and based on the experience of the authors with creating value functions for a wide range of test cases [16,49,50,51,52,53,54,55,56,57], we believe that creating a mathematical value function that can capture all the attributes and their interactions is an extremely challenging and time-consuming task. Although researchers in Decision Analysis have provided some guidelines [8,48,58] on formulating preference functions, there is still a lack of a mathematically rigorous method that can facilitate formulation.
With the consideration of uncertainty, capturing preferences becomes more challenging. For instance, eliciting a utility function from the stakeholder is a time-intensive task and typically the method of elicitation dictates how the utility function is formed. Multi-attribute utilities are much harder to deal with since formulating a multi-attribute utility function requires a significant time investment. In addition, communicating preferences using linearized value and utility functions has some challenges including, local minima due to linearization, ensuring consistency in physics, time-consuming decision iterations between hierarchical levels to ensure consistency, etc.
In addition to the representation of stakeholder preferences, significant challenges exist in identifying inconsistencies in stakeholder preferences. Researchers have emphasized the importance of identifying and resolving conflicts in requirements during the early phases of the system lifecycle to avoid schedule delays and cost overruns [59,60,61,62,63]. Some researchers in SE associate the notion of consistency with the absence of conflicting requirements within a requirement set [64,65,66,67,68,69]. Researchers in SE have proposed a set of heuristics [64] that are derived from literature and experience and a method [64] that operationalizes the set of heuristics to identify conflicts in requirements. Work done so far in requirement conflict identification has been procedural in nature and lacks theoretical foundation. Conflict identification has been extensively studied in software systems [64,67,68,70], where the primary focus is identifying conflicts in functional requirements. Multiple techniques based on propositional logic have been proposed to identify conflicts in functional requirements pertaining to software systems [70,71,72]. Systems engineering, on the other hand, consists of multiple categories of requirements including performance, resource, interface, and functional [12], thereby making it challenging to leverage the conflict identification techniques used in software systems.
3. Preference Representation—Formalism
Formal logic emerged in the late 19th and early 20th century as a way to model reasoning with mathematically precise structures. In its modern form, each such logic consists of three parts: (i) a set of symbolic representations, called sentences, defined recursively for a set of base symbols comprising a formal language; (ii) a precise and rigid semantics for interpreting the sentences; and (iii) a proof theory that defines a relation of proof between sets of sentences (premises) and another sentence (the conclusion) [73]. Formal logics can be used as powerful tools for reasoning automatically in the domains they describe. Representing statements that capture the cognitive attitudes of agents through formal logic enables mathematical or logical reasoning, which aids in making inferences based on the premises.
Modal logic was developed as an extension from propositional [74,75] and first order (predicate) logic [76] to reason about statements involving modality [77]. For instance, in the statements “It is necessary that p” and “It is possible that p”, necessary and possible are the modals. Multiple logics have been derived based on modal logic that help reason about various modalities including obligatory, permissible, will always be, will be, and, central to our concerns here, prefers. Stakeholder preferences in systems engineering are expressed over the desired characteristics (or attributes) of the system, perceived in the mind of the stakeholder, and are intuitively comparative in nature. Here, the stakeholder is an entity that can claim complete ownership of the system during development. Stakeholder preferences are generalized into categories as shown in Table 1, all of which are formally defined in later sections. In Table 1, target-oriented preferences represent preferences on specific targets, whereas design-dependent preferences represent preferences on solution alternatives. In objective-oriented preferences, preferred directions on attributes of interest are specified. In this article, we will implement a preference logic that can handle the inherent comparative nature of preferences, the different types of preferences in Table 1, and can aid in evaluating consistency in a given preference set. We will base our formal language on the modal preference logic systems in [43] to provide theoretical foundations for systems engineering, specifically relating stakeholder preferences and solution spaces. This modal preference logic is based on the classic possible-worlds approach.

Table 1.
Preferences in systems engineering.
3.1. Syntax for Modal Preference Logic
As with any formal language, the syntax for a Modal preference logic consists of a non-empty set () of atomic propositions that represent basic facts about the situation under consideration and are usually denoted by p, q, r, etc. “The system is a satellite” and “The system has stealth capability” are examples of atomic propositions. Compound sentences or formulas typically represented using Greek symbols , , etc., can be formed by closing off under conjunction and negation. Additionally, we have a modal operator, , which represents whether an agent prefers something or not. is formally defined in Section 3.2.2.
Definition 1 (Modal preference language).
The modal preference language (Lp) is given by the following Backus–Naur/Backus–Normal Form (BNF) [78].
BNF is a formal notation representing the grammar of the formal language. “:=” means “may be expanded to” or “replaced with”. In the above notation, the formula can be replaced with simple propositions p, and/or compounded formulas with the preference operator.
3.2. Semantics for Modal Preference Logic
Preferences are evaluated based on the classical possible-worlds approach for the modal preference logic implemented in this article. The semantics of such a language will be developed based on Kripke structures that were extensively used to represent and reason about knowledge and beliefs [45,46]. The elements necessary to evaluate preferences based on worlds are represented by the preference structure, which is discussed in the following section.
3.2.1. Preference Structure
Definition 2 (Preference structure).
A preference structure, similar to Kripke structure [79], is a tuple , where is the set of all states, also sometimes called the domain of . In the context of large-scale systems, can be considered as the set of all alternatives that a decision-maker considers possible. In other words, represents the entire solution space (see Definition 10). Here is a binary relation called the betterness relation that is used to evaluate preferences. The preference structure contains all the necessary elements required to represent preference as a modal and will be used to evaluate the preference statements elicited from the stakeholder. The in the structure M is a valuation function, as defined in the following definition.
Definition 3 (Valuation function).
In the preference structure , is a valuation function, that assigns truth values to each of the atomic propositions in at each state, i.e., = TRUE means that the proposition p is true at state w. The state w is emphasized here as the truth assignment changes when the state changes.
With the elements of the preference structure defined, the semantic relation can be recursively defined as which can be read equivalently as “ is true in structure M at state w” or “structure M satisfies at state w”. Equation (2) states that atomic proposition p is TRUE at state w in structure , if and only if assigns TRUE.
Moreover, we have
The notation is used to indicate that it is not the case that , which it true if and only if .
Definition 4 (Partial order/partially ordered set or poset).
A partial order is a binary relation that is reflexive, transitive, and antisymmetric. Given a set S and a partial order, the pair is called a partially ordered set or a poset.
Definition 5 (Total order).
A total order is a partial order that also has the property of totality, i.e., all the pairs of distinct elements are comparable. Given a set S, and a total order , , totality means either or .
Definition 6 (Betterness relation).
Betterness relation in the preference structure (definition 2) is a binary relation that has a partial order defined by the following equation.
Here, is read as is at least as good as . If and ’, then is strictly better than , i.e., (). The order on the betterness relation can be specified based on the context of the decision problem. For instance, having a partial order for the betterness relation allows for incomparability between states. This allows to represent and reason about preferences over attributes that are incomparable. Theorems 2 and 3 discuss the relationship between the betterness relation and the solutions.
3.2.2. Types of Preferences
In the development of large-scale complex engineered systems, stakeholders may express their preferences in many ways including requirements, business goals, a preferred direction for an attribute, etc., as seen in Table 1. The following definitions will provide a mathematical structure to represent these different types of stakeholder preferences.
Definition 7 (Attributes, propositions, and preference statements).
The stakeholder has preferences over certain desired characteristics of the system. These characteristics are called attributes. For example, the stakeholder may prefer low mass and high resolution, where mass and resolution are the attributes. Propositions are defined on such attributes. For instance, in “p: The system has low mass”, and “q: The system has high resolution”, p and q represent propositions on attributes. These propositions (p and q) are then used to form preference statements. For example, “The stakeholder prefers p”.
Before formally defining the types of preferences in Table 1, first we need to define maximal/minimal and greatest/least elements in a partially ordered set (also called poset).
Definition 8 (Maximal/minimal element in a poset).
Let be a partially ordered set. For an element then a is a minimal element. For an element then a is a maximal element.
Definition 9 (Greatest/least element in a poset).
Let be a partially ordered set. For an element , then a is the greatest element. For an element , then a is the least element. The key difference between minimal and least elements (also maximal and greatest) is that for an element to be a least (or greatest) element, all the distinct elements in the set have to be comparable. A partially ordered set that allows for incomparability does not have a unique greatest or least element, but only a set of maximal or minimal elements.
Definition 10 (Solution space).
The solution space, , is defined as the set of all possible worlds that are considered by all the key decision-makers in the organization. These possible worlds are the alternatives that define the system.
Definition 11 (Acceptable solutions).
The set of acceptable solutions relative to a preference structure are the maximal elements of the solution space.
Definition 12 (Optimal solutions).
Optimal solutions (OS) are the set of greatest elements (definition 9), i.e., highest-ranked elements, based on the betterness relation in the solution space (S) that satisfy all the preference statements that are elicited from the stakeholder.
Definition 13 (Comparative preference).
Comparative preference between two propositions is defined as “An agent prefers to if and only if all the states where holds is better than all the states where holds”. In other words, all -states are better than all -states. The following equation mathematically represents comparative preference.
For example, let us assume that the stakeholder in a company that manufactures satellites has preferences over two attributes, mass and SNR, in particular, low mass and high SNR, and low mass is preferred over high SNR. Under no circumstances will the stakeholder choose a design alternative that has high SNR but also high mass. In other words, low mass is her first priority, and it overrides any design alternatives where the SNR may be high but so is the mass. A more detailed example that discusses both absolute and comparative preferences is provided in the following section.
Definition 14 (Absolute preference).
Absolute preferences can be defined in terms of comparative preference. An agent can be said to prefer simpliciter if the agent prefers to . In other words, any state in which is true is as good or better than states in which it is false. In the modal preference language given in definition 1, this can be written as . It will be convenient to define a new derivative symbol . Strictly speaking, it is not part of the modal preference language, but is definable in it. Semantically,
Example 1 (Absolute preference).
Let us consider a scenario where a decision-maker is deciding between two choices for a wing based on his/her preferences over proposition p.
p: The wing has capability X
Let the two choices for the wing be , where = swept wing, and = rectangular wing. Let us say that the decision-maker has the following preferences.
From the definition of “prefers” represented in Equation (5), the above equation means that p is preferred if and only if all worlds at which p is true are considered at least as good as worlds where it is false. Figure 1 represents a preference structure for which this preference statement evaluates to true. It shows the worlds of S along with a list of propositions true at each world. The arrows in Figure 1 represent the betterness relation with a total order, i.e., . It should be noted that, for convenience, edges from a world () into itself (representing the fact that are not shown throughout the paper. This is the only structure for which the given preference evaluates as true, and so it is the only ordering of the design space consistent with the stakeholder’s preference. It happens to contain a greatest element, w1 (swept wing), which would thus be the preferred choice of the decision-maker.
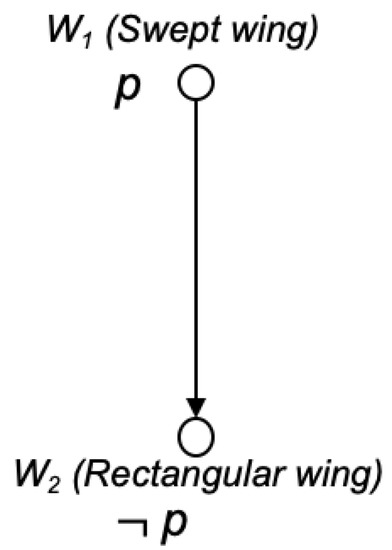
Figure 1.
Absolute preference—Example.
Example 2 (Absolute and comparative preferences).
Let us consider a scenario where a decision-maker is deciding between four choices for a wing based on her preferences over propositions p and q that represent the capabilities of a wing.
p: The wing has capability X
q: The wing must hold at least 10,000 gal of fuel
Let the three choices for the wing be , where w1 = swept wing, w2 = rectangular wing, and w3 = elliptical wing. In order to make a decision, the decision-maker has to imagine multiple worlds with each element in S as a choice by taking the propositions p and q into consideration. Let us say that the decision-maker has the following preferences.
Equation (8) means that the decision-maker prefers worlds where p is true (over those where it is not). Equation (9) means that the decision-maker prefers worlds where q is true to worlds where p is true. The diagram in Figure 2 depicts one preference structure, that satisfies these preferences. The arrows in Figure 2 represent the betterness relation . From Figure 2., it can be seen that , and . The intention here is to find the greatest element (optimal solution—Definition 12) with respect to the betterness relation. World is the greatest in this case.
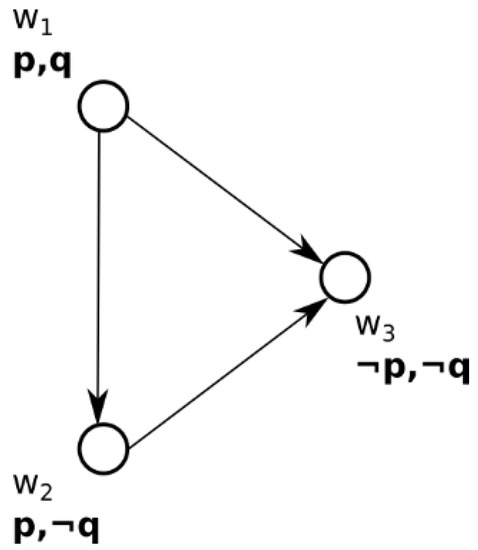
Figure 2.
Comparative preference—example.
Definition 15 (Conditional preference).
A conditional preference is defined in a preference statement as a ceteris paribus preference, where in this context “ceteris paribus” means “all other things being normal [43]. For example, “the agent prefers high horsepower to high torque, unless it is an electric vehicle”. Being an electric vehicle changes the preference of the agent on these attributes. Conditional preference can be formally represented through a simple conjunction operator as shown below.
The statement above means that according to the agent, all -states are better than all -states, given a condition C1.
Definition 16 (Target-oriented preferences).
A target-oriented preference is specified on targets. The targets may be satisfied or not satisfied. Let be the set of all target-oriented propositions. For example, = The satellite has continuous communication with the ground station at a data rate of 10 Mbps, and the preference statement is “Stakeholder prefers ”, where the target is specified. Mathematically, this is represented as . can only be true or false and the stakeholder prefers all the worlds where is true. Target-oriented preferences can be considered analogous to system requirements, which define the boundary of the solution space, that are specified in traditional systems engineering practices.
Definition 17 (Design-dependent preferences).
A design-dependent preference is one in which the stakeholder directly specifies preferences over propositions on solution alternatives. Let be the set of all design-dependent propositions. = The system is a single satellite, and = The system is a fragmented satellite. Preferences over such design-dependent propositions can be represented as , which means that “Stakeholder prefers single satellite to a fragmented satellite system”. Similar to target-oriented preferences, design dependent preferences are also evaluated based on the truth value. Here, the stakeholder prefers all the states where is true to all states where is true.
Definition 18 (Objective-oriented preferences).
An objective-oriented preference is one in which the stakeholder indicates the direction (high- or low-) without encroaching on the solution space. For example, “Stakeholder prefers low launch cost” is objective-oriented, where the stakeholder has preferences over the attributes of the system. Here, there is no restriction on how the objective is to be achieved. Objective-oriented preferences are specified over propositions on attributes that are of interest to the stakeholder. Let be the set of all objective-oriented propositions that the stakeholder has preferences over. For example, can represent a proposition “The satellite system has low mass”.
Each attribute of a design can be described by an atomic proposition, e.g., : The mass is between 8 and 10 kg, or : The mass is at least 2 kg. Since the design space is bounded, there are only finitely many of such propositions. In that case, objective-oriented preferences can be expressed by a (finite) conjunction of absolute or comparative preferences, depending upon the choice of how attributes are encoded in the stock of atomic propositions. For example, suppose we want to express “Stakeholder prefers low mass for the satellite system”, denoted by . Let the solution space (S) be defined by four designs as shown in Table 2.

Table 2.
Solution Space—Example.
Suppose the set of atomic propositions has the form, The mass is between and , for , with the propositions labelled . For instance,
p0,1: The mass is between 0 and 1 kg;
p1,2: The mass is between 1 and 2 kg, etc.
Then . Based on the definition of comparative preferences, the optimal solution is world (or design) w1, which is the greatest element in the solution space (S) based on the betterness relation that satisfies the preference statement . Such an extension using conjunction can be done automatically to any finite set of masses or mass ranges. One will seldom have a need to fully unpack the expression because we need only find acceptable solutions. While a stakeholder’s statements can be compactly represented by terms like , the point is that these can be syntactically defined (or axiomatically connected) to finite conjunctions of claims using only comparative preference.
There may be scenarios where the stakeholder might not have a preference between propositions in set . For example, the stakeholder might prefer low mass and high SNR at the same time but may not have a preference between low mass and high SNR. Situations like these are similar to multi-objective optimization problems that result in pareto optimal solutions based on low mass and high SNR. On the other hand, the stakeholder might have a preference between low mass and high SNR —“Stakeholder prefers low mass to high SNR”. Both the situations can be represented using a conjunction of statements involving comparative preferences.
3.2.3. Relationship between Stakeholder Preferences and Solution Space
In a systems engineering context, the problem of stakeholder preferences involves elicitation, representation, and communication. All these elements have an effect on the realization of the system. In this article, we are interested in understanding the relationship between some of the aspects of these key elements and the solution space. The following definitions and theorems provide an understanding of how the solution space is affected by
- The mathematical structure (betterness relation) of preferences;
- Types of preferences;
- Inconsistency in preferences;
- Changes in preferences.
Definition 19 (Preference base).
A preference base
is the union of all preference statements that are elicited from the stakeholder, where are the set of target-oriented, objective-oriented and design-dependent preference statements respectively. For instance, represents the set of all preference statements that are design-dependent, whereas represent the set of all preference statements that are objective-oriented.
Theorem 1.
Every finite poset has at least one maximal element.
This theorem is fundamental in nature but is necessary for proofs in Theorems 2 and 3, where we investigate the relationship between the structure of preference, represented through the betterness relation, and the solution space.
Proof.
Let be a finite partially ordered set. Let us consider an element . If is a maximal element, we can conclude now that S has a maximal element. If not, there must be another element such that but . Now if is the maximal element, our search can conclude here, else we move on to the next element but , and so on. This gives rise to one of two results: (1) We find a maximal element in the poset S, or (2) we iterate infinitely. We will present a proof by contradiction for case 2, thereby proving that the poset does indeed have a maximal element.
Let us assume there is an infinite sequence of elements of S such that and However, since the sequence is infinite and the elements are drawn from the finite set S, every element will recur more than once. Thus, we can assume i < j such that . The partial sequence may be depicted as , and by transitivity, . The next element in the sequence is such that , but since , . We now have both and, so by antisymmetry, . However, by definition, , leading to a contradiction. This proves that the sequence cannot be infinite and there is indeed a maximal element in the poset S. □
Next, we will investigate the impact of the mathematical structure of preferences, i.e., betterness relation, on the solution space. During elicitation of stakeholder preferences, one may run into two scenarios. One scenario is where the stakeholder has definite preferences over all the attributes that are comparable. In this case, the betterness relation has a total order, i.e., the preferences are complete. This is consistent with the theory of rational choice, where one of the axioms is completeness. In the other scenario, the stakeholder may have preferences over attributes that are incomparable, allowing for the betterness relation to be a partial order. This incompleteness (lack of totality) in the betterness relation may be due to the following reasons:
(1) Lack of knowledge.
For example, during elicitation, the stakeholder might not have enough knowledge about certain attributes of the system, resulting in an incomparability. This can be resolved with new knowledge generated as the design progresses. In this case, the incomparability in the betterness relation will now be resolved, leading to a total order.
(2) No possible way for the decision-maker to distinguish or compare the attributes.
For example, let us consider a government agency (e.g., NASA) as the stakeholder. In this case, it might not be possible to resolve the incomparability between environmental attributes (e.g., space debris) and the economic attributes (e.g., cost) of a launch system.
Theorems 2 and 3 serve to understand how such elicited preferences impact the final solution.
Theorem 2.
A betterness relation with a total order always results in an optimal solution, given a finite non-empty set of possible worlds/states.
Proof.
Let be a non-empty finite set of all states/worlds. Here are the worlds that are used to evaluate the preference statements. For example, means that the agent prefers all worlds where holds. From Definition 6, is a binary relation, called betterness relation, that is defined on the set . Theorem 1 says that every finite poset has at least one maximal element. Let be one such maximal element in and be an arbitrary element in . Since is a maximal element and is a total order defined on , we have . Suppose is a maximal element, then . Since is also a maximal element in with respect to , we have . Additionally, since is also a maximal element in with respect to , we have . From and , we have , which means that all the maximal elements are equal. By Definitions 5, 8, and 9, for a totally ordered set, the greatest element is the same as the maximal element. The existence of the greatest element proves that an optimal solution exists. □
Example 3.
The same example used to demonstrate comparative preferences (definition 13) can be used here. The decision-maker is deciding between four choices for a wing based on his/her preferences over propositions p and q.
p: The wing has capability X
q: The wing must hold at least 10,000 gal of fuel
Total order was one of the necessary conditions that enabled comparison of all the worlds based on the truth values of the preference statements. This exhaustive comparison is what resulted in an optimal solution w1 where both p and q are true.
Theorem 3.
If some of the attributes are incomparable for the stakeholder, then optimal solutions may not exist.
Proof.
Let p, q, and s be distinct propositions. Suppose that the stakeholder does not express any preferences explicitly involving s and that s is not implicitly related by any objective-oriented preferences to p and q. Then it is possible to find structures that satisfy sets of target-oriented preferences with no optimal solution.
As a proof by example, consider a set of worlds and the following set of preference statements:
Then the structure shown in Figure 3 satisfies these preferences but does so with a preference relation that is only a partial order. From the definition of optimal solutions (Definition 11), this implies that an optimal solution does not exist relative to this structure. □
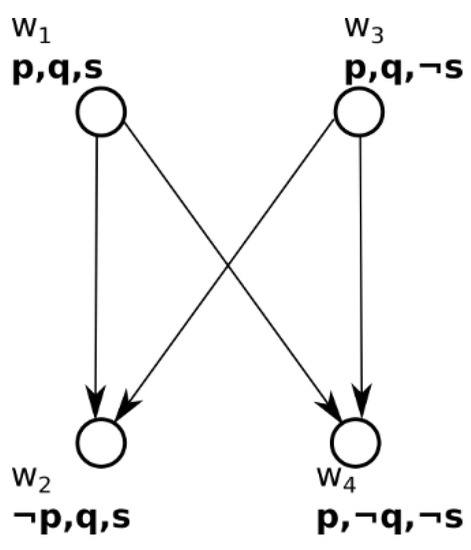
Figure 3.
Incomparable worlds.
Example 4.
Let be the set of possible worlds, where w1 = System A, w2 = System B, w3 = System C, and w4 = System D. Let us assume that the following propositions are in consideration.
p: The system has cost less than $10M
q: The system has capability X
s: The system is eco-friendly
Let us say that the decision-maker has the following preferences:
Equation (13) means that the decision-maker prefers worlds where p is true. Equation (14) means that the decision-maker prefers worlds where q is true. These preferences are satisfied by the structure represented graphically in Figure 3. In Figure 3, worlds w1 and w2 and worlds w3 and w2 are comparable based on the truth values of propositions p, whereas worlds w3 and w4 and worlds w1 and w4 are comparable based on the truth value of proposition q. However, worlds w1 and w3 are incomparable with each other. For a case like this, the betterness relation is a partial order that allows for incomparability, i.e., no arrows exist between these worlds as shown in Figure 3. In this case, worlds w1 and w3 are preferred over worlds w2 and w4, respectively, as shown by the arrows in Figure 3, but the decision-maker cannot compare worlds w1 and w3, which leads to no decision.
Stakeholders may express preferences over desired characteristics of the system through targets, goals, and preferred directions on certain attributes. We will see how the different types of preferences in systems engineering impact the solution space—Theorems 4 and 5.
Theorem 4.
Target-oriented preferences may constrain the solution space.
Proof.
To prove that target-oriented preferences may constrain the solution space, it is sufficient to prove that the cardinality of the set of solutions satisfying these target-oriented preferences is less than the cardinality of the original solution space in at least one circumstance. Let be a target-oriented proposition in . means that the stakeholder prefers worlds where holds. Let be a non-empty finite set of all states/worlds. Let be the set of all worlds where holds. There are three possible outcomes here—either (1) is true at all worlds in S, (2) is false at all worlds in S, or (3) is true at a proper subset of S. In the first two cases, the target-oriented preference, , neither requires nor precludes any edges in structures that satisfy any set of preferences to which it belongs. In the third case, however, any structure that satisfies must have an edge from worlds where is true to those where it is false. This in turn guarantees that the worlds where is false cannot be maximal, and thus, the cardinality of the set of acceptable solutions has decreased . □
Example 5.
The same examples used before to demonstrate absolute and comparative preferences can be applied here to see how the solution space may get constrained due to the presence of target-oriented preferences.
Theorem 5.
Design-dependent preferences will always constrain the solution space.
Proof.
Let be the set of all distinct propositions that the stakeholder has preference on. Let be a design-dependent proposition. means that the stakeholder prefers worlds where holds. By Definition 17, design-dependent preferences are specified directly in terms one or more aspects of the solution. Let be a non-empty finite set of all worlds. Let be the set of all worlds where holds. Assuming that there are other alternatives for , the cardinality of the set is always less than the cardinality of the set , i.e., . This implies that the solution space reduces in size, in other words gets constrained, due to specifying such a design-dependent preference. □
Example 6.
Let us consider a satellite with a propulsion subsystem. For simplicity, let us assume that the solutions of the propulsion subsystem are defined using the following design variables: Propulsion type, Propellant type, and Propellant tank material type. The solution space is denoted by where are vectors defining the design of the propulsion subsystem. For example, = [Liquid propulsion, Hydrazine, carbon fibre], =[Solid propulsion, Composite solid propellant, Al alloy], etc. The decision-maker has several alternatives with multiple combinations of the variables defined above.
Let p: The system has liquid propulsion subsystem
Assuming that the decision-maker has the following preferences as in Equation (15), now the “acceptable” solution space is narrowed down to the worlds (or alternatives) with only liquid propulsion system.
Definition 20 (Satisfiability).
A formula is satisfiable if there exists some structure M and some state for M such that [45,74,76,77]. A set of formulas is satisfiable if and only if there exists some structure M and some state for M such that [45,74,76,77]. This formal notion of satisfiability will be used in this article to determine consistency in the elicited stakeholder preference statements.
Definition 21 (Consistency in preferences).
An agent has a consistent preference base (definition 19) if and only if there exists a structure and a world such that
During elicitation, it is possible that the elicited stakeholder preferences may contradict each other. While each preference statement may hold good independent of the others, the set is said to be consistent only if they can hold good in relation to one another. It is highly unlikely to achieve a meaningful outcome with inconsistent preference statements. For instance, consider the following statements: Stakeholder prefers high SNR to low mass; Stakeholder prefers high resolution to high SNR; Stakeholder prefers low mass to high resolution. We can observe that it is impossible for all the three statements to be true collectively. In order for a set to be consistent, it must be possible for all the premises in the set to be true collectively. In our context, any contradictory statements will need to be abandoned or modified. The sort of consistency discussed so far corresponds to the formal notion of satisfiability (Definition 20). That is, for the set of stakeholder preferences to be consistent, all the preference statements in the set that are expressed in the formal logic have to be satisfiable simultaneously. Theorems 6 and 7 deal with the effect of an inconsistent PB on the solution space.
Theorem 6.
An inconsistent preference base results in no acceptable solutions.
Proof.
By definition, an inconsistent preference base PB is one for which there does not exist a structure and world that satisfies PB. That is, the set of all structures and such that is empty. Let be the set of maximal elements, i.e., acceptable solutions, that is the subset of worlds in the structure that describes the decision problem. These worlds satisfy the conjunction of the statements in the preference base. If PB is inconsistent, the set of acceptable solutions that satisfy PB is empty for every structure M, and so empty for . □
Theorem 6 emphasizes the need to check for consistency in the preference base before the beginning of the design process. During elicitation, it is possible to have preference statements that contradict each other. As proved in Theorem 6, proceeding with such conflicting preferences will ultimately result in no solutions, leading to the need for iterations later in the lifecycle, which results in schedule delays and cost overruns. With the provided formalism, a consistency check can be made very early in the lifecycle to ensure that solutions will exist.
Large-scale complex engineered systems are developed by multi-agent organizations over a period of many years. During the development time, factors that are external and internal to the organization affect how the system is realized. For example, an announcement or a broad directive from the government, policy changes in the organization, market demand fluctuations, competition, unexpected time-critical needs due to war, natural disasters, energy crises, etc., are some of the factors that affect the stakeholder preferences, which in turn affect the chosen system. The NASA systems engineering consortium and INCOSE have emphasized through a postulate that a change in stakeholder expectations is inevitable in a systems engineering context and must be accounted for during the system lifecycle [80]. Theorem 7 discusses a similar message as the postulate in the white paper.
Theorem 7.
A change (update, addition, or deletion of preference statements) in the stakeholder preference base requires a new consistency check.
Proof.
It is taken for granted that one always wants a solution to exist, and therefore, it is necessary to check for consistency whenever it may fail to obtain. Assume that stakeholder preferences are consistent and not tautologous (i.e., their conjunction is not a logical truth). Assume that changes to the stakeholder preferences always involve the addition of a self-consistent set of sentences or replacement of a proper subset of sentences with a self-consistent set or some combination of the two. Then it suffices to show that the operation of addition or replacement can result in contradiction.
It is always possible through replacement of a non-empty, non-tautologous proper subset of sentences in a consistent set with a new set that is itself consistent to obtain an inconsistent set . Let be any non-empty subset of sentences of that is not tautologous. Necessarily, is consistent because is. Let be the negation of the single sentence that is the conjunction of every sentence in . Then for any model and world , iff . Consequently, there can be no such that .
Similarly, the addition of the single sentence that is the negation of the conjunction of all sentences in renders the new set unsatisfiable and thus inconsistent. It is therefore always possible to create an inconsistent set of sentences through the replacement or addition (or both) of a consistent set. □
In Theorem 7, it was proved that it is always possible to create an inconsistent PB through any changes (update, addition and/or deletion) in the sentences. Even a simple addition of a new preference statement in PB might result in an inconsistent PB. In Theorem 6, it was proved that an inconsistent PB results in no acceptable solutions. Therefore, such a simple addition of a new preference statement in PB can result in no acceptable solutions. Since changes in PB are sometimes unavoidable due to the external and internal factors discussed before, this theorem implies that one needs to check for consistency again to ensure that any acceptable solutions exist, when any changes are made to PB.
4. Discussion
The various aspects involved in the stakeholder preference problem include elicitation, representation, and communication of stakeholder preferences. Theorems 2 and 3 discuss the impact of the mathematical structure (betterness relation) of preferences on the solution space. The mathematical structure has to do with how the preferences are elicited from the stakeholder. For example, the elicited stakeholder preference base may consist of incomparable attributes resulting in no optimal solutions, as opposed to a fully comparable set of attributes in the preference base that leads to optimal solutions. Incomparable attributes may exist due to lack of knowledge or no possible way to compare certain attributes. Theorems 2 and 3 imply that during the stages of elicitation, engineers can have a discussion with the stakeholders on the kind of outcomes they can expect based on the structure of the preferences. Stakeholders and the engineers can engage in a conversation to resolve such incomparability to allow for the betterness relation to be a total order so that optimal solutions can be achieved.
Theorems 4 and 5 discuss how different preference types impact the solution space. It can be seen that both design-dependent and target-oriented preferences constrain the solution space. Objective-oriented preferences, on the other hand, do not constrain the solution space since only preferred directions in the solution space are specified, which aid in identifying optimal solutions.
Theorem 6 emphasizes the need to obtain consistent preferences from the stakeholder during elicitation in order to have meaningful and optimal solutions. Traditional requirements-based systems engineering practices lack a mathematically rigorous method of checking for conflicts. Oftentimes, design is carried forward with conflicting requirements, ultimately resulting in stakeholder needs not being satisfied. In these traditional methods, there is no easy way to identify if conflicts exist or not. In this paper, we have defined a preference base (PB) as the set of all stakeholder preference statements. We have further defined what a consistent preference base looks like and have proved (Theorem 6) that an inconsistent preference base results in no solution. This has significant implications for combating schedule delays and cost overruns in that, if stakeholder preferences are represented using the formalism provided in the paper, one can tell if any solutions exist even before the process of design.
Theorem 7 tells us that, when any changes are made to the preference base of the stakeholder, one needs to evaluate consistency again to determine if any solutions exist. One of the postulates identified by the NASA Systems Engineering consortium and INCOSE [80] is “Stakeholder needs can change and must be accounted for over the system lifecycle”. Due to the long development time, it is inevitable that the stakeholder preferences change due to internal and external factors (e.g.,: announcement or a broad directive from the government, policy changes in the organization, market demand fluctuations, competition, unexpected time-critical needs due to war, natural disasters, energy crisis, etc.). Theorem 7 emphasizes that whenever a change (addition/deletion/updates in preference statements) in stakeholder preferences is encountered, past solutions that the stakeholder preferred may no longer hold. This will potentially lead to project delays and/or cost overruns.
The delays in schedule and cost overruns, which often lead to the cancellation of projects altogether, are some of the fundamental problems associated with the development of LSCES. The formal mathematical representation of stakeholder preferences and the relationships between preferences and the solution space studied in this paper enable the creation of a consistent preference base from the beginning of the design process and provide both the stakeholders and the system designers a means for understanding the impact of the preference base on the design solutions. This approach, with its foundations grounded in mathematical theory, can help in reducing the delays associated with the rework of requirements, integration problems, and system redesign due to the inconsistencies in stakeholder preferences at later stages in the system design cycle. A significant amount of time and money can be saved in this process, thus enabling the realization of systems faster and cheaper.
5. Conclusions and Future Work
Although recent work on model-based requirements [81] and value models continues to emphasize the need for mathematical rigor in SE, there is still a lack for a formalism that can enable direct and rigorous representation of stakeholder preferences, facilitate evaluation of consistency in preferences, and enable distributed decision-making in a multi-agent organization. This article moves towards a holistic model-centric approach for preference representation and communication. In this article, formal definitions are provided for the different types of stakeholder preferences that may be encountered in the development of large-scale complex engineered systems. These formal definitions were formulated using a modal preference logic [43] that was developed based on epistemic modal logic [45,46]. A definition for consistent/inconsistent preferences was also provided. A summary of key definitions is provided in Table 3.

Table 3.
Key definitions.
In addition to the definitions, the article provides fundamental theorems that help improve the understanding of the relationship between stakeholder preferences and the solution space. A high-level summary of the theorems and their implications is provided in Table 4. The formal definitions provided in this paper for the different types of preferences and the various elements of the proposed preference logic establish rigor in theory for systems engineering preferences. The benefits of this work include enabling common understanding among engineers and preventing misinterpretations and, ultimately, enabling rigorous communication of stakeholder preferences for decision-making in a multi-agent organization. Although engineers may be heuristically familiar with these types of preferences, formally dividing them into categories give engineers a better understanding of the outcomes that may be expected from these different stakeholder preference types.

Table 4.
Theoretical Contributions.
In addition to the stakeholder, the development of engineered systems involves a number of key decision-makers, who are also subject matter experts, making decisions across the hierarchy. Therefore, it is crucial to consider the knowledge of these individuals, in addition to the stakeholder preferences, in order to make system-wide consistent decisions. Future work will focus on creating a formal logic framework that can handle both stakeholder preferences and knowledge of other entities in a multi-agent organization. Some potential future directions include:
- How can we represent domain knowledge of engineers in a formal manner?
- What is the impact of the knowledge structure on the solution space?
- How can one formally accommodate for changes in stakeholder preferences?
- How does a change in preference base affect the knowledge of engineers?
- Issue of consistency in the knowledge base.
- Issue of consistency between preference and knowledge bases.
- A mathematical framework that can aid in resolving incomparability.
- How can we leverage modal preference logic in formulating value functions?
- Another future direction is a study involving multiple stakeholders in a game theoretic context.
Author Contributions
Conceptualization, H.K.; methodology, H.K. and B.J.; writing—original draft preparation, H.K., B.L.M., and B.J.; writing—review and editing, G.V.B., B.L.M., and B.J.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- United States Department of Defense. Technology and Logistics. In Performance of the Defense Acquisition Systems: 2016 Annual Report; Defense Pentagon: Washington, DC, USA, 2016. [Google Scholar]
- Simpson, T.W.; Martins, J.R. Multidisciplinary design optimization for complex engineered systems: Report from a national science foundation workshop. J. Mech. Des. 2011, 133, 101002. [Google Scholar] [CrossRef]
- Paul, D.C. Report on the Science of Systems Engineering Workshop. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Bloebaum, C.L.; Collopy, P.; Hazelrigg, G.A. NSF/NASA Workshop on the Design of Large-Scale Complex Engineered Systems—From Research to Product Realization. In Proceedings of the 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, IN, USA, 17–19 September 2012. [Google Scholar]
- DARPA/NSF. DARPA/NSF Systems Engineering and Design of Complex Aerospace Systems Workshop; DARPA/NSF: Arlington, VA, USA, 2009.
- Collopy, P. Final Report: National Science Foundation Workshop on the Design of Large Scale Complex Systems; National Science Foundation: Alexandria, VA, USA, 2011. [Google Scholar]
- Hazelrigg, G.A. Fundamentals of Decision Making for Engineering Design and Systems Engineering; Pearson Education, Inc.: New York, NY, USA, 2012. [Google Scholar]
- Abbas, A.E.; Howard, R.A. Foundations of Decision Analysis; Pearson Higher Education: New York, NY, USA, 2015. [Google Scholar]
- Blanchard, B.S.; Fabrycky, W.J.; Fabrycky, W.J. Systems Engineering and Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1990; Volume 4. [Google Scholar]
- Wasson, C.S. System Engineering Analysis, Design and Development: Concepts, Principles and Practices; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- NASA. NASA Systems Engineering Handbook; Volume NASA/SP-2007-6105, Rev1; NASA: Washington, DC, USA, 2007.
- Buede, D.M. The Engineering Design of Systems: Models and Methods; John Wiley & Sons: New York, NY, USA, 2009; Volume 55. [Google Scholar]
- NDIA Systems Engineering Division and Software Committee. Top Software Engineering Issues in the Defense Industry. 2006. Available online: https://ndiastorage.blob.core.usgovcloudapi.net/ndia/2006/systems/Wednesday/rassa6.pdf (accessed on 12 December 2019).
- National Defense Industrial Association Systems Engineering Division. Top Five Systems Engineering Issues in Defense Industry. 2003. Available online: https://www.ndia.org/-/media/sites/ndia/divisions/systems-engineering/studies-and-reports/ndia-top-se-issues-2016-report-v7c.ashx?la=en. (accessed on 12 December 2019).
- Collopy, P.D.; Hollingsworth, P.M. Value-Driven Design. J. Aircr. 2011, 48, 749–759. [Google Scholar] [CrossRef]
- Kannan, H.; Mesmer, B.; Bloebaum, C.L. Increased System Consistency through Incorporation of Coupling in Value-Based Systems Engineering; Systems Engineering (INCOSE): Hoboken, NJ, USA, 2015; Under Review. [Google Scholar]
- Mesmer, B.L.; Bloebaum, C.L.; Kannan, H. Incorporation of Value-Driven Design in Multidisciplinary Design Optimization. In Proceedings of the 10th World Congress of Structural and Multidisciplinary Optimization (WCSMO), Orlando, FL, USA, 19–24 May 2013. [Google Scholar]
- Cheung, J.; Scanlan, J.; Wong, J.; Forrester, J.; Eres, H.; Collopy, P.; Hollingsworth, P.; Wiseall, S.; Briceno, S. Application of Value-Driven Design to Commercial Aero-Engine Systems. In Proceedings of the 10th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Fort Worth, TX, USA, 13–15 September 2010. [Google Scholar]
- Claudia, M.; Price, M.; Soban, D.; Butterfield, J.; Murphy, A. An Analytical Study of Surplus Value using a Value Driven Design Methodology. In Proceedings of the 11th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference, Virginia Beach, VA, USA, 20–22 September 2011. [Google Scholar]
- Collopy, P.; Poleacovschi, C. Validating Value-Driven Design. In Proceedings of the Third International Air Transport and Operations Symposium, Delft, The Netherlands, 18–20 June 2012; IOS Press: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hollingsworth, P. An Investigation of Value Modelling for Commercial Aircraft. In Proceedings of the Second International Air Transport and Operations Symposium, Delft, The Netherlands, 28–29 March 2011; IOS Press Inc.: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Bhatia, G.; Mesmer, B. Integrating Model-Based Systems Engineering and Value-Based Design with an NEA Scout Small Satellite Example. In Proceedings of the AIAA SPACE and Astronautics Forum and Exposition, Orlando, FL, USA, 12–14 September 2017. [Google Scholar]
- Miller, S.W.; Simpson, T.W.; Yukish, M.A.; Stump, G.; Mesmer, B.L.; Tibor, E.B.; Bloebaum, C.L.; Winer, E.H. Toward a Value-Driven Design Approach for Complex Engineered Systems Using Trade Space Exploration Tools. In Proceedings of the ASME 2014 International Design Engineering Technical Conference & Computers and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014. [Google Scholar]
- Neumann, L.J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1947. [Google Scholar]
- Von Wright, G.H. The Logic of Preference Reconsidered. Theory Decis. 1972, 3, 1401–1469. [Google Scholar] [CrossRef]
- Von Wright, G.H. The Logic of Preference; Edinburgh University Press: Edinburgh, UK, 1963. [Google Scholar]
- Moutafakis, N.J. The Logics of Preference: A Study of Prohairetic Logics in Twentieth Century Philosophy; Springer Science & Business Media: New York, NY, USA, 2012; Volume 14. [Google Scholar]
- Hansson, S. Preference Logic in Handbook of Philosophical Logic; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Hansson, S.O. Preference-based deontic logic (PDL). J. Philos. Log. 1990, 19, 75–93. [Google Scholar] [CrossRef]
- Van Benthem, J.; Liu, F. Dynamic logic of preference upgrade. J. Appl. Non Class. Log. 2007, 17, 157–182. [Google Scholar] [CrossRef]
- Liu, F. Von wright’s “the logic of preference” revisited. Synthese 2010, 175, 69–88. [Google Scholar] [CrossRef]
- Van Benthem, J.; van Otterloo, S.; Roy, O. Preference Logic, Conditionals and Solution Concepts in Games; University of Amsterdam: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Lang, J. Logical Representation of Preference: A Brief Survey. In Decision Theory and Multi-Agent Planning; Springer: Berlin/Heidelberg, Germany, 2006; pp. 65–88. [Google Scholar]
- Hansson, B. Fundamental axioms for preference relations. Synthese 1968, 18, 423–442. [Google Scholar] [CrossRef]
- Hansson, S.O. A new semantical approach to the logic of preference. Erkenntnis 1989, 31, 1–42. [Google Scholar] [CrossRef]
- Chisholm, R.M. The intrinsic value in disjunctive states of affairs. Noûs 1975, 295–308. [Google Scholar] [CrossRef]
- Chisholm, R.M.; Sosa, E. On the Logic of “Intrinsically Better”. Am. Philos. Q. 1966, 3, 244–249. [Google Scholar]
- Quinn, P.L. Improved foundations for a logic of intrinsic value. Philos. Stud. 1977, 32, 73–81. [Google Scholar] [CrossRef]
- Pigozzi, G.; Tsoukias, A.; Viappiani, P. Preferences in artificial intelligence. Ann. Math. Artif. Intell. 2016, 77, 361–401. [Google Scholar] [CrossRef]
- Wilson, N. Extending CP-Nets with Stronger Conditional Preference Statements. In Proceedings of the national conferenec on Artificial Intelligence, San Jose, CA, USA, 25–29 July 2004; pp. 735–741. [Google Scholar]
- Boutilier, C.; Brafman, R.I.; Domshlak, C.; Hoos, H.H.; Poole, D. CP-nets: A tool for representing and reasoning withconditional ceteris paribus preference statements. J. Artif. Intell. Res. 2004, 21, 135–191. [Google Scholar] [CrossRef]
- Allen, T.E. CP-nets: From theory to practice. In Proceedings of the International Conference on Algorithmic Decision Theory, Lexington, KY, USA, 27–30 September 2015. [Google Scholar]
- Van Benthem, J.; Girard, P.; Roy, O. Everything else being equal: A modal logic for ceteris paribus preferences. J. Philos. Log. 2009, 38, 83–125. [Google Scholar] [CrossRef]
- Divers, J. Possible Worlds; Routledge: Abingdon, UK, 2006. [Google Scholar]
- Ditmarsch, H.; Halpern, J.Y.; van der Hoek, W.; Kooi, B.P. Handbook of Epistemic Logic; College Publications: London, UK, 2015. [Google Scholar]
- Fagin, R.; Halpern, J.Y.; Moses, Y.; Vardi, M. Reasoning about Knowledge; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Keeney, R.L. Value-Focused Thinking: A Path to Creative Decisionmaking; Harvard University Press: Cambridge, MA, USA; London, UK, 1992. [Google Scholar]
- Abbas, A.E. Foundations of Multiattribute Utility; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Murugaiyan, S.; Kannan, H.; Mesmer, B.L.; Abbas, A.; Bloebaum, C. A comprehensive study on modeling requirements into value formulation in a satellite system application. In Proceedings of the 14th Annual Conference on Systems Engineering Research (CSER 2016), Huntsville, AL, USA, 22–24 March 2016. [Google Scholar]
- Bhatia, G.V.; Kannan, H.; Bloebaum, C.L. A Game Theory approach to Bargaining over Attributes of Complex Systems in the context of Value-Driven Design: An Aircraft system case study. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Kannan, H. An MDO Augmented Value-Based Systems Engineering Approach to Holistic Design Decision-Making: A Satellite System Case Study. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2015. [Google Scholar]
- Kannan, H.; Shihab, S.; Zellner, M.; Salimi, E.; Abbas, A.; Bloebaum, C.L. Preference Modeling for Government-Owned Large-Scale Complex Engineered Systems: A Satellite Case Study. In Disciplinary Convergence in Systems Engineering Research; Springer: Berlin/Heidelberg, Germany, 2018; pp. 513–529. [Google Scholar]
- Kwasa, B.; Kannan, H.; Bloebaum, C.L. Impact of Organization Structure in a Value-based Systems Engineering Framework. In Proceedings of the 2015 ASEM International Annual Conference, Indianapolis, IN, USA, 7–10 October 2015. [Google Scholar]
- Bhatia, G.; Mesmer, B.; Weger, K. Mathematical Representation of Stakeholder Preferences for the SPORT Small Satellite Project. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0708. [Google Scholar]
- Clerkin, J.H.; Mesmer, B.L. Representation of knowledge for a NASA stakeholder value model. Syst. Eng. 2019, 22, 422–432. [Google Scholar] [CrossRef]
- Goetzke, E.D.; Bloebaum, C.L.; Mesmer, B. Value-driven design of non-commercial systems using bargain modeling. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 0134. [Google Scholar]
- Jung, S.; Simpson, T.W.; Bloebaum, C.; Kannan, H.; Winer, E.; Mesmer, B. A value-driven design approach to optimize a family of front-loading washing machines. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016. [Google Scholar]
- Keeney, R.L. Value-Focused Thinking; Harvard University Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Malone, P.; Apgar, H.; Stukes, S.; Sterk, S. Unmanned aerial vehicles unique cost estimating requirements. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–8. [Google Scholar]
- Malone, P.; Wolfarth, L. Measuring system complexity to support development cost estimates. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–13. [Google Scholar]
- Dwyer, M.; Selva, D.; Cameron, B.; Crawley, E.; Szajnfarber, Z. The impact of technical complexity on the decision to collaborate and combine. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–11. [Google Scholar]
- Bearden, D.A. A complexity-based risk assessment of low-cost planetary missions: When is a mission too fast and too cheap? Acta Astronaut. 2003, 52, 371–379. [Google Scholar] [CrossRef]
- Leising, C.J.; Wessen, R.; Ellyin, R.; Rosenberg, L.; Leising, A. Spacecraft complexity subfactors and implications on future cost growth. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–11. [Google Scholar]
- Salado, A.; Nilchiani, R. The Tension Matrix and the concept of elemental decomposition: Improving identification of conflicting requirements. IEEE Syst. J. 2015, 11, 2128–2139. [Google Scholar] [CrossRef]
- Salado, A.; Nilchiani, R. The concept of order of conflict in requirements engineering. IEEE Syst. J. 2014, 10, 25–35. [Google Scholar] [CrossRef]
- Carson, R.S. 1.6. 4 Requirements Completeness: A Deterministic Approach. In INCOSE International Symposium; Wiley Online Library: New York, NY, USA, 1998. [Google Scholar]
- Robertson, S.; Robertson, J. Mastering the Requirements Process: Getting Requirements Right; Addison-Wesley: New York, NY, USA, 2012. [Google Scholar]
- Liu, X.F.; Yen, J. An analytic framework for specifying and analyzing imprecise requirements. In Proceedings of the 18th International Conference on Software Engineering, London, UK, 13–14 May 2014; pp. 60–69. [Google Scholar]
- Salado, A.; Nilchiani, R.; Verma, D. Aspects of a Formal Theory of Requirements Engineering: StaNeholder Needs, System Requirements, Solution Spaces, and RequirementsГ Qualities. Syst. Eng. 2013. submitted. [Google Scholar]
- Van Lamsweerde, A.; Darimont, R.; Letier, E. Managing conflicts in goal-driven requirements engineering. IEEE Trans. Softw. Eng. 1998, 24, 908–926. [Google Scholar] [CrossRef]
- Gervasi, V.; Zowghi, D. Reasoning about inconsistencies in natural language requirements. ACM Trans. Softw. Eng. Methodol. 2005, 14, 277–330. [Google Scholar] [CrossRef]
- Ali, R.; Dalpiaz, F.; Giorgini, P. Reasoning with contextual requirements: Detecting inconsistency and conflicts. Inf. Softw. Technol. 2013, 55, 35–57. [Google Scholar] [CrossRef]
- Van Dalen, D. Logic and Structure; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Gensler, H.J. Introduction to Logic; Routledge: London, UK, 2012. [Google Scholar]
- Pospesel, H. Propositional Logic; Prentice-Hall: Englewood Cliffs, NJ, USA, 1974. [Google Scholar]
- Smullyan, R.R. First-Order Logic; Springer Science & Business Media: New York, NY, USA, 2012; Volume 43. [Google Scholar]
- Blackburn, P.; van Benthem, J.F.; Wolter, F. Handbook of Modal Logic; Elsevier: Amsterdam, The Netherlands, 2006; Volume 3. [Google Scholar]
- McCracken, D.D.; Reilly, E.D. Backus-naur form (BNF). In Encyclopedia of Computer Science, 4th ed.; John Wiley and Sons Ltd.: Chichester, UK, 2003. [Google Scholar]
- Kripke, S. Semantical Considerations of the Modal Logic. 2007. Available online: https://philpapers.org/rec/KRISCO (accessed on 11 December 2019).
- NASA. Systems Engineering Postulates, Principles, Hypotheses. Available online: https://www.nasa.gov/consortium/postulates-principles-hypotheses (accessed on 11 December 2019).
- Salado, A.; Wach, P. Constructing True Model-Based Requirements in SysML. Systems 2019, 7, 19. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).