1. Introduction
Naturally, produced electromagnetic fields (EMF) have existed for millions of years. Examples of natural sources of EMFs include lightning storms and the magnetic field of the Earth itself. However, with the advancement of technology, man has created numerous artificial sources of EMFs arising from our needs (pylons, wireless, broadcasting, mobile telephones, etc.), so the level of electromagnetic radiation to which the world population is subjected has increased. Accordingly, the following issues may arise: If both radiation levels and the number of sources of EMFs are continually increasing, could these radiation sources negatively affect everyone’s health? Should we take preventive measures and implement controls in relation to this issue? These are open questions that, unfortunately and for now, have neither been confirmed nor denied with adequate studies.
However, there are results indicating that active users of mobile phones and computers can show various symptoms including headaches, joint pain, anxiety, dizziness, and even insomnia [
1]. Furthermore, these symptoms are significantly higher in people living near mobile phone base-stations (<300 m), compared to those who live further from these (>300 m) [
2].
In addition, the IARC (International Agency for Research on Cancer) has classified the EMF radio frequency (RF) as “possibly carcinogenic” to humans (a group 2B carcinogen), according to the increased risk in developing glioma (Glioma is a type of brain tumor) associated with the use of mobile phones [
3].
In this sense, because of the high level of concern by the population and the significant media interest in the topic, the first Eurobarometer survey on EMF exposure was conducted in 2006. Eurobarometer is a series of surveys that the Commission European has conducted in EU member states since 1973, in order to follow the evolution of public opinion, and to provide relevant information with which to make decisions and evaluate the perception of citizens on a variety of issues: these include culture, information technology, and the environment.
In this article, we examined the data from Eurobarometer 73.3 June 2010 [
4] corresponding to various aspects of electromagnetic fields in the EU population. The big number of elements involved advise us to investigate different alternatives of statistical treatment and to propose a novel approach based on the general systems theory.
In speaking about cause-effect relationships between variables within a system it is essential to mention the father of general systems theory: Ludwig Von Bertalanffy. In the late 1960s, this author justified the need for a theory that is able to formulate basic principles governing systems from a general perspective, regardless of the nature of the basic elements that compose them, and the relationships between them [
5]. In contrast, classical physics has focused on closed systems, i.e., systems that are considered isolated from the environment around them. We should note that in nature we often find open systems, i.e., systems that do have interaction and feedback with the environment in which they find themselves. Therefore, we need a formal theory that is able to treat this type of system from a global point of view, as a “whole” where the system’s functioning is greater than the sum of its parts. However, it was not until 1975 that M. Mesarovic and Y. Takahara published their General Theory of Systems and grounded the concept of system in the mathematical terms of set theory [
6].
There are authors like Peter M. Senge who claim that, although we can see straight lines of cause–effect relationships (linear causality), reality consists of circles (circular causality) [
7]. In linear causality, when a case appears to produce a certain effect, this effect does not have any influence on the initial cause. In circular causality, a cause has an effect and this effect in turn influences the initial cause, thus forming a loop or a causal circle illustrating the feedback in the system. Whereupon, it seems logical when studying systems in reality that we use a language of relationships based on circular reasoning.
Understanding causality gives the ability to predict results or consequences of certain events in the future. Therefore, one can claim that a representation of a phenomenon is causal if we are able not only to recognize the associations between causes and their effects, but also to describe how we arrived from the causes to the effects.
Now consider the problem that arises when one wants to model a certain system. One can study not only what variables are present and how they are interrelated, but also their behavior and whether it tends toward a particular pattern over time. It is also important to know the limits of the system, how far the relationships develop, and whether the system is independent of other systems.
This idea of circularity along with various concepts related to different branches of mathematics including set theory, systems theory, graph theory and a qualitative version of the theory of discrete chaos, will allow us to model systems. We will conclude that indirect effects present a greater impact on changes in a system than direct effects.
2. Methodology
First, we selected the data of the first domain of the survey, which deals with health and environmental factors. Specifically, respondents in each EU country were asked: to what extent do they believe that various elements (food quality, mobile phone antennas, etc.) can affect your health? Each element is to be a variable to study, and we selected 15 of these variables.
To determine if two pairs of any set of variables are related, we examine a correlation matrix using the IBM SPSS Statistics software v.22 (IBM Corp, Armonk, NY, USA). Depending on our decision concerning the valid correlation threshold, we can determine that there are more or less strongly related pairs. Then, we categorize variables using Microsoft Office Excel 2007. In our study, we used a process to reassign variable values as follows: when the value of a variable was less than the mean, we assigned a 0; when the value was greater than the mean, we assigned a1.
The next step is to use the concept of limiting factor, i.e., examining the direction of the relationship when two variables A and B are correlated. To do this, we must calculate conditional probabilities, so that if (If A is an event within the sample space S of an activity or experiment, the complement of A (denoted ) consists of all outcomes in S that are not in A.), A will be the cause of effect B.
From known pairs of cause-effect relationships, we produce the corresponding directed graph [
8] for each correlation threshold established; from these, we apply the theory of discrete chaos in order to track trends in the system from the attractors found.
3. Attractor of a Complex System
An attractor A of a complex system is a set that will stop all orbits of the variables that are within the basin of attraction C. Since the basin of attraction C always contains the attractor A, we will say that .
Figure 1 shows this concept graphically. As we see, we can imagine the basin of attraction
C as a paraboloid, so that if we choose a variable that is within the basin and follow its orbit, it will go to the bottom of the basin, an area that will lead the rest of the variables’ orbits, i.e., the attractor.
An analytical definition of attractors can be found in [
9,
10,
11,
12,
13]. Attractors are areas that define the seemingly disorganized behavior of the variables and thus are essential for predicting the behavior or trend that a complex system will follow over time. In this paper, they allow us to analyze the implications of electromagnetism for health.
4. Selection of Variables
We chose the domain of the survey related to health and environmental factors for various reasons: it is a domain of the survey that has more variables, so one may achieve more traction in terms of cause-effect relationships; it contains several variables relating to electromagnetic fields; and it may be interesting to analyze the extent to which variables may be related in terms of EMF with the other variables. Respondents were asked the following questions: “Please indicate to what extent you think each of the following affects your health,” where the elements were
- ■
Quality of air outside air (CAE) (The acronyms follow Spanish terms for the variables and are relevant for interpreting Tables).
- ■
Quality of the inside air (CAI).
- ■
Quality of the drinking water (CAP).
- ■
Quality of river and lake water (CAR).
- ■
Landfill (VR).
- ■
Food quality (CAC).
- ■
Chemicals (QMS).
- ■
Living conditions (CDV).
- ■
High voltage lines (LAT).
- ■
Mobile telephone antennae (ATM).
- ■
Mobile telephones (TFM).
- ■
Computers (CPS).
- ■
Household electrical equipment (EEH).
- ■
Noise (RDO).
- ■
Exposure to the sun (EAS).
To carry out the study, we selected all of the above variables, but only used the data for those people who answered “to a large extent” and “to some extent,” and which responded with an affirmative answer.
5. Results
5.1. Correlation Analysis
A correlation matrix between the selected variables was produced using SPSS. For the analysis, we reviewed the table noting those pairs of variables whose correlation coefficients are greater than or equal to 0.7 (
rxy ≥ 0.7). The couple we obtained with
rxy ≥ 0.7 are grouped in
Table 1.
Initially, we know what pairs of variables are related through the correlation coefficient, but do not know which variable causes the other, i.e., we do not know the direction of the relationship.
The concept of a limiting factor is crucial in determining this direction and is based on the concept of conditional probability.
5.2. Development of Directed Graphs
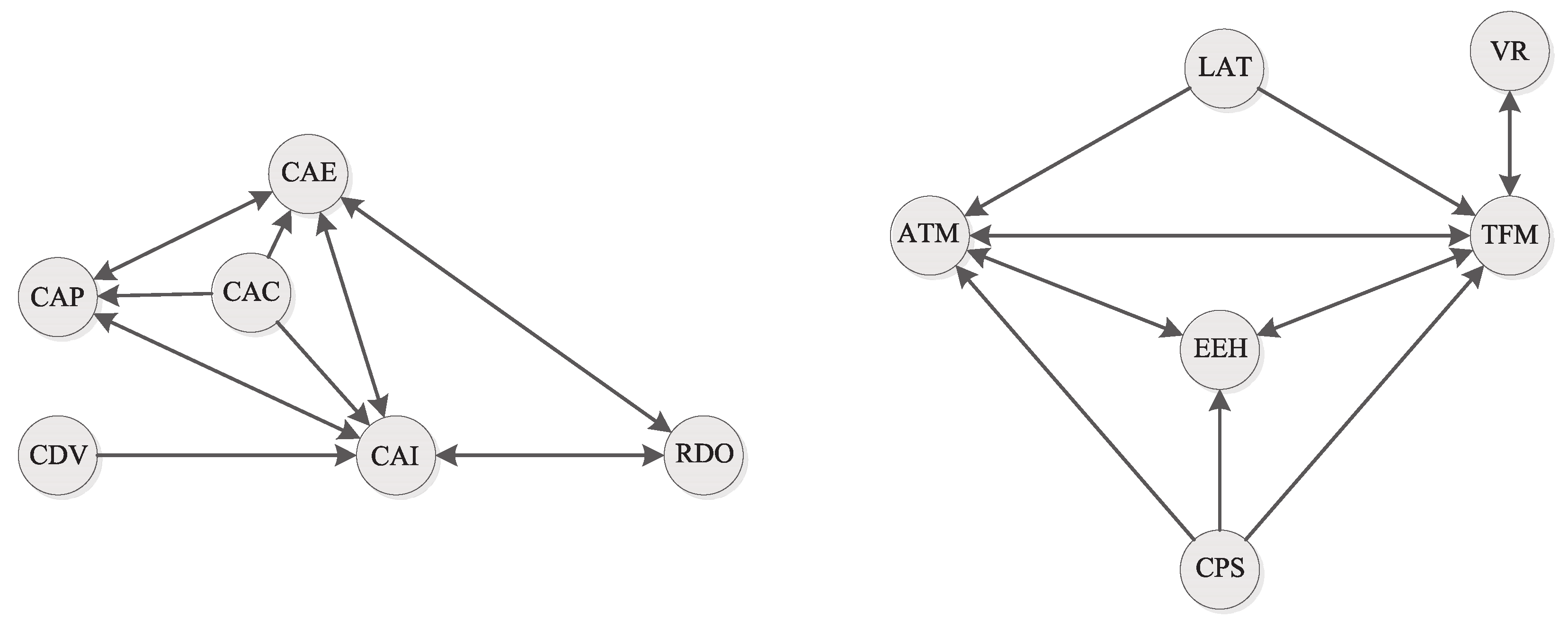
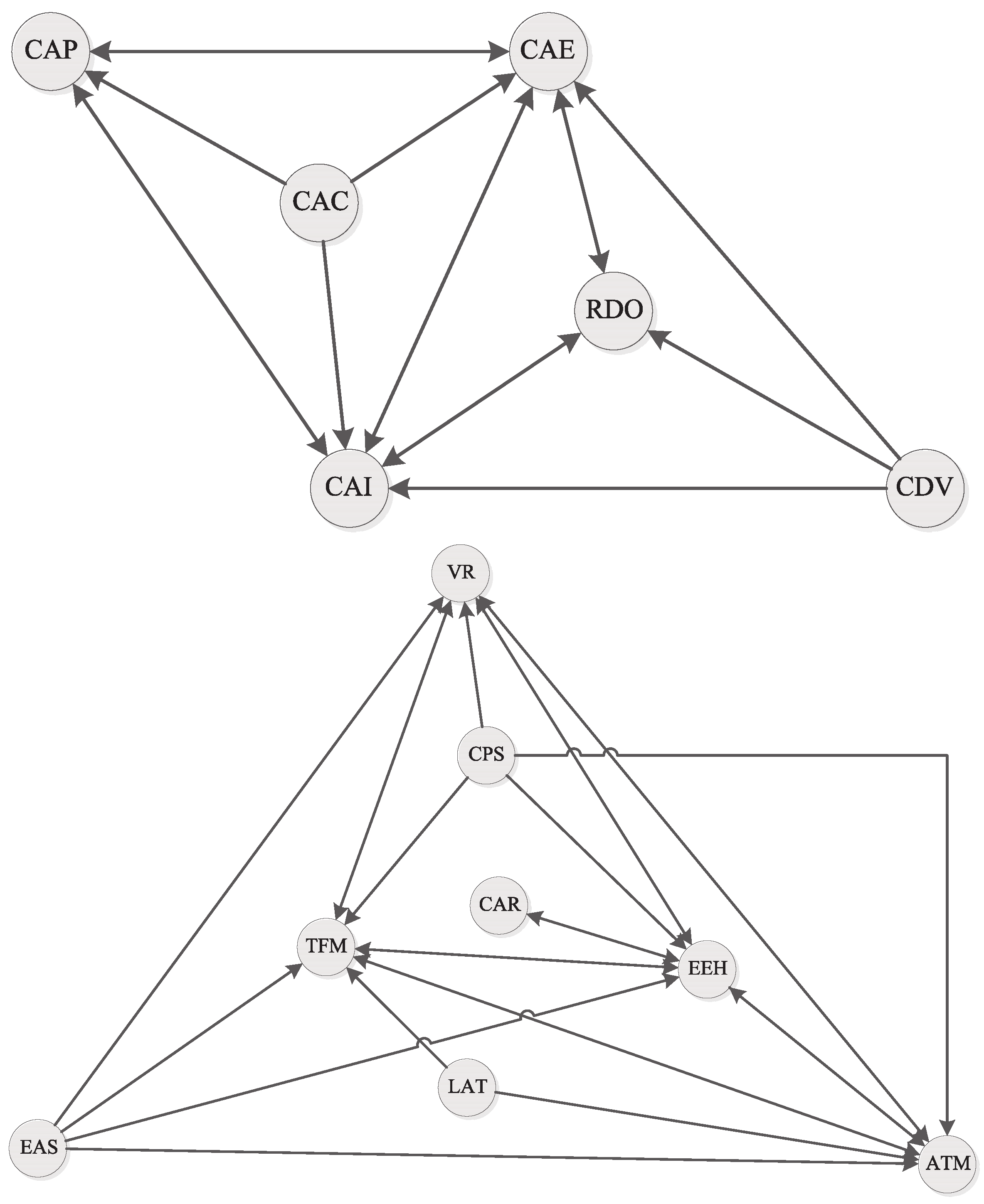
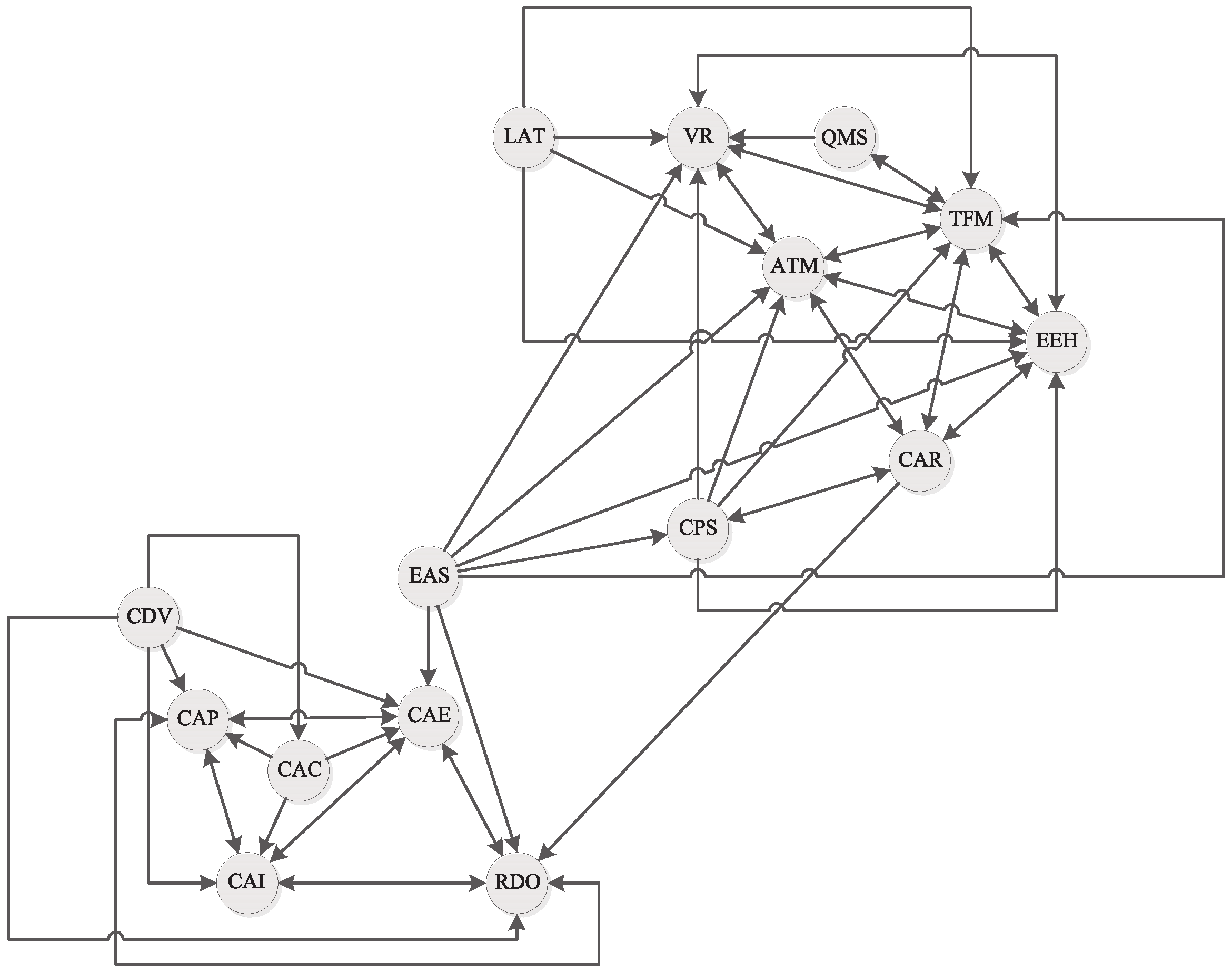
If the correlation coefficient has a lower value, we are being more permissive with the threshold and thus can represent more pairs of cause-effect relationships, and the graph can be more complex. On the contrary, if we increased the correlation coefficient, we are being stricter since only those pairs that have a very high correlation would be represented in the graph. Therefore, we would have fewer relationships and a simpler graph. In the present case, we decided to obtain directed correlation graphs with three thresholds: correlation coefficients greater than or equal to 0.8, 0.75, and 0.7 (We cannot choose a higher correlation value because the requirements would eliminate the edges of the graph and thus the possibility of obtaining attractors.).
The results of these directed graphs with these three correlation thresholds are shown in
Figure 2,
Figure 3 and
Figure 4, respectively.
6. Discussion
First, it is noteworthy that, when the required correlation is lower, we obtain a graph with the highest number of causalities, but the information obtained is also less detailed, as it is more difficult to observe trends in cause-effect relationships in the system.
Analyzing the graph for correlation coefficients greater than or equal to 0.7 (
Figure 4), we can discern that there is a set attractor
A:
where the basin of attraction C is equivalent to the following set:
On this occasion, the basin coincides with the entire system. The identified attractor A does not provide much information, although it links causally the group of variables related to electromagnetism (ATM, TFM, CPS, and EEH) with other variables related to various health factors (VR, QMS, CAR, RDO, CAE, CAP, and CAI).
We can also see that the variable relating to noise (RDO) is the point that connects the sets of electromagnetic variables (upper graph) with the other variables on health factors (bottom graph).
This graph indicates that the evolution of the system practically goes to an attractor set that is almost as large as the entire system, so the interpretation to highlight could be confusing, since it would mean that most of the responses (both in relation to electromagnetic forces and health issues) provided by the European citizens in the survey would be substantially interrelated. In short, we cannot draw a clear conclusion from this graph.
However, if we move to the graph with correlation coefficients greater than or equal to 0.75 (
Figure 3), the two sets that were previously united by the variable RDO have now separated and thus have two independent graphs and, in turn, two different attractors, each corresponding to a graph.
The first subgraph reflects the attractor:
With the basin of attraction,
Therefore, we can understand that the first subgraph (upper subgraph of
Figure 3) relates variables whose nature corresponds only to factors relating to health. In this sense, what the citizens of the European community really value as the most important health factors are the quality of drinking water (CAP), outdoor air quality (CAE), internal air quality (CAI), and noise (RDO).
Continuing with the second subgraph, we find the attractor:
whose basin of attraction would be
This subgraph primarily relates variables with an electromagnetic character, except for the variables concerning water quality in rivers and lakes (CAR) and waste disposal (VR). The attractor A2 explains that the five variables therein have a similar level of concern among these European citizens.
The graphs with the most demanding correlation threshold of greater than or equal to 0.8 are shown in
Figure 2. Again, there are two subgraphs. The first graph shows an attractor set
A3, with a basin of attraction
C3, and both sets are identical to the correlation graph 0.75, i.e.,
A2 and
A3 = C2 = C3.
However, in the second subgraph, there is a considerable loss of cause–effect relationships due to increased correlation, and the disappearance of the variables EAS and CAR can be seen (i.e., exposure to sun and water quality of rivers and lakes, respectively). Thus, the attractor
A4 can be seen below:
Its basin of attraction is as follows:
Despite the changes, the tendency of the system is to remain stable in comparison with the graph whose correlation is 0.75. As a result, we think that these European respondents have made decisions with similar responses depending on the domain of the variables: those related to health and environmental factors, and those focused on electromagnetism.
Thus, although variables appear in the survey in these two areas, the answers to one domain do not appear to influence the other, i.e., the fact that variables appear related to electromagnetism would not affect decisions about the group of variables concerning health factors, and vice versa.
On the other hand, in the subgraph electromagnetism corresponding to the correlation threshold (rxy ≥ 0.8), the variable high voltage lines (LAT) are not part of the attractor and the response to this variable could be the cause of the effects of both ATM and TFM (mobile antennas and mobile phones).
The interpretation of this result would be that, when the respondent answers about how they think power lines will affect them, the answer could be based on the answers about the variables concerning mobile phone antennas and mobile phones. Similarly, the variable concerning computers (CPS) also appears to be due to the effects of mobile phone antennas and mobile phones, in addition to household electrical equipment (EEH).
This reasoning could be also valid for the variable quality of food (CAC) in the subgraph of health factors regarding the variables effecting drinking water quality (CAP), outdoor air quality (CAE), and indoor air quality (CAI).
7. Conclusions
Causal analysis of databases using a qualitative version of chaos theory is an alternative method to statistical procedures, such as principal component analysis or correspondence analysis, widely used in the field of data analysis. The technique used is based on correlations between pairs of variables, as well as in determining conditional probabilities to determine the causal relationships between these pairs. The main advantage of this method compared to traditional statistical methods is that it allows us to understand the tendencies of an apparently chaotic system when we find sets of attractors in it. This enables us to predict the behavior of the system under study in the immediate future, unlike statistical methods, which provide information about the present moment. With respect to the results obtained, we can emphasize that, since we have become increasingly demanding with pairs of causal relationships, as we increase the correlation coefficient threshold, the number of relationships is reduced proportionately, making it possible to distinguish attractors or system trends when it stabilizes over time.
In this sense, we have seen that, for the section of the Eurobarometer database analyzed, European citizens independently valued the variables related to environmental and health factors, compared to those related to the context of electromagnetism. Therefore, respondents did not consider the same level of importance to both sets of variables. One possible explanation could be the lack of information received regarding EMF exposure, that is, they do not really know how to evaluate the harmfulness of EMF for varying levels of exposure. Fortunately, in the case of Spain, we verified that, although electromagnetic fields can become harmful above a certain level of exposure (depending on the frequency band), there is no risk for the population subjected to non-ionizing radiation such as in the RF band, since the levels emitted are well below the limits harmful to the body [
14,
15,
16,
17]. Moreover, we also found significant variables outside the attractors, as in the case of pylons (LAT) or the quality of the food (CAC), whose answers can directly influence the responses of other related variables that are perhaps less important for respondents (ATM, TFM, CAP, CAE, and CAI). Regarding the results of the Eurobarometer study, we verified that the public believes that the sources that generate EMFs are potentially less harmful to one’s health than other sources such as chemicals, food quality, or even the quality of the drinking water. This phenomenon is reflected in our study by the separation of the two subgraphs as possible groups of variables related by their potential danger to health. When the survey focused exclusively on EMF sources, the pylons and mobile phone antennas were what most concerned respondents (35% and 33%, respectively). However, responses concerning mobile phones only concerned 26% of respondents, being one of the closest devices that radiate EMF. Indeed, if we compare the survey results with those of our study, high voltage towers (LAT) directly influence the responses in relation to mobile phone antennas (ATM).
In general, the objectives of the article have been met: a database of special importance in the context of the study of electromagnetism and health was located and studied, and the mathematical tools necessary to carry out the causal analysis were explained. We selected the most relevant variables of the database and showed their causal relationships using specific software (SPSS and Excel), and finally we analyzed the results by means of cause-effect relationships, orbits, and sets of attractors. Currently, there is an exponential and unstoppable growth in the generation, storage, and processing of data. This has produced a global revolution in the world of business and companies—so much so that the volume of data is growing at a rate faster than the infrastructure can manage.