A Research on Active Control to Synchronize a New 3D Chaotic System

Abstract

This paper presents the robust synchronization problem of a 3D chaotic system by using the active control technique. Based on the Gershgorin theorem and Routh-Hurwitz criterion, sufficient algebraic conditions are derived to design a linear controller gain matrix. The conditions are then applied for the robust stability of the synchronization error dynamics in the presence of an unknown bounded smooth external disturbance. The proposed active control strategy with a suitable computation of the linear controller gain matrix is simple in design and establishes fast convergence rates of the synchronization error signals. Numerical simulation results further verified the analytical results.

1. Introduction

For the last two decades, chaos synchronization has been widely explored in various research fields [1,2,3]. The ever present demand for secure communication is one of the foremost form of motivation for studying chaos synchronization [4,5,6]. Various linear and nonlinear control techniques have been developed to carry out synchronization behavior. Some of these include, adaptive control [7], linear error state feedback control [8], backstepping method [9], active control [10], sliding mode control [11], and nonlinear control [12] are worth citing here, among others.

Recently, active control strategies have received considerable interest among many researchers due to the simple implementation for chaotic synchronization. Using the active control algorithm, Agiza and Yaseen [13] presented the synchronization of two identical Rossler and two identical Chen chaotic systems. Lei et al. [14] reported the synchronization problem of two identical nonlinear gyros using the active control based on the Routh-Hurwitz criterion and Lyapunov stability theory. Ucar et al. [15] utilized the active control technique for chaos synchronization in RCL-shunted Josephson function. Njah and Vincent [16] investigated the synchronization and anti-synchronization of two identical extended BVP chaotic oscillators by using the generalized active control method. Based on the Routh-Hurwitz criterion and Lyapunov stability theory and using the active control strategy, Shahzad and Ahmad [17] showed an experimental study of synchronization and anti-synchronization for the spin orbit problem of Enceladus. Recently, Ahmad et al. [10], addressed the synchronization problem of two identical and two non-identical chaotic systems using the active control technique based on the Lyapunov stability theory. A modification has been made based on the Lyapunov stability theory [18] for the globally, asymptotically-stable synchronization.

However, the finding of these studies [10,13,14,15,16,17] guarantee the asymptotic stability of the resulting synchronization error dynamics by allocating negative eigenvalues of the coefficient matrix in the closed-loop system that simply obeys the Routh-Hurwitz criterion. Convergence rates of the synchronization error signals depend on the numeric values of the controller gain coefficients. In real-life applications, selecting high controller gain coefficients may lead to automatic signal saturations and the two coupled chaotic/hyperchaotic systems may lose synchronization stability completely. In fact, the above notable results [10,13,14,15,16,17] affect each other mutually and need a systematic approach to compute suitable linear controller gains. In addition, the chaotic systems are considered free of the unknown external disturbance.

In this article, based on the Gershgorin theorem [19] and Routh-Hurwitz criterion [20] and using the active control strategy, a generalized approach is proposed to compute a suitable linear controller gain matrix that establishes globally asymptotical synchronization under the effect of unknown external disturbance.

There are three main aims for this paper. The first aim is to study the synchronization problem of a newly reported 3D chaotic system [21] in the presence of an unknown external disturbance. The second aim is to discuss the active control method for the synchronization of two identical and two non-identical 3D chaotic systems. The third aim is to derive analytically the sufficient algebraic conditions to compute a suitable linear control gain matrix that guarantees globally asymptotical stability of the closed-loop system. Two illustrative examples are given to verify the robustness and the performance of the proposed approach; complete synchronization between two identical chaotic systems [21], and the generalized synchronization between the chaotic system [21] and the Liu-Chen chaotic system [22].

The rest of the paper is organized as follows: In Section 2, the problem statement is given and derived the generic criterion to construct a proper linear control gain matrix using the active control technique. In Section 3, description of a new 3D chaotic system [21] is briefly described and synchronization behavior of two identical chaotic systems [21] are given, followed by the analysis of synchronization between the new chaotic and the Liu-Chen chaotic systems in Section 4. The paper concludes in Section 5.

2. Problem Statement and a Theory for the Proposed Active Control Strategy

Let us consider a drive-response chaotic system synchronization scheme is described as follows:

$$\{\begin{array}{ll}\text{Drive}\hspace{0.17em}\text{System}:& \dot{X}\left(t\right)=X\left(t\right)A_1+F\left(X\left(t\right)\right)+\Delta \left(t\right)\\ \text{Response}\hspace{0.17em}\text{System}:& \dot{Y}\left(t\right)=Y\left(t\right)A_2+G\left(Y\left(t\right)\right)+\mathsf{\Omega }\left(t\right)+\mathit{\delta }\left(t\right)\end{array}$$

(1)

where $X\left(t\right)={\left[x_1\left(t\right),\hspace{0.17em}{x}_2\left(t\right),\dots ,x_n\left(t\right)\right]}^T\in R^n \text{and} Y\left(t\right)={\left[y_1\left(t\right),\hspace{0.17em}{y}_2\left(t\right),\dots ,y_n\left(t\right)\right]}^T\in R^n$ are the state vectors, $F\left(X\left(t\right)\right) \text{and} G\left(Y\left(t\right)\right)$ are the nonlinear bounded smooth functions, and $A_1,A_2\in R^{n\times n}$ are the matrices of the chaotic drive and response systems parameters alternatively, $\Delta \left(t\right) \text{and} \mathsf{\Omega }\left(t\right)$ are the vectors of the unknown bounded smooth external disturbances present in the drive and response systems, respectively and $\delta \left(t\right)\in R^n$ is the control input to be designed later.

Assumption 1. 

It is assumed that the unknown external disturbances are norm-bounded [2].

$$\left|{\Delta }_i\left(t\right)\right|\le a_i^n,\left|{\mathsf{\Omega }}_i\left(t\right)\right|\le b_i^n \text{and} \left|{\Delta }_i\left(t\right)-{\mathsf{\Omega }}_i\left(t\right)\right|\le {\mathsf{\Phi }}_i i=1,2,\dots ,n$$

(2)

where $a_i^n,b_i^n \mathrm{and} {\mathsf{\Phi }}_i$ are positive constants.

Definition 1. 

Let us define the synchronization error system as follows:

$$\Vert \mathit{e}\left(t\right)\Vert =\Vert Y\left(t\right)-X\left(t\right)\Vert ,\hspace{0.17em}i=1,2,...n$$

(3)

where $\Vert \hspace{0.17em}·\hspace{0.17em}\Vert$ represents the Euclidean norm in $R^n$.

From the drive-response system arrangement Equation (1), it follows that:

$$\begin{array}{ll}& \dot{\mathit{e}}\left(t\right)=Y\left(t\right)A_2-X\left(t\right)A_1+G\left(Y\left(t\right)\right)-F\left(X\left(t\right)\right)+\mathsf{\Omega }\left(t\right)-\Delta \left(t\right)+\mathit{\delta }\left(t\right)\\ \Rightarrow & \dot{\mathit{e}}\left(t\right)=A_3\mathit{e}\left(t\right)+H\left(X\left(t\right),Y\left(t\right),\mathit{e}\left(t\right)\right)+\mathsf{\Omega }\left(t\right)-\Delta \left(t\right)+\mathit{\delta }\left(t\right)\\ \Rightarrow & \dot{\mathit{e}}\left(t\right)=A_3\mathit{e}\left(t\right)+H\left(X\left(t\right),Y\left(t\right),\mathit{e}\left(t\right)\right)+\left|\mathsf{\Omega }\left(t\right)-\Delta \left(t\right)\right|+\mathit{\delta }\left(t\right)\end{array}$$

(4)

where $H\left(X\left(t\right),Y\left(t\right),e\left(t\right)\right)=G\left(Y\left(t\right)\right)-F\left(X\left(t\right)\right)+\left(A_2-{\overline{A}}_2\right)Y\left(t\right)-\left(A_1-{\overline{A}}_1\right)X\left(t\right)$ is the function of residual terms and ${\overline{A}}_2-{\overline{A}}_1=A_3$ is the (n × n) coefficient matrix of the error system Equation (4) [23].

If $A_1=A_2$, then, $X\left(t\right)\hspace{0.17em}\text{and}\hspace{0.17em}Y\left(t\right)$ are the states of two identical chaotic systems and if, $A_1\ne A_2$, then, $X\left(t\right)\hspace{0.17em}\text{and}\hspace{0.17em}Y\left(t\right)$ are the states of two different chaotic systems.

Corollary 1. 

The two coupled chaotic systems Equation (1) are globally asymptotically synchronized in a sense:

$$\underset{t\to \infty }{\lim }\Vert \mathit{e}\left(t\right)\Vert =\underset{t\to \infty }{\lim }\Vert Y\left(t\right)-X\left(t\right)\Vert =0,\hspace{0.17em}\text{for} \text{all}\hspace{0.17em}{e}_i(0)\in R^n$$

(5)

The chaotic synchronization problem can be considered as a stabilization of the synchronization error at the origin by a suitable controller $\mathsf{\delta }\left(t\right)\in R^n$. This means that the controller directs the synchronization error trajectories to the origin for all $t\ge t_0\ge 0$, where $t_0$ is the time of control activation.

Active Controller Design

Theorem 1. 

Let us define the following control function:

$$\mathsf{\delta }\left(t\right)=-H\left(X\left(t\right),Y\left(t\right),\mathit{e}\left(t\right)\right)-{\mathsf{\Phi }}_i+\mathit{v}\left(t\right)$$

(6)

where $\mathit{v}\left(t\right)=-K\mathit{e}\left(t\right)=-K\left(Y\left(t\right)-X\left(t\right)\right)=-K\mathit{e}\left(t\right)$ is the sub-controller function with $K\in R^{n\times n}$ is a linear controller gain matrix that regulates the strength of the feedback controller into the response system.

Proof of Theorem 1. 

It is assumed that the parameters of the drive and response systems are available and measurable. Using systems of Equations (4) and (6) that yields:

$$\begin{array}{c}\dot{\mathit{e}}\left(t\right)=A_3\mathit{e}\left(t\right)+v\left(t\right)\\ \Rightarrow \hspace{1em}\dot{\mathit{e}}\left(t\right)=A_3\mathit{e}\left(t\right)-K\mathit{e}\left(t\right)\\ \Rightarrow \hspace{1em}\dot{\mathit{e}}\left(t\right)=\left(A_3-K\right)\mathit{e}\left(t\right)\\ \Rightarrow \hspace{1em}\dot{\mathit{e}}\left(t\right)=B\mathit{e}\left(t\right)\end{array}$$

(7)

$\text{where},\hspace{0.17em}{A}_3-K=B\in R^{n\times n}$.

At this stage, the problem is reduced to show that the matrix $B\in R^{n\times n}$ of the closed-loop Equation (7) is Hurwitz.

Lemma 1. 

The necessary and sufficient condition for the matrix $B\in R^{n\times n}$ of the closed-loop system Equation (7) being a Hurwitz matrix, if all eigenvalues of the matrix $B\in R^{n\times n}$ have negative real parts, then, the zero solution of the closed-loop system Equation (7) is globally asymptotically stable.

The proof for Lemma 1 can be found in [20].

Now, we state the main theorem.

Theorem 2. 

The coefficient matrix $B\in R^{n\times n}$ of the closed-loop system Equation (7) is Hurwitz if the linear controller gain matrix $K\in R^{n\times n}$ is design such that coefficient matrix $B\in R^{n\times n}$ in Equation (7) satisfies the following two conditions:

$$\begin{array}{ll}\text{(i)}.& \left|b_{ii}\right|>{\displaystyle \sum _{i\ne j}\left|b_{ij}\right|}\hspace{0.17em}\text{with}\hspace{0.17em}{b}_{ij}\le 0,\hspace{0.17em}\text{for} \text{all}\hspace{1em}i,\hspace{0.17em}j=1,2,\dots ,n\\ \text{(ii)}.& b_{ii}<0,\hspace{0.17em}\text{for} \text{all}\hspace{1em}i=1,2,\dots ,n\end{array}$$

(8)

Then, the closed-loop system Equation (7) is globally asymptotically stable.

Proof of Theorem 2. 

Let us assumed that $B\in R^{n\times n}$ be a real symmetric matrix. Further, it is assumed that the coefficients of the feedback controller gain matrix $K\in R^{n\times n}$ are designed such that the system matrix $B\in R^{n\times n}$ satisfies the two conditions of the Theorem 2. Then, the matrix $B\in R^{n\times n}$ is a strictly diagonally dominant (SDD) non-singular matrix. By the Gershgorin theorem [19], if a matrix is SDD and all its diagonal elements are negative, then, every eigenvalue of the system matrix $B\in R^{n\times n}$ is also negative. Thus, by the Routh-Hurwitz criterion [20], the matrix $B\in R^{n\times n}$ is Hurwitz. Hence, by the linear control theory [20], the closed-loop system Equation (7) is globally asymptotically stable. This implies that the two coupled chaotic systems Equation (1) are globally asymptotical synchronized.

3. Identical Chaos Synchronization

3.1. Description of the New 3D Chaotic System

Recently, a new 3D chaotic system is reported [21], which is contructed by replacing a constant parameter e with a switching function in Qi four-wing chaotic attractor and generated an eight-wing chaotic attractor. The system of differential equations describing the chaotic system [21] are given as follows:

$$\begin{array}{l}\dot{x}\left(t\right)=p\left(y\left(t\right)-x\left(t\right)\right)+f(t)y\left(t\right)z\left(t\right)\\ \dot{y}\left(t\right)=qx+ry\left(t\right)-x\left(t\right)z\left(t\right)\\ \dot{z}\left(t\right)=x\left(t\right)y\left(t\right)-sz\left(t\right)\end{array}\}$$

(9)

where ${\left[x\left(t\right),y\left(t\right),z\left(t\right)\right]}^T\in R^3$ are the state vectors and $p,q,r\hspace{0.17em}\text{and}\hspace{0.17em}s$ are all real positive system parameters and $f\left(t\right)=\mathsf{\xi }\mathrm{sgn}(\sin \mathsf{\omega }t)+\mathsf{\lambda }$, is a parameter function with $\mathsf{\omega }$ as the switching frequency, $\mathsf{\xi }$, and $\mathsf{\lambda }$ are the constant parameters which takes values within a certain range. It has been investigated [21] that when $f\left(t\right)=1$ , originally the system [21] shows a four-wing chaotic attractor and when $\mathsf{\xi }=9$ and λ = 10, the parameter function $f\left(t\right)=\mathsf{\xi }\mathrm{sgn}(\sin \mathsf{\omega }t)+\mathsf{\lambda }$ with $\mathsf{\omega }=0.04\mathsf{\pi }$, then, the new system displays an eight-wing chaotic attractor (mother butterfly) and the new four-wing attractor (Baby butterfly) is very close to the origin [21]. The proposed eight-wing chaotic attractor has a complex dynamics and topologically different structure than the original Qi four-wing chaotic attractor as shown in Figure 1. Due to the complex properties of the system Equation (9), it is now significant to synchronize the chaotic system [21] for further research purposes on theoretical ground in order to implement it for hybrid image encryption, secure communications, and chaotic masking, etc.

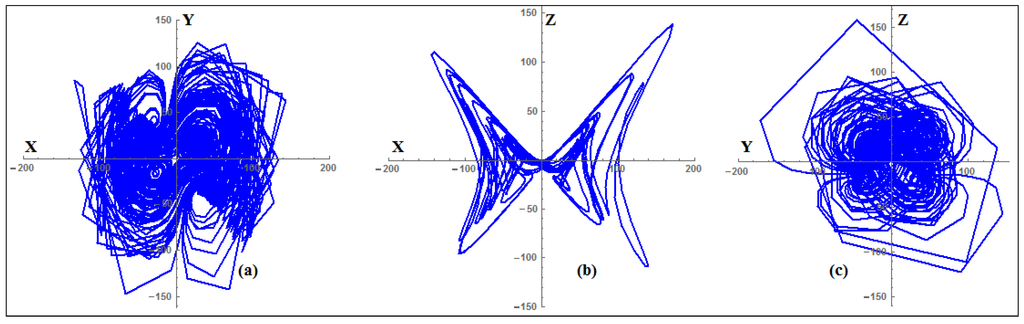
Figure 1. (a) 2D phase portrait of the new 3D chaotic system in XY-space; (b) XZ-space; and (c) YZ-space. Note. For our own simplicity, we will use $\left[x,y,z\right]$ for $\left[x\left(t\right),y\left(t\right),z\left(t\right)\right]$ alternatively.

3.2. Problem Statement

In this sub-section of the paper, we briefly describe the identical synchronization scheme for the two coupled chaotic systems [21]. The drive chaotic system Equation (9) with three state variables denoted by the subscript 1 drives the response chaotic system having identical equations denoted by the subscript 2. Although, the initial conditions of the two systems are different. The two coupled chaotic systems [21] are described in a drive-response system synchronization scheme as follows:

$$\begin{array}{ll}\text{Drive}\hspace{0.17em}\text{system}:& \{\begin{array}{l}{\dot{x}}_1=p\left(y_1-x_1\right)+f\left(t\right)y_1{z}_1+{\Delta }_1\left(t\right)\\ {\dot{y}}_1=q{x}_1+r{y}_1-x_1{z}_1+{\Delta }_2\left(t\right)\\ {\dot{z}}_1=x_1{y}_1-s{z}_1+d_3\left(t\right)+{\Delta }_3\left(t\right)\end{array}\\ \mathrm{Re}\text{sponse}\hspace{0.17em}\text{system}:& \{\begin{array}{l}{\dot{x}}_2=p\left(y_2-x_2\right)+f\left(t\right)y_2{z}_2+{\mathsf{\Omega }}_1\left(t\right)+{\mathsf{\delta }}_1\left(t\right)\\ {\dot{y}}_2=q{x}_2+r{y}_2-x_2{z}_2+{\mathsf{\Omega }}_2\left(t\right)+{\mathsf{\delta }}_2\left(t\right)\\ {\dot{z}}_2=x_2{y}_2-s{z}_2+{\mathsf{\Omega }}_2\left(t\right)+{\mathsf{\delta }}_3\left(t\right)\end{array}\end{array}$$

(10)

where ${\left[x_1,y_1,z_1\right]}^T \text{and} {\left[x_2,y_2,z_2\right]}^T\in R^3$ are the state vectors and $p,q,r,s,f\left(t\right)$ are the positive parameters of the drive and response systems Equations (10) alternatively, $\mathsf{\delta }\left(t\right)={\left[{\mathsf{\delta }}_1\left(t\right),{\mathsf{\delta }}_2\left(t\right),{\mathsf{\delta }}_3\left(t\right)\right]}^T\in R^3$ as the control input injected to the response system, and ${\Delta }_i\left(t\right) \text{and} {\mathsf{\Omega }}_i\left(t\right)\in R^3$ are the vectors of unknown bounded smooth external disturbances present in the drive and response systems respectively.

Definition 2. 

The error dynamical system for the synchronization scheme Equation (10) is described as follows:

$$\begin{array}{ll}& \left(\begin{array}{l}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{l}p\left(e_2\left(t\right)-e_1\left(t\right)\right)+f(t)\left(y_2{z}_2-y_1{z}_1\right)\\ e_1\left(t\right)+r{e}_2\left(t\right)-x_2{z}_2+x_1{z}_1\\ -s{e}_3\left(t\right)-x_1{y}_1+x_2{y}_2\end{array}\right)+\left(\begin{array}{c}{\mathsf{\Omega }}_1\left(t\right)-{\Delta }_1\left(t\right)\\ {\mathsf{\Omega }}_2\left(t\right)-{\Delta }_2\left(t\right)\\ {\mathsf{\Omega }}_3\left(t\right)-{\Delta }_3\left(t\right)\end{array}\right)+\left(\begin{array}{l}{\mathsf{\delta }}_1\left(t\right)\\ {\mathsf{\delta }}_2\left(t\right)\\ {\mathsf{\delta }}_3\left(t\right)\end{array}\right)\\ \Rightarrow & \left(\begin{array}{l}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{l}p\left(e_2\left(t\right)-e_1\left(t\right)\right)+f(t)\left(y_2{z}_2-y_1{z}_1\right)\\ e_1\left(t\right)+r{e}_2\left(t\right)-x_2{z}_2+x_1{z}_1\\ -s{e}_3\left(t\right)-x_1{y}_1+x_2{y}_2\end{array}\right)+\left|\begin{array}{c}{\mathsf{\Omega }}_1\left(t\right)-{\Delta }_1\left(t\right)\\ {\mathsf{\Omega }}_2\left(t\right)-{\Delta }_2\left(t\right)\\ {\mathsf{\Omega }}_3\left(t\right)-{\Delta }_3\left(t\right)\end{array}\right|+\left(\begin{array}{l}{\mathsf{\delta }}_1\left(t\right)\\ {\mathsf{\delta }}_2\left(t\right)\\ {\mathsf{\delta }}_3\left(t\right)\end{array}\right)\end{array}$$

(11)

$\text{where},\hspace{0.17em}{e}_1\left(t\right)=x_2-x_1,e_2\left(t\right)=y_2-y_1,e_3\left(t\right)=z_2-z_1$.

Theorem 3. 

Let us define the following active control functions:

$$\left(\begin{array}{l}{\mathsf{\delta }}_1\left(t\right)\\ {\mathsf{\delta }}_2\left(t\right)\\ {\mathsf{\delta }}_3\left(t\right)\end{array}\right)=\left(\begin{array}{c}f(t)\left(y_1{z}_1-y_2{z}_2\right)\\ x_2{z}_2-x_1{z}_1\\ x_1{y}_1-x_2{y}_2\end{array}\right)-\left(\begin{array}{c}{\mathsf{\Phi }}_1\\ {\mathsf{\Phi }}_2\\ {\mathsf{\Phi }}_3\end{array}\right)+\left(\begin{array}{l}{v}_1\left(t\right)\\ v_2\left(t\right)\\ v_3\left(t\right)\end{array}\right)$$

(12)

Then, the two coupled identical chaotic systems Equation (10) are globally asymptotically synchronized.

Proof of Theorem 3. 

It is assumed that all the variables and parameters of the two chaotic systems Equation (10) are available and measureable. Using systems of Equations (11) and (12), that yields:

$$\left(\begin{array}{l}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{c}p\left(e_2\left(t\right)-e_1\left(t\right)\right)\\ q{e}_1\left(t\right)+r{e}_2\left(t\right)\\ -s{e}_3\left(t\right)\end{array}\right)+\left(\begin{array}{l}{v}_1\left(t\right)\\ v_2\left(t\right)\\ v_3\left(t\right)\end{array}\right)$$

(13)

where $\left(\begin{array}{c}{v}_1\left(t\right)\\ v_2\left(t\right)\\ v_3\left(t\right)\end{array}\right)=-\left(\begin{array}{ccc}{k}_{11}& k_{12}& k_{12}\\ k_{21}& k_{22}& k_{23}\\ k_{31}& k_{32}& k_{33}\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)$.

Re-write system of Equation (13) as follows:

$$\left(\begin{array}{c}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-p& p& 0\\ q& r& 0\\ 0& 0& -s\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)-\left(\begin{array}{ccc}{k}_{11}& k_{12}& k_{13}\\ k_{21}& k_{22}& k_{23}\\ k_{31}& k_{32}& k_{33}\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)$$

(14)

$$\Rightarrow \hspace{1em}\left(\begin{array}{c}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-p-k_{11}& p-k_{12}& -k_{13}\\ q-k_{21}& r-k_{22}& -k_{23}\\ -k_{31}& -k_{32}& -s-k_{33}\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)$$

(15)

$$\Rightarrow \hspace{1em}\dot{\mathit{e}}\left(t\right)=B\mathit{e}\left(t\right)$$

(16)

where

$$B=\left(\begin{array}{ccc}-p-k_{11}& p-k_{12}& -k_{13}\\ q-k_{21}& r-k_{22}& -k_{23}\\ -k_{31}& -k_{32}& -s-k_{33}\end{array}\right)$$

(17)

The closed-loop system Equation (15) to be controlled is a linear system with control input $v_1\left(t\right),v_2\left(t\right)\hspace{0.17em}\text{and}\hspace{0.17em}{v}_3\left(t\right)$ as a function of $e_1\left(t\right),e_2\left(t\right)\hspace{0.17em}\text{and}\hspace{0.17em}{e}_3\left(t\right)$ alternatively, where the constants $k_{ij},\text{i, j}=1,2,3$ are the linear controller gains. As long as these controller gains stabilize the closed-loop system Equation (15), the $e_1\left(t\right),e_2\left(t\right)\hspace{0.17em}\text{and}\hspace{0.17em}{e}_3\left(t\right)$ converge to zero as time goes to infinity [16], then, the zero solution of the closed-loop system Equation (15) is obvious. This implies that the two coupled identical chaotic systems Equation (10) are globally asymptotically synchronized.

At this stage, the problem is reduced to show that the matrix $B\in R^{3\times 3}$ of the closed-loop system Equation (15) is Hurwitz.

Corollary 2. 

If the coefficient matrix $B\in R^{3\times 3}$ in Equation (17) of the closed-loop system Equation (15) is Hurwitz, then the zero solution of the error system Equation (15) is globally asymptotically stable.

Theorem 4. 

The matrix $B\in R^{3\times 3}$ is Hurwitz, if the linear controller gain matrix $K\in R^{3\times 3}$ is constructed such that the coefficient matrix $B\in R^{3\times 3}$ in Equation (17) satisfies the following two conditions:

$$\begin{array}{l}(i).\hspace{0.17em}\{\begin{array}{l}\left|-p-k_{11}\right|>{\displaystyle \sum _{i\ne j}\left|\left(p-k_{12}\right)+\left|-k_{13}\right|\right|} \\ \left|r-k_{22}\right|>{\displaystyle \sum _{i\ne j}\left|\left(q-k_{21}\right)+\left|-k_{23}\right|\right|}\\ \left|-s-k_{33}\right|>{\displaystyle \sum _{i\ne j}\left|-k_{31}+\left|-k_{32}\right|\right|}\end{array}\hspace{0.17em}\\ \text{and}\\ (ii).\hspace{0.17em}\{-p-k_{11}<0,\hspace{0.17em}r-k_{22}<0,\hspace{0.17em}-s-k_{33}<0\end{array}$$

(18)

Proof of Theorem 4. 

The controller Equation (12) is associated to the feedback controller gain matrix $K\in R^{3\times 3}$ so that the design of $K\in R^{3\times 3}$ is to make all eigenvalues of the coefficient matrix $B\in R^{n\times n}$ of the closed-loop system Equation (15) are in the open left-half of the complex plane. For the particular choice of the gain coefficients, which satisfies the conditions Equation (18) are selected as follows:

$$\left(\begin{array}{ccc}{k}_{11}& k_{12}& k_{13}\\ k_{21}& k_{22}& k_{23}\\ k_{31}& k_{32}& k_{33}\end{array}\right)=\left(\begin{array}{ccc}-p+2& p& 0\\ q& r+2& 0\\ 0& 0& -s+2\end{array}\right)$$

(19)

With this specific choice of the controller gains and considering: $a=0.4,b=5,$ $c=12,p=14,q=-1,r=16 \text{and} s=43$, the closed-loop system Equation (15) yields:

$$\left(\begin{array}{c}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-2& 0& 0\\ 0& -2& 0\\ 0& 0& -2\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)$$

(20)

Thus, by the Routh-Hurwitz criterion, the matrix $B\in R^{n\times n}$ is Hurwitz. This proves that the closed-loop system Equation (15) is globally asymptotically stable. Consequently Theorem 4 and Corollary 2 are obvious. Hence Theorem 3 is proved.

3.3. Numerical Simulation and Discussion

Numerical simulation results are furnished to validate the advantages and effectiveness of the proposed approach by using Mathematica 10. The parameters for the chaotic system [21] are set as $p=14,$ $q=-1,r=16,s=43,f\left(t\right)=7$ with initial values of the state variables of the drive and response systems being chosen as ${\left[x_1\left(0\right),y_1\left(0\right),z_1\left(0\right)\right]}^T=\left[10,-10,-15\right]$ $\text{and }{\left[x_2\left(0\right),y_2\left(0\right),z_2\left(0\right)\right]}^T=\left[-25,-50,-40\right]$ respectively. In the simulation, the following external disturbances are applied to the drive and response systems respectively.

$$\begin{array}{l}{\Delta }_1\left(t\right)=0.3\cos \left(\frac{\mathsf{\pi }}{2}t\right),{\Delta }_2\left(t\right)=-0.2\cos \left(\mathsf{\pi }t\right),{\Delta }_3\left(t\right)=0.4\cos \left(\frac{3\mathsf{\pi }}{2}t\right)\\ {\mathsf{\Omega }}_1\left(t\right)=-0.1\sin \left(\frac{\mathsf{\pi }}{2}t\right),{\mathsf{\Omega }}_2\left(t\right)=0.3\cos \left(\frac{3\mathsf{\pi }}{2}t\right),{\mathsf{\Omega }}_3\left(t\right)=-0.2\sin \left(\frac{5\mathsf{\pi }}{6}t\right)\end{array}$$

(21)

Subsequently, ${\mathsf{\Phi }}_1=0.4, {\mathsf{\Phi }}_2=0.5\text{ and }{\mathsf{\Phi }}_3=0.6$, that satisfies the assumption 1.

For the identical chaotic systems [21], the time series of the state vectors of the synchronized and unsynchronized trajectories are depicted in Figure 2, Figure 3 and Figure 4. The state trajectories of the drive system converged to the state trajectories of the response system under the control action Equation (12).

The time series of the error system Equation (11) for identical synchronization are shown in Figure 5. As expected, one can notice the smoothness of the synchronized error signals while converging to the zero state quickly, when the controllers are activated at $t<2s$. This demonstrates the robustness and performance of the control action Equation (12) for the complete synchronization under the effect of unknown external disturbance.

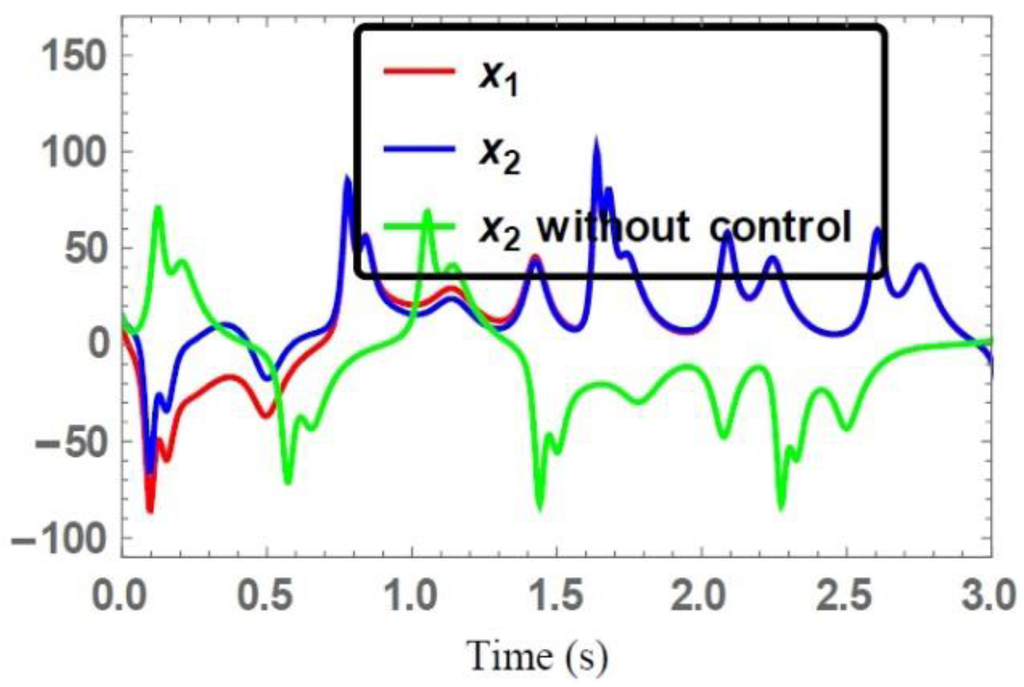
Figure 2. Time series of the state trajectories $x_1\hspace{0.17em}\text{and}\hspace{0.17em}{x}_2$.

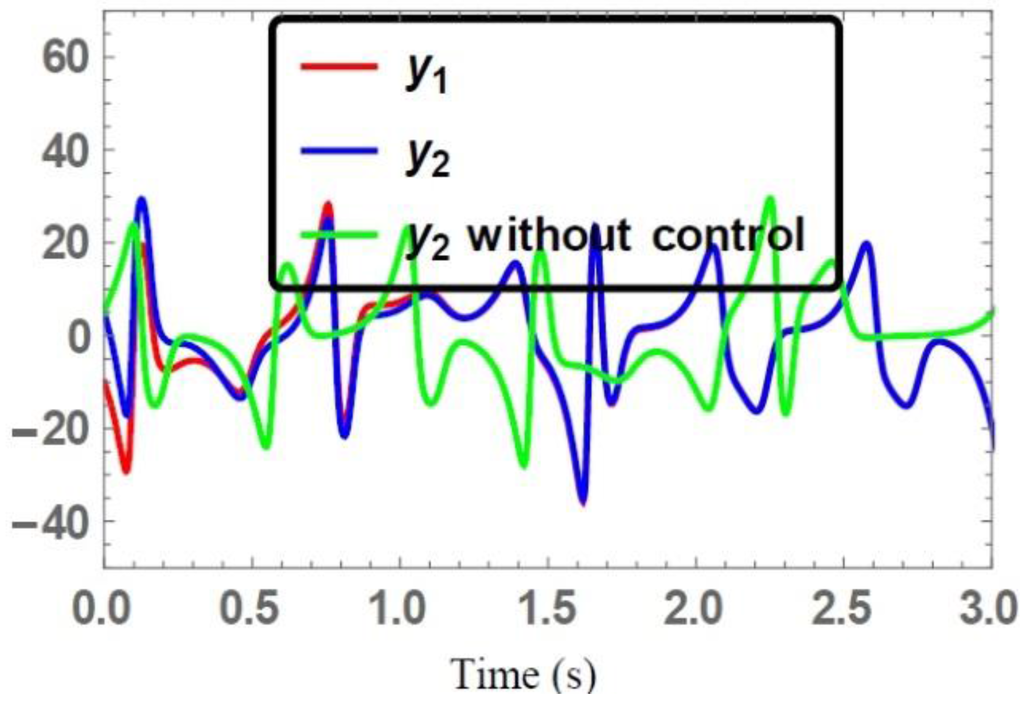
Figure 3. Time series of the state trajectories $y_1\hspace{0.17em}\text{and}\hspace{0.17em}{y}_2$.

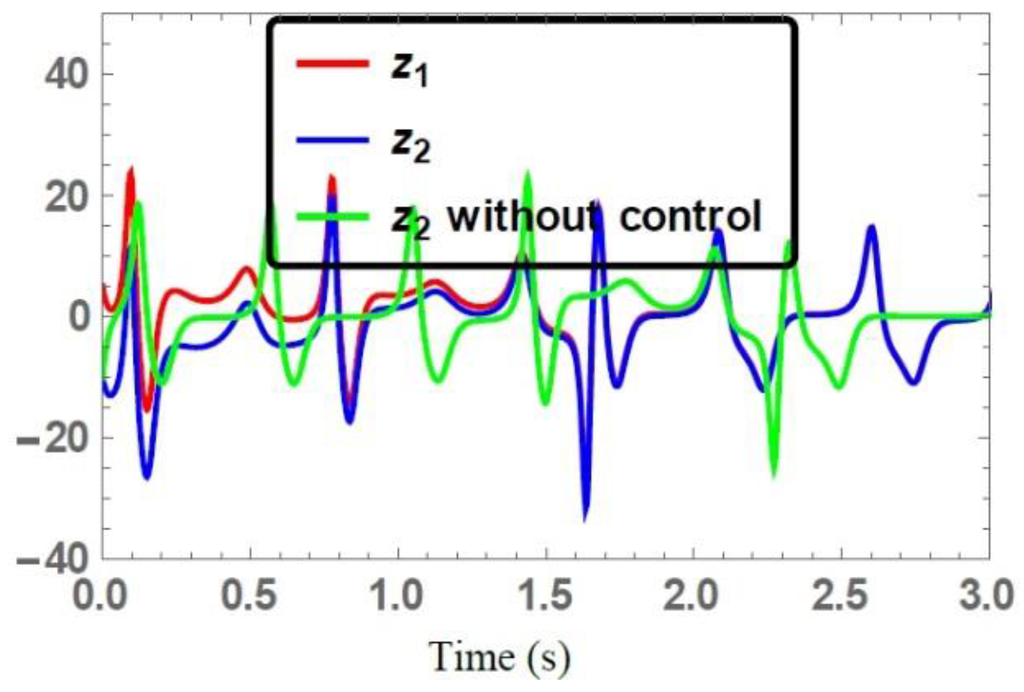
Figure 4. Time series of the state trajectories $z_1\hspace{0.17em}\text{and}\hspace{0.17em}{z}_2$.

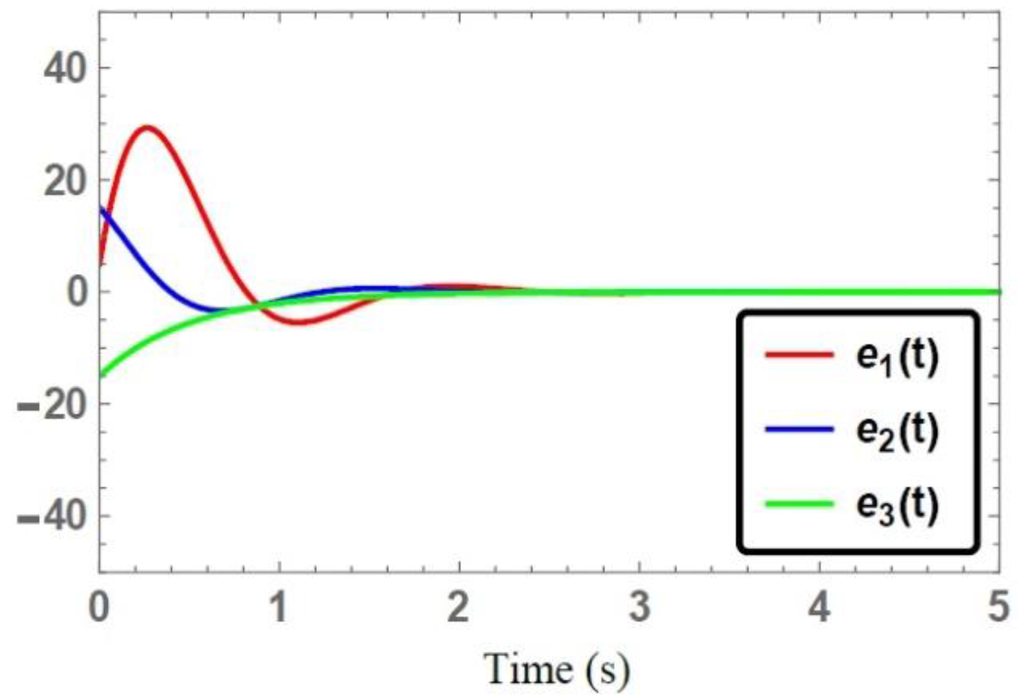
Figure 5. Time series of the controlled synchronization error system Equation (11).

4. Non-Identical Synchronization

4.1. Problem Formulation

To study the generalized synchronization problem for the chaotic system [21], it is assumed that the chaotic system [21] drives the Liu-Chen chaotic system [22]. Thus, the drive-response system synchronization scheme is described as follows:

$$\begin{array}{ll}\text{Drive}\hspace{0.17em}\text{system}:& \{\begin{array}{l}{\dot{x}}_1=p\left(y_1-x_1\right)+f\left(t\right)y_1{z}_1+{\Delta }_1\left(t\right)\\ {\dot{y}}_1=q{x}_1+r{y}_1-x_1{z}_1+{\Delta }_2\left(t\right)\\ {\dot{z}}_1=x_1{y}_1-s{z}_1+{\Delta }_3\left(t\right)\end{array}\\ \mathrm{Re}\text{sponse}\hspace{0.17em}\text{system}:& \{\begin{array}{l}{\dot{x}}_2=a{x}_2-y_2{z}_2+{\mathsf{\Omega }}_1\left(t\right)+{\mathsf{\delta }}_1\left(t\right)\\ {\dot{y}}_2=-c{y}_2+x_2{z}_2+{\mathsf{\Omega }}_2\left(t\right)+{\mathsf{\delta }}_2\left(t\right)\\ {\dot{z}}_2=x_2{y}_2-b{z}_2+{\mathsf{\Omega }}_3\left(t\right)+{\mathsf{\delta }}_3\left(t\right)\end{array}\end{array}$$

(22)

where ${\left[x_1,y_1,z_1\right]}^T\in R^3 \text{and} {\left[x_2,y_2,z_2\right]}^T\in R^3$ are the corresponding state vectors, $p,q,r \hspace{0.17em}\text{and}\hspace{0.17em}s$ and $a,b\hspace{0.17em}\text{and}\hspace{0.17em}c$ are the parameters of the drive and response systems respectively, ${\Delta }_i\left(t\right) \text{and} {\mathsf{\Omega }}_i\left(t\right)\in R^3$ are the vectors of unknown bounded smooth external disturbances present in the drive and response systems Equation (22) respectively, and $\mathsf{\delta }\left(t\right)={\left[{\mathsf{\delta }}_1\left(t\right),{\mathsf{\delta }}_2\left(t\right),{\mathsf{\delta }}_3\left(t\right)\right]}^T\in R^3$ as the active controller that is to be designed yet.

Definition 3. 

The error dynamical system for the synchronization scheme Equation (22) is be described as follows:

$$\begin{array}{ll}& \left(\begin{array}{l}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{c}p\left(e_2\left(t\right)-e_1\left(t\right)\right)+\left(p+a\right)x_2-p{y}_2-f\left(t\right)y_1{z}_1-y_2{z}_2\\ q{e}_1\left(t\right)-c{e}_2\left(t\right)-q{x}_2-\left(c+r\right)y_1+x_1{z}_1+x_2{z}_2\\ -s{e}_3\left(t\right)+\left(s-b\right)z_2-x_1{y}_1+x_2{y}_2\end{array}\right)+\left(\begin{array}{c}{\mathsf{\Omega }}_1\left(t\right)-{\Delta }_1\left(t\right)\\ {\mathsf{\Omega }}_2\left(t\right)-{\Delta }_2\left(t\right)\\ {\mathsf{\Omega }}_3\left(t\right)-{\Delta }_3\left(t\right)\end{array}\right)+\left(\begin{array}{c}{\mathsf{\delta }}_1\left(t\right)\\ {\mathsf{\delta }}_2\left(t\right)\\ {\mathsf{\delta }}_3\left(t\right)\end{array}\right)\\ \Rightarrow & \left(\begin{array}{l}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{c}p\left(e_2\left(t\right)-e_1\left(t\right)\right)+\left(p+a\right)x_2-p{y}_2-f\left(t\right)y_1{z}_1-y_2{z}_2\\ q{e}_1\left(t\right)-c{e}_2\left(t\right)-q{x}_2-\left(c+r\right)y_1+x_1{z}_1+x_2{z}_2\\ -s{e}_3\left(t\right)+\left(s-b\right)z_2-x_1{y}_1+x_2{y}_2\end{array}\right)+\left|\begin{array}{c}{\mathsf{\Omega }}_1\left(t\right)-{\Delta }_1\left(t\right)\\ {\mathsf{\Omega }}_2\left(t\right)-{\Delta }_2\left(t\right)\\ {\mathsf{\Omega }}_3\left(t\right)-{\Delta }_3\left(t\right)\end{array}\right|+\left(\begin{array}{c}{\mathsf{\delta }}_1\left(t\right)\\ {\mathsf{\delta }}_2\left(t\right)\\ {\mathsf{\delta }}_3\left(t\right)\end{array}\right)\end{array}$$

(23)

Theorem 5. 

Let us define the following active control functions:

$$\left(\begin{array}{l}{\mathsf{\delta }}_1\left(t\right)\\ {\mathsf{\delta }}_2\left(t\right)\\ {\mathsf{\delta }}_3\left(t\right)\end{array}\right)=\left(\begin{array}{c}\left(p+a\right)x_2+p{y}_2+y_2{z}_2+f\left(t\right)y_1{z}_1\\ \left(c+r\right)y_1+q{x}_2-x_2{z}_2-x_1{z}_1\\ \left(b-s\right)z_2+x_1{y}_1-x_2{y}_2\end{array}\right)-\left(\begin{array}{c}{\mathsf{\Phi }}_1\\ {\mathsf{\Phi }}_2\\ {\mathsf{\Phi }}_3\end{array}\right)+\left(\begin{array}{l}{v}_1\left(t\right)\\ v_2\left(t\right)\\ v_3\left(t\right)\end{array}\right)$$

(24)

Then, the two coupled non-identical chaotic systems Equation (22) are globally asymptotically synchronized.

Proof of Theorem 5. 

It is assumed that all the variables and parameters of the two systems Equation (22) are available and measureable. Using systems of Equations (23) and (24), that yields:

$$\left(\begin{array}{l}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{c}p\left(e_2\left(t\right)-e_1\left(t\right)\right)\\ q{e}_1\left(t\right)-c{e}_2\left(t\right)\\ -s{e}_3\left(t\right)\end{array}\right)+\left(\begin{array}{l}{v}_1\left(t\right)\\ v_2\left(t\right)\\ v_3\left(t\right)\end{array}\right)$$

(25)

where $\left(\begin{array}{c}{v}_1\left(t\right)\\ v_2\left(t\right)\\ v_3\left(t\right)\end{array}\right)=-\left(\begin{array}{ccc}{k}_{11}& k_{12}& k_{12}\\ k_{21}& k_{22}& k_{23}\\ k_{31}& k_{32}& k_{33}\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)$.

Re-writing the system of Equation (25) as follows:

$$\begin{array}{cc}& \left(\begin{array}{c}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-p& p& 0\\ q& -c& 0\\ 0& 0& -s\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)-\left(\begin{array}{ccc}{k}_{11}& k_{12}& k_{13}\\ k_{21}& k_{22}& k_{23}\\ k_{31}& k_{32}& k_{33}\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)\\ \Rightarrow & \left(\begin{array}{c}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-p-k_{11}& p-k_{12}& -k_{13}\\ q-k_{21}& -c-k_{22}& -k_{23}\\ -k_{31}& -k_{32}& -s-k_{33}\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)\end{array}$$

(26)

$$\Rightarrow \hspace{1em}\dot{\mathit{e}}\left(t\right)=B\mathit{e}\left(t\right)$$

(27)

where

$$B=\left(\begin{array}{ccc}-p-k_{11}& p-k_{12}& -k_{13}\\ q-k_{21}& -c-k_{22}& -k_{23}\\ -k_{31}& -k_{32}& -s-k_{33}\end{array}\right)$$

(28)

Theorem 6. 

The matrix $B\in R^{3\times 3}$ is Hurwitz, if the feedback controller gain matrix $K\in R^{3\times 3}$ is constructed such that the coefficient matrix $B\in R^{3\times 3}$ Equation (28) of the closed-loop system Equation (26) satisfies the following two conditions:

$$\begin{array}{l}i).\hspace{0.17em}\{\begin{array}{l}\left|-p-k_{11}\right|>{\displaystyle \sum _{i\ne j}\left|\left(p-k_{12}\right)+\left|-k_{13}\right|\right|} \\ \left|-c-k_{22}\right|>{\displaystyle \sum _{i\ne j}\left|\left(q-k_{21}\right)+\left|-k_{23}\right|\right|}\hspace{0.17em}\\ \left|-s-k_{33}\right|>{\displaystyle \sum _{i\ne j}\left|-k_{31}+\left|-k_{32}\right|\right|}\end{array}\hspace{0.17em}\\ \text{and}\\ ii).\hspace{0.17em}\{-p-k_{11}<\hspace{0.17em}0,\hspace{0.17em}-c-k_{22}<\hspace{0.17em}0,\hspace{0.17em}-s-k_{33}<\hspace{0.17em}\hspace{0.17em}0\end{array}$$

(29)

Proof of Theorem 6. 

For the particular choice of the linear controller gains which satisfies the conditions Equation (28) are selected as follows:

$$\left(\begin{array}{ccc}{k}_{11}& k_{12}& k_{13}\\ k_{21}& k_{22}& k_{23}\\ k_{31}& k_{32}& k_{33}\end{array}\right)=\left(\begin{array}{ccc}-p+2& p& 0\\ q& -c+2& 0\\ 0& 0& s+2\end{array}\right)$$

(30)

With this specific selection of the linear controller gains and considering: $a=0.4,b=5,$ $c=12,p=14,$ $q=-1,r=16 \text{and} s=43$, the closed-loop system Equation (26) yields:

$$\left(\begin{array}{c}{\dot{e}}_1\left(t\right)\\ {\dot{e}}_2\left(t\right)\\ {\dot{e}}_3\left(t\right)\end{array}\right)=\left(\begin{array}{ccc}-2& 0& 0\\ 0& -2& 0\\ 0& 0& -2\end{array}\right)\left(\begin{array}{c}{e}_1\left(t\right)\\ e_2\left(t\right)\\ e_3\left(t\right)\end{array}\right)$$

(31)

This completes the proof.

4.2. Simulation Studies

The parameters for the chaotic system [21] and Liu-Chen system [22] are set as $p=14,q=-1,r=16,$ $s=43,f\left(t\right)=7 \text{and} a=0.4,\hspace{0.17em}b=5,\hspace{0.17em}c=12$ with initial values of the drive [21] and response [22] systems being chosen as ${\left[x_1\left(0\right),y_1\left(0\right),z_1\left(0\right)\right]}^T=\left[10,-10,-15\right]$ and ${\left[x_2\left(0\right),y_2\left(0\right),z_2\left(0\right)\right]}^T=\left[15,7,6\right]$ alternatively. In the simulation, the following bounded smooth disturbances are applied to the drive and response systems, respectively:

$$\begin{array}{l}{\Delta }_1\left(t\right)=0.2\sin \left(\frac{5\mathsf{\pi }}{6}t\right),{\Delta }_2\left(t\right)=-0.5\cos \left(\frac{3\mathsf{\pi }}{2}t\right),{\Delta }_3\left(t\right)=0.3\cos \left(\frac{\mathsf{\pi }}{2}t\right)\\ {\mathsf{\Omega }}_1\left(t\right)=-0.2\cos \left(\mathsf{\pi }t\right),{\mathsf{\Omega }}_2\left(t\right)=-0.1\sin \left(\frac{5\mathsf{\pi }}{6}t\right),{\mathsf{\Omega }}_3\left(t\right)=-0.3\cos \left(\frac{2\mathsf{\pi }}{3}t\right)\end{array}$$

(32)

Accordingly, ${\mathsf{\Phi }}_1=0.4,{\mathsf{\Phi }}_2=0.6\text{ and }{\mathsf{\Phi }}_3=0.6$.

For the non-identical chaotic systems [21,22], the time series of the state vectors of the synchronized and unsynchronized trajectories are illustrated in Figure 6, Figure 7 and Figure 8. These figures demonstrated that the state trajectories of the response system converged to that state trajectories of the drive system under the synthesized control action Equation (24), while the uncontrolled state trajectories of the response system are completely different from the drive system state trajectories. Time series of the error system Equation (23) to the zero state are depicted in Figure 9. One can notice the smoothness of the synchronized error trajectories while converging to the zero state with fast converging rates, which illustrates the performance of the control action Equation (24) for non-identical synchronization. This feature shows that the investigated controllers are robust to the accidental parameters mismatch and unknown external disturbances in the transmitter and receiver.

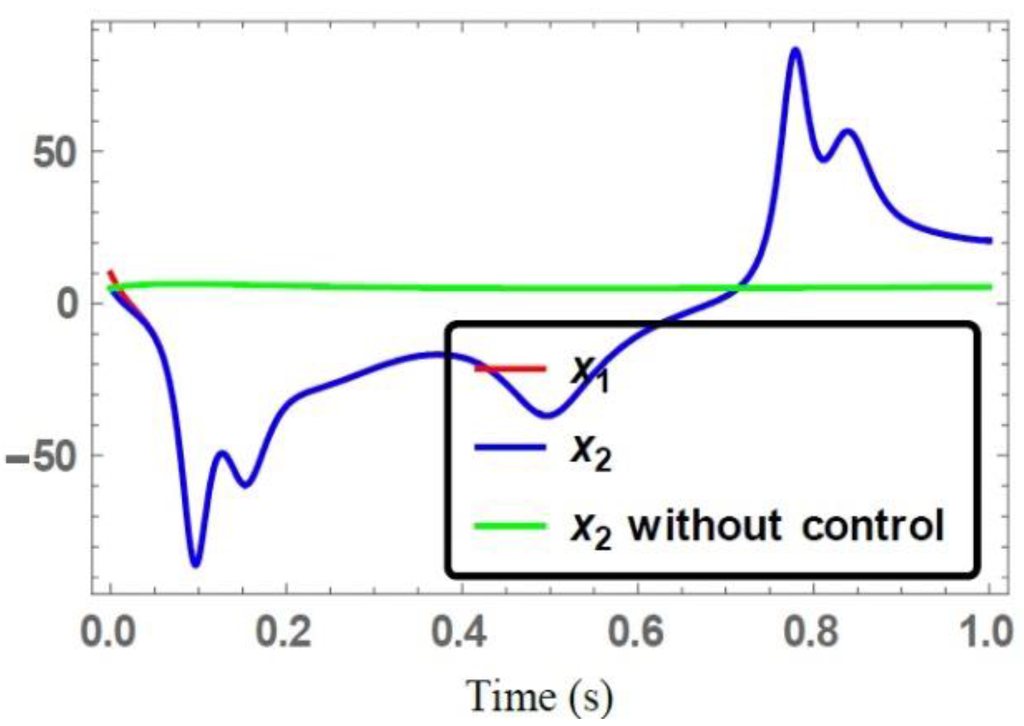
Figure 6. Time series of the state trajectories $x_1\hspace{0.17em}\text{and}\hspace{0.17em}{x}_2$.

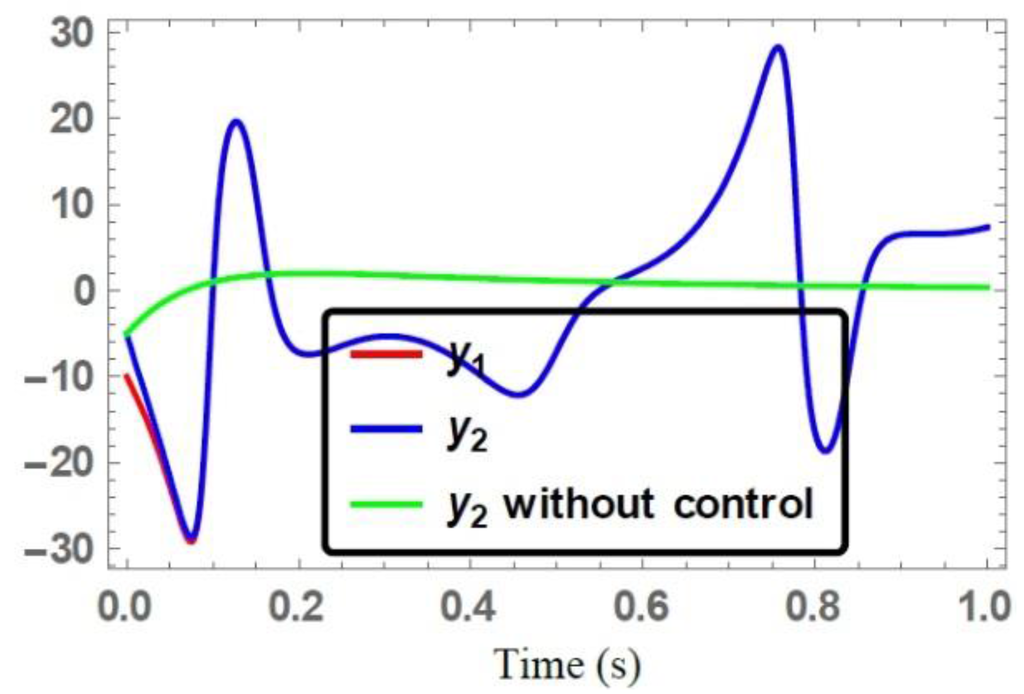
Figure 7. Time series of the state trajectories $y_1\hspace{0.17em}\text{and}\hspace{0.17em}{y}_2$.

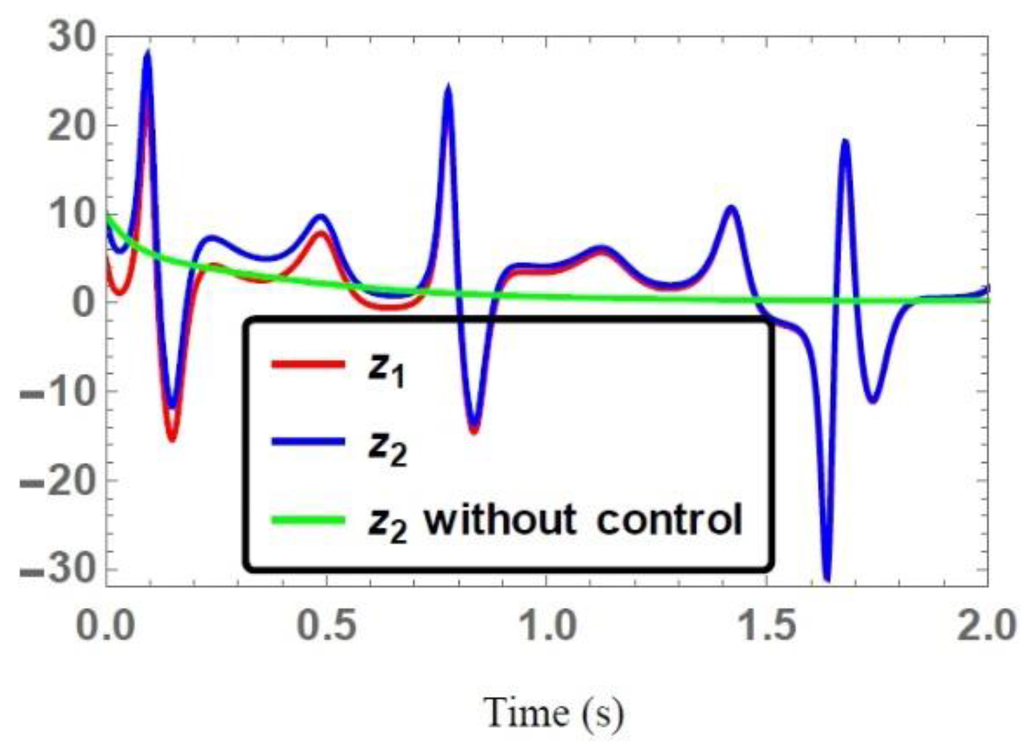
Figure 8. Time series of the state trajectories $z_1\hspace{0.17em}\text{and}\hspace{0.17em}{z}_2$.

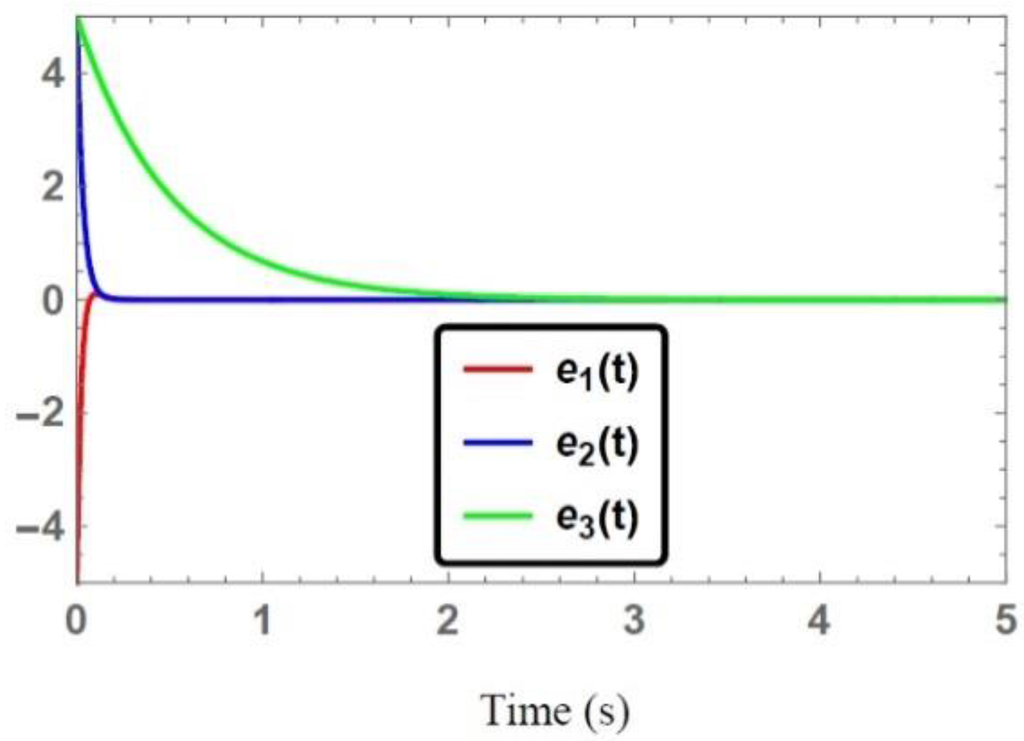
Figure 9. Time series of the controlled synchronization error system Equation (26).

5. Conclusions

The robust synchronization problem of two identical and two non-identical chaotic systems has been investigated. Based on the Gershgorin theorem and Routh-Hurwitz criterion and using the active control strategy, sufficient conditions are derived to construct a suitable linear gain matrix that established the globally asymptotical synchronization under the effect of an unknown external disturbance. Numerical simulation results show that the proposed approach works very well and can be applied to a class of chaotic as well as hyperchaotic systems successfully.

In comparison with some published related works, there are three main advantages of the proposed approach which are summarized as follows.

(a)

The synchronization speed is fast as well as the amplitude of the oscillations is smaller.

(b)

In the proposed active synchronization control approach, the eigenvalues of the coefficient matrix of the closed-loop system can be adjusted to have a desirable synchronization time.

(c)

Most of the chaotic systems in real practical applications have different structures, thus, we believe that the proposed active control approach will be a helpful tool in synchronizing a class of chaotic/hyperchaotic systems.