Electric Multiple Unit Spare Parts Vendor-Managed Inventory Contract Mechanism Design
Abstract
1. Introduction
- Existing research on the EMU spare parts mainly focuses on demand forecasting, inventory optimization, and maintenance strategy and only considers decision optimization for individual entities in the supply chain, with insufficient attention to cooperation between upstream and downstream enterprises in the supply chain. This paper studies the design of the contract mechanism for EMU spare parts under the VMI model, aiming to improve the overall efficiency and responsiveness of the supply chain, enriching the research on spare parts coordination.
- The coordination role of different contracts under uncertain demand environments in various supply methods is explored in depth, enriching the perspective of scenario description in the design of contractmechanisms under the VMI model. The model takes into account factors such as the downtime loss cost of spare parts and the difficulty of spare parts procurement, thereby expanding the research perspective of the VMI model.
2. Literature Review
3. Problem Description and Model Assumptions
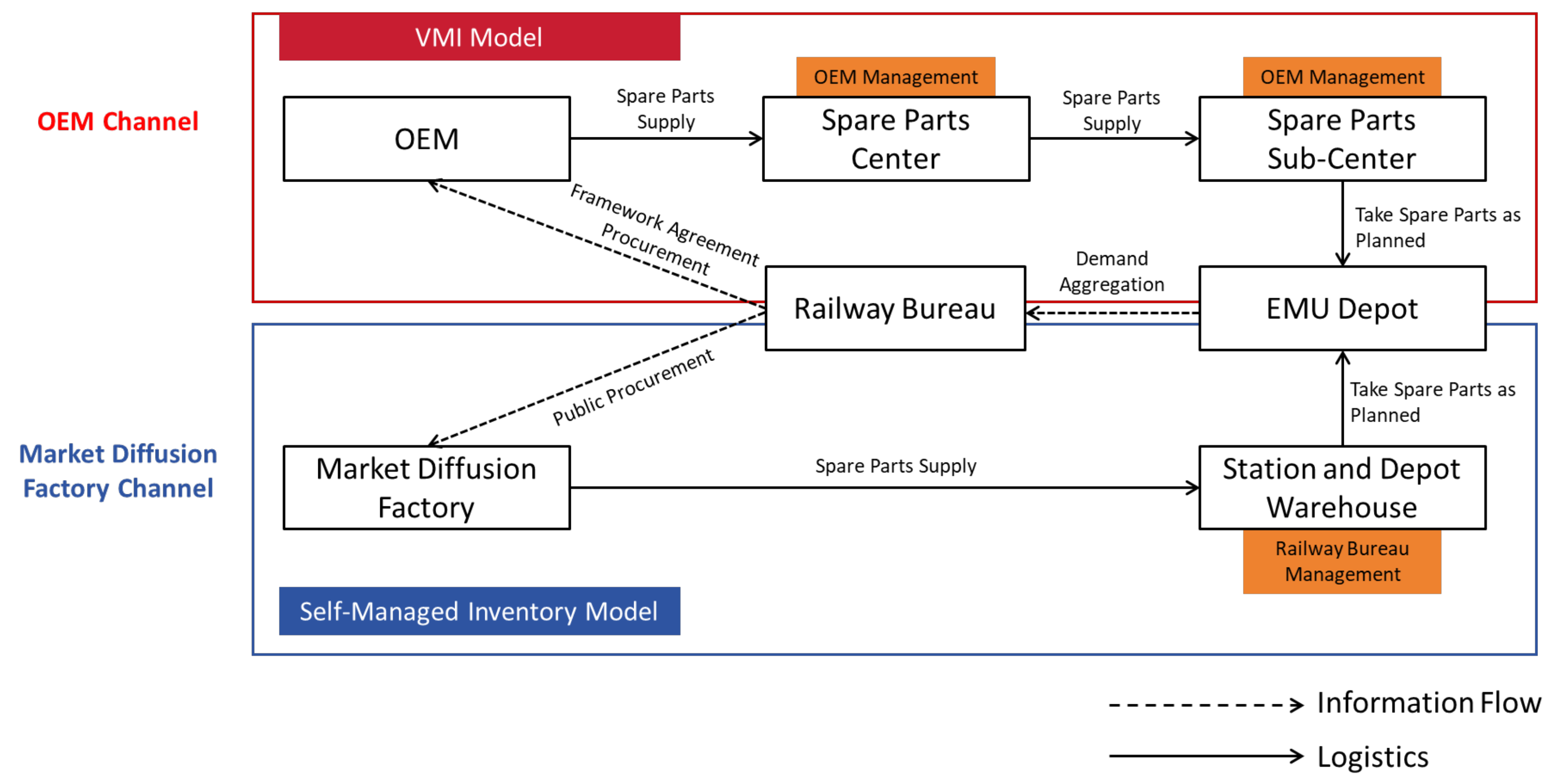
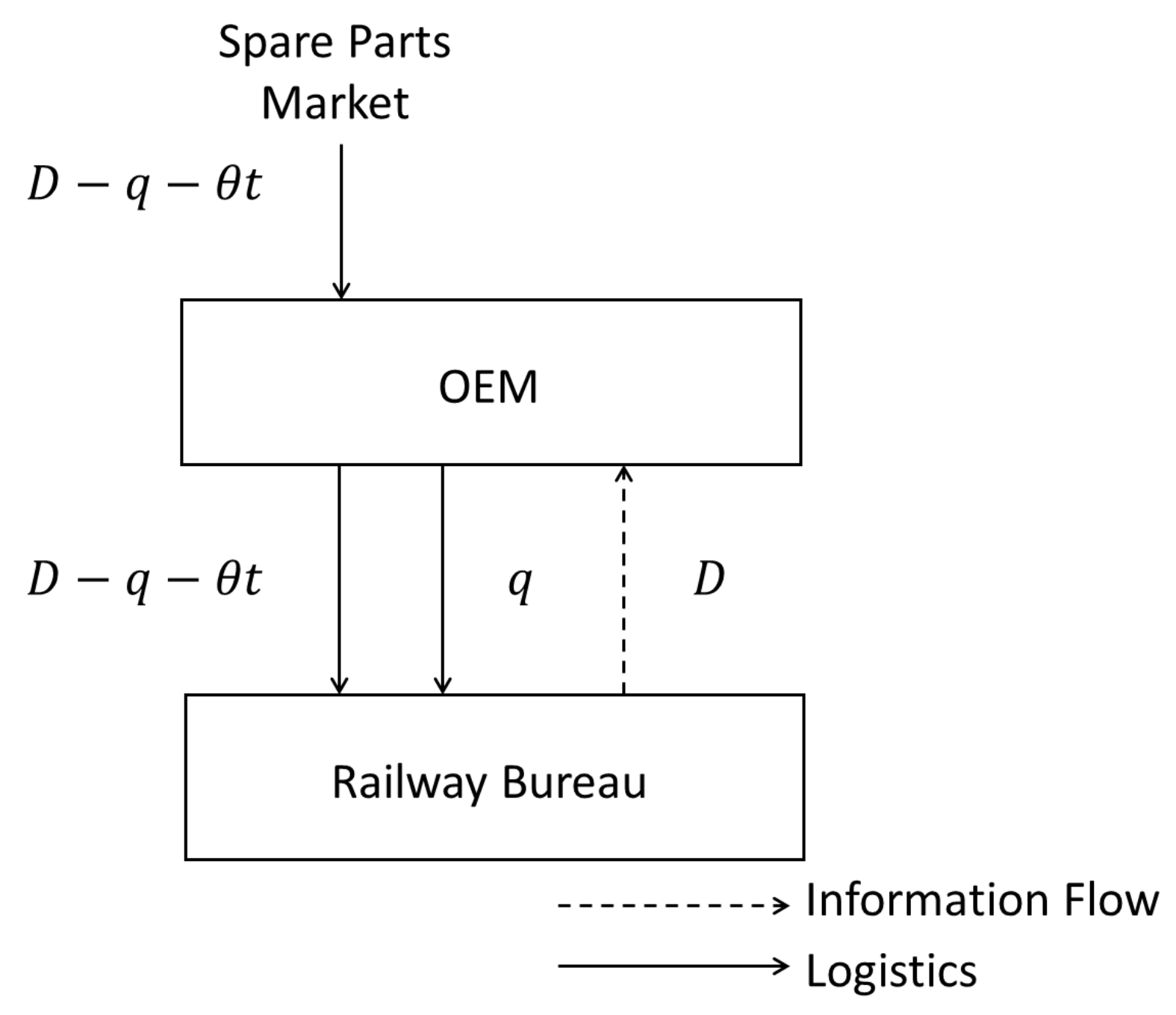
3.1. Problem Description
3.2. Model Assumptions
- Both the OEM and the railway bureau are fully rational decision-makers with complete information symmetry. That is, both parties are aware of the probability density and cumulative distribution functions of spare parts demand, which is similar to general equipment supply chain studies [29].
- Spare parts repair is not considered. Damaged parts must be replaced. Spare parts reserved at the OEM but unused by the railway bureau during the stock period are transferred or scrapped, retaining some residual value .
- Spare parts shortages may lead to maintenance delays or failures. A unit shutdown loss cost is introduced to measure the adverse effects of such situations.
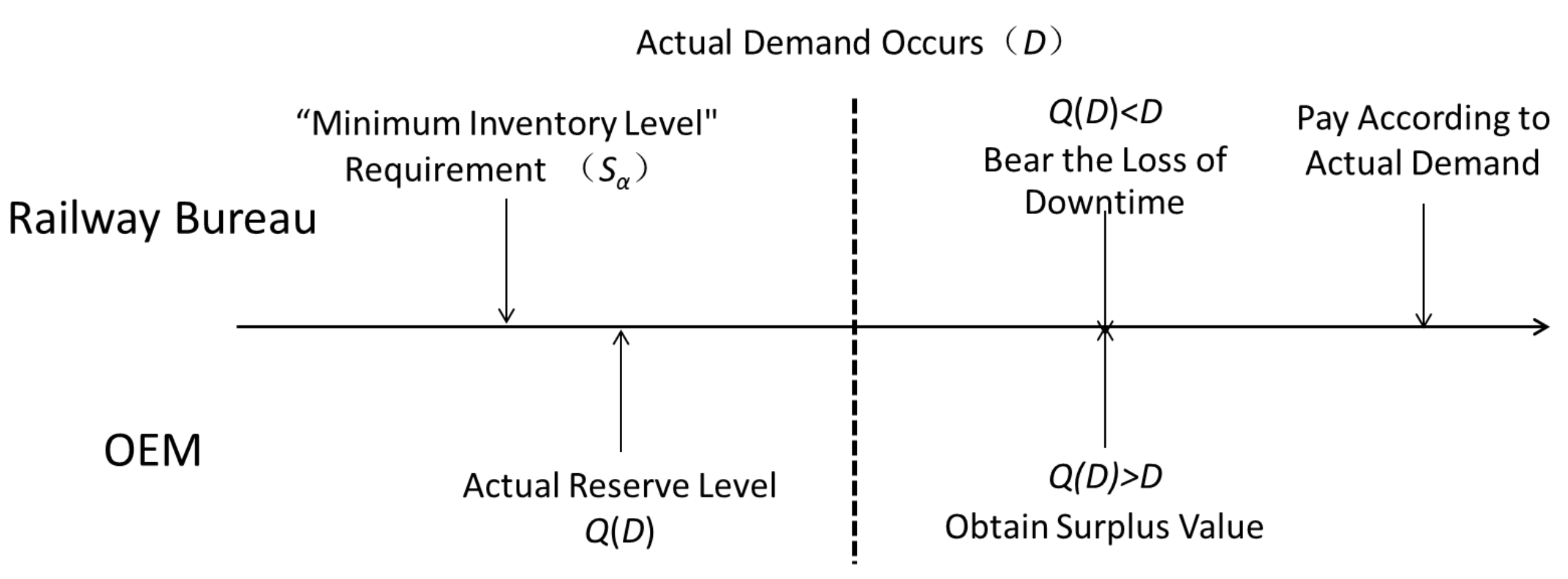
- ensures the OEM always gains profit; is the condition for the railway bureau to purchase spare parts, ; otherwise, the primary manufacturer would infinitely stockpile parts.
- Different parts have varying procurement difficulties. Let represent the procurement difficulty. When , the difficulty is normal. Higher difficulty requires greater response-effort costs.
- Market procurement involves response-effort costs, such as supplier collaboration and channel development. Response-effort cost is defined as the increase in the marginal cost of accelerating response time. Following the research of Yang, X. et al. [30], the following quadratic form is used to represent response-effort cost: , where is the maximum response-effort cost and is the cost saved by delaying a unit’s response time . Larger response-effort costs enable meeting more spare parts demand.
- In real-world railway operations, long response times for non-emergency critical parts may delay EMU maintenance and cause shutdown losses. Following Wen et al. [31], we introduce as the spare parts order loss coefficient. For each unit time delay in response, the OEM loses orders, leading to spare parts-related shutdown losses for the EMU depot.
4. Spare Parts Supply Chain VMI Contract Mechanism Design
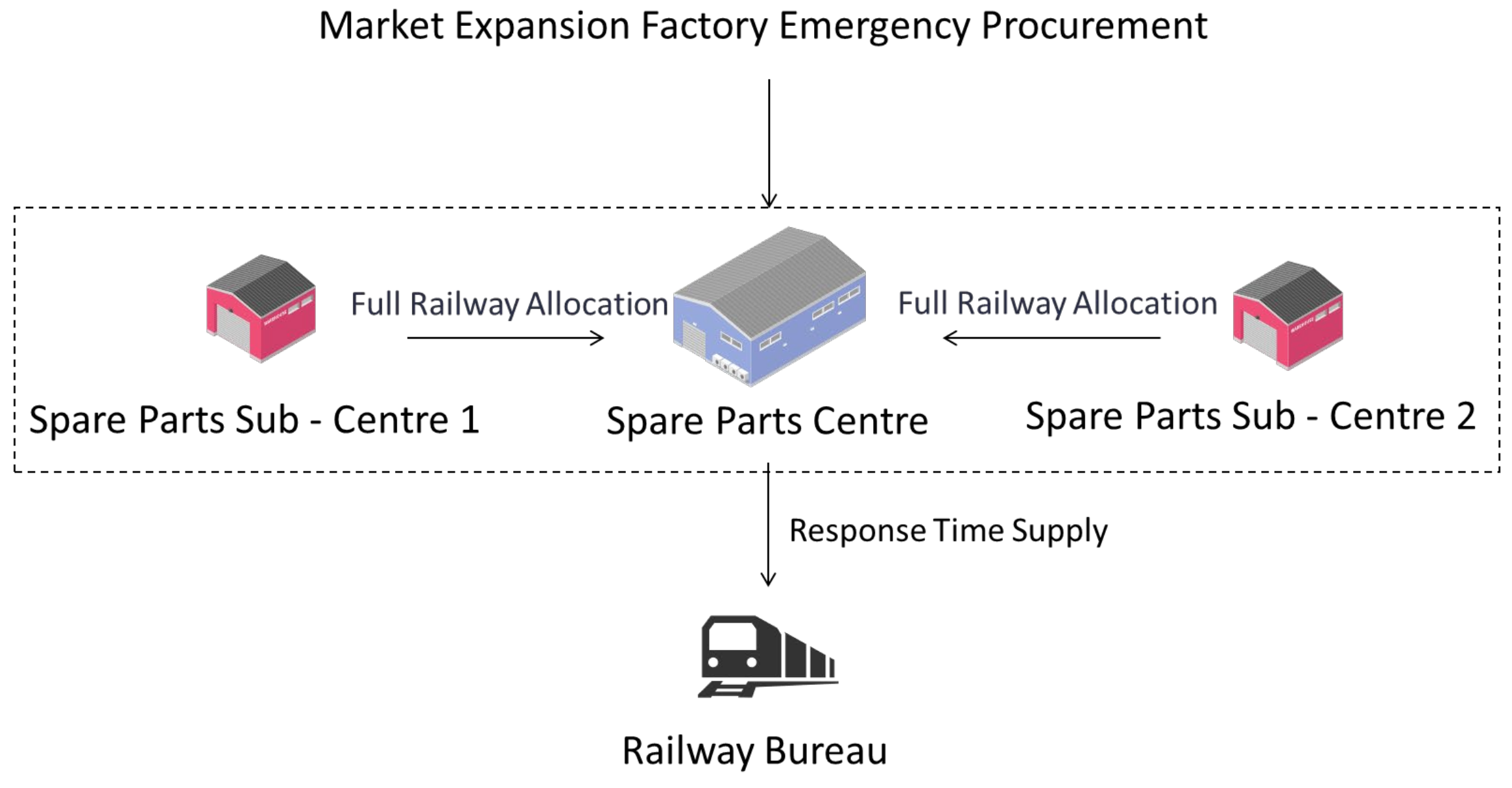
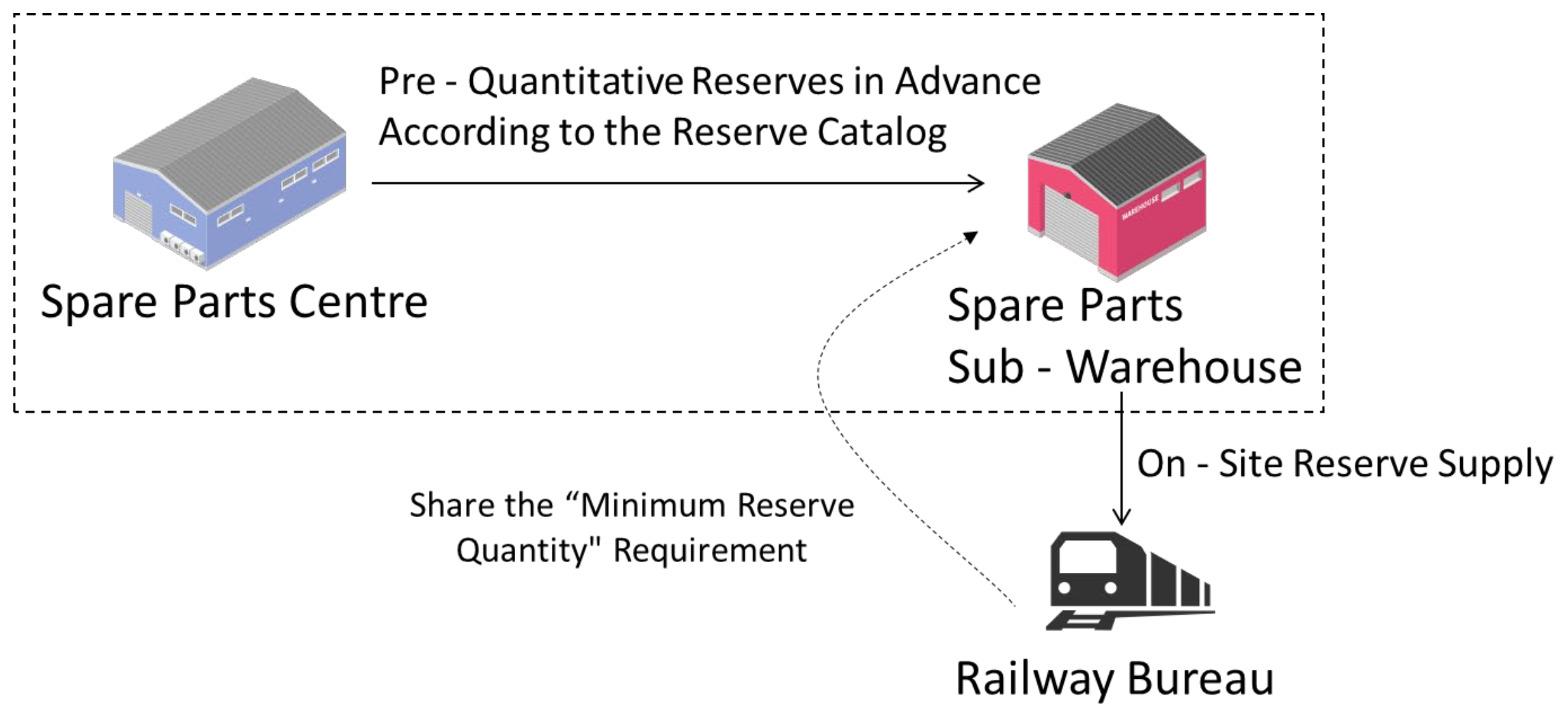
4.1. Reward–Punishment Mechanism for Emergency Critical Spare Parts: A Quantity Commitment-Based Design
4.1.1. Without Reward and Penalty Mechanism
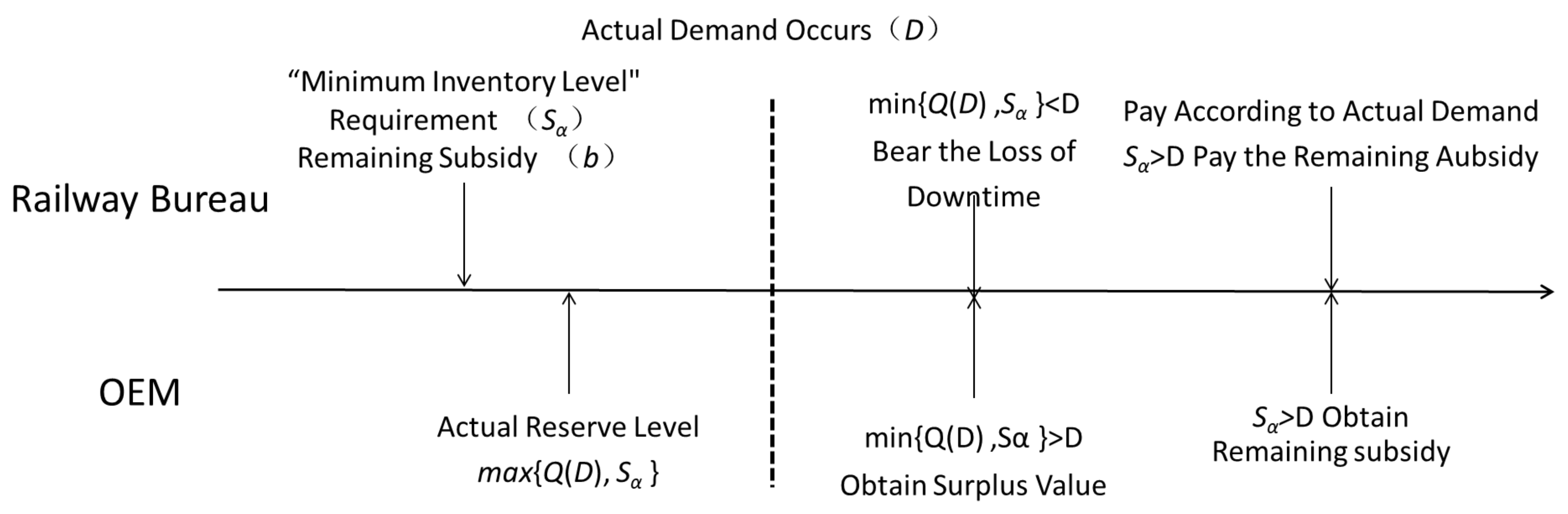
4.1.2. Residual-Subsidy Mechanism Under the Quantity Commitment
- (1)
- When , is a concave function and a monotonically decreasing function with respect to , ;
- (2)
- When , , is a concave function with respect to , .
- (1)
- When , the OEM rejects the contract;
- (2)
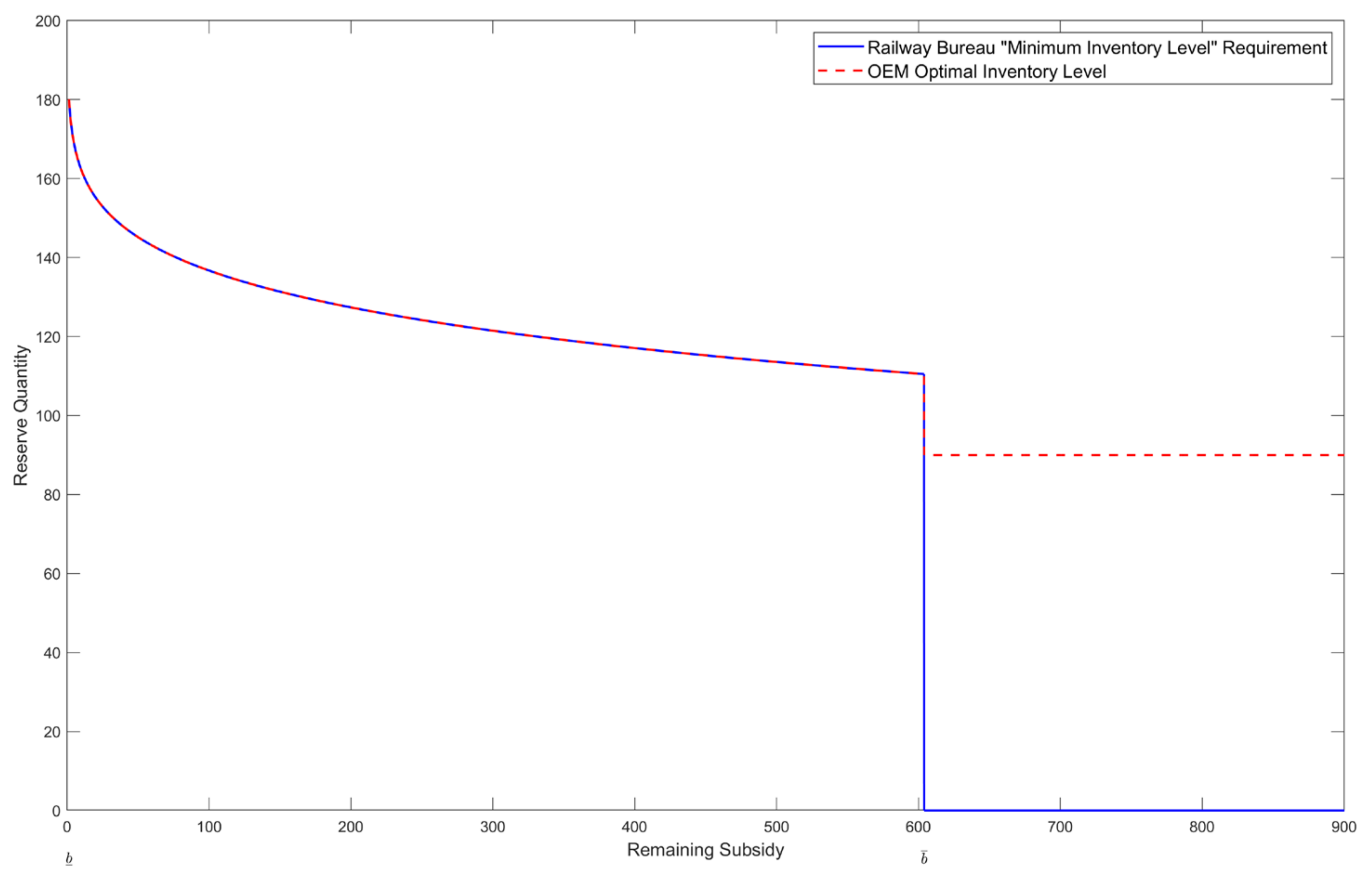
- When , the railway bureau’s optimal “minimum reserve quantity” is , and the OEM’s reserve quantity is , with and ;
- (3)
- When , the railway bureau’s optimal “minimum reserve quantity” is , and the OEM’s reserve quantity is , aligning with decentralized decisions.
4.2. Reward–Punishment Mechanism for Non-Emergency Critical Spare Parts: A Response Time-Based Design
4.2.1. No Reward–Punishment Mechanism
- (1)
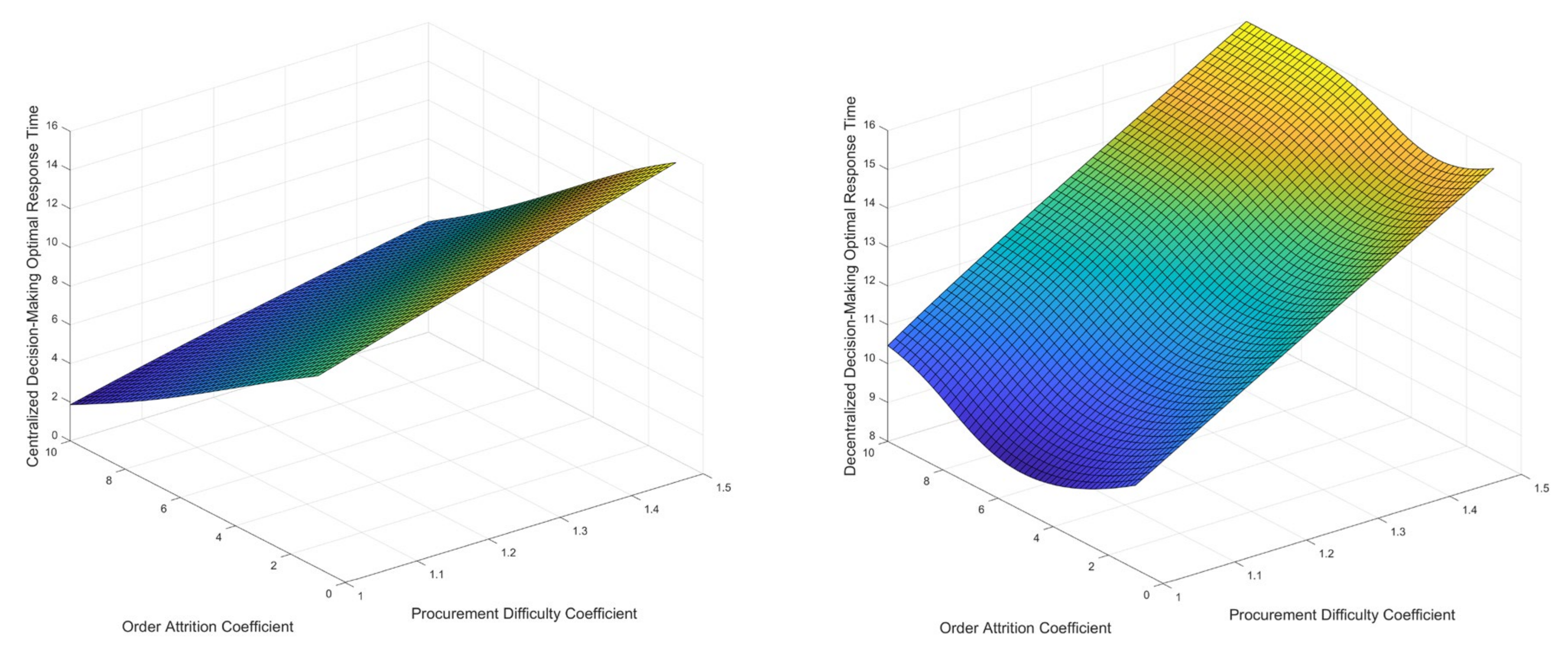
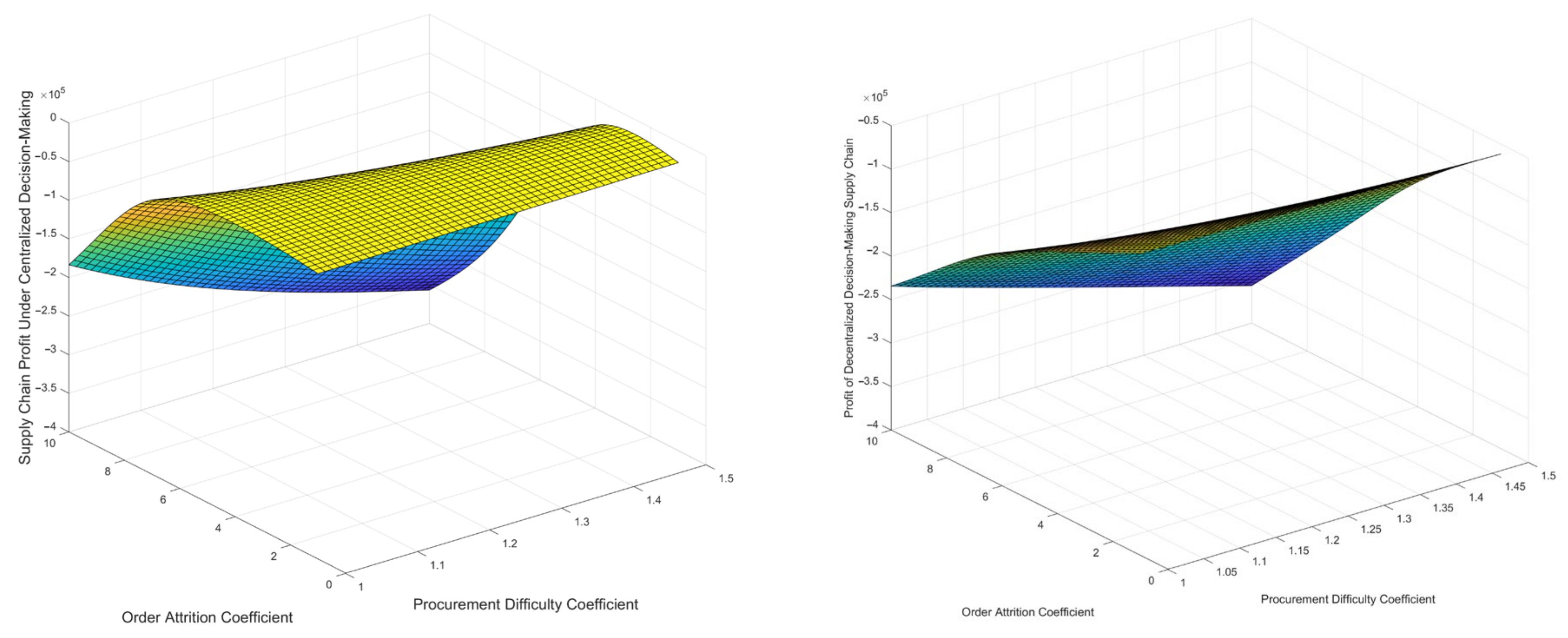
- Under both decentralized decision-making and centralized decision-making, as the procurement difficulty coefficient increases, the optimal response time will increase, and the total profit of the supply chain will decrease;
- (2)
- Under centralized decision-making, as the spare parts order loss coefficient increases, the optimal response time decreases, and the total profit of the supply chain decreases; under decentralized decision-making, as the spare parts order loss coefficient increases, the optimal response time first decreases and then increases, and the total profit of the supply chain decreases.
4.2.2. Residual-Subsidy Mechanism Under Response Time
5. Case Analysis
5.1. Effectiveness Analysis of the Residual-Subsidy Mechanism Under Quantity Commitment
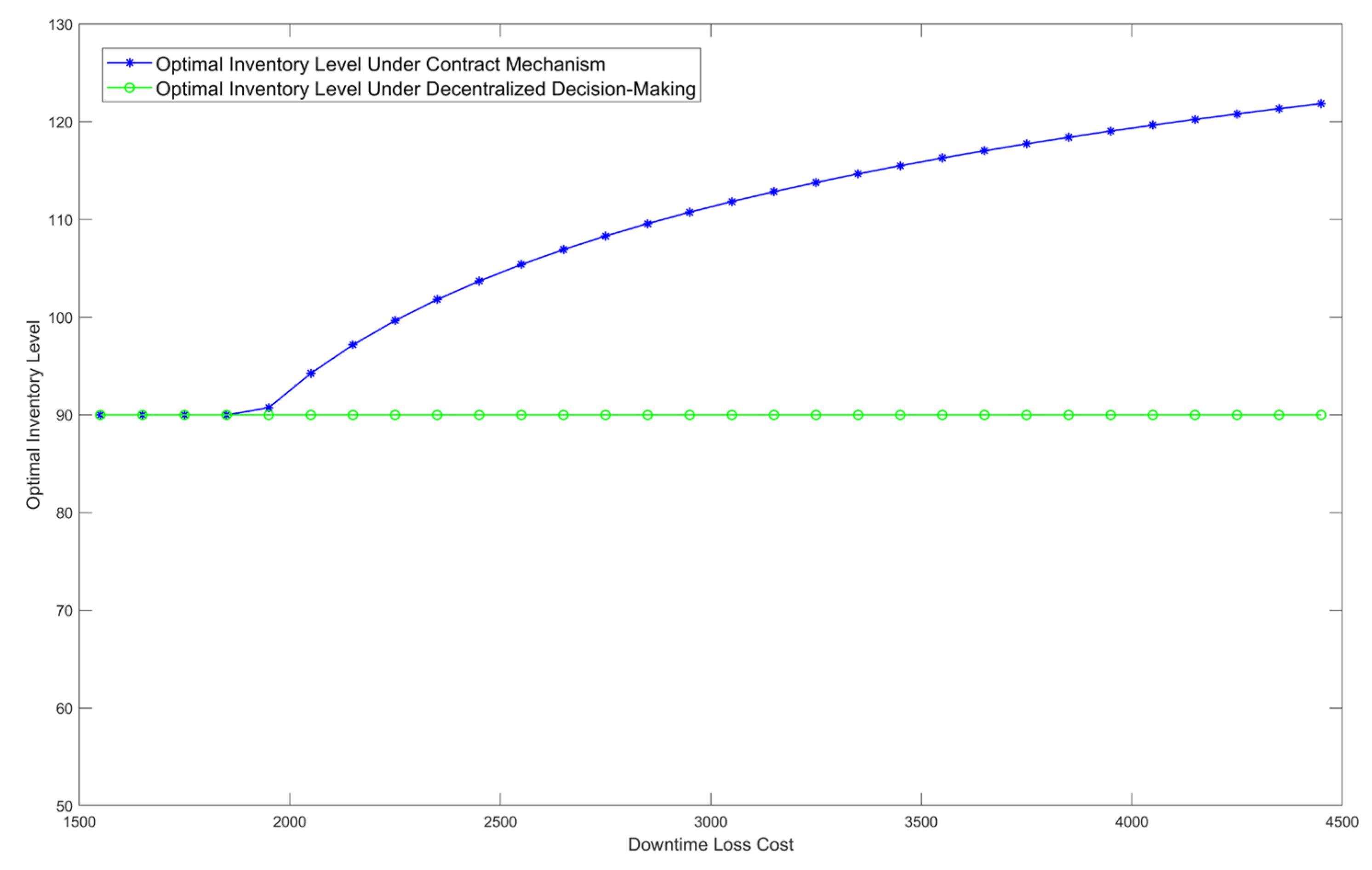
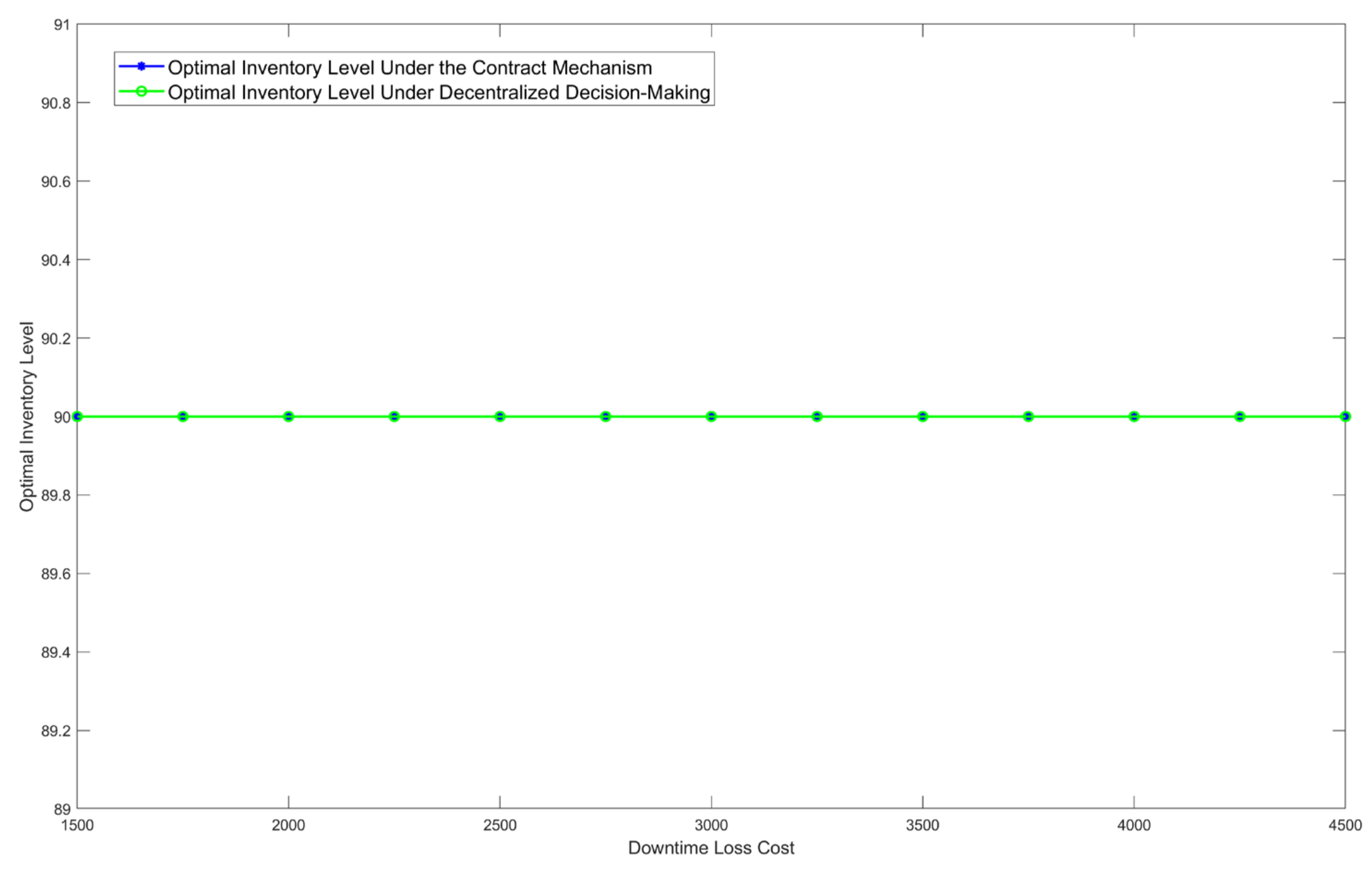
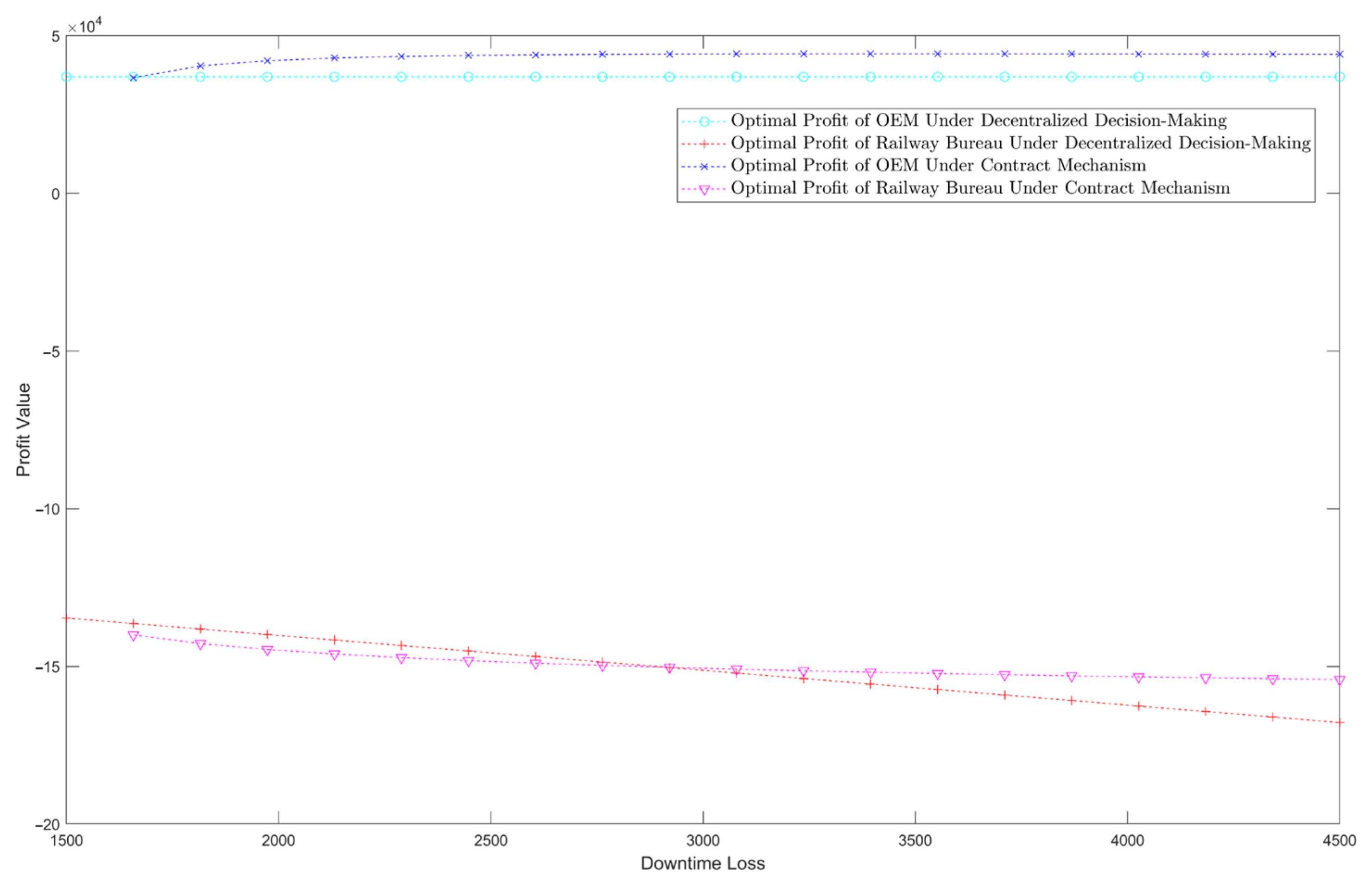
5.1.1. The Impact of Downtime Loss on Supply Chain Members’ Optimal Decision and Optimal Expected Profit
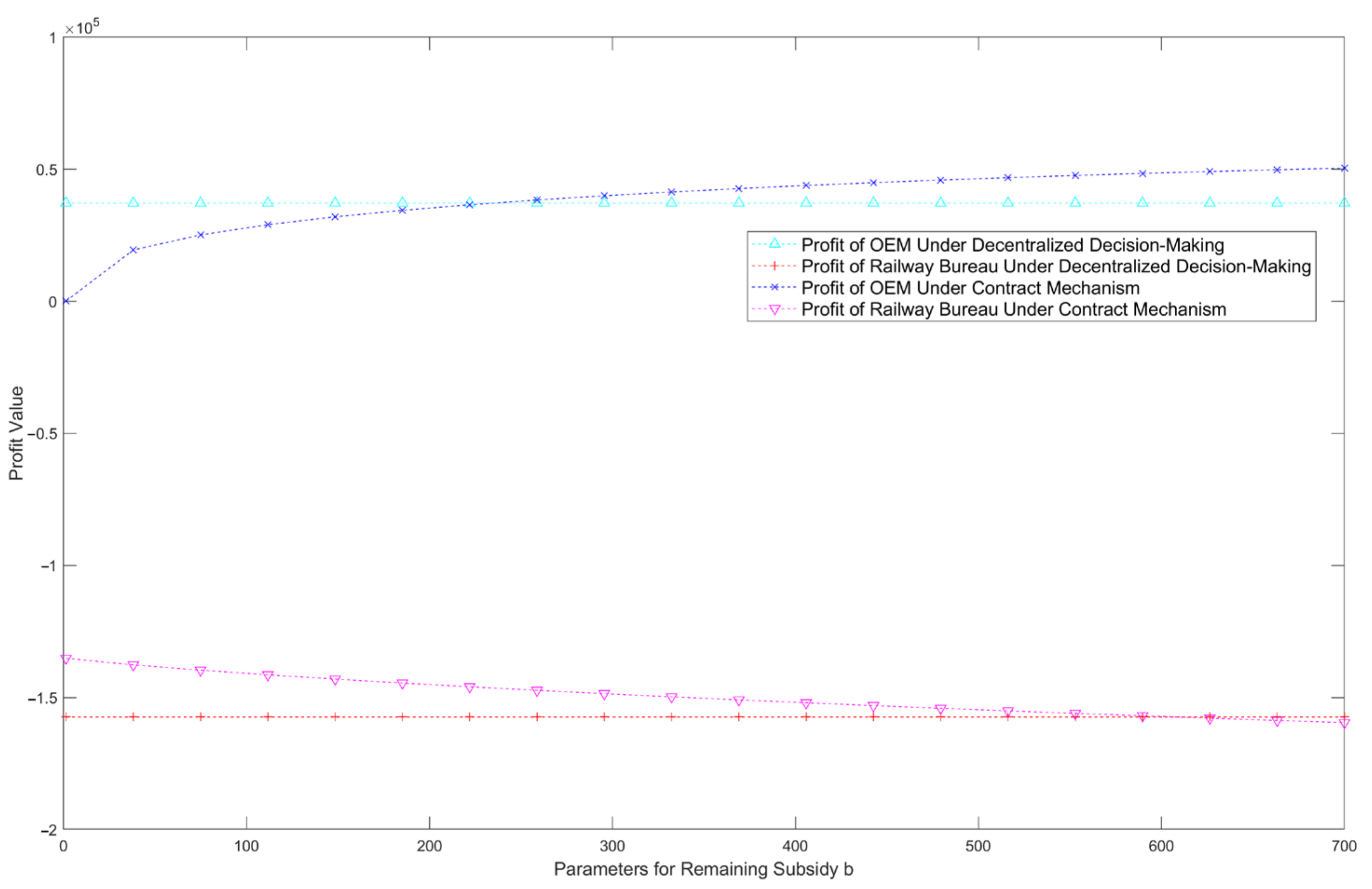
5.1.2. Impact of Contract Residual-Subsidy Parameters on Optimal Decision and Optimal Expected Profit of Supply Chain Members
5.2. Effectiveness Analysis of Cost-Sharing Mechanism Under Response Time
5.2.1. The Impact of Procurement Difficulty Coefficient and Order Loss Coefficient on the Optimal Decision and Optimal Expected Profit of Supply Chain Members
5.2.2. The Impact of Contract Cost-Sharing Parameters on Optimal Expected Profit
6. Conclusions
- Consider the circumstance where emergency critical spare parts are supplied by the OEM at the parts sub-center under on-site inventory supply conditions. A residual-subsidy system under quantity commitment is proposed. Through the building and study of both centralized decision-making and decentralized decision-making models, it is found that the optimal decision attained under the centralized decision-making model is superior to the decisions made under the decentralized decision-making model. The primary research findings are as follows:
- The decision of whether the railway bureau provides a “minimum inventory level” requirement and executes the residual-subsidy plan hinges on comparing the downtime loss to a certain threshold. If the downtime loss exceeds this threshold, the railway bureau is motivated to issue the requirement and implement the subsidy; conversely, if the downtime loss is below this threshold, it is optimal to maintain the decision not to issue the “minimum inventory level” requirement;
- When the downtime loss of spare parts is significant, setting a residual subsidy within a certain parameter range is necessary to increase the inventory levels and reduce the risk of stockouts, indicating the potential for supply chain coordination. Case studies show that after the residual-subsidy contract mechanism was introduced, the OEM’s spare parts inventory increased from 90 under the decentralized decision-making mode to 115, and the total profit of the supply chain also increased accordingly, achieving a Pareto improvement for the supply chain. Within this range, as the residual subsidy increases, the OEM’s inventory level reduces, and the expected profit increases, while the railway bureau’s expected profit decreases. Additionally, the higher the downtime loss cost, the more pronounced the coordination effect produced by the contract mechanism.
- In the setting where non-emergency critical spare parts are centrally stored by the OEM at the parts center and supplied through market procurement, a cost-sharing mechanism based on response time has been designed. Initially, by creating and studying two models, centralized decision-making and decentralized decision-making, it is discovered that the optimal decision achieved under the centralized decision-making model is superior to that under the decentralized decision-making model. The principal research conclusions are as follows:
- In both decentralized decision-making and centralized decision-making, the optimal response time is directly proportional to the procurement difficulty coefficient, while the total profit of the supply chain is inversely proportional to both the procurement difficulty coefficient and the order loss coefficient;
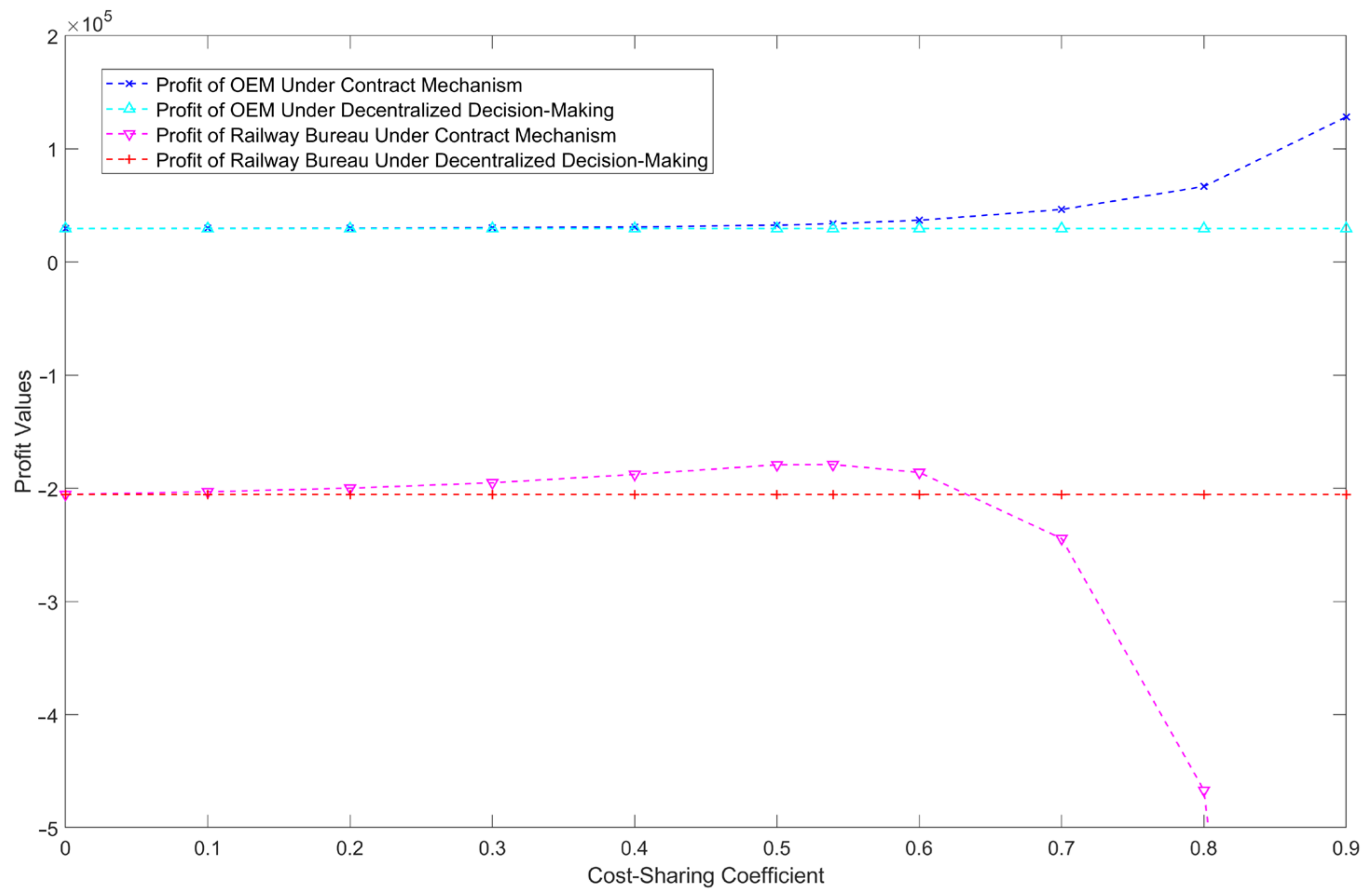
- Compared to decentralized decision-making without a contract, the cost-sharing contract can accelerate the response time, increase the demand satisfaction rate, and enhance the profit of the OEM as the cost-sharing coefficient increases. Meanwhile, the cost for the railway bureau initially decreases and then increases with the rise in the cost-sharing coefficient;
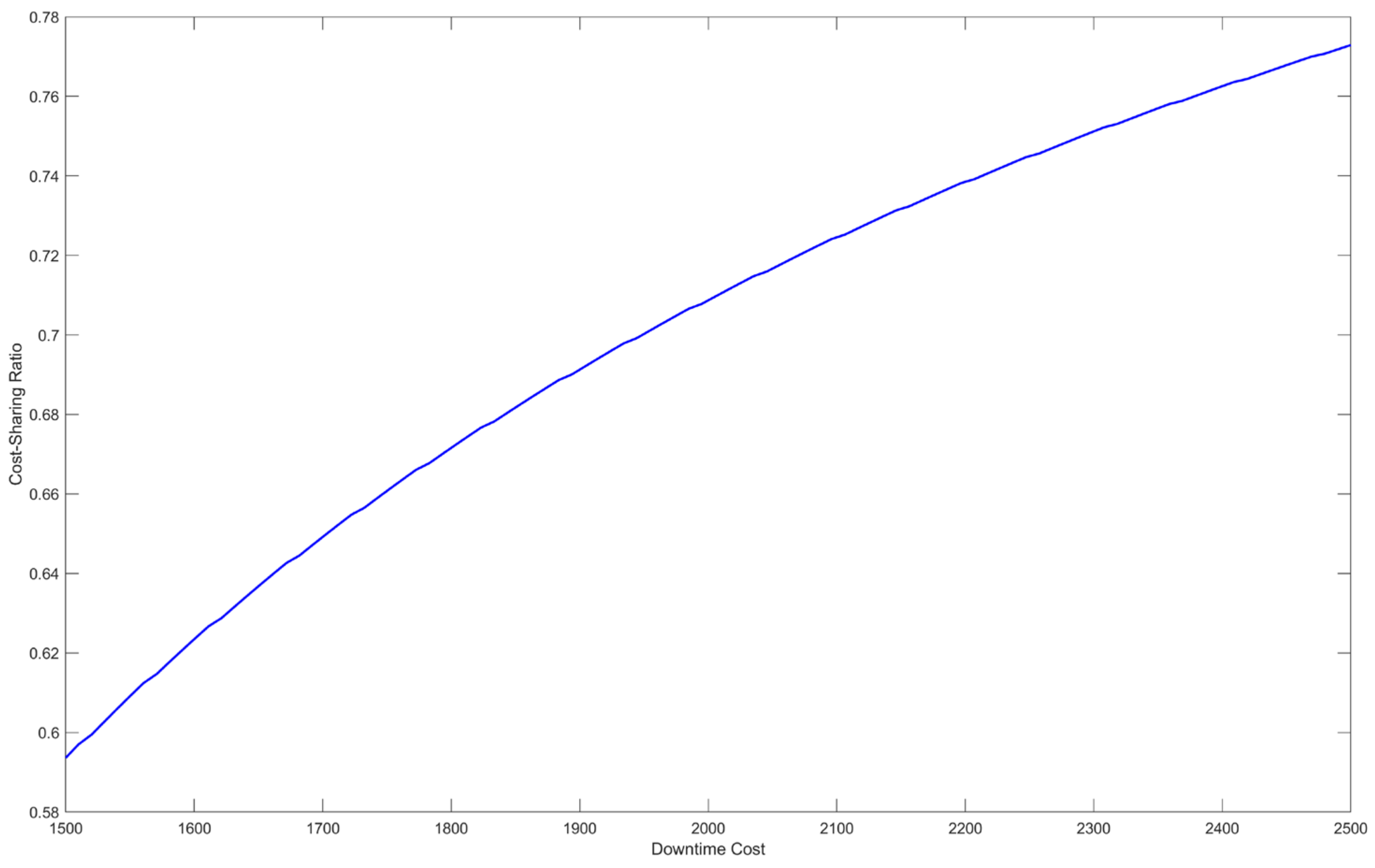
- Upon introducing the contract mechanism, it is observed that the OEM consistently benefits, while the railway bureau needs to meet certain conditions of the cost-sharing parameters to achieve cost reduction. Consequently, by modifying the pertinent parameters in the contract, the distribution of costs among members can be efficiently managed to achieve Pareto improvement. Case studies reveal that after implementing the response time-based cost-sharing mechanism, the OEM’s reaction time decreased from 9.6 days under the decentralized decision-making model to 4.3 days. Furthermore, the total cost of the supply chain was reduced by 15.5%, and the total profit approached the level of the centralized decision-making model. Additionally, the cost-sharing coefficient necessary for the supply chain to attain a coordinated condition grows with the rise in the downtime loss cost of spare parts. For spare parts with high downtime loss costs, the railway bureau must take higher response cost-sharing to assure timely supply.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EMU | Electric Multiple Unit |
| OEM | Original Equipment Manufacturer |
| VMI | Vendor-Managed Inventory |
Appendix A
References
- Bacchetti, A.; Saccani, N. Spare parts classification and demand forecasting for stock control: Investigating the gap between research and practice. Omega 2012, 40, 722–737. [Google Scholar] [CrossRef]
- Teixeira, C.; Lopes, I.; Figueiredo, M. Classification methodology for spare parts management combining maintenance and logistics perspectives. J. Manag. Anal. 2018, 5, 116–135. [Google Scholar] [CrossRef]
- He, Y.; Wang, H.; Yang, G.J. Multi-attribute model on phased sequential preventive maintenance model for component of electric multiple unit. Ind. Eng. Manag. 2021, 26, 18–23. [Google Scholar]
- Zhang, D.; Yang, S.; Li, S.; Fan, J.; Ji, B. Integrated Optimization of the Location–Inventory Problem of Maintenance Component Distribution for High-Speed Railway Operations. Sustainability 2020, 12, 5447. [Google Scholar] [CrossRef]
- Li, D.; Zhao, J.; Peng, Q.; Wang, D.; Zhong, Q. Rolling stock rescheduling in high-speed railway networks via a nested Benders decomposition approach. Transp. Res. Part C Emerg. Technol. 2025, 171, 105001. [Google Scholar] [CrossRef]
- Rahimi-Ghahroodi, S.; Al Hanbali, A.; Zijm, W.; Timmer, J. Multi-resource emergency supply contracts with asymmetric information in the after-sales services. Int. J. Prod. Econ. 2020, 229, 107761. [Google Scholar] [CrossRef]
- Qin, X.; Shao, L.; Jiang, Z.Z. Contract design for equipment after-sales service with business interruption insurance. Eur. J. Oper. Res. 2020, 284, 176–187. [Google Scholar] [CrossRef]
- Kim, S.H.; Cohen, M.A.; Netessine, S.; Veeraraghavan, S. Contracting for infrequent restoration and recovery of mission-critical systems. Manag. Sci. 2010, 56, 1551–1567. [Google Scholar] [CrossRef]
- Lamghari-Idrissi, D.; Basten, R.; van Houtum, G.J. Reducing risks in spare parts service contracts with a long downtime constraint. IISE Trans. 2021, 53, 1067–1080. [Google Scholar]
- Zhang, M.; Wei, K.; He, S.; He, Z.; Yan, W. Performance-based maintenance contract for mission-critical equipment considering spare parts inventory cost-sharing and suppliers’ risk attitudes. Int. J. Prod. Res. 2023, 61, 7524–7539. [Google Scholar] [CrossRef]
- Zhen-Yang, S.; Shao-Xuan, L. Spare parts supply chain coordination based on buy-back contract during end-of-life period. Ind. Eng. Manag. 2019, 24, 23–30. [Google Scholar]
- He, J.; Ma, C.; Pan, K. Capacity investment in supply chain with risk averse supplier under risk diversification contract. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 255–275. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Chen, X. Pricing and order decisions with option contracts in the presence of customer returns. Int. J. Prod. Econ. 2017, 193, 422–436. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Chan, H.K. Channel coordination through subsidy contract design in the mobile phone industry. Int. J. Prod. Econ. 2016, 171, 97–104. [Google Scholar] [CrossRef]
- Ma, C.; He, J.; Huang, F.; Liu, J. Coordination of VMI Supply Chain with Loss Aversion and Replenishment Tactic. Oper. Res. Manag. Sci. 2024, 33, 69. [Google Scholar]
- Wang, D.; Wang, Z.; Zhang, B.; Zhu, L.X. Vendor-managed inventory supply chain coordination based on commitment-penalty contracts with bilateral asymmetric information. Enterp. Inf. Syst. 2020, 16, 508–525. [Google Scholar] [CrossRef]
- Zhu, X.; Xie, L.; Lin, G.; Ma, X. Decision analysis of individual supplier in a vendor-managed inventory program with revenue-sharing contract. Int. J. Ind. Eng. Comput. 2022, 13, 405–420. [Google Scholar] [CrossRef]
- Liu, J.; Huang, F.; Ma, C. Coordination of VMI supply chain with replenishment tactic under risk aversion and sales effort. 4OR 2021, 19, 389–414. [Google Scholar] [CrossRef]
- Qu, J.-L.; Hu, B.-Y. Optimization and Coordination of Supply Chain with Revenue Sharing Contracts Under Supply and Demand Uncertainty. J. Univ. Electron. Sci. Technol. China (Soc. Sci. Ed.) 2017, 19, 57–61. [Google Scholar]
- Cai, J.; Zhong, M.; Shang, J.; Huang, W. Coordinating VMI supply chain under yield uncertainty: Option contract, subsidy contract, and replenishment tactic. Int. J. Prod. Econ. 2017, 185, 196–210. [Google Scholar] [CrossRef]
- Fan, C.; Wang, W.-L.; Ding, C.; Su, Q. On contracts with risk share for vmi program under replenishment strategy. Chin. J. Manag. Sci. 2015, 23, 92–98. [Google Scholar]
- Yin, Z.; Ma, S. Incentives to improve the service level in a random yield supply chain: The role of bonus contracts. Eur. J. Oper. Res. 2015, 244, 778–791. [Google Scholar] [CrossRef]
- Gong, X.; Chen, Y.F.; Yuan, Q. Coordinating Inventory and Pricing Decisions Under Total Minimum Commitment Contracts. Prod. Oper. Manag. 2022, 31, 511–528. [Google Scholar] [CrossRef]
- Cai, J.; Hu, X.; Jiang, F.; Zhou, Q.; Zhang, X.; Xuan, L. Optimal input quantity decisions considering commitment order contracts under yield uncertainty. Int. J. Prod. Econ. 2019, 216, 398–412. [Google Scholar] [CrossRef]
- Han, X.; Yu, Y.; Hu, G. A dynamic newsvendor problem with goodwill-dependent demands and minimum commitment. Omega 2019, 89, 242–256. [Google Scholar] [CrossRef]
- Qiu, R.; Chu, X.; Sun, Y. Dual-channel supply chain decision model based on robust optimization under price and delivery-time dependent demand. Chin. J. Manag. Sci. 2021, 29, 1–12. [Google Scholar]
- Modak, N.M.; Kelle, P. Managing a dual-channel supply chain under price and delivery-time dependent stochastic demand. Eur. J. Oper. Res. 2019, 272, 147–161. [Google Scholar] [CrossRef]
- Cachon, G.P. Supply chain coordination with contracts. Handb. Oper. Res. Manag. Sci. 2003, 11, 227–339. [Google Scholar]
- Sun, J.H.; Zhang, H.B.; Zhao, L.M. Quality control behavior in the three-echelon equipment manufacturing supply chain. Chin. J. Manag. Sci. 2018, 26, 71–83. [Google Scholar]
- Yang, X.; Jing, F.; Ma, N.; Nie, F. Supply chain pricing and effort decisions with the participants’ belief under the uncertain demand. Soft Comput. 2020, 24, 6483–6497. [Google Scholar] [CrossRef]
- Wen, X.; Wang, C. Optimal-quality choice and committed delivery time in build-to-order supply chain. Sustainability 2022, 14, 11746. [Google Scholar] [CrossRef]
| Parameter | Parameter Description |
|---|---|
| Railway bureau spare parts demand probability density function | |
| Railway bureau spare parts demand cumulative distribution function | |
| Maximum railway bureau spare parts demand, with a value of | |
| Railway bureau spare parts “minimum inventory level” requirement | |
| OEM spare parts inventory at parts sub-center | |
| OEM production or procurement unit cost for spare parts | |
| OEM selling price of spare parts | |
| OEM unit inventory holding cost at parts sub-center | |
| Unit spare parts salvage value | |
| Railway bureau unit subsidy for OEM remaining spare parts | |
| Unit downtime loss incurred by railway bureau due to unmet demand | |
| OEM expected profit | |
| Railway bureau expected profit | |
| OEM response time | |
| Difficulty of spare parts procurement | |
| OEM advance reserve quantity, i.e., centralized reserve quantity at parts center | |
| OEM response-effort cost | |
| Spare parts order loss coefficient | |
| Response-effort cost coefficient | |
| Cost-sharing coefficient |
| Variable | Centralized Decision-Making | Decentralized Decision-Making | Residual-Subsidy Contract Decision |
|---|---|---|---|
| 115 | 90 | 115 | |
| — | 37,212.58 | 44,631.92 | |
| — | −157,340.77 | −152,702.10 | |
| −108,070.18 | −120,128.19 | −108,070.18 |
| Variable | Centralized Decision-Making | Decentralized Decision-Making | Cost-Sharing Contract Decision |
|---|---|---|---|
| 4.3 days | 9.6 days | 4.3 days | |
| — | 23,845.59 | 33,867.84 | |
| — | −195,619.44 | −178,947.43 | |
| −145,079.59 | −171,773.85 | −145,079.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, Z.; Xu, J.; Lei, C. Electric Multiple Unit Spare Parts Vendor-Managed Inventory Contract Mechanism Design. Systems 2025, 13, 585. https://doi.org/10.3390/systems13070585
Shao Z, Xu J, Lei C. Electric Multiple Unit Spare Parts Vendor-Managed Inventory Contract Mechanism Design. Systems. 2025; 13(7):585. https://doi.org/10.3390/systems13070585
Chicago/Turabian StyleShao, Ziqi, Jie Xu, and Cunjie Lei. 2025. "Electric Multiple Unit Spare Parts Vendor-Managed Inventory Contract Mechanism Design" Systems 13, no. 7: 585. https://doi.org/10.3390/systems13070585
APA StyleShao, Z., Xu, J., & Lei, C. (2025). Electric Multiple Unit Spare Parts Vendor-Managed Inventory Contract Mechanism Design. Systems, 13(7), 585. https://doi.org/10.3390/systems13070585





