Abstract
Improving the performance of the operations of ride-hailing platforms (RHPs) by adequately considering drivers’ switching behaviors is becoming crucial for their profitability and sustainability. This study explores how to optimize the operations of RHPs by investigating the impact of commission rates on drivers’ switching behaviors in a dynamic mobility market. Two queue-theory-based mathematical models have been developed to explore the relationship between commission rates, drivers’ switching behaviors, and critical platform parameters in optimizing the operations of RHPs. Numerical examples are presented to demonstrate the applicability of such models in determining the best commission rate to optimize the operations of RHPs in duopoly and fully competitive market conditions. The findings suggest that understanding the intricate relationship between commission rates, drivers’ switching behaviors, and critical platform parameters is significant for RHPs in formulating appropriate strategies and policies to ensure their sustainable operations.
1. Introduction
Ride-hailing is an emerging shared mobility solution focusing on the delivery of prearranged mobility services that connect drivers of private vehicles with customers through ride-hailing platforms (RHPs) [1,2]. It is becoming increasingly popular due to the rapid development of digital technologies [3] and the increasing availability of mobile applications for facilitating booking, paying, and rating mobility services in a holistic manner [4,5,6]. This results in growing competition between these platforms [7,8,9].
There are increasing initiatives in the development of RHPs in China for improving the mobility of individuals [10], exemplified by the average daily order volume of about 29 million trips on more than 349 RHPs [11]. This leads to fierce competition between and among RHPs for their profitability and sustainability in a dynamic mobility market. More and more platforms have joined the ride-hailing market due to the increasing demand for shared mobility services after the pandemic [12], further exacerbating the competition. As a result, determining how to improve the performance of ride-hailing operations of these digital platforms is becoming critical [13].
The operations of RHPs are running in a two-sided market by connecting drivers with customers in a dynamic environment [14,15]. Improving the operations of RHPs, therefore, is becoming complex and challenging [16,17]. There are various variables that must be adequately considered in formulating appropriate strategies and policies for optimizing the operations of RHPs in a profitable and sustainable manner [13,18,19,20].
Drivers are the vital resource in the mobility market for providing ride-hailing services through their employment in RHPs [10,21]. They often change their employment from one platform to another, commonly referred to as drivers’ switching behaviors [22], in pursuing better working conditions including higher income [23,24]. Such switching behaviors adversely affect the sustainable operations of RHPs due to the potential shortage of platform drivers, resulting in increased customer waiting time and poor customer service quality, ultimately leading to the deterioration of the profitability and sustainability of individual RHPs [8,25,26].
Understanding how drivers’ switching behaviors affect the profitability and sustainability of RHPs is critical for improving their operations [19,27]. Such behaviors are usually related to the determination of the commission rate between RHPs and drivers. Setting a high commission rate, i.e., the proportion of the fare to the platform, can increase the revenue of the platform in the short term. This, however, may lead to more frequent drivers’ switching behaviors. It, therefore, weakens the overall profitability and sustainability of individual RHPs in the long term [17,26]. This suggests that exploring the interplay between commission rates, drivers’ switching behaviors, and critical platform parameters is crucial for ensuring the profitable and sustainable operations of RHPs.
Many studies have been conducted to explore how to develop effective operations strategies through leveraging various pricing mechanisms and non-monetary incentives for optimizing the operations of RHPs [13]. Cohen and Zhang [28], for example, develop an endogenous model to simulate the operations of two-sided RHPs, leading to the determination of the optimal service price and the most appropriate commission rate in an analytical manner. Sun and Ertz [26] propose a system dynamic modeling framework to explore the ride-hailing operations, discovering that commission rates, order prices, and investment levels are the critical variables for optimizing the operations of RHPs. Zhong et al. [22] examine how RHPs compete with traditional taxi companies, resulting in designing specific pricing strategies under unregulated and regulated environments in optimizing the operations of RHPs. The studies above have provided insights into how to improve the operations of RHPs from different perspectives.
Existing studies concentrate on understanding how to improve the operations of RHPs by maximizing platform revenue [29], improving customer service utility [30], and increasing customers’ social welfare [24,28]. While commission rates are widely considered in most studies, the findings on the impact of commission rates on the profitability and sustainability of platform operations are inconclusive [26]. There is a lack of understanding of the relationship between commission rates, drivers’ switching behaviors, and critical platform parameters in optimizing the operations of RHPs. To address these gaps, a research question that this study aims to address is formulated as follows: How do commission rates affect drivers’ switching behaviors in optimizing the operations of RHPs in the dynamic mobility market?
This study examines the impact of commission rates on drivers’ switching behaviors for optimizing the operations of RHPs. The related literature has been comprehensively reviewed, leading to the development of two queue-theory-based mathematical models for exploring the relationship between commission rates, drivers’ switching behaviors, and critical platform parameters in optimizing the operations of RHPs. Numerical examples are presented to demonstrate the applicability of the two models in optimizing the operations of RHPs. The study reveals that there is an intricate relationship between commission rates, drivers’ switching behaviors, and critical platform parameters in optimizing platform operations. These findings highlight the importance of understanding such a complex relationship for formulating appropriate strategies and policies to ensure the profitability and sustainability of RHPs in a dynamic mobility market.
In what follows, Section 2 presents a literature review, followed by the formulation of the research problem in Section 3. Section 4 develops two queue-theory-based mathematical models. Section 5 describes three examples for demonstrating the applicability of the two models in optimizing the operations of RHPs in the dynamic ride-hailing market. Section 6 presents the research findings followed by the concluding remarks.
2. Literature Review
Ride-hailing is operated in a dynamic mobility market [13,19]. Optimizing ride-hailing operations involves making timely decisions with respect to specific demand and supply issues while considering the requirements and expectations of various stakeholders [10]. This brings substantial complexity and challenges to individual RHPs [19,26,31,32,33,34].
Much research has been conducted to understand the operations of RHPs from different perspectives. An examination of such research shows that existing studies can be classified into three streams including (a) operations, (b) critical factors, and (c) market evolution and platform competition. Such studies have provided insights into how to optimize the operations of RHPs in the dynamic ride-hailing market. Table 1 presents an overview of these studies from these three perspectives.

Table 1.
An overview of the related studies on optimizing ride-hailing operations.
Operations-based studies focus on the formulation of specific strategies and policies for improving the performance of RHPs [8,9,13,30,35,36,37,38,39,40,41,42]. Bahrami et al. [8], for example, establish an analytical model to understand the impact of operational variables in matching supply with demand to maximize the profit of RHPs. Lin et al. [9] examine the impact of an asset-heavy model on the profitability of RHPs, revealing that such a model can provide a “win–win–win” outcome for platforms, customers, and drivers in the competitive mobility market. Guo et al. [13] analyze the impact of three service mode selection strategies on customers and drivers, leading to the identification of the conditions that bring the optimal platform revenue. Chen et al. [30] develop a dynamic model for characterizing the matching process between waiting customers and vacant cars in ride-sourcing for optimizing the operations of RHPs. Alonso-Mora et al. [35] present an algorithm for optimizing the operations of large-scale RHPs focusing on more passenger assignments and less waiting time via an experiment using real-world data. Di and Ban [36] propose a conceptual framework for exploring the interaction between private vehicles and service fleets for developing sustainable transport. Ke et al. [37] investigate the benefits of ride-pooling with respect to different levels of customer demands using specific strategies, finding that the level of customer demand and the range of the matching window are the two critical platform parameters for optimizing their operations. Sun et al. [38] discover that two types of order assignment strategies have distinct impacts on the operations of RHPs. Xu et al. [39] propose a generalized fluid framework incorporating appropriate commission rate setting for modeling ride-hailing to improve the operations of RHPs. Ke and Qian [34] develop an optimal pricing scheme for improving the operations of RHPs. Bandiera et al. [40] present a mathematical model to simulate the interaction between service providers and customers. Xi et al. [41] develop a multi-leader–multi-follower model in which platforms compete to optimize their operations. Yao and Zhang [42] adopt a many-to-many matching framework for solving the pricing problem that RHPs face in a multi-modal transport network.
Critical-factor-aligned studies concentrate on understanding the critical factors affecting the operations of RHPs in the dynamic ride-hailing market [10,14,19,22,43,44,45,46]. Zhou et al. [10], for example, offer an empirical explanation for the turnover intention of ride-hailing drivers in which drivers’ income satisfaction is critical for affecting the operations of RHPs. Mourad et al. [14] discover that demand attributes, drivers’ behaviors, driver supply, and platform service capacity are critical for optimizing the operations of RHPs. Wang and Yang [19] reveal that service quality, driver income, customer demand, and driver supply are crucial for influencing the efficiency of the operations of RHPs. Zhong et al. [22] find that the intensity of the competition between platforms, commission rates, and drivers’ opportunity costs are critical for affecting the operations of RHPs. Acheampong et al. [43] show that socio-demographic factors, perceived benefits, ease of use, perceived risks, and car-dependent lifestyle influence the utilization of ride-hailing services. Dean and Kockelman [44] find that trip length, day of the week, pedestrian density, multi-modal infrastructure, and socioeconomic characteristics have a substantial impact on ride-hailing operations. Li et al. [45] examine the critical factors for using different types of ride-hailing services, showing that there are different critical factors that influence the utilization of respective ride-hailing services. Chen et al. [46] argue that drivers’ income satisfaction is critical for the operations of RHPs.
Market-evolution-and-platform-competition-oriented studies try to understand the interaction between platform operations, service competition, and market evolution in delivering ride-hailing services [2,15,19,26,47,48,49,50]. Wang and Li [2], for example, study the competition between an emerging autonomous RHP and a traditional RHP by characterizing the equilibrium of their competition, finding that the transfer of autonomous vehicles between the two types of platforms can lead to a win–win outcome in an increasingly competitive mobility market. Zhang et al. [15] examine the competition between RHPs in a shared economy, revealing that the competition is more intense in a shared economy than in a traditional one. Wang and Yang [19] examine the strategic and operational issues with respect to different types of digital platforms for understanding how to improve the operations of RHPs. Sun and Ertz [26] explore the growth mechanism of a simulated digital platform from a systematic perspective for investigating the sustainable growth mechanism in optimizing the operations of RHPs. Cachon [47] states that pricing mechanism, location, and control of the supply side are the substantial factors influencing the competition between RHPs and market evolution. Benjaafar and Hu [48] argue that understanding how incentives are affected by multisided platforms is critical for optimizing platform operations. Rietveld and Schilling [49] present a comprehensive review of the platform competition literature for developing sustainable operations of RHPs. Sun et al. [50] investigate the influence of various regulatory policies on the operations of RHPs with respect to the growth of individual platforms.
The discussion above has provided a better understanding of how to improve the operations of RHPs from three perspectives. There is, however, a lack of studies on how to achieve a subtle trade-off between platform profitability and customer service quality in optimizing the operations of RHPs. The interplay between commission rates, drivers’ switching behaviors, and critical platform parameters in optimizing the operations of RHPs is unclear. This demonstrates an urgent need to address the current research problem as detailed above in this study.
3. Problem Formulation
There are various platform variables that affect the operations of RHPs in the dynamic ride-hailing market [15,26]. Such variables can be classified into three perspectives including the supply side, the demand side, and the operations side. Supply-side factors include drivers’ commission rates, drivers’ quantity, drivers’ switching behaviors, and drivers’ income. Demand-side variables consist of customers’ socio-demographics, trip attributes, and psychological or behavioral factors. Operations-side factors include price and income-related factors in which commission rates are employed as a main income lever for the profitability of individual RHPs.
Commission rates are critical for optimizing the operations of RHPs. Increasing the commission rate can lead to higher platform profitability while introducing drivers’ switching behaviors. This negatively affects the platform’s customer service quality, thus reducing the number of orders and leading to a decline in platform profitability [15,26].
This section formulates the research problem to facilitate the development of the mathematical model for optimizing the operations of RHPs. To pave the way for the problem formulation process, a comprehensive overview of the operations of RHPs is discussed. How the commission rate affects the platform performance is elaborated. Some basic assumptions are proposed together with notations and specifications employed in the study. All these underpin the development of the mathematical model for addressing the research problem formulated in this section.
3.1. The Mechanism and Evolution of the Operations of RHPs
There are three stages in the development of the ride-hailing market including (a) a monopolistic market, (b) an oligarchic market, and (c) a competitive market [4,31,32,33]. Stage one is characterized by the use of conventional taxis in the market, referred to as hailing systems RT. Stage two is exemplified by the introduction of RHPs, indicated as hailing systems R1. Stage three features the addition of more RHPs in the market, referred to as RHP follow-up systems R2.
Determining the commission rate directly affects the relationship between RHPs and their drivers, leading to drivers’ switching behaviors [17,33]. Excessive commission rates encourage drivers to transfer from one platform to another, therefore reducing the availability of drivers in specific RHPs. As a result, the service capacity of such RHPs suffers. This leads to customers waiting for a longer time for expected services [19]. The profitability of RHPs and their sustainability in the long term are, therefore, adversely affected.
As critical platform performance indicators, customer waiting time and platform productivity have a crucial impact on the customer service quality of RHPs [19,21]. Excessive customer waiting time or poor productivity have a negative impact on platform customer service quality. Customers can cancel orders due to long waiting time, leading to a reduction in platform revenue. The decrease in platform revenue affects the determination of the commission rate in the platform. RHPs, therefore, have an evident motivation to increase the commission rate to pursue higher operational revenue, while contemplating their commission rate decisions for achieving the trade-off between operations revenue in the short term and profitable operations in the long term, especially when facing increasingly fierce market competition [22,26,34]. Figure 1 presents an overview of the mechanism of the operations of RHPs in a dynamic ride-hailing market.
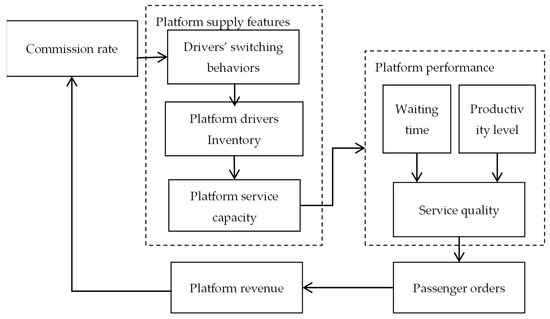
Figure 1.
An overview of the mechanism of the operations of RHPs.
3.2. Drivers’ Switching Behaviors
This study explores the impact of commission rates on drivers’ switching behaviors for optimizing the operations of RHPs in a dynamic mobility market. Without the loss of generality, the study assumes that the ride-hailing market is open and dynamic in which drivers are free to move from one platform to another to pursue individual benefits.
The availability of drivers influences customer service quality and platform profitability [10,50]. As a result, the leading platform needs to set up a reasonable commission rate to mitigate the loss of drivers in ensuring its customer service quality. Platform customer service quality is measured by customer waiting time, which is a function of the number of drivers in the platform. The number of platform drivers is correlated with the commission rate. Excessive commission rates reduce drivers’ income, thus resulting in drivers’ switching behaviors [21,46].
The total number of RHPs in the market is assumed as N. The starting time that drivers begin their switching behaviors is T1. The ending time that drivers stop their switching behaviors from the leading RHP R1 to Ri is Ti. The number of drivers switching from R1 to the other RHP Ri is x1i. Here, subscript i denotes 2, 3, …, N. It is assumed that the leading RHP R1 has sufficient operations information; i.e., the drivers’ switching quantities x12, x13, …, x1N are well known. The switching process of individual drivers between the leading RHP and other RHPs is illustrated in Figure 2.
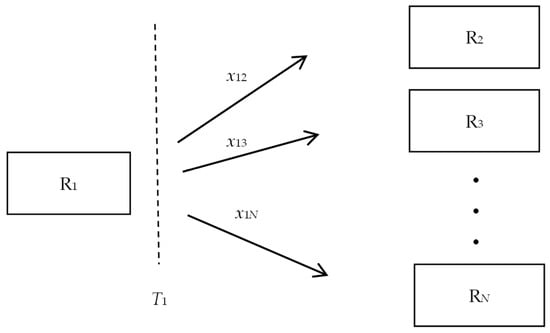
Figure 2.
Overview of drivers’ switching behaviors in a dynamic ride-hailing market.
3.3. Theoretical Foundation and Assumptions
This study treats the ride-hailing market as a queueing system [19,27]. It is assumed that there are no restrictions on the number of customers and platform capacity. Ride-hailing services are provided according to the principle of first-in and first-served [8,19]. Customers waiting for rides on the roadside or sending orders on their smart devices, such as mobile phones or tablets, are regarded as the “generation” of customers’ demand [27]. Drivers pick up passengers on the roadside or accept customer orders on their smart devices through ride-hailing apps, which are regarded as starting to provide the services. Customers are regarded as “leaving” when they arrive at their destinations.
With the assumptions above, the ride-hailing market is treated as an M/M/S queueing system [27,51]. Based on the premise of knowing the arrival rate of customer orders and the vehicle service rate, crucial platform parameters such as customer queue length, customer waiting time, and average queue length can be derived. See Appendix A for the details.
Drivers’ switching behaviors have a substantial impact on the operations of RHPs [14,19]. To better understand the relationship between commission rates, drivers’ switching behaviors, and critical platform parameters in optimizing the operations of RHPs, several further assumptions are proposed in this study as follows:
Assumption 1:
The average trip distance and the unit price for the average trip distance are exogenous, determined by the travel demand and the current ride-hailing market properties.
Assumption 2:
The generation of customer demand orders is a Poisson process with parameter , and the time interval for drivers to provide services follows the exponential distribution with parameter .
Assumption 3:
Drivers’ switching rate between RHPs is proportional to the commission rate r and inversely proportional to platform productivity p.
There are some notations that this study uses in addressing the problem above. Such notations are detailed in Table 2.

Table 2.
Notations and specifications.
4. The Model
Two queue-theory-based mathematical models are developed for exploring the relationship between commission rates, drivers’ switching behaviors, and crucial platform parameters including platform drivers’ market share proportion , platform productivity , and driver switching lasting time period from the leading RHP R1 to the ith RHP Ri in optimizing the operations of RHPs. The operational revenue of the ith RHP is formulated as the cumulative order income as follows:
This operational revenue function characterized as in Equation (1) has general applicability for different shared mobility modes such as ride-sourcing and ride-splitting [7]. The presence of ride-splitting means a decrease in the amount of customer orders in the market. All these situations can be addressed by changing the value of variable Vi in the operational revenue function as in Equation (1).
A duopoly competitive market in which there are two platforms, R1 and R2, is considered first. Here, R1 is the leader, and R2 is the follower. Drivers switch from R1 to R2 in the period . To ensure the customer service quality of the platform, platform R1 must set an appropriate commission rate to ensure that the average waiting time is not higher than that of R2. As a result, the number of drivers switched x must satisfy the following condition:
To optimize the operations of RHPs, the best commission rate must be determined as follows:
Model 1:
A fully competitive mobility market is considered here in which there are N platforms R1, …, RN existing in the market. R1 is the leading platform, and R2, …, RN are the followers. Drivers switch from R1 to R2 in the period . Drivers switch from R1 to R3 in the period , …, and from R1 to RN in the period . To ensure the level of customer service quality, R1 must set an appropriate commission rate to guarantee that the average waiting time is not higher than all other platforms R2~RN. As a result, the number of drivers switched must satisfy the condition as follows:
To optimize the ride-hailing operations of RHPs, the optimal commission rate must be determined as follows:
Model 2:
To obtain the optimal solution of Model 1 and Model 2, the objective function must be examined first. Indeed, . This shows that the objective function is a non-negative linear function with a single independent variable with Assumption 1.
To determine the optimal commission rate based on Model 1 and Model 2, it is required to articulate the explicit expression of the commission rate according to the constraint condition of Model 1 and Model 2. The constraint conditions of the two models comprise a set of inequalities which are described as a customer waiting time function . If the monotonic features of the function could be garnered, the explicit expression of the commission rate can be derived analytically. Proposition 1 shows that the function is monotonic with the independent variable x.
Proposition 1.
It is claimed that is a monotonic descent function. Here, independent variable , parameters , and satisfies . See Appendix B for the proof.
Both Model 1 and Model 2 are examined with respect to their characteristics and functionalities. With respect to Model 1, , drivers’ switching quantity satisfies based on Proposition 1. It is easy to know . From Assumption 3, the driver switching rate . In the time period , the cumulative drivers’ switching quantity . This means that . The commission rate can then be derived immediately as follows:
The optimal commission rate in Model 1 is from Equation (4). This means that the optimal commission rate is related to four operation parameters including (a) : the total number of drivers in the market, (b) : the difference between drivers’ market share proportion of the leading platform and that of the following platform, (c) : the productivity level of the leading platform, and (d) : the time period between the start time and the end time of drivers’ switching behaviors.
For a given ride-hailing market with the total number of drivers fixed, the optimal commission rate is positively proportional to the difference between the drivers’ market share proportion between two RHPs and the productivity of the leading platform R1. It is inversely proportional to the period between the start time and the end time of drivers’ switching behavior .
An examination of Model 2, , finds that drivers’ switching quantity satisfies based on Proposition 1. Assumption 3 indicates that the drivers’ transferring rate . In the period , the cumulative drivers’ switching quantity .
Substituting into , this can lead to . That means .
Based on this relationship, the upper boundary of the commission rate can be obtained as follows:
It is easy to know that if the number of RHPs equals 2 (), Model 2 is equivalent to Model 1. There are platforms in a general ride-hailing market in which . As a result, the optimal commission rate in Model 2 can be presented as follows:
This means that the leading platform R1 should adopt the operations strategy by setting the commission rate as . This can ensure that the leading platform R1 is more competitive than other following RHPs.
The solution algorithm for calculating the optimal commission rate upper boundary in Model 1 is straightforward and simple. The solution algorithm for Model 2 is presented as follows:
- Step 1:
- Initialization. Given the total available number of drivers in the market , the productivity level of platform R1, the market share information of RHP ,. The starting time that a driver begins switching in the market is , and the ending times that a driver stops switching to the ith RHP are ,;
- Step 2:
- Calculate the real number sequence , where ;
- Step 3:
- Search the minimum value of sequence , ;
- Step 4:
- Set the optimal commission rate as , .
5. Examples
Three numerical examples are presented to demonstrate the applicability of the models above for optimizing the operations of RHPs in the dynamic ride-hailing market. The first one is based on Model 1 with a focus on obtaining the commission rate upper boundary and exploring the relationship between commission rates, drivers’ switching behaviors, and the critical platform parameters under the duopoly competitive condition. The second one is based on Model 2 for demonstrating how the optimal commission rate is determined for optimizing the operations of RHPs in the fully competitive ride-hailing market. The third one is used to demonstrate the validity of the two models for different shared mobility modes.
5.1. Example One
The first numerical example is the simulation of a duopoly competitive market in which there are two platforms, R1 and R2. The objective of R1 is to maximize its revenue while ensuring its customer service quality. The objective function and constraint conditions of Model 1 proposed in Section 4 characterize this situation.
To explore how various platform parameters affect the determination of the optimal commission rate in this numerical example, a comparative analysis between eight different scenarios is conducted, as shown in Table 3. Three platform parameters are incorporated in the proposed queue-theory-based mathematical model. When one parameter is changed every time, there are three independent scenarios produced. When two of the three parameters are changed every time, there are three more independent scenarios. When all three parameters are changed simultaneously, there is another scenario. With the consideration of the basic scenario as the comparative baseline, a total of eight scenarios are formulated in the study to investigate the impact of changing the platform parameters on the best commission rate in optimizing the operations of RHPs. Here, the values of these parameters refer to empirical observations of real platform operations.

Scenario 1 offers a fundamental benchmark to demonstrate how the change in related platform parameters influences the determination of the optimal commission rate. For the given drivers’ market share proportion of two platforms (0.7), (0.3), the time period between the starting time and the ending time of drivers’ switching behaviors (5000), the productivity level of the platform (0.45), and the total available number of drivers in the market (10,000), the optimal commission rate c* is calculated at 36%.
Scenario 2 investigates the impact of drivers’ market share proportion on the optimal commission rate. When the difference in drivers’ market share proportion between two RHPs decreases ( is changed from 0.4 to 0.15), the optimal commission rate of leading platform R1 is decreased from 36% to 13.5%. This reveals that if the platform has a higher drivers’ market share proportion, it will have the chance to set a higher commission rate in optimizing its operations.
Scenario 3 examines the impact of drivers’ switching behavior lasting time on the optimal commission rate. When the drivers’ switching behavior lasting time R1 increases ( is changed from 5000 to 10,000), the optimal commission rate of the leading platform R1 is decreased from 36% to 18%. This shows that the drivers’ switching time period affects adversely the optimal commission rate. The longer the period of drivers’ switching behaviors lasts, the smaller the commission rate that the platform should adopt.
Scenario 4 explores the joint impact of drivers’ market share proportion and drivers’ switching behavior lasting time on the optimal commission rate. When the difference in the drivers’ market share proportion between two RHPs is becoming smaller ( is changed from 0.4 to 0.15), and the drivers’ switching behavior lasting time is longer ( is changed from 5000 to 10,000), the optimal commission rate of the leading platform R1 is decreased from 36% to 6.75%. The optimal commission rate is smaller than that in Scenario 3 (6.75% compared to 18%). This demonstrates that drivers’ market share proportion and drivers’ switching behavior lasting time amplify the impact on the optimal commission rate of the leading platform.
Scenario 5 studies the impact of the productivity of the leading platform on the optimal commission rate. When the productivity of the leading platform R1 is higher (0.45 to 0.65), the optimal commission rate of the leading platform R1 is increased from 36% to 52%. This reveals that higher productivity allows the leading platform to set up higher commission rates in optimizing its operations. It means that RHPs should endeavor to improve their productivity so that they have more chances to set higher commission rates for optimizing their operations in the competitive mobility market.
Scenario 6 probes the joint impact of the productivity and drivers’ market share proportion on the commission rate in optimizing the operations of RHPs. When the productivity of the leading platform R1 is higher (0.45 to 0.65), and the difference in the drivers’ market share proportion between two RHPs is becoming smaller (0.4 to 0.15), the optimal commission rate of the leading platform R1 is decreased from 36% to 19.5%. This reveals that the increase in the platform productivity and the decrease in the drivers’ market share proportion can cause the leading platform to reduce its commission rate to pursue more operations revenue.
Scenario 7 concentrates on investigating the joint effect of the platform productivity and the drivers’ switching behavior lasting time on the optimal commission rate. When the productivity of the leading platform R1 is higher (0.45 to 0.65), and the drivers’ switching behavior lasting time is longer ( is changed from 5000 to 10,000), the optimal commission rate of the leading platform R1 is decreased from 36% to 26%. This demonstrates that the leading platform must reduce its commission rate to pursue more operations revenue when its productivity increases and drivers’ switching behavior lasts longer.
Scenario 8 studies the joint effect of platform productivity, drivers’ market share proportion and drivers’ switching behavior lasting time on the optimal commission rate. When the productivity of the leader platform R1 is higher (0.45 to 0.65), the difference in the drivers’ market share proportion between two RHPs becomes smaller (0.4 to 0.15), and the drivers’ switching behavior lasting time is longer (from 5000 to 10,000), the optimal commission rate of the leading platform R1 is decreased from 36% to 9.75%, which is lower than that in Scenario 6 (19.5%) and Scenario 7 (26%), while higher than that in Scenario 4 (6.75%). There are two parameters changed in Scenarios 4, 6, and 7. This means that there are intricate relationships between platform productivity, platform drivers’ market share proportion, and drivers’ switching behavior lasting time and the optimal commission rate.
The discussion above demonstrates that Model 1 can be used as an informative instrument to understand how the optimal commission rate is determined in a duopoly competitive market. Multiple platform parameters including drivers’ market share proportion, platform productivity, and drivers’ switching behavior lasting time can be employed to garner the optimal commission rate in optimizing the operations of RHPs. The numerical experiment results above imply that the change in one or more of these platform parameters has a significant impact on the optimal commission rate. This suggests that RHPs should carefully consider these variables in optimizing their operations.
5.2. Example Two
Example Two has three RHPs competing in the ride-hailing mobility market. They are denoted as R1, R2, and R3 respectively. This example is used to simulate a fully competitive market where drivers can switch from the leading R1 to R2, or from R1 to R3. Table 4 presents an overview of the simulation result.

Table 4.
Numerical results of Example Two for Model 2 (M = 10,000).
Table 4.
Numerical results of Example Two for Model 2 (M = 10,000).
| p1 | r1 | r2 | r3 | T1 | T2 | T3 | ||
| 0.65 | 0.5 | 0.3 | 0.2 | 10,000 | 13,000 | 15,000 | ||
| c | 5.91% | 7.5% | ||||||
| c* | 5.91% |
The leading platform in the market R1 has the largest drivers’ market share at 50% of the ride-hailing market. The other two RHPs, R2 and R3, have 30% and 20% drivers’ market share, respectively. The start time of drivers’ switching behaviors in R1 is at time point T1 = 10,000. The stop time of drivers’ switching behaviors from R1 to R2 is at time point T2 = 13,000. The lasting time of drivers’ switching behaviors from R1 to R2 equals T2 − T1 = 3000. The stop time of drivers’ switching behaviors from R1 to R3 is at time point T3 = 15,000. The lasting time of drivers’ switching behaviors from R1 to R3 equals T3 − T1 = 5000. The total number of available drivers in the current market is M = 10,000. The productivity of the leading platform R1 is p1 = 0.65. The optimal commission rate is determined as 5.91%, which is calculated by using the solution algorithm presented in Section 4.
The results above show that the leading platform R1 should set its commission rate as 5.91% to ensure that it can provide customers with better services than its competitors R2 and R3. Although the leading platform R1 has more advantages than R3 in drivers’ market share proportion compared with R2 (r1 − r3 = 0.3 > r1 − r2 = 0.2), the drivers’ switching behavior lasting time is longer (T3 − T1 = 5000 > T2 − T1 = 3000), and the optimal commission rate between R1 and R3 (7.5%) is higher than that with R1 and R2 (5.91%). The optimal commission rate for the leading platform R1 is 5.91%. This can ensure that platform R1 is competitive in the fully competitive ride-hailing market.
5.3. Example Three
Example Three demonstrates the generality and validity of the proposed mathematical models between different ride-hailing modes. It considers two on-demand ride services including ride-sourcing and ride-splitting based on Model 1. The first scenario indicates ride-souring, and the second scenario indicates ride-splitting. The total order volume of Scenario 1 is Vi referring to the ride-sourcing mode, and the total order volume of Scenario 2 is Vj referring to the ride-splitting mode. Here, Vj < Vi means ride-splitting mode will merge multiple orders, thus having similar passengers’ routes into one order leading to a decrease in the total order volume. It reveals that the optimal commission rate is irrelevant to the type of ride-hailing modes. As a result, the optimal commission rates of two on-demand ride services are the same, as listed in Table 5.

Table 5.
Numerical results of Example Three for two modes (M = 10,000).
Table 5.
Numerical results of Example Three for two modes (M = 10,000).
| Scenarios | r1 | r2 | r1 − r2 | p1 | T2 − T1 | c* |
|---|---|---|---|---|---|---|
| Mode 1 | 0.7 | 0.3 | 0.4 | 0.45 | 5000 | 36% |
| Mode 2 | 0.7 | 0.3 | 0.4 | 0.45 | 5000 | 36% |
The three numerical examples above provide some insights for optimizing the operations of RHPs. First, RHPs which have a dominant supply market share can set relatively higher commission rates for achieving higher revenue under the guarantee of customer service quality. Second, drivers’ switching behaviors have a negative impact on the commission rate of RHPs. If drivers’ switching behaviors last too long, RHPs must decrease their optimal commission rates to attract more drivers to join the platform to sustain their operations. Third, RHPs should endeavor to improve their productivity to obtain the opportunity to set higher commission rates. Fourth, RHPs should pay close attention to the relationship between commission rates, drivers’ switching behavior, and critical platform parameters in optimizing their operations for profitability and sustainability. Fifth, the proposed two models could be used in different on-demand ride service modes such as ride-sourcing or ride-splitting.
6. Conclusions and Discussion
This study explores how to optimize the operations of RHPs with a focus on understanding the impact of the commission rate on drivers’ switching behaviors in a dynamic ride-hailing market. This leads to the development of two specific mathematical models within the theoretical background of the queue theory for better explaining the interplay between commission rates, drivers’ switching behaviors, and the critical platform parameters in optimizing platform operations. The study makes several theoretical contributions as follows.
First, this study formulates the problem of how to optimize the operations of RHPs with a focus on investigating the impact of the commission rate on drivers’ switching behaviors, which has not been addressed in existing studies. Two queue-theory-based mathematical models are developed to better explain the impact of drivers’ switching behaviors on the operations of RHPs. This addresses an existing research gap in optimizing the operations of RHPs in which drivers’ switching behaviors have not been adequately considered. This is the first attempt to consider drivers’ switching behaviors in optimizing the operations of RHPs. It enriches existing research in mobility operations management.
Second, the proposed models explore the trade-off between commission rates, drivers’ switching behaviors, and critical platform parameters for optimizing the operations of RHPs while sustaining customer service quality, which is not considered sufficiently in prior studies. RHPs strive to maximize their revenue by developing various pricing strategies in which commission rates are treated as a main component of such strategies. Two analytical models are formulated to maximize the operations revenue of RHPs while sustaining customer service quality in the platform.
Third, the analytical solutions of the models are derived in the examples given. This provides RHPs with feasible strategies for optimizing their operations in the dynamic ride-hailing market, which has not been addressed in existing studies. Numerical experiments provide a comprehensive analysis to examine how commission rate setting is associated with drivers’ switching behaviors and crucial platform parameters in optimizing the ride-hailing operations of RHPs. This leads to a better understanding of the interplay between commission rates, drivers’ switching behaviors, and critical platform parameters for optimizing the ride-hailing operations of RHPs.
The findings of this study have several practical implications. First, the findings of the study suggest that RHPs should strive to improve their drivers’ market share so that they can set higher commission rates for optimizing their operations in the dynamic ride-hailing market, which is similar to the prior studies of [9,22]. Second, the findings state that RHPs should try to adopt proper incentives to shorten drivers’ switching behavior lasting time as much as possible. If drivers’ switching behavior occurs in a relatively short time interval, RHPs then could set higher commission rates to pursue more operations revenue. The drivers’ switching behavior is associated with drivers’ income satisfaction, which is verified in a recent study [10], while the relationship between drivers’ switching behavior and commission rates shows that there is a complex interplay between them in the dynamic market conditions. Third, the findings advise that RHPs should commit to improving their productivity to optimize their operations. As a key platform parameter, the productivity of RHPs has a substantial influence on the optimal commission rate setting and the platform revenue, which are discussed in different service mode contexts [13]. Fourth, the study finds that all three operations instruments can be utilized for optimizing the operations of RHPs. RHPs should determine a rational configuration within drivers’ market share, drivers’ switching behavior lasting time, and platforms’ productivity for developing competitive operations strategies.
There are some limitations in this study. First, there is specific simplification about drivers’ behaviors in developing the two mathematical models for optimizing the operations of RHPs in the dynamic mobility market. The variation in the driver quantity for a long time, for example, is not considered. The total driver quantity in the ride-hailing market is assumed to be stable in this study. This can be further explored on the impact of the variation in the total driver quantity on the optimal commission rate. Second, the cooperation between RHPs is not considered. In practice, there usually exists not only competition but also cooperation between platforms, which is taken as a coopetition relationship in aggregated platform contexts [51,52]. The presence of the aggregation mode intensifies the complexity of drivers’ supplies in the market. If the adoption of the aggregation mode is considered, how does it affect the determination of the optimal commission rate? This is an interesting problem that is worthy of further exploration. Third, no sensitivity analysis is conducted in the current study with the inclusion of more platform operations variables such as market density and price elasticity. Future studies can be carried out in further exploring the relationship between those critical platform operations variables in determining the best commission rate for optimizing platform operations. Fourth, emerging technological innovations in the transport domain such as the use of autonomous vehicles in the mobility market have a substantial impact on the operations of RHPs. Considering these advances in optimizing the operations of RHPs in the dynamic mobility market is a direction worthy of attention in the future.
Author Contributions
Conceptualization, X.C. and H.D.; methodology, X.C. and H.D.; software, X.C. and H.D.; validation, X.C. and H.D.; formal analysis, X.C. and H.D.; investigation, X.C. and H.D.; resources, X.C. and H.D.; data curation, X.C. and H.D; writing—original draft preparation, X.C. and H.D; writing—review and editing, X.C. and H.D; visualization, X.C. and H.D; supervision, X.C.; project administration, X.C.; funding acquisition, X.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the National Natural Science Foundation of China grant number [72171102].
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
For the M/M/S queueing system with arrival rate and service rate , we have the following results [53]:
According to the Little formula [54], the number of customers in the system queue can be calculated.
where
Queue waiting time:
System waiting time:
Average number of customers in the system:
Appendix B
Proof of Proposition 1.
According to the Little formula [51,52], we can derive a variation form of waiting time function from Equation (A2) as .
As a result,
where . Assuming that , we have
That means because and . We have
; thus, . The proof is completed. □
References
- Jin, S.T.; Kong, H.; Wu, R.; Sui, D.Z. Ridesourcing, the sharing economy, and the future of cities. Cities 2018, 76, 96–104. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S. Competition between autonomous and traditional ride-hailing platforms: Market equilibrium and technology transfer. Transp. Res. Part C: Emerg. Technol. 2024, 165, 104728. [Google Scholar] [CrossRef]
- Chen, X.G.; Deng, H. Latent pattern analysis of conscious cooperation for developing sustainable transport. Transp. Res. Part F Traffic Psychol. Behav. 2022, 86, 356–369. [Google Scholar] [CrossRef]
- Shaheen, S.; Cohen, A.; Yelchuru, B.; Sarkhili, S. Mobility on Demand Operational Concept Report. Technical Report. 2017. Available online: https://rosap.ntl.bts.gov/view/dot/34258 (accessed on 17 September 2017).
- Duan, S.X.; Tay, R.; Molla, A.; Deng, H. Predicting Mobility as a Service (MaaS) use for different trip categories: An artificial neural network analysis. Transp. Res. Part A Policy Pract. 2022, 166, 135–149. [Google Scholar] [CrossRef]
- Terentyev, A.; Marusin, A.; Evtyukov, S.; Marusin, A.; Shevtsova, A.; Zelenov, V. Analytical model for information flow management in intelligent transport systems. Mathematics 2023, 11, 3371. [Google Scholar] [CrossRef]
- Chen, Y.J.; Dai, T.; Korpeoglu, C.G.; Körpeoğlu, E.; Sahin, O.; Tang, C.S.; Xiao, S. Innovative online platforms: Research opportunities. Manuf. Serv. Oper. Manag. 2020, 22, 430–445. [Google Scholar] [CrossRef]
- Bahrami, S.; Nourinejad, M.; Nesheli, M.M.; Yin, Y. Optimal composition of solo and pool services for on-demand ride-hailing. Transp. Res. Part E Logist. Transp. Rev. 2022, 161, 102680. [Google Scholar] [CrossRef]
- Lin, X.; Jin, K.; Lin, Q.; Zhou, Y.W.; Fu, W. Asset-light or asset-heavy? Implications for ride-hailing platforms’ profits, consumer surplus, and driver surplus. Comput. Ind. Eng. 2024, 194, 110336. [Google Scholar] [CrossRef]
- Zhou, M.; Yin, J.; Tang, Y.; Yi, H.; Kong, N.; Campy, K.S. What drives the drivers away? An empirical study on the factors influencing the turnover intention of full-time online ride-hailing drivers in China. Transp. Res. Part A Policy Pract. 2024, 186, 104134. [Google Scholar] [CrossRef]
- China Industry and Information News (www.cnii.com.cn). The Number of Orders for Ride Hailing Services in China Has Reached 897 Million. 2024. Available online: https://www.cnii.com.cn/rmydb/202405/t20240531_572651.html (accessed on 31 May 2024).
- Shokouhyar, S.; Shokoohyar, S.; Sobhani, A.; Gorizi, A.J. Mobility in Post-COVID Era:New Challenges and Opportunities. Sustain. Cities Soc. 2021, 67, 102714. [Google Scholar] [CrossRef] [PubMed]
- Guo, D.; Fan, Z.P.; Liu, Y. The strategic analysis of service mode selection for a ride-hailing platform. Int. Trans. Oper. Res. 2024, 31, 3135–3172. [Google Scholar] [CrossRef]
- Mourad, A.; Puchinger, J.; Chengbin, C. A survey of models and algorithms for optimizing shared mobility. Transp. Res. Part B Methodol. 2019, 123, 323–346. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, J.; Raghunathan, S. Two-Sided Platform Competition in a Sharing Economy. Manag. Sci. 2022, 68, 8909–8932. [Google Scholar] [CrossRef]
- Henao, A.; Marshall, W.E. The impact of ride-hailing on vehicle miles traveled. Transportation 2019, 46, 2173–2194. [Google Scholar] [CrossRef]
- Benjaafar, S.; Bernhard, H.; Courcoubetis, C.; Kanakakis, M.; Papafragkos, S. Drivers, Riders, and Service Providers: The Impact of the Sharing Economy on Mobility. Manag. Sci. 2021, 68, 123–142. [Google Scholar] [CrossRef]
- Erhardt, G.D.; Roy, S.; Cooper, D.; Sana, B.; Chen, M.; Castiglione, J. Do transportation network companies decrease or increase congestion? Sci. Adv. 2019, 5, eaau2670. [Google Scholar] [CrossRef]
- Wang, H.; Yang, H. Ridesourcing systems: A framework and review. Transp. Res. Part B Methodol. 2019, 129, 122–155. [Google Scholar] [CrossRef]
- Yang, H.; Qin, X.; Ke, J.; Ye, J. Optimizing matching time interval and matching radius in on-demand ride-sourcing markets. Transp. Res. Part B Methodol. 2020, 131, 84–105. [Google Scholar] [CrossRef]
- Guo, X.; Haupt, A.; Wang, H.; Qadri, R.; Zhao, J. Understanding multi-homing and switching by platform drivers. Transp. Res. Part C Emerg. Technol. 2023, 154, 104233. [Google Scholar] [CrossRef]
- Zhong, Y.; Yang, T.; Cao, B.; Cheng, T.C.E. On-demand ride-hailing platforms in competition with the taxi industry: Pricing strategies and government supervision. Int. J. Prod. Econ. 2022, 243, 108301. [Google Scholar] [CrossRef]
- Yu, J.; Mo, D.; Xie, N.; Hu, S.; Chen, X. Exploring multi-homing behavior of ride-sourcing drivers via real-world multiple platforms data. Transp. Res. Part F Traffic Psychol. Behav. 2021, 80, 61–78. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, X.; Gu, Q. Pricing strategy and platform competition with partial multi-homing agents: When the aggregation platform exists in ride-sharing market. Transp. Res. Part E Logist. Transp. Rev. 2024, 184, 103483. [Google Scholar] [CrossRef]
- Hu, J.W.; Creutzig, F. A systematic review on shared mobility in China. Int. J. Sustain. Transp. 2022, 16, 374–389. [Google Scholar] [CrossRef]
- Sun, S.; Ertz, M. Dynamic evolution of ride-hailing platforms from a systemic perspective: Forecasting financial sustainability. Transp. Res. Part C Emerg. Technol. 2021, 125, 103003. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Zhang, Y.; Malenje, J.O.; Han, Y. Optimizing taxi-pooling operations to enhance efficiency and revenue: A queuing model approach. Mathematics 2024, 12, 3210. [Google Scholar] [CrossRef]
- Cohen, M.C.; Zhang, R. Competition and coopetition for two-sided platforms. Prod. Oper. Manag. 2020, 31, 1997–2014. [Google Scholar] [CrossRef]
- Yan, C.; Zhu, H.; Korolko, N.; Woodard, D. Dynamic pricing and matching in ride-hailing platforms. Nav. Res. Logist. 2019, 67, 705–724. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, H.; Ke, J.; Yang, H. Dynamic optimization strategies for on-demand ride services platform: Surge pricing, commission rate, and incentives: Surge pricing, commission rate, and incentives. Transp. Res. Part B Methodol. 2020, 138, 23–45. [Google Scholar] [CrossRef]
- Shaheen, S.; Cohen, A.; Zohdy, I. Shared Mobility: Current Practices and Guiding Principles. U.S. Department of Transportation, Federal Highway Administration. 2016. Available online: https://ops.fhwa.dot.gov/publications/fhwahop16022/fhwahop16022.pdf (accessed on 13 May 2020).
- Mardešić, N.; Erdelić, T.; Carić, T.; Đurasević, M. Review of stochastic dynamic vehicle routing in the evolving urban logistics environment. Mathematics 2024, 12, 28. [Google Scholar] [CrossRef]
- Benjaafar, S.; Kong, G.; Li, X.; Courcoubetis, C. Peer-to-peer product sharing: Implications for ownership, usage and social welfare in the sharing economy. Manag. Sci. 2019, 65, 477–493. [Google Scholar] [CrossRef]
- Ke, J.; Qian, S. Leveraging ride-hailing services for social good: Fleet optimal routing and system optimal pricing. Transp. Res. Part C Emerg. Technol. 2023, 155, 104284. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; Samaranayake, S.; Wallar, A.; Frazzoli, E.; Rus, D. On-demand high-capacity ride-sharing via dynamic trip vehicle assignment. Proc. Natl. Acad. Sci. USA 2017, 114, 462–467. [Google Scholar] [CrossRef] [PubMed]
- Di, X.; Ban, X.J. A unified equilibrium framework of new shared mobility systems. Transp. Res. Part B Methodol. 2019, 129, 50–78. [Google Scholar] [CrossRef]
- Ke, J.; Yang, H.; Zheng, Z. On ride-pooling and traffic congestion. Transp. Res. Part B Methodol. 2020, 142, 213–231. [Google Scholar] [CrossRef]
- Sun, L.; Teunter, R.H.; Hua, G.; Wu, T. Taxi-hailing platforms: Inform or Assign drivers? Transp. Res. Part B Methodol. 2020, 142, 197–212. [Google Scholar] [CrossRef]
- Xu, Z.; Yin, Y.; Chao, X.; Zhu, H.; Ye, J. A generalized fluid model of ride-hailing systems. Transp. Res. Part B Methodol. 2021, 150, 587–605. [Google Scholar] [CrossRef]
- Bandiera, C.; Connors, R.D.; Viti, F. Mobility service providers’ interacting strategies under multi-modal equilibrium. Transp. Res. Part C Emerg. Technol. 2024, 168, 104766. [Google Scholar] [CrossRef]
- Xi, H.; Li, M.; Hensher, D.A.; Xie, C.; Gu, Z.; Zheng, Y. Strategizing sustainability and profitability in electric Mobility-as-a-Service (E-MaaS) ecosystems with carbon incentives: A multi-leader multi-follower game. Transp. Res. Part C Emerg. Technol. 2024, 166, 104758. [Google Scholar] [CrossRef]
- Yao, R.; Zhang, K. Design an intermediary mobility-as-a-service (MaaS) platform using many-to-many stable matching framework. Transp. Res. Part B Methodol. 2024, 189, 102991. [Google Scholar] [CrossRef]
- Acheampong, R.A.; Siiba, A.; Okyere, D.K.; Tuffour, J.P. Mobility-on-demand: An empirical study of internet-based ride-hailing adoption factors, travel characteristics and mode substitution effects. Transp. Res. Part C Emerg. Technol. 2020, 115, 102638. [Google Scholar] [CrossRef]
- Dean, M.D.; Kockelman, K.M. Spatial variation in shared ride-hail trip demand and factors contributing to sharing: Lessons from Chicago. J. Transp. Geogr. 2021, 91, 102944. [Google Scholar] [CrossRef]
- Li, X.; Du, M.; Zhang, Y.; Yang, J. Identifying the factors influencing the choice of different ride-hailing services in Shenzhen, China. Travel Behav. Soc. 2022, 29, 53–64. [Google Scholar] [CrossRef]
- Chen, X.; Bai, S.; Wei, Y.; Jiang, H. How income satisfaction impacts driver engagement dynamics in ride-hailing services. Transp. Res. Part CEmerging Technol. 2023, 157, 104418. [Google Scholar] [CrossRef]
- Cachon, G.P. A Research Framework for Business Models: What Is Common Among Fast Fashion, E-Tailing, and Ride Sharing? Manag. Sci. 2019, 66, 1172–1192. [Google Scholar] [CrossRef]
- Benjaafar, S.; Hu, M. Operations Management in the Age of the Sharing Economy: What Is Old and What Is New? Manuf. Serv. Oper. Manag. 2020, 22, 93–101. [Google Scholar] [CrossRef]
- Rietveld, J.; Schilling, M.A. Platform competition: A systematic and interdisciplinary review of the literature. J. Manag. 2020, 47, 014920632096979. [Google Scholar] [CrossRef]
- Sun, S.; Wang, Z.; Wang, W. The impact of regulatory policy on the growth of ride-hailing platform: System dynamics perspective. Phys. A Stat. Mech. Appl. 2023, 632, 1–21. [Google Scholar] [CrossRef]
- Chen, X.G.; Deng, H.; Guan, S.Q.; Han, F.X.; Zhu, Z.H. Cooperation-oriented multi-modal shared mobility for sustainable transport: Developments and challenges. Sustainability 2024, 16, 11207. [Google Scholar] [CrossRef]
- Ma, L.; Tao, Z.; Wei, Q.; Huo, B. Cooperate with aggregation platform or not? Optimal decision for the on-demand ride service platform. Res. Transp. Bus. Manag. 2025, 59, 101251. [Google Scholar] [CrossRef]
- Gross, D.; Shortle, J.F.; Thompson, J.M.; Harris, C.M. Fundamentals of Queueing Theory, 4th ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Little, J.D.C. A Proof for the Queueing Formula: L=W. Oper. Res. 1961, 9, 383–387. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).