Dynamic Railcar Flow Assignment of Railway Terminal with Multiple Marshalling Stations

Abstract

This paper deals with the optimization of railcar flow assignment among multiple marshalling stations oriented to making a stage plan. We aimed to minimize the total dwell time of the on-time and delayed allocated railcar flow at the station within a stage plan. Considering the limitations of the disassembly and assembly capacity of marshalling stations, the limitation of the transfer operation capacity between marshalling stations, the connection time limit of inbound and outbound trains, and the limitation of trains with different full workloads, we constructed a multi-marshalling station railcar flow assignment optimization model. Furthermore, for comparison, we built a model that only satisfied the train equivalent length limitation and a model that only satisfied the train hauling weight limitation. Finally, we designed experimental scenarios and conducted comparative analyses of the proposed model and a model that considered only a single full workload limitation. The results show that the railcar flow assignment scheme that considers different full workload limitations shortens the dwell time of railcar flow at the station, reduces the number of undispatched outbound trains within the time range of the stage plan, and effectively improves the terminal operation efficiency within the stage plan. Thus, the proposed scheme can achieve an effective railcar flow assignment within a multi-marshalling station railroad terminal while minimizing the dwell time.

1. Introduction

In China’s freight transportation system, railway transportation has received widespread attention owing to its suitability for long distances, large freight volume, and resistance to extreme weather. According to statistics from China’s transport authorities, the total freight volume shipped in 2023 was 5.035 billion tons, an increase of 1.0% over the previous year, and the total freight turnover volume was 3646 billion ton-kilometers, an increase of 1.4%. Railway transportation accounts for approximately 70% of the annual freight turnover achieved by modern transportation [1]. Thus, railway freight transportation plays an important role in China.

In railway transportation, railway terminals are the core of the railway network. Railroad terminals must handle various operations efficiently, such as train arrival and departure, railcar classification, engine maintenance, and cargo handling. Thus, the railcar-flow assignment of railway terminals is crucial, and their operating efficiency significantly affects the throughput capacity of the entire railway network [2].

As the core component of railroad terminals, marshalling stations primarily handle the operation of reconfiguring and transshipping trains, undertaking the task of disassembling and assembling a substantial number of freight trains. These stations significantly enhance the turnover speed of railway vehicles across the entire network and contribute to the enhancement of transportation capacity, thus holding an extremely important position within the railway network [3]. A marshalling station generally has a dedicated operation yard, which also includes equipment for shunting (e.g., shunting lines, humps, and pull-out lines), traffic (e.g., arrival and departure lines, communications, and signals), and maintenance (e.g., maintenance warehouses, fuel, and spare parts).

Railcar flow assignment is the core of technical operations at marshalling stations. Specifically, the railcar flow assignment aims to disassemble inbound freight trains from different directions, classify them according to the final destination of the goods, gather the same type of railcars with the same final destination, and group them into a new outbound train. If the new outbound train meets the full workload limitation (e.g., the hauling weight of the train, hauling railcar number of the outbound train, and equivalent length of the train), it is sent to the next marshalling station. Otherwise, the new outbound train will not be dispatched, and the railcars that make-up the train will be assigned to other outbound trains [4]. Therefore, the assignment process will require additional transfer time and will also cause these railcars to be delayed in leaving the marshalling station. Thus, whether the full workload limitation is met affects whether the outbound train can leave the marshalling station on time, which, in turn, affects the dwell time of the railcar flow at the station as well as the system operation efficiency.

Clearly, railcar flow assignment at a marshalling station is subject to various constraints in terms of technical capabilities, such as the disassembly and dispatch of trains and the passage of trains between different stations (see Section 3). In addition, it is related to technical personnel competence, weather conditions, equipment operation, and failure conditions. To avoid overcomplexity of the model, we did not consider these factors in this study.

With global economic development in recent years, large railroad terminals with multiple marshalling stations have emerged to meet the growing demand for goods transport. For example, the Chicago railroad terminal in the United States contains 11 marshalling stations, and the Lyon railroad terminal in France contains six marshalling stations. Similar examples have been reported in China. The Beijing railroad terminal includes Fengtai West Station, Fengtai Station, and Shuangqiao Station, and the Tianjin railroad terminal includes Nanchang Station, Beitang West Station, and Chagu Port Station. Compared with a railroad terminal with a single marshalling station, a large railroad terminal with multiple marshalling stations has more connecting line directions and undertakes heavier disassembly and assembly tasks. If the allocation and coordination of various technical tasks between different marshalling stations within the terminal cannot be handled effectively, then the allocation of railcars will not be efficient. This will cause severe roundabouts of railcar flow in the station, thereby affecting the efficiency of terminal operation. This results in a longer train dwell time at the terminal, an increase in the number of outbound trains out of service, and an increase in operating expenses [5].

Therefore, how to assign the railcar flow within a multi-marshalling station railroad terminal is worth studying. In this paper, we present a model for minimizing the dwell time of railcar flow in a terminal. It comprehensively considers the actual constraints, such as the connection time and traffic capacity, and it relaxes the full workload limitation of the outbound train to reduce the dwell time of the railcar flow at the station, increase the number of dispatched outbound trains, and increase the terminal efficiency. This study is only applicable to the railcar flow organization problem under the condition of balanced arrival and departure railcar flows. Distinct from the actual operations in railway production, we have not considered factors such as shunting resource constraints, classification line utilization, and railcar flow variability. The specific research assumptions regarding this issue will be elaborated in Section 3.1.

2. Literature Review

In this section, we review the literature related to the optimization of the railcar flow assignment to be studied in this paper. The literature review revealed that research on railcar flow assignment can be divided into two categories: railcar flow allocation at marshalling stations and the optimization of train formation plans. In addition, we also compiled relevant research on the full workload limitation of outbound trains. At the end of this section, we will review and analyze the literature.

2.1. Railcar Flow Allocation of Marshalling Station

The railcar-flow assignment of a single-direction marshalling station has been studied previously with some valuable results. Schasfoort [6] considered the uncertainty of the train arrival time and the impact of emergencies, studied the real-time assignment problem of trains at railway stations, and constructed a mathematical model with the goal of minimizing train delay time; they presented a genetic algorithm and a first-come, first-serve heuristic algorithm to solve the mathematical model, and compared the results of the two algorithms. Bruck [7] considered the impact of railroad terminals on multimodal transportation and studied issues such as splitting access trains into freight train sequences, assigning freight trains to outbound trains, and arranging parking tracks for freight trains. Haahr et al. [8] studied the flow allocation problem based on the use of classification tracks, built a mixed-integer programming model to minimize the average dwell time of railcars in the marshalling station, and designed a greedy heuristic algorithm to solve it. Khadilkar [9] conducted rule-based discrete event simulation optimization research to solve the classification track application in the railcar flow allocation problem and the design of the train disassembly and assembly scheme. Furthermore, Gestrelius [10] comprehensively considered using a hairline and the disassembly plan to construct an integer programming model.

Shi [11] first introduced shunting locomotive operation schemes for hump break-up and make-up processes at marshalling stations based on empirical field experience. Subsequently, considering the finite track resources in actual hump yards, a scheme was proposed for the prompt break-up of inbound trains. Ultimately, by integrating the HSS model, an optimization scheme for shunting locomotive operations was established. Zhou [12] provided a more comprehensive analysis, addressing the limited resources of both the shunting yard and the marshalling yard. Simulation methods were combined to conduct a study on the operation of shunting locomotives in marshalling stations that closely align with practical conditions, with solutions derived using genetic algorithms. David [13] integrated computer information network security technology into the optimization of the departure train make-up sequence in railcar flow allocation at marshalling stations. A neural network approach was utilized to establish an optimization model for station make-up sequences, leading to a significant improvement in the fulfillment rate of various operations and a substantial reduction in train make-up time. Shi [14] applied heuristic algorithms to formulate shunting locomotive operation methods for the break-up of arriving trains at stations, and developed a mixed-integer programming model with the objective function of minimizing the time that vehicles spend at the station. Rauts [15] constructed a mixed-integer linear temporal programming model to address similar problems and designed a rolling horizon algorithm for their resolution. Qian [16] focused on the development of integrated planning schemes for marshalling stations, leveraging computer software to achieve rapid and optimized station work plan formulation. Lusby [17] conducted research on the robustness of work plans within marshalling stations, examining the station’s ability to continue planning and operations based on the continuity of various technical operations, even in the face of severe delays or halts in the previous work plan. Given the inevitability of robustness in marshalling station operations, it is essential to fully consider the robustness of plan execution in the compilation of station work plans, incorporating robust measures and objectives to ensure that the station can continue to operate according to plan in the event of deviations.

2.2. Optimization of Train Formation Plan

Gulbrodsen [18], Hein [19], Glover et al. [20], and Gupta et al. [21] were among the first to introduce operational research, queuing theory, modern mathematics, and computer technology into the automation of marshalling station work plans and the optimization of stage plans, providing new avenues for subsequent research on related issues. Assad A [22], from the perspective of network optimization and combinatorial optimization, described a class of models for handling train routing and marshalling plans on the railway network, comparing them with previous railway network models. Some scholars have treated this issue as a multi-commodity flow problem by constructing network models for solutions. Bodin et al. [23] established a nonlinear mixed-integer model for the compilation of marshalling plans, studying it as a multi-commodity flow problem with many other ancillary conditions. Crainic et al. [24] researched train routing and marshalling plans within the railway network, taking the example of the Canadian National Railway, constructing a spatiotemporal network model that incorporates the principle of reachability to determine the sequence of inbound trains and ingeniously transforming the stage plan compilation problem into a two-dimensional structured network model for solution, applying heuristic algorithms to address the multi-commodity flow problem. Subsequently, scholars have integrated marshalling plan problems with practical experience and real-case studies. Ferreira [25] focused on Australia’s operational planning practices, applying operational research knowledge to the optimization of train marshalling plans to enhance transportation timeliness and arrival reliability. Marton et al. [26] utilized integer programming methods and computer simulation tools to successfully develop and validate an improved classification timetable for actual trains, simulating the compilation of freight train marshalling plans to achieve optimal marshalling plans. Bohlin et al. [27], in their study on the optimization of marshalling station work plans in Sweden, established a mixed-integer programming model and successively employed branch-and-price column generation and dynamic decision-making to solve the problem.

Keaton [28,29], considering the fixed costs of train operations, proposes innovative designs for further operational optimization solutions and resolution strategies and conducts research on the optimization of railway transportation plans.

2.3. Research on Limitation for Full Workload of Outbound Trains

Most of the abovementioned studies only used a single-train full workload limitation, among which the hauling railcar number of outbound trains was mostly used. Specifically, the hauling railcar number of outbound trains was used as a full workload limitation, which means that the number of railcars attached to the outbound train must exceed a certain value before the train can be dispatched. Most researchers have adopted this constraint. For instance, Peng et al. [30] considered the weight and length of the outbound train but set the parameters of the connecting railcar flow at average values, which is not significantly different from using the number of railcars of an outbound train as the full-axle constraint. Some researchers have also discussed the assembly and dispatch of under-axle outbound trains under special circumstances; that is, the number of railcars attached to an outbound train is lower than the required number, but the train is still allowed to be assembled and dispatched. Moreover, Wang [31,32] constructed a model to solve the minimum number of railcars in the time-fixed mode. By studying the changes in the operating indicators in the two assembly modes, they proposed the concept of beneficial numbers of railcars for different situations. Subsequently, through an analysis of the operating income and losses of freight trains under the time-fixed mode, they presented a calculation plan for the minimum number of railcars and discussed its relationship with section running time and traffic volume. After comparing the characteristics and applicable conditions of the two assembly modes, Liu et al. [33] selected the time-fixed-point mode with relaxed conditions, which has the advantages of both the time-fixed mode and railcar-number-fixed mode. Starting from the disassembly and assembly operation, they analyzed the impact of this assembly mode on the disassembly operation, built a corresponding model, and validated the effectiveness of the model using the example of the Fengtai West Marshalling Station. Considering the real-time performance of freight train transportation, Lin [34] conducted an in-depth study on the impact of different assembly modes on railway economic benefits. Based on queuing theory, the author constructed an optimization model for railroad cars in the assembly system and the adjacent station’s disassembly system under different assembly modes. By analyzing the impact of different parameters on economic benefit values, they analyzed the applicable range of railcar-number-fixed and time-fixed modes. Li [35] conducted a systematic study on the railcar assembly process at marshalling stations and built a queuing model for railcar assembly under different circumstances based on queuing theory and a relaxed time-fixed mode. On this basis, they optimized the number of trains under competitive market conditions.

As mentioned in the introduction, the full workload limitation affects whether the outbound train can leave the marshalling station on time, which in turn affects the dwell time of the railcar flow at the station and the efficiency of the system operation. Therefore, a broader, more qualified, and full workload limitation is more suitable for the actual needs of railway transportation. According to Chinese railway regulations, the connection and allocation of railcar flow should take into account the full-axle constraints of the outbound train’s hauling weight and equivalent length. As long as one of the constraints is met, the train can be dispatched. Hauling weight refers to the maximum weight that a locomotive or power head can pull under specified conditions, encompassing both the weight of the train itself and the cargo it carries. The equivalent length refers to the ratio of the distance between the inner sides of the couplers at both ends of the railway vehicle to the standard vehicle length of 11 m. This measurement is used to standardize the lengths of various railway vehicles for operational calculations. For example, if the train length is 13 m, we can convert it into an equivalent length of 13/11 = 1.2.

It should be noted that the Chinese railway department has established length and hauling weight standards for outbound trains and allows them to fluctuate within a certain range. The train hauling weight standard and length standard will affect the hauling railcar number of outbound trains such that the number of railcars attached to the outbound train is within an observable range; however, the hauling railcar number of outbound trains is not a formal full workload limitation. Therefore, in this article, we will use the hauling weight and equivalent length as the full workload limitation of trains. In the subsequent discussion of this paper, for the sake of convenience, the terms “hauling weight” and “equivalent length” are, respectively, abbreviated as “weight” and “length”.

2.4. Research Gaps

The following two points can be made: (1) Recent research on railcar flow assignment of railroad terminals has mainly focused on railroad terminals with single marshalling stations, but there has been insufficient research on large railroad terminals with multiple marshalling stations. When a railcar flow assignment is made in a railroad terminal with multiple marshalling stations, the information isolation between marshalling stations should be broken. We should not only consider the optimal transportation indicators of a specific marshalling station, which would lead to resource waste and traffic backlogs, thus affecting the overall transportation efficiency of the terminal. (2) When considering the full-axle constraint of a train, considering only a single full-axle constraint may cause a waste of railcar flow resources and cause a backlog of railcar flow, thereby reducing the transportation efficiency of the marshalling stations and even the terminal. Therefore, it is necessary to study the collaborative dispatch of railcar flow between multiple marshalling stations with different full-axle constraints.

3. Problem Formulation

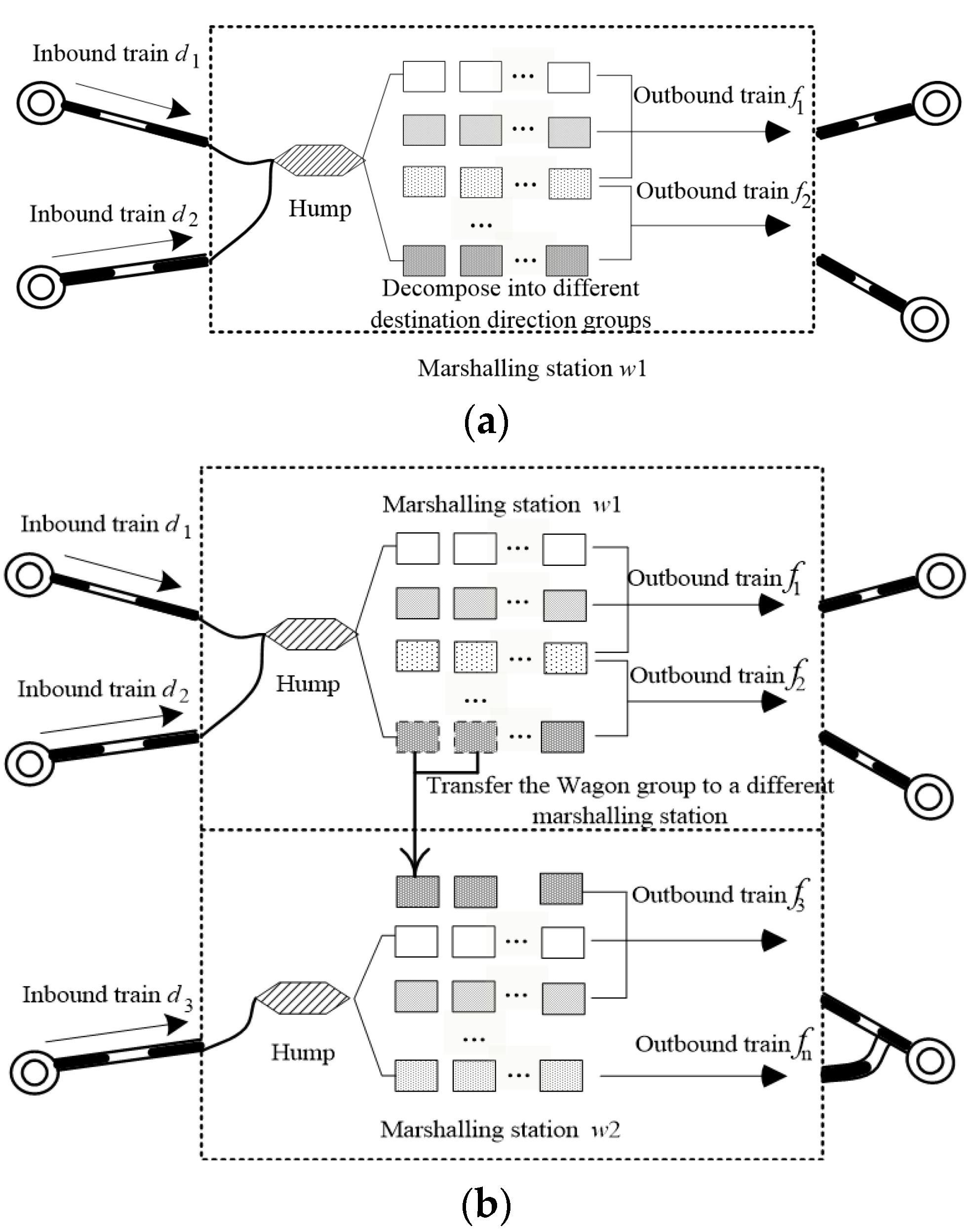
3.1. Problem Description

First, we will introduce the problem of railcar flow assignment in a single marshalling station. The railroad terminal has only one marshalling station, which has an arrival yard, classification yard, and departure yard. At the beginning of the dispatching period, after inbound trains access each marshalling station, they are disassembled through the hump into a transfer railcar flow with different destinations, as well as a local arrival railcar flow. According to the marshalling direction, connection time, and transfer capacity restrictions, an outbound train is assembled from the transfer flow, railcars are unallocated to outbound trains from the previous stage of the plan, and local railcars are retrieved from each loading and unloading station, leaving the terminal when the axle is full. The locally arriving railcars are sent to the destination loading station using exchange trains. The diagram of railcar flow assignment in a single marshalling station is shown in Figure 1a.

The main differences between the railcar flow assignment problem in multiple marshalling stations and in a single marshalling station to be studied in this article are as follows. First of all, there are multiple marshalling yards in the railway terminal, and different marshalling yards are connected by lines. Secondly, after the outbound trains are disassembled, if the transfer railcar flow cannot meet the full-axle requirement at the marshalling station, they arrive. In order to minimize the dwell time of the railcar flow in the terminal, we can send the transfer railcar flow to a different station according to the marshalling direction, connection time, and transfer capacity restrictions. Finally, unlike previous studies, we use weight and length as the full workload limitation for outbound trains from each marshalling station. The diagram of railcar flow assignment in multiple marshalling stations is shown in Figure 1b.

To simplify the model and reduce the complexity of the solution, the following assumptions are made in the study of optimization models for the organization of railcar flow in multiple marshalling stations within a railway terminal:

(1)

The railway terminal maintains a balance in the stage plan for arrival and departure railcar flows, which means that the quantity of arrival railcar flows is essentially equal to the quantity of railcar flows that should be dispatched according to the marshalling plan.

(2)

The division of labor among the marshalling stations within the railway terminal is predetermined; that is, the freight trains that are routed to or dispatched from a particular marshalling station are known.

(3)

There is an abundance of shunting locomotive resources at each marshalling station within the terminal, which is sufficient to satisfy the requirements of freight train break-up and make-up operations.

(4)

Freight trains arrive and depart from marshalling stations strictly according to the timetable, without additional consideration of the variability in train arrival or departure times.

(5)

The scope of this study is limited to arrival and break-up trains, self-assembled departure trains, and terminal short-haul trains, excluding other types of freight trains, such as non-marshaling transit trains and partially marshaling transit trains.

(6)

After accounting for the technical service capacity occupied by other types of trains (e.g., the technical service capacity occupied by non-marshaling transit trains and partially marshaling transit trains) and the necessary reserve capacity, the remaining capacity for receiving and dispatching trains at each station and the capacity for disassembly and assembly operations in the shunting yards meet the requirements. The technical service for freight trains can satisfy the requirement of immediate inspection upon arrival. Concurrently, the line section passing capacity is ample.

(7)

The sequence of train disassembly is determined by the order of arrival of the inbound trains, and the sequence of train marshalling is determined by the order of departure of the outbound trains.

3.2. Parameters and Variables

The notations used throughout this paper are listed below.

Sets
M	Set of marshalling stations in the terminal. Define m = {m|m = I,II,···,$\tilde{m}$},where $\tilde{m}$ is the total number of marshalling stations, and $m^{\prime }$ represents a marshalling station different from m.
R	Set of destination directions. Define R = { r|r = 1, 2, ···, $\tilde{r}$}, where $\tilde{r}$ is the total number of destination directions.
K	Set of the railcar flow number stored at the initial station of the stage plan. Define K = {k|k = 1, 2, ···, $\tilde{k}$}, where $\tilde{k}$ is the total number of railcar flows in the stations. Railcar-flow groups at different stations have different destinations.
A	Set of inbound trains in the stage plan. Define A = { a|a = 1, 2, ···, $\tilde{a}$}, where $\tilde{a}$ is the total number of inbound trains.
D	Set of outbound trains within the stage plan. Define D = { d|d = 1, 2, ···, $\tilde{d}$}, where $\tilde{d}$ is the total number of outbound trains.
Γ	Train type. Define Γ = {τ|τ = 0, 1}, At τ = 0, the trains are those that cannot be underloaded, such as district trains, through trains, and direct trains. At τ = 1, the trains are those that can be underloaded, such as pickup goods trains and district transfer trains.
H	Set of train technical operations. Define h = {h|h = 1, 2, 3, 4}, including arrival, disassembly, assembly, and departure operations.
Parameters
ts	Stage plan start time.
te	Stage plan end time.
$t_{am\tau }$	The actual arrival time of inbound train a (type τ) at marshalling station m in the stage plan.
$t_{dm\tau }$	The actual departure time of outbound train d (type τ) departing from marshalling station m in the stage plan.
$c_m^1$	The disassembly ability of marshalling station m.
$c_m^2$	The assembly capacity of marshalling station m.
$c_{m{m}^{\prime }}$	The maximum number of transit railcars between marshalling stations m and $m^{\prime }$ where $m^{\prime }\in M,m^{\prime }\ne m$.
$t_{m{m}^{\prime }}$	The maximum transit time of railcars from marshalling station m to marshalling station $m^{\prime }$.
tm,h	The time it takes for trains to handle technical operations, h, at marshalling station m.
ma	The number of inbound trains at marshalling station m in the stage plan.
md	The number of outbound trains from marshalling station m in the stage plan.
mk	The number of station-stored railcar groups in marshalling station m at the beginning of the stage plan.
nmar	The number of railcars arriving at marshalling station m and going to r in train a.
nmkr	The number of railcars of station-stored railcar group k destined for r at marshalling station m.
lmar	The equivalent length of railcars destined for r in the inbound train a at marshalling station m.
lmkr	The equivalent length of the station-stored railcar group k destined for r at marshalling station m.
wmar	The weight of railcars arriving at marshalling station m and destined for r in inbound train a.
wmkr	The weight of the railcars destined for r in-station-stored railcar group k at marshalling station m.
$l_{md,\max }$	The maximum equivalent length of outbound train d at marshalling station m, as specified in the assembly plan.
$l_{md,\min }$	The minimum equivalent length of outbound train d at marshalling station m, as specified in the assembly plan.
$w_{md,\max }$	The maximum weight of outbound train d at marshalling station m, as specified in the assembly plan.
$w_{md,\min }$	The minimum weight of outbound train d at marshalling station m, as specified in the assembly plan.
Discriminant variables
$x_{m^{\prime }kr}^{md}$	The discriminant variable of outbound trains with station-stored railcar group. $x_{m^{\prime }kr}^{md}$ = 1 means that the railcars destined for r in-station-stored railcars k at station $m^{\prime }$ provides the railcar-flow source for outbound train d departing from station m; otherwise, it is 0. $m^{\prime }$ = m means that the station-stored trains provide the railcar source for outbound trains departing from this station, and $m^{\prime }$ ≠ m means that the station-stored trains provide the railcar source across the stations.
$u_{m^{\prime }kr}^{md}$	The number of railcars destined for r in-station-stored railcar group k at station $m^{\prime }$ is allocated to the number of outbound train d departing from station m.
$y_{m^{\prime }ar}^{md}$	The discriminant variable for allocating the inbound trains to the outbound trains. $y_{m^{\prime }ar}^{md}$ = 1 means that the railcars destined for r in inbound train a arriving at station $m^{\prime }$ provides the railcar-flow source for outbound train d departing from the station m; otherwise, it is 0. $m^{\prime }$ = m means that the inbound train provides the railcar-flow source for the outbound train departing from this station, and $m^{\prime }$ ≠ m means that the inbound train provides the railcar-flow source across the stations.
$v_{m^{\prime }ar}^{md}$	The number of railcars destined for r in train a arriving at station $m^{\prime }$ is allocated to train d departing from station $m^{\prime }$.
${\lambda }_{md}^{ld}$	The discriminant variable for the length of the outbound train. ${\lambda }_{md}^{ld}$ = 1 means that outbound train d departing from station m meets the length requirement; otherwise, it is 0.
${\lambda }_{md}^{wd}$	The discriminant variable of outbound train weight. ${\lambda }_{md}^{wd}$ = 1 means that outbound train d departing from the station m meets the weight requirement; otherwise, it is 0.

3.3. Objective Function

The objective is to minimize the total railcar-hour consumption at the railway terminal.

Terminal railcar flow can be divided into two categories: on-time allocated railcar flow in the stage plan and delayed allocated railcar flow in the stage plan, based on whether the connecting and linking arrangements can be completed within the time specified in the stage plan.

(1)

Dwell time of on-time railcar flow

We intend to minimize the total time of on-time railcar-flow and delayed railcar-flow dwelling on the marshalling station. The on-time railcar flow implies that they can be allocated to an outbound train within the time range of the stage plan. The railcar flow that cannot be assigned to the outbound train within the time range of the stage plan is named the delayed railcar flow.

The allocated railcar flow in the stage plan consists of two parts: the newly connected railcar flow and the station-stored railcar flow. Within the stage plan, the inbound trains are connected to the corresponding marshalling station, and before the end of the stage plan, the railcar flow of the outbound train constitutes a newly connected and allocated railcar flow, where the quantity is ${\displaystyle \sum _{m=1}^{\tilde{m}}{\displaystyle \sum _{m^{\prime }=1}^{\tilde{m}}{\displaystyle \sum _{a=1}^{m_a}{\displaystyle \sum _{d=1}^{m_d}{\displaystyle \sum _{r=1}^{\tilde{r}}{v}_{m^{\prime }ar}^{md}}}}}}$. If the train fails to be dispatched at the end of the previous stage plan, the railcar flow of trains scheduled to depart at this stage will constitute the flow of the dispatched station-stored railcars at the station, where the quantity is ${\displaystyle \sum _{m=1}^{\tilde{m}}{\displaystyle \sum _{m^{\prime }=1}^{\tilde{m}}{\displaystyle \sum _{k=1}^{w_k}{\displaystyle \sum _{d=1}^{w_d}{\displaystyle \sum _{r=1}^r{u}_{m^{\prime }kr}^{md}}}}}}$. Moreover, the station dwell time of the allocated train flow at this stage will be $t_{dm\tau }$ − $t_{am\tau }$; therefore, the total dwell time of the allocated railcar flow at this stage can be obtained as follows:

$$z_1={\displaystyle \sum _{m=1}^{\tilde{m}}{\displaystyle \sum _{m^{\prime }=1}^{\tilde{m}}{\displaystyle \sum _{d=1}^{w_d}{\displaystyle \sum _{a=1}^{w_a}{\displaystyle \sum _{k=1}^{w_k}{\displaystyle \sum _{r=1}^{\tilde{r}}(u_{m^{\prime }kr}^{md}+v_{m^{\prime }ar}^{md})(t_{dm\tau }-t_{am\tau })}}}}}}$$

(1)

(2)

Dwell time of delayed railcar flow

In the stage plan, as the inbound trains are connected to the corresponding marshalling stations, and before the end of the stage plan, the number of railcar flows that cannot be assigned to the outbound train is ${\displaystyle \sum _{m=1}^{\tilde{m}}{\displaystyle \sum _{m^{\prime }=1}^{\tilde{m}}{\displaystyle \sum _{d=1}^{w_d}{\displaystyle \sum _{a=1}^{w_a}{\displaystyle \sum _{k=1}^{w_k}{\displaystyle \sum _{r=1}^r(n_{mdr}+n_{mkr}-u_{m^{\prime }kr}^{md}-v_{w^{\prime }ar}^{md})}}}}}}$. The dwell time of this type of railcar flow at the station is $t_e-t_{am\tau }$; therefore, the total number of delayed allocated railcar flows at this stage can be obtained as follows:

$$z_2={\displaystyle \sum _{m=1}^{\tilde{m}}{\displaystyle \sum _{m^{\prime }=1}^{\tilde{m}}{\displaystyle \sum _{d=1}^{w_d}{\displaystyle \sum _{a=1}^{w_a}{\displaystyle \sum _{k=1}^{w_k}{\displaystyle \sum _{r=1}^{\tilde{r}}{\displaystyle \sum _{\tau =0}^1(n_{mar}+n_{mkr}-u_{m^{\prime }kr}^{md}-v_{w^{\prime }ar}^{md})(t_e-t_{am\tau })}}}}}}}$$

(2)

3.4. Constraints

(1)

Destination direction of outbound train

When the allocated outbound train d at marshalling station m is connected with the number of railcars going to r with the railcar flow k at the station $m^{\prime }$, $x_{m^{\prime }kr}^{md}$ = 1 and $u_{m^{\prime }kr}^{md}$ > 0; when the allocated outbound train d at the marshalling station m is not connected to the number of railcars destined for r of the station-stored traffic flow k at station $m^{\prime }$, $x_{m^{\prime }kr}^{md}$ = 0 and $u_{m^{\prime }kr}^{md}$ = 0. To express the above logical relationship, we introduce a large positive number Ω, so that

$$u_{m^{\prime }kr}^{md}\le \Omega \cdot x_{m^{\prime }kr}^{md},\forall k\in K,\forall r\in R$$

(3)

When allocated outbound train d at marshalling station m is connected with the number of railcars going to r that is connected to railcar flow a at station $m^{\prime }$, $y_{m^{\prime }ar}^{md}$ = 1 and $v_{m^{\prime }ar}^{md}$ > 0; when the number of outbound train d allocated at marshalling station m is not connected to the number of railcars destined for r of the continuous railcar flow a at the station $m^{\prime }$, $y_{m^{\prime }ar}^{md}$ = 0 and $v_{m^{\prime }ar}^{md}$ = 0. To express the above logical relationship, we introduce a large positive number Ω, so that

$$v_{m^{\prime }ar}^{md}\le \Omega \cdot y_{m^{\prime }ar}^{md},\forall a\in A,\forall r\in R$$

(4)

When the number of railcars unallocated into the outbound trains provided by the marshalling station $m^{\prime }$ transfer to a different marshalling station m, it cannot exceed the number of railcars unallocated into the outbound trains of the marshalling station $m^{\prime }$, that is

$${\displaystyle \sum _{m=1}^{\tilde{m}}{\displaystyle \sum _{d=1}^{\tilde{d}}{u}_{m^{\prime }kr}^{md}}}\le n_{m^{\prime }kr},\forall k\in K,\forall r\in R$$

(5)

The number of transfer railcar flows provided by the marshalling station $m^{\prime }$ to a different marshalling station, m, cannot exceed the number of stock connecting railcars at the marshalling station $m^{\prime }$; that is,

$${\displaystyle \sum _{m=1}^{\tilde{m}}{\displaystyle \sum _{d=1}^{\tilde{d}}{v}_{m^{\prime }ar}^{md}}}\le n_{m^{\prime }ar},\forall a\in A,\forall r\in R$$

(6)

(2)

In-station railcar flow connection time

When the station-stored railcars at marshalling station m provide a railcar-flow source for train d departing from this station, its disassembly, assembly, and departure operations are completed earlier than the train departure time; that is,

$$(T_s+{\displaystyle \sum _{h=2}^4{t}_{m,h}})\cdot x_{mkr}^{md}\le t_{dm\tau },\forall k\in K$$

(7)

When inbound train a at marshalling station m provides a railcar-flow source for outbound train d departing from the station, its arrival, disassembly, assembly, and departure operations are completed earlier than the train departure time. That is,

$$(t_{am\tau }+{\displaystyle \sum _{h=1}^4{t}_{mh}})\cdot y_{m^{\prime }ar}^{md}\le t_{dm\tau },\forall a\in A,\forall r\in R$$

(8)

(3)

Transit railcar flow connection time

When the station-stored train group at the marshalling station $m^{\prime }$ provides a railcar-flow source for outbound train d departing from a different marshalling station m, it handles disassembly $t_{m\prime ,2}$, assembly $t_{m\prime ,3}$, and transit $t_{m\prime ,m}$ at the station $m^{\prime }$, and then it proceeds to a different marshalling station, m. The moment after the secondary disassembly t_m,2, assembly t_m,3, and departure t_m,4 operations must be earlier than the train departure time t_dmτ. That is,

$$(T_s+{\displaystyle \sum _{h=2}^3{t}_{m^{\prime }h}}+t_{m^{\prime }m}+{\displaystyle \sum _{h=2}^4{t}_{mh}})\cdot x_{mkr}^{md}\le t_{dm\tau },\forall k\in K$$

(9)

When inbound train a at marshalling station $m^{\prime }$ provides the railcar-flow source for outbound train d at a different marshalling station m, it handles arrival $t_{m\prime ,1}$, disassembly $t_{m\prime ,2}$, assembly $t_{m\prime ,3}$, and transit $t_{m\prime ,m}$ at the station $m^{\prime }$, and then it proceeds to a different marshalling station w. The time after the station handles the secondary disassembly t_m,2, assembly t_m,3, and departure t_m,4 operations must be earlier than the train departure time, t_dmτ. That is,

$$(t_{am\tau }+{\displaystyle \sum _{h=1}^3{t}_{m^{\prime }h}}+t_{m^{\prime }m}+{\displaystyle \sum _{h=2}^4{t}_{mh}})\cdot y_{m^{\prime }ar}^{md}\le t_{dm\tau },\forall a\in A,\forall r\in R$$

(10)

(4)

Railcar transit constraint

In a railroad terminal with multiple marshalling stations, cross-station transit railcar flow can be provided to outbound trains to improve the efficiency of the terminal railcar flow. Considering the capacity of the connecting lines between marshalling stations, the cross-station transit railcar flow should meet the limit of the number of transiting railcars.

$${\displaystyle \sum _{a=1}^{\tilde{a}}{\displaystyle \sum _{d=1}^{\tilde{d}}{\displaystyle \sum _{k=1}^{\tilde{k}}{\displaystyle \sum _{r=1}^{\tilde{r}}(}}}}{u}_{m^{\prime }kr}^{md}+v_{m^{\prime }ar}^{md})\le c_{m^{\prime }m}(m^{\prime }\ne m),\forall m,m^{\prime }\in M$$

(11)

(5)

Train full workload

According to the train marshalling plan, the allocated trains should meet the minimum weight or minimum length requirements, or they should meet the weight and length requirements at the same time. Considering factors such as the type of cargo loaded, gradient of the railway line, and braking distance, the hauling weight regulations and equivalent length regulations that different departing trains must meet are not entirely the same. Among the above two full workload constraints, the values of train weight and length are not fixed values but have certain value ranges. Therefore, outbound train d departing from station m should meet the train length requirements:

$$l_{md,\min }\le {\displaystyle \sum _{m^{\prime }=1}^{\tilde{m}}{\displaystyle \sum _{k=1}^{\tilde{k}}{\displaystyle \sum _{r=1}^{\tilde{r}}(u_{m^{\prime }kr}^{md}\cdot l_{m^{\prime }kr}+v_{m^{\prime }ar}^{md}\cdot l_{m^{\prime }ar})\cdot {\lambda }_{md}^{ld}\le l_{md,\max }}}}$$

(12)

Train d departing from station m should meet the weight requirement of the train:

$$w_{md,\min }\le {\displaystyle \sum _{m^{\prime }=1}^{\tilde{m}}{\displaystyle \sum _{k=1}^{\tilde{k}}{\displaystyle \sum _{r=1}^{\tilde{r}}(u_{m^{\prime }kr}^{md}\cdot w_{m^{\prime }kr}+v_{m^{\prime }ar}^{md}\cdot w_{m^{\prime }ar})\cdot {\lambda }_{md}^{wd}\le w_{md,\max }}}}$$

(13)

In addition, the outbound train d departing from station m must satisfy either the length or weight full-axle constraints; otherwise, the outbound train will not be dispatched:.

$${\lambda }_{md}^{ld}+{\lambda }_{md}^{wd}\ge 1,\forall m\in M,\forall d\in D$$

(14)

In the above equations, ${\lambda }_{md}^{ld}$ and ${\lambda }_{md}^{wd}$ are binary variables, representing whether the outbound train d from station m meets the train’s equivalent length and hauling weight requirements, respectively. Regarding Equation (14), there are four possible value scenarios: “${\lambda }_{md}^{ld}$ = 0 and ${\lambda }_{md}^{wd}$ = 0”, “${\lambda }_{md}^{ld}$ = 0 and ${\lambda }_{md}^{wd}$ = 1”, “${\lambda }_{md}^{ld}$ = 1 and ${\lambda }_{md}^{wd}$ = 0”, “${\lambda }_{md}^{ld}$ = 1 and ${\lambda }_{md}^{wd}$ = 1”. Among all these four scenarios, Equation (14) requires that the sum of ${\lambda }_{md}^{ld}$ and ${\lambda }_{md}^{wd}$ must be greater than or equal to 1; thus, the scenario “${\lambda }_{md}^{ld}$ = 0 and ${\lambda }_{md}^{wd}$ = 0” is not permitted within the model as it does not satisfy the model’s constraints. The remaining three scenarios all meet the requirements of Equation (14). Together with Equations (12) and (13), these three constraints jointly operate within the mathematical model to ensure that the outbound train d from station m satisfies the dispatch conditions.

3.5. Optimization Model

The model is established with the goal of minimizing the total dwell time of on-time and delayed allocated railcar flows in the stage plan under constraints such as the hauling railcar number of outbound trains and railcar flow connection time:

$$\min z=z_1+z_2$$

(15)

• st. Destination direction of outbound train: (3)–(6)
• In-station railcar-flow connection time: (7)–(8)
• Transit railcar-flow connection time: (9)–(10)
• Railcar transit constraint: (11)
• Train full workload: (12)–(14)

4. Case Study

4.1. Scenario Setting of the Experiments

Shenyang is a central metropolis in Northeast China and serves as a pivotal industrial base, commercial hub, and integrated transportation junction nationwide. The Shenyang railway hub encompasses three principal marshalling stations: Sujiatun Station, Yuguo Station, and Shenyang East Station. Among them, Sujiatun Marshalling Station, a superior-grade freight station (the highest rank among China’s freight marshalling stations), features a bidirectional three-tier and seven-yard layout, equipped with two automated hump yards and ten shunting locomotives, totaling 54 shunting tracks. It is one of China’s primary network marshalling stations, capable of handling over 20,000 vehicles in disassembly and assembly daily, and able to receive and dispatch more than 400 trains. Yuguo Station, a superior-grade freight station, has a mixed two-tier and six-yard layout with 14 arrival and departure tracks, including one automated hump, and handles over 14,000 vehicles in disassembly and assembly daily, capable of receiving and dispatching more than 240 trains. Shenyang East Station, a first-class freight station, currently has nine freight-dedicated lines and six arrival and departure tracks.

Taking the Shenyang railway hub as a prototype [36], we refer to the layout and daily operational data of large-scale railway hubs with multiple marshalling stations [37,38,39]. For marshalling stations where relevant information could not be found, we draw on the technical parameters and daily operational data of other marshalling stations of equivalent scale to design the experimental scenarios as follows: three marshalling stations (I, II, and III) were distributed in the railroad terminal, responsible for the dispatching of trains for eight marshalling destinations. A plan view of a railroad terminal with multiple marshalling stations is shown in Figure 2.

The disassembly, assembly, and inter-station transfer capabilities of each marshalling station and the train running time between marshalling stations are shown in

Table 1. Coupling/decoupling capacity of marshalling station, transship capacity, and trip time among marshalling stations.

Marshalling Station	Coupling/Decoupling Capacity (Railcar)		The Transship Capacity (Railcar)			Trip Time Among Marshalling Stations (min)
	Break-Up	Make-UP	I	II	III	I	II	III
I	480	450	-	65	50	-	31	38
II	390	420	-	-	60	-	-	27
III	400	380	-	-	-	-	-	-

. In the context of actual railway transportation in China, the number and direction of railcar flows arriving at marshalling stations daily are determined by the dispatching center based on various factors, including freight demand and locomotive supply. Subsequently, the daily work plan is divided into several phase plans (with each phase lasting 3 to 4 hours), yielding the quantity and transportation direction of railcar flows within each phase plan. In the test cases set up in this paper, a total of 24 inbound trains were received from 9:00 to 11:00. The station-stored railcar flow information at the beginning of the stage plan is shown in

Table 2. Information on railcar groups existed at the beginning of the stage plan.

Railcar-Flow Number	Marshalling Station	Destination Station Direction	Number of Railcars	Weight of Every Railcar (t)	Equivalent Length of Every Railcar
1	I	2	3	58/65/66	1.3/1.3/1.3
2	I	4	8	54/54/54/58/58/60/59/60	1.1/1.1/1.2/1.2/1.2/1.2/1.2/1.2
3	I	6	5	58/57/62/65/63	1.3/1.4/1.4/1.4/1.4
4	II	5	6	54/52/65/53/56/64	1.2/1.1/1.4/1.1/1.2/1.3
5	II	7	8	52/53/54/54/53/52/55/56	1.1/1.1/1.2/1.2/1.1/1.2/1.2/1.2
6	II	1	4	63/58/60/65	1.4/1.4/1.4/1.4
7	III	3	3	60/67/65	1.3/1.4/1.3
8	III	8	5	66/63/60/52/65	1.4/1.4/1.3/1.3/1.4

Note: The equivalent length refers to the ratio of the distance between the inner sides of the couplers at both ends of a railway vehicle to the standard vehicle length of 11 m; therefore, the equivalent length in the table does not have units. Table 4 and Table 6, Table 7, Table 8 and Table 9 are the same.

. The inbound train numbers and composition information are shown in

Table 3. Information on the inbound train in the stage plan.

Inbound Trains	Arrival Marshalling Station	Time of Arrival at the Marshalling Station	Train Type	Inbound Trains	Arrival Marshalling Station	Time of Arrival at the Marshalling Station	Train Type
1	I	9:05	0	13	I	9:56	0
2	II	9:09	0	14	II	9:59	0
3	I	9:15	0	15	III	10:03	0
4	III	9:18	1	16	I	10:06	1
5	II	9:21	0	17	II	10:17	0
6	III	9:32	0	18	III	10:21	1
7	I	9:32	0	19	I	10:25	0
8	II	9:39	0	20	I	10:31	0
9	III	9:45	1	21	III	10:37	0
10	I	9:47	0	22	II	10:45	0
11	III	9:52	0	23	I	10:52	0
12	II	9:55	0	24	III	10:56	0

and

Table 4. Composition information of the inbound trains in the stage plan.

Inbound Trains	Destination Station Direction	Number of Railcars	Weight of Every Railcar (t)	Equivalent Length of Every Railcar
1	2	8	58/65/72/65/48/52/54/55	1.2/1.4/1.5/1.2/1.3/1.3/1.2/1.2
1	4	14	52/54/58/60/54/55/52/53/55/ 52/52/53/54/54	1.1/1.1/1.3/1.3/1.1/1.2/1.2/1.2/1.2/ 1.2/1.2/1.2/1.2/1.2
1	7	12	54/54/54/58/58/60/59/60/65/53/56/64	1.1/1.1/1.1/1.3/1.3/1.3/1.3/1.3/1.4/1.1/1.2/1.4
2	4	10	54/54/54/58/58/60/59/60/52/48	1.1/1.1/1.2/1.2/1.2/1.2/1.2/1.2/1.1/1.1
2	6	7	62/63/59/72/58/59/60	1.4/1.4/1.3/1.6/1.4/1.4/1.4
2	7	8	52/53/54/54/53/52/55/56	1.1/1.1/1.2/1.2/1.1/1.2/1.2/1.2
2	8	10	52/54/58/60/54/55/52/53/55/52	1.1/1.1/1.3/1.3/1.1/1.2/1.2/1.2/1.2/1.1
3	3	8	54/54/54/58/58/60/59/60	1.1/1.1/1.1/1.3/1.3/1.3/1.3/1.3
3	5	12	66/63/60/52/65/52/54/58/60/54/55/52	1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
3	7	12	64/62/59/54/60/51/56/57/60/54/54/54	1.3/1.4/1.3/1.4/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
4	4	12	66/61/60/55/65/52/53/58/60/53/54/53	1.4/1.3/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
4	6	9	54/58/60/54/55/52/53/55/52	1.1/1.3/1.3/1.1/1.2/1.2/1.2/1.2/1.1
5	1	12	54/54/54/58/58/60/59/60/65/53/56/64	1.1/1.1/1.1/1.3/1.3/1.3/1.3/1.3/1.4/1.1/1.2/1.4
5	2	10	54/55/52/53/55/52/52/53/54/54	1.1/1.2/1.2/1.2/1.2/1.2/1.2/1.2/1.2/1.2
5	5	10	60/52/65/52/54/58/60/54/55/52	1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
5	8	9	54/60/51/56/57/60/54/54/54	1.4/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
6	3	12	55/57/52/56/60/62/63/59/72/58/59/60	1.1/1.1/1.2/1.2/1.1/1.4/1.4/1.3/1.6/1.4/1.4/1.4
6	6	11	57/60/54/54/54/54/58/60/ 54/55/52	1.3/1.3/1.1/1.2/1.2/1.1/1.3/1.3/1.2/1.2/1.2
6	8	15	53/55/52/66/61/60/55/65/52/53/58/60/53/54/53	1.2/1.2/1.1/1.4/1.3/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
7	1	8	68/60/54/55/52/53/65/72	1.6/1.3/1.1/1.2/1.2/1.2/1.5/1.6
7	5	14	63/53/65/62/59/52/65/52/54/58/60/54/55/52	1.4/1.1/1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
7	7	12	56/52/53/52/72/63/54/54/53/52/55/66	1.2/1.1/1.1/1.2/1.6/1.4/1.2/1.2/1.1/1.2/1.2/1.4
8	4	8	60/51/56/57/60/54/54/54	1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
8	6	15	62/53/53/65/62/59/52/65/52/54/58/60/54/55/52	1.4/1.1/1.1/1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
8	7	12	64/62/59/54/60/51/56/57/60/54/54/54	1.3/1.4/1.3/1.4/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
9	5	12	56/56/52/56/60/62/63/59/72/58/59/60	1.2/1.2/1.1/1.2/1.1/1.4/1.4/1.3/1.6/1.4/1.4/1.4
9	7	8	68/60/54/55/52/53/65/62	1.5/1.3/1.1/1.2/1.2/1.2/1.5/1.4
10	2	15	52/54/52/68/62/60/55/65/52/53/58/60/53/54/53	1.1/1.2/1.1/1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
10	4	10	52/54/58/60/54/55/52/53/55/52	1.1/1.1/1.3/1.3/1.1/1.2/1.2/1.2/1.2/1.1
10	8	15	54/54/52/66/61/60/55/65/52/53/58/60/ 53/54/53	1.2/1.2/1.1/1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
11	3	6	60/54/58/52/53/67	1.3/1.1/1.4/1.2/1.2/1.5
11	5	14	53/52/65/63/60/52/65/52/54/58/60/54/55/52	1.1/1.1/1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
11	7	16	52/53/56/55/66/61/60/55/65/52/53/58/60/53/54/53	1.1/1.2/1.2/1.1/1.4/1.3/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
12	2	12	66/63/60/52/65/52/54/58/60/54/55/52	1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
12	4	9	59/68/60/54/55/52/53/65/72	1.4/1.6/1.3/1.1/1.2/1.2/1.2/1.5/1.6
12	7	15	52/56/52/66/61/60/55/65/52/53/58/60/ 53/54/53	1.2/1.2/1.1/1.4/1.3/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
13	4	14	52/54/66/62/59/52/65/52/54/58/60/54/55/52	1.1/1.1/1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
13	6	6	64/65/72/53/65/72	1.4/1.4/1.6/1.2/1.5/1.6
13	7	15	52/53/53/65/62/59/52/65/52/54/58/60/ 54/55/52	1.1/1.1/1.1/1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
14	4	15	53/55/52/66/61/60/55/65/52/53/58/60/ 53/54/53	1.2/1.2/1.1/1.4/1.3/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
14	5	8	61/68/60/54/58/52/53/67	1.4/1.6/1.3/1.1/1.4/1.2/1.2/1.5
14	7	14	53/53/65/62/59/52/65/52/54/58/60/54/55/52	1.1/1.1/1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
15	3	14	52/53/66/63/60/52/65/52/54/58/60/54/55/52	1.1/1.1/1.4/1.4/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.2/1.2/1.2
15	6	12	55/57/52/56/60/62/63/59/72/58/59/60	1.1/1.1/1.2/1.2/1.1/1.4/1.4/1.3/1.6/1.4/1.4/1.4
15	7	8	59/68/60/54/58/52/53/65	1.4/1.6/1.3/1.1/1.4/1.2/1.2/1.5
15	8	5	65/72/53/65/72	1.4/1.6/1.2/1.5/1.6
16	5	12	56/52/53/52/72/63/54/54/53/52/55/66	1.2/1.1/1.1/1.2/1.6/1.4/1.2/1.2/1.1/1.2/1.2/1.4
16	7	8	54/60/51/56/57/60/54/54	1.4/1.4/1.1/1.1/1.3/1.3/1.1/1.2
17	1	12	55/57/52/56/60/62/63/59/72/58/59/60	1.1/1.1/1.2/1.2/1.1/1.4/1.4/1.3/1.6/1.4/1.4/1.4
17	5	5	68/59/68/60/54	1.5/1.4/1.6/1.3/1.1
17	7	12	57/52/53/52/72/63/54/54/53/52/55/66	1.3/1.1/1.1/1.2/1.6/1.4/1.2/1.2/1.1/1.2/1.2/1.4
17	8	9	66/68/60/54/55/52/53/65/72	1.5/1.6/1.3/1.1/1.2/1.2/1.2/1.5/1.6
18	4	6	64/65/72/53/65/72	1.4/1.4/1.6/1.2/1.5/1.6
18	6	8	61/68/60/54/58/52/53/67	1.4/1.6/1.3/1.1/1.4/1.2/1.2/1.5
18	7	9	68/59/68/60/54/58/52/53/65	1.5/1.4/1.6/1.3/1.1/1.4/1.2/1.2/1.5
19	4	8	68/60/54/55/52/53/65/72	1.6/1.3/1.1/1.2/1.2/1.2/1.5/1.6
19	5	16	51/53/55/52/66/61/60/55/65/52/53/58/60/ 53/54/53	1.1/1.2/1.2/1.1/1.4/1.3/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
19	7	14	55/52/52/52/53/52/72/63/54/54/53/52/55/66	1.2/1.2/1.2/1.1/1.1/1.2/1.6/1.4/1.2/1.2/1.1/ 1.2/1.2/1.4
20	3	8	68/60/54/55/52/53/65/72	1.6/1.3/1.1/1.2/1.2/1.2/1.5/1.6
20	4	14	52/56/56/52/53/52/72/63/54/54/53/52/55/66	1.1/1.2/1.2/1.1/1.1/1.2/1.6/1.4/1.2/1.2/1.1/ 1.2/1.2/1.4
20	6	16	52/52/56/54/66/61/60/55/65/52/53/58/60/ 53/54/53	1.1/1.2/1.2/1.1/1.4/1.3/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
21	4	8	72/63/54/54/53/52/55/66	1.6/1.4/1.2/1.2/1.1/1.2/1.2/1.4
21	7	15	53/55/52/66/61/60/55/65/52/53/58/60/ 53/54/53	1.2/1.2/1.1/1.4/1.3/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
21	8	12	55/52/53/52/72/63/54/54/53/52/55/66	1.2/1.1/1.1/1.2/1.6/1.4/1.2/1.2/1.1/1.2/1.2/1.4
22	5	12	55/57/52/56/60/62/63/59/72/58/59/60	1.1/1.1/1.2/1.2/1.1/1.4/1.4/1.3/1.6/1.4/1.4/1.4
22	6	7	60/54/55/52/53/65/72	1.3/1.1/1.2/1.2/1.2/1.5/1.6
22	7	14	51/56/55/52/53/52/72/63/54/54/53/52/55/66	1.1/1.2/1.2/1.1/1.1/1.2/1.6/1.4/1.2/1.2/1.1/1.2/1.2/1.4
23	4	15	55/53/54/57/60/54/55/52/53/55/53/53/52/55/54	1.3/1.1/1.1/1.3/1.3/1.1/1.2/1.2/1.2/1.2/ 1.2/1.2/1.2/1.2/1.2
23	5	15	56/52/54/58/60/54/55/52/53/55/ 52/52/53/54/54	1.3/1.1/1.1/1.3/1.3/1.1/1.2/1.2/1.2/1.2/ 1.2/1.2/1.2/1.2/1.2
23	6	7	62/63/59/72/58/59/60	1.4/1.4/1.3/1.6/1.4/1.4/1.4
24	4	9	59/68/60/54/55/52/53/65/72	1.6/1.3/1.1/1.2/1.2/1.2/1.5/1.6
24	6	16	51/53/55/52/66/61/60/55/65/52/53/58/60/ 53/54/53	1.1/1.2/1.2/1.1/1.4/1.3/1.3/1.3/1.4/1.1/1.1/1.3/1.3/1.1/1.2/1.2
24	7	11	52/53/52/72/63/54/54/53/52/55/66	1.1/1.1/1.2/1.6/1.4/1.2/1.2/1.1/1.2/1.2/1.4

. A total of 24 outbound trains were available from 11:00–13:00. The train numbers and directions are shown in

Table 5. Information on outbound trains in the stage plan.

Outbound Trains	Departure Marshalling Station	Time of Departure at the Marshalling Station	Train Type	Destination Station Direction	Outbound Trains	Departure Marshalling Station	Time of Departure at the Marshalling Station	Train Type	Destination Station Direction
1	I	11:00	0	4,6	13	I	11:58	0	4,7,8
2	II	11:03	1	1	14	III	12:02	0	5,7
3	I	11:07	1	2,3	15	II	12:07	0	4,6,7
4	III	11:18	0	6,8	16	II	12:15	0	4,5,7
5	I	11:17	0	4,7	17	III	12:20	1	3
6	III	11:18	0	2,3	18	II	12:23	0	5,6
7	II	11:26	0	5,7,8	19	I	12:28	0	4,5,6
8	I	11:28	0	4,5,6	20	I	12:34	0	4,5,7
9	II	11:37	0	4,6,7	21	III	12:38	0	6,7
10	I	11:45	0	4,6	22	I	12:44	0	4,5,7
11	III	11:48	0	4,5	23	III	12:46	0	4,6,7
12	II	11:50	1	2,3	24	II	12:56	0	5,7,8

. In Table 5, trains with property 0 are those that cannot be underloaded, such as district trains, through trains, and direct trains, and trains with property 1 are those that can be underloaded, such as pickup goods trains and district transfer trains. Information on the outbound train’s full workload limitation is shown in

Table 6. Information on the outbound train’s full workload limitation.

Outbound Trains	Train Weight Range (t)	Train Length Range	Outbound Trains	Train Weight Range (t)	Train Length Range
1	[1550,1820]	[35,42]	13	[1750,2100]	[38,48]
2	[1320,2100]	[28,40]	14	[1120,1560]	[28,38]
3	[1550,1860]	[28,48]	15	[1350,2200]	[35,48]
4	[1560,2100]	[35,42]	16	[1360,1820]	[31,42]
5	[1320,1820]	[28,42]	17	[1420,1860]	[31,42]
6	[1350,2100]	[28,48]	18	[1520,1820]	[31,42]
7	[1760,2400]	[35,48]	19	[1500,1860]	[31,38]
8	[1360,1820]	[28,42]	20	[1420,1860]	[31,38]
9	[1360,1820]	[31,40]	21	[1320,1820]	[31,38]
10	[1320,1800]	[31,38]	22	[1520,1800]	[31,42]
11	[1550,1800]	[28,42]	23	[1360,1800]	[28,38]
12	[1420,1800]	[31,48]	24	[1750,1820]	[35,42]

.

4.2. Model Validation and Analysis

All the proposed approaches are coded using CPLEX 12.10 to solve the models. The experiments are executed on a PC with an Intel I7 14700HX 20-Core 5.50 GHz Processor, 16 GB RAM, and Windows 11 64-bit operating system. The railcar-flow allocation scheme is shown in

Table 7. Railcar flow assignment scheme with different full workloads for multiple marshalling stations.

Outbound Trains	Departure Marshalling Station	Time of Departure at the Marshalling Station	Hauling Weight (t)	Equivalent Length	Outbound Trains	Departure Marshalling Station	Time of Departure at the Marshalling Station	Hauling Weight (t)	Equivalent Length
1	I	11:00	-	-	13	I	11:58	1839	40
2	II	11:03	1337	30	14	III	12:02	1198	30.1
3	I	11:07	1999	45.5	15	II	12:07	2081	46.6
4	III	11:18	2006	46.4	16	II	12:15	1734	40.5
5	I	11:17	1444	30.7	17	III	12:20	1426	32.6
6	III	11:18	1815	40	18	II	12:23	1304	33.8
7	II	11:26	2282	50.9	19	I	12:28	1530	36.8
8	I	11:28	1642	39.1	20	I	12:34	1468	35.9
9	II	11:37	1730	38.9	21	III	12:38	1347	32.7
10	I	11:45	1479	30.3	22	I	12:44	1561	34.9
11	III	11:48	1292	30.4	23	III	12:46	1388	30
12	II	11:50	1726	40	24	II	12:56	-	-

Note: The bold font indicates compliance with the full workload constraint for this column.

.

According to the solution results, we made the following observations:

(1)

According to the solution results, considering different full workload constraint scenarios, the railcar-flow dwell time at the station was 19.48 railcar hours, the number of railcars in the station after the stage plan had ended was 67 railcars, and a total of two outbound trains were not dispatched owing to an insufficient traffic connection. Marshalling station I and station II each had one train;

(2)

Among the 22 outbound trains allocated on time within the stage plan, 17 trains could meet both the weight and length constraints. If only considering the train weight constraints, two additional outbound trains cannot be dispatched (the 11th and 18th trains). If only considering the train length constraints, three additional outbound trains cannot be dispatched (the 4th, 7th, and 10th trains). This result indicates that considering different full workload constraints reduces the occurrence of undispatched outbound trains.

4.3. Comparison of Railcar Flow Allocation Schemes Under Three Full Workload Constraints

To validate the model’s effectiveness, we introduced railcar-flow allocation schemes under a single full-axis constraint for comparison. First, the multi-marshalling station flow allocation model with different full-axle constraints was adjusted, and the expressions of the parameters w_mar, w_mkr, $w_{md,\max }$, and $w_{md,\min }$ related to the weight of the outbound train were removed, as was the related discriminant variable ${\lambda }_{md}^{wd}$. Additionally, the weight constraint (14) and constraint (15) for outbound trains were deleted from the model. A multi-marshalling station railroad terminal allocation model that only considers the outbound train length constraint was obtained. Then, the CPLEX solver was used to solve the model on microcomputers with the same configuration. A railcar-flow allocation scheme was obtained, as shown in

Table 8. Railcar flow assignment scheme with hauling length limitation for multiple marshalling stations.

Outbound Trains	Departure Marshalling Station	Time of Departure at the Marshalling Station	Hauling Weight (t)	Equivalent Length	Outbound Trains	Departure Marshalling Station	Time of Departure at the Marshalling Station	Hauling Weight (t)	Equivalent Length
1	I	11:00	-	-	13	I	11:58	2021	44.1
2	II	11:03	1650	37	14	III	12:02	1536	37.2
3	I	11:07	1587	37	15	II	12:07	1706	37.6
4	III	11:18	1745	39.6	16	II	12:15	1578	37
5	I	11:17	-	-	17	III	12:20	1606	37.1
6	III	11:18	2031	45.2	18	II	12:23	1420	37
7	II	11:26	1993	44.3	19	I	12:28	1482	37.2
8	I	11:28	1655	38.5	20	I	12:34	1575	37.1
9	II	11:37	1741	38.2	21	III	12:38	1547	37.2
10	I	11:45	1710	37	22	I	12:44	1656	37.6
11	III	11:48	1580	37.1	23	III	12:46	1785	37.7
12	II	11:50	2004	46	24	II	12:56	-	-

Note: The bold font indicates compliance with the full workload constraint for this column.

.

Following a similar method, we introduced a multi-marshalling station railroad terminal railcar-flow allocation model that considers only train weight constraints. First, the original model was adjusted to remove the parameter expressions l_mar, l_mkr, $l_{md,\max }$, and $l_{md,\min }$ related to the outbound train length, as well as the related discriminant variables ${\lambda }_{md}^{ld}$. At the same time, the outbound train length constraints (13) and (15) in the model were removed to obtain another model. Then, we used the CPLEX solver to run the solution on a microcomputer with the same configuration, and we obtained the railcar-flow allocation scheme, as shown in

Table 9. Railcar flow assignment scheme with hauling weight limitation for multiple marshalling stations.

Outbound Trains	Departure Marshalling Station	Time of Departure at the Marshalling Station	Hauling Weight (t)	Equivalent Length	Outbound Trains	Departure Marshalling Station	Time of Departure at the Marshalling Station	Hauling Weight (t)	Equivalent Length
1	I	11:00	-	-	13	I	11:58	1983	61.1
2	II	11:03	1752	39.3	14	III	12:02	-	-
3	I	11:07	1753	40.4	15	II	12:07	2171	48
4	III	11:18	1817	40.9	16	II	12:15	1784	41.3
5	I	11:17	-	-	17	III	12:20	1770	40.6
6	III	11:18	1986	44.1	18	II	12:23	1751	44.9
7	II	11:26	2065	45.6	19	I	12:28	1770	43.9
8	I	11:28	1775	41.4	20	I	12:34	1806	43.5
9	II	11:37	1782	39.7	21	III	12:38	1785	43.6
10	I	11:45	1751	35.5	22	I	12:44	1774	38.8
11	III	11:48	1751	41.1	23	III	12:46	-	-
12	II	11:50	1783	41.5	24	II	12:56	-	-

Note: The bold font indicates compliance with the full workload constraint for this column.

.

According to the solution results, we made the following observations:

(1)

According to Table 8, when only considering the train length constraint, the railcar flow stayed at the station for 19.9 railcar hours, the number of railcars in stock at the station after the stage plan had ended was 81 railcars, and a total of three outbound trains were not dispatched, owing to insufficient traffic connection. Marshalling station I had two trains, and marshalling station II had one train.

(2)

According to Table 9, when only considering the train weight constraint, the railcar flow stayed at the station for 20.93 railcar hours, the number of railcars in the station after the end of the stage plan was 128 railcars, and a total of five outbound trains were not dispatched, owing to insufficient traffic connection. Marshalling stations I and II each had two trains, while Marshalling Station III had one train.

To better demonstrate the superior performance of the model proposed in this paper, we selected four indicators: station dwell time, number of undispatched outbound trains, number of transfer railcars, and number of station-stored railcars. Then, three multi-marshalling station railcar-flow allocation schemes under full-axle constraints were compared, as shown in

Table 10. Testing results of the three models.

Comparative Indicators	Comparative models
	Different Full Workload	Equivalent Length Limitation	Hauling Weight Limitation
CPU running time (s)	322	376	451
Dwell time of terminal railcar flow (h)	1169	1194	1256
Railcars unallocated into the outbound trains (railcar)	67	81	128
Outbound trains not dispatched within the time range of the stage plan (train)	2	3	5

.

According to the validation results, we made the following observations:

(1)

From the perspective of the CPU running time, for the three models, good solutions could be obtained within a reasonable time range, meeting real-world application requirements. The model that considers different full workload constraints took less time to run than the model that only considers the train length constraint and the one that only considers the train weight constraint.

(2)

Judging from the indicators of the number of station-stored railcars at the station and the number of undispatched outbound trains at the end of the stage plan, when considering different full workload constraints, we found that there were fewer station-stored railcars at the station at the end of the stage plan, and the undispatched outbound trains were also fewer.

In summary, the multi-marshalling station railroad terminal allocation scheme that considers different full workload constraints can effectively improve the efficiency of railroad terminal operations in the stage plan.

4.4. Experimental Evaluation and Key Parameter Analysis Under Different Scales

Utilizing the technical parameters of the Shenyang railway hub, which incorporates multiple marshalling stations, we use varying scales of inbound and outbound train numbers to test the applicability of the model proposed in this paper under different railcar flow conditions. Simultaneously, we have taken into account that the distances between different marshalling stations within the railway hub affect the transit time of railcar flows, thereby impacting the effectiveness of coordinated railcar flow allocation. Therefore, it is necessary to further discuss the impact of transit times on railcar flows between marshalling stations in the allocation scheme.

Firstly, we establish a case study with a larger scale of train arrival and departure: within the phase plan, there are 42 inbound trains entering the railway hub, and simultaneously, 42 outbound trains are leaving the railway hub. Subsequently, following the chronological order of train entry into the railway hub, we randomly select a specified number of arriving trains, and correspondingly, the same number of outbound trains is chosen using this method, forming different scales of train arrival and departure. The specifics are as follows: ① 24 inbound trains and 24 outbound trains; ② 30 inbound trains and 29 outbound trains; ③ 36 inbound trains and 37 outbound trains; and ④ 42 inbound trains and 42 outbound trains. For ease of representation,

Table 11. Comparison of Solution Results under Different Scenarios.

Comparative Indicators	Scenario Configuration
	Scale ①			Scale ②			Scale ③			Scale ④
	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12
CPU running time (s)	316	356	374	896	966	1120	3600	3600	3600	#	#	#
Dwell time of terminal railcar flow (h)	1178	1189	1232	1312	1346	1425	1620 *	1677 *	1783 *	#	#	#
Railcars unallocated into the outbound trains (railcar)	47	61	117	103	131	147	137 *	151 *	226 *	#	#	#
Outbound trains not dispatched within time range of the stage plan (train)	2	2	4	4	5	6	5 *	5 *	8 *	#	#	#

Note: “*” denotes the satisfactory solution obtained by CPLEX within the prescribed time; “#” indicates that CPLEX failed to find a feasible solution within the time limit.

denotes the four problem scales as Scale ①–Scale ④.

Secondly, we categorize the transit time for railcar flows between different marshalling stations within the railway hub into three classes, with the mutual transit times between Marshalling Station I, Marshalling Station II, and Marshalling Station III being 30 min, 50 min, and 70 min, respectively.

Based on the established foundation, we combine different scales of inbound and outbound trains with various transit distances to form 12 experimental scenarios. Among these, Scenarios 1 to 3 represent the experimental settings under the condition of Scale ① for inbound and outbound trains, with transit times of 30 min, 50 min, and 70 min, respectively. Similarly, Scenarios 4 to 6, 7 to 9, and 10 to 12 are set according to the aforementioned matching method. For ease of representation, the 12 experimental scenarios in Table 11 are denoted as S1–S12.

Finally, the experiments are executed on a PC with an Intel I7 14700HX 20-Core 5.50 GHz Processor, 16 GB RAM, and Windows 11 64-bit operating system. Considering the practical application value, the runtime limit for CPLEX is set to 3600 seconds, where the symbol “∗” denotes the satisfactory solution obtained by CPLEX within the prescribed time, and “#” indicates that CPLEX failed to find a feasible solution within the time limit. A comparison of the solution results under 12 different scenarios is illustrated in Table 11, where the numerical values represent the average of five consecutive tests for each scenario.

From the solution results, it can be observed that

(1)

As the problem size increases, at problem scale ③, CPLEX can only obtain satisfactory solutions within the specified time, whereas at problem scale ④, CPLEX is unable to find a feasible solution within the specified time. However, considering the Sujiatun Station, which has the strongest operational load capacity within the Shenyang railway hub, its current average daily number of arrival and departure trains is only over 400 (in an approximate conversion, equivalent to about 17 trains per hour), we believe that the performance of CPLEX in solving problems is sufficient to meet the daily operational needs.

(2)

The transit time between marshalling stations significantly affects the allocation outcomes. The solution results at problem scales ① and ② indicate that an increase in transit time leads to a corresponding increase in the number of trains not dispatched, with an average increase of one to two trains for every additional 20 min of transit time ( this value is subject to factors such as the structure of railcar flows). Concurrently, an increase in transit time also results in varying degrees of increase in the dwell time of railcar flows at stations and the number of unallocated railcars. Furthermore, the satisfactory solutions at problem scale ③ also validate this trend. We conclude that this is primarily because the increased transit time for railcar flows between stations encroaches on other technical operations, reducing the sources of railcar flows available for allocation to departing trains. Consequently, this leads to an increase in the number of trains not dispatched, the dwell time of railcar flows at stations, and the number of unallocated railcars.

5. Conclusions

This paper proposes a railcar-flow assignment optimization model that considers different full workload limitations of outbound trains to improve the operation efficiency of multiple marshalling stations at railroad terminals. Specifically, we built a model with the goal of minimizing the dwell time of railcar flow in the railroad terminals, comprehensively considering constraints such as connection time and traffic capacity, and relaxing the full workload limitation of the outbound train to reduce the dwell time of the railcar flow at the station, effectively improving the number of outbound trains and terminal operation efficiency. At the same time, in order to verify the effect of the model, we constructed two comparison models that only consider a single full workload constraint: a model that only satisfies the train length constraint and a model that only satisfies the train weight constraint.

By designing experimental scenarios and comparing results, we found that the railcar-flow allocation scheme considering different full-axle constraints can effectively reduce the number of undispatched outbound trains caused by a single full-axis constraint, which is conducive to optimizing railcar flow connections, reducing the number of trains stocked at stations, and shortening the transfer time between stations. However, determining the upper and lower limits of different full workload constraints of the outbound train will be the focus of the next step of research.

From the solution results, it can be observed that the organization of railcar flows of multiple marshalling stations is a complex combinatorial optimization problem that is highly deserving of exploration and research. This paper draws on existing studies and proposes incorporating various full workload constraints for outbound trains into the railcar flow organization of multiple marshalling stations. Although certain research outcomes have been achieved, there are still many aspects that require improvement. Future research can be further deepened in the following areas:

(1)

Railcar flow organization optimization is characterized by its multi-objective nature, and the process of planning is a complex decision-making process. This paper only considers the continuity of railcar flows and different full workload constraints for outbound trains without taking into account the utilization of classification tracks, the arrangement of shunting resources, and the priority levels of railcar flow organization, which are influential factors. Therefore, comprehensive optimization considering all aspects of the station is a key direction for future research.

(2)

The information required for railcar flow organization in multiple marshalling stations often exhibits uncertainty in actual field compilation, and the on-site environment is prone to changes (such as changes in railcar flow information and equipment failures). Therefore, it is necessary to further enhance the robustness of the plan and design real-time adjustment strategies.

(3)

The existing railcar flow origins and quantities are based on the train arrival times confirmed by the stage plan, without additional consideration for the variability in train arrival times. However, in actual railway operations, the size of railcar flows exhibits more randomness. Future plans include incorporating other methods to determine the size of railcar flows, such as Fuzzy logic and neural networks.