Abstract
To scientifically evaluate the implementation of the River Chief System (RCS), accelerate the overall improvement of the water ecological environment, and promote the sustainable development of river and lake functions, this study selects 26 evaluation indicators from six aspects, including the effectiveness of organization and management, the effectiveness of water resources protection, the effectiveness of water environment management, the effectiveness of water pollution prevention and control, the effectiveness of water ecological restoration, and the effectiveness of the management of the waterside shoreline, and establishes an evaluation system for the effectiveness of the implementation of the RCS. Among the 26 indicators, data for the qualitative indicators mainly come from a series of statistical yearbooks and RCS reports, while data for the quantitative indicators are obtained through scoring by more than 20 experts and calculating the average. The CRITIC objective weighting method is improved from three aspects of comparison intensity, correlation coefficient, and degree of variation, and the subjective weighting of indicators is carried out using the AHP 1–5 scale method. The optimal linear combination of subjective and objective weighting results is obtained using the combination weighting method with game theory, which is auxiliary to the set pair analysis. Considering the “certainty” and “uncertainty” in the evaluation process, the four-element connection number model of set pair analysis is established to evaluate the implementation effect of the RCS in Henan Province from 2018 to 2021. The results show that the implementation effect of the RCS in Henan Province improves year by year and reaches excellent in 2019. The results of this study can be used as a reference for evaluating the work of the RCS in other regions and can also provide a reference for the study of evaluation problems in other fields.
1. Introduction
With its large population and severe resource constraints, China has been facing great challenges in terms of water environment issues. In the course of past development, a large amount of wastewater, sewage, pesticides, and fertilizers discharged from industry, urban life, and agricultural activities have directly or indirectly led to the pollution of the water environment [1]. In addition, rapid economic development, increased water use in industry and agriculture, and climate change have also caused water scarcity in some parts of China [2,3]. Water pollution and water shortage have not only caused very serious impacts on Chinese society but also caused great damage to the ecological environment and biodiversity [4]. As the water problem is becoming more and more obvious, the development of Chinese society has been hindered to a great extent. In response to China’s high demand for pollution control and water resource protection and to effectively improve the water environment, China has begun to implement the River Chief System (RCS) in different regions [5]. With the gradual popularization of the RCS, how to improve the efficiency of water environment management has become the main problem facing the construction of water ecological civilization in China [6].
In 2018, Henan, Jiangsu, Shanghai, and other provinces and municipalities became the first pilot areas for the full implementation of the RCS, followed by Guangdong, Zhejiang, Fujian, Hunan, Anhui, and other provinces. After practicing in various regions, the General Office of the CPC Central Committee and the General Office of the State Council put forward the opinion of comprehensively implementing the RCS, which has been actively implemented in various regions and is now being carried out nationwide, participating in the governance of coastal areas and large and medium-sized cities [7,8]. So far, about 300,000 river chiefs have been set up nationwide, covering 15 types of rivers, lakes, and reservoirs to ensure comprehensive management and integrated governance of rivers. The Essentials of River and Lake Management in 2022 proposes to strictly evaluate the assessment and evaluation of the RCS and evaluate the fulfillment of the objectives of the work of river chiefs [9]. How to scientifically evaluate the effectiveness of the implementation of the RCS and improve the efficiency of water environment management is extremely important for the improvement of water environment management policies and in-depth study of China’s water environment management.
In the existing literature, most research studies focus on policy, and few scholars use mathematical modeling to evaluate the effectiveness of the implementation of the RCS. Longfei Wang et al. [10] conducted a study on the development of the RCS in China over the past decade. They elucidated the advantages of the RCS in terms of responsibility, authority, and interdepartmental collaboration while also highlighting some remaining issues. Their research findings provide new insights for the design of river management systems in other developing countries. Wang Juan et al. [11] conducted a study on the game theory between enterprise pollution management and the implementation strategies of local government pollution permits, as well as the game theory between different strategies of pollution permit implementation among local governments, and provided positive recommendations for the evolution direction of the RCS. Zhang Zihao et al. [12] conducted a study on water quality data in the Huai River Basin over the past 5 years and analyzed the effectiveness of the RCS based on the “embeddedness theory”. In addition, many other scholars have put forward many different suggestions for the policy on the RCS.
The use of appropriate methods to assess the effectiveness of the implementation of the RCS will help to identify problems promptly and summarize experiences and lessons learned in response to them. According to the evaluation results, targeted improvement measures can be put forward to optimize the river and lake governance model, which can make it more adaptable to the actual situation and needs, which is very necessary for the implementation of scientific governance and the promotion of river protection and restoration, and also one of the necessary means to promote the development of the system of river chiefs and enhance the effectiveness of governance. Therefore, it is of great significance to use appropriate methods to judge the implementation effect of the RCS to maintain the healthy life of rivers and lakes and to realize the sustainable use and development of river and lake functions.
In this study, the effectiveness of implementing the RCS was investigated using mathematical modeling. The study of implementation effectiveness is typically considered a problem of multi-indicator comprehensive evaluation. This method comprehensively evaluates phenomena by synthesizing multiple indicators, enabling the rational integration of evaluation factors from diverse perspectives and fields, thus providing an objective and comprehensive reflection of their essence and characteristics [13]. In domains such as environmental protection and water resource management, this evaluation method is frequently employed to assess the functionality of rivers [14] and the effectiveness of policy implementation [15]. Similarly, applying research on the effectiveness of implementation to the RCS can offer vital foundations for scientific management and decision-making.
The evaluation of multiple indicators often encounters conflicts, uncertainties, and incompatibilities. To address these challenges, it is crucial to first acknowledge the existence of uncertainties and systematically characterize the objects being evaluated. Subsequently, specific analysis and distinct dialectical evaluations can be conducted on these objects. Set pair analysis is an evaluation method that possesses the aforementioned advantages. It studies the uncertainties of two entities from the perspectives of “identity, diversity, and opposition”, treating certainty and uncertainty as a determinate–uncertain system and comprehensively depicts the correlation between these two entities [16]. In this system, certainty and uncertainty are interconnected, mutually influencing and constraining each other, and under certain conditions, they can transform into one another [17].
Traditional set pair analysis uses three-element connection numbers [18] for evaluation, neglecting the uncertainties in the “degree of difference”, which leads to imprecise evaluation results. In this study, we expand on the concept of the “degree of difference” and extend the traditional set pair analysis to a four-element connection number model. This model is suitable for comprehensive evaluation and allows for qualitative and quantitative analysis of the information reflected in the four-element connection numbers. Furthermore, set pair analysis itself cannot determine the weights of the evaluation criteria and requires the assistance of appropriate weighting methods. However, to date, there is no unified method for assigning weights in set pair analysis. This study aims to improve the traditional CRITIC objective weighting method in three aspects: the intensity of comparison, correlation coefficient, and degree of variation. In addition, a subjective weighting of indicators is performed using the Analytic Hierarchy Process (AHP) 1–5 scale method. The average scores of over 20 experts’ rating results on the importance of indicators were calculated and sorted. This process was used to construct a judgment matrix and examine the consistency of the matrix to determine the usability of the scoring results. The combination weighting method based on game theory is then employed to optimize the results of subjective and objective weighting, thereby reducing the impact of data fluctuations and subjective judgments on the weighting results and assisting set pair analysis in evaluating the indicators. By establishing the game theory combination weighting-set pair analysis model, the comprehensive evaluation results of the implementation effectiveness of the RCS in the evaluated region can be determined, resulting in more accurate and reasonable evaluation outcomes. These indicator data used in this study were sourced from various statistical yearbooks and reports. The quantitative indicators were scored by more than 20 experts, and the average scores were calculated to obtain the final values. Additionally, this approach aims to ensure that provincial governments pay more attention to improving water environmental governance efficiency, making water environmental investments achieve higher standards of return.
2. Literature Review
The purpose of the literature review in this study is to provide a deeper understanding of the relevant research on which this study is based.
2.1. CRITIC, AHP, and Game Theory for Weighting Method
In the evaluation process, determining the weights of selected indicators is crucial for generating the final results. To address the issue of the inability of set pair analysis methods to determine weights, appropriate weighting methods are required as assistance. The weighting determination methods can be categorized into two major types: subjective weighting methods and objective weighting methods [19]. The CRITIC method, proposed by Diakoulaki et al. [20], is a method for determining objective weights. This method mainly utilizes the conflict and contrast intensity among indicators to obtain the information contained in the indicators, thus determining the objective weights of the evaluation indicators [21]. Regarding the CRITIC method, many studies have combined it with other multi-attribute evaluation methods for application, making it a more comprehensive objective weighting method [22].
The Analytic Hierarchy Process (AHP) is a typical subjective weighting method proposed by American operations researcher T. L. Saaty [23] in the early 1970s. AHP combines quantitative and qualitative analysis by expressing subjective judgments in a numerical way. The AHP has garnered increasing recognition among scholars worldwide owing to its broad applicability and growing popularity [24]. Due to its wide applicability, scholars have continually extended and improved the AHP method, leading to the development of methods such as Exponential Scale Analytic Hierarchy Process (ESAHP) [25], Fuzzy Analytic Hierarchy Process (FAHP) [26], and AHP three-scale method [27], which have enhanced the effectiveness and feasibility of the AHP method. Since its inception, AHP has been widely applied in economics [28], mathematics [29], energy science [30], computer software applications [31], and architecture [32], among other fields.
For objective weighting methods, the fluctuation and errors in data may unavoidably affect the weighting results. Subjective weighting methods, on the other hand, can lead to irrational weight allocation due to overly subjective judgments based on expert experiences. The game theory-based combination weighting method addresses these issues by optimizing the linear relationship between different types of weighting methods, combining two or more weighting results to obtain more effective indicator weights. As a result, this method has been continuously validated for its scientific and rational results [33].
2.2. River Chief System and Set Pair Analysis Methodology
As a new water environment management system, the RCS has an indispensable positive force in water pollution prevention, water resources protection, and water ecological restoration [34]. Due to the relatively late implementation of the RCS, the current research literature is still very limited. From the perspective of RCS research, the majority of the relevant literature focuses on the implementation of the system nationwide [7]. In terms of research content, it primarily includes studies on the current state of implementation [12], analysis of the effects of the RCS [35], the impact of the system on enterprise development [36,37], evaluation of river chief work [5], and the control of agricultural pollution under the RCS [38]. A few scholars have also explored the effectiveness of the implementation of the RCS, and the identified evaluation factors are mainly related to water pollution, water ecology, and organizational supervision. Up to now, the research on the implementation status quo and regional differences of the RCS in some regions, the audit evaluation system of river chiefs, the performance evaluation system of river chiefs, and the effectiveness of the implementation of the RCS in some provinces and municipalities [39] has produced some results. However, there is no unified method to evaluate the effectiveness of the implementation of the RCS. The aims of the RCS are many, the task is heavy, and the impact on the ecology of rivers and lakes, as well as the development of the environment, is very significant, so it is very necessary to use a suitable method to evaluate the effectiveness of the implementation of the RCS in Henan Province. Through the judgment of the operation of the RCS, it can be targeted to put forward relatively scientific solutions.
From the perspective of comprehensive evaluation, most scholars apply hierarchical analysis [40], gray correlation analysis [41], fuzzy comprehensive evaluation [42], the TOPSIS method [43], and other methods to solve practical problems, and they have all produced very good results. Compared with the aforementioned evaluation methods, the set pair analysis method analyzes the systematic certainty and uncertainty of a practical problem from three different aspects: “identity, diversity, and opposition”. This allows for a comprehensive and three-dimensional evaluation of the problem from multiple perspectives [44]. Set pair analysis was proposed by Zhao Keqin in 1989, and its application is becoming increasingly widespread [45]. By considering the evaluation indexes and evaluation levels in the comprehensive evaluation problem as two different sets and systematically analyzing them, the analysis exhibits a distinct dialectical nature. This approach yields results closer to the actual outcomes after this study. Therefore, set pair analysis has become an effective method among the various approaches for solving problems related to multi-objective decision-making and multi-attribute evaluation in uncertain systems. In recent years, set pair theory has been successfully applied to various fields, including evaluation [46], management [47], decision-making [48], forecasting [49], planning [50], and artificial intelligence [51].
To fill the gap in the research direction of RCS, this study establishes a reasonable evaluation model for the implementation effectiveness of RCS. First, use the combination weighting method with game theory in combination with the weighting results of the improved CRITIC method and the AHP 1–5 scale method to determine the final weight, and then establish a set pair analysis four-element connection number framework to evaluate the selected indicators, obtain scientific evaluation results, and give reasonable suggestions for the evaluation results.
3. Determination of Indicator Weights
Considering the characteristics of fuzziness and uncertainty associated with the evaluation indicators for assessing the effectiveness of the implementation of the RCS, as well as the need to distinguish the importance of these indicators in the evaluation process, we employ a combined weighting method that integrates the improved CRITIC method and the AHP 1–5 scale method. This approach allows us to calculate the weights of the indicators accurately. The objective weight and subjective weight of each indicator are obtained accordingly. Additionally, the combination weighting method with game theory is utilized to optimize the weighting results and determine the combined weight.
3.1. AHP for Determining Subjective Weight of Indicators
The Analytic Hierarchy Process (AHP) is a multi-level analytical structural model based on the construction of evaluation indicators. It comprehensively calculates the subjective weights of the indicators by considering the relative importance between levels and between indicators [52]. The steps of calculation are as follows.
- (1)
- According to the selected set of indicators, construct the corresponding hierarchical structure. Using the RCS as the evaluation object, establish a three-level hierarchy, including the goal level, criterion level, and indicator level. The goal level represents the effectiveness of implementing the RCS, and the criterion level consists of six aspects: organizational management effectiveness, water resource protection effectiveness, water environment governance effectiveness, water pollution prevention and control effectiveness, water ecological restoration effectiveness, and water area shoreline management effectiveness. The goal level provides a detailed description and explanation of the criterion level.
- (2)
- Construct the judgment matrix. To reduce errors caused by subjective judgments during the evaluation process, a 1–5 scale method is used. By consulting expert opinions, scores are given to each indicator based on their importance to the effectiveness of implementing the RCS, and the judgment matrix is constructed.
- (3)
- Calculation of eigenvectors, eigenvalues, and weights. Using the maximum eigenvalue method, calculate the maximum eigenvalue and the corresponding normalized eigenvector for the judgment matrix.
- (4)
- Consistency test. If the consistency test is passed, it indicates that the judgment matrix is reasonable and has an explanatory value.
If the consistency test is not passed, the judgment matrix needs to be reviewed and modified, and if the revised judgment matrix satisfies the consistency test, subjective weights for evaluating the RCS can be determined. Further analysis can then be carried out based on the derived weights.
3.2. Improved CRITIC Method for Determining Objective Weights of Indicators
The CRITIC method assigns objective weights to indicators by considering both the relative importance and conflicts among them [53]. This study proposes the following improvements to the traditional CRITIC method:
- (1)
- For measuring the conflicts among indicators, the traditional CRITIC method typically uses the Pearson correlation coefficient. However, the Pearson coefficient may not accurately represent the correlation when data do not follow a normal distribution, or the sample size is less than 30 [54]. Therefore, this study replaces the Pearson coefficient with the Spearman correlation coefficient.
- (2)
- The correlation coefficient can be positive or negative, but in this study, absolute values of the correlation coefficients are used to avoid unnecessary biases during the calculation.
- (3)
- The traditional CRITIC method uses the standard deviation to measure the relative importance of indicators. However, in practical applications, it has been found that using the standard deviation is not sufficient. Instead, using the average deviation can provide better reliability and reduce errors caused by non-normality and skewness in these data. Therefore, this study replaces the standard deviation with the average deviation to measure the relative importance of indicators.
Considering the above improvements, the main steps of the revised CRITIC weighting method are as follows:
Step 1. Firstly, use the collected sample data to establish a decision matrix for evaluating the effectiveness of the RCS implementation
where represents the indicator value of the i-th indicator in the j-th year.
Step 2. Normalize these data to obtain the standardized decision matrix
If the indicator is a benefit-type indicator, the element of the standardized decision matrix after normalization is given by
If the indicator is a cost-type indicator, the element of the standardized decision matrix after normalization is given by
Step 3. Calculate the average deviation of these processed data
where represents the average value of evaluation criteria, and represents the average deviation of the evaluation criteria.
Step 4. Calculate the coefficient matrix of indicator correlation based on the Spearman correlation coefficient
In this case, the symbol represents the correlation coefficient between the indicators, and its expression is denoted as
where and represent the rankings of different elements in the normalized decision matrix after sorting the indicators in descending or ascending order.
Step 5. Calculate the amount of information contained in the evaluation indicators.
Step 6. Calculate the objective weights () of each evaluation indicator.
3.3. Game Theory-Based Weight Optimization
To avoid the subjective bias of expert judgments and the over-reliance on data in determining weight allocation, this study adopts a combination weighting method to determine the weights of indicators, aiming to achieve a more reasonable weight distribution [55].
Assuming there are different weighting methods, the weight vector represents the weights of indicators [33]. Through calculations, the basic weight set is obtained, and the combined weight is defined as the linear combination of these basic weights, i.e.,
Among them, is the allocation coefficient for the l-th basic weight. Since there are different weighting methods, there are infinitely many linear combinations of these basic weights, denoted as , where represents the optimal combination weight. This study utilizes game theory principles to optimize the allocation coefficients of the basic weights in the formula to minimize the discrepancy between the optimal combination weight and all the basic weights. This can be expressed as
where represents the second norm of vector ; is the variable to be determined and .
Using the MATLAB solver for calculations, obtaining the optimal value of , the combination weights based on game theory can be represented as
4. Model for Evaluating the Effectiveness of River Chief System
The core idea of set pair analysis is to consider certainty and uncertainty as a deterministic–uncertain system, recognizing that the “identity, diversity, and opposition” in things are interrelated, interdependent, and mutually constrained. Under certain conditions, they can also transform into each other, and this relationship is described using the degree of association [56]. The mathematical expression for the four-element connection number model of set pair analysis is denoted as
In the equation, , , , and represent the components of the connection numbers. denotes the degree of identity, and represents the degree of diversity, and and represent the coefficient of diversity degree with the relationship . is the coefficient of opposition degree and satisfies the constraint . Following the principle of equal division, the range of values for the connection numbers is evenly divided into three parts, corresponding to the values of , , and , resulting in , , and . The symbol represents the degree of opposition in set pair analysis, and the components of connection numbers satisfy the equation , with the additional conditions that , , , and .
Based on the fundamental concept of set pair analysis, an evaluation model for assessing the effectiveness of the RCS implementation is constructed. The specific steps are as follows.
Step 1. Calculate the four-element connection number between the sample value and the evaluation level based on the evaluation index standards. Evaluation indices that increase (decrease) as the evaluation level increases are referred to as benefit-type (cost-type) indices. Taking the benefit-type indices in the evaluation index system of the effectiveness of the implementation of the RCS as an example, the formulas for calculating the four-element connection numbers of set pair analysis corresponding to different levels of the indices are as follows.
where , represent the thresholds between adjacent evaluation criterion levels, and represents another critical value for the first-level evaluation criterion.
Step 2. Calculate the relative membership degree of the single index belonging to the standard level through normalization and then obtain the single index connection number .
Step 3. The calculation of the evaluation coefficient for the implementation effectiveness of the RCS corresponding to the sample .
In the equation, , , , , and the represents the weight of the evaluation indicator, which satisfies the condition and .
Step 4. Determine the evaluation level of the effectiveness of the implementation of the RCS. By using the principle of equal division, divide the interval into equal parts to obtain the standard intervals for the evaluation levels of the sample I~IV. Specifically, when the value falls within interval , it is classified as Level I; when it falls within interval , it is classified as Level II; when it falls within interval , it is classified as Level III; when it falls within interval , it is classified as Level IV.
5. Application Case
This study takes Henan Province as an example and combines the actual provincial situation to study the implementation of the RCS in Henan Province from six aspects: organizational and management effectiveness, water resource protection effectiveness, water environment governance effectiveness, water pollution prevention, and control effectiveness, water ecological restoration effectiveness, and water area shoreline management effectiveness. A total of 26 evaluation indicators were selected from 2018 to 2021. The set pair analysis was expanded from the three-element connection number to the four -element connection number. The game theory combination weighting method was adopted to optimize the weighting results of the 1–5 scale AHP method and the improved CRITIC method. This was performed to assist in the set pair analysis by incorporating the game theory approach. Through this process, an evaluation model for the implementation effectiveness of the RCS was established. The established model was then utilized to evaluate the implementation effectiveness of the RCS in Henan Province.
5.1. Study Area Overview
Henan Province is located in the Central Plains of China. It borders Anhui and Shandong to the east, Hebei and Shanxi to the north, Shaanxi to the west, and Hubei to the south. As shown in Figure 1, it spans across four major river basins: the Yellow River, Yangtze River, Huai River, and Hai River. Henan Province is an important transportation hub and center for the flow of people, goods, and information, earning the reputation of being the “heartland of the nine provinces and a thoroughfare of ten provinces”. The province has a complex topography, with higher elevations in the west and lower elevations in the east. There are numerous rivers, lakes, and canals, providing a rich and diverse water ecosystem. The total area of the province is 167,000 square kilometers, with 493 rivers larger than 100 square kilometers in their basin area. The rivers crisscross the province in an east-west and north-south pattern, connecting all four major river basins. To fully implement the concept of green development, promote ecological civilization construction, and respond to the call of the Central Committee of the Communist Party of China and the State Council, Henan Province established a comprehensive RCS at the end of 2017, creating a five-level RCS that covers the provincial, municipal, county, township, and village levels.
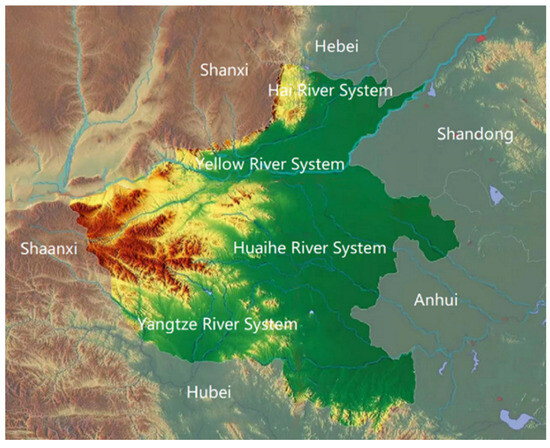
Figure 1.
Watershed distribution map of Henan Province.
5.2. System of Indicators
Evaluating the effectiveness of the RCS cannot rely solely on a single indicator; instead, multiple indicators should be carefully selected to provide a comprehensive analysis and yield reasonable results. The selection of these evaluation indicators should adhere to principles of scientific rigor, representativeness, rationality, accessibility, and feasibility. Currently, the choice of evaluation indicators for assessing the implementation of the RCS primarily focuses on factors such as river and lake health, water quality, and the ecological environment. Building upon prior research, this study focuses on the comprehensive governance effectiveness of river and lake areas since the implementation of the RCS in Henan Province. It takes into account the “Provincial Assessment Plan for the Integrated Governance of Four Waters under the River Chief System for the Year 2021” issued by Henan Province, public announcements, press conferences held since the implementation of the RCS, expert consultations, and the practical situation and challenges in the region. A total of 26 representative indicators were selected from six aspects: organizational and managerial effectiveness, water resource protection effectiveness, water environment governance effectiveness, water pollution control effectiveness, water ecological restoration effectiveness, and water area shoreline management effectiveness. This selection was used to construct an evaluation indicator system for assessing the implementation effectiveness of the RCS in Henan Province, which includes a goal layer, criterion layer, and indicator layer. The criterion layer reflects the focal points and challenges of the work of the RCS, while the indicator layer provides explanations and further elaboration of the criterion layer. For a detailed indicator system, please refer to Table 1 in this study.

Table 1.
Evaluation Index System for Assessing the Implementation Effectiveness of the RCS in Henan Province.
5.3. Data Sources and Indicator Values
Data used in this study are sourced from “China Statistical Yearbook [57,58,59,60]”, “Henan Statistical Yearbook [61,62,63,64]”, “Henan Water Resources Bulletin [65,66,67,68]”, “Henan Ecological and Environmental Status Bulletin [69,70,71,72]”, “China Water Resources Statistical Yearbook [73,74,75,76]”, “China Urban Construction Statistical Yearbook [77,78,79,80]”, official announcements and bulletins from Henan Water Resources Department, as well as reports, documents, and plans related to water pollution prevention, ecological environment protection, and released by Henan Water Resources Department, Ecological Environment Department, Agriculture and Rural Affairs Department, and other relevant units. The satisfaction results were obtained through survey questionnaires, while other qualitative indicators were scored by invited experts. Performing a reliability analysis on the obtained indicator data reveals an Alpha coefficient of 0.99, indicating a very high level of internal consistency in the numerical values of the indicators. This suggests that the data source exhibits high reliability and accuracy. Please refer to Table 2 for the specific indicator system.

Table 2.
Values of Indicators for Evaluating the Implementation Effectiveness of the RCS in Henan Province.
Sensitivity analysis of the indicators was conducted using Stata’s stepwise exclusion method, and the results indicate that even after excluding any single indicator out of the 26, the results still exhibit a high level of stability and consistency. This implies that the variation in the results is nearly independent of the number of indicators, indicating that the current number of indicators is reasonable and statistically significant. Please refer to Figure 2 for specific results.
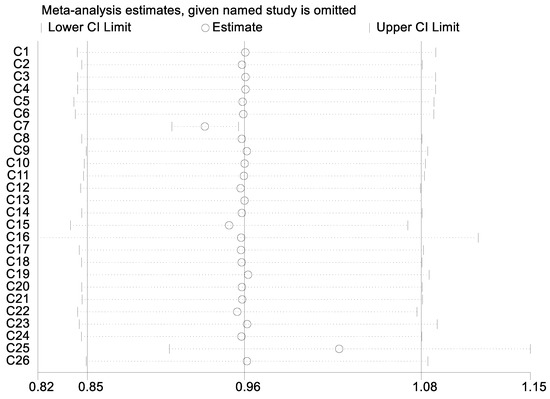
Figure 2.
Sensitivity Analysis Results of Indicators.
5.4. Evaluation Grading Criteria
Drawing from the grading standards of the Chinese water conservancy modernization index system and the “Implementation Plan for the 2022 Henan Province’s Battle against Air, Water, and Soil Pollution and Agricultural and Rural Pollution Control”, and considering the target values and actual values of selected indicators in the regional development plan, in conjunction with expert opinions, the evaluation indicators have been categorized into four levels: Level I (Excellent), Level II (Good), Level III (Qualified), and Level IV (Not Qualified). Specific criteria for indicator evaluation can be found in Table 3.

Table 3.
Grading Criteria for Indicators Used to Evaluate the Implementation Effectiveness of the RCS in Henan Province.
5.5. Evaluation Results of River Chief System in Henan Province
5.5.1. Weighting Results of Evaluation Indicators
The basic weights to be combined in this study are the objective weights based on improved CRITIC and the subjective weights based on the 1–5 scale AHP. The combined weights minimize the deviation between the combined weights and the subjective and objective weights. This balances the importance of indicators reflected by subjective and objective weights, allowing the combined weights to reflect both the attributes of the indicators themselves and effectively utilize the information from these original data of the indicators. This study uses game theory to combine weights for the improved CRITIC method and the 1–5 scale AHP method. The objective weighting result is denoted as , the subjective weighting result is denoted as , and the optimal linear combination obtained is denoted as . The final weighting results can be found in Table 4.

Table 4.
Weights of Indicators for Evaluating the Implementation Effectiveness of the RCS in Henan Province.
5.5.2. Comprehensive Evaluation Result and Analysis
Using the four-element connection number model of set pair analysis, the effectiveness of the RCS implementation in Henan Province from 2018 to 2021 was evaluated. By calculating the single-indicator connection numbers, the final connection numbers for the effectiveness of the RCS implementation in different years in Henan Province were obtained. Based on the principle of average score, the evaluation grade of the RCS implementation in Henan Province from 2018 to 2021 was determined. Additionally, the entropy weight TOPSIS method was used to evaluate the indicators with both positive and negative directions (process omitted). The evaluation results from this method were compared with the results derived from the set pair analysis model, and the outcomes of both evaluation models were presented in Table 5.

Table 5.
Evaluation Results of the Implementation Effectiveness of the RCS in Henan Province.
According to the four-element connection number model of set pair analysis, the evaluation of the implementation effectiveness of the RCS in Henan Province from 2018 to 2021 revealed correlation coefficients of 0.4454, 0.5289, 0.5734, and 0.6455, corresponding to the grades of “good”, “excellent”, “excellent”, and “excellent”, respectively. The increasing connection numbers indicate the gradual popularization and improvement of the RCS. Among them, the highest connection number in 2021 indicates that the river and lake management mechanism has gradually improved, achieving good results in river and lake protection. The connection number in 2020 is also relatively high, which is in line with the policies implemented by Henan Province. In 2020, Henan Province started the “Clearing-Up the Four Chaotic Practices” campaign and fully implemented the “River Chief+” mechanism. Building on the foundation of 2020, in 2021, the “River Chief+” mechanism was further implemented, integrating the work of River Chiefs with that of the Procurator, Police Chief, River Custodian, Civilian River Chiefs, and Grid Chiefs. Additionally, the implementation was improved through the utilization of the Internet with the establishment of the “River Chief+ Internet” system, greatly enhancing the effectiveness of the RCS. In 2018, the evaluation grade for the implementation effectiveness of the RCS in Henan Province was “good”, as it was just getting started, with the establishment of five levels of River Chiefs at the end of 2017. After a year of effort, the RCS in Henan Province transitioned from being “in name” to “in practice”. As the RCS was further promoted in 2019, Henan Province embarked on a new model of ecological river governance, achieving an evaluation grade of “excellent”. Overall, the implementation effectiveness of the RCS in Henan Province is significant. The evaluation scores have been increasing year by year, indicating the deepening of the RCS work. The evaluation results are consistent with the actual situation, demonstrating the feasibility of the evaluation model. Overall, the use of the four-element connection number model of set pair analysis for evaluating the effectiveness of the RCS implementation in Henan Province yielded consistent final ranking results with the entropy weight TOPSIS method. However, the entropy weight TOPSIS method did not consider the relative proximity of different indicators to different levels. Compared with the set pair analysis model, the evaluation of the ranking results using the entropy weight TOPSIS method was slightly rough and deviated from the actual situation. In contrast, the four-element connection number model of set pair analysis is more accurate, reasonable, feasible, and in line with the actual circumstances.
5.5.3. Analysis of Single Indicator Evaluation Results
Based on the four-element connection numbers of the set pair analysis model, the coefficients for individual indicators were calculated. The calculation results can be found in Table 6 and Table 7.

Table 6.
Evaluation Results of Single Indicator for the Implementation Effectiveness of the RCS in Henan Province, 2018–2019.

Table 7.
Evaluation Results of Single Indicator for the Implementation Effectiveness of the RCS in Henan Province, 2020–2021.
From the evaluation results, it can be seen that the organizational system of the RCS at all levels in Henan Province has been continuously improved. The implementation of the RCS has been strengthened, and the institutional framework has become increasingly sound. Various systems have been effectively implemented. The work mechanism has been continuously optimized, leading to improvements in the ecological environment of rivers and lakes. The conditions for guaranteeing the implementation of the RCS have been continuously strengthened. The construction of organizational systems and institutional development of the RCS at all levels in Henan Province has achieved significant results. There has been a noticeable improvement in the ecological environment of rivers and lakes, and the water quality of rivers and lakes has been effectively enhanced.
In terms of organizational management, unlike in 2018, the evaluation grades for the informatization of supervision and the soundness of laws and regulations for the years 2019–2021 were rated as “excellent”. This is because, over the past three years, Henan Province has been dedicated to the development of informatization in supervision while incorporating different provisions based on the actual provincial situation. In terms of informatization supervision, in 2019, Henan Province began promoting the RCS information system throughout the city, establishing the “Smart River Chief” river monitoring system, enabling important rivers and lakes to be “instantly visible and traceable” throughout the entire process. In 2020, drones were utilized for river patrols, and the use of the Henan Province River Chief App was actively promoted, resulting in the construction of a municipal-level smart river and lake management platform. In 2021, Henan Province actively employed means such as satellite remote sensing and drones to investigate and identify issues related to “disorderly” practices, followed by appropriate rectification. Regarding laws and regulations, in 2019, the Henan Provincial Procuratorate and the Provincial River Chief Office jointly issued the “Interim Measures for Establishing the Henan Provincial People’s Procuratorate River Chief Office”, becoming one of the leading provinces along the Yellow River to establish procuratorate river chief offices. From 2020 to 2021, Henan Province has made great efforts to implement the “River Chief+” system, facilitating joint law enforcement.
In terms of water resources conservation, at the end of 2019, to implement the “National Water Conservation Action Plan” issued by the National Development and Reform Commission and the Ministry of Water Resources, as well as the “Notice on the Division of Work for Implementing the National Water Conservation Action Plan” issued by the Office of the National Development and Reform Commission and the Office of the Ministry of Water Resources, Henan Province formulated the “Henan Province Water Conservation Action Implementation Plan” based on local conditions and began its implementation. The evaluation results indicated that the total groundwater resources were rated as “pass” in 2019 and remained consistently rated as “excellent” in the following two years.
In terms of water environment management and aquatic ecological restoration, in 2021, the General Office of the People’s Government of Henan Province issued the “Henan Province Integrated Water Governance Plan (2021–2035)”, which includes specific plans for water environment management, aquatic ecological restoration, water disaster prevention and control, and comprehensive groundwater management. The plan was diligently implemented throughout the province, leading to significant improvements in the compliance rate of centralized drinking water sources, surface water environmental quality, and soil and water conservation rate.
In terms of water pollution prevention and control, starting in 2018, Henan Province has made great efforts to promote the treatment and resource utilization of waste from livestock and poultry farming. By 2021, the comprehensive utilization rate of livestock and poultry manure had reached the level of “excellent”. To fully implement the decisions and deployments of the CPC Central Committee, the State Council, the Provincial Party Committee, and the Provincial Government regarding the pollution prevention and control battle, various levels of river chiefs have been actively engaged in the implementation of the “2021 Water Pollution Prevention and Control Battle Implementation Plan”. This has resulted in significant progress in the battle against water pollution, as indicated by the transformation of the harmless treatment rate of sludge from a “passing” grade in 2020 to an “excellent” grade. However, due to Henan Province being an agricultural province, it is challenging to effectively control the use of fertilizers and pesticides. Continuous efforts are still needed in this regard.
In terms of waterway and shoreline management, Henan Province has carried out extensive activities to rectify the “disorderly” practices in rivers and lakes. River chiefs at all levels have actively conducted river patrols and, with the assistance of various departments, implemented joint law enforcement measures to address numerous instances of “disorderly” practices. As a result, significant improvements have been made in the treatment of black and odorous water bodies, with a consistently high level of rectification achieved in addressing the “disorderly” practices. The compliance rate of embankments has also improved significantly, shifting from a “failing” grade in 2018 to an “excellent” grade. Additionally, river chiefs at various levels have coordinated efforts to promote comprehensive basin management.
In addition, the treatment rate of rural domestic sewage has shifted from unqualified to qualified, indicating an increasing emphasis on the construction of river chief organizational systems in rural areas. Higher-level authorities should increase financial support for rural RCS work, expand the team of river chief offices, and provide strong support for the implementation of the rural RCS. This collective effort aims to protect the health and well-being of rivers and lakes by ensuring effective management and conservation of water environments.
Overall, the majority of indicators are rated as “excellent”, reflecting the effective implementation of responsibilities by river chiefs at all levels, the strengthening of targeted problem rectification, and the integral role of innovative work systems and mechanisms. This is inextricably linked to the fact that the people of Henan have kept in mind General Secretary Xi Jinping’s ardent wish of “guarding the blue water of a river”. Henan Province has consistently implemented the national “14th Five-Year Plan”, reinforcing the RCS and constructing happy rivers and lakes. Efforts are being made to comprehensively upgrade river and lake management and protection, following the working arrangements of the Provincial Party Committee, Provincial Government, and Ministry of Water Resources while considering the reality of Henan Province. Steady progress is being made toward the goal of “clean water, unobstructed rivers, green shores, and ecological balance”. However, continuous efforts are still needed to advance the RCS. There is still significant room for improvement in the protection of water ecological environment and water environmental governance in Henan Province. It is necessary to persistently strive for improvement and sustain innovation, and these experiences are also valuable for other regions as a reference.
6. Conclusions
The implementation of the RCS is not only aimed at improving the ecological environment of river basins but also at enhancing the quality of life for residents, improving people’s happiness index, and promoting harmonious coexistence between humans and nature. Based on this, this study constructs an evaluation index system for the implementation effectiveness of the RCS. It includes six aspects with a total of 26 evaluation indicators: organizational management effectiveness, water resource protection effectiveness, water environmental governance effectiveness, water pollution prevention and control effectiveness, water ecological restoration effectiveness, and water body and shoreline management effectiveness. This index system can provide a reference for evaluating the implementation effectiveness of the RCS in different regions.
Due to the limitations of the traditional CRITIC method in the process of weighting, this study proposes improvements to the traditional CRITIC objective weighting method from three aspects: contrast intensity, correlation coefficient, and variation degree. These improvements aim to achieve objective weighting of evaluation indicators. Additionally, considering the significant errors associated with the use of the 1–9 scale, the AHP 1–5 scale method is used for the subjective weighting of indicators. The combination weighting method with game theory is employed to optimize the results obtained from the subjective and objective weighting methods, thus obtaining the optimal weighting results and determining the weights of evaluation indicators. Taking Henan Province as an example, the traditional set pair analysis coefficient is expanded to the four-element connection numbers, and an evaluation model for the implementation effectiveness of the RCS is constructed.
The evaluation results show that the implementation effectiveness of the RCS in Henan Province from 2018 to 2021 was rated as “good” and “excellent”, with the evaluation scores increasing year by year. Based on the evaluation results, it can be seen that by the end of 2021, the RCS in Henan Province has been established, and a working mechanism has been formed. The organizational system is continuously improving, and the integration and development of river and lake management and protection are gradually being realized. With the continuous improvement of the river chief responsibility system, significant achievements have been made in river and lake management and protection. Public participation has been strengthened, and social supervision mechanisms have been continuously improved. These evident achievements are consistent with the actual situation, which validates the scientific and accurate nature of this method.
However, there are still some significant issues in river and lake management and protection that cannot be ignored. For example, the task of river pollution control remains challenging, the enforcement and supervision of river and lake regulations need to be strengthened, and there is a weak capacity for grassroots governance. Based on these issues, the comprehensive implementation of the RCS in Henan Province should focus on the following aspects: First, it is necessary to increase the promotion and training of policies and regulations related to the RCS to enhance public awareness and involvement in the system. Second, it is important to strengthen administrative law enforcement and supervision and intensify efforts to combat illegal activities in rivers and lakes. Finally, it is crucial to enhance the capacity building for grassroots river and lake management and protection, increase financial investment in the RCS, and further promote the standardization and information management of the system. By addressing these issues and strengthening the key aspects mentioned above, Henan Province can make further progress in the comprehensive implementation of the RCS and improve the effectiveness of river and lake management and protection.
Using this model to evaluate the effectiveness of the RCS has multiple advantages. Firstly, the model allows for year-by-year research and analysis of the implementation effectiveness in the same region, providing insights into the progress and trends. Secondly, it enables comparative analysis of the implementation effectiveness among different regions during the same period, facilitating the exchange of experiences and lessons learned. Additionally, the model can identify weak areas and influencing factors in the implementation process, helping implementers to provide targeted recommendations and take appropriate measures to enhance river and lake management capabilities more efficiently. Most importantly, this evaluation model is of great significance in maintaining the health of rivers and lakes and achieving the sustainable utilization of their functions. Through a scientific assessment of the implementation effectiveness of the RCS, it can drive improvements and optimization in river and lake management, leading to more sustainable water resource management.
Author Contributions
Methodology, J.L. and L.S.; Software, X.C.; Formal analysis, L.S.; Investigation, L.Q.; Data curation, L.Q.; Writing—original draft, X.C.; Writing—review & editing, J.L. and L.S.; Supervision, J.L.; Project administration, Y.L. and Y.X.; Funding acquisition, Y.L. and Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (No.52179015); Key Science and Technology Projects in Henan Province (No.201300311400); Key Science and Technology Projects in Henan Province (No.232102321114); Ministry of Education “Chunhui plan” cooperative scientific research project (No.HZKY20220268).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data used in this study are sourced from “China Statistical Yearbook”, “Henan Statistical Yearbook”, “Henan Water Resources Bulletin”, “Henan Ecological and Environmental Status Bulletin”, “China Water Resources Statistical Yearbook”, “China Urban Construction Statistical Yearbook”, official announcements and bulletins from Henan Water Resources Department, as well as reports, documents, and plans related to water pollution prevention, ecological environment protection, and released by Henan Water Resources Department, Ecological Environment Department, Agriculture and Rural Affairs Department, and other relevant units. The satisfaction results were obtained through survey questionnaires, while other qualitative indicators were scored by invited experts.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bashir, I.; Lone, F.A.; Bhat, R.A.; Mir, S.A.; Dar, Z.A.; Dar, S.A. Concerns and threats of contamination on aquatic ecosystems. In Bioremediation and Biotechnology: Sustainable Approaches to Pollution Degradation; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–26. [Google Scholar]
- Zhou, H.; Zhang, X.; Xu, H.; Ling, H.; Yu, P. Influences of climate change and human activities on Tarim River runoffs in China over the past half century. Environ. Earth Sci. 2012, 67, 231–241. [Google Scholar] [CrossRef]
- Deng, X.P.; Shan, L.; Zhang, H.; Turner, N.C. Improving agricultural water use efficiency in arid and semiarid areas of China. Agric. Water Manag. 2006, 80, 23–40. [Google Scholar] [CrossRef]
- Luo, P.; Mu, Y.; Wang, S.; Zhu, W.; Mishra, B.K.; Huo, A.; Zhou, M.; Lyu, J.; Hu, M.; Duan, W.; et al. Exploring sustainable solutions for the water environment in Chinese and Southeast Asian cities. Ambio 2021, 51, 1199–1218. [Google Scholar] [CrossRef]
- Li, Y.; Tong, J.; Wang, L. Full implementation of the river chief system in China: Outcome and weakness. Sustainability 2020, 12, 3754. [Google Scholar] [CrossRef]
- Hao, Y.; Wan, T. Top-Down Mechanisms: Governmental River Chiefs. In The River Chief System and an Ecological Initiative for Public Participation in China; Springer Nature Singapore: Singapore, 2023; pp. 17–45. [Google Scholar]
- Ouyang, J.; Zhang, K.; Wen, B.; Lu, Y. Top-down and bottom-up approaches to environmental governance in China: Evidence from the River Chief System (RCS). Int. J. Environ. Res. Public Health 2020, 17, 7058. [Google Scholar] [CrossRef]
- Ding, R.; Sun, F. Impact of River Chief System on Green Technology Innovation: Empirical Evidence from the Yangtze River Economic Belt. Sustainability 2023, 15, 6575. [Google Scholar] [CrossRef]
- Zhang, L. Implementation effectiveness evaluation of grass-roots river chief system based on fuzzy evaluation. Yangtze River 2022, 53, 8–13. [Google Scholar]
- Wang, L.; Tong, J.; Li, Y. River Chief System (RCS): An experiment on cross-sectoral coordination of watershed governance. Front. Environ. Sci. Eng. 2019, 13, 64. [Google Scholar] [CrossRef]
- Wang, J.; Wan, X.; Tu, R. Game Analysis of the Evolution of Local Government’s River Chief System Implementation Strategy. Int. J. Environ. Res. Public Health 2022, 19, 1961. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiong, C.; Yang, Y.; Liang, C.; Jiang, S. What Makes the River Chief System in China Viable? Examples from the Huaihe River Basin. Sustainability 2022, 14, 6329. [Google Scholar] [CrossRef]
- Wang, C.; Ding, Z.; Jiang, P.; Pan, X. Systematic review and perspective of the application of multi-index comprehensive evaluation method. Plant Prot. 2022, 48, 187–192+206. [Google Scholar]
- Fu, Y.; Liu, Y.; Xu, S.; Xu, Z. Assessment of a Multifunctional River Using Fuzzy Comprehensive Evaluation Model in Xiaoqing River, Eastern China. Int. J. Environ. Res. Public Health 2022, 19, 12264. [Google Scholar] [CrossRef]
- Li, C.; Peng, W.; Shen, X.; Gu, J.; Zhang, Y.; Li, M. Comprehensive Evaluation of the High-Quality Development of the Ecological and Economic Belt along the Yellow River in Ningxia. Sustainability 2023, 15, 11486. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Xu, J. Study on the Multifactor Degree Set Pair Analysis in Guizhou Drought Early Warning. Math. Pract. Theory 2015, 45, 199–206. [Google Scholar]
- Chen, W.; Yang, Y. Safety evaluation of coal enterprise based on comprehensive weighting and set pair analysis. Min. Saf. Environ. Prot. 2020, 47, 105–109. [Google Scholar]
- Zhao, J.; Gao, H.; Cheng, J. Research on Evolution of Participation Willingness in Network Public Opinion: Based on Three-element Connection Number. Inf. Sci. 2017, 35, 118–120+140. [Google Scholar]
- Wang, T.C.; Lee, H.D. Developing a fuzzy TOPSIS approach based on subjective weights and objective weights. Expert Syst. Appl. 2009, 36, 8980–8985. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Ocampo, L.; Aro, J.L.; Evangelista, S.S.; Maturan, F.; Casinillo, L.; Yamagishi, K.; Selerio, E., Jr. Composite ecotourism potential index based on an integrated stochastic CRITIC-weighted sum method. Curr. Issues Tour. 2023, 26, 2513–2542. [Google Scholar] [CrossRef]
- Su, J.; Su, K.; Wang, S. Evaluation of digital economy development level based on multi-attribute decision theory. PLoS ONE 2022, 17, e0270859. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process [M]; Mc Graw Hill Company: New York, NY, USA, 1980. [Google Scholar]
- Yu, D.; Kou, G.; Xu, Z.; Shi, S. Analysis of collaboration evolution in AHP research: 1982–2018. Int. J. Inf. Technol. Decis. Mak. 2021, 20, 7–36. [Google Scholar] [CrossRef]
- Xiang, M.; Huang, H.; He, C.; Li, R.; Zeng, L. Comprehensive Performance Evaluation Strategy for Communication Networks Selection in Smart Grid. Cybern. Inf. Technol. 2016, 16, 39–56. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, L.; Li, M.; Zheng, R. A Novel Fire Risk Assessment Approach for Large-Scale Commercial and High-Rise Buildings Based on Fuzzy Analytic Hierarchy Process (FAHP) and Coupling Revision. Int. J. Environ. Res. Public Health 2021, 18, 7187. [Google Scholar] [CrossRef]
- Haoyu, Z.; Wensheng, W.; Hao, W. TOC prediction using a gradient boosting decision tree method: A case study of shale reservoirs in Qinshui Basin. J. Pet. Sci. Eng. 2023, 221, 111271. [Google Scholar]
- Saraswat, S.; Sharma, V.; Khan, M.A. Finding the target customers through new approach in Analytic Hierarchy Process (AHP) using Big 5 personality traits. Int. J. Syst. Assur. Eng. Manag. 2023, 14, 1028–1039. [Google Scholar] [CrossRef]
- Chen, C.Y.; Huang, J.J. Deriving Fuzzy Weights from the Consistent Fuzzy Analytic Hierarchy Process. Mathematics 2022, 10, 3499. [Google Scholar] [CrossRef]
- Lobzang, C.; Kumar, S.G. Evaluation of groundwater heavy metal pollution index through analytical hierarchy process and its health risk assessment via Monte Carlo simulation. Process Saf. Environ. Prot. 2023, 170, 855–864. [Google Scholar]
- Pascoe, S. A Simplified Algorithm for Dealing with Inconsistencies Using the Analytic Hierarchy Process. Algorithms 2022, 15, 442. [Google Scholar] [CrossRef]
- Kara, C.; Iranmanesh, A. Modelling and Assessing Sustainable Urban Regeneration for Historic Urban Quarters via Analytical Hierarchy Process. Land 2022, 12, 72. [Google Scholar] [CrossRef]
- Huang, W.G.; Zhang, S.W.; Wang, G.Z.; Huang, J.; Lu, X.; Wu, S.L.; Wang, Z.T. Modeling Methodology for Site Selection Evaluation of Underground Coal Gasification Based on Combination Weighting Method with Game Theory. ACS Omega 2023, 8, 11544–11555. [Google Scholar] [CrossRef]
- Wang, B.; Wan, J.; Zhu, Y. River Chief System: An institutional analysis to address watershed governance in China. Water Policy 2021, 23, 1435–1444. [Google Scholar] [CrossRef]
- Li, J.; Shi, X.; Wu, H.; Liu, L. Trade-off between economic development and environmental governance in China: An analysis based on the effect of River Chief System. China Econ. Rev. 2020, 60, 101403. [Google Scholar] [CrossRef]
- Xu, X.; Cheng, Y.; Meng, X. River Chief System, Emission Abatement, and Firms’ Profits: Evidence from China’s Polluting Firms. Sustainability 2022, 14, 3418. [Google Scholar] [CrossRef]
- Gao, D.; Liu, C.; Wei, X.; Liu, Y. Can River Chief System Policy Improve Enterprises’ Energy Efficiency? Evidence from China. Int. J. Environ. Res. Public Health 2023, 20, 2882. [Google Scholar] [CrossRef]
- Li, Z.; Ling-zhi, L.; Ji-kun, H. The River Chief System and agricultural non-point source water pollution control in China. J. Integr. Agric. 2021, 20, 1382–1395. [Google Scholar]
- Li, W.; Zhou, Y.; Deng, Z. The Effectiveness of “River Chief System” Policy: An Empirical Study Based on Environmental Monitoring Samples of China. Water 2021, 13, 1988. [Google Scholar] [CrossRef]
- Vahedi, N.; Ghassemieh, M. Preference of Hybrid Steel Frame with Exclusive Seismic Performance Using the Analytic Hierarchy Process. J. Earthq. Eng. 2022, 26, 5425–5446. [Google Scholar] [CrossRef]
- Zhu, H.; Liao, Q.; Qu, B.; Hu, L.; Wang, H.; Gao, R.; Zhang, Y. Relationship between the main functional groups and complex permittivity in pre-oxidised lignite at terahertz frequencies based on grey correlation analysis. Energy 2023, 278, 127821. [Google Scholar] [CrossRef]
- Chen, H.; Xu, Z.; Liu, Y.; Huang, Y.; Yang, F. Urban Flood Risk Assessment Based on Dynamic Population Distribution and Fuzzy Comprehensive Evaluation. Int. J. Environ. Res. Public Health 2022, 19, 16406. [Google Scholar] [CrossRef]
- de Lima Silva, D.F.; Ferreira, L.; de Almeida Filho, A.T. Preference disaggregation on TOPSIS for sorting applied to an economic freedom assessment. Expert Syst. Appl. 2023, 215, 119341. [Google Scholar] [CrossRef]
- Zhao, K.Q.; Xuan, A.L. Set Pair Theory—A New Theory Method of Non-Define and Its Applications. Syst. Eng. 1996, 14, 18–23+72. [Google Scholar]
- Xiang, W.; Yang, X.; Babuna, P.; Bian, D. Development, Application and Challenges of Set Pair Analysis in Environmental Science from 1989 to 2020: A Bibliometric Review. Sustainability 2021, 14, 153. [Google Scholar] [CrossRef]
- Li, B.; Zhang, W.; Liu, Z.; Meng, H. Groundwater Quality Evaluation Model Based on Set Pair Analysis and Its Application. Proc. Inst. Civ. Eng.-Water Manag. 2021, 176, 212–222. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H. Construction Risk Assessment of Deep Foundation Pit Projects Based on the Projection Pursuit Method and Improved Set Pair Analysis. Appl. Sci. 2022, 12, 1922. [Google Scholar] [CrossRef]
- Shen, Q.; Lou, J.; Liu, Y.; Jiang, Y. Hesitant fuzzy multi-attribute decision making based on binary connection number of set pair analysis. Soft Comput. 2021, 25, 14797–14807. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, L.; Li, Y.; Wang, Y.; Ma, T.; Luo, X. Set pair prediction for Chinese natural gas energy security based on higher-order Markov chain with risk attitude. Resour. Policy 2022, 77, 102741. [Google Scholar] [CrossRef]
- Han, Z.; Meng, J.; Zhu, L.; Cheng, H.; Wu, Y.; Wei, C. Quantifying trade-offs of land multifunctionality evaluated by set pair analysis in ecologically vulnerable areas of northwestern China. Land Degrad. Dev. 2022, 33, 1999–2013. [Google Scholar] [CrossRef]
- Jiang, Y.L.; Zhao, K.Q. Application and development of set pair analysis inartificial intelligence: A survey. CAAI Trans. Intell. Syst. 2019, 14, 28–43. [Google Scholar]
- Bojan, S.; Zorica, S. Prioritisation in the analytic hierarchy process for real and generated comparison matrices. Expert Syst. Appl. 2023, 225, 120015. [Google Scholar]
- Sun, H.; Wei, G.W.; Chen, X.D.; Mo, Z.W. Extended EDAS method for multiple attribute decision making in mixture z-number environment based on CRITIC method. J. Intell. Fuzzy Syst. 2022, 43, 2777–2788. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, Y.; Liu, Y.; He, J. Hybrid HVDC line pilot protection method based on EMD and Spearman correlation coefficient. Power Syst. Prot. Control. 2021, 49, 1–11. [Google Scholar]
- Yang, Y.; Sun, H.; Dai, Z.; Wu, M.; Fu, S. Comprehensive evaluation of majors offered by universities based on combination weighting. Eval. Program Plan. 2023, 97, 102202. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.Q. Disposal and Description of Uncertainties Basedon The Set Pair Analysis. Inf. Control. 1995, 24, 162–166. [Google Scholar]
- National Bureau of Statistics of the People’s Republic of China. China Statistical Yearbook 2019; Statistics Press: Beijing, China, 2020.
- National Bureau of Statistics of the People’s Republic of China. China Statistical Yearbook 2020; Statistics Press: Beijing, China, 2021.
- National Bureau of Statistics of the People’s Republic of China. China Statistical Yearbook 2021; Statistics Press: Beijing, China, 2022.
- National Bureau of Statistics of the People’s Republic of China. China Statistical Yearbook 2022; Statistics Press: Beijing, China, 2023.
- National Bureau of Statistics of the People’s Republic of China. Henan Statistical Yearbook 2019; Statistics Press: Beijing, China, 2020.
- National Bureau of Statistics of the People’s Republic of China. Henan Statistical Yearbook 2020; Statistics Press: Beijing, China, 2021.
- National Bureau of Statistics of the People’s Republic of China. Henan Statistical Yearbook 2021; Statistics Press: Beijing, China, 2022.
- National Bureau of Statistics of the People’s Republic of China. Henan Statistical Yearbook 2022; Statistics Press: Beijing, China, 2023.
- Henan Provincial Department of Water Resources, China. Henan Province Water Resources Bulletin 2018; Henan Hydrological and Water Resources Survey and Evaluation Center: Zhengzhou, China, 2019.
- Henan Provincial Department of Water Resources, China. Henan Province Water Resources Bulletin 2019; Henan Hydrological and Water Resources Survey and Evaluation Center: Zhengzhou, China, 2020.
- Henan Provincial Department of Water Resources, China. Henan Province Water Resources Bulletin 2020; Henan Hydrological and Water Resources Survey and Evaluation Center: Zhengzhou, China, 2021.
- Henan Provincial Department of Water Resources, China. Henan Province Water Resources Bulletin 2021; Henan Hydrological and Water Resources Survey and Evaluation Center: Zhengzhou, China, 2022.
- Henan Provincial Department of Ecology and Environment, China. Henan Province Ecological and Environmental Status Bulletin 2018; Henan Provincial Department of Ecology and Environment: Zhengzhou, China, 2019.
- Henan Provincial Department of Ecology and Environment, China. Henan Province Ecological and Environmental Status Bulletin 2019; Henan Provincial Department of Ecology and Environment: Zhengzhou, China, 2020.
- Henan Provincial Department of Ecology and Environment, China. Henan Province Ecological and Environmental Status Bulletin 2020; Henan Provincial Department of Ecology and Environment: Zhengzhou, China, 2021.
- Henan Provincial Department of Ecology and Environment, China. Henan Province Ecological and Environmental Status Bulletin 2021; Henan Provincial Department of Ecology and Environment: Zhengzhou, China, 2022.
- Ministry of Water Resources of the People’s Republic of China. China Water Resources Statistical Yearbook 2019; Water Resources and Hydropower Press: Beijing, China, 2020.
- Ministry of Water Resources of the People’s Republic of China. China Water Resources Statistical Yearbook 2020; Water Resources and Hydropower Press: Beijing, China, 2021.
- Ministry of Water Resources of the People’s Republic of China. China Water Resources Statistical Yearbook 2021; Water Resources and Hydropower Press: Beijing, China, 2022.
- Ministry of Water Resources of the People’s Republic of China. China Water Resources Statistical Yearbook 2022; Water Resources and Hydropower Press: Beijing, China, 2023.
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. China Urban Construction Statistical Yearbook 2018; China Architecture & Building Press: Beijing, China, 2019.
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. China Urban Construction Statistical Yearbook 2019; China Architecture & Building Press: Beijing, China, 2020.
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. China Urban Construction Statistical Yearbook 2020; China Architecture & Building Press: Beijing, China, 2021.
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. China Urban Construction Statistical Yearbook 2021; China Architecture & Building Press: Beijing, China, 2022.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).