Evaluating Information Risk Propagation in Complex Public Opinion Environments Based on the Improved Grey Relational Analysis—Decision Making Trial and Evaluation Laboratory Method
Abstract
:1. Introduction
- (a)
- Introduced the “Probability Splitting Algorithm” to handle probability hesitant fuzzy sets and proposed Dice similarity and Jaccard similarity in the context of probability hesitant fuzzy sets. Based on these two similarity measures, two distance measurement methods for probability hesitant fuzzy elements were proposed.
- (b)
- Improved the GRA-DEMATEL method using Dice distance and Jaccard distance in the framework of probability hesitant fuzzy sets to calculate the weights of evaluation criteria. Additionally, a combination of objective and subjective weights was used to derive comprehensive weights for each evaluation criterion.
- (c)
- Improved the standardization process of the traditional CoCoSo method using similarity measures to effectively handle probability hesitant fuzzy information. Presented a novel multi-criteria group decision-making and evaluation method.
- (d)
- Summarized information propagation pathways in complex public opinion environments and identified relevant evaluation criteria, providing a theoretical reference and research basis for future related studies.
2. Literature Review
2.1. Complex Public Opinion Environment and Information Risk Propagation
2.2. Information Risk Evaluation Based on Multi-Criteria Decision-Making Methods
2.3. Weight Determination Methods
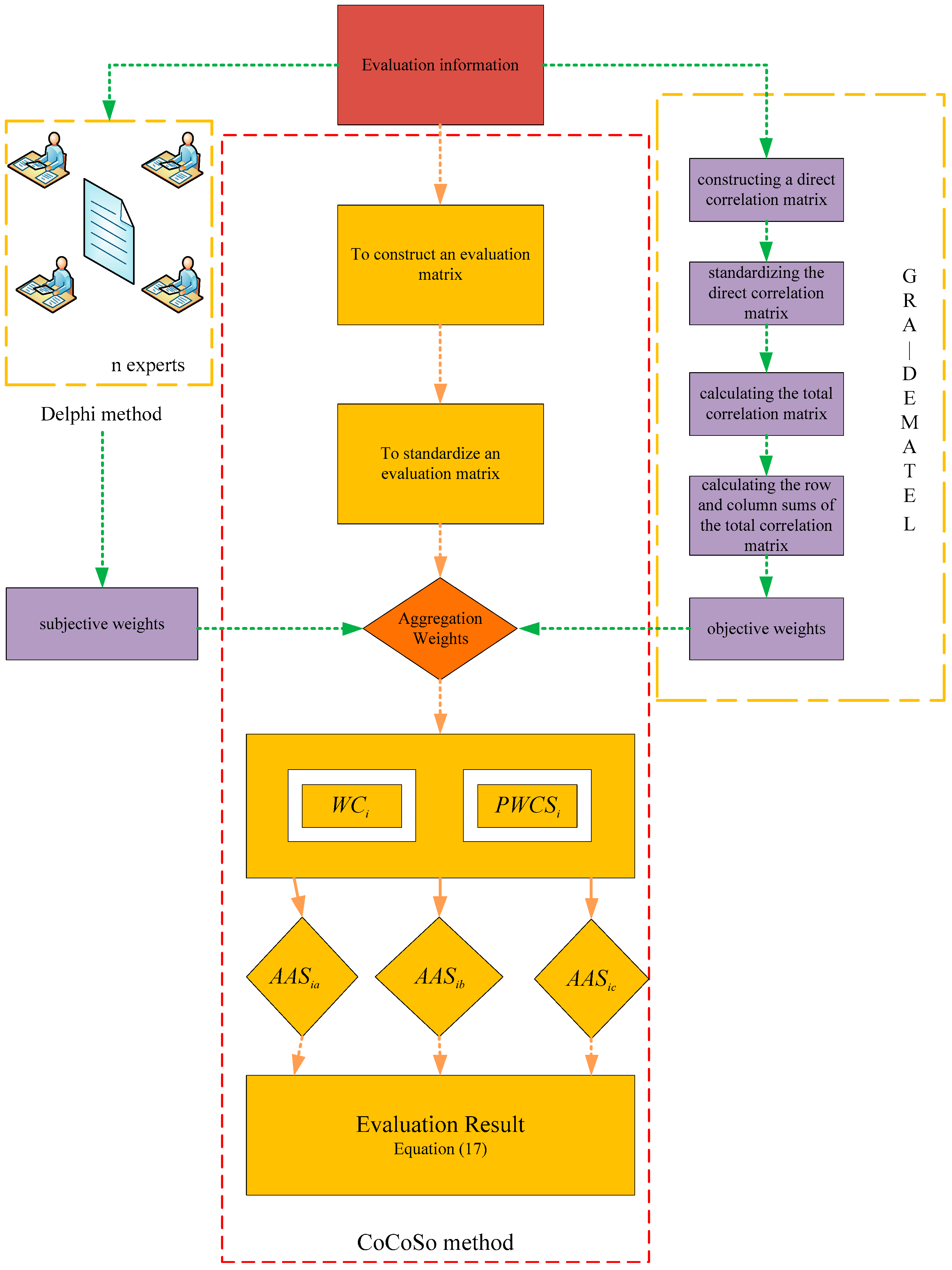
3. Methodology
3.1. A Brief Review of Probabilistic Hesitant Fuzzy Sets
- (a)
- If , then ;
- (b)
- If , thenIf , then ; if , then .
3.2. Some New Similarity and Distance Measures for Probabilistic Hesitant Fuzzy Sets
- (1)
- ,
- (2)
- ,
- (3)
- if , then .
- (1)
- ,
- (2)
- ,
- (3)
- if , then .
3.3. Weight Determination Method Combining Subjective and Objective Approaches
3.4. PHFS-CoCoSo Method Based on Similarity
4. Evaluation of Information Risk Propagation in Complex Public Opinion Environments
4.1. Information Risk Propagation Channels
4.2. Construction of Evaluation Indicators
5. Case Study
6. Discussion
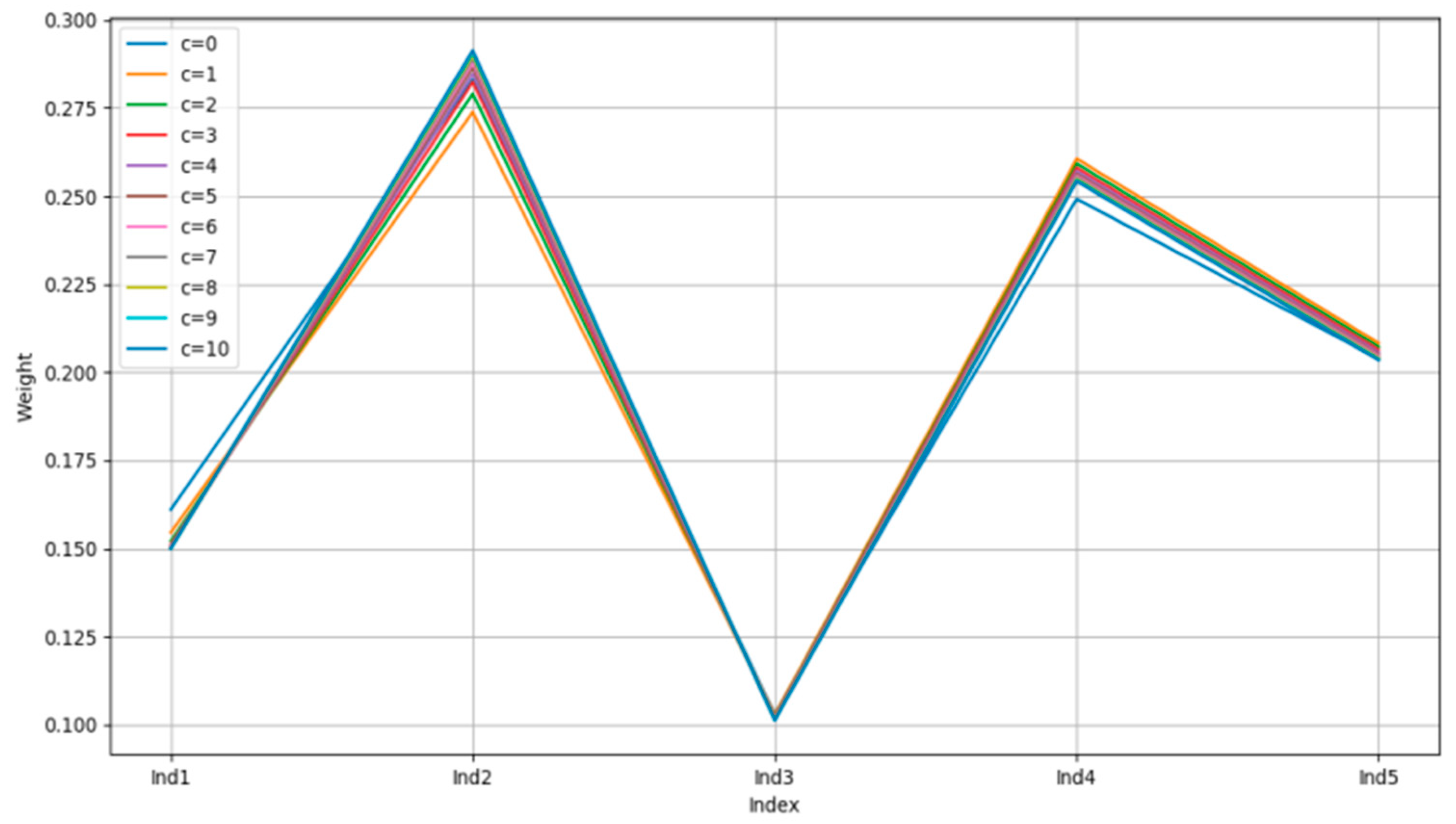
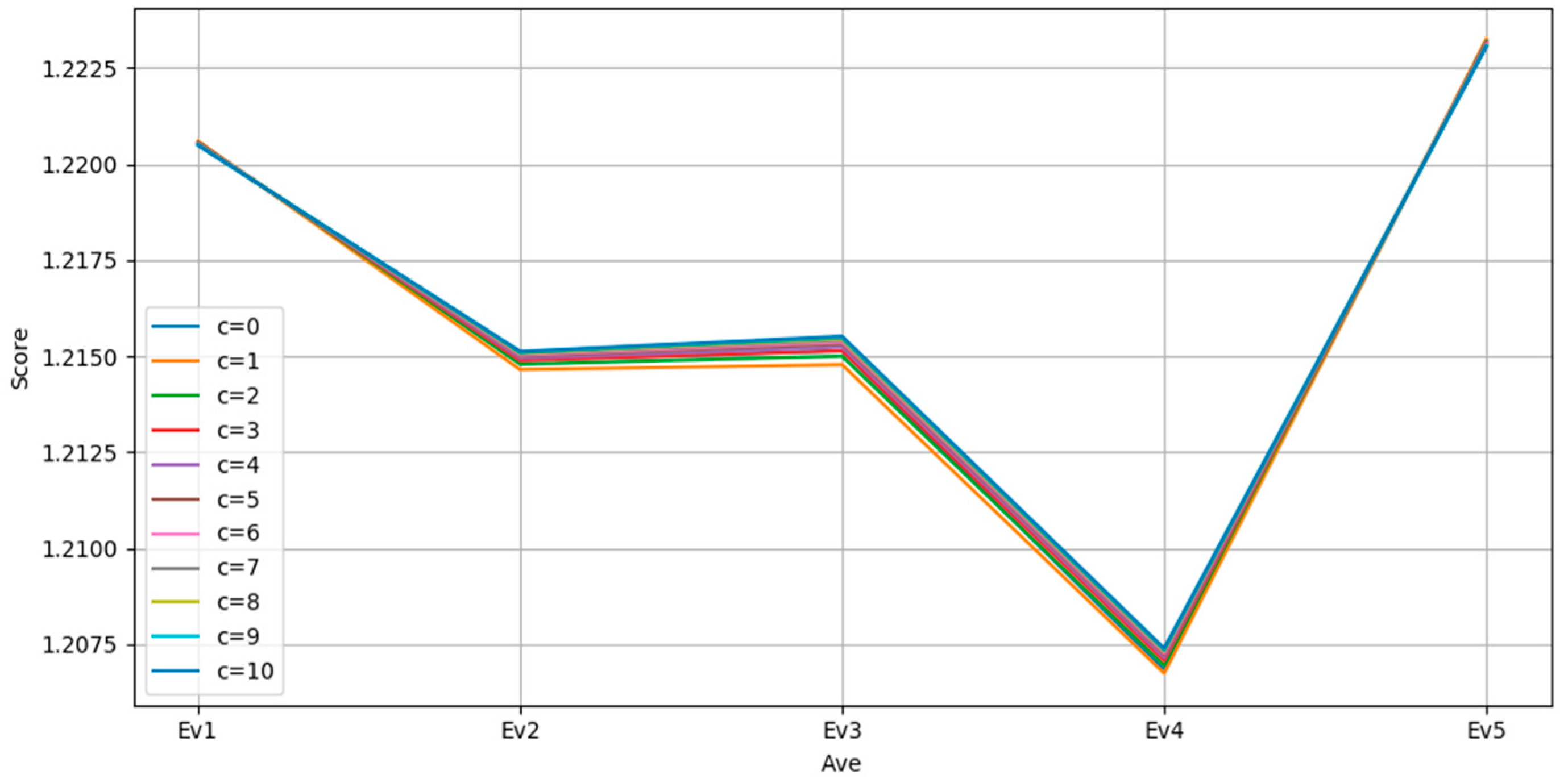
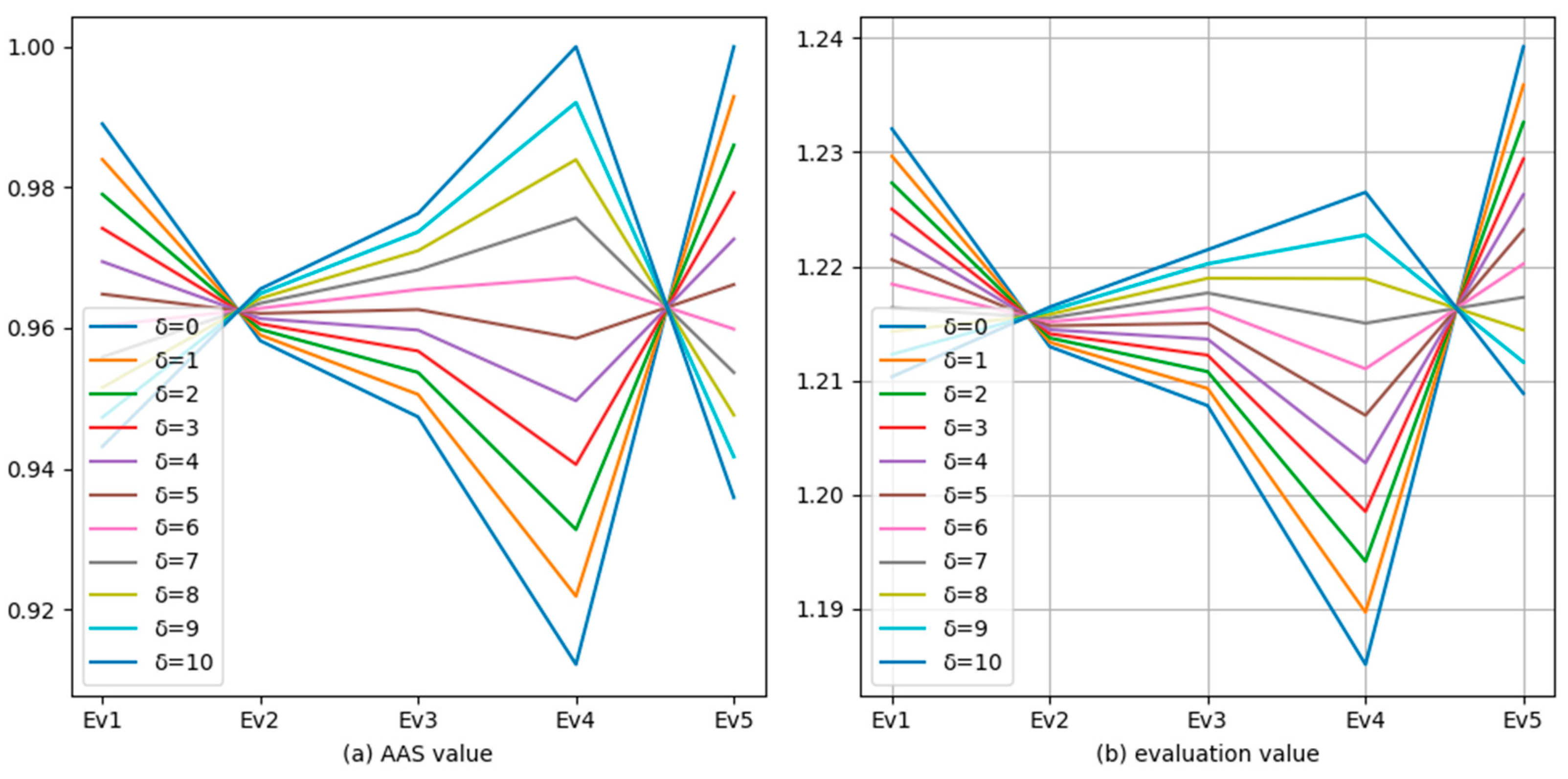
6.1. Sensitivity Analysis
6.2. Effectiveness Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, B. Analysis of Factors Influencing Public Opinion and Study of Psychological Effects in Public Opinion. Tianjin Soc. Sci. 2018, 6, 33–39. [Google Scholar] [CrossRef]
- Peng, Z. Misleading Public Opinion Research from the Perspective of Disinformation. Inf. Stud. Theory Appl. 2023, 46, 59–113. [Google Scholar]
- Torkayesh, A.E.; Pamucar, D.; Ecer, F.; Chatterjee, P. An integrated BWM-LBWA-CoCoSo framework for evaluation of healthcare sectors in Eastern Europe. Socio-Econ. Plan. Sci. 2021, 78, 101052. [Google Scholar] [CrossRef]
- Erdal, H.; Kurtay, K.G.; Dagistanli, H.A.; Altundas, A. Evaluation of Anti-Tank Guided Missiles: An integrated Fuzzy Entropy and Fuzzy CoCoSo multi criteria methodology using technical and simulation data. Appl. Soft Comput. 2023, 137, 110145. [Google Scholar] [CrossRef]
- Saraswat, S.K.; Digalwar, A.K. Evaluation of energy alternatives for sustainable development of energy sector in India: An integrated Shannon’s entropy fuzzy multi-criteria decision approach. Renew. Energy 2021, 171, 58–74. [Google Scholar] [CrossRef]
- Garg, H.; Krishankumar, R.; Ravichandran, K.S. Decision framework with integrated methods for group decision-making under probabilistic hesitant fuzzy context and unknown weights. Expert Syst. Appl. 2022, 200, 117082. [Google Scholar] [CrossRef]
- Torra, V. Hesitant Fuzzy Sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Fang, B. Some uncertainty measures for probabilistic hesitant fuzzy information. Inf. Sci. 2023, 625, 255–276. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, W. Consensus building with a group of decision makers under the hesitant probabilistic fuzzy environment. Fuzzy Optim. Decis. Mak. 2016, 16, 481–503. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Z.; He, Y. Operations and integrations of probabilistic hesitant fuzzy information in decision making. Inf. Fusion 2017, 38, 1–11. [Google Scholar] [CrossRef]
- Jiang, F.; Ma, Q. Multi-attribute group decision making under probabilistic hesitant fuzzy environment with application to evaluate the transformation efficiency. Appl. Intell. 2018, 48, 953–965. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, X.; Zhang, L. Evaluation of the survival of Yangtze finless porpoise under probabilistic hesitant fuzzy environment. Int. J. Intell. Syst. 2022, 37, 7665–7684. [Google Scholar] [CrossRef]
- Shan, X.; Qi, J.; Cao, Y.; Chen, H. Research on the Formation Path of Online Public Opinion Crisis of Listed Companies. Inf. Stud. Theory Appl. 2023, 1–11. [Google Scholar]
- Deng, J.; Wu, L.; Qi, J.; Xu, X.; Liu, Y. Risk Classification and Prediction of Negative Network Public Opinion Based on Information Correlation. Inf. Sci. 2022, 40, 38–43. [Google Scholar] [CrossRef]
- He, Q.; Luo, X.; Wang, X. Stochastic Evolutionary Game Analysis of Resolving Negative Network Public Opinion in Emergencies. Econ. Manag. 2023, 37, 20–29. [Google Scholar]
- Jin, D.; Xia, Y.; Zhu, P. The Mechanism of Network Public Opinion Group Polarization Dynamics from the Perspective of Emotional Evolution. Inf. Sci. 2023, 41, 57–65. [Google Scholar] [CrossRef]
- Trivedi, S. A risk management framework for life insurance companies. J. Corp. Gov. Insur. Risk Manag. 2022, 9, 89–111. [Google Scholar] [CrossRef]
- Bozanic, D.; Tešić, D.; Komazec, N.; Marinković, D.; Puška, A. Interval fuzzy AHP method in risk assessment. Rep. Mech. Eng. 2023, 4, 131–140. [Google Scholar] [CrossRef]
- Hua, Z.; Jing, X.; Martínez, L. An ELICIT information-based ORESTE method for failure mode and effect analysis considering risk correlation with GRA-DEMATEL. Inf. Fusion 2023, 93, 396–411. [Google Scholar] [CrossRef]
- Jasiński, D.; Cinelli, M.; Dias, L.C.; Meredith, J.; Kirwan, K. Assessing supply risks for non-fossil mineral resources via multi-criteria decision analysis. Resour. Policy 2018, 58, 150–158. [Google Scholar] [CrossRef]
- Yazdani, M.; Gonzalez, E.; Chatterjee, P. A multi-criteria decision-making framework for agriculture supply chain risk management under a circular economy context. Manag. Decis. 2019, 59, 1801–1826. [Google Scholar] [CrossRef]
- Su, J.; Wang, D.; Zhang, F.; Xu, B.; Ouyang, Z. A Multi-Criteria Group Decision-Making Method for Risk Assessment of Live-Streaming E-Commerce Platform. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 1126–1141. [Google Scholar] [CrossRef]
- Deivanayagampillai, N.; Jacob, K.; Manohar, G.V.; Broumi, S. Investigation of industry 5.0 hurdles and their mitigation tactics in emerging economies by TODIM arithmetic and geometric aggregation operators in single value neutrosophic environment. Facta Univ. Ser. Mech. Eng. 2023. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Gamal, A.; Chakrabortty, R.K.; Ryan, M. Development of a hybrid multi-criteria decision-making approach for sustainability evaluation of bioenergy production technologies: A case study. J. Clean. Prod. 2021, 290, 125805. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Kazimieras Zavadskas, E.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. Sustainable supplier selection: A novel integrated fuzzy best worst method (F-BWM) and fuzzy CoCoSo with Bonferroni (CoCoSo’B) multi-criteria model. J. Clean. Prod. 2020, 266, 121981. [Google Scholar] [CrossRef]
- Deveci, M.; Pamucar, D.; Gokasar, I. Fuzzy Power Heronian function based CoCoSo method for the advantage prioritization of autonomous vehicles in real-time traffic management. Sustain. Cities Soc. 2021, 69, 102846. [Google Scholar] [CrossRef]
- Ghoushchi, S.J.; Jalalat, S.M.; Bonab, S.R.; Ghiaci, A.M.; Haseli, G.; Tomaskova, H. Evaluation of Wind Turbine Failure Modes Using the Developed SWARA-CoCoSo Methods Based on the Spherical Fuzzy Environment. IEEE Access 2022, 10, 86750–86764. [Google Scholar] [CrossRef]
- Wang, W.; Deng, X.; Xu, H. A new index weight calculation method of group DEMATEL based on the three-dimensional density operator. Chin. J. Manag. Sci. 2021, 29, 179–190. [Google Scholar] [CrossRef]
- Zou, Z.H.; Yun, Y.; Sun, J.N. Entropy method for determination of weight of evaluating indicators in fuzzy synthetic evaluation for water quality assessment. J. Environ. Sci. 2006, 18, 1020–1023. [Google Scholar] [CrossRef]
- Chen, C.; Pai, P.; Hung, W. An Integrated Methodology using Linguistic PROMETHEE and Maximum Deviation Method for Third-party Logistics Supplier Selection. Int. J. Comput. Intell. Syst. 2010, 3, 438–451. [Google Scholar] [CrossRef]
- Podvezko, V. Application of AHP Technique. J. Bus. Econ. Manag. 2009, 10, 181–189. [Google Scholar] [CrossRef]
- Luo, Z.; Zhou, Z.; Hao, Y.; Feng, J.; Gong, Y.; Li, Y.; Huang, Y.; Zhang, Y.; Li, S. Establishment of an indicator framework for the transmission risk of the mountain-type zoonotic visceral leishmaniasis based on the Delphi-entropy weight method. Infect. Dis. Poverty 2022, 11, 122. [Google Scholar] [CrossRef]
- Taherdoost, H.; Madanchian, M. Understanding Applications and Best Practices of DEMATEL: A Method for Prioritizing Key Factors in Multi-Criteria Decision-Making. J. Manag. Sci. Eng. Res. 2023; in progress. [Google Scholar] [CrossRef]
- Paul, T.K.; Jana, C.; Pal, M.; Simic, V. Sustainable carbon-dioxide storage assessment in geological media using modified Pythagorean fuzzy VIKOR and DEMATEL approach. Int. J. Hydrogen Energy 2023, 48, 9474–9497. [Google Scholar] [CrossRef]
- Mao, Q.; Chen, J.; Lv, J.; Guo, M.; Xie, P. Selection of plastic solid waste treatment technology based on cumulative prospect theory and fuzzy DEMATEL. Environ. Sci. Pollut. Res. Int. 2023, 30, 41505–41536. [Google Scholar] [CrossRef]
- Gandomi, M.; Pirooz, M.D.; Nematollahi, B.; Nikoo, M.R.; Varjavand, I.; Etri, T.; Gandomi, A.H. Multi-criteria decision-making optimization model for permeable breakwaters characterization. Ocean Eng. 2023, 280, 114447. [Google Scholar] [CrossRef]
- Tutak, M.; Brodny, J. Progress towards the innovation potential of the European union member states using grey relational analysis and multidimensional scaling methods. Decis. Mak. Appl. Manag. Eng. 2023, 6, 186–218. [Google Scholar] [CrossRef]
- Silva, N.F.; dos Santos, M.; Gomes, C.F.S.; de Andrade, L.P. An integrated CRITIC and Grey Relational Analysis approach for investment portfolio selection. Decis. Anal. J. 2023, 8, 100285. [Google Scholar] [CrossRef]
- Jagatheswari, S.; Ramalingam, P.; Chandra Priya, J. Improved grey relational analysis-based TOPSIS method for cooperation enforcing scheme to guarantee quality of service in MANETs. Int. J. Inf. Technol. 2022, 14, 887–897. [Google Scholar] [CrossRef]
- Zhou, L.; Wan, S.; Dong, J. A Fermatean Fuzzy ELECTRE Method for Multi-Criteria Group Decision-Making. Informatica 2022, 33, 181–224. [Google Scholar] [CrossRef]
- Li, P.; Xu, Z.; Wei, C.; Bai, Q.; Liu, J. A novel PROMETHEE method based on GRA-DEMATEL for PLTSs and its application in selecting renewable energies. Inf. Sci. 2022, 589, 142–161. [Google Scholar] [CrossRef]
- Yang, X.; Xu, Z.; Xu, J. Large-scale group Delphi method with heterogeneous decision information and dynamic weights. Expert Syst. Appl. 2023, 213, 118782. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, Z. Probability Calculation and Element Optimization of Probabilistic Hesitant Fuzzy Preference Relations Based on Expected Consistency. IEEE Trans. Fuzzy Syst. 2018, 26, 1367–1378. [Google Scholar] [CrossRef]
- Gao, J.; Xu, Z.; Liao, H. A Dynamic Reference Point Method for Emergency Response Under Hesitant Probabilistic Fuzzy Environment. Int. J. Fuzzy Syst. 2017, 19, 1261–1278. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.-x. Consensus Building for Probabilistic Hesitant Fuzzy Preference Relations with Expected Additive Consistency. Int. J. Fuzzy Syst. 2018, 20, 1495–1510. [Google Scholar] [CrossRef]
- Jaccard, P. Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bull. Soc. Vaudoise Sci. Nat. 1901, 37, 241–272. [Google Scholar]
- Dice, L.R. Measures of the Amount of Ecologic Association between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Jin, C.; Ran, Y.; Wang, Z.; Zhang, G. Prioritization of key quality characteristics with the three-dimensional HoQ model-based interval-valued spherical fuzzy-ORESTE method. Eng. Appl. Artif. Intell. 2021, 104, 104271. [Google Scholar] [CrossRef]
- Lin, M.; Zhan, Q.; Xu, Z. Decision making with probabilistic hesitant fuzzy information based on multiplicative consistency. Int. J. Intell. Syst. 2020, 35, 1233–1261. [Google Scholar] [CrossRef]
- Yazdani, M.; Torkayesh, A.E.; Chatterjee, P. An integrated decision-making model for supplier evaluation in public healthcare system: The case study of a Spanish hospital. J. Enterp. Inf. Manag. 2020, 33, 965–989. [Google Scholar] [CrossRef]
- Wu, L.; Yang, Y. The strategy of psychological restraint on risk amplification of information in online public opinion events. J. Northwest Norm. Univ. (Soc. Sci.) 2019, 56, 108–115. [Google Scholar]
- Liu, Z.; Ma, L. The Integrated Application of Internet Public Opinion Information under the Big Data Framework of Smart Information Service. Inf. Sci. 2022, 40, 84–89. [Google Scholar] [CrossRef]
- Li, C.; Wu, F.; Sun, Q. Research on information spreading effects in the social interaction context. J. Ind. Eng. Eng. Manag. 2023, 37, 22–34. [Google Scholar]
- Bi, H.; Tian, H. Analysis and reflection on the Phenomenon of “Quasi—reversal” in Public Opinion: Taking the “Wanzhou Bus Falling into the river Incident” as an Example. J. Intell. 2019, 38, 103–110. [Google Scholar]
- Di, Z.; Mingchen, L. Communication Mechanism of Network Language Information from the Perspective of Information Ecology. Inf. Sci. 2021, 39, 28–34. [Google Scholar] [CrossRef]
- Djerf-Pierre, M.; Shehata, A. Still an Agenda Setter: Traditional News Media and Public Opinion During the Transition From Low to High Choice Media Environments. J. Commun. 2017, 67, 733–757. [Google Scholar] [CrossRef]
- Li, L.; Xiao, X.; Wang, U. Research on Government Guidance to Online Public Opinion in the Era of Micro—Video. J. Xiangtan Univ. (Philos. Soc. Sci.) 2021, 45, 80–84. [Google Scholar] [CrossRef]
- Hajli, M.N.; Sims, J.; Featherman, M.; Love, P.E.D. Credibility of information in online communities. J. Strateg. Mark. 2014, 23, 238–253. [Google Scholar] [CrossRef]
- Song, S.; Zhang, Y.; Yu, B. Interventions to support consumer evaluation of online health information credibility: A scoping review. Int. J. Med. Inf. 2021, 145, 104321. [Google Scholar] [CrossRef]
- Glenski, M.; Weninger, T.; Volkova, S. Propagation From Deceptive News Sources Who Shares, How Much, How Evenly, and How Quickly? IEEE Trans. Comput. Soc. Syst. 2018, 5, 1071–1082. [Google Scholar] [CrossRef]
- Tian, Z.-W.; Wang, L.; Liu, C. Information Dissemination Mechanism Analysis and Model Construction of Micro-blog Based on Complex Network. Inf. Sci. 2015, 33, 15–21. [Google Scholar] [CrossRef]
- Denizci Guillet, B.; Mattila, A.; Gao, L. The effects of choice set size and information filtering mechanisms on online hotel booking. Int. J. Hosp. Manag. 2020, 87, 102379. [Google Scholar] [CrossRef]
- Woo-Young, C. Online civic participation, and political empowerment: Online media and public opinion formation in Korea. Media Cult. Soc. 2016, 27, 925–935. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, X. Modeling and Simulation Research of Interactive Public Opinion Evolution under Multi-Agent Interventions. Processes 2022, 10, 1379. [Google Scholar] [CrossRef]
- You, G.; Gan, S.; Guo, H.; Dagestani, A.A. Public Opinion Spread and Guidance Strategy under COVID-19: A SIS Model Analysis. Axioms 2022, 11, 296. [Google Scholar] [CrossRef]
- Feng, Z. Hot news mining and public opinion guidance analysis based on sentiment computing in network social media. Pers. Ubiquitous Comput. 2018, 23, 373–381. [Google Scholar] [CrossRef]

| Channels | Mark | Content | References |
|---|---|---|---|
| Social media platforms | Social media platforms such as Facebook, Twitter, and Weibo have become the main channels for information dissemination. Users can spread information through various means, including posting messages, sharing links, and commenting, which may include various types of content, such as real, false, or misleading information. | Wu and Yang [52] Liu and Ma [53] Li et al. [54] | |
| News media | News agencies and media play a crucial role in information dissemination. They spread information through reporting, interviews, commentary, and other means. However, at times, media can also engage in inaccurate reporting, sensationalism, or biased coverage, leading to risks in information propagation. | Bi and Tian [55] | |
| Online forums and blogs | Online forums and blogs provide platforms for discussion and communication, but they also come with information dissemination risks. Users can spread information through posting threads, comments, and replies, including false information, malicious attacks, and hate speech, among other things. | Wu and Yang [52] | |
| Traditional media | Traditional media, including television, radio, newspapers, and magazines, still play a significant role in information dissemination. These media channels deliver information to the public through news reports, opinion articles, television programs, and more. | Di and Mingchen [56] Djerf-Pierre and Shehata [57] | |
| Short video platforms | Short video platforms have become increasingly popular in recent years, providing a quick and engaging way for users to share and consume information. These platforms, such as TikTok and Instagram Reels, allow users to create and share short videos, making them a powerful tool for information dissemination. However, similar to other social media platforms, there is a risk of spreading misinformation, false content, and potentially harmful messages through short video content. | Li et al. [58] |
| Indicators | Mark | Content | References |
|---|---|---|---|
| Trustworthiness and reliability | When evaluating information dissemination pathways, the primary criteria to consider are their trustworthiness and reliability. The dissemination pathways should be based on credible sources, authoritative institutions, or reliable platforms to ensure the authenticity and accuracy of the information. | Hajli et al. [59]; Song et al. [60] | |
| Dissemination speed and breadth | In the complex public opinion environment, information dissemination tends to be rapid and extensive. When evaluating dissemination pathways, it is important to consider their speed of propagation and the breadth of their influence. Some pathways may have the ability to spread rapidly, while others may have a more significant impact within specific social circles or target audiences. | Glenski et al. [61] Tian et al. [62] | |
| Information filtering mechanisms | When evaluating communication channels, it is essential to consider their information filtering mechanisms. Some channels may have robust information screening and quality control mechanisms, which can reduce the dissemination of false, misleading, or harmful information. On the other hand, other channels may be relatively loose, making it easier for low-quality and inaccurate information to spread. | Denizci Guillet et al. [63] | |
| Participation and interactivity | In complex public opinion environments, it is important to consider the level of participation and interactivity when evaluating communication channels. Some channels may actively encourage user engagement, interaction, and information sharing, thereby promoting information dissemination. On the other hand, other channels may be more passive, with information dissemination primarily controlled by media or organizations. | Woo-Young [64] Chen and Zhao [65] | |
| Social impact and public opinion orientation | When evaluating communication pathways, it is essential to consider their social impact and public opinion orientation. Some pathways may have a significant influence on public opinion, social emotions, and attitudes, which in turn can affect the public’s decision making and behavior. Assessing the public opinion orientation of communication pathways helps understand their impact on society. | You et al. [66] Feng [67] |
| {0.8|0.2, 0.9|0.6, 0.95|0.2} | {0.7|0.1, 0.8|0.4, 0.9|0.4, 0.95|0.1} | {0.9|0.6, 0.95|0.4} | {0.85|0.2, 0.9|0.4, 0.95|0.4} | {0.8|0.1, 0.9|0.6, 0.95|0.3} | |
| {0.9|0.7, 0.95|0.3} | {0.6|0.3, 0.7|0.4, 0.8|0.2, 0.9|0.1} | {0.8|0.4, 0.85|0.4, 0.9|0.2} | { 0.8|0.1, 0.9|0.5, 0.95|0.4} | {0.8|0.4, 0.9|0.4, 0.95|0.2} | |
| {0.8|0.2, 0.9|0.8} | {0.5|0.2, 0.6|0.4, 0.7|0.4} | {0.9|0.5, 0.95|0.5} | { 0.8|0.2, 0.9|0.6, 0.95|0.2} | {0.7|0.1, 0.8|0.2, 0.9|0.5, 0.95|0.2} | |
| {0.8|0.1, 0.9|0.7, 0.95|0.2} | {0.5|0.3, 0.6|0.4, 0.65|0.3} | {0.7|0.2, 0.8|0.4, 0.85|0.4} | {0.6|0.3, 0.7|0.5, 0.8|0.2} | {0.7|0.2, 0.8|0.4, 0.9|0.4} | |
| {0.9|0.9, 0.95|0.1} | {0.85|0.6, 0.9|0.4 } | {0.9|0.2, 0.95|0.8} | {0.9|0.4, 0.95|0.6} | {0.85|0.1, 0.9|0.4, 0.95|0.5} |
| The i-th Row/Column/Indicator | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Sums of Rows | 22.51176 | 19.07755 | 22.84532 | 22.85205 | 22.85653 |
| Sums of Columns | 21.78701 | 21.57026 | 21.9155 | 22.45196 | 22.41849 |
| Objective Weights of Evaluation Indicators | 0.2011 | 0.18452 | 0.20319 | 0.20566 | 0.20553 |
| Indicator | |||||
|---|---|---|---|---|---|
| The Subjective Weights | 0.15 | 0.3 | 0.1 | 0.25 | 0.2 |
| The Objective Weights | 0.2011 | 0.18452 | 0.20319 | 0.20566 | 0.20553 |
| The Comprehensive Weights | 0.15207 | 0.27907 | 0.10244 | 0.2592 | 0.20722 |
| 1.02684 | 1.05124 | 1.06292 | 1.08874 | 1.01894 | |
| 0.96407 | 0.93401 | 0.92345 | 0.88915 | 0.97476 | |
| 0.20041 | 0.19984 | 0.19995 | 0.19910 | 0.20069 | |
| 2.09200 | 2.08215 | 2.08174 | 2.06850 | 2.09628 | |
| 0.96482 | 0.96208 | 0.96262 | 0.95851 | 0.96618 | |
| 1.22058 | 1.21480 | 1.21500 | 1.20695 | 1.22321 | |
| Ranking | 2 | 4 | 3 | 5 | 1 |
| Original Evaluation Results | 1.22058 | 1.21480 | 1.21500 | 1.20695 | 1.22321 |
| Original Rankings | 2 | 4 | 3 | 5 | 1 |
| Modified Evaluation Results | 2.84894 | 54.43592 | 51.99502 | 43.26278 | 62.10789 |
| Modified Ranking | 5 | 2 | 3 | 4 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Xue, Y.; Su, J. Evaluating Information Risk Propagation in Complex Public Opinion Environments Based on the Improved Grey Relational Analysis—Decision Making Trial and Evaluation Laboratory Method. Systems 2023, 11, 472. https://doi.org/10.3390/systems11090472
Luo Z, Xue Y, Su J. Evaluating Information Risk Propagation in Complex Public Opinion Environments Based on the Improved Grey Relational Analysis—Decision Making Trial and Evaluation Laboratory Method. Systems. 2023; 11(9):472. https://doi.org/10.3390/systems11090472
Chicago/Turabian StyleLuo, Zhanyang, Yumei Xue, and Jiafu Su. 2023. "Evaluating Information Risk Propagation in Complex Public Opinion Environments Based on the Improved Grey Relational Analysis—Decision Making Trial and Evaluation Laboratory Method" Systems 11, no. 9: 472. https://doi.org/10.3390/systems11090472
APA StyleLuo, Z., Xue, Y., & Su, J. (2023). Evaluating Information Risk Propagation in Complex Public Opinion Environments Based on the Improved Grey Relational Analysis—Decision Making Trial and Evaluation Laboratory Method. Systems, 11(9), 472. https://doi.org/10.3390/systems11090472







