Abstract
Uncertain yield and demand often result in unbalanced revenue and risk sharing among agriculture supply chain (ASC) members. Agricultural cooperatives help smallholder farmers enhance their bargaining power via revenue and risk sharing and are a significant bridge between farmers and retailers. Therefore, this study aimed to design a contractual mechanism considering a cooperative’s participation in the coordination of ASCs that face random yield and demand in pursuit of risk and benefit equivalence. We first compared two- and three-echelon decentralized ASCs with a centralized system, and the results indicate that the cooperative’s participation is conducive to redistributing profit between the retailer and farmer. As a verified revenue-sharing (RS) contract cannot coordinate a two-echelon ASC under uncertain yield and demand, we developed a double revenue-sharing (DRS) contract, which has been demonstrated to coordinate an ASC system with the cooperative’s participation. A numerical analysis was conducted to show that the cooperative can influence profit distribution among the upstream and downstream members via wholesale prices. Therefore, equivalence of risk and benefit is realized and fairly allocated among the members under the DRS contract, which is of great significance to the ASC system’s stable and sustainable development.
1. Introduction
Agricultural cooperatives play a significant role in helping farmers integrate resources. They expand sales channels, provide social services, and grant access to the advantages of industrialized agricultural economies of scale; they thus, to a certain extent, improve farmers’ income, especially in developing countries [1,2,3]. Cooperatives facilitate the organic connection between farmers and modern agriculture by mitigating issues, including weak bargaining power, high transaction costs, and a high default rate, etc., for farmers who directly sign contracts with leading enterprises or supermarkets, thereby contributing to the vertical integration of agricultural supply chains (ASCs) [4]. Accordingly, farmers can benefit from participating in ASCs with agricultural cooperatives as intermediates, with the main functions of processing and marketing; in turn, the ASC offers a promising approach to the stable and sustainable supply of agricultural food.
In practice, however, the relationships between agricultural cooperatives and their members are not as stable as expected, which weakens their cooperative efficiency and hinders the ASC system’s sustainability. Internally, improper governance arrangements of the upstream cooperative are liable to cause the compression of farmers’ interests [3,5], leading to inequality in risk sharing and benefit allocation among members of the chain. Externally, natural and market risks exacerbate internal inequality via the upstream and downstream relationships [6,7]. On the one hand, crop-growing is particularly sensitive to the natural factors of seasons, weather, pests, and diseases. Similar levels of agricultural input may result in different output levels, thus leading farmers to reduce their risks by reducing inputs. As farmers are unable to bear the yield risk alone, a phenomenon emerges in which they are unwilling to share losses with cooperatives [8]. On the other hand, uncertain market demand for the final product plagues downstream buyers. They may respond to the demand risk by cutting down order quantity. Especially when the market is in a slump, buyers may be reluctant to purchase a predetermined quantity of crops due to their low market price, often resulting in default [9]. Hence, low input and under-ordering issues threaten the stability of upstream and downstream contract relationships, thus compromising the sustainability of the agriculture supply chain system.
The inequivalence of risk sharing and benefit allocation among ASC members is the fundamental issue that challenges the stability and sustainability of cooperation relationships and the ASC system. Downstream risk sharing and benefit allocation between the cooperative and the buyer are generally expressed in the form of contracts, e.g., wholesale price contracts. While a cooperative’s governance structure inherently determines the risk sharing and benefit allocation between the cooperative and its members, different contracts designate various risk sharing and benefit allocation combinations [5]. Practically, profit distribution in farmer cooperatives generally consists of two parts. With the profit from the transaction with the downstream buyer, the cooperative must first pay for the farmers’ delivered quantity at a pre-agreed price. Then, the remainder of the profit, after deducting the cooperative’s production and operation costs to ensure its viability, is shared between the cooperative and the farmers [3], e.g., the two-step profit distribution policy implemented in rural China [8]. That is to say, the cooperative and the farmers also determine their risk sharing and benefit allocation by signing an agreement. Furthermore, the contract structure is similar to a classic revenue-sharing (RS) contract, widely used between cooperatives and retailers in contract farming or agriculture supply chains [9].
In the context of contract coordination, a centralized system in which all of the members make decisions together pursues the maximization of the entire supply chain’s profit, which is set as a benchmark for comparison. In a decentralized system, each member acts to maximize their own profit. The total supply chain profit is the sum of all members’ profits, which tends to be lower than that in the centralized system. When the whole supply chain profit under the decentralized decision is equal to that under the centralized decision, the contracts can coordinate the supply chain. Thus, risk sharing and benefit allocation combinations among members is observed.
Therefore, this study aimed to explore risk sharing and benefit allocation issues in a multi-echelon agriculture supply chain setting in terms of the coordinating mechanisms used to design upstream and downstream contracts in order to improve the stability and sustainability of the cooperative and the entire ASC. To develop coordinating mechanisms based on classic news vendor models, we built a three-echelon agriculture supply chain composed of a farmer, a cooperative, and a retailer, where the farmer confronts uncertain yield originating from uncontrollable natural conditions and the retailer faces random demand in the end consumer market. The respective upstream and downstream revenue- and risk-sharing relationships are integrated into the same agriculture supply chain system by extending the ASC from two to three tiers. In this case, we can focus on risk sharing and benefit allocation between the cooperative and its members internally as well as between the cooperative and the downstream buyer externally. Meanwhile, the mutual influence of internal and external contractual relationships can be further taken into account.
On the basis of the three-echelon ASC, a two-layer ASC, in the absence of the cooperative, was constructed in which the retailer combines the tasks of processing crops and selling finished products. Via comparative analysis between the two-level and three-level ASCs, we explored the influence of the cooperative’s participation on the contract structure and ASC’s profit distribution. Under the circumstances, based on classic coordinating contracts, we aimed to design an extra-dyadic double revenue-sharing (DRS) contract as a revenue- and risk-sharing mechanism for a multi-echelon supply chain to achieve benefit and risk equivalence among the ASC members. We constructed the ASC facing yield and demand uncertainties, which is beneficial for a more in-depth investigation of risk sharing and benefit allocation in contract form. According to the coordinated contracts, further insights can be obtained for improving the performance of the integrated ASC system and its members, thus enhancing the stability and sustainability of the cooperatives and the ASC systems. The main contributions of this paper to the literature are as follows:
(1) We compared the ASC’s total profits in different scenarios, including a three-tier decentralized decision, two-echelon decentralized decision, and coordinated DRS contract or centralized ASC. The results show that the third scenario has the highest supply chain profit, followed by the second scenario, with the first scenario having the lowest profit. In the second scenario, the retailer receives the majority of the ASC’s profit. In the three-level ASC, however, if the ASC is coordinated, the cooperative can share a portion of the retailer’s profit, implying a more conducive situation to achieve risk sharing and benefit allocation equivalence.
(2) We considered yield and demand risks resulting from natural and market factors outside the ASC system. These exogenous risks impact the ASC members’ decision-making and exacerbate the original inequality of risk sharing and benefit allocation under circumstances where yield and demand risks are not considered. Our analysis showed that a revenue-sharing contract could not coordinate a two-echelon ASC, while a DRS contract can coordinate the three-echelon ASC. This corrects the farmer’s low input and the retailer’s under-ordering problems due to yield and demand uncertainties.
(3) In the coordinated three-level ASC, with regard to the upstream relationship, we found that the cooperative could share risk and benefit with farmers and alter the risk and revenue distribution ratio through wholesale prices. Furthermore, we investigated the impacts of the crop replenishment cost and found that it was inversely related to the profits of the entire chain and its members, except for the cooperative. Similar to wholesale prices, the upstream replenishment cost also influences the downstream retailer’s profit. Concerning the downstream relationship, the risk and revenue could be redistributed between the cooperative and the retailer by adjusting the wholesale price. In addition, the results indicate that changes in the downstream wholesale price affect upstream members’ profits. Combining the findings from upstream and downstream, it was implied that the ASC members could achieve equivalences in risk sharing and benefit allocation. Therefore, upstream and downstream contractual mechanisms interacted, which verified the significance of placing the upstream and downstream contractual arrangements in the same supply chain.
We have organized the rest of this paper as follows. In Section 2, we review the relevant literature. Section 3 provides the problem description, notations, and the centralized benchmark. Section 4 analyzes a decentralized three-echelon ASC system under classic wholesale price contracts. A semi-integrated two-echelon ASC system is constructed for comparative analysis in Section 5. Section 6 presents the model of a double revenue-sharing contract to coordinate the three-echelon ASC with random yield and demand. In Section 7, we present a numerical analysis to verify the results of the above models. We conclude the main findings in this paper and related issues for future research in Section 8.
2. Literature Review
2.1. Relationships among the ASC Members
From the perspective of contract arrangements, the literature has widely discussed the pairwise relationships between the farmer, cooperative, and buyer. With regard to the relationships between cooperatives and their members, Hovelaque et al. [10] examined the economic effect of an agricultural cooperative offering differential price contracts to its heterogeneous members while considering constrained supply. Candemir et al. [3] reviewed and discussed the influence of cooperatives’ economic characteristics on members’ welfare and the main challenges cooperatives face when improving farm sustainability. Zhong et al. [5] conducted empirical studies on risk sharing and benefit allocation under three contract forms in the dairy sectors of China. With regard to the relationships between cooperatives and buyers (the buyer may be a supermarket or an agricultural company as a distributor or retailer selling the final products to consumers), the empirical research of Jia and Huang [11] discussed vertical coordination issues from the perspective of contract arrangements between farmer cooperatives and buyers. Ge et al. [12] investigated the bargaining power of a dairy cooperative and milk processors in Florida through price negotiations. In the case of contract farming, the previous literature has explored the relationships between farmers and buyers. Federgruen et al. [13] studied a manufacturer’s decision model for selecting an optimal set of farmers to contract with for supplying agricultural products, one in which the farmers chose from a menu of contracts to maximize their expected profit. Ton et al. [14] explored the effectiveness of research on contractual arrangements for improving the incomes of smallholders who contracted with a firm. Tang et al. [15] proposed a partially guaranteed price contract to enhance mutual benefit and promote the sustainable relationship between smallholder farmers and buying firms.
Previous literature has analyzed the upstream or downstream adjacent contractual relationship of the cooperative in depth. However, in a setting of agriculture supply chains, the upstream and downstream contractual relationships interact with each other and are also critical for the stability and sustainability of the entire chain. For example, farmers’ incomes are not only affected by their contracts with cooperatives but also by the contractual arrangements between cooperatives and buyers. To our knowledge, few studies have simultaneously considered the interrelated contractual relationships among farmers, cooperatives, and buyers. Only a small number of studies have focused on the differences in the participation of two and three members in the same supply chain. For example, Zhong et al. [16] compared two-stage and three-stage e-commerce logistics of service supply chains with cooperative distribution. They found that the profit of a centralized decision-making system was higher than both a two- or a three-stage decentralized system, indicating the significance of designing a suitable profit distribution mechanism under revenue-sharing contracts. Giri and Bardhan [17] constructed a three-level manufacturing supply chain and compared the total supply chain profits under the centralized, decentralized, and upstream and downstream semi-integrated decisions based on wholesale price contracts. The results showed that the profit of the decentralized system is the lowest, the profit of the centralized system is the highest, and the profit of the semi-integrated system falls in between. However, the above studies originated from different industry backgrounds, leading to different contract arrangements. In an agricultural setting, this study aimed to integrate upstream and downstream contractual relationships into the same ASC system, thus investigating the risk sharing and benefit allocation among the members.
2.2. Contract Coordination under Yield and Demand Risk
ASC members’ relationships can be formulated as contract coordination problems so as to examine risk sharing and benefit allocation between them. From the perspective of contract coordination, particularly while considering yield and demand risk, classic contracts (such as wholesale price, revenue-sharing, buyback contracts, etc.) are usually studied under a two-echelon supply chain with uncertainties. Coordinating a two-tier supply chain under uncertain yield and demand has been widely studied in the literature. It has been found that the classic contracts, except for wholesale price contracts, i.e., revenue-sharing contracts [18] and buyback contracts [19], cannot redistribute the yield risk and thus fail to coordinate the chain facing random yield and demand. However, based on the classic contracts [18,19,20], such as surplus subsidy mechanisms [19], improved or combined contracts [20] can achieve supply chain coordination. The adjacent members should sign contracts separately when the agriculture supply chain is extended from two to three tiers.
Moreover, the variability in risk taking by different supply chain members complicates coordination. Therefore, contract designs under a two-echelon supply chain may expose the participants to limitations. Previous studies have shown that pairwise (where each pair of adjacent members in the supply chain signs the same contract) revenue-sharing contracts [21,22] or return policy contracts [23] can coordinate three-tier supply chains under uncertain demand conditions. Formentini and Romano [24] defined this kind of contract as an extra-dyadic contract. In the case of a fresh produce agricultural supply chain, both considering random demand and fresh-keeping efforts, Yang and Liu [25] and Ma et al. [26] developed combined contracts, including cost sharing and revenue-sharing contracts. In contrast, while considering only the uncertain yield affected by changes in weather conditions, Anderson and Monjardino [27] proposed a double discount contract to share the grower’s yield risk in the middle of a three-echelon agriculture supply chain.
In cases of the simultaneous consideration of random yield and demand, only a small number of relevant studies have focused on the contract design of multi-level manufacturing supply chains. Under a three-tier supply chain with manufacturers at the core, He and Zhao [28] considered that raw material suppliers at the forefront of the supply chain faced random outputs. In contrast, retailers at the end of the chain faced demand uncertainty. They assumed that when the supplier’s production was insufficient, it could be replenished through the spot market. It is indicated that the combined upstream wholesale price contracts and downstream buyback contracts could achieve supply chain coordination. Giri and Bardhan [17] considered a three-echelon manufacturing supply chain where the upstream supplier and midstream manufacturer confronted random yield, and the downstream retailer was affected by stochastic demand. Their results show that neither pairwise wholesale price contracts nor separate alliances between upstream and downstream members could achieve system coordination. With the same case of yield and demand randomness corresponding to members in the three-tier supply chain, Jian and Wang [29] designed a combined contract with yield risk sharing and buyback to achieve coordination upon the assumption that the supplier could replenish through the spot market when underproducing. Adhikari [30] constructed a five-level textile supply chain under demand and supply uncertainties. They proved that even if suppliers at all levels were allowed to replenish the output through the spot market, wholesale price contracts could not achieve supply chain coordination. In contrast, buyback contracts and options contracts could coordinate the supply chain.
The most relevant literature to our study is that of Zhong et al. [16], Giri and Bardhan [17], and Giannoccaro and Pontrandolfo [21]. However, Zhong et al. [16] did not consider uncertain yield and demand, and Giannoccaro and Pontrandolfo [21] only considered random demand. The first two studies only conducted comparative analysis on the two- and three-level supply chains without designing coordinating contracts. In addition, these studies focused on e-commerce or manufacturing supply chains. Our study considered random yield and demand and proposes a coordinating mechanism for a three-echelon agricultural supply chain. As mentioned above, the contract arrangement in an agricultural supply chain setting will differ due to the characteristics of smallholder farmers or agricultural products. For example, due to the disadvantaged position of farmers, cooperatives may practically purchase all of their agricultural products to share their output risk, rather than purchasing via a strict accordance with the order quantity. Furthermore, the buyback contract, commonly used in manufacturing sectors, is not applicable in the agricultural setting due to the special nature of agricultural products. Previous research has shown that revenue-sharing contracts are commonly used in agricultural settings compared with research focusing on the manufacturing industry but are less common in multi-echelon supply chain coordination. As shown in Table 1, we have made a comparison between the related literature and our study. Considering the significance of farm cooperatives for ASCs, this study aimed to design a double revenue-sharing contract, where the contractual arrangements between adjacent members are both based on classic revenue-sharing contracts. Then, we examined risk sharing and benefit allocation issues under the circumstances of ASC coordination, thus gaining further insights into the members’ risk and benefit equivalence.

Table 1.
Overview of the related literature.
3. Problem Description, Notations, and the Centralized Benchmark
3.1. Problem Description, Notations, and Assumptions
Consider a three-echelon agriculture supply chain for a single crop consisting of a farmer, a cooperative, and a retailer. Affected by weather, pests, or diseases, the actual yield of the upstream farmer growing crops may be less than the planned amount for a given agricultural material input . Thus, we assume the crop yield to be randomly represented as , with being a nonnegative random variable. The midstream cooperative plays a role in processing crops and transacting them with the retailer at a predetermined order quantity. The downstream retailer buys final agricultural products from the cooperative and sells them in the end consumer market. The market demand is supposed to be stochastic. The unit cost of the agricultural material input is , and the unit sale price of the final products in the market is . We assume that neither the farmer nor the retailer can influence the market price compared with the national or global market. Hence, both and are exogenously determined. The sequence of events is given as follows:
- Before the sowing season, the cooperative declares the unit purchase price and unit wholesale price . Accordingly, the farmer decides the input quantity units, and the retailer determines his order quantity units of the finished agricultural products;
- The cooperative determines the order quantity of crops to be processed into final products. Without a loss of generality, we assume that one unit of the crop is necessary to produce one unit of the finished agricultural product. Hence, the amount of crops the cooperative orders from the farmer is the same as the retailer’s order quantity . Suppose the cooperative will purchase all of the farmer’s realized output. Consequently, the input amount will be actually determined by the cooperative’s order decision, which equals the farmer’s planned yield ;
- The growing season begins, and the farmer grows crops with a given agricultural material input determined by the cooperative, as above. Due to weather, pests, or disease factors, the farmer is faced with yield uncertainty. As the cooperative agrees to purchase all of the yield of the given input, partial yield risk is transferred to the cooperative. However, the farmer still bears the risk resulting from the loss of the input costs that cannot produce the planned quantity;
- After harvest, the realized crop yield is delivered to the cooperative to be processed into the finished agricultural products at unit processing cost . If the delivered amount is less than the retailer’s order quantity, the cooperative will buy the deficit from the crop spot market at a higher price ; if it is more, the excess amount will be salvaged at a reduced price . Then, the cooperative transacts the order quantity with the retailer at a unit wholesale price .
- The market demand is realized as the selling season begins. It assumed that there is no salvaged value of the unsold product and no shortage cost for the retailer.
In addition, we assume that the farmer, the cooperative, and the retailer are all risk-neutral and rationally pursuing self-profit maximization. Information is common knowledge among them. To avoid the uninteresting trivial cases, we make the following assumptions referring to [17,28]: (i) , to keep the farmer, the cooperative, and the retailer willing to participate; (ii) , to avoid the cooperative directly buying from the crop spot market; and (iii) , to prevent the cooperative from infinitely purchasing the crops. The notations are summarized in Table 2.

Table 2.
Main notations used in this paper.
3.2. The Centralized Benchmark
In this subsection, we have built a centralized model to provide a benchmark case, in which all the members as a whole pursue the maximization of the profit of the integrated supply chain. Based on the centralized benchmark, supply chain coordination requires that the profit added up from all members under coordinating contracts is equal to that under the centralized situation. In the centralized system, the ASC sells the minimum value of planned output and market demand at a unit retail price and pays unit processing cost for planned output and unit input cost for market demand . When the actual yield is lower than the planned output , the unit replenishment cost should be paid for purchasing agricultural material from other farmers; conversely, the unit salvage value can be obtained by handling the excess output. Thus, the expected profit of the entire ASC is formulated as
where . The first term is the total sales revenue. The second and third terms are input costs for the agricultural material and processing costs for the final products, respectively. The fourth term is the cost of buying crops from the spot market to fulfill the retailer’s order quantity when the farmer’s yield falls short. The last term refers to revenue derived from selling the excess amount.
Proposition 1.
is jointly concave in and , and the optimal values satisfy
Proof of Proposition 1.
From Equation (1), we have the second-order partial derivatives associated with and , respectively.
Then, we obtain the Hessian matrix .
It is easy to see that , and ; thus, is a negative definite matrix that completes the proof and the unique optimal and satisfy the first-order conditions, as shown in Equations (2) and (3). Therefore, we obtain Proposition 1.
By substituting Equations (2) and (3) into Equation (1), we can obtain the optimal expected profit of the integrated supply chain.
4. The Three-Echelon Decentralized ASC System
Under the decentralized ASC system, there are three self-profit maximizing entities. A double (pairwise) wholesale price contract is adopted where two adjacent members sign contracts. The farmer determines the agricultural material input quantity by the order amount of the cooperative. The cooperative will purchase all of the realized yield according to the given input quantity. Therefore, the low yield risk is partly transferred to the cooperative, equivalent to the input quantity determined by the cooperative. Hence, following backward induction, the problem of the retailer, the cooperative, and the farmer is solved as follows.
Firstly, given the wholesale price and , the retailer’s excepted profit is represented as
The first term is the revenue obtained by selling the finished products to the consumer market, and the second is the cost of buying the ordered quantity from the cooperative.
From Equation (5), we have the first- and second-order conditions with respect to , and . Thus, the unique solution of the retailer’s optimal order quantity satisfies
By substituting Equation (6) into Equation (5), we obtain the optimal expected profit of the retailer.
Then, the cooperative’s expected profit function is expressed as
The first term represents the revenues derived from selling the final products to the retailer. The second term refers to the crop purchasing costs from the farmer. The third term refers to the replenishing costs to compensate for the shortage of crops needed to produce the retailer’s order quantity. The last term refers to revenues derived from processing excess crops and selling them at crop purchase markets. Similarly, from Equation (8), we have the first- and second-order derivatives concerning , and .
Hence, the optimal agricultural material input satisfies
Let and substitute Equation (9) into Equation (8). Then, we have the optimal cooperative’s profit:
Next, the farmer’s optimal expected profits are formulated as
The first term is the revenue from selling the crops to the cooperative, and the second is the costs of necessary input to grow crops.
Finally, using Equations (7), (10), and (11), we have the maximized expected profit of the whole three-echelon ASC:
It is assumed that both and are positive to ensure that the farmer and the cooperative are willing to participate in the chain. Therefore, we have from Equation (11) and from Equation (10). Then, comparing Equation (9) with Equation (2), we have , and comparing Equation (6) with Equation (3), we have . Consequently, it is easy to obtain , indicating that the pairwise wholesale price contract cannot coordinate the three-echelon agriculture supply chain under random yield and demand. In the decentralized system, low input and under-ordering issues arise and lead to the total profit of the entire chain being lower than that in the centralized system.
Furthermore, we aim to investigate the impacts of wholesale prices and . From Equation (6), we have
Using Equations (10) and (11), we obtain . The CDF is assumed to conform to an increasing generalized failure rate (IGFR, refer to [18]); thus, , and then the optimal wholesale price is uniquely determined by the first-order condition as
Accordingly, it is easy to see that . Therefore, we can obtain the Hessian matrix as a negative definite matrix. Then, we have the following proposition:
Proposition 2.
The cooperative’s expected profit is jointly concave in and .
From Equation (9), we have
From Equation (6), using Equations (14) and (15), we obtain and . Simultaneously solving these two equations, we have
Equation (17) indicates that the cooperative’s wholesale price for the final agricultural products increases in the farmer’s wholesale price for the crops. Equations (13) and (16) show that the retailer’s optimal order quantity decreases in both and .
Using Equations (15) and (16) to solve the first-order condition from Equation (11), we have
5. The Two-Echelon ASC System without the Cooperative’s Participation
5.1. The Decentralized Two-Echelon ASC
Without the participation of cooperatives, the ASC system becomes two layers, consisting of one farmer and one retailer. The retailer practically carries out the role of both processing the crops and selling the finished products, similar to the semi-integrated channel in Giri and Bardhan [17]. Compared with the decentralized three-echelon ASC, the wholesale price of the processed crops will not be present here, and the retailer will decide the farmer’s input quantity because they will buy all of the farmer’s realized yield. The sequence of events is as follows:
- Before the sowing season, the retailer declares the unit purchase price and decides the order quantity units of the crops;
- The farmer takes the order quantity as their planned output and determines the input amount units. Similarly, the retailer will purchase all of the farmer’s realized output units, indirectly deciding the farmer’s input quantity.
The expected profit of the farmer is the same as Equation (11), and that of the retailer is given by
As before, it will be shown that is jointly concave in and . The optimal order and input decisions satisfy Equations (9) and
The optimal expected profits of the farmer, the retailer, and the whole two-echelon ASC are expressed as
Compare the decentralized two-echelon scenario with the centralized benchmark case in Section 3. With the same assumptions of and , it is easy to show that and . On the one hand, this indicates that the wholesale price contracts cannot coordinate the two-echelon ASC; on the other hand, the resulting total two-level ASC profit will be lower than that of the decentralized system due to the concavity of the profit functions.
Compare the decentralized two-echelon with the three-echelon scenarios in Section 4. First, we can obtain from Equation (9). Second, using and Equations (6) and (19), we have and , indicating that the total maximum profit of the decentralized two-echelon ASC is higher than that of the decentralized three-echelon ASC.
To summarize the above comparison, we have the following proposition:
Proposition 3.
(1) The relationships of the planned and input quantity among the decentralized two- and three-echelon ASCs and the centralized system are and , respectively; (2) the optimal profits among the three scenarios are .
Statement (1) of Proposition 3 states that the planned and input quantities in the centralized scenario are the highest; in contrast, those in the three-echelon decentralized system are the lowest, and those in the two-echelon decentralized scenario fall in between. The increased planned and input quantities bring the ASC more profit, which is manifested in statement (2). Proposition 3 highlights the necessity of ASC coordination, and thus we aim to investigate whether classic revenue-sharing contracts can coordinate the two-echelon ASC.
5.2. The Two-Echelon ASC under Revenue-Sharing Contracts
Under the two-echelon ASC, the retailer provides the farmer with revenue-sharing contracts, in which the retailer pays a lower wholesale price for crops. Meanwhile, they share their sales revenue partially with the farmer. The sequence of events is similar to the scenario in the decentralized two-echelon ASC, and we first solve the retailer’s problem following backward induction. The retailer’s expected profit function is expressed as
where designates the proportion of the retailer’s sales revenue share with the farmer. Thus, under the revenue-sharing contract, the farmer’s profit consists of the sales revenue, input costs, and the profit shared from the retailer’s sales revenue. Then, the farmer’s expected profit is formulated as
As before, it can be easily proved that the retailer’s expected profit function is jointly concave in the order quantity and input amount ; thus, the resulting optimal order decisions satisfy
and the optimal input decision satisfies
Substituting Equations (26) and (27) into Equation (24), we can obtain the maximum profit of the retailer under the revenue-sharing contract as
Let and substitute Equations (26) and (27) into Equation (25). Then, we have the cooperative’s maximum profit under the revenue-sharing contract as
Compared with Equation (22) in Section 5.1, Equation (29) indicates that the farmer can share a portion of the retailer’s sales revenue under revenue-sharing contracts; a possibility which does not exist in the decentralized two-echelon ASC. To sum up the above analysis, we can use the following proposition.
Proposition 4.
Under the revenue-sharing contract, the retailer’s expected profit is jointly concave in and , and the optimal values satisfy Equations (26) and (27); the revenue-sharing contract cannot coordinate the two-echelon ASC.
Proof of Proposition 4.
If the revenue-sharing contract can coordinate the two-echelon ASC, we have and , if and only if and . At this time, however, the farmer’s profit equals zero, i.e., , contrary to our previous hypothesis. Therefore, the two-echelon ASC cannot achieve coordination under revenue-sharing contracts.
Proposition 4 implies that the profit of the non-coordinated two-echelon ASC is less than that of the centralized system, which is consistent with the literature [18,19,20]. In order to explore the influence of the cooperative’s participation in the ASC on the profit distribution in the following section, we analyzed the coordination problem of the two-tier ASC without the participation of cooperatives in this section. The scenarios under wholesale price contracts in Section 5.1 and revenue-sharing contracts in Section 5.2 were constructed to compare with the corresponding scenarios in the three-tier ASC. The numerical analysis in Section 7 will demonstrate that the profits of the two-layer decentralized supply chain are higher than those of the three-layer decentralized chain. However, the retailers account for the vast majority of the total ASC’s profits in the former scenario; in contrast, the retailer’s partial profits are shared by the cooperative in the latter situation. Hence, we aimed to investigate the cooperative’s role in improving the farmer’s revenue and the performance of the integrated ASC and to design the coordinated contracts under the three-echelon ASC in the next section.
6. Coordination Using a Double Revenue-Sharing Contract
Since the pairwise wholesale price contracts cannot coordinate the agriculture supply chain with random yield and demand, as mentioned in Section 2, we designed a double revenue-sharing contract. Under the DRS contract, the retailer shares with the cooperative fraction of its revenue from selling the order quantity, and the cooperative gives the retailer a lower wholesale price . Meanwhile, the cooperative allows the farmer to share , a fraction of its revenue, from selling crops and disposing of the excess order quantity of the final products after deducting the costs for buying the shortfall quantity of the crops. The farmer gives the cooperative a lower wholesale price . The DRS contract aims to reallocate the yield risk between the adjacent upstream members and the demand risk between the neighboring downstream entities to correct the low input and under-ordering issues.
The upstream revenue-sharing contract allows the cooperative to replenish a shortage from the crop spot market when the farmer suffers from low production. However, the replenishment costs are subtracted from the sales income, and the remaining revenue is shared with the farmer. Similar to practice, cooperatives take on the yield risk together with members by sharing a portion of the sales revenue after deducting the production and operational costs [5]. This is in contrast with classic revenue-sharing contracts where cooperatives share a percentage of all sales revenue. The DRS contract assumes that the cooperative buys all of the farmer’s realized output, which requires the cooperative to take on most of the yield risk. However, the cooperative can adjust the wholesale price to impact the extent to which the yield risk is transferred downstream. Consequently, the above revenue-sharing arrangement can encourage the cooperative’s participation in the supply chain.
The expected profit function of the retailer, the cooperative, and the farmer can be given as follows:
Solving the first- and second-order conditions of Equations (30) and (31), we obtain the following equations:
Substitute Equations (33) and (34) into Equations (30), (31), and (32). Then the maximum expected profit functions of the retailer, the cooperative, and the farmer can be written as follows:
To induce the retailer to order and the farmer to input the same amount as in the centralized system, i.e., and , using Equations (33) and (34), respectively, we can have the following proposition:
Proposition 5.
The DRS contract can coordinate the agriculture supply chain if the share fractions and satisfy
The optimal expected profit of the entire ASC can be arbitrarily distributed among the retailer, the cooperative, and the farmer by varying and .
7. Numerical Analysis
This section conducts a numerical analysis to verify the above analytic results and gain deep insights for guiding the practice. Maize production in Heilongjiang province, one of the main producing areas of China, is taken as an example. For simplicity, both the stochastic demand and yield are assumed to follow a uniform distribution. The random demand has mean and standard deviation . The mean and standard of the stochastic yield rate are and , respectively. Under the DRS contract, the retailer shares fraction of his sales revenue with the cooperative; meanwhile, the cooperative provides the farmer with portion of his sales revenue after deducting the replenishment costs. The farmer’s input cost per unit is 1.8. The cooperative buys crops to replenish the farmer’s underproduction at price and processes the crops at cost . If the farmer produces more than the ordered quantity, the excess amounts are salvaged at price . The price for the final products sold in the consumer market is . The data are directly available or indirectly estimated from the national cost and income compilation of agricultural products in 2015 [31].
First, we compare the total ASC profit and its distribution among the members in the two-level decentralized ASC, three-level decentralized ASC, and coordinated DRS contract. As is illustrated in Figure 1, the results are consistent with Proposition 3, the three-echelon decentralized ASC’s total profit is lower than that of the two-echelon decentralized ASC , and both are lower than that under the coordinated DRS contract or the centralized ASC . In the two-level decentralized ASC, however, the retailer accounts for the vast majority of the total ASC’s profits. In contrast, the retailer’s partial profit is shared by the cooperative in the three-level decentralized ASC, regardless of whether the ASC is coordinated. It designates that the cooperative shares a portion of the retailer’s revenue and the profit redistributed in the three-echelon ASC compared with that in the two-echelon ASC. If the cooperative’s nature is beneficial to the farmer, the weak position of the farmer can be improved. In this case, the participation of cooperatives implies a more conducive situation in which to achieve risk sharing and benefit allocation equivalence in the ASC. Further, compared with the three-level decentralized ASC, all the members achieve a Pareto improvement, and the farmer’s profit is the highest under the coordinated DRS contract.
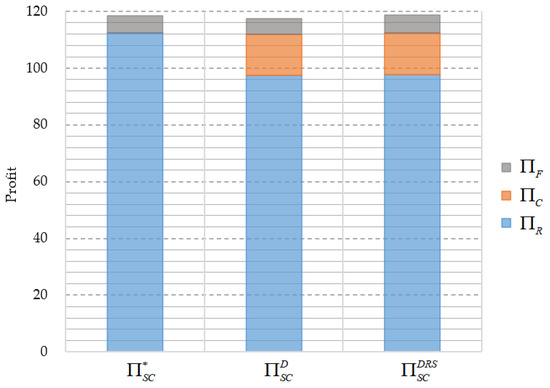
Figure 1.
Comparison of profits under different contract structures.
Second, we examine the effect of stochastic demand on the supply chain and its members’ profits. As is shown in Figure 2, the standard deviation of demand designates the demand uncertainty. As declines, the ASC and its members’ profits appear to exhibit a downward trend, whether under a non-coordinated or coordinated contract. The ASC’s earnings in the centralized system are always higher than in the decentralized system.
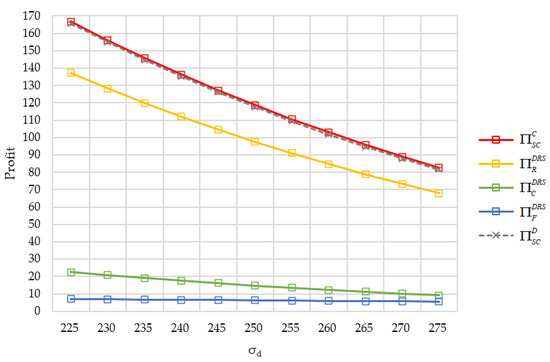
Figure 2.
The impact of demand uncertainty on the profits of the supply chain and its members.
Next, Figure 3 illustrates how the random yield influences the profit changes. Due to the increase in yield uncertainty, the profits reduce in the centralized and decentralized supply chain; however, the former is always slightly higher. Furthermore, the retailer and the farmer’s profits decrease as the yield uncertainty increases under the DRS contract. In contrast, when the yield uncertainty drops, the cooperative’s profit undergoes a rising trend. This indicates that the DRS contract transfers yield risk to the downstream member.
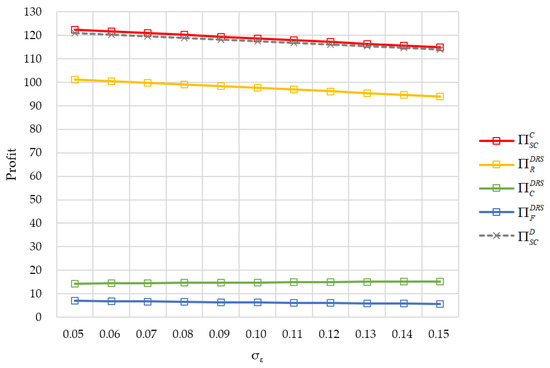
Figure 3.
The impact of yield uncertainty on the profits of the supply chain and its members.
Furthermore, the random yield will affect the members’ profit change tendencies when adjusting wholesale prices or revenue-sharing ratios. The cooperative can share risk and benefit with farmers and adjust the risk and revenue distribution ratio through or . Similarly, risk and benefit can also be reallocated between the cooperative and the retailer by adjusting and . In our numerical analysis, only the effect of wholesale prices is considered, and revenue-sharing ratios are assumed to be given exogenously.
As is illustrated in Figure 4, the cooperative and the farmer’s profits increase with . Conversely, this does not affect the retailer’s profit. Hence, the increase in the wholesale price will benefit the cooperative but reduce the farmer’s revenue. Although the rise in the revenue-sharing ratio will also increase the farmer’s profit, the increase is less than the decrease in profit caused by the rising wholesale price.
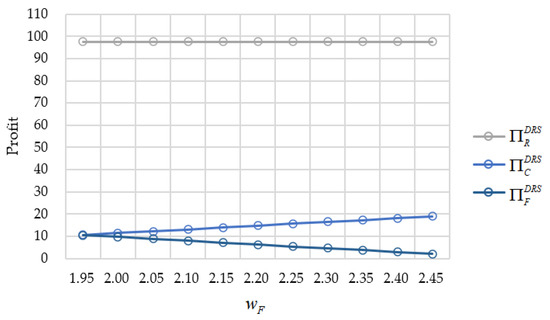
Figure 4.
The influence of on the supply chain members’ profits under the coordination.
In Figure 5, when increases, the retailer and the farmer’s profits increase; in contrast, the cooperative’s profit declines. This implies that the cooperative can adjust to impact the extent to which yield risk transfers to the downstream member, which also signifies that the downstream contractual arrangements influence the upstream members’ profits. Figure 4 and Figure 5 show that the cooperative can impact the upstream and downstream members by wholesale prices, i.e., and , respectively. Therefore, the DRS contract can reallocate the yield and demand risk among the supply chain members.
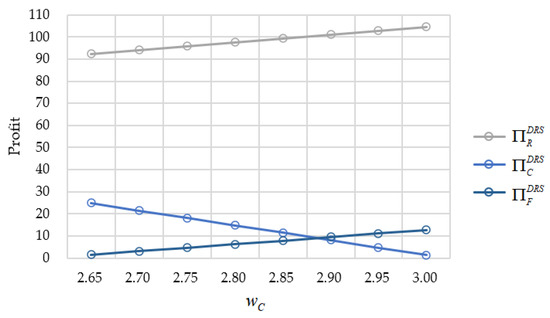
Figure 5.
The influence of on the supply chain members’ profits under the coordination.
Finally, Figure 6 illustrates that an exogenous crop purchasing price reduces all of the profits except for the cooperatives. This is because the cooperative shares a portion of its sales revenue with the farmer after deducting the replenishment cost , implying that the cooperative only takes on a partial yield risk, despite buying all of the farmer’s realized output. In addition, similar to the impact of wholesale prices and , the upstream replenishment cost also affects the downstream retailer’s profit.
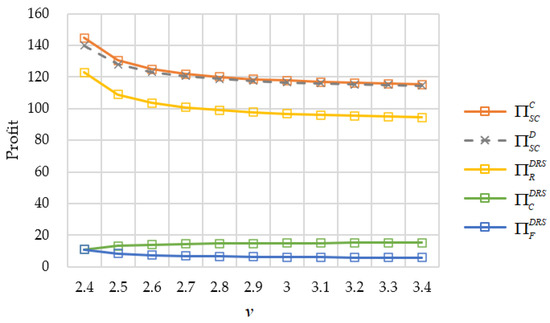
Figure 6.
The impact of replenishment costs on the profits of the supply chain and its members.
8. Conclusions
This study investigated the contract design for coordinating a three-echelon agriculture supply chain considering the participation of the cooperative, which faces yield and demand uncertainties. We examined how the cooperative’s involvement affects the contract structure, the ASC’s profit distribution, and whether it benefits the farmer’s revenue. Furthermore, the randomness of yield and demand hinders the coordination that underlies the decision to employ a two- or three-echelon ASC. This leads to low-input and under-ordering issues compared with the optimal levels in centralized systems. Previous studies have shown that extra-dyadic contracts are needed to coordinate a multi-echelon supply chain. Therefore, we focused on designing the contract structure and parameters based on classic contracts to coordinate this type of supply chain.
We first designed a centralized system as a benchmark representing the maximum value of the integrated ASC. Based on this, a decentralized model was constructed with pairwise wholesale price contracts. It was found that classic wholesale price contracts between adjacent supply chain members cannot achieve coordination under stochastic yield and demand, consistent with previous studies. In the absence of the cooperative, the retailer plays a role in processing crops and selling the finished products, similar to the semi-integration of the three-level decentralized chain. Accordingly, a two-echelon ASC was modeled to conduct a comparative analysis examining the cooperative’s influence on the contract structure and ASC’s profit distribution.
We then explored the wholesale price contract and revenue-sharing contract in a two-echelon ASC without the cooperative’s participation. In the decentralized decision under wholesale price contracts, the total profit of the two-echelon ASC was higher than that of the three-echelon ASC, and the results are consistent with those of Zhong et al. [16] and Giri and Bardhan [17]. However, the retailer obtains most of the chain’s profit in the former. Further, in the three-level ASC, the cooperative can share a portion of the retailer’s profit regardless of whether the ASC is coordinated, implying a more conducive situation to achieve risk sharing and benefit allocation equivalence. Further, we investigated the revenue-sharing mechanism in the absence of the cooperative, which was proven to be unable to coordinate the two-echelon ASC. The reason may be that random yield and demand were considered in our study, and the resulting low-input or under-ordering issues were exacerbated. As a result, the supply chain can only be coordinated when farmers’ profits are zero. The above results indicate that the cooperative’s participation significantly improves the farmer’s revenue. However, the extent to which cooperatives benefit farmers also depends on the nature of the cooperatives.
Due to the inability of the revenue-sharing contract to coordinate a two-echelon ASC and the fact that the total profit in the two-echelon decentralized ASC was higher than that in the three-echelon decentralized ASC, we designed a double revenue-sharing contract to cope with yield and demand uncertainties. The upstream revenue-sharing contract between the farmer and the cooperative was developed to correct the low-input problem. In contrast, the downstream revenue-sharing contract between the cooperative and the retailer targets a revamping of the retailer’s under-ordering behavior. Under the DRS contract, we assumed that the cooperative buys all of the realized output from the farmer and shares part of the revenue that subtracts the replenishment costs from the sales income. The results indicate that the DRS contract could coordinate the three-echelon ASC facing random yield and demand.
A numerical example was included to indicate that the cooperative’s participation impacts the profit distribution of the integrated ASC and that this is promising for the farmer’s revenue improvement. It was proven that, in a three-level ASC, regardless of whether it was coordinated, the cooperative can share a portion of the retailer’s profit compared with a two-echelon ASC. This signifies that the cooperative has an opportunity to redistribute the profits between itself and the farmer. Further, the numerical analysis demonstrated that the cooperative can influence the extent to which the yield risk is shared upstream and transferred downstream by adjusting the wholesale prices, i.e., and . This suggests that various combinations of contractual arrangements of risk and benefit equivalence exist under the coordinated ASC. With regard to the upstream relationship, the cooperative can share risk and benefit with farmers and alter the risk and revenue distribution ratio through wholesale prices. In line with the results of empirical analysis, the farmer benefits more if the cooperative is a not-for-profit organization; conversely, as the cooperative receives more profit, especially when the cooperative is an investor-owned organization, the interests of farmers are remarkably compressed. Contract forms chosen between the cooperative and the farmer mainly depend on the cooperative’s governance structure [3,5], which was not within the scope of our study. Concerning the downstream relationship, the risk and revenue can be redistributed between the cooperative and the retailer by adjusting the wholesale price. In addition, the results indicate that changes in the downstream wholesale price affect upstream members’ profits.
Further, we explored the influence of the exogenous replenishment costs, i.e., , when the farmer suffers a low-production situation. We found that the crop replenishment cost was inversely related to the profits of the entire chain and its members, except for the cooperative. As with wholesale prices, the upstream replenishment cost also influences the downstream retailer’s profit. Therefore, upstream and downstream contractual mechanisms interact, which verifies the significance of placing the upstream and downstream contractual arrangements in the same ASC system.
The above results suggest that our research can be extended into the future to consider the impact of uncertain purchasing price issues between the cooperative and the farmer. In future studies, we can explore other combined contracts to coordinate a multi-echelon supply chain facing uncertain yield and demand. Furthermore, investigating the risk preference of the supply chain members may provide more managerial insight for practical application. In summary, contracting with risk- and revenue-sharing equivalence is of great significance to the stable and sustainable development of cooperative membership and the ASC systems.
Author Contributions
Conceptualization, Y.S. and F.W.; methodology, Y.S.; data curation, Y.S.; writing—original draft preparation, Y.S.; writing—review and editing, Y.S. and F.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Heilongjiang Philosophy and Social Science Research Planning Project, grant number 21JYB147.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bijman, J.; Iliopoulos, C. Farmers’ cooperatives in the EU: Policies, strategies and organization. Ann. Public Coop. Econ. 2014, 85, 497–508. [Google Scholar] [CrossRef]
- Mangnus, E.; Schoonhoven-Speijer, M. Navigating dynamic contexts: African cooperatives as institutional bricoleurs. Int. J. Agric. Sustain. 2020, 18, 99–112. [Google Scholar] [CrossRef]
- Candemir, A.; Duvaleix, S.; Latruffe, L. Agricultural Cooperatives and Farm Sustainability—A Literature Review. J. Econ. Surv. 2021, 35, 1118–1144. [Google Scholar] [CrossRef]
- Mojo, D.; Fischer, C.; Degefa, T. The determinants and economic impacts of membership in coffee farmer cooperatives: Recent evidence from rural Ethiopia. J. Rural Stud. 2017, 50, 84–94. [Google Scholar] [CrossRef]
- Zhong, Z.; Jia, F.; Long, W.; Chen, K.Z. Risk sharing, benefit distribution and cooperation longevity: Sustainable development of dairy farmer cooperatives in China. Int. J. Agric. Sustain. 2022, 20, 982–997. [Google Scholar] [CrossRef]
- Wan, J.; Zeng, L. Cooperative types, governance mechanisms and operating performance. Chin. Rural Econ. 2020, 422, 33–48, (In Chinese with English Abstract). [Google Scholar]
- Yang, J. Profit Distribution of Farmer-Supermarket Direct Purchase Model with Unequal Power. Issues Agric. Econ. 2019, 7, 93–102, (In Chinese with English Abstract). [Google Scholar]
- Shen, M.; Shen, J. Evaluating the cooperative and family farm programs in China: A rural governance perspective. Land Use Policy 2018, 79, 240–250. [Google Scholar] [CrossRef]
- Lin, Q.; Ye, F. Coordiantion for “company + farmer” contract-farming supply chain under Nash negotiation model. Syst. Eng. -Theory Pract. 2014, 34, 1769–1778, (In Chinese with English Abstract). [Google Scholar]
- Hovelaque, V.; Duvaleix-Tréguer, S.; Cordier, J. Effects of constrained supply and price contracts on agricultural cooperatives. Eur. J. Oper. Res. 2009, 199, 769–780. [Google Scholar] [CrossRef]
- Jia, X.; Huang, J. Contractual arrangements between farmer cooperatives and buyers in China. Food Policy 2011, 36, 656–666. [Google Scholar] [CrossRef]
- Ge, J.; Flores-Lagunes, A.; Kilmer, R.L. An analysis of bargaining power for milk cooperatives and milk processors in Florida. Appl. Econ. 2015, 47, 5159–5168. [Google Scholar] [CrossRef]
- Federgruen, A.; Lall, U.; Şimşek, A.S. Supply Chain Analysis of Contract Farming. Manuf. Serv. Oper. Manag. 2019, 21, 361–378. [Google Scholar] [CrossRef]
- Ton, G.; Vellema, W.; Desiere, S.; Weituschat, S.; D’Haese, M. Contract farming for improving smallholder incomes: What can we learn from effectiveness studies? World Dev. 2018, 104, 46–64. [Google Scholar] [CrossRef]
- Tang, C.S.; Sodhi, M.S.; Formentini, M. An analysis of partially-guaranteed-price contracts between farmers and agri-food companies. Eur. J. Oper. Res. 2016, 254, 1063–1073. [Google Scholar] [CrossRef]
- Zhong, Y.; Guo, F.; Wang, Z.; Tang, H. Coordination Analysis of Revenue-sharing in E-Commerce Logistics Service Supply Chain With Cooperative Distribution. SAGE Open 2019, 9, 1–15. [Google Scholar] [CrossRef]
- Giri, B.C.; Bardhan, S. Sub-supply chain coordination in a three-layer chain under demand uncertainty and random yield in production. Int. J. Prod. Econ. 2017, 191, 66–73. [Google Scholar] [CrossRef]
- Luo, J.; Chen, X. Coordination of random yield supply chains with improved revenue-sharing contracts. Eur. J. Ind. Eng. 2016, 10, 81–102. [Google Scholar] [CrossRef]
- He, Y.; Zhao, X. Contracts and coordination: Supply chains with uncertain demand and supply. Nav. Res. Logist. 2016, 63, 305–319. [Google Scholar] [CrossRef]
- Xie, L.; Ma, J.; Goh, M. Supply chain coordination in the presence of uncertain yield and demand. Int. J. Prod. Res. 2020, 59, 4342–4358. [Google Scholar] [CrossRef]
- Giannoccaro, I.; Pontrandolfo, P. Supply chain coordination by revenue-sharing contracts. Int. J. Prod. Econ. 2004, 89, 131–139. [Google Scholar] [CrossRef]
- Van der Rhee, B.; Van der Veen, J.A.A.; Venugopal, V.; Nalla, V.R. A new revenue-sharing mechanism for coordinating multi-echelon supply chains. Oper. Res. Lett. 2010, 38, 296–301. [Google Scholar] [CrossRef]
- Ding, D.; Chen, J. Coordinating a three level supply chain with flexible return policies. Omega 2008, 36, 865–876. [Google Scholar] [CrossRef]
- Formentini, M.; Romano, P. Towards supply chain collaboration in B2B pricing. Int. J. Oper. Prod. Manag. 2016, 36, 734–756. [Google Scholar] [CrossRef]
- Yang, H.; Liu, R. Three-stage Supply Chain Coordination of Connecting Agriculture with Supermarkets Considering Loss and Effort Level. J. Syst. Sci. 2018, 26, 47–52, (In Chinese with English Abstract). [Google Scholar]
- Ma, X.; Wang, S.; Jin, H.; Bai, Q. Coordination and optimization of three-echelon agricultural product supply chain considering freshness-keeping effort and quantity/quality elasticity. Chin. J. Manag. Sci. 2018, 26, 175–185, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Anderson, E.; Monjardino, M. Contract design in agriculture supply chains with random yield. Eur. J. Oper. Res. 2019, 277, 1072–1082. [Google Scholar] [CrossRef]
- He, Y.; Zhao, X. Coordination in multi-echelon supply chain under supply and demand uncertainty. Int. J. Prod. Econ. 2012, 139, 106–115. [Google Scholar] [CrossRef]
- Jian, M.; Wang, Y. Risk Sharing Combined Contract Design for Three-level Supply Chain with Output Uncertainty. Oper. Res. Manag. Sci. 2017, 26, 74–81, (In Chinese with English Abctract). [Google Scholar] [CrossRef]
- Adhikari, A.; Bisi, A.; Avittathur, B. Coordination mechanism, risk sharing, and risk aversion in a five-level textile supply chain under demand and supply uncertainty. Eur. J. Oper. Res. 2020, 282, 93–107. [Google Scholar] [CrossRef]
- DPNDRC. National Cost and Income Compilation of Agricultural Products; Department of Price in National Development and Reform Commission, Statistics Press: Beijing, China, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).