1. Introduction
Estimation of distribution algorithms (EDAs) is a family of evolutionary optimization algorithms that have received increasing attention in recent years. Also known as probabilistic model-building genetic algorithms (PMBGAs) [
1,
2,
3], EDAs replace the crossover and mutation operators of genetic algorithms (GAs) [
4] with a building and sampling of learned probabilistic model. EDAs based on the idea of modeling the problem’s distribution in order to guide the search process to explore the search space. To construct the next generation EDAs samples, the built model. The algorithm terminates when a given criterion is reached, such as a limited number of generations, a stable population, or a lack of progress in recent generations. This algorithm has been successfully applied to a wide range of optimization problems, including continuous and combinatorial problems [
2,
5,
6,
7].
Among the combinatorial problems, permutation-based problems have been the focus of significant research efforts [
8]. Permutation-based problems are problems in which the solutions are encoded with permutations of a set of elements. The permutation-based problems pose significant challenges for EDAs, due to the large solution space and the mutual exclusivity constraints.
In the literature, many EDAs have been proposed to solve permutation-based problems, and most of these solutions are extensions of conventional EDAs that were developed to address problems relating to discrete or continuous domains [
8]. However, several EDAs have been proposed specifically for permutation problems, including the Node Histogram-based Sampling Algorithm (NHBSA) [
9], the Edge Histogram-based Sampling Algorithm (EHBSA) [
3], the Random Key EDA (RK-EDA) [
7], and the Generalized Mallows Model EDA (GM-EDA) [
10]. These algorithms have shown promising results on various permutation-based problems, such as the Traveling Salesman Problem (TSP) [
11], the Quadratic Assignment Problem (QAP) [
12], and the Permutation Flow-shop Scheduling Problem (PFSP) [
13]. However, there is still a need for further improvement in the efficiency and quality of solutions found by EDAs for permutation problems.
Based on the general framework, many EDAs are designed to deal with permutation problems. Ceberio et al. in [
8] grouped these algorithms into three principal classes. The first class includes a set of EDAs adapted from the algorithms developed first to solve the problems in continuous domains. Bosman et al. suggests a continuous iterated density estimation evolutionary algorithm (IDEAs) [
14] to deal with permutation problems. Univariate Marginal Distribution Algorithm UMDAc [
15], Mutual Information Maximization for Input Clustering MIMICc [
15] and Estimation of Gaussian Networks Algorithm EGNAc [
15], adapted from continuous domain by Lozano and Mendiburu to tackle Jop Shop Scheduling Problem. All approaches in this category are based on the Random Keys algorithm [
14].
Although the random key strategy can generate a possible permutation of any vector with a real value by ranking method, the major disadvantage of this technique is the redundancy. The ranking of different vectors of real values may provide the same permutation. The second class of EDAs suggested to solve permutation-based problems is those algorithms adopted from the originally designed to solve problems where the solution is represented as a vector of discrete values. To guarantee obtaining a permutation, the sampling phase was modified, usually, the Probabilistic Logic Sampling algorithm is used. The adapted sampling method is based on the idea of setting 0 to the probability of the previous sampled values and normalizing the probabilities of the remainder of the values to a total of 1.
Furthermore, in recent years many algorithms have been proposed especially to deal with permutation-based problems. In [
3] Tsutsui et al propose a new algorithm, Edge Histogram-Based Sampling Algorithm (EHBSA). In EHBSA, an edge is a link between two nodes, the model is built by learning the dependencies between edges and represented with an edge histogram matrix. To generate a new individual, the authors propose two methods of sampling, without and with a template, denoted EHBSA/WO and EHBSA/WT, respectively. The first sampling method samples the edge histogram matrix in ordered positions starting with position 0 and a randomly selected node, and then a roulette wheel is constructed for each row to sample a new node in a way similar to Probabilistic Logic Sampling. The sampling with template uses a parent individual chosen from the previous generation at random as a template, then this template is divided into
segments, choose at random one segment to sample it and the other
segments are copied without changes into the offspring. Another histogram-based algorithm introduced in [
9] by the same authors is called the Node Histogram-Based Sampling Algorithm (NHBSA). The NHBSA uses a node histogram matrix which models the distribution of nodes over string absolute positions in the selected individuals. The same two sampling techniques used in EHBSA can be applied in NHBSA.
Another family of EDAs is designed to solve permutation problems in particular. This kind of algorithm is relative to probability models for ranking such as [
16,
17] in which distance-based exponential models like Mallows Model and Generalized Mallows Model are introduced in EDAs. In [
18], the Plackett-Luce probability model is also proposed to learn the distribution over permutation space in the EDA framework. The Generalized Mallows-EDA [
17], and PlackettLuce-EDA [
18] obtain good results for PFSP and LOP, respectively.
A random key EDA (RK-EDA) proposed in [
7] builds a univariate distribution model like UMDAc with predefined variance. To overcome the redundancy issue of classical random key-based EDAs, the generated RK vectors are rescaled and normalized between
. In RK-EDA, the authors suggest using a cooling rate parameter to control exploration and exploitation. The RK-EDA tested in different permutation problems and they have good results in the PFSP with respect to the makespan in [
7], then using Total Flow Time in [
19].
Many estimation of distribution algorithms (EDAs) designed for permutation problems focus on sampling nodes rather than positions. However, this approach can be problematic because the relationship between elements and their positions can significantly affect the algorithm’s performance. Furthermore, there is no established method for assigning a node to a specific position, which is often done sequentially or randomly. To our knowledge, no existing EDA for permutation problems has not addressed this issue.
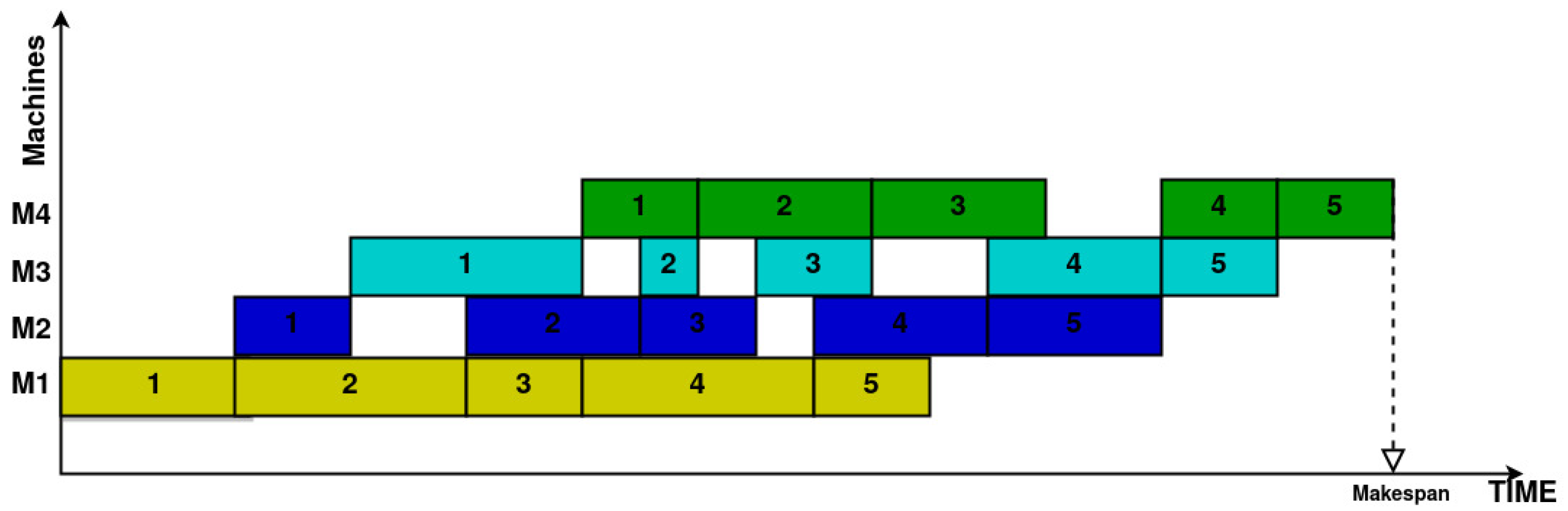
The PFSP is one of the permutation-based problems that has gained more attention in the community due to its wide range of applications, including manufacturing, production planning, textiles, and logistics [
20,
21]. The PFSP involves scheduling a set of jobs on a set of machines to minimize a specific performance measure. The most used objective function in the studies is makespan [
22,
23], which refers to the total time necessary to perform all of the jobs on all of the machines. The PFSP is a well-studied problem that has been widely used as a benchmark for various optimization algorithms [
19,
22].
To minimize the makespan of the PFSP, various approaches have been proposed. These include exact algorithms like the branch and bound algorithm [
24,
25]. However, as the number of jobs and machines increases, solving PFSP optimally using exact methods becomes computationally challenging due to its NP-hard nature. As a result, heuristic and metaheuristic methods are widely used to tackle this challenge. Several heuristic algorithms have been proposed to obtain approximate solutions for PFSP [
26,
27,
28,
29]. Additionally, metaheuristic optimization techniques have revolutionized combinatorial optimization, leading to a diverse range of strategies for solving PFSP, including genetic algorithms [
30,
31], simulated annealing [
32], estimation of distribution algorithms [
7,
10,
33], and particle swarm optimization [
34,
35]. In [
36], a parallel metaheuristic approach is designed to tackle PFSP.
In this paper, we propose an EDA for solving permutation-based problems and specifically test it on the PFSP. The proposed algorithm (PGS-EDA) uses a novel sampling technique. The novel sampling method is designed in this work to go deeper into the exploitation of the information captured by the model. Furthermore, our sampling operation is guided by a sequence vector (SV) constructed during the modeling phase. Each element is assigned to a specific position based on the presented order in the sequence vector extracted from the model. This guided sampling approach enables the algorithm to exploit the captured information and effectively explore promising areas in the search space. Our proposal uses a dynamic updating mechanism to adapt the distribution model to the search progress, enabling it to balance exploration and exploitation effectively. We show that the proposed algorithm is able to find high-quality solutions efficiently and outperforms existing state-of-the-art algorithms, through a comprehensive experimental study on a set of benchmark instances of the PFSP.
In the remainder of this paper, an introduction to EDAs is given and PFSP is introduced in detail in the next section. In
Section 3, we present the proposed algorithm in detail, including its distribution model, updating mechanism, and selection mechanism.
Section 4 describes the experimental setup, including the benchmark instances and the performance measures used. Then, we present the experimental results and a detailed analysis of the performance of the proposed algorithm. Finally, we draw conclusions and suggest directions for future research in
Section 5.
3. The Proposed PGS-EDA Algorithm
In this section, we describe our proposed algorithm in detail. We start with the individual representation and initialization. We then present the new method of modeling and sampling. Finally, we discuss how the population is updated across generations.
The proposed algorithm is based on the standard EDA outline present in
Section 2.1. The general steps of PGS-EDA are shown in Algorithm 3.
| Algorithm 3: A pseudo code of PGS-EDA |
![Systems 11 00389 i003 Systems 11 00389 i003]() |
3.1. Individuals Representation and Initialization
Random initialization strategy is one commonly employed approach for generating the initial population in evolutionary algorithms. To achieve an initial population with a desired level of diversity, the initial population is randomly and uniformly generated [
43]. In this work, the individuals are represented by permutations of jobs. Each permutation corresponds to a particular arrangement of jobs. During the scheduling process, the jobs are allocated to the machines in the order specified by the permutation.
3.2. Modeling
At each generation, a set of individuals are selected according to their fitness. Each individual in the population is represented by a permutation
as described in Equation (
4).
where
n is the problem size. The proposed algorithm learns a probabilistic model that indicates a particular element’s count or frequency at that position across the population. In other words, it describes how often the element
i appears in position
j.
The model is represented as a matrix M of
elements, as follows:
where
m in the size of selected individuals, and
is a function used to count the appearance of the elements defined as:
and
is a user-defined constant used to contribute to the diversification in the sampling phase, and used for numerical stability and avoiding mathematical complications when dealing with zero-valued.
Therefore, we can formulate our model (M) as a matrix of size
, as follows:
Adding epsilon
to all elements of
M:
Once the model is constructed, the extraction of the sequence vector (SV) from matrix M plays a crucial role in guiding the subsequent sampling phase. SV, a vector of size n, represents a permutation of elements. The key characteristic of SV is that its elements are arranged based on the frequency of their occurrence in the same position across all individuals or samples. The element that appears most frequently in a specific position across the selected individuals takes precedence and occupies the corresponding position in SV. This arrangement continues for each position, ensuring that the most common elements in each position are placed at the beginning of the SV.
For example, let
be the population at the generation
kThe matrix
, which represents the probabilistic model, is constructed for each generation
k according to the process described above. Specifically,
is constructed by considering the distribution of elements across string positions in the population
at that particular generation. The value of
is added to all elements of
M.
From the matrix M, we can extract the SV. In this example, the SV will be because the element 2 appears three times in the same position 2. Since the element 0 has less frequency, it occurs just one time in each position.
3.3. Sampling
In contrast to other algorithms like NHBSA, EHBSA, or UMDA, where the sampling of a new individual of size
n revolves around selecting the element that will occupy the
position, starting from the first position and progressing to the last, our proposed algorithm takes a different approach by shifting the focus to the position itself rather than the element. The SV represents the order in which elements should be placed in the offspring and serves as a crucial component in our algorithm. During sampling, we extract elements from the SV and determine the appropriate position for each element. By assigning positions based on the SV, we aim to optimize the arrangement of elements within the individual, see Algorithm 4.
| Algorithm 4: The sampling algorithm |
![Systems 11 00389 i004 Systems 11 00389 i004]() |
Input: The algorithm takes two inputs, Matrix model M: This represents a matrix containing some information or values. Sequence vector : This is a vector containing a sequence of elements.
Initializing the offspring: The algorithm initializes the offspring variable , which represents the new offspring. Initially, it is empty or contains default values.
Iterating over the sequence vector: The algorithm iterates over each element e in the sequence vector .
Computing the probability vector: For each element e, the algorithm computes the probability vector by normalizing the corresponding row of the matrix model M. This step ensures that the values in sum up to 1 and represent a valid probability distribution.
Sampling a position: The algorithm samples a position p from the probability vector . This step uses a roulette wheel to select an index from based on the probabilities associated with each index.
Assigning the element to the offspring: The algorithm assigns the value of e to the position p in the offspring . This step determines where the element e will be placed in the offspring based on the sampled position.
Updating the matrix model: The algorithm sets the value at position p in the matrix model M to 0. This step ensures that the same position will not be selected again in future iterations, as the corresponding probability will be 0.
Repeat the process: The algorithm continues iterating over the remaining elements in the sequence vector and performs steps 4 to 7 for each element.
Output: Once the iteration is complete, the algorithm returns the resulting offspring , which contains the elements from the sequence vector arranged based on the sampled positions.
In summary, the algorithm probabilistically assigns elements from the sequence vector to positions in the offspring based on the probabilities computed from the matrix model M. By sampling positions and updating the matrix model, the algorithm ensures that each element is placed in a unique position in the offspring, taking into account the probability distribution derived from M.
3.4. Replacement Strategy
The replacement strategy in EDAs determines how the newly generated offspring are incorporated into the existing population. The proposed replacement strategy suggests that an offspring will be added to the population if its fitness exceeds that of the worst individual in the current generation. This selection process ensures that only individuals with superior fitness levels are included in the population, aiming to improve the overall quality of the population over time. Additionally, the strategy ensures that no duplicate individuals are added, maintaining diversity within the population. This approach strikes a balance between exploration and exploitation, gradually replacing weaker individuals with stronger ones to drive the evolution of the population toward better solutions.
4. Experiments and Results
4.1. Experiments
In order to prove the performance of our proposed algorithm, we carried out a set of experiments using a set of 45 instances of the PFSP from Taillard’s benchmark of instances [
44]. The chosen instances were divided into nine sets of different size (number of jobs × number of machines) as follows:
. We selected the five (05) first instances for each size.
In this work, we compared our proposed method with a set of state-of-the-art EDAs, including Random-Key estimation of Distribution Algorithm (RK-EDA) [
7], Univariate Marginal Distribution (UMDA) [
15], Generalized Mallows EDAs (GM-EDA) [
45], Node Histogram-Based Sampling Algorithm (NHBSA) [
9], and the Edge Histogram-Based Sampling Algorithm (EHBSA) [
3]. All the algorithms considered for comparison in our study are pure EDAs without hybridization. We specifically excluded hybrid algorithms such as HGM-EDA [
10] from our comparison. Our proposed algorithm (PGS-EDA), UMDA, NHBSA, and EHBSA are implemented in Python. The GM-EDA and RK-EDA codes are available on the GitHub of the authors. The parameters used during the experiments for all algorithms are presented in
Table 1. The stopping criterion was set to
fitness evaluation for all algorithms because it is used in many studies [
7,
8,
16]. In addition, we set experimentally
, and
interchange operations between two elements in SV before the sampling phase.
During the comparison of different algorithms, we ensured that the parameters recommended by the respective authors were used. It is worth noting that both methods employed sampling without a template for NHBSA and EHBSA. The parameters of RK-EDA used were those suggested by the authors in [
7]. Many variants of EDAs use probability distance-based models for ranking, depending on the distance function that is used. In this comparison, we picked GM-EDAs under Kendall
distance [
45,
46].
Each algorithm taken into consideration for the experiment was run 10 times for each instance. The average relative percentage deviation (ARPD) was used to measure the performance of the proposed algorithm. , where is the value returned by the algorithm under experiment in the repetition i, and is the best-known value for the used instance.
4.2. Results and Discussion
To better understand the behavior of the algorithms, we divided the Taillard benchmark instances into three sets: the small instances with 20 jobs, the medium instances with 50 jobs, and the large instances with 100 jobs, all on 5, 10, and 20 machines.
Bayesian Performance Analysis (BPA) [
47] was used to conduct a statistical analysis of the results obtained in the experiments. BPA is a statistical technique that can be used to study the uncertainty of the results of an experiment. The first step involves transforming the results from ARDP (Average Relative Deviation Percentage) to rankings for each test instance. Then, samples are drawn from the posterior probability distribution of the weights in the Plackett–Luce model, which is a probability model specifically designed for rankings. These sampled weights are used to calculate the probability of each algorithm winning. This process allows us to assess the relative performance of the algorithms based on their rankings and provides a probabilistic measure of their chances of success.
The ARPD results for each algorithm on the selected instances of 20 jobs are presented in
Table 2. The best results values are indicated in bold. Our proposed algorithm achieves the best results in terms of the minimum ARPD value in 11 among 15 of the small instances considered. The second most successful algorithm is GM-EDA, outperforming the other methods in 13.33% of the instances, then the RK-EDA and NHBSA both in 6.33%. The UMDA also has good results compared to the EHBSA. The average value of all 15 instances was calculated for each algorithm. In terms of the average ARPD, PGS-EDA demonstrates its effectiveness by achieving the lowest average value compared to the other algorithms. This indicates that PGS-EDA consistently performs well across different instances and showcases its ability to generate high-quality solutions.
Figure 2 illustrates the posterior distribution of the probability of each algorithm being the top one. The empirical probabilities are depicted as black dots. It can be observed that the probability of PGS-EDA being the winning algorithm is the highest, often equal to
. According to the results of the Bayesian analysis, the NHBSA is the second-best algorithm. GM-EDA and RK-EDA follow with probabilities around
.
The ARPD results for each algorithm in the selected instances of 50 jobs are presented in
Table 3. The best ARPD values are indicated in bold. Our proposed algorithm achieves the best results in terms of the minimum ARPD value in nine of the instances considered. The second most successful algorithm is RK-EDA, outperforming the other methods in four of the instances. The UMDA and NHBSA also have good results compared to the GM-EDA and EHBSA. The makespan of the PFSP is greatly affected by the precise positioning of nodes (jobs). The success of algorithms such as PGS-EDA, RK-EDA, UMDA, and NHBSA can be attributed to their utilization of node-position sampling techniques.
Notably, our algorithm consistently achieves competitive performance across multiple instances. Our algorithm outperforms other algorithms in 8 out of 15 instances, demonstrating its effectiveness in minimizing the makespan. It is particularly noteworthy that our algorithm achieves the optimal solution in all 10 runs for the first instance of 50 × 5, with ARPD = 0.000, showcasing its superiority in scenarios with a smaller number of machines. On the other hand, the RK-EDA algorithm exhibits strong performance outperforming our algorithm in 4 other instances.
On average, PGS-EDA has the lowest mean ARPD value of 1.456, indicating its overall superior performance across the instances of 50 jobs. GM-EDA, NHBSA, RK-EDA, and UMDA follow with mean ARPD values of 1.754, 2.213, 1.539, and 3.078, respectively. EHBSA has the highest mean ARPD value of 7.607, suggesting that it may struggle to find solutions close to optimality on average.
Figure 3 shows the posterior distribution of the probability of being the top algorithm for each algorithm. The black dots represent the empirical probability for each algorithm to be the best. We can observe that the probability of PGS-EDA being the winning algorithm is the highest, with a probability that can exceed 70%. It has an average probability of around 0.4, followed by RK-EDA and GM-EDA, with probabilities of around 0.3 and 0.2, respectively.
Furthermore, the results of benchmarks on Taillard’s instances of 100 jobs are depicted in
Table 4. As can be observed, for instances of 5 machines the ARPD values of PSG-EDA, RK-EDA, GM-EDA, and NHBSA are closely the same. The RK-EDA reach a minimum ARPD value in three instances out of five, while the PGS-EDA and NHBSA had one minimum value for both of them. The results indicate that there is no statistically significant difference between the top four algorithms in the small number of machines. This means that the observed difference in performance between those algorithms could reasonably occur by random chance, and there is no strong evidence to support the claim that one algorithm performs better than the other in this specific scenario.
In the subset of instances with 10 machines, we observe a slight decrease in the performance of PGS-EDA and NHBSA compared to RK-EDA and GM-EDA. However, it is important to note that PGS-EDA and NHBSA remain competitive in terms of ARPD. Specifically, RK-EDA outperforms the other algorithms in three out of the five instances, demonstrating its effectiveness. Additionally, GM-EDA achieves the minimum ARPD in the remaining two instances, showcasing its strong performance as well. Overall, while there is a variation in performance among the algorithms in this particular subset, PGS-EDA and NHBSA still demonstrate their competitiveness in terms of ARPD. However, when the number of machines increases, the RK-EDA algorithm outperforms all other algorithms and achieves the minimum ARPD among all five instances of . GM-EDA, as the second successful algorithm, outperforms PGS-EDA and NHBSA. Regarding the average value of ARPD, PGS-EDA ranked at position three with 1.471 after RK-EAD and GM-EDA with 0.624 and 0.954, respectively. These findings highlight the importance of considering the specific problem characteristics and the potential impact of varying parameters, such as the number of machines, when comparing and selecting appropriate algorithms for solving permutation-based problems.
The results of the BPA for instances of size 100, which illustrate the probability of each algorithm being the top, are shown in
Figure 4. Based on these results, we can conclude that the RK-EDA has the highest probability of being the best algorithm, with an empirical probability of approximately 0.8. Following closely behind are GM-EDA and PSG-EDA, both with a probability of 0.4.
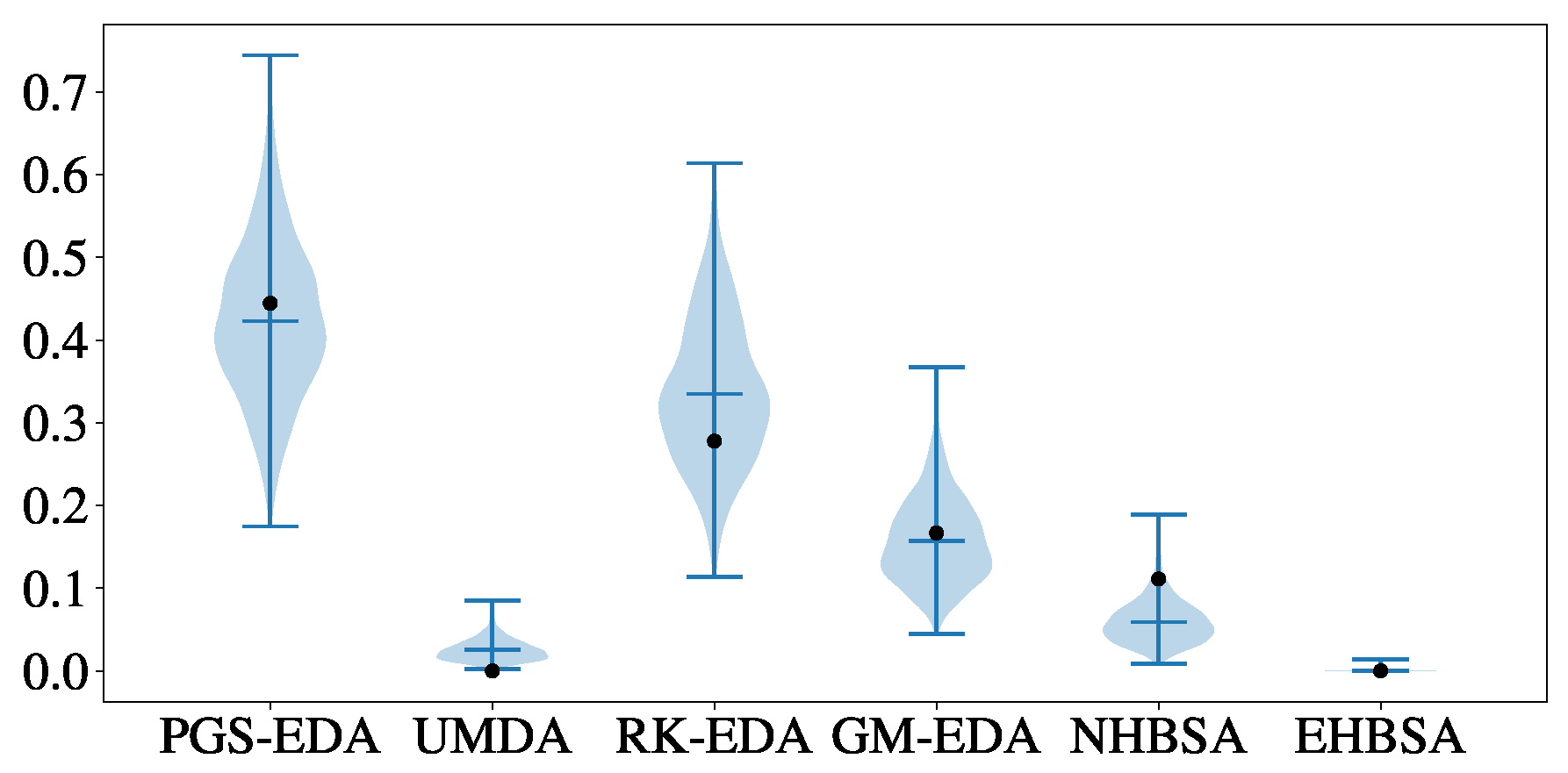
To conclude the statistical analysis, we conducted a Bayesian performance analysis to compare the performance of all the considered algorithms on instances with 20, 50, and 100 jobs. The results, shown in
Figure 5, indicate that PGS-EDA has the highest probability of winning, with a probability exceeding
. The second-best algorithm is RK-EDA, followed by GM-EDA and NHBSA, respectively. The remaining algorithms have lower probabilities, below
.
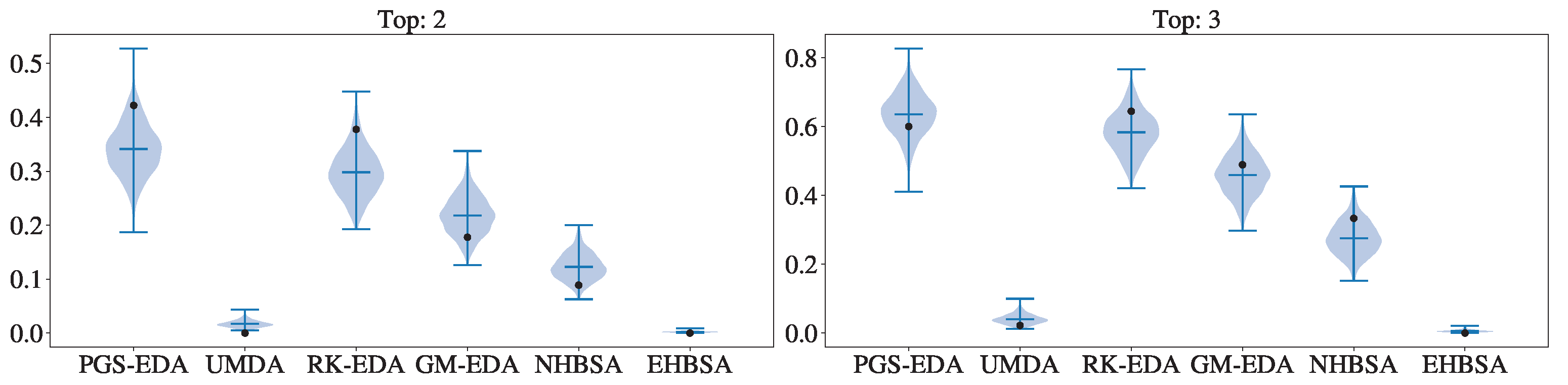
Figure 6 provides insights into the probabilities of each method being among the top two and top three algorithms, as determined by Bayesian performance analysis. The analysis encompassed all instances of size 20, 50, and 100 jobs. The results further validate our previous findings, highlighting the strong performance of PGS-EDA and RK-EDA, which are the most probable algorithms to rank among the top two. This suggests that these algorithms are likely to be the most effective in solving this type of problem. Additionally, when considering the top three algorithms, PGS-EDA maintains its high confidence level, while RK-EDA and GM-EDA closely follow. Notably, NHBSA also exhibits a probability of approximately 0.4 of being among the top three algorithms.
As a summarization of the statistical results, the Bayesian performance analysis conducted on instances of 20, 50, and 100 jobs reveals significant insights into the relative performance of the algorithms under consideration. PGS-EDA consistently demonstrates the highest probability of being the best algorithm, followed closely by RK-EDA, confirming the authors’ suggestion that RK-EDA excels in large-scale problems [
19]. GM-EDA and NHBSA also exhibit competitive probabilities, particularly in the top three rankings. However, the remaining algorithms have lower probabilities of being among the top performers. These findings underscore the importance of selecting algorithms based on problem characteristics and varying parameters, highlighting the effectiveness of PGS-EDA and RK-EDA in solving permutation-based problems.
While our algorithm demonstrates promising results on the PFSP, there are limitations to our study that should be acknowledged. The performance of our algorithm may suffer as the problem size increases, and further investigations on a wider range of problem instances would enhance the generalizability of our findings. Additionally, the performance of PGS-EDA may vary when applied to different problem domains or problem sizes.