Addressing Environmental Protection Supplier Selection Issues in a Fuzzy Information Environment Using a Novel Soft Fuzzy AHP–TOPSIS Method

Abstract

With the current heightened promotion of environmental awareness, issues related to environmental protection have become a critical component of economic development. The emergence of new environment-friendly materials and simple packaging, and other environmental awareness demands in recent years, have prompted manufacturers to pay more attention to planning greener production and supply processes than before. Many scholars have been urged to investigate the issues related to environmental protection and the sustainable economy of green suppliers. However, many factors needed to be considered, such as the price, cost, benefit, reputation, and quality involved in the process of green supplier selection. These factors require quantitative and qualitative analysis information, making the issue of environmental protection a multi-criteria decision making (MDCM) problem. Traditional research methods are unable to effectively and objectively handle the MCDM problem of green supplier selection due to the problem’s complexity and the method’s inclination towards biased conclusions. To resolve the complicated problem of green supplier selection, this study combined the fuzzy analytic hierarchy process (AHP), the technique for order preference by similarity to ideal solution (TOPSIS), and the 2-tuple fuzzy linguistic model (2-tuple FLM) and corrected the ranking of the possible green suppliers. The computation results were also compared with the typical TOPSIS and AHP–TOPSIS methods. Through the numerical verification of the actual case for the green supplier, the test results suggested that the proposed method could perform an objective evaluation of expert-provided information while also retaining all their valuable insights.

1. Introduction

With modern technological advancements, businesses have started utilizing technological equipment to shorten their production times (from product design to market launch) and enhance their competitive advantage. However, mass production has resulted in environmental destruction, such as in wastewater, gas emissions, and energy consumption. The environmental changes caused by global warming have posed a serious threat to ecological and economic development. As a result, many countries are gradually shifting their attention to environmental protection issues by developing innovative product materials and striving to achieve a balance between environmental protection and business economics. In this regard, the key to environment-friendly processes lies in the manufacturing industry’s upstream supply of raw materials, with the problem of raw material supplier selection being an essential issue in supply chain management. The problem of raw materials supplier selection involves factors such as cost, benefit, reputation, and efficiency, among others. Different suppliers have different backgrounds and advantages, and procurement personnel’s expertise and experiences influence decision-making. Therefore, finding the most suitable supplier is a complicated, multi-criteria decision-making (MCDM) issue. To date, many scholars have applied different algorithms to address the complicated MCDM problem related to supplier selection (such as [1,2,3,4]).

To solve the complicated MCDM problem, academic scholars have devised several research methods in the past few decades. In 1968, Roy suggested the elimination et choice translating reality (ELECTRE) [5], while Charnes et al. [6] introduced the data envelopment analysis (DEA) approach. On the other hand, Saaty [7] proposed the analytical hierarchy process (AHP) method, while Hwang and Yoon [8] initiated the technique for order preference by similarity to an ideal solution (TOPSIS) method, and Yazdani et al. [9] proposed the combined compromise solution (CoCoSo) method. In 1973, the Battelle Memorial Institute of the Geneva Research Center proposed the decision-making trial and evaluation laboratory (DEMATEL) method [10], while Brans and Vincke [11] introduced the preference ranking organization method for enrichment evaluation (PROMETHEE) method and Opricovic [12] proposed the VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method. These research methods can be used to solve management or decision-making problems in various fields, such as renewable energy sources [13], military simulation training systems [14], occupational safety and health [15], cloud service [16], battery electric vehicles [17], healthcare waste treatment technology [18], contractor selection [19], and vaccine selection [20]. However, each method has its limitations, specificities, and perspectives; hence, no method is perfect or suitable for all problems. To obtain a suitable method and solve problems efficiently, researchers must clearly understand the nature of the problem.

The AHP method is an MCDM approach that was developed by Saaty in 1971 [7]. It is mainly used in MCDM situations involving multiple evaluation criteria and dealing with quantitative and qualitative information. The AHP method systematically and structurally decomposes complex decision-making problems into multiple levels, establishes relationships between the levels, and addresses the issue of available alternatives using multiple criteria. The AHP method focuses primarily on the importance of criteria weights to provide decision-makers with sufficient decision-making information through a survey approach, reducing the risk of decision-making errors. At present, the AHP method is extensively utilized across numerous fields as it can effectively assist scholars and decision-makers in solving complex decision-making problems, such as techno-entrepreneurship [21], renewable energy [22], road selection [23], sewer networks [24], and smart buildings [25].

Evaluating, comparing, and selecting different alternatives are among the most common issues among MCDM problems. In 1981, Hwang and Yoon introduced the TOPSIS method, which is based on the proximity ideal targets between a limited number of evaluated alternatives and ideal targets for ranking. By performing geometric calculations to approach ideal solutions, relative evaluations of the existing alternatives can be conducted. The basic principle of this method is to detect various criteria related to the evaluated alternatives, select the best and worst solutions, and calculate the geometric distances between each alternative for sorting. The evaluated alternative is considered to be the best solution if it is farthest from the worst solution and closest to the ideal solution. This method has the advantage of simple geometric calculations and greater flexibility when using weights. Therefore, this approach has been used extensively across numerous fields, such as medical equipment supplier selection [26,27], failure mode and effects analysis [28], group decision making [29], economic freedom assessment [30], medical treatment selection [31], and performance evaluation [32].

The presentation and processing of data are essential parts of MCDM problems. However, due to the experts’ diverse experiences, backgrounds, and professional knowledge, collected opinions sometimes lack consensus, and cannot be expressed or solved using ordinary positive integers. As a result, the concept of fuzzy numbers emerged. Zadeh [33] proposed a mathematical theory of fuzzy sets, which are extensions of ordinary sets in mathematics. The principle of defuzzification involves providing a span for a single numerical value and forming a range interval where the values within the intervals represent possible results of opinions. This allows experts to express their opinions more precisely and provide better perspectives on events, which is different from the absolute representation of positive integers. Due to the flexibility of fuzzy methods and their alignment with real-world situations, many scholars have adopted and utilized this method in various methods and models, while also applying it in various fields. For example, Faizi et al. [34] used hesitant fuzzy sets to manage uncertain decision problems. Garg and Kumar [35] proposed the concept of a linguistic interval-valued Atanassov intuitionistic fuzzy set to address group decision making problems. Mathew et al. [36] integrated spherical fuzzy set, AHP, and TOPSIS methods to deal with problems in manufacturing systems selection. Wen et al. [37] addressed the risk assessment problem by integrating a hesitant fuzzy linguistic term set and subjective and objective weights. On the other hand, Zadeh [38] proposed linguistic expression variables based on natural language semantics to define the linguistic variables provided by experts more clearly. These expressions convey information through subjective language descriptions. Building on Zadeh’s concept, Herrera and Martinez [39] introduced a method for expressing linguistic transformations, which was called the 2-tuple fuzzy linguistic model (2-tuple FLM). This model establishes a semantic scale (from poor to good) and assigns corresponding fuzzy intervals to convert indicator calculation results into scoring properties. The calculation results are then re-expressed as a 2-tuple based on the semantic scale. The application of the 2-tuple FLM allows for the thorough examination of useful information. For instance, when evaluating product quality, multiple fuzzy language terms such as “very good”, “good”, “fair”, “poor”, and “very poor” can be used. A membership degree value can be used for each fuzzy linguistic term to describe the strength of the product quality. In recent years, the 2-tuple FLM has also been widely applied to address problems in various fields, such as group decision-making [40], personnel selection [41], cloud computing for e-commerce [42], failure mode and effects analysis [43], and the selection of material suppliers [44].

Recently, Utama [45] combined AHP and TOPSIS approaches to manage green supplier selection among color painting and printing enterprises in Indonesia. Utama [45] used eight criteria to select suppliers, and the results revealed that the criteria of quality had the highest importance. However, the said study failed to consider that experts’ diverse backgrounds, experiences, and expertise caused the collected opinions to contain some vague information, leading to certain deviations in the solution results. To address the aforementioned issue, this study combined the fuzzy AHP method, the TOPSIS method, and the 2-tuple FLM to manage the supplier selection problem with uncertain and imprecise information. The proposed method exhibits novelty and several advantages. Firstly, it utilizes the fuzzy AHP approach to determine the weights of different evaluation criteria, taking into account the differences in criterion importance. Secondly, the proposed method employs the TOPSIS approach to consider the Euclidean distance of each alternative from both the optimal and worst solutions. This ensures a comprehensive evaluation of alternatives. Finally, the method integrates the 2-tuple FLM approach, enabling the simultaneous handling of qualitative and quantitative information. This allows for the thorough consideration of all available information.

The remainder of this study is organized as follows. Section 2 discusses the basic concepts and some fundamental definitions related to 2-tuple FLM, the fuzzy AHP method, and the TOPSIS method. Section 3 presents a novel soft fuzzy AHP–TOPSIS model to solve environmental protection supplier selection under a fuzzy environment. Section 4 presents a numerical example of selecting a green supplier, and discusses how the research results compare with other related methods to demonstrate the effectiveness of the proposed novel soft fuzzy AHP–TOPSIS method. Section 5 draws the conclusion and contributions of this study together and highlights suggestions for future researchers.

2. Preliminary

2.1. Fuzzy AHP Method

Saaty introduced the AHP method, which is a research methodology suitable for addressing complex MCDM problems with hierarchical structures, in 1971. This approach systematically and structurally decomposes decision problems into several levels while considering and processing both quantitative and qualitative information, resolving the challenge of comparing multiple solutions [7]. However, the conventional AHP methodology is inadequate when handling the fuzzy information that experts provide. To manage imprecise and uncertain information, Zadeh [33] suggested the concept of fuzzy sets, which can be used to leverage fuzzy logic and address the uncertainty of the decision problem. The fuzzy AHP method combines mathematical theory (fuzzy set) and the MCDM approach (AHP method) to consider both uncertain and imprecision information in its evaluation. The following presents the computation rules related to the triangular fuzzy number (TFN).

Definition 1 

([46]). Considering that two TFN are $M_1=\left(l_1,m_1,u_1\right)$ and $M_2=\left(l_2,m_2,u_2\right)$, the basic operational laws are as follows:

$$M_1\oplus M_2=\left(l_1,m_1,u_1\right)\oplus \left(l_2,m_2,u_2\right)=\left(l_1+l_2,m_1+m_2,u_1+u_2\right)$$

(1)

$$M_1\ominus M_2=\left(l_1,m_1,u_1\right)\ominus \left(l_2,m_2,u_2\right)=\left(l_1-u_2,m_1-m_2,u_1-l_2\right)$$

(2)

$${\left(l_1,m_1,u_1\right)}^{-1}=\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$u_1,$}\right.\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$m_1$}\right.,\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$l_1$}\right.\right)$$

(3)

The fuzzy AHP approach procedure is as follows.

• Step 1. Establish a hierarchy and determine the evaluation criteria.

The hierarchical structure of the problem can be divided into multiple levels (from top to bottom), while the actual level size depends on the problem analysis. Evaluation criteria are determined based on the hierarchical structure, and pairwise comparisons are used to assess the relative importance of the evaluation criteria. A rating scale of 1–9 is employed, with larger numbers indicating greater importance. The evaluation scale is shown in

Table 1. AHP method evaluation scale.

Evaluation Degree	Importance Comparison	Definition
1	Equally	Both elements are regarded as equally important
3	Slightly	Tend to slightly value the more important element
5	Strongly	Strongly value the element that is more important
7	Very strongly	The element is highly associated with importance
9	Absolutely	Absolutely considers the element as more important than the other
2, 4, 6, 8	Between each semantic	Importance is a compromise between the criteria above

[7].

• Step 2. Perform a questionnaire survey based on a fuzzy scale and make a pairwise comparison.

Convert the evaluation scale of the AHP method to the evaluation scale of the TFN, as shown in

Table 2. Linguistic evaluation conversion in a triangular fuzzy set.

Linguistic Variable	Evaluation Scale	Triangular Fuzzy Set	The Reciprocal of the Scale	The Reciprocal of the Triangular Fuzzy Set
Same importance	1	(1, 1, 1)	1	(1, 1, 1)
	2	(3/2, 2, 5/2)	1/2	(2/5, 1/2, 2/3)
Slight importance	3	(5/2, 3, 7/2)	1/3	(2/7, 1/3, 2/5)
	4	(7/2, 4, 9/2)	1/4	(2/9, 1/4, 2/7)
Strong importance	5	(9/2, 5, 11/2)	1/5	(2/11, 1/5, 2/9)
	6	(11/2, 6, 13/2)	1/6	(2/13, 1/6, 2/11)
Very strong importance	7	(13/2, 7, 15/2)	1/7	(2/15, 1/7, 2/13)
	8	(15/2, 8, 17/2)	1/8	(2/17, 1/8, 2/15)
Absolute importance	9	(17/2, 9, 9)	1/9	(1/9, 1/9, 2/17)

(adapted from [47]). Then, complete the expert questionnaire. After performing the questionnaire survey, use the semantic scales answered by the experts’ questionnaires to establish matrix A. Let $A={\left(a_{ij}\right)}_{n\times m}$ be a fuzzy pairwise comparison judgments matrix, $M_{ij}=(l_{ij},m_{ij},u_{ij})$ be a TFN, and adopt both to execute pairwise comparisons between the different assessment elements, where $a_{ij}$ is the importance comparison value of the i-th assessment criteria to the j-th assessment criteria, $a_{ij}=1$, $\forall i=j$, and $a_{ji}=\frac{1}{a_{ij}}$, $\forall i=1,2,\dots ,n$, $j=1,2,\dots ,m$, as shown in Equation (4).

$$A=\left[a_{ij}\right]=\left[\begin{array}{ccc}{a}_{11}& a_{12}& \begin{array}{cc}\dots & a_{1m}\end{array}\\ a_{21}& a_{22}& \begin{array}{cc}\dots & a_{2m}\end{array}\\ \begin{array}{c}⋮\\ a_{n1}\end{array}& \begin{array}{c}⋮\\ a_{n2}\end{array}& \begin{array}{cc}\begin{array}{c}\ddots \\ \dots \end{array}& \begin{array}{c}⋮\\ a_{nm}\end{array}\end{array}\end{array}\right]$$

(4)

• Step 3. Defuzzify the TFN value.

Use the center of area (COA) method to defuzzify the pairwise comparison matrix in Step 2. Equation (5) illustrates the process of defuzzifying a TFN value $D{F}_{ij}$ [48].

$$D{F}_{ij}=l_{ij}+\frac{\left[\left(u_{ij}-l_{ij}\right)+\left(m_{ij}-l_{ij}\right)\right]}{3}$$

(5)

• Step 4. Calculate the consistency ratio (CR) value.

To verify the consistency of expert-provided opinions, examine the aggregated value of the TFN in Step 3. Then, apply the AHP method to calculate the CR and consistency index (CI) value, as shown in Equations (6)–(8).

Table 3. RI value for different matrix sizes.

Size of matrix (n)	1	2	3	4	5	6	7	8	9	10
RI	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

shows that ${\lambda }_{max}$ is the largest eigenvector and n is the size of the fuzzy pairwise comparison matrix A, while the value of random index (RI) is based on the matrix size [7]. It should be noted that the CR value must be less than 0.1 to prove the consistency of expert-provided assessments and opinions.

$$Aw={\lambda }_{max}w,\mathrm{and}{\sum }_{i=1}^n{w}_i=1$$

(6)

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

(7)

$$CR=\frac{CI}{RI}$$

(8)

• Step 5. Calculate the optimal weight and rank the criteria and alternatives.

Once the weight of each evaluation criteria has been determined in Step 5, it is then multiplied by each alternative in the decision-making problem to obtain the weighted score. To select the best alternative, the results of weighted scores are ranked from high to low.

2.2. The TOPSIS Method

Hwang and Yoon developed the TOPSIS method in 1981, which is a widely used technique for multi-criteria decision analysis [8]. The TOPSIS method is primarily used in addressing issues involving solution and combination selection. The method involves comparing the candidate solutions with the positive ideal solution (PIS) and negative ideal solutions (NIS), as well as evaluating the superiority and ranking of each solution by examining their geometric distances from the best and worst solutions. The evaluated solution is considered the best if it is the closest to the best solution and farthest from the worst solution. The steps involved in this method are explained below.

• Step 1. Construct and compute the normalized decision matrix.

Establish a decision matrix for various criteria of different units, digits, and alternatives. Then, perform the normalization process to obtain the data to be compared using values ($a_{ij}$) of the same sizes and digits. The formula is as follows, where $x_{ij}$ is the evaluation value of ith alternatives with respect to jth criteria.

$$a_{ij}=\frac{x_{ij}}{\sqrt{{\sum }_{i=1}^n{x}_{ij}^2}},i=1,\dots ,n,j=1,\dots ,m$$

(9)

• Step 2. Compute the weighted normalized decision matrix.

Multiply the normalized values obtained in Step 1 by the corresponding weights to compute the weighted normalized decision matrix ($z_{ij}$). Experts typically determine the weights in the TOPSIS in a subjective manner. It can also be calculated using other research methods to assign weights to the criteria in the normalized matrix. The formula is as follows, where $w_j$ is the weight of the jth criteria, and ${\sum }_{j=1}^m{w}_j=1$:

$$z_{ij}=w_j{a}_{ij},i=1,\dots ,n,j=1,\dots ,m$$

(10)

• Step 3. Select the PIS and the NIS of each alternative.

The PIS and the NIS are the two basic concepts of the TOPSIS method. The PIS refers to the best conceived solution, with all its attribute values reaching the best values among all alternative solutions. On the other hand, the NIS is the worst conceived solution, with all its attribute values reaching the worst values among all alternative solutions. The attributes of the evaluation index should be used in the evaluation of its solution, from which the value that maximizes the benefit and minimizes the cost will be selected.

For the benefit criteria:

$$z_j^{+}=max\left\{z_{1j},z_{2j},\dots ,z_{nj}\right\}$$

(11)

$$z_j^{-}=min\left\{z_{1j},z_{2j},\dots ,z_{nj}\right\}$$

(12)

For the cost criteria:

$$z_j^{+}=min\left\{z_{1j},z_{2j},\dots ,z_{nj}\right\}$$

(13)

$$z_j^{-}=max\left\{z_{1j},z_{2j},\dots ,z_{nj}\right\}$$

(14)

The PIS ($Z^{+}$) and NIS are ($Z^{-}$) as follows:

$$Z^{+}=\left[z_1^{+},z_2^{+},\dots ,z_m^{+}\right]$$

(15)

$$Z^{-}=\left[z_1^{-},z_2^{-},\dots ,z_m^{-}\right]$$

(16)

• Step 4. Calculate the Euclidean distance of each alternative from the optimal solution and the worst solution.

After completing the screening of the optimal and the worst solution, the relative distance between the scores of each alternative and the best and worst solutions is calculated. Equation (17) can be summed to obtain the distance between the selected alternative and the best solution ($S_i^{+}$), and Equation (18) can be summed to obtain the distance between the selected alternative and the worst solution ($S_i^{-}$). The formula is as follows.

$$S_i^{+}=\sqrt{{\sum }_{j=1}^m{\left(z_{ij}-Z_j^{+}\right)}^2},i=1,2,\dots ,n.$$

(17)

$$S_i^{-}=\sqrt{{\sum }_{j=1}^m{\left(z_{ij}-Z_j^{-}\right)}^2},i=1,2,\dots ,n.$$

(18)

• Step 5. Compute the closeness coefficient ($C_i$) of the alternatives.

The final step is to compare the distance ratio of each alternative with the ideal and the negative ideal solutions. If the distance ratio from the worst solution is the highest (the farthest distance), and the proportion of distance from the optimal solution is the smallest (the distance is the shortest), it is identified as the optimal alternative. The value of $C_i$ is used as the basis for ranking the alternative. The greater the value, the farther away from the worst solution obtained, and the better the alternative. The formula is as follows:

$$C_i=\frac{S_i^{-}}{S_i^{-}+S_i^{+}}$$

(19)

2.3. The 2-Tuple FLM

Herrera and Martinez proposed the 2-tuple FLM as an expression semantic conversion method in 2000 [39]. According to the semantic expression variables proposed by Zadeh [38], numerous different expression modes are set, such as good, very good, poor, very poor, and so on. However, each person observes a difference between the expression variables to varying degrees. As a result, the 2-tuple FLM assigns absolutely fixed scoring positions for the abovementioned semantic scales, corresponding to $s_1,s_2,\cdots ,s_9$, respectively, where $s_1$ is absolutely poor, $s_3$ is fairly poor, $s_5$ is common, $s_7$ is fairly good, and $s_9$ is absolutely good, leading to a fixed distance level between semantic variables.

The 2-tuple FLM is composed of two elements, such as a fuzzy language word (s) and an associated membership value (α), and develops a semantic description in a binary group format, where L = (s, α). The range α of the fuzzy interval is limited within the range of ±0.5, by converting the semantic scale to give the corresponding fuzzy interval. Using 5.25 as an example, it can be expressed as (s5, 0.25). Figure 1 depicts the overall model.

Definition 2 

([39,49]). Assume $S=\left\{s_{1,}{s}_{2,}\dots ,s_k\right\}$ is a set of linguistic representation and $\beta \in \left[0,k\right]$ is an operation result of symbolic aggregation, and then the function represents the 2-tuple linguistic as follows:

$$∆:S\times \left[-0.5,0.5\right)\to \left[0,k\right]$$

(20)

$$∆\left(\beta \right)=\left(s_i,\alpha \right),with\left\{\begin{array}{cc}{s}_i,& k=round\left(\beta \right)\\ \alpha =\beta -i,& \alpha \in \left[-0.5,\left.0.5\right)\right.\end{array}\right.$$

(21)

where $s_i$ is the index closest to $\beta$, $\alpha$ is the deviation between the actual value and the fuzzy linguistic, and round (.) is the usual round operation.

Definition 3 

([39]). Assume $x=\left\{\left(s_1,{\alpha }_1\right),\left(s_2,{\alpha }_2\right),\dots ,\left(s_n,{\alpha }_n\right)\right\}$ is a set of the 2-tuple linguistic representation, and then the calculation of the arithmetic mean ${\stackrel{-}{\chi }}^e$ is as follows:

$${\stackrel{-}{\chi }}^e=∆\left({\sum }_{i=1}^n\frac{1}{n}{∆}^{-1}\left(s_i,{\alpha }_i\right)\right)=∆\left(\frac{1}{n}{\sum }_{i=1}^n{\beta }_i\right)$$

(22)

Definition 4 

([39]). Assume $\left(s_e,{\alpha }_1\right)$ and  $\left(s_f,{\alpha }_2\right)$ are two 2-tuple linguistic representations, and then their comparison law as is follows.

(i) 

If e > f, then  $\left(s_e,{\alpha }_1\right)>\left(s_f,{\alpha }_2\right)$.

(ii) 

If e = f, then

(A) 

If ${\alpha }_1={\alpha }_2$, then $\left(s_e,{\alpha }_1\right)$ and $\left(s_f,{\alpha }_2\right)$ indicate the same information.

(B) 

If ${\alpha }_1>{\alpha }_2$, then $\left(s_e,{\alpha }_1\right)>\left(s_f,{\alpha }_2\right)$.

3. The Proposed Novel Soft Fuzzy AHP–TOPSIS Method

3.1. The Planning of the Proposed Method

The goal of choosing green suppliers is to reduce the environmental impact of enterprise development, and emphasize the selection of environmentally responsible suppliers for procurement activities. However, selecting green suppliers involves multiple factors, including environmental management system certification, energy and carbon emission reduction, social responsibility, and eco-friendly product production, among others. Hence, green supplier selection is considered to be an MCDM issue. To effectively address this issue, this study integrated the fuzzy AHP method with the TOPSIS method and 2-tuple FLM to evaluate green supplier selection. On the other hand, with the ongoing development of the digital economy, there has been a significant increase in the volume of data being generated. The proposed method is well-suited for environments involving big data. This study first used the AHP approach to determine the weight of the different evaluation criteria, assess the significance of each evaluation criterion, minimize subjective bias, and enhance evaluation precision. Then, the researchers used the TOPSIS method to assist the evaluators in identifying the optimal solution by measuring the geometric distance between the best and worst solutions. During the selection process, experts must evaluate the comprehensiveness of the suppliers’ environmental protection policy and determine if the product promote environmental protection. However, there are often uncertainties and ambiguities in these types of evaluations. Therefore, using the fuzzy logic of fuzzy sets, fuzzy subjective judgments are transformed into numerical values. Meanwhile, the 2-tuple FLM can be used to consider available information fully, improving the accuracy and credibility of green supplier evaluations and selecting suppliers that best meet the enterprises’ environmental protection requirements.

3.2. Steps Involved in the Proposed Method

Based on the research plan described in Section 3.1, the implementation techniques of the proposed research method are explained below, and the flowchart of the proposed novel soft fuzzy AHP–TOPSIS method is shown in Figure 2.

• Step 1. Define the decision problems and build problem hierarchies.

This step involves organizing a decision-making committee to analyze the problem, defining the structure of the MCDM problem, and constructing problem hierarchies (including goal, criteria, and alternative) to aid in understanding the evaluation criteria and identifying potential alternatives.

• Step 2. Determine the different evaluation criteria and conduct a questionnaire survey.

Experts with professional experience in specialized fields design evaluation criteria based on different evaluation criteria to complete the questionnaire survey. This step involves performing a questionnaire survey with experts using the 1 to 9 rating scale of the AHP method. This approach is beneficial for analyzing the alternatives in the subsequent MCDM problem.

• Step 3. Decide the assessment criteria weight.

Equation (5) is used to defuzzify the TFN value in the evaluation criteria comparison matrix and convert it into the crisp value. Equations (6)–(8) are then adopted to evaluate the relative priorities of the criteria. The CR value is calculated to confirm that the expert-provided information meets the consistency standard (CR < 0.1) and to determine the criteria weight value.

• Step 4. Calculate performance values of the alternative.

Based on the original data collected in Step 2, this step uses the 2-tuple FLM for the semantic conversion and calculates the algebraic average to obtain the average performance. The evaluation criterion weight value obtained in Step 3 is then multiplied by the alternative’s average performance value.

• Step 5. Rank the alternative.

This step involves the ranking of the alternatives in the MCDM problem using Equations (11)–(16) to obtain the input data of the PIS and NIS. After applying Equations (17)–(19) to calculate the values of $S^{+}$, $S^{-}$, and $C_i$, the alternatives are ranked based on the $C_i$ value.

• Step 6. Provide suggestions for decision-making.

After completing the priorities of the alternatives in Step 5, managers (decision-makers) can make informed decisions based on the ranking from large to small, and provide the best green supplier selection suggestion.

4. Case Study

4.1. Overview

The rising trends in promoting environmental awareness and achieving sustainable economic development goals warrant the consideration of the performance of environmental protection, economic development, and social feedback by each enterprise in their business operations. As reflected in previous studies, scholars examined environmental protection issues and proposed several solutions. 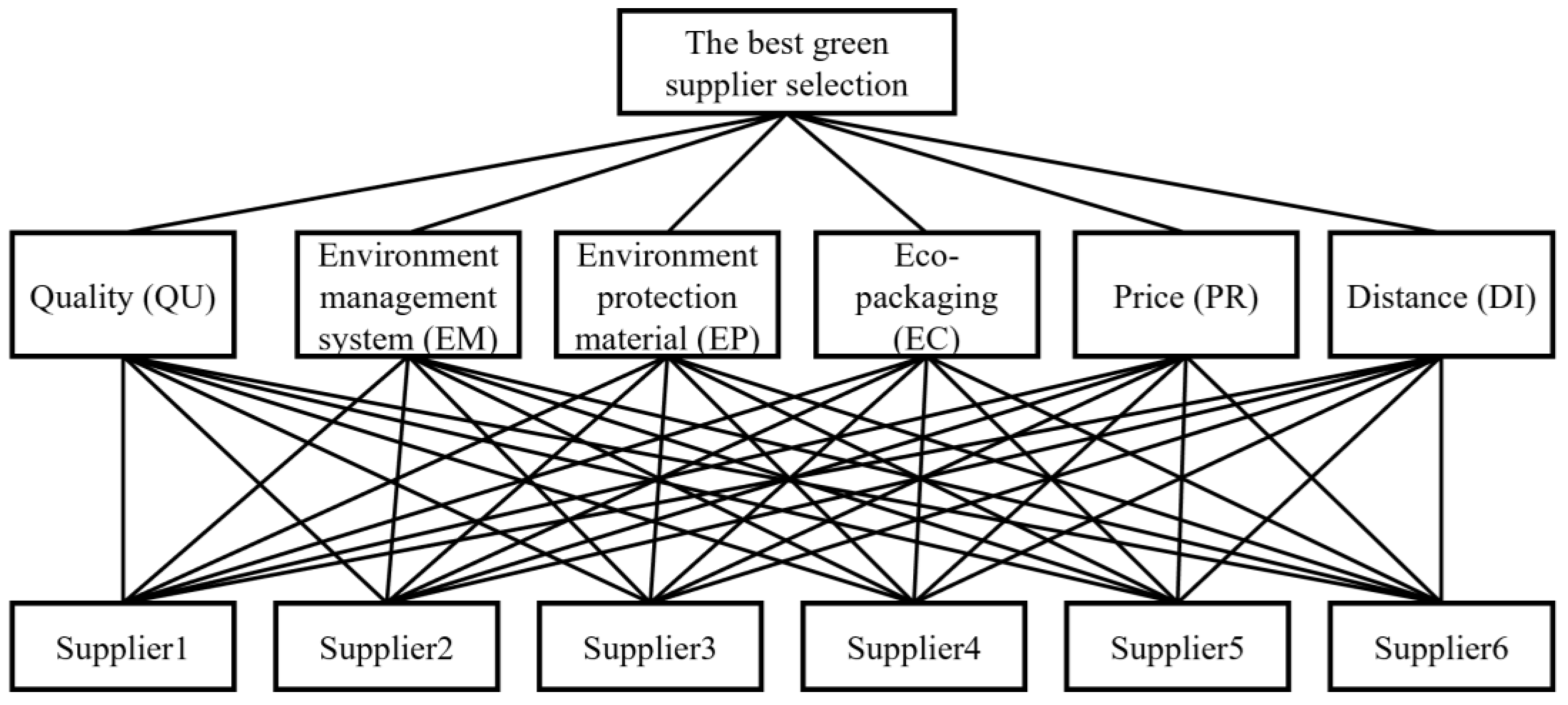This study adapted an example involving the selection of raw material suppliers among color painting and printing companies in Indonesia (adapted from [45]), and investigated how to cope with the problem of environmental protection supplier selection. The evaluation criteria distinguished two attributes of benefit and cost, totaling six criteria including quality (QU), environment management system (EM), environmental protection material (EP), eco-package (EC), price (PR), and distance (DI). Experts provided the evaluation scores’ qualitative data for QU, EM, EP, and EC (i.e., s1: normal, s3: slightly good, s5: fairly good, s7: very good, and s9: absolutely good, where s2, s4, s6, and s8 are an intermediate judgment between two adjacent judgments). Meanwhile, the evaluation scores for PR and DI were quantitative data.

Table 4. List of evaluation criteria.

Item	Evaluation Criteria	Classification
QU	Quality	Benefit
EM	Environment management system	Benefit
EP	Environmental protection material	Benefit
EC	Eco-package	Benefit
PR	Price	Cost
DI	Distance	Cost

Note: The unit of PR is per hundred thousand IDR; the unit of DI is kilometers.

shows the assessment results for the six suppliers in each criterion, while Figure 3 presents the structure. To evaluate and select the best among the six selected suppliers (S1–S6), we formed an advisory committee for green supplier selection comprising four experts (Expert 1, Expert 2, Expert 3, and Expert 4) who possess extensive practical experience in the fields of environmental protection and supplier selection. These experts conducted the fuzzy information evaluation of the supplier selection goals, as demonstrated in

Table 5. Indicators’ pairwise comparison matrix for the selection of a green supplier of raw materials.

	Expert	QU	EM	EP	EC	PR	DI
QU	E1	(1, 1, 1)	(9/2, 5, 11/2)	(9/2, 5, 11/2)	(13/2, 7, 15/2)	(1, 1, 1)	(7/2, 4, 9/2)
	E2	(1, 1, 1)	(3/2, 2, 5/2)	(7/2, 4, 9/2)	(9/2, 5, 11/2)	(2/7, 1/3, 2/5)	(9/2, 5, 11/2)
	E3	(1, 1, 1)	(5/2, 3, 7/2)	(5/2, 3, 7/2)	(11/2, 6, 13/2)	(2/7, 1/3, 2/5)	(5/2, 3, 7/2)
	E4	(1, 1, 1)	(7/2, 4, 9/2)	(11/2, 6, 13/2)	(13/2, 7, 15/2)	(2/5, 1/2, 2/3)	(9/2, 5, 11/2)
EM	E1	(2/11, 1/5, 2/9)	(1, 1, 1)	(1, 1, 1)	(9/2, 5, 11/2)	(2/11, 1/5, 2/9)	(2/7, 1/3, 2/5)
	E2	(2/5, 1/2, 2/3)	(1, 1, 1)	(5/2, 3, 7/2)	(7/2, 4, 9/2)	(2/9, 1/4, 2/7)	(2/11, 1/5, 2/9)
	E3	(2/7, 1/3, 2/5)	(1, 1, 1)	(3/2, 2, 5/2)	(11/2, 6, 13/2)	(2/5, 1/2, 2/3)	(2/9, 1/4, 2/7)
	E4	(2/9, 1/4, 2/7)	(1, 1, 1)	(7/2, 4, 9/2)	(9/2, 5, 11/2)	(2/7, 1/3, 2/5)	(2/5, 1/2, 2/3)
EP	E1	(2/11, 1/5, 2/9)	(1, 1, 1)	(1, 1, 1)	(5/2, 3, 7/2)	(2/9, 1/4, 2/7)	(2/7, 1/3, 2/5)
	E2	(2/9, 1/4, 2/7)	(2/7, 1/3, 2/5)	(1, 1, 1)	(3/2, 2, 5/2)	(2/13, 1/6, 2/11)	(2/9, 1/4, 2/7)
	E3	(2/7, 1/3, 2/5)	(2/5, 1/2, 2/3)	(1, 1, 1)	(7/2, 4, 9/2)	(2/11, 1/5, 2/9)	(2/13, 1/6, 2/11)
	E4	(2/13, 1/6, 2/11)	(2/9, 1/4, 2/7)	(1, 1, 1)	(9/2, 5, 11/2)	(2/9, 1/4, 2/7)	(2/7, 1/3, 2/5)
EC	E1	(2/15, 1/7, 2/13)	(2/11, 1/5, 2/9)	(2/7, 1/3, 2/5)	(1, 1, 1)	(2/15, 1/7, 2/13)	(2/11, 1/5, 2/9)
	E2	(2/11, 1/5, 2/9)	(2/9, 1/4, 2/7)	(2/5, 1/2, 2/3)	(1, 1, 1)	(2/13, 1/6, 2/11)	(2/17, 1/8, 2/15)
	E3	(2/13, 1/6, 2/11)	(2/13, 1/6, 2/11)	(2/9, 1/4, 2/7)	(1, 1, 1)	(2/15, 1/7, 2/13)	(2/13, 1/6, 2/11)
	E4	(2/15, 1/7, 2/13)	(2/11, 1/5, 2/9)	(2/11, 1/5, 2/9)	(1, 1, 1)	(2/17, 1/8, 2/15)	(2/13, 1/6, 2/11)
PR	E1	(1, 1, 1)	(9/2, 5, 11/2)	(7/2, 4, 9/2)	(13/2, 7, 15/2)	(1, 1, 1)	(7/2, 4, 9/2)
	E2	(5/2, 3, 7/2)	(7/2, 4, 9/2)	(11/2, 6, 13/2)	(11/2, 6, 13/2)	(1, 1, 1)	(5/2, 3, 7/2)
	E3	(5/2, 3, 7/2)	(3/2, 2, 5/2)	(9/2, 5, 11/2)	(13/2, 7, 15/2)	(1, 1, 1)	(9/2, 5, 11/2)
	E4	(3/2, 2, 5/2)	(5/2, 3, 7/2)	(7/2, 4, 9/2)	(15/2, 8, 17/2)	(1, 1, 1)	(7/2, 4, 9/2)
DI	E1	(2/9, 1/4, 2/7)	(5/2, 3, 7/2)	(5/2, 3, 7/2)	(9/2, 5, 11/2)	(2/9, 1/4, 2/7)	(1, 1, 1)
	E2	(2/11, 1/5, 2/9)	(9/2, 5, 11/2)	(7/2, 4, 9/2)	(15/2, 8, 17/2)	(2/7, 1/3, 2/5)	(1, 1, 1)
	E3	(2/7, 1/3, 2/5)	(7/2, 4, 9/2)	(11/2, 6, 13/2)	(11/2, 6, 13/2)	(2/11, 1/5, 2/9)	(1, 1, 1)
	E4	(2/11, 1/5, 2/9)	(3/2, 2, 5/2)	(5/2, 3, 7/2)	(11/2, 6, 13/2)	(2/9, 1/4, 2/7)	(1, 1, 1)

and

Table 6. Suppliers’ evaluation scores.

Suppliers	Expert	QU	EM	EP	EC	PR	DI
Supplier 1	E1	s3	s4	s4	s4	6.50	20
	E2	s4	s5	s6	s5
	E3	s5	s6	s5	s3
	E4	s6	s4	s4	s2
Supplier 2	E1	s5	s3	s4	s3	6.00	25
	E2	s4	s5	s5	s2
	E3	s6	s5	s5	s2
	E4	s6	s3	s4	s2
Supplier 3	E1	s4	s4	s3	s3	6.25	30
	E2	s3	s3	s3	s5
	E3	s3	s2	s2	s4
	E4	s4	s3	s4	s2
Supplier 4	E1	s5	s4	s5	s3	7.00	50
	E2	s5	s4	s4	s4
	E3	s6	s5	s6	s5
	E4	s4	s3	s5	s3
Supplier 5	E1	s4	s3	s3	s4	6.20	30
	E2	s4	s5	s4	s5
	E3	s6	s6	s6	s5
	E4	s5	s4	s5	s3
Supplier 6	E1	s3	s3	s4	s3	6.20	30
	E2	s5	s3	s3	s4
	E3	s4	s3	s4	s3
	E4	s4	s2	s5	s3

Note: The unit of PR is per hundred thousand IDR; the unit of DI is kilometers.

(adapted from [45]).

4.2. Application of the Typical TOPSIS Method

The TOPSIS method is commonly used to solve MCDM problems by comparing the geometric distances between the alternative properties and the PIS and NIS. Aires and Ferreira [50] applied the TOPSIS method to effectively rank the alternatives in an MCDM problem, where the weight of the criteria was assumed to be the same. Table 6 shows that the normalized average data value was multiplied by the weighted value of each index 0.167 to determine the average weighted value, as depicted in

Table 7. Calculation results of the typical TOPSIS method.

Suppliers	QU	EM	EP	EC	PR	DI	${\mathit{S}}_{\mathit{i}}^{+}$	${\mathit{S}}_{\mathit{i}}^{-}$	${\mathit{C}}_{\mathit{i}}$	Rank
S1	0.073	0.083	0.075	0.076	0.069	0.042	0.005	0.088	0.943	1
S2	0.073	0.067	0.075	0.038	0.064	0.053	0.043	0.065	0.604	3
S3	0.058	0.050	0.045	0.076	0.067	0.063	0.052	0.057	0.526	4
S4	0.073	0.067	0.075	0.076	0.075	0.106	0.066	0.053	0.444	6
S5	0.073	0.083	0.075	0.076	0.066	0.063	0.021	0.074	0.778	2
S6	0.058	0.050	0.060	0.057	0.066	0.063	0.049	0.049	0.504	5
$Z^{+}$	0.073	0.083	0.075	0.076	0.064	0.042
$Z^{-}$	0.058	0.050	0.045	0.038	0.075	0.106

.

Equations (11)–(16) were used to determine the PIS ($Z^{+}$) and NIS ($Z^{-}$) for the six criteria, and the Euclidean distance of each alternative to the $S_i^{+}$ and $S_i^{-}$ was measured using Equations (17) and (18). Equation (19) was utilized to calculate the closeness coefficient ($C_i$). The complete calculation results are shown in Table 7.

4.3. Application of the Typical AHP–TOPSIS Method

The typical AHP–TOPSIS method combines the AHP and TOPSIS methods. This method first uses the AHP method to compute the different evaluation criteria weight for problem-solving and then ranks the alternatives effectively through the TOPSIS method. Azimifard et al. [27] used the AHP–TOPSIS methodologies to select a sustainable steel industry supplier, and the research results proved that this method can assist managers in handling supplier selection issues at the macro level. This study also utilized the AHP–TOPSIS method to evaluate and choose suitable green suppliers.

Table 5 shows that the weights of the six criteria were calculated using the AHP method. Since the AHP method can only handle crisp information, the TFN contents in Table 5 were converted to a crisp information comparison criteria matrix, as shown in

Table 8. Comparison matrix of the typical AHP method.

Criteria	QU	EM	EP	EC	PR	DI
QU	1	4	5	6	1/2	4
EM	1/4	1	3	5	1/3	1/3
EP	1/5	1/3	1	4	1/5	1/4
EC	1/6	1/5	1/4	1	1/7	1/6
PR	2	3	5	7	1	4
DI	1/4	3	4	6	1/4	1

.

Table 5 shows that the weights of the six criteria were calculated using the AHP method. Since the AHP method can only handle crisp information, the TFN contents in Table 5 were converted to a crisp information comparison criteria matrix. The operation procedure involves first performing the arithmetic mean calculation of the values obtained by the four experts in Table 5. Subsequently, defuzzification is carried out using Equation (5) to obtain a single value, as illustrated in Table 8.

As shown in Table 8, Equations (6)–(8) were used to determine the CR values by calculating ${\lambda }_{max}=6.585$. The CI value was 0.117 and the CR value was 0.094. The calculation procedure is shown as follows:

$$CI=\frac{{\lambda }_{max}-n}{n-1}=\frac{6.585-6}{6-1}=0.117$$

$$CR=\frac{CI}{RI}=\frac{0.117}{1.240}=0.094$$

After confirming that the CR value is <0.1, the expert-provided judgement can be tagged as consistent. The weight calculation can then be performed to obtain the weighted vectors (0.298, 0.101, 0.057, 0.029, 0.360, 0.156)^T, with the results indicating that PR had the most important weight value, at 0.360, followed by the weights of QU (0.298), DI (0.156), EM (0.101), EP (0.057), and EC (0.029).

Data in Table 6 and Equation (9) were used to conduct the mean calculation, which was then multiplied by the respective weighted value of the six criteria. Following that, the weighted average value was determined, as shown in

Table 9. Calculation results of the typical AHP–TOPSIS method.

Suppliers	QU	EM	EP	EC	PR	DI	${\mathit{S}}_{\mathit{i}}^{+}$	${\mathit{S}}_{\mathit{i}}^{-}$	${\mathit{C}}_{\mathit{i}}$	Rank
S1	0.130	0.051	0.025	0.013	0.150	0.040	0.012	0.070	0.858	1
S2	0.130	0.040	0.025	0.007	0.139	0.049	0.016	0.062	0.799	2
S3	0.104	0.030	0.015	0.013	0.144	0.059	0.040	0.044	0.521	5
S4	0.130	0.040	0.025	0.013	0.162	0.099	0.064	0.030	0.320	6
S5	0.130	0.051	0.025	0.013	0.143	0.059	0.020	0.056	0.734	3
S6	0.104	0.030	0.020	0.010	0.143	0.059	0.039	0.044	0.530	4
$Z^{+}$	0.130	0.051	0.025	0.013	0.139	0.040
$Z^{-}$	0.104	0.030	0.015	0.007	0.162	0.099

. Table 9 and Equations (11)–(16) illustrate how to find out the PIS ($Z^{+}$) and NIS ($Z^{-}$) for the s criteria, while Equations (17) and (18) depict how the Euclidean distances of each alternative to the $S_i^{+}$ and $S_i^{-}$ were measured. Equation (19) was used to calculate the closeness coefficient ($C_i$), and the complete calculation results are illustrated in Table 9.

4.4. Application of the Proposed Novel Soft Fuzzy AHP–TOPSIS Method

This section used the proposed novel soft fuzzy AHP–TOPSIS method to evaluate the performance of the six suppliers. The method integrates the fuzzy AHP method, the TOPSIS method, and the 2-tuple FLM. Steps 1 to 6 are outlined in Section 3.2.

• Step 1. Define decision problems and build problem hierarchies.

This step involves organizing a supplier selection committee to analyze the problem, defining the hierarchical structure of the MCDM problem, formulating feasible evaluation criteria, and looking for best green supplier.

• Step 2. Determine the different evaluation criteria and conduct a questionnaire survey.

Experts discussed and determined the evaluation criteria based on the case of raw material suppliers of color painting and printing companies. Table 2 shows the expert-provided weight indicators of the pairwise comparison matrix for the green supplier selection of raw materials. The fuzzy evaluation scores for supplier selection objectives were also depicted in Table 2.

• Step 3. Decide the assessment criteria weight.

As shown in Table 5 and Equation (5), the TFN value of each evaluation criteria in the comparison matrix was defuzzified and converted into the exact value. For example, Expert E1 gave the degree of importance of criteria EM for pairwise comparisons of criteria QU as (2/11, 1/5, 2/9), as shown in Table 5. Using the calculation involved in the COA method, the obtained score was 0.201.

$$D{F}_{ij}=l_{ij}+\raisebox{1ex}{$\left[\left(u_{ij}-l_{ij}\right)+\left(m_{ij}-l_{ij}\right)\right]$}\!\left/ \!\raisebox{-1ex}{$3$}\right.=2/11+\raisebox{1ex}{$\left[\left(2/9-2/11\right)+\left(1/5-2/11\right)\right]$}\!\left/ \!\raisebox{-1ex}{$3$}\right.=0.201$$

As shown in Table 5, Equation (22) was used to aggregate experts’ opinion and obtain the comparison matrix of fuzzy AHP methods expressed in

Table 10. Linguistic comparison matrix of the proposed novel soft fuzzy AHP–TOPSIS method.

Criteria	QU	EM	EP	EC	PR	DI
QU	$∆$(1.000)	$∆$(3.500)	$∆$(4.500)	$∆$(6.250)	$∆$(0.550)	$∆$(4.250)
EM	$∆$(0.286)	$∆$(1.000)	$∆$(2.500)	$∆$(5.000)	$∆$(0.329)	$∆$(0.329)
EP	$∆$(0.222)	$∆$(0.400)	$∆$(1.000)	$∆$(3.500)	$∆$(0.219)	$∆$(0.275)
EC	$∆$(0.160)	$∆$(0.200)	$∆$(0.286)	$∆$(1.000)	$∆$(0.145)	$∆$(0.165)
PR	$∆$(1.817)	$∆$(3.040)	$∆$(4.576)	$∆$(6.903)	$∆$(1.000)	$∆$(4.000)
DI	$∆$(0.235)	$∆$(3.040)	$∆$(3.638)	$∆$(6.046)	$∆$(0.250)	$∆$(1.000)

.

As illustrated in Table 8, Equations (6)–(8) were used to determine the CR values by calculating the ${\lambda }_{max}=6.513$. The computed CI value was 0.103 and the CR value was 0.083, confirming that the expert-provided information met CR < 0.1. The PR weight value (0.354) appeared to be the most important, followed by the weights of QU (0.301), DI (0.156), EM (0.100), EP (0.060), and EC (0.029).

• Step 4. Calculate performance values of the alternative.

The proposed method adopted Equations (20)–(22) to perform semantic conversion on the questionnaire results in Table 6. The arithmetic mean of the supplier’s performance score was calculated and then it was multiplied by the evaluation criteria weighted value obtained in Step 3.

Table 11. Calculation results of the proposed method.

Suppliers	QU	EM	EP	EC	PR	DI	${\mathit{S}}^{+}$	${\mathit{S}}^{-}$	Ci	Rank
S1	$∆$(0.122)	$∆$(0.050)	$∆$(0.027)	$∆$(0.012)	$∆$(0.148)	$∆$(0.040)	$∆$(0.023)	$∆$(0.070)	$∆$(0.750)	2
S2	$∆$(0.142)	$∆$(0.042)	$∆$(0.025)	$∆$(0.008)	$∆$(0.136)	$∆$(0.049)	$∆$(0.015)	$∆$(0.074)	$∆$(0.835)	1
S3	$∆$(0.095)	$∆$(0.031)	$∆$(0.017)	$∆$(0.012)	$∆$(0.142)	$∆$(0.059)	$∆$(0.056)	$∆$(0.043)	$∆$(0.436)	5
S4	$∆$(0.135)	$∆$(0.042)	$∆$(0.028)	$∆$(0.013)	$∆$(0.159)	$∆$(0.099)	$∆$(0.064)	$∆$(0.044)	$∆$(0.408)	6
S5	$∆$(0.129)	$∆$(0.047)	$∆$(0.025)	$∆$(0.015)	$∆$(0.141)	$∆$(0.059)	$∆$(0.025)	$∆$(0.059)	$∆$(0.705)	3
S6	$∆$(0.108)	$∆$(0.029)	$∆$(0.023)	$∆$(0.011)	$∆$(0.141)	$∆$(0.059)	$∆$(0.045)	$∆$(0.046)	$∆$(0.505)	4
$Z^{+}$	$∆$(0.142)	$∆$(0.050)	$∆$(0.028)	$∆$(0.015)	$∆$(0.136)	$∆$(0.040)
$Z^{-}$	$∆$(0.095)	$∆$(0.029)	$∆$(0.017)	$∆$(0.008)	$∆$(0.159)	$∆$(0.099)

shows the obtained weighted average performance values of the alternatives.

• Step 5. Rank the alternative.

This step applied Equations (11)–(16) to determine the PIS ($Z^{+}$) and the NIS ($Z^{-}$) for the six criteria in Table 11. Equations (17) and (18) were then used to measure the separation distance of each alternative to the $S_i^{+}$ and $S_i^{-}$. Equation (19) was used to calculate the closeness coefficient ($C_i$). The alternatives were ranked based on the $C_i$ value. Table 11 shows the whole calculation results.

• Step 6. Provide suggestions for decision-making.

After completing the priorities of the alternatives in Step 5, decision makers or managers can sort the findings from large to small and provide the best green supplier selection suggestion.

4.5. Comparison and Discussion

This study proposed a soft fuzzy AHP–TOPSIS method that combines the fuzzy AHP method, the TOPSIS method, and the 2-tuple FLM to address issues relating to environmental protection supplier selection under a fuzzy information environment. To prove the accuracy and effectiveness of the proposed method, the calculation results compared the typical TOPSIS method and the AHP–TOPSIS method. Table 7, Table 9 and Table 11 show the calculation results of the three different research methods, while

Table 12. Comparison of the calculation results of the three different research methods.

Research Method	Score			Ranking
	TOPSIS Method [50]	AHP–TOPSIS Method [27]	Proposed Method	TOPSIS Method [50]	AHP–TOPSIS Method [27]	Proposed Method
Supplier 1	0.943	0.858	$∆$(0.750)	1	1	2
Supplier 2	0.604	0.799	$∆$(0.835)	3	2	1
Supplier 3	0.526	0.521	$∆$(0.436)	4	5	5
Supplier 4	0.444	0.320	$∆$(0.408)	6	6	6
Supplier 5	0.778	0.734	$∆$(0.705)	2	3	3
Supplier 6	0.504	0.530	$∆$(0.505)	5	4	4

shows the summarized results. The differences in the three different research methods in terms of information processing and weights were considered in evaluating the criteria, as shown in

Table 13. Differences in information processing and weights considered for the three different research methods.

Research Method	Handle Qualitative and Quantitative Information Simultaneously	Fully Consider the Differences of Weight between Criteria	Objectively Estimate Information Provided by Experts	Fully Consider Available Information
TOPSIS method [50]	X	X	X	X
AHP–TOPSIS method [27]	O	O	X	X
Proposed method	O	O	O	O

.

The following explains the several advantages of the proposed method.

(1)

Ability to handle qualitative and quantitative information simultaneously

The typical TOPSIS method can perform geometric calculations to obtain ideal solutions and conduct relative evaluations for existing alternatives and rankings. However, it cannot consider qualitative and quantitative information simultaneously. Both the AHP–TOPSIS method and the proposed method maximize the solving features of the AHP method, effectively decomposing complex decision-making problems into multiple levels and easy-to-handle subproblems, quantifying experts’ subjective scores on the evaluation criteria, and converting qualitative scores into quantitative values while ensuring that all qualitative and quantitative information is fully considered to improve the accuracy and reliability of their decision-making.

(2)

Ability to fully consider the differences of the weights between criteria

The traditional TOPSIS method ignores weight considerations, causing the evaluation results to deviate from the actual situation. Both the AHP–TOPSIS method and the proposed method can distinguish the relative importance of each criterion, making the evaluation results more suitable for the actual situation.

(3)

Objectively estimates the expert information

The AHP–TOPSIS method and the typical TOPSIS method can only deal with the crisp value and cannot handle fuzzy information. The proposed method can simultaneously consider the interval values of the fuzzy information, including the lower limit, center, and upper limit, and can consider the expert-provided information more objectively. Through the proposed method, subjective interpretations of the experts’ opinions can be avoided, as this may lead to biased results, thereby improving the accuracy of the evaluation. The proposed method also suits the actual situation of the evaluation and comparison results.

(4)

Fully consider available information

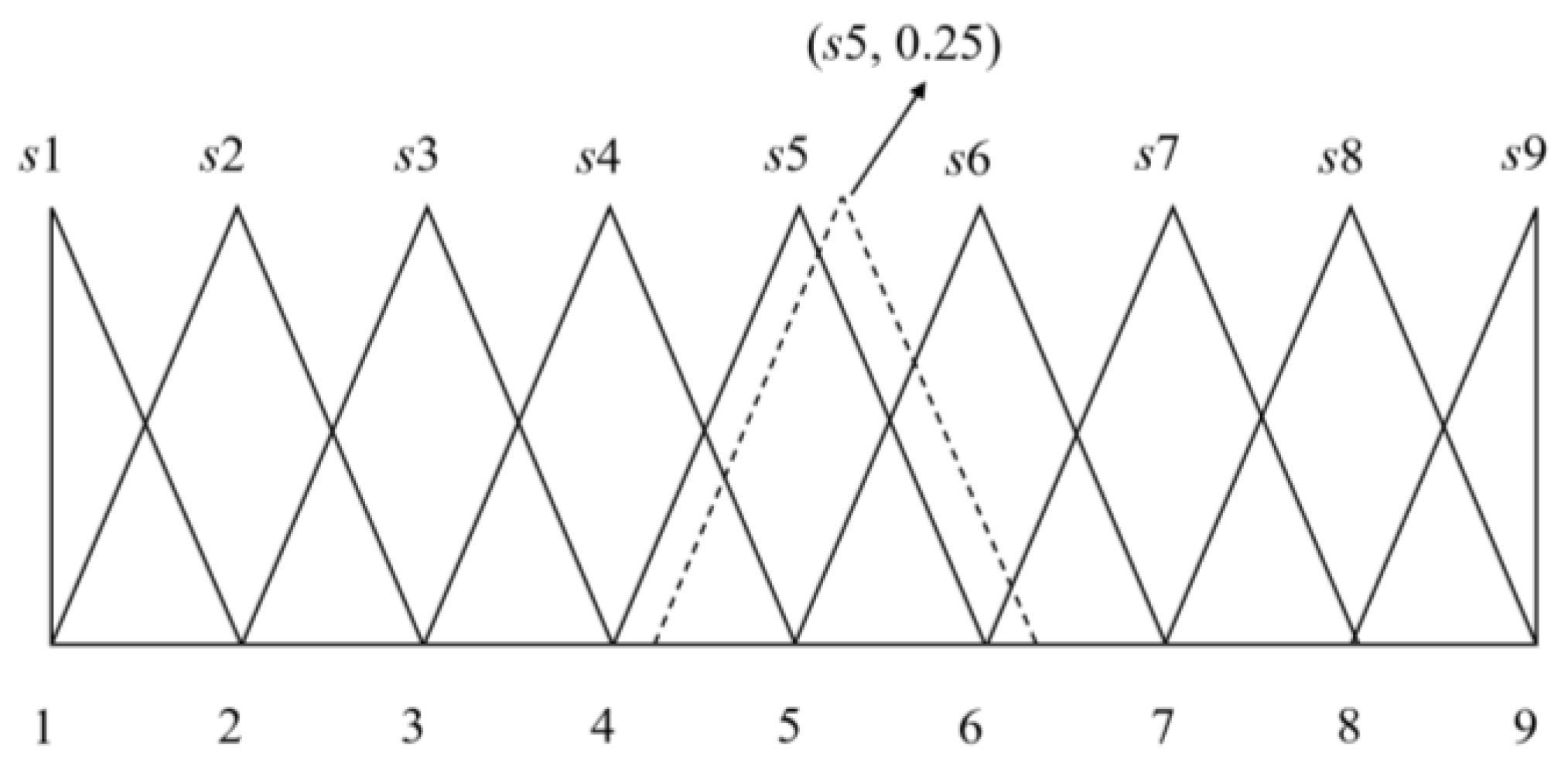
Since the traditional TOPSIS and AHP–TOPSIS methods calculate the arithmetic mean to obtain the crisp value during the operation process, some subtle information will be ignored or vanished easily. As seen in Table 6, the average mean value of Suppliers 2, 4, and 5 was 5 when grading the “QU” criteria, even though managers (decision makers) did not have the complete information. These conditions may result in some bias in the subsequent calculations. Therefore, the characteristics of the 2-tuple FLM were used in this study to deal with the aforementioned problems. In the “QU” criteria, the average mean values of Suppliers 2, 4, and 5 were (𝑠5, 0.250), (𝑠5, 0.000), and (𝑠5, −0.250), respectively. Therefore, the proposed novel soft fuzzy AHP–TOPSIS method can provide complete information and prevent erroneous analysis.

Although the proposed method has several advantages, there is one aspect that requires attention when applying the method. The proposed method utilizes the fuzzy AHP to calculate the relative weights of evaluation criteria. Therefore, it is essential for experts to have a basic understanding of the fuzzy AHP method in order to provide a suitable pairwise comparison matrix for the selection of a green supplier of raw materials.

5. Conclusions

Businesses are grappling with balancing economic development and sustainable environmental practices amidst a growing emphasis on environmental and ecological preservation. Issues related to environment-friendly materials, packaging, eco-landscaping, and production pollution management have become focal points of concern for industry and academia alike. Numerous scholars have shown interest in performing research to evaluate green manufacturing suppliers, particularly those in various industrial chains, aiming to mitigate the adverse impact of producing non-environment-friendly materials. In the past, weight evaluation methods commonly assumed equal weights for evaluation indices. However, the AHP enables the calculation of individual weights for each evaluation index, thereby minimizing subjective bias and effectively addressing MCDM problems. Nevertheless, assessments of this nature often involve uncertainty and ambiguity. To enhance the evaluation accuracy, this study employs the fuzzy AHP method to process fuzzy information. Regarding ranking, many research methods rely on simple weighted calculations. In contrast, the TOPSIS method aids evaluators in identifying the optimal solution by measuring the geometric distance between the optimal and worst solutions. This approach allows for a more objective and comprehensive assessment of the advantages and disadvantages of each option. Based on the above reasons, this study integrates the fuzzy AHP method, the TOPSIS method, and the 2-tuple FLM to evaluate the performance of green suppliers. Through numerical verification and a comparison between the AHP–TOPSIS and the traditional TOPSIS methods, the proposed novel soft fuzzy AHP–TOPSIS method presented the following advantages:

(1)

The proposed novel soft fuzzy AHP–TOPSIS method can simultaneously process qualitative and quantitative information in MCDM problems.

(2)

The proposed novel soft fuzzy AHP–TOPSIS method can fully consider the weight of different criteria in MCDM problems.

(3)

The proposed novel soft fuzzy AHP–TOPSIS method can take into account the objectively estimated information fully provided by experts.

(4)

The proposed novel soft fuzzy AHP–TOPSIS method can fully consider all relevant and available information.

As the overall economic environment remains unclear after the COVID-19 epidemic, experts are vulnerable to the unclear, missing, or incomplete evaluation of information when selecting suppliers. Future researchers may consider different fuzzy membership functions such as trapezoid and Gaussian, or pursue intuitionistic and picture fuzzy sets to fully consider the available fuzzy information offered by different experts to accurately reflect their inner thoughts. In terms of alternative performance evaluation, various research methods can be considered, such as CoCoSo, ELECTRE, and DEA. Additionally, the evaluation of expert decision preferences can also be incorporated. By doing so, not only can the breadth of research be expanded, but it can also align more closely with real-world problems.