Lifecycle Value Sustainment and Planning Mission Upgrades for Complex Systems: The Case of Warships
Abstract
1. Introduction
- (1)
- Existing systems may not have been designed with changeability in mind. When a system is designed and implemented, the design choices made at that time can limit the ability of the system to change or evolve over time. These limitations may not become apparent until the system needs to be modified, and the cost of making these modifications can be high.
- (2)
- Existing systems may not have been well-documented, making it difficult to understand how the system works or how changes might impact the system. This lack of documentation can make it challenging to identify areas of the system that are most in need of change or to understand how changes might impact other parts of the system.
- (3)
- Another factor that can make it difficult to apply changeability analysis to existing systems is the lack of a clear understanding of the system’s requirements or the environment in which it operates. If the system’s requirements or operating environment have changed since the system was designed, the original design may no longer be appropriate, and changes may be required to ensure that the system continues to meet its intended goals.
- (4)
- The cost of making changes to an existing system can be high, both in terms of time and resources. This cost can make it difficult to justify making changes to the system, particularly if the benefits of those changes are not clear.
2. Background
2.1. Changeability Analysis Methods
2.2. Applying Changeability Analysis Methods to In-Service Systems
- System path dependence: akin to the butterfly effect, the lifecycle path of an existing system is dependent on the system’s response to evolving requirements through time; had one system design decision been made differently, the system’s performance for its remaining service life may be drastically altered. Hence, it is critical to understand the consequences of all perceivable decisions. Since many decisions are available to stakeholders in response to a new set of requirements, decision-makers can only be sure of the best decision if all possible design alternatives and consequent lifecycle paths are understood. Applying this understanding, decisions that increase value in the short-term (e.g., major technology upgrade) though inhibit further increases in value in the long-term (e.g., consume all margins preventing future upgrades) can be avoided, allowing all decisions to be optimised for lifecycle value. However, the current state of the EEA (Ross & Rhodes, 2008) does not allow for a full enumeration of path-dependent system lifecycles. This work pays particular attention to path dependency, as an addition to the EEA framework.
- Issue of short-term underperforming designs: the generation of all possible lifecycle paths, dependent upon a proposed sequence of context and perception-driven requirements, yields many possible system end states. A subset of these system end states may underperform against a subset of contexts and preferences. In the traditional application of EEA, a strategy or goal is applied to each epoch individually [9]. The best performing system end state(s) for that strategy is (are) selected, initializing the creation of a new epoch to analyse the selected system state(s). In this manner, underperforming system end states are not analysed further, and stakeholders fail to gain knowledge of their subsequent performance in later epochs. It is possible that underperforming design options in the short-term evolve to become the best-performing designs in the long term. While [7,9] acknowledge this concept as an important consideration for the current state of EEA, the concept can only be suitably achieved through a full enumeration of path-dependent system lifecycles.
- Changing the change variables: The fundamental principle of changeability analysis implies that complex engineered systems need to change over time as a strategic response to maintain value. Such systems, however, change by adding/upgrading subsystems, which may be regarded as complex systems in their own right. For example, [32] and [35] applied changeability analysis to the conceptual design of a warship and missile system, respectively; albeit, the missile subsystem commonly evolves over the life of a warship. Factoring the rate at which subsystems change, i.e., their performance and physical specifications, is an important consideration to more accurately predict the impact of changes on a system. Accordingly, factoring subsystem changes compounds the importance of path dependence since the design parameters used for subsystem upgrades can become time-dependent. Combining system path dependence and the principles of change to both systems and subsystems in a single analysis can help rectify the hindrances of current changeability analysis methods. However, we emphasize that this work is not intended to consider all types of uncertainty. The only type of uncertainty of interest to this research is tactical uncertainty in operational scenarios of a system.
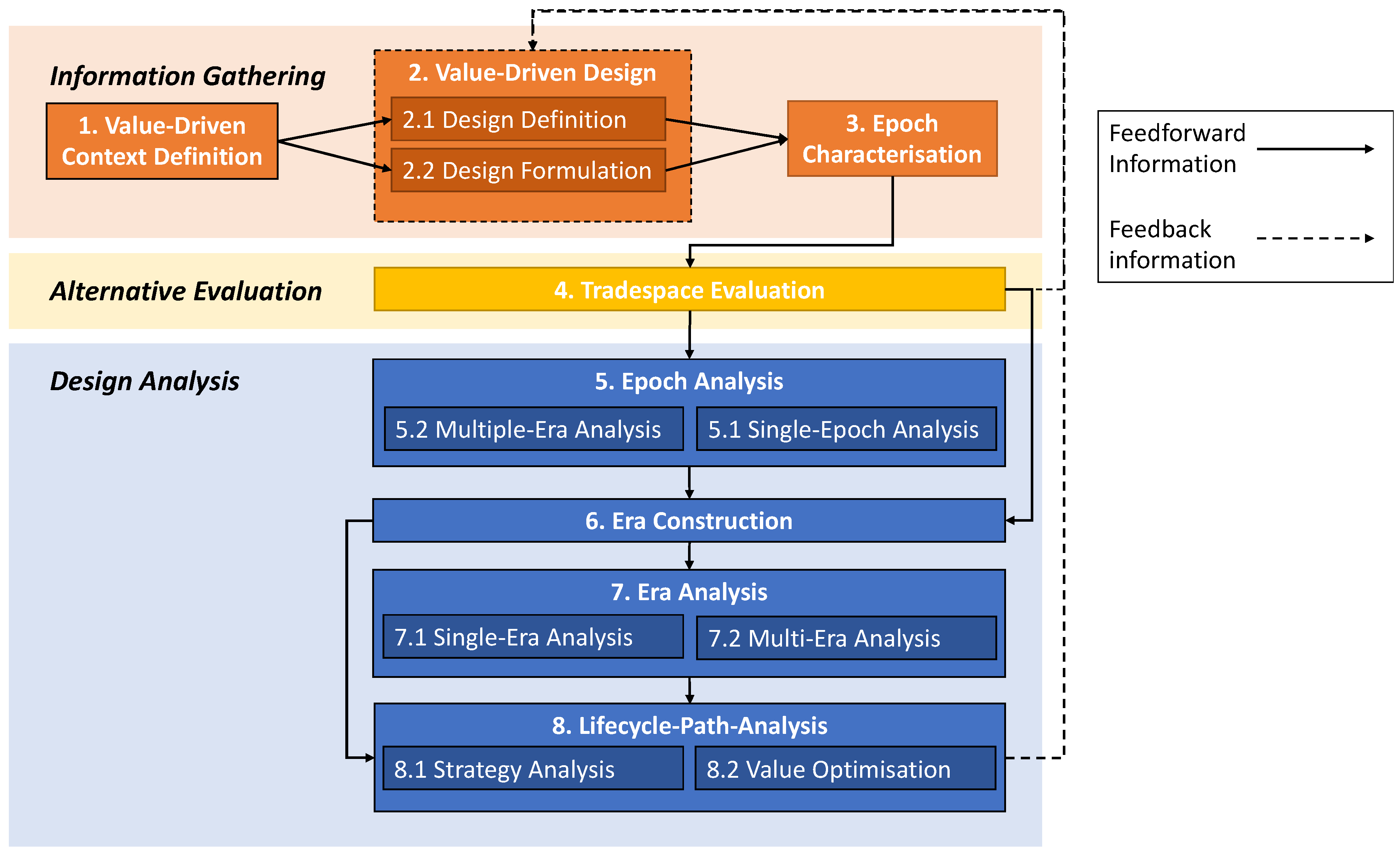
3. RSC Method: Epoch-Era Networks
- Information gathering;
- Alternatives evaluation;
- Design analysis.
3.1. Information Gathering
3.2. Alternatives Evaluation
3.3. Design Analysis
3.4. Constructing and Analysing Epoch-Era Networks
4. Case Study
- (1)
- Acquiring information about system parameters (that are usually well documented for defence systems and not so well for other systems) is a challenge;
- (2)
- Assessment of cost of changes might not be knowable a priori in the case of some systems. This is because changes are not planned in advance for some existing systems, so the cost issue becomes a major challenge;
- (3)
- Assessing the value of changes relative to future requirements is also a major challenge. Here, we demonstrate the value evaluations for three neatly defined requirements that are gearing the vessel for anti-air and anti-submarine operations. However, these requirements might not be as clear for other systems and might be accompanied by ambiguities which make the changes in value estimation challenging.
4.1. Transition Rules, Attributes and Design Variables
4.2. Epoch Requirements and Era Construction
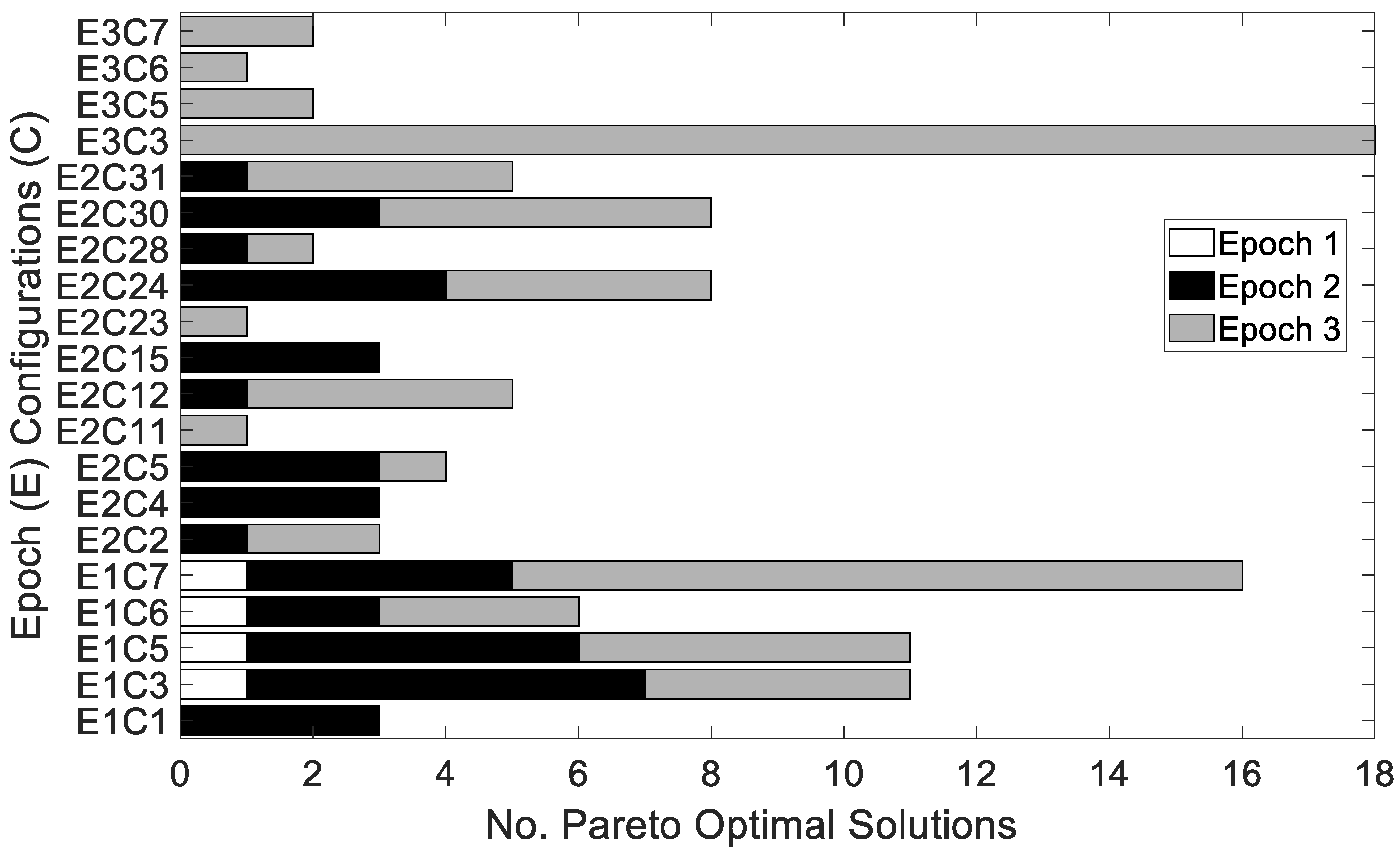
5. Results and Discussion
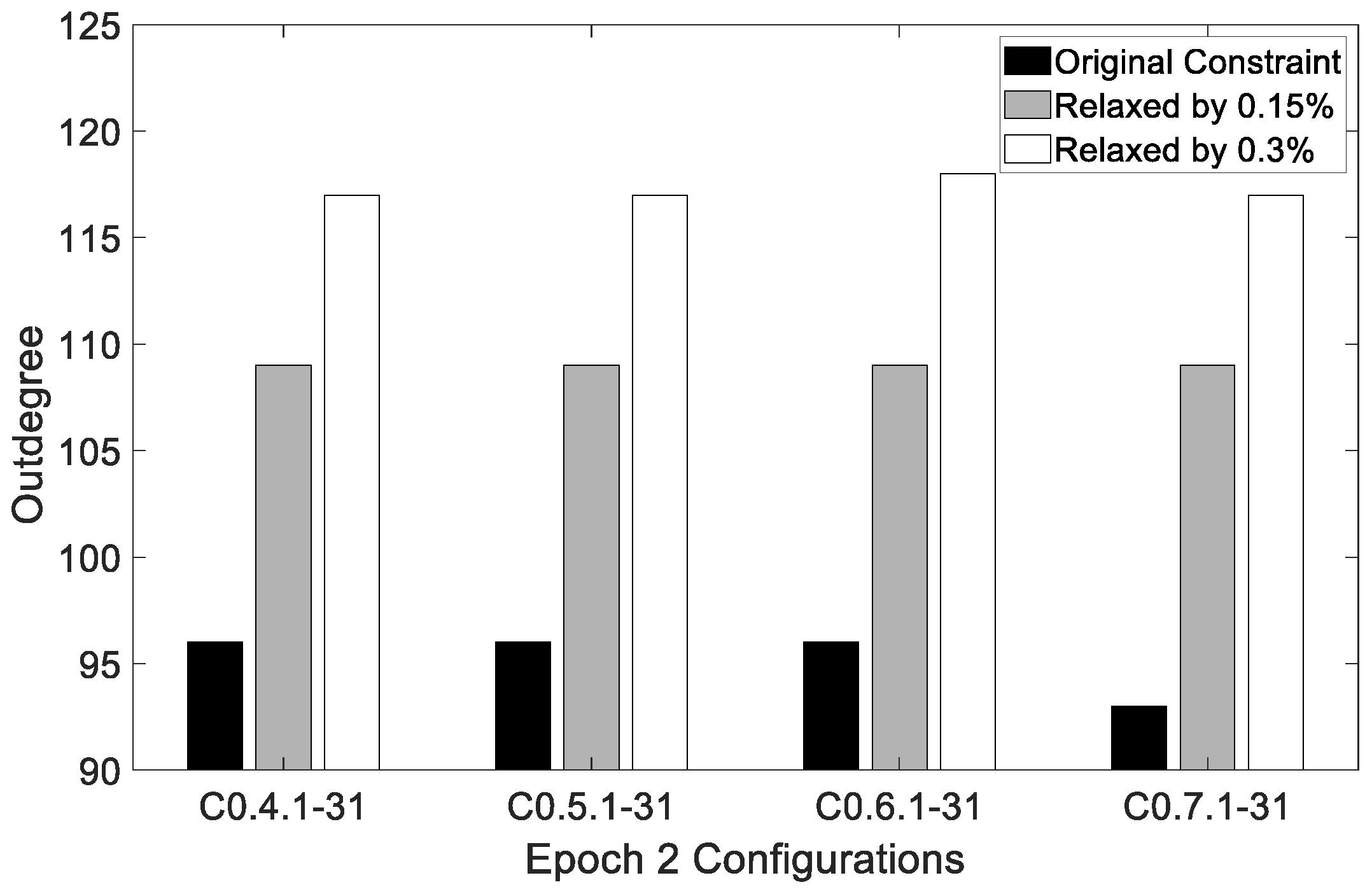
5.1. Strategy Analysis: Maximising Utility
5.2. Strategy Analysis: Maximising Utility for a Given Expense
5.3. Comparing Strategies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Acronyms
References
- Ahuja, R.K.; Mehlhorn, K.; Orlin, J.; Tarjan, R.E. Faster algorithms for the shortest path problem. J. ACM 1990, 37, 213–223. [Google Scholar] [CrossRef]
- Bauernhansl, T.; Mandel, J.; Diermann, S. Evaluating changeability corridors for sustainable business resilience. Procedia CIRP 2012, 3, 364–369. [Google Scholar] [CrossRef]
- Clarkson, P.J.; Simons, C.; Eckert, C. Predicting change propagation in complex design. J. Mech. Des. 2004, 126, 788–797. [Google Scholar] [CrossRef]
- Clempner, J.B. Necessary and sufficient Karush–Kuhn–Tucker conditions for multiobjective Markov chains optimality. Automatica 2016, 71, 135–142. [Google Scholar] [CrossRef]
- de Neufville, R. Architecting/Designing Engineering Systems Using Real Options; Massachusetts Institute of Technology: Boston, MA, USA, 2002. [Google Scholar]
- De Weck, O.L.; De Neufville, R.; Chaize, M. Staged deployment of communications satellite constellations in low earth orbit. J. Aerosp. Comput. Inf. Commun. 2004, 1, 119–136. [Google Scholar] [CrossRef]
- Deshmukh, A.; Wortman, M.; Boehm, B.; Jacques, D.; Housel, T.; Sullivan, K.; Collopy, P. Value of flexibility-Phase 1; Systems Engineering Research Concil, Stevens Inst Of Tech: Hoboken, NJ, USA, 2010; Report no SERC-2010-TR-010-1. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Dwyer, D.M. Toward Changeability Analysis for New and Existing Systems: A Foundational Definition and Comparison of Methods; Defence Science and Technology Group: Canberra, ACT, Australia, 2020.
- Dwyer, D.M.; Efatmaneshnik, M. Changeability analysis for existing systems. Aust. J. Multi-Discip. Eng. 2020, 16, 43–53. [Google Scholar] [CrossRef]
- Dwyer, D.M.; Morris, B.A. A Ship Performance Modelling and Simulation Framework to Support Design Decisions throughout the Capability Life Cycle: Part 2-Acquisition and in Service; Defence Science and Technology Group: Canberra, ACT, Australia, 2019.
- Eckert, C.; Clarkson, P.J.; Zanker, W. Change and customisation in complex engineering domains. Res. Eng. Des. 2004, 15, 1–21. [Google Scholar] [CrossRef]
- Efatmaneshnik, M.; Shoval, S.; Qiao, L. A Standard Description of the Terms Module and Modularity for Systems Engineering. IEEE Trans. Eng. Manag. 2018, 67, 365–375. [Google Scholar] [CrossRef]
- El-Akruti, K.; Dwight, R.; Zhang, T. The strategic role of engineering asset management. Int. J. Prod. Econ. 2013, 146, 227–239. [Google Scholar] [CrossRef]
- Engel, A.; Browning, T.R. Designing systems for adaptability by means of architecture options. Syst. Eng. 2008, 11, 125–146. [Google Scholar] [CrossRef]
- Fitzgerald, M.E.; Ross, A.M. Mitigating contextual uncertainties with valuable changeability analysis in the multi-epoch domain. In Proceedings of the 2012 IEEE International Systems Conference SysCon 2012, Vancouver, BC, Canada, 19–22 March 2012. [Google Scholar]
- Fitzgerald, M.E.; Ross, A.M. Sustaining lifecycle value: Valuable changeability analysis with era simulation. In Proceedings of the 2012 IEEE International Systems Conference SysCon 2012, Vancouver, BC, Canada, 19–22 March 2012. [Google Scholar]
- Fricke, E.; Gebhard, B.; Negele, H.; Igenbergs, E. Coping with changes: Causes, findings, and strategies. Syst. Eng. 2000, 3, 169–179. [Google Scholar] [CrossRef]
- Fricke, E.; Schulz, A.P. Design for changeability (DfC): Principles to enable changes in systems throughout their entire lifecycle. Syst. Eng. 2005, 8, no. 4, 342–359. [Google Scholar] [CrossRef]
- Frolov, V.; Mengel, D.; Bandara, W.; Sun, Y.; Ma, L. Building an ontology and process architecture for engineering asset management. In Proceedings of the 4th World Congress of Engineering Asset Lifecycle Management 2009, Athens, Greece, 28–30 September 2009. [Google Scholar]
- Hooper, R.; Armitage, R.; Gallagher, A.; Osorio, T. Whole-Life Infrastructure Asset Management: Good Practice Guide for Civil Infrastructure; Construction Industry Research and Information Association: London, UK, 2009; CIRIA Report C, Issue. [Google Scholar]
- Jnitova, V.; Efatmaneshnik, M.; Joiner, K.F.; Chang, E. Improving Enterprise Resilience by Evaluating Training System Architecture: Method Selection for Australian Defense. In A Framework of Human Systems Engineering: Applications and Case Studies; Handley, H.A.H., Tolk, A., Eds.; Wiley-IEEE Press: New York, NY, USA, 2020; pp. 143–183. [Google Scholar]
- McManus, H.; Hastings, D.E. A Framework for Understanding Uncertainty and Its Mitigation and Exploitation in Complex Systems; INCOSE international symposium: Rochester, NY, USA, 2005. [Google Scholar]
- Rehn, C.F.; Agis, J.J.G.; Erikstad, S.O.; de Neufville, R. Versatility vs. retrofittability tradeoff in design of non-transport vessels. Ocean. Eng. 2018, 167, 229–238. [Google Scholar] [CrossRef]
- Rehn, C.F.; Pettersen, S.S.; Garcia, J.J.; Brett, P.O.; Erikstad, S.O.; Asbjørnslett, B.E.; Ross, A.M.; Rhodes, D.H. Quantification of changeability level for engineering systems. Syst. Eng. 2019, 22, 80–94. [Google Scholar] [CrossRef]
- Roberts, C.J.; Richards, M.G.; Ross, A.M.; Rhodes, D.H.; Hastings, D.E. Scenario planning in dynamic multi-attribute tradespace exploration. In Proceedings of the 2009 3rd Annual IEEE Systems Conference, Vancouver, BC, Canada, 23–26 March 2009. [Google Scholar]
- Ross, A. Managing Unarticulated Value: Changeability in Multi-Attribute Tradespace Exploration; MIT: Cambridge, MA, USA, 2006. [Google Scholar]
- Ross, A.; Hastings, D.E. Assessing Changeability in Aerospace Systems Architecting and Design Using Dynamic Multi-Attribute Tradespace Exploration; Space: San Jose, CA, USA, 2006. [Google Scholar]
- Ross, A.; Hastings, D.E.; Warmkessel, J.M.; Diller, N.P. Multi-attribute tradespace exploration as front end for effective space system design. J. Spacecr. Rocket. 2004, 41, 20–28. [Google Scholar] [CrossRef]
- Ross, A.; McManus, H.; Rhodes, D.; Richards, M.; Hastings, D.; Long, A. Responsive systems comparison method: Case study in assessing future designs in the presence of change. In Proceedings of the AIAA SPACE 2008 Conference Exposition 2008, San Diego, CA, USA, 9–11 September 2008. [Google Scholar]
- Ross, A.; Rhodes, D. Using natural value-centric time scales for conceptualizing system timelines through epoch-era analysis. In Proceedings of the INCOSE International Symposium 2008, Utrecht, The Netherlands, 15–19 June 2008. [Google Scholar]
- Ross, A.; Rhodes, D.H.; Hastings, D.E. Defining changeability: Reconciling flexibility, adaptability, scalability, modifiability, and robustness for maintaining system lifecycle value. Syst. Eng. 2008, 11, 246–262. [Google Scholar] [CrossRef]
- Ross, A.M.; Rhodes, D.H. Towards a prescriptive semantic basis for change-type ilities. Procedia Comput. Sci. 2015, 44, 443–453. [Google Scholar] [CrossRef]
- Schaffner, M.A.; Ross, A.M.; Rhodes, D.H. A method for selecting affordable system concepts: A case application to naval ship design. Procedia Comput. Sci. 2014, 28, 304–313. [Google Scholar] [CrossRef]
- Schaffner, M.A.; Shihong, M.W.; Ross, A.M.; Rhodes, D.H. Enabling design for affordability: An epoch-era analysis approach. In Proceedings of the Tenth Annual Acquisition Research Symposium, Monterey, CA, USA, May 2013. [Google Scholar]
- Siddiqi, A.; de Weck, O.L. Modeling methods and conceptual design principles for reconfigurable systems. ASME J. Mech. Des. 2008, 130, 101102. [Google Scholar] [CrossRef]
- Sidoti, D.; Avvari, G.V.; Mishra, M.; Zhang, L.; Nadella, B.K.; Peak, J.E.; Hansen, J.A.; Pattipati, K.R. A Multiobjective Path-Planning Algorithm With Time Windows for Asset Routing in a Dynamic Weather-Impacted Environment. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 3256–3271. [Google Scholar] [CrossRef]
- Sullivan, B.P.; Rossi, M.; Ramundo, L.; Terzi, S. Characteristics for the implementation of changeability in complex systems. In Proceedings of the XXIV Summer School “Francesco Turco”—Industrial Systems Engineering 2019, Brescia, Italy, 11–13 September 2019. [Google Scholar]
- Tan, W.; Sauser, B.J.; Ramirez-Marquez, J.E.; Magnaye, R.B. Multiobjective Optimization in Multifunction Multicapability System Development Planning. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 785–800. [Google Scholar] [CrossRef]
- Viscito, L. Quantifying Flexibility in the Operationally Responsive Space Paradigm; MIT: Cambridge, MA, USA, 2009. [Google Scholar]
- Viscito, L.; Chattopadhyay, D.; Ross, A.M. Combining pareto trace with filtered outdegree as a metric for identifying valuably flexible systems. In Proceedings of the 7th Annual CSER, Loughborough, UK, 20–23 April 2009. [Google Scholar]
- Viscito, L.; Ross, A. Quantifying flexibility in tradespace exploration: Value-weighted filtered outdegree. In Proceedings of the AIAA SPACE 2009 Conference Exposition, Pasadena, CA, USA, 14–17 September 2009. [Google Scholar]
- Wojtaszek, D.; Wesolkowski, S. Evaluating the Flexibility of Military Air Mobility Fleets. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 435–445. [Google Scholar] [CrossRef]







| Characteristic | Value (Units) |
|---|---|
| Mass | 3600 (tons) |
| Length Overall | 118 (m) |
| Beam | 14.8 (m) |
| Draft | 4.35 (m) |
| Max Speed Range | 27 (knots) 6000 (nautical miles) |
| Complement | 179 (officers, sailors, crew) |
| Transitional Rules | Units | Available (A)/Limit (L) |
|---|---|---|
| Area Margin | m2 | 717 (A) |
| Volume Margin | m3 | 346 (A) |
| Mass Margin | tons | 3800 (L) |
| VCG Margin | m | 6.28 (L) |
| Utility Attributes (U) | Units | Level Range (X) (Worst–Best) | Weighting (k) |
|---|---|---|---|
| Technological Capability | Nil | 0–1 | 0.7 |
| Seakeeping | Nil | 0–1 | 0.1 |
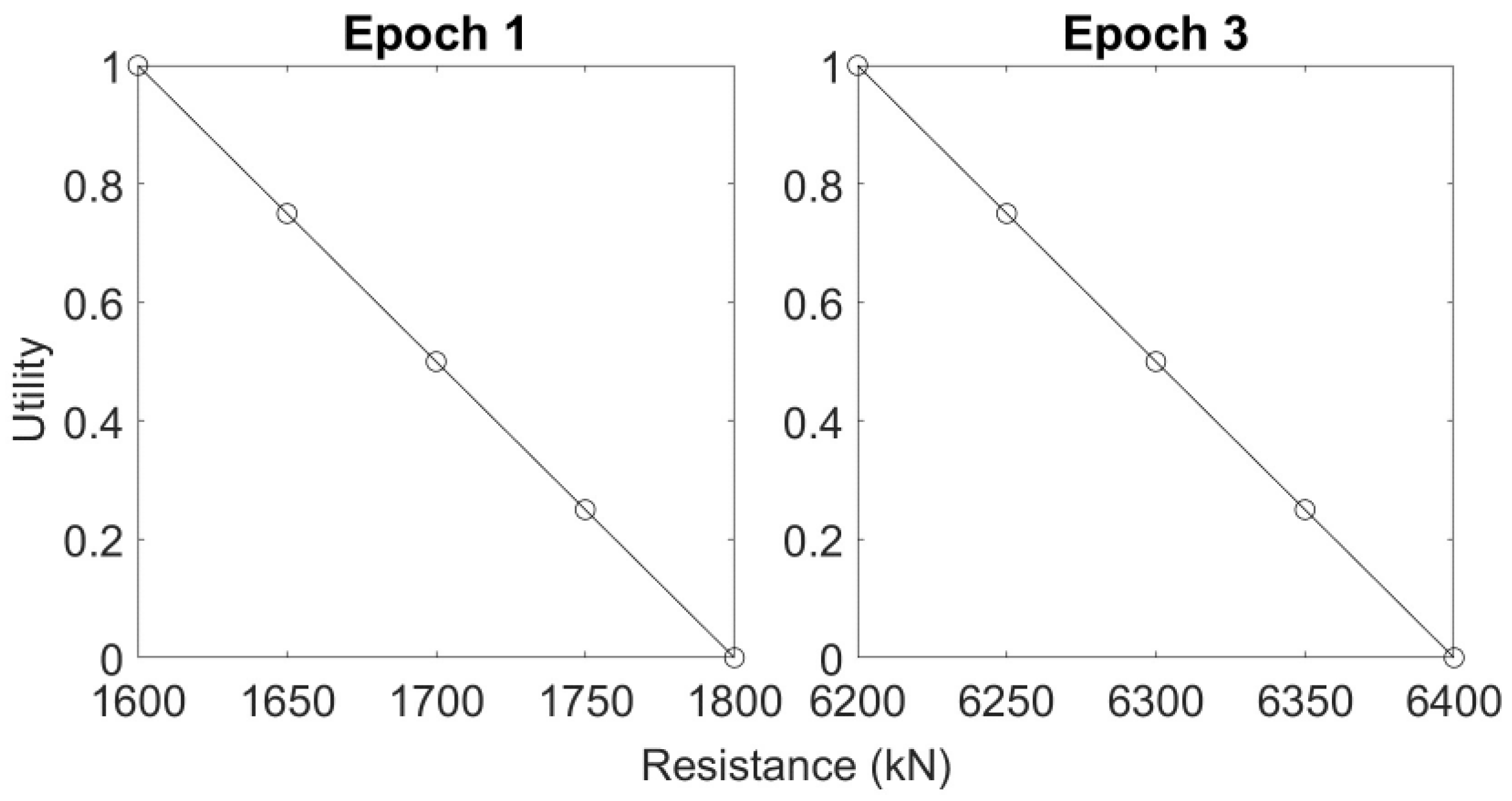
| Resistance | kN | 6400–1600 | 0.1 |
| Stability (Metacentric Height) | m | 0.6–1.45 | 0.1 |
| Expense Attributes (E) | Units | Level Range (X) (Worst–Best) | Weighting (k) |
| Area Margin Remaining | % | 0–100 | 0.25 |
| Volume Margin Remaining | % | 0–100 | 0.25 |
| Mass Margin Remaining | % | 0–100 | 0.25 |
| VCG Margin Remaining | % | 0–100 | 0.25 |
| Design Variable (Acronym) | Range (Units) |
|---|---|
| Mass a | 3600–3800 (tons) |
| Length Waterline | 109–110 (m) |
| Draft | 4.4–4.6 (m) |
| Vertical Centre of Gravity (VCG) a | 5.9–6.3 (m) |
| Cruising Speed Profile | 15–19 (kn) |
| Operating Wave- Length + Height | 9–13 (s) + 3–5 (m) |
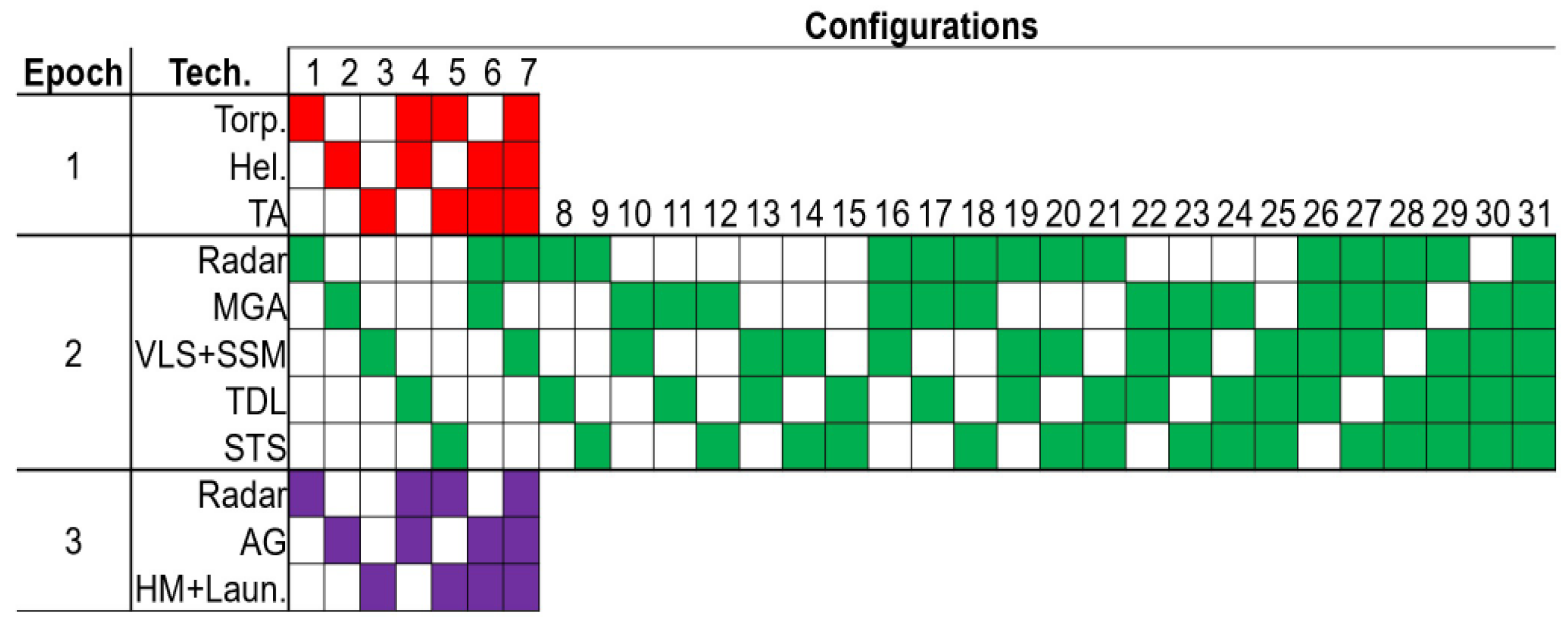
| Torpedoes (Torp.) a | No, Yes |
| Helicopter (Hel.) a | No, Yes |
| Towed Array (TA) a | No, Yes |
| Radar a | No, Yes |
| Main Gun Ammo (MGA) a | No, Yes |
| Vertical Launch System (VLS) a + Seasparrow Missiles (SSM) a | No, Yes |
| Tactical Data Link (TDL) a | No, Yes |
| Search and Track System (STS) a | No, Yes |
| Automatic Guns (AG) a | No, Yes |
| Harpoon Missiles (HM) a + Launcher (Laun.) a | No, Yes |
| Uncertainty Category | Epoch Variable | Values (Units) |
|---|---|---|
| ASW Capability | Upgrade Torp. b | No, Yes (-) |
| Upgrade Hel. b | No, Yes (-) | |
| Upgrade TA b | No, Yes (-) | |
| AAW Capability | Upgrade Radar b | No, Yes (-) |
| Add VLS + Upgrade SSM b | No, Yes (-) | |
| Upgrade MGA b | No, Yes (-) | |
| Add TDL | No, Yes (-) | |
| Add STS | No, Yes (-) | |
| ASuW Capability | Upgrade Radar b | No, Yes (-) |
| Upgrade AG b | No, Yes (-) | |
| Add Launch. + Upgrade HM b | No, Yes (-) | |
| Operating Condition | Dominant cruise speed | 15, 17, 19 (kn) |
| Operating Environment | Sea State | 3, 4, 5 (-) |
| Epoch 1 ASW | Epoch 2 AAW | Epoch 3 ASuW |
|---|---|---|
| EVs (values) | EVs (values) | EVs (values) |
| Up. Torp. (no, yes) | Up. Radar (no, yes) | Up. Radar (no, yes) |
| Up. Hel. (no, yes) | Add VLS + Up. SSM (no, yes) | Add Launch. + Up. HM (no, yes) |
| Up. TA (no, yes) | Up. MGA (no, yes) | Up. AG (no, yes) |
| Cruise Speed (15) | Add TDL (no, yes) | Cruise speed (19) |
| Sea State (3) | Add STS (no, yes) | Sea State (5) |
| Cruise Speed (17) | ||
| Sea State (4) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dwyer, D.; Efatmaneshnik, M. Lifecycle Value Sustainment and Planning Mission Upgrades for Complex Systems: The Case of Warships. Systems 2023, 11, 183. https://doi.org/10.3390/systems11040183
Dwyer D, Efatmaneshnik M. Lifecycle Value Sustainment and Planning Mission Upgrades for Complex Systems: The Case of Warships. Systems. 2023; 11(4):183. https://doi.org/10.3390/systems11040183
Chicago/Turabian StyleDwyer, Dylan, and Mahmoud Efatmaneshnik. 2023. "Lifecycle Value Sustainment and Planning Mission Upgrades for Complex Systems: The Case of Warships" Systems 11, no. 4: 183. https://doi.org/10.3390/systems11040183
APA StyleDwyer, D., & Efatmaneshnik, M. (2023). Lifecycle Value Sustainment and Planning Mission Upgrades for Complex Systems: The Case of Warships. Systems, 11(4), 183. https://doi.org/10.3390/systems11040183







