Abstract
After the COVID-19 pandemic has subsided, the catering industry has returned to its previous thriving scene. Many restaurants have launched group buying services and collaborate with third-party online platforms to attract more customers. For the optimal decisions and maximum profits of restaurants and online platforms, a two-layer supply chain model is designed to investigate and study the price strategies and service strategies. Considering the service levels of restaurants and platforms, we construct the mathematical expressions of the offline retail model, online retail model, and online group buying model, respectively, and solve the game equilibrium. The results are shown as follows: (1) With cooperation between the restaurant and platform, both the restaurant and platform can obtain their maximum profits when they apply optimal pricing strategies. (2) The optimal pricing strategies of the restaurant are influenced by the sensitivity coefficients of customers to the restaurant and platform’s service levels, and the cost coefficients of the restaurant and platform’s service levels. (3) The maximum profit of the restaurant is directly proportional to the number of new potential consumers who are attracted. The more potential consumers who are attracted, the higher the profit the restaurant earns. The research results provide a reference for restaurants and platforms to formulate price strategies and service strategies, to help restaurants and platforms achieve more profits.
1. Introduction
O2O (Online to Offline) is a business model that utilizes e-commerce platforms to combine online information with offline products [1]. Consumers can browse product information online, complete payments, and obtain goods or services offline. In recent years, e-commerce platforms have developed rapidly, and increasingly more consumers have become accustomed to purchasing goods or booking services online. For restaurants, collaborating with third-party online platforms and providing group buying services are also common ways to increase sales channels and expand sales.
Group buying, also, namely, group purchase or Tuangou in Chinese, refers to a shopping model which consumers with the same needs group together to purchase with discounted prices [2]. In recent years, various industries have been conducting group buying businesses to attract more consumers [3]. As early as the late 20th century, the group buying model appeared in people’s vision, and a large number of group buying websites emerged at that time. However, due to the complexity of the trading mechanism and other factors, group buying websites did not achieve the expected profits, and most were subsequently shut down [4]. At present, there are well-known group buying websites like Pinduoduo (pinduoduo.com), Meituan (meituan.com), and Groupon (groupon.com). In China, Pinduoduo provides many kinds of groups with logistics distribution. The catering group buying (CGB) service is mainly provided by Meituan, which is a mode of placing orders online and dining at the restaurant. Both platforms have community group buying business branches, which is another O2O consumption model. The objective of this study is to look at one of the Meituan’s CGB models, which mostly focuses on on-demand dining and does not require delivery.
At present, this group buying model is gradually being integrated into people’s daily lives. According to data released by China Chain Store and Franchise Association (CCFA) and Huaxing Capital, the market size of Chinese group meals in 2022 reached 1.98 trillion CNY, and it is gradually increasing.
The COVID-19 pandemic has had a huge impact on many industries, among which the catering industry is one of the most severely affected [5]. During the pandemic, many restaurants were forced to close due to a sharp decline in sales. People trapped by the pandemic also found it difficult to eat food outside. After the pandemic, people have a strong desire to consume and amuse themselves. Consumers’ emotional states are more positive than before [6]. Many restaurants have also issued coupons to further stimulate consumption. Nowadays, China’s catering industry is in a stage of rapid growth by O2O, while many restaurants are often experiencing empty seats and queues. According to the National Bureau of Statistics, from January to February 2023, national catering revenue increased by 9.2% year-by-year [7]. People’s lives and work have returned to normal in all aspects. Most people choose to travel together, and dining with friends is an important way to connect with each other. At this point, meal purchasing in groups is often more cost-effective than purchasing separately. Taking a barbecue buffet in Shanghai, China, as an example, a separate order costs 59 CNY, with a meal for two people costing 103 CNY (51.5 CNY per person) and a meal for three people costing 154 CNY(51.3 CNY per person). Reasonable group buying prices and retail prices can attract more consumers to purchase food and increase restaurant revenue. Therefore, it is particularly important for restaurants to establish scientific and reasonable group buying and retail prices.
Nowadays, most restaurants have opened online channels [8]. The platform provides online stores for restaurants, which need to pay a certain percentage of commission to the platform based on sales revenue. Therefore, the more sales, the higher the revenue for restaurants and platforms. The service level of restaurants (such as the environment, service quality of waiters, etc.) and the service level of platforms (such as ease of use, customer quality, etc.) are both factors that affect the sales volume of food. Consequently, the service qualities of restaurants and platforms require careful decision-making. However, restaurants mostly rely on experience and lack scientific basis when setting group buying and retail prices, making it difficult to maximize profits. Possible malicious competition and price wars among platforms are hidden dangers that restrict the development of CGB. Therefore, reasonable price setting can help restaurants acquire more revenue and earn a good reputation.
This article focuses on the catering supply chain, establishes the demand function based on consumer utility theory and perceived value theory, and constructs a game model solving the price and service strategies of restaurants and platforms to maximize profits, so that both restaurants and platforms can obtain more profits from it. The aim of this study is to address the following two issues:
(1) What are the optimal prices, best service levels, and maximum profits for both parties in these models of offline retail, online retail, and online group buying for restaurants and platforms?
(2) How do the sensitivity coefficients, the cost coefficients of service levels, the cost coefficients of grouping, and the number of potential consumers attracted to each model affect the optimal decision-making and maximum profits of restaurants and online platforms?
The main contributions of this study are as follows:
(1) The business of online group buying catering supply chain is studied, including offline retail, online retail, and online group buying. We establish several game models to study the optimal price strategies and service strategies, providing a reference for restaurants and platforms to make decisions.
(2) The impact of the sensitivity coefficient, cost coefficient of service level, cost of assembling a group, and the number of potential consumers attracted by each model on the optimal decisions and maximum profits of both parties is analyzed, and reasonable suggestions are provided for the catering supply chain.
(3) The impact of the numbers of new potential consumers attracted by the online retail and online group buying models on the profits of restaurants and platforms is discussed. The more new consumers who are attracted, the greater the profits.
2. Literature Review
The development of information technology has promoted the prosperity of e-commerce and the emergence of new sales models, with online group buying being one of them. Among this, related research mainly focuses on three aspects: online group buying pricing strategies, factors affecting online group buying, and O2O supply chain pricing strategies. This paper will review the relevant literature from these three aspects.
2.1. Online Group Buying Pricing Strategies
In terms of pricing strategies for online group buying, scholars have conducted much research from different perspectives in various situations. For example, Zhu et al. [9] proposed a pricing method for online group buying based on continuous price functions, which dynamically set prices based on the buyer’s demand and thereby encouraged the buyer to provide realistic quotations. Zhang et al. [10] proposed a pricing method for online group buying based on buyer fixed bidding, aiming at the impact of buyer demand quantity on the participant population. Ming and Tunca [11] established a continuous-time dynamic game theory model to study consumer behavior and solve its equilibrium, mathematically explaining the extent to which group buying can increase profit.
Some scholars have also studied group buying pricing strategies in specific situations. For example, Ni [12] considered both positive and negative network effects and proposed three possible sales strategies for group buying, individual buying, and hybrid buying, as well as their optimal decision on price. Wu et al. [13] studied the method for restaurants to set group buying prices and the optimal promotion strategy for the platform, given the promotion level of group buying websites. He et al. [14] explored fairness-focused behavior in the group buying supply chain and found that the retailer’s fairness-focused behavior does not always harm the supplier’s profits. Guan et al. [15] explored the optimal group buying price strategy in social e-commerce with information sharing. They found that when the cost of information sharing is small or the cost function is a quadratic function, sellers would choose to share information independently. To ensure the quality of fresh food and the profitability of merchants in community group buying, Shui and Li [16] designed a community group buying pricing model and a cold chain vehicle route planning model. Wang and Song [17] found that the emergence of community group buying caused concern about the fairness of businesses. They also found that online retailers would weaken the market position of offline sellers after entering the market. Ando [18] analyzed the pricing strategy of merchants by predicting the market demand and competitive environment. Although there have been many studies on group buying pricing strategies, few scholars have studied catering group buying (CGB). Therefore, it is worthwhile focusing on the issue of online CGB, considering the characteristics of the catering industry while developing pricing strategies and other strategies.
2.2. Factors Affecting Online Group Buying
The second stream of research is the factors affecting online group buying. Hsu et al. [19] conducted a survey on members of online group buying platforms in Taiwan and found that the expected value, hedonic value, and social value of online group buying could affect customer loyalty. Chou [20] studied the influence of different countdown time units on consumers’ willingness to participate in group buying with limited time. He argued that using countdowns expressed with a contracted scale (vs. an expanded scale) can increase their willingness. Kozáková [21] studied the impact of reputation and perceived scale, system quality, information quality, and service quality of online group buying websites on customer confidence and satisfaction in Xi’an group buying, finding that reputation and perceived scale were the most important factors. Ou et al. [22] found that customer consistency behavior had a significant positive impact on online group buying willingness, and that perceived risk had a disruptive effect. Chow et al. [23] constructed an inverted U-shaped relationship between the popularity of group buying and consumers’ purchase intention and found that popularity can promote group buying at low levels, while reaching a certain value would have an inhibitory effect on group buying. Hongsuchon and Li [24] explored the impact of consumer privacy concerns on the willingness to group purchase in communities. Hossain and Rahman [25] studied five personality traits that affect group buying in China, among which extroversion, affinity, and responsibility directly affect the group buying behavior of China customers. Klein and Sharma [26] studied the influence of consumers’ decision-making style and consumers’ intervention (the energy spent by consumers in searching and processing commodity-related information) on consumers’ group purchase intention. Xiao [27] used qualitative methods to explore the factors that motivate consumers to participate in online group buying and explanatory structure modeling to develop a context-specific hierarchical motivation model. Many scholars have analyzed the factors that affect group buying intention by constructing utility functions, which also provides a certain theoretical basis for the following model constructed.
2.3. O2O Supply Chain Pricing Strategies
The third stream of research related to this article is about O2O supply chain pricing strategies. In the related research of O2O supply chain pricing strategy, most scholars used game theory to build a model and solved the best decision. Lin and Hu [28] reviewed the commonly used game models for supply chain pricing and discussed the maximization of supply chain benefits and coordination mechanism. They believed that the profit maximization of agricultural companies and the consumer-centered research perspective would become the focus of future research. Song et al. [29] summarized the types of dual-channel supply chain considering consumers’ green preference and thought that the influence of politics and media should be considered when studying this issue. Yu and Ren [30] used a Stackelberg game model and a Bertrand game model to formulate the best pricing strategy for each member of the food supply chain from online to offline. Some scholars have studied the pricing strategy of O2O retail supply chain. Considering the dynamic reference quality effect of consumers, Qiu et al. [31] established an O2O retail supply chain model composed of suppliers and retailers, and designed a wholesale price, cost sharing, and two-part tariff contract to coordinate the supply chain. Amrouche et al. [32] studied the O2O competition game model in three scenarios: no service input, full compensation for offline service by retailers, and online service by manufacturers. It was found that the cooperation mechanism of full payment for offline service by retailers and revenue sharing could coordinate the O2O supply chain. Datta et al. [33] discussed the dynamic pricing problem of retailers under the condition of stochastic price and sensitive demand of sales efforts, arguing that O2O retail and sales work can help retailers improve profits and reduce waste.
Some scholars studied the pricing strategy of the catering supply chain, which is also the focus of this part. Zheng and Guo [34] believed that not all restaurants should be encouraged to participate or offer online price discounts. Especially for restaurants with fixed service capacity, it was recommended to participate in online price discounts when the number of loyal offline customers is relatively small. The following year [35], they studied a hybrid game model consisting of Nash games between multiple restaurants and Stackelberg games between these restaurants and third-party websites. Xu et al. [36] explored the different strategies that restaurants and third-party online platforms should adopt when collaborating on retail prices within different ranges. Tong et al. [37] compared the impact of dynamic pricing and static pricing strategies on platform profits, based on more than 2.4 million orders traded on the three platforms in China, and found that dynamic pricing performed better. Niu et al. [38] discussed the cooperation strategy between fast food restaurants and third-party online sales platforms when considering logistics strategies (platform logistics and self-logistics). Zhang et al. [39] studied the impact of price subsidies on product pricing and revenue in a single channel supply chain, as well as the impact of price subsidies and fairness concerns on supply chain revenue in a dual giant supply chain. Guo et al. [40] studied the impact of online ordering and in-store dining strategies on restaurant optimal decision-making and maximum profit; they found that when the unit carbon tax price is relatively high, using this strategy can reduce carbon tax costs. Du et al. [41] discussed four combinations of the pricing strategies (online and offline unified pricing and differential pricing) and delivery modes (self-distribution and platform distribution) of restaurants. By comparing the profits in four scenarios, the restaurant can choose the appropriate strategy. Zhang et al. [42] explored the take-away mode of restaurants and found that only when the income from take-away reaches a certain level can restaurants benefit from it. Webb et al. [43] put forward a priority mixed bundling strategy to solve the problems faced by traditional pricing methods and demonstrated its theoretical feasibility in the meantime. In these studies, few scholars have discussed the pricing and other strategies of group buying in catering.
Through a review of the relevant literature, it was found that although there are many studies on group buying and O2O pricing strategies, few scholars have studied the pricing strategies of CGB and how catering merchants using the O2O model set retail prices and group buying prices when collaborating with third-party online platforms. Therefore, the optimal decisions and maximum profits of restaurants and online platforms under each model are calculated, providing a reference for both parties’ decision-making.
3. Problem Description and Assumptions
Considering the service levels of restaurants and third-party online platforms, O2O catering supply chain models are established for three scenarios: offline retail model (OFM), online retail model (ONM), and online group buying model (GBM). Because the real scene is very complicated, the models are reasonably simplified before being established and some assumptions are put forward.
3.1. Problem Description
Consider a scenario where an offline restaurant collaborates with a third-party online sales platform. The restaurant offers online food reservation services through a third-party online platform. Customers can book meals or seats on the third-party online platform and use their reservation voucher to enter the restaurant for dining purposes. The third-party online platform charges a certain amount of commission to the restaurant. In the process, the service levels of the third-party online platform and restaurant could affect customer utility, thereby affecting the sales volume of meals, and ultimately the profits of the restaurant and platform.
The pricing methods of restaurants cooperating with Meituan are shown in Figure 1. Usually, the original price and discount price of the meal are set by the restaurants, with some restaurants with group buying services setting the group buying price based on the original price. To increase customer traffic, the platform would issue platform coupons during special periods (such as holidays), which are normally universal across the platform. Since all restaurants will set a discounted price (the final price shown to the customer), it is the only decision-making goal, without considering the original price of the restaurants and the platform’s discounts.
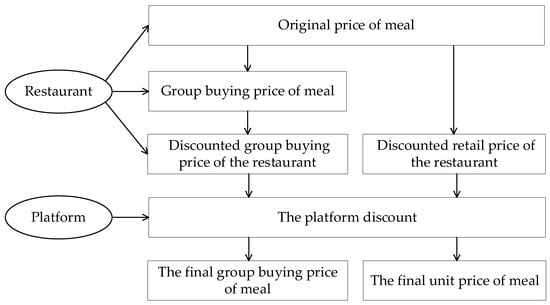
Figure 1.
Price-making diagram for restaurant and Meituan cooperation.
This article uses the Stackelberg game model to study the pricing and service strategies of restaurants and third-party online platforms. In this game, third-party online platforms and restaurants are the relationship between the leaders and the followers. Before collaborating with third-party platforms, restaurants only had retail services, namely, the offline retail model (OFM). When restaurants choose to settle on third-party online platforms, they can choose to continue their previous sales model, namely, the online retail model (ONM). It is also possible to sell multiple meals simultaneously at a lower price using the online group buying model (GBM). This article will consider the best strategies of restaurants and platforms using these three models.
3.2. Assumptions
Assumption 1.
Retail price and unit meal cost
Assuming that the restaurant only sells one type of meal, its retail price is . The unit cost of the meal is , including the unit cost of water, electricity, and rent, and the sensitivity coefficient of consumers to meal prices is .
Assumption 2.
Third-party online platform’s service level
On the one hand, the third-party online platform is responsible for the operation and maintenance of the website, such as the beauty and comfort of the website interface, the ease of operation, and the response speed of customer service, which all belong to the platform’s service level. On the other hand, third-party online platforms will also invest in advertisements to attract an audience, which is also a way for the platform to improve its service level. Assuming that the service level selected by the third-party online platform is , the sales volume will increase and the amount required is , where is the sensitivity coefficient of consumers to the service level of the platform and is the cost coefficient of the service level of the third-party platform, [44].
Assumption 3.
Restaurant’s service level
The sales volume of meals is closely related to the restaurant’s service level. The restaurant’s service level here refers to the service attitude of the restaurant staff (including waiting time) and the environment of the restaurant (customer capacity, decoration style, completeness of facilities, geographical location of the restaurant, etc.). Since these factors are all services provided by restaurants to consumers and can affect consumers’ perceived value, these factors are categorized as the restaurant’s service level, represented by . When the restaurant’s service level is , the sales volume will increase , which will require where is the sensitivity coefficient of consumers to the restaurant’s service level and is the cost coefficient of the restaurant’s service level, .
Assumption 4.
Customer’s valuation of the meal
Different customers have different estimates of the value of the meal. Assuming that follows a uniform distribution on and that the consumer utility is , only when the consumer’s utility is greater than 0 () will consumers purchase meals.
Assumption 5.
Group buying price and grouping cost
The group buying price (the average price of each meal in the case of group purchase) is . Generally, . The average cost that each person needs to pay for a successful group purchase is , including time, energy, and other costs. When the required number of group buyers is n, the cost of group buying is and the average cost per person is . In order to calculate the method, is recorded as .
Assumption 6.
Number of potential customers in each model
Assume that the original potential customers of the restaurant offline is . In the online retail model, the number of new potential customers that can be attracted by entering the online platform is . (Potential customers refer to customers who are likely to make a purchase, and only those with utility greater than 0 will really make a purchase.) The number of new potential customers that the restaurant can attract by directly entering the online platform through the group purchase model is .
Assumption 7.
Commission rate
Suppose that when a restaurant sells products through a third-party online platform, it needs to pay a sales commission of to the platform for each order. The platform will evaluate the restaurant before the game and determine the commission rate . Generally, .
Assumption 8.

Online sales of meals
Suppose that in order to increase online sales, restaurants also require customers to place orders online when receiving offline customers. In other words, there is essentially only an online sales channel. The retail sales volume under each model is and the sales volume of group purchase is .
Superscripts F, N, and G indicate the offline retail model, online retail model, and group purchase model, respectively. To make the total profit of the supply chain greater than 0 and make the model meaningful, assume , , and . All notations and meanings used in this paper are shown in Table 1.

Table 1.
Notations description.
4. Decision-Making Model Analysis
This paper constructs demand functions based on consumer utility theory and perceived value theory. The price of food and the service strategies of restaurants and third-party online platforms will all affect consumers’ perceived value, thus affecting consumers’ utility. The demand function is expressed as the part of potential consumers whose utility is greater than 0, so the price and service levels will affect the sales volume of restaurants, thus affecting the income of restaurants and platforms. For restaurants and third-party online platforms, it takes a cost to improve their service levels. And the service strategies will also affect the expenditure of restaurants and platforms. Therefore, according to the relationship between price and service strategies and the profits of supply chain members, three catering supply chain are established in the offline retail model (OFM), online retail model (ONM), and online group buying model (GBM), respectively.
4.1. Offline Retail Model (OFM)
Before the restaurant enters a third-party online platform, it adopts the offline retail model. Its sales volume is only related to price, restaurant service level, and the number of potential consumers, which is:
The profit of the restaurant is:
According to the principle of profit maximization, the best pricing strategy of the restaurant can be obtained as follows:
The maximum profit of the restaurant is:
It shows that in the OFM, when the restaurant sets the price of food as and the service level is , the restaurant can achieve the maximum profit .
4.2. Online Retail Model (ONM)
When a restaurant cooperates with a third-party online sales platform in a retail model, customers can only purchase meals separately. Restaurants and third-party online platforms aim to maximize their respective profits and choose the strategy that is most advantageous to them. When entering the platform, the number of new potential consumers attracted is , and the total number of potential consumers is . The decision-making order is, first, the platform determines its own service level , and then the restaurant decides the retail price of the meal and restaurant’s service level . At this point, the platform is the leader and the restaurant is the follower.
Figure 2 is a schematic diagram of the pricing process. There are three participants in the catering supply chain, namely, restaurant, customer, and third-party online platform (TP-OLPM). Among them, the customer chooses and buys food in the restaurant after browsing the third-party online platform. The relationship between the restaurant and third-party online platform is cooperative, and the two are mutually beneficial. Both the restaurant and platform aim at profit maximization, and their profits can be calculated based on income minus cost. The restaurant sells through the platform, and at the same time gives the platform a commission according to the sales, that is, , and is the commission rate. The customer’s willingness to spend directly determines the sales volume of the restaurant. It is related to the price, the service levels of the restaurant (Restaurant’s S.L.) and platform (Platform’s S.L.). And the sensitivity coefficients (Sensitivity Coef.) of two service levels are and . When the Restaurant’s S.L. is and the Platform’s S.L. is , the consumption willingness will increase by and , and the cost is and , respectively. The sales volume is also related to the number of potential customers of the restaurant . For the restaurant, the profit of each order is the price after deducting the commission from each order minus the cost . The profit of the restaurant is calculated as the profit of each order multiplied by the sales volume minus the service cost of . The profit of the platform is the commission income from the restaurant minus the platform service cost .
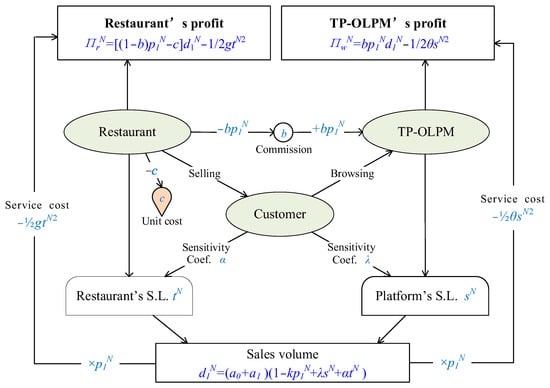
Figure 2.
Pricing diagram of the online retail model.
The actual sales volume of meals is:
The profit of the restaurant is:
The profit of third-party online platforms is:
Theorem 1.
The equilibrium result of the online retail model is:
At this time, the maximum profits of the restaurant and third-party online platform are:
Proof of Theorem 1.
The proof process is shown in Appendix A.1. □
Theorem 1 shows that in the ONM, when the restaurant sets the price of food as , the service level as , and the service level of the platform is , both the restaurant and the platform can achieve the maximum profit. The maximum profit of the restaurant is , and that of the platform is .
Corollary 1.
, , .
, , .
Corollary 1 shows that as the sensitivity coefficient of customers to the third-party online platform or restaurant’s service levels increases, the optimal price and service levels will both increase, and the total profits of the restaurant and third-party online sales platform will also increase. This indicates that the service levels of the restaurant and platform have a greater impact on customer purchasing the more motivated they are to improve their own service levels, so the optimal service levels will increase. The optimal price and maximum profits for both parties will also increase. When the cost coefficient of the restaurant or platform increases, it will cost more to improve the same service level than before, which will lead to the platform and restaurant’s reluctance to improve their own service levels. As the cost of spending increases, the corresponding optimal price and maximum profits for both parties will decrease.
Proof of Corollary 1.
The proof process is shown in Appendix A.2. □
4.3. Online Group Buying Model (GBM)
The online group buying model refers to the restaurant only providing a group buying service during the cooperation process with third-party platforms. In this model, customers need to group together to purchase a specified quantity of meals in order to enjoy price discounts. Figure 3 is a schematic diagram of the pricing process. Unlike the online retail model, during a group buying transaction, customers need to spend additional time, effort, and other resources searching for group members, which is the cost of grouping .
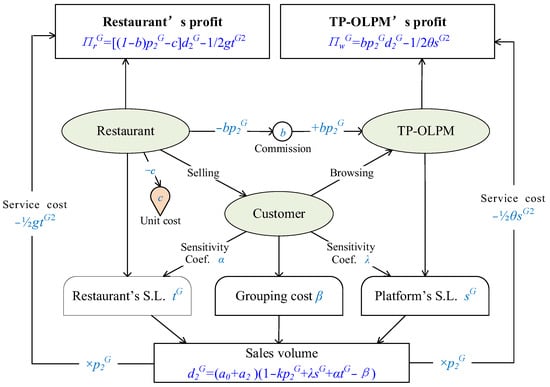
Figure 3.
Pricing diagram of the group buying model.
The group buying sales volume of meals is:
The profit of the restaurant is:
The profit of third-party online platforms is:
Theorem 2.
The equilibrium result of the online group buying model is:
The maximum profits for the restaurant and third-party online platform are:
Theorem 2 shows that in the GBM, when the group purchase price of the restaurant is , the service level is , and the service level of the platform is , both the restaurant and the platform can achieve the maximum profits .
Corollary 2.
; ;
; ; .
Corollary 2 indicates that in the online group buying model, the optimal price of the restaurant and the optimal service level of the platform will also increase with the increase of customer sensitivity to service levels, and that they will decrease with the increase of the service cost coefficient. Meanwhile, as the grouping cost increases, the optimal price of meals, the optimal service level of the platform, and the maximum profits of restaurants and platforms will all decrease. The cost of assembling a group will reduce the total utility of the customer, and the higher the cost, the more utility will be reduced. As a result, restaurants need to set slightly lower prices to motivate customers to make purchases. The cost of group buying is to some extent influenced by the number of group purchases. The more meals that need to be purchased in a single group transaction, the higher the cost of group buying.
Proof of Corollary 2.
The proof process is shown in Appendix A.3. □
5. Numerical Analysis
Further analysis follows of the sensitivity coefficient of the third-party online platform’s service level (), cost coefficient of the third-party online platform’s service level (), sensitivity coefficient of the restaurant’s service level (), cost coefficient of the restaurant’s service level (), grouping cost (), and the number of new potential customers attracted by each model (). This section conducts numerical analysis. Assume that , , , , , , , , , , and . Unless otherwise specified, all values in Part 5 are based on the above content. In this part, coef. is short for coefficient, TP-OLPM is the abbreviation of third-party online platform, and S.L. means service level.
5.1. Sensitivity Coefficient of Third-Party Online Platform’s Service Level ()
Firstly, this paper analyzed the sensitivity coefficient of the third-party online platform’s service level (). The value range is [0, 0.5]. Figure 4 and Figure 5 show that there are positive correlations between the sensitivity coefficient of the third-party online platform’s service level and the optimal retail price, group buying price, optimal service levels, and maximum profits of the restaurant and platform in each model. When the sensitivity coefficient of consumers to the platform’s service level increases, the optimal retail price, group buying price, and platform’s optimal service level of restaurants will all increase. This is because as consumers attach greater importance to the service level of the platform, increasing the service level of the platform will attract more new consumers than before, and sales of meals will also increase. In this case, both the optimal price and service levels will increase, and the profits of restaurants and platforms will also increase.
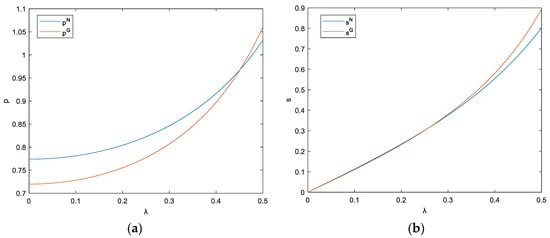
Figure 4.
(a) The impact of sensitivity coef. of TP-OLPM’s S.L. on retail price and group buying price; (b) The impact of sensitivity coef. of TP-OLPM’s S.L. on platform’s S.L.
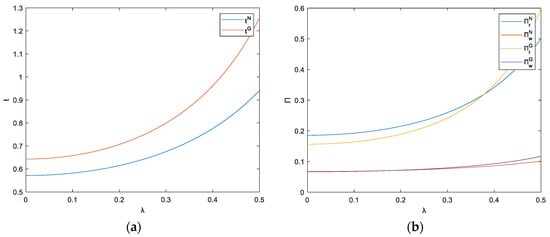
Figure 5.
(a) The impact of sensitivity coef. of TP-OLPM’s S.L. on restaurant’s S.L.; (b) The impact of sensitivity coef. of TP-OLPM’s S.L. on restaurant and platform profits.
In fact, in today’s era, consumers value the quality of meals and they care increasingly about the experience of the purchasing process. Therefore, consumers are increasingly sensitive to the service level of the platform. For example, to earn more money, many software place multiple advertisements at the screen opening and inside the software. Users often click on advertisements and are redirected to new software or websites by mistake when using the software, greatly reducing the user experience. Users who often encounter this situation could develop an aversion to the app. Therefore, there is a negative correlation between service level and the number of advertising placements. Reducing the number of placements will greatly increase user experience and user utility. Although it will reduce advertising revenue, it will also increase sales and enhance the platform’s reputation. In the long run, the advantages outweigh the disadvantages. In addition, the ease, smoothness of use, aesthetic appearance of the interface, and customer service response speed of the platform are also of increasing concern for consumers.
5.2. Cost Coefficient of Third-Party Online Platform’s Service Level ()
The value range of is [0, 0.5]. Figure 6 and Figure 7 show that there is a negative correlation between the cost coefficient of the third-party online platform’s service level and the optimal retail price, group buying price, optimal service levels of both sides, and the maximum profits of the restaurant and platform in each model. When the cost coefficient of the third-party online platform’s service increases, it means that the marginal cost required to improve the service level increases, and the platform will not be willing to improve the service level. For example, when the running speed is relatively high, if the platform wants to continue improving the running speed, it will incur high costs but the benefits will be very small. Consequently, when the cost coefficient increases, the optimal service level of the platform will decrease, leading to a decrease in customer utility. The optimal retail price and group buying price will also decrease, leading to a decrease in the maximum profits of restaurants and platforms.
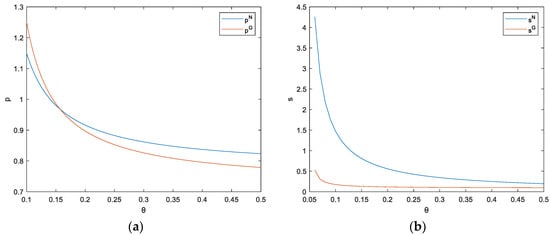
Figure 6.
(a) The impact of cost coef. of TP-OLPM’s S.L. on retail price and group buying price; (b) The impact of cost coef. of TP-OLPM’s S.L. on platform’s S.L.
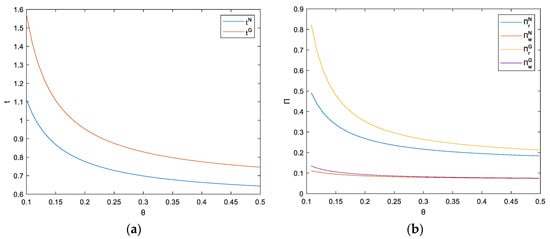
Figure 7.
(a) The impact of cost coef. of TP-OLPM’s S.L. on restaurant’s S.L.; (b) The impact of cost coef. of TP-OLPM’s S.L. on restaurant and platform profits.
5.3. Sensitivity Coefficient of Restaurant’s Service Level ()
The value range of is [0, 0.5]. Figure 8 and Figure 9 show that there is a positive correlation between the sensitivity coefficient of the restaurant’s service level and the optimal retail price, group buying price, optimal service levels of both sides, and the maximum profits of the restaurant and platform in each model. The service level of a restaurant will greatly affect the perceived value of customers. The convenient geographical location, short waiting time, exquisite decoration, complete service facilities, and comfortable waiters all make customers feel the intention and sincerity of the restaurant, thus leaving a good impression on them. When customers are more concerned about these conditions, then, for restaurants, improving these service levels can increase sales volume, and the maximum profits of the restaurant and platform will also increase.
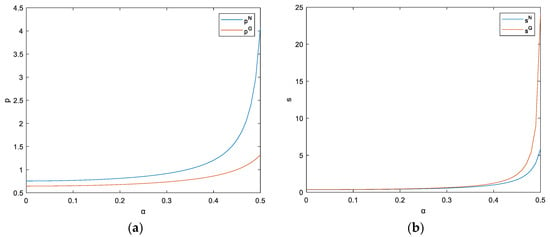
Figure 8.
(a) The impact of sensitivity coef. of restaurant’s S.L. on retail prices and group buying prices; (b) The impact of sensitivity coef. of restaurant’s S.L. on platform’s S.L.
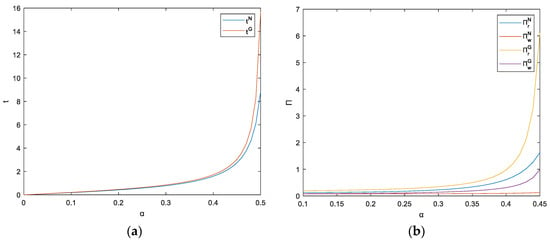
Figure 9.
(a) The impact of sensitivity coef. of restaurant’s S.L. on restaurant’s S.L.; (b) The impact of sensitivity coef. of restaurant’s S.L. on restaurant and platform profits.
5.4. Cost Coefficient of Restaurant’s Service Level ()
The value range of is [0, 0.5]. Figure 10 and Figure 11 show that there is a negative correlation between the cost coefficient of the restaurant’s service level and the optimal retail price, group buying price, optimal service levels of both sides, and the maximum profits of the restaurant and platform in each model. Restaurants need to pay more costs to improve their service levels. For example, restaurants in good locations need to pay higher rent. The improvement of decoration and facilities, as well as the professional level of service personnel, also require the restaurant to invest more funds. When the cost coefficient increases, restaurants need to pay more for improving unit service levels. Therefore, the optimal price and service level in both models will decrease, and the maximum profits of both parties will also decrease.
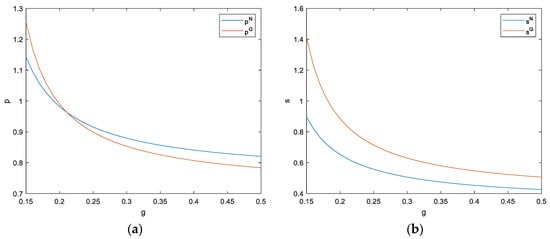
Figure 10.
(a) The impact of cost coef. of restaurant’s S.L. on retail price and group buying price; (b) The impact of cost coef. of restaurant’s S.L. on platform’s S.L.
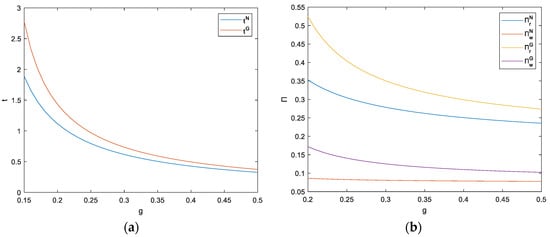
Figure 11.
(a) The impact of cost coef. of restaurant’s S.L. on restaurant’s S.L.; (b) The impact of cost coef. of restaurant’s S.L. on restaurant and platform profits.
5.5. Grouping Cost ()
The value range of is [0, 0.1]. Figure 12 shows that there is a negative correlation between the grouping cost and the optimal group buying price, optimal service level, and the maximum profit in the online group buying model. When the cost of group buying increases, the additional cost that users need to bear for group buying also increases, and some customers will abandon group buying. In order to retain this group of customers as much as possible, the optimal group buying price needs to be reduced. In the online retail model, the retail price does not change with the change of the grouping cost.
Figure 12.
The impact of grouping cost on decision-making variables.
The cost of group buying is mainly related to the setting of the number of group purchases (the number of meals to be purchased in a group purchase). The larger the number of group purchases, the more group members need to be found, and the higher the cost of group buying. For example, the grouping cost of “six people’s meals” is significantly higher than that of “three people’s meals”. When the cost of grouping increases, customers need to spend more time and energy searching for group members, which will reduce their willingness to purchase. Therefore, restaurants need to set a reasonable number of group purchases to achieve the goal of expanding sales while ensuring that the cost of grouping is not too high.
5.6. Numbers of New Potential Customers Being Attracted ()
The numbers of new potential consumers attracted by each model and the changes in the maximum profits of restaurants and platforms are shown in Figure 13. The values range of () is [0, 1]. Based on the two graphs, the maximum profits of both restaurant and platform increase with the increase of new potential consumers that they attract. The number of new potential consumers depends on both the restaurant’s business model and the platform’s user base. The more users the platform has, the greater the number of new potential consumers it will have. Therefore, for restaurants, the larger the scale of online platforms they collaborate with, the more users they have, and the greater their profits.
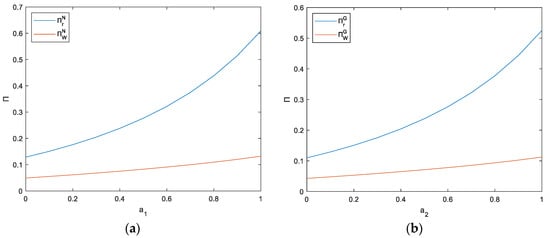
Figure 13.
(a) The impact of the number of new potential consumers attracted by the ONM on restaurant and platform profits; (b) The impact of the number of new potential consumers attracted by the GBM on restaurant and platform profits.
6. Discussion and Conclusions
This paper studies a catering supply chain system composed of a restaurant and a third-party online platform. Considering the impact of the service levels of the third-party online platform and restaurant on the demand for meals in the market, three game models are established: offline retail model (OFM), online retail model (ONM), and online group buying model (GBM). The optimal decisions and maximum profits are calculated, respectively. Then, based on the analysis of several exogenous variables, it is found that the sensitivity coefficients of consumers to the platform and restaurant’s service levels are positively correlated with restaurant retail prices, group purchase prices, two service levels, and restaurant and platform profits, while the cost coefficients of the platform and restaurant’s service levels are negatively correlated with these variables. More importantly, there is a significant positive correlation between the maximum profit of a restaurant and the number of new potential consumers attracted by each model, which is consistent with Xing et al.’s [45] research results.
From a theoretical perspective, this study expands the research of Li et al. [46] and Kim et al. [47], which mentioned the importance of geographical location. This paper also considers the geographical location of the restaurant, which is included in the service of the restaurant. A good geographical location means high rent, which requires the restaurant to bear more service costs at the same time. Considering the impact of these services on revenue and cost to make the best decision, this study discusses the pricing strategies and service strategies of an O2O catering supply chain. Different from Reis et al. [48], who focused on the migration of online services to offline channels and analyzed the importance of recovery measures in multi-channel services and the transitional role of O2O in multi-channel services through qualitative analysis, the scenario we study is to add online sales channels in the traditional offline retail scenario. In addition, we use quantitative research methods to establish a mathematical model and analyze the service levels of restaurants and platforms to study the group purchase pricing problem when restaurants cooperate with third-party platforms. The model built in this paper is in line with the current business model of offline restaurants cooperating with Meituan, so the conclusion can help them formulate better price strategies, service strategies, and obtain more profits. It is conducive to the continuous and stable cooperation between restaurants and platforms, thus promoting the steady development of the catering industry in China. In addition, this paper also supplements the research bank of group purchase supply chain in the catering industry.
However, this model still has limitations. For example, the model only applies to the three scenarios mentioned above. Although there are many such scenes in China, some restaurants also provide a take-away service. This model is not suitable for restaurants that provide a take-away service, because it does not pay attention to delivery service. In addition, the model is not suitable for the scenario of differential pricing between online and offline channels. At present, part of the latest food-related research focuses on the take-away service in restaurants. For instance, Kilders et al. [49] used FM-BBCE to study consumers’ needs and preferences when eating in restaurants and ordering take-away; they found that the price elasticity of consumers when eating in restaurants is greater than when ordering take-away, and the meals provided by in-house food and take-away food were complementary. Du et al. [41] discussed the selection of two pricing strategies (unified pricing and differential pricing) and two distribution strategies (platform delivery and self-delivery) of Chinese restaurants in O2O dual-channel sales, and the best pricing strategies of restaurants and platforms before and after the online take-out platform launched a paid on-time delivery service [50]. There were also scholars [51] who paid attention to the manipulation of online comments by restaurants and discussed the influence of the quantity and quality of competitors on the manipulation of positive and negative comments by restaurants. Future research can extend group buying to the take-away industry and pay more attention to the factors that consumers care about, such as delivery quality and delivery fee.
It is suggested that both restaurants and third-party online platforms pay close attention to consumers’ considerations regarding pricing sensitivity and their expectations for platform service levels, and that they adjust pricing and service strategies in a timely manner based on consumers’ different sensitivity and cost coefficients to meet consumer needs. It is also recommended that restaurants establish reasonable group buying quantity requirements to control group buying costs and maintain them within an acceptable range.
In the cooperation between restaurants and third-party online platforms, due to the significant difference in strength between the platforms and restaurants, online platforms often control the discourse power. Therefore, restaurants are suggested to be cautious when collaborating with third-party online platforms, and they should choose the appropriate platform for cooperation based on the platform’s reputation, cooperation attitude, strength, and incremental demand [42]. At the same time, it is suggested that restaurants improve their service level, increase customers’ perceived value, and thereby increase sales volume and obtain more profits. For restaurants, choosing a group buying model may generate a significant amount of costs in a short period of time. However, as a traditional marketing way, group buying can effectively expand sales and help restaurants achieve the goal of increasing popularity and brand awareness.
This study also has some limitations which provide ideas for future research. Firstly, this paper considered the situation where the offline and online sales of restaurants in collaboration with third-party online platforms are unified as the total sales volume but did not consider the situation of calculating them individually. Secondly, this article only studies the cooperation between a restaurant and a third-party online platform. In real life, a third-party online platform often cooperates with multiple restaurants, and there is also competition between similar restaurants. A restaurant may also collaborate with more than one platform. These are all directions that can be improved in the future.
Author Contributions
Conceptualization, D.D.; methodology, D.D., H.M. and M.Z.; validation, H.M., M.Z. and T.F.; writing—original draft preparation, H.M.; writing—review and editing, M.Z. and T.F.; visualization, H.M.; guidance and supervision, D.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China: 72032001, 71972071.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors thank the editors and reviewers for their hard work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1
The Proof of Theorem 1.
Calculate the first partial derivatives of and , make the first derivative equal to 0, and then find the Hessian matrix of .
Owing to and , the first-order principal sub-equation of is less than 0. And the second-order principal sub-equation of is greater than 0. Therefore, is a joint concave function of and . The restaurant has the maximum profit. By making and equal to 0, the expression of and about can be obtained. ,
Substitute the above into and calculate the first derivative of and make it equal to 0, so that the expression of can be obtained. As the second derivative is , which is less than 0, then when , the maximum value of can be obtained. Substitute into the expression of and and finally calculate the maximum profit of restaurants and platforms in the online retail model.
The equilibrium solution and the restaurant and platform’s profits of the online group buying model can be calculated in the same way. □
Appendix A.2
The Proof of Corollary 1.
According to the assumption , and , it can be determined that and . Owing to , it can be inferred that . According to these inferences, Corollary 1 can be proved. The specific calculation is as follows:
□
Appendix A.3
The Proof of Corollary 2.
Corollary 2 can be proved in the same way as Corollary 1. The derivation process of Corollary 2 is as follows:
□
References
- Chen, J.; Yu, C.; Jin, H. Evaluation Model for Business Sites Planning Based on Online and Offline Datasets. Future Gener. Comput. Syst. 2019, 91, 465–474. [Google Scholar] [CrossRef]
- Wang, J.J.; Zhao, X.; Li, J.J. Group Buying: A Strategic Form of Consumer Collective. J. Retail. 2013, 89, 338–351. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Y.; Pan, H.; Xu, A. Influence of Multi-Role Interactions in Community Group-Buying on Consumers’ Lock-In Purchasing Intention From a Fixed Leader Based on Role Theory and Trust Transfer Theory. Front. Psychol. 2022, 13, 903221. [Google Scholar] [CrossRef]
- Ni, G.; Xu, Y.; Xu, J.; Dong, Y. Optimal Decisions for Fixed-Price Group-Buying Business Originated in China: A Game Theoretic Perspective. Int. J. Prod. Res. 2015, 53, 2995–3005. [Google Scholar] [CrossRef]
- Zhang, J. Faced with the Epidemic, the Top Ten Industries of “Ice and Fire”. Available online: https://www.gmw.cn/xueshu/2020-02/10/content_33541661.htm (accessed on 9 April 2023).
- Zhang, C.; Jiang, J.; Jin, H.; Chen, T. The Impact of COVID-19 on Consumers’ Psychological Behavior Based on Data Mining for Online User Comments in the Catering Industry in China. Int. J. Environ. Res. Public Health 2021, 18, 4178. [Google Scholar] [CrossRef] [PubMed]
- National Bureau of Statistics. From January to February, the National Economy Stabilized and Rebounded. Available online: http://www.stats.gov.cn/sj/zxfb/202303/t20230315_1937190.html (accessed on 9 April 2023).
- Song, B.; Xu, H.; Zhao, L. Open or Not? Operation Strategies of Competitive eCommerce Platforms from an Ecosystem Perspective. Systems 2023, 11, 6. [Google Scholar] [CrossRef]
- Zhu, J.; Teng, L.; Zhu, Z.; Lu, H. A Pricing Method of Online Group-Buying for Continuous Price Function. Neural Comput. Appl. 2020, 32, 4453–4461. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Z.; Li, B.; Zhu, J. Allocation and Pricing of Group-Buying Based on the Fixed Bidding. Multimed. Tools Appl. 2020, 79, 14689–14710. [Google Scholar] [CrossRef]
- Ming, L.; Tunca, T.I. Consumer Equilibrium, Demand Effects, and Efficiency in Group Buying. Manuf. Serv. Oper. Manag. 2022, 24, 1437–1456. [Google Scholar] [CrossRef]
- Ni, G. A Pricing Model for Group Buying Based on Network Effects. PLoS ONE 2019, 14, e0211109. [Google Scholar] [CrossRef]
- Wu, Y.; Li, D.; Li, T. Coordination of Traditional and Online Group-Buying Channels Considering Website Promotion Effort. Sci. Iran. 2020, 27, 2069–2092. [Google Scholar] [CrossRef]
- He, N.; Jiang, Z.-Z.; Sun, M.; Sheng, Y. Group Buying of Competing Retailers with Fairness Concerns. J. Syst. Sci. Syst. Eng. 2020, 29, 655–674. [Google Scholar] [CrossRef]
- Guan, L.; Chen, H.; Ma, H.; Zhang, L. Optimal Group-Buying Price Strategy Considering the Information-Sharing of the Seller and Buyers in Social e-Commerce. Int. Trans. Oper. Res. 2022, 29, 1769–1790. [Google Scholar] [CrossRef]
- Shui, W.; Li, M. Integrated Pricing and Distribution Planning for Community Group Purchase of Fresh Agricultural Products. Sci. Program. 2020, 2020, e8839398. [Google Scholar] [CrossRef]
- Wang, Y.; Song, H. A Game Theoretic Strategic Model for Understanding the Online-Offline Competition and Fairness Concern under Community Group Buying. J. Ind. Manag. Optim. 2023, 19, 1670–1696. [Google Scholar] [CrossRef]
- Ando, T. Merchant Selection and Pricing Strategy for a Platform Firm in the Online Group Buying Market. Ann. Oper. Res. 2018, 263, 209–230. [Google Scholar] [CrossRef]
- Hsu, S.-W.; Qing, F.; Wang, C.-C.; Hsieh, H.-L. Evaluation of Service Quality in Facebook-Based Group-Buying. Electron. Commer. Res. Appl. 2018, 28, 30–36. [Google Scholar] [CrossRef]
- Sharma, V.M.; Klein, A. Consumer Perceived Value, Involvement, Trust, Susceptibility to Interpersonal Influence, and Intention to Participate in Online Group Buying. J. Retail. Consum. Serv. 2020, 52, 101946. [Google Scholar] [CrossRef]
- Kozáková, P. Ověření Důvěry a Spokojenosti Zákazníků Na Českých Slevových Portálech Metodou Modelování Strukturních Rovnic. Polit. Ekon. 2020, 68, 381–404. [Google Scholar] [CrossRef]
- Ou, C.-C.; Chen, K.-L.; Tseng, W.-K.; Lin, Y.-Y. A Study on the Influence of Conformity Behaviors, Perceived Risks, and Customer Engagement on Group Buying Intention: A Case Study of Community E-Commerce Platforms. Sustainability 2022, 14, 1941. [Google Scholar] [CrossRef]
- Chow, C.W.C.; Chow, C.S.F.; Lai, J.Y.M.; Zhang, L.L. Online Group-Buying: The Effect of Deal Popularity on Consumer Purchase Intention. J. Consum. Behav. 2022, 21, 387–399. [Google Scholar] [CrossRef]
- Hongsuchon, T.; Li, J. Accessing the Influence of Consumer Participation on Purchase Intention Toward Community Group Buying Platform. Front. Psychol. 2022, 13, 887959. [Google Scholar] [CrossRef]
- Hossain, M.A.; Rahman, S. Investigating the Success of OGB in China: The Influence of Personality Traits. Inf. Syst. Front. 2021, 23, 543–559. [Google Scholar] [CrossRef]
- Klein, A.; Sharma, V.M. Consumer Decision-Making Styles, Involvement, and the Intention to Participate in Online Group Buying. J. Retail. Consum. Serv. 2022, 64, 102808. [Google Scholar] [CrossRef]
- Xiao, L. Analyzing Consumer Online Group Buying Motivations: An Interpretive Structural Modeling Approach. Telemat. Inform. 2018, 35, 629–642. [Google Scholar] [CrossRef]
- Lin, K.-Y.; Hu, L. Supply and Demand Optimization of Agricultural Products in Game Theory: A State-of-the-Art Review. J. Eng. Manag. Syst. Eng. 2022, 1, 76–86. [Google Scholar] [CrossRef]
- Song, C.; Xu, B.; Song, C.; Xu, B.; Xu, L. Dual-Channel Supply Chain Pricing Decisions for Low-Carbon Consumers: A Review. J. Intell. Manag. Decis. 2023, 2, 57–65. [Google Scholar] [CrossRef]
- Yu, X.; Ren, X. The Impact of Food Quality Information Services on Food Supply Chain Pricing Decisions and Coordination Mechanisms Based on the O2O E-Commerce Mode. J. Food Qual. 2018, 2018, e8956820. [Google Scholar] [CrossRef]
- Qiu, R.; Yu, Y.; Sun, M. Supply Chain Coordination by Contracts Considering Dynamic Reference Quality Effect under the O2O Environment. Comput. Ind. Eng. 2022, 163, 107802. [Google Scholar] [CrossRef]
- Amrouche, N.; Pei, Z.; Yan, R. Service Strategies and Channel Coordination in the Age of E-Commerce. Expert Syst. Appl. 2023, 214, 119135. [Google Scholar] [CrossRef]
- Datta, A.; Sarkar, B.; Dey, B.K.; Sangal, I.; Yang, L.; Fan, S.-K.S.; Sardar, S.K.; Thangavelu, L. The Impact of Sales Effort on a Dual-Channel Dynamical System under a Price-Sensitive Stochastic Demand. J. Retail. Consum. Serv. 2024, 76, 103561. [Google Scholar] [CrossRef]
- Zheng, X.; Guo, X. E-Retailing of Restaurant Services: Pricing Strategies in a Competing Online Environment. J. Oper. Res. Soc. 2016, 67, 1408–1418. [Google Scholar] [CrossRef]
- Guo, X.; Zheng, X. Examination of Restaurants Online Pricing Strategies: A Game Analytical Approach. J. Hosp. Mark. Manag. 2017, 26, 659–673. [Google Scholar] [CrossRef]
- Xu, J.; Hu, L.; Guo, X.; Yan, X. Online Cooperation Mechanism: Game Analysis between a Restaurant and a Third-Party Website. J. Revenue Pricing Manag. 2020, 19, 61–73. [Google Scholar] [CrossRef]
- Tong, T.; Dai, H.; Xiao, Q.; Yan, N. Will Dynamic Pricing Outperform? Theoretical Analysis and Empirical Evidence from O2O on-Demand Food Service Market. Int. J. Prod. Econ. 2020, 219, 375–385. [Google Scholar] [CrossRef]
- Niu, B.; Li, Q.; Mu, Z.; Chen, L.; Ji, P. Platform Logistics or Self-Logistics? Restaurants’ Cooperation with Online Food-Delivery Platform Considering Profitability and Sustainability. Int. J. Prod. Econ. 2021, 234, 108064. [Google Scholar] [CrossRef]
- Zhang, H.; Luo, K.; Ni, G. The Effects of Price Subsidy and Fairness Concern on Pricing and Benefits of Take-Away Supply Chain. J. Comb. Optim. 2022, 43, 1106–1124. [Google Scholar] [CrossRef]
- Guo, Q.; He, L.; He, Y. Omnichannel Service Operations with Order-Online-and-Dine-in-Store Strategy. Manag. Decis. Econ. 2022, 43, 2311–2325. [Google Scholar] [CrossRef]
- Du, Z.; Fan, Z.-P.; Sun, F. O2O Dual-Channel Sales: Choices of Pricing Policy and Delivery Mode for a Restaurant. Int. J. Prod. Econ. 2023, 257, 108766. [Google Scholar] [CrossRef]
- Zhang, P.; Ju, S.; Huang, H. Can a Restaurant Benefit from Joining an Online Take-Out Platform? Mathematics 2022, 10, 1392. [Google Scholar] [CrossRef]
- Webb, T.; Ma, J.; Cheng, A. Variable Pricing in Restaurant Revenue Management: A Priority Mixed Bundle Strategy. Cornell Hosp. Q. 2023, 64, 22–33. [Google Scholar] [CrossRef]
- Lan, C.; Yu, X. Revenue Sharing-Commission Coordination Contract for Community Group Buying Supply Chain Considering Promotion Effort. Alex. Eng. J. 2022, 61, 2739–2748. [Google Scholar] [CrossRef]
- Xing, P.; Yao, J.; Wang, M. Quality Effort Strategy of O2O Takeout Service Supply Chain under Three Operation Modes. Complexity 2022, 2022, e8177186. [Google Scholar] [CrossRef]
- Li, L.; Feng, R.; Xi, J.; Wang, F. Spatial Drivers and Effects of Urban Food Accessibility: Comparison of Conventional and Online-to-Offline Services. Appl. Geogr. 2023, 152, 102894. [Google Scholar] [CrossRef]
- Kim, J.; Lee, M.; Kwon, W.; Park, H.; Back, K.-J. Why Am I Satisfied? See My Reviews—Price and Location Matter in the Restaurant Industry. Int. J. Hosp. Manag. 2022, 101, 103111. [Google Scholar] [CrossRef]
- Reis, J.; Amorim, M.; Melão, N. Multichannel Service Failure and Recovery in a O2O Era: A Qualitative Multi-Method Research in the Banking Services Industry. Int. J. Prod. Econ. 2019, 215, 24–33. [Google Scholar] [CrossRef]
- Kilders, V.; Caputo, V.; Lusk, J.L. Consumer Preferences for Food Away from Home: Dine in versus Delivery. Am. J. Agric. Econ. 2023, 1–30. [Google Scholar] [CrossRef]
- Du, Z.; Fan, Z.-P.; Chen, Z. Implications of On-Time Delivery Service with Compensation for an Online Food Delivery Platform and a Restaurant. Int. J. Prod. Econ. 2023, 262, 108896. [Google Scholar] [CrossRef]
- Li, H.; Ji, H.; Luo, J.M.; Zhang, Z. Competition and Restaurant Online Review Manipulations: A Dynamic Panel Data Analysis. Int. J. Hosp. Manag. 2023, 115, 103605. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).