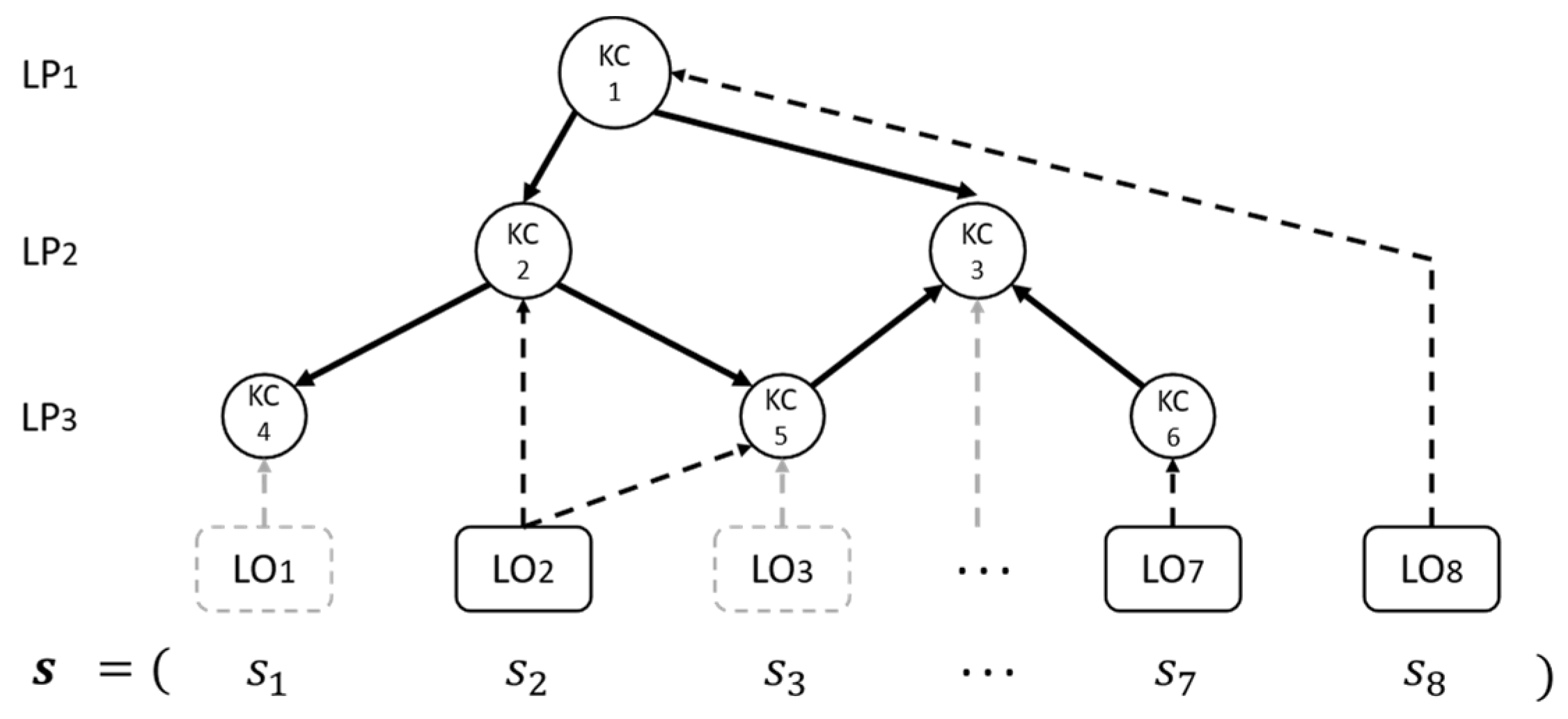
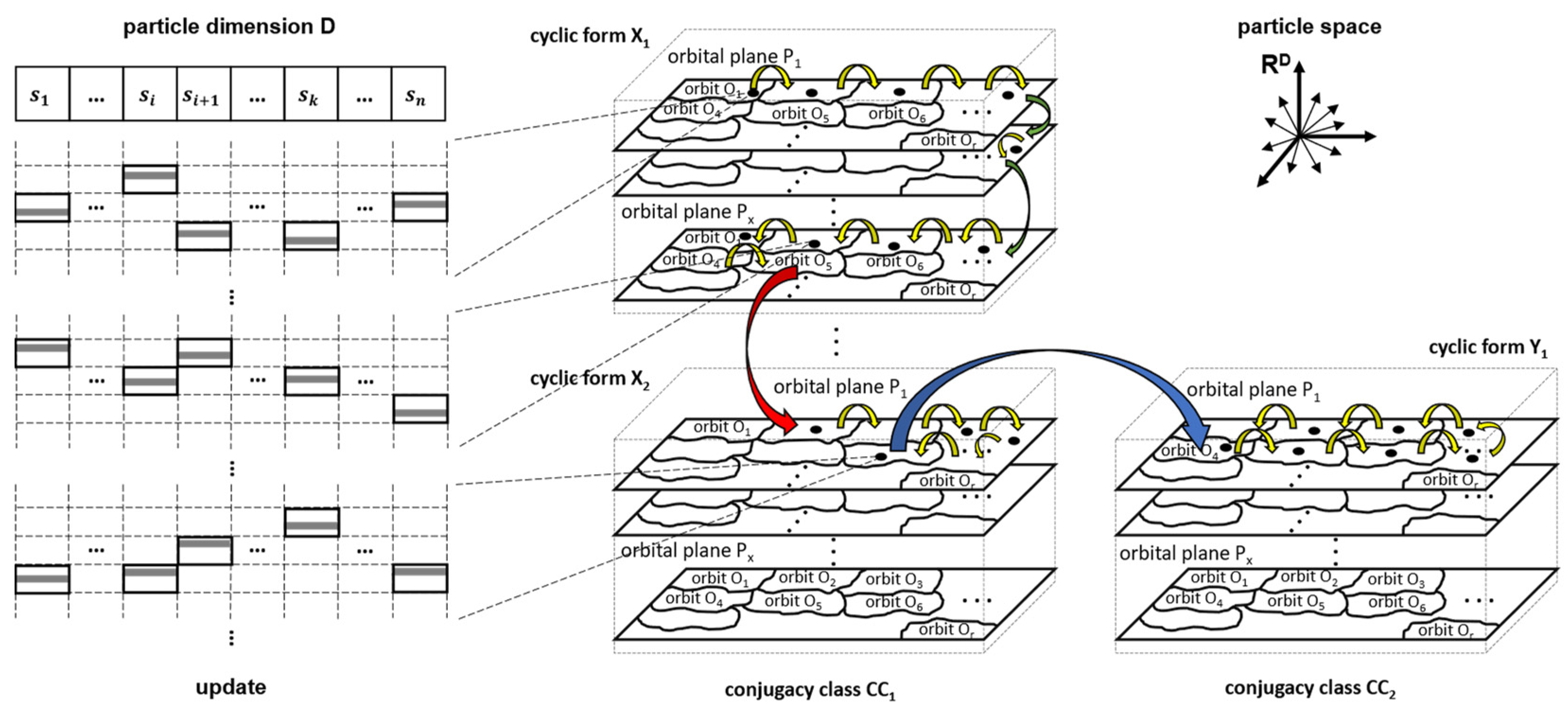
1. Introduction
With the rapid development of information technology and rising amounts of communication demand, the popularization of online education is growing and there have been great achievements in the last few decades. This social phenomenon has facilitated the advancement of e-education technologies, and distance education has become more and more widely recognized. Meanwhile, the relationship between teachers and students has been dispersed spatially and temporally, for the boundaries of the physical classrooms are expanded to the new space through e-education and e-classrooms [
1]. The demands of online meeting and remote conference also come from various entities such as elementary schools, universities, governments, private companies, non-profit social organizations, etc. [
2,
3].
Especially since the beginning of 2020, because of the epidemic of coronavirus, social structures have been massively rebuilt, and more and more social interactions and communications quickly transferred from physical form to electronic form [
4]. Furthermore, the traditional online education system is still imperfect and has many limitations such as lack of reusability and flexibility, as well as possible incompatibility with updating management systems over time, which could compromise the quality of education. Therefore, improving and perfecting online education systems is an imminent and crucial task [
5]. One of the possible improvements could be developing the function of producing a curriculum with new ways of content delivery and innovative pedagogic strategies, customized to fit each user in the system. In this way, user satisfaction, teaching efficiency, and learning outcome could all be improved, and in the meantime avoid possible educational defects such as lack of commitment, cognitive overload, disorientation, distraction, etc.
However, because of the NP-hard nature of the Curriculum Sequencing (CS) problem, as well as the fact that nowadays the CS process is still mainly performed by teaching staff manually, customizing personal curricula for different students is a difficult and consuming process. Therefore, offering the optimal sequence of a curriculum with intelligent tutoring, personalized scenarios, and adaptive education according to each student’s skills and learning content, is known as the Adaptive Curriculum Sequencing (ACS) problem in the education management system. Specifically, ACS problems are divided into two separate categories: Individual Sequencing (IS) problem [
6] and Social Sequencing (SS) problem [
7]. The users’ own background information is the only item considered by IS, whereas SS treats the users’ both previous and current experiences as the impacting factors for final ruling. To tackle this task, a metaheuristic approach involving evolutionary computation and swarm intelligence could be considered and implemented to approximate optimal solutions [
8]. These methods are endowed with a non-deterministic framework that can search the solution space based on the guidance of better candidates, trial-and-error interactions, and random components to some extent.
The challenge of the ACS problem mainly focuses on the automatic progress of reaching the most suitable sequence in terms of users’ profiles and goals, and different types of metaheuristic algorithms are dedicated to improving the approximation of optimal solutions. Previous research showed that the trending methods of metaheuristics such as Genetic Algorithm (GA), Differential Evolution (DE), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Prey–Predator Algorithm (PPA) are increasingly being applied to IS and SS problems recently.
Vanitha et al. [
9] propose the adaptation of ACO to select the optimal path for maximizing users’ acquisitions according to their pedagogical experiences. The improved ACO is unitary by integrating the individual profile, collective factors, and mutual interactions of the optimization approach. Birjali et al. [
10] present e-learning paradigm optimization based on big data technologies to enhance the capacity of a large number of educational resources. The model consists of several levels using MapReduce-based GA, MapReduce-based ACO, and MapReduce-based Social Networks Analysis (SNA) for adequate e-assessment, adaptive learning path, and social productivity, respectively. Christudas et al. [
11] introduce the Compatible Genetic Algorithm (CGA) to force the compatibility of unimplemented learning contents in the e-learning system, which further reduces the complexity of the search space of personalized learning contents. Peng et al. [
12] use the Hybrid PSO by adding the components of a competitive-genetic crossover operator, adaptive polynomial mutation, and a curriculum scheduling model to ensure the practicability of their proposed model for the ACS problem under certain constraints. Govindarajan et al. [
13] observe the competence and meta-competence values of students and utilize the Parallel PSO to predict the dynamic path for them, and it is able to auto-configure and auto-customize the proposed system simultaneously. Menai et al. [
14] modify the swarm search with a random walk mechanism (SwarmRW) using incremental and random heuristic strategies, and the quantitative results show that the best trade-off between quality and time is obtained by SwarmRW_inc. Meanwhile, the maximum number of satisfied constraints are achieved by SwarmRW_rnd. Machado et al. [
15] investigate the adaptive version of the Prey–Predator Algorithm (PPA) for the CS problem, and the performance is tested on both real-life and synthetic datasets, but it is not yet explored under the adaptive environment of e-learning. Martins et al. [
16] conduct a series of metaheuristic algorithms including aforementioned GA, PSO, PPA, and DE. This comprehensive study analyzes the influence of multiple learning contents while matching the requirements of learning resources with learning paths, and it highlights the effort of DE compared to other algorithms as well.
Generally speaking, the abovementioned methods are proven to be effective in respect of their convergence and the performance of objective functions during the optimization process. The experimental results illustrated the contributions of their valuable works but there is still room for improvement. Many of the pedagogical works take only into account the intrinsic characteristics of users and evaluate the optimal path mainly based on synthetic datasets. As for the search behavior, the trade-off between diversification (exploration) and intensification (exploitation) is significant to the solution quality and the dynamically balanced relationship should be investigated for ACS optimization.
Group theory is the study about algebraic structures known as groups [
17]. Groups are special sets equipped with an operation (such as multiplication, addition, composition, etc.) that satisfies certain basic rules of properties. In practice, many combinatorial applications from multiple disciplines can be modeled by the framework of a symmetric group, especially for those with symmetric characteristics of the whole system. The theory of the symmetric group usually embodies the internal symmetry of some structures in the form of permutation and combination representations. It is also the case that the symmetric relationship resides in the path of curriculum sequences for the ACS problem. The internal symmetry of the underlying structure often exists as an invariant property of the system, which is a great effort in solving the combinatorial optimization problem simultaneously.
The objective of this study is to propose a novel metaheuristic mechanism named Group-Theoretic Particle Swarm Optimization (GT-PSO) for the ACS problem in the education management system. GT-PSO is the extension of traditional PSO with the solid mathematical foundation of a symmetric group to rebuild the search paradigm from four aspects, which are, respectively, particle representation, landscape decomposition, moving neighborhood, and swarm topology. GT-PSO is originally designed for the combinatorial optimization problem and trends of searching characteristics are implemented via the utilization of group theory concept. The ACS problem is formulated as the combination of users’ preferences, learning subjects, and knowledge concepts, and this sort of NP-hard problem is addressed in the form of the systematic procedure of GT-PSO. The main contributions of this paper are summarized as follows:
A new search paradigm combining symmetric group theory with metaheuristics is proposed for tackling an NP-hard problem;
Both intrinsic and extrinsic characteristics of users are involved in the learning process as the objective function;
The balanced relationship between diversification and intensification is maintained during the optimization procedure.
The remainder of this paper is organized as follows:
Section 2 describes the materials and methodology of our proposed work;
Section 3 presents the results generated from experiments on real-life datasets;
Section 4 discusses the performance and analyzes the behavior of the proposed method;
Section 5 concludes the paper.
3. Results
In the case study of the real-life application of OULAD, the fitness scores of objective function and convergence of the compared algorithms are the main factors to measure the performance. The number of learning materials varies from 50 to 1000, which means that the difficulty of finding the optimal curriculum path covering users’ preferences, learning contents, and knowledge concepts increases severely. The quantitative results of fitness scores returned by the fused objective functions of multiple metaheuristics are tabulated in
Table 2 with respect to corresponding numbers of learning materials. Best results are in bold for emphasis. In most situations, all methods can obtain good solutions and it can be inferred that the proposed GT-PSO achieves the best averaged fitness score among them. For instance, GT-PSO generates the superior averaged fitness score of 9.266 on OULAD with 50 learning materials, which is almost 0.4 higher than that of GA with its fitness score of 9.642. ATSA is the second best of all, followed by IChOA and DE. The fitness score of PSO occupies the position almost equivalent to ACO because there is a slight variation between them, and the worst results are produced by GA. The fitness scores of metaheuristics become higher with the incremental extension of material size, and the trend underlying this seems to be proportional.
In addition to mean value of the fitness score, the standard deviation and best value of the fitness score and
p-value of the hypothesis test are shown in
Table 2 to evaluate solution qualities as well. The significance level
, and if the
p-value of the given method is less than that, then there is indeed a significant difference between those two comparative algorithms, and vice versa. It can be revealed from
Table 2 that the proposed GT-PSO provides the best performance among all except for one case, i.e., the pairwise comparison between GT-PSO and ATSA under the circumstance of 500 learning materials in a path of the curriculum sequence. Its
p-value is much greater than 0.05 and there exists no significant difference between them, and GT-PSO has inferior performance to ATSA, which is further evidenced by the statistical results of mean and best values of the fitness score. Please also note that the standard deviation of GT-PSO fitness score diverges as the number of learning materials increases. In spite of this, DE shows a relatively converged standard deviation regardless of material numbers, while GA acts the opposite of DE.
Figure 5 displays the visualizations of fitness scores divided by different numbers of learning materials. Result curves of the compared methods are represented in different colors. The total number of iterations is set to be 1000 since nearly all methods would converge after 800 iterations in the later stage of the search procedure. From all subfigures in
Figure 5, we can observe that searching difficulty also rises while the number of learning materials increases, which is reflected in the convergence speed of the compared algorithms as well. In
Figure 5a of 50 materials, almost all methods converge at the iterations less than 300 except for DE and the convergence situation happens around 400 iterations in
Figure 5b of 200 materials except for DE and IChOA. In
Figure 5c of 500 materials, the number of iterations is near 400 to 500 and finally in
Figure 5d of 1000 materials it is around 800. From
Figure 5a,b it can be observed that the convergence speed of ACO is relatively slow, on the contrary, the trend of GT-PSO decreases rapidly, and the other five algorithms have intermediate results. However,
Figure 5c,d indicate that GT-PSO has relatively lower convergence, and DE and ATSA show the relatively fair performance.
4. Discussion
The experimental results show that, in general, all selected algorithms tested in the experiment could handle the ACS problem with the feature of NP hardness using their own search strategies. Basically, the population-based metaheuristic can be regarded as the trial-and-error method of multi-agent collaborative search. On the other hand, it contains the approximation approach of random technology. It is worth mentioning that GT-PSO is built based on the mathematical foundation of symmetric group theory and its search paradigm is classified into the categories of diversification and intensification, and the adaptive control of the balanced relationship between these two is maintained by parameter configuration and hierarchical operation. When the dataset size is relatively small, GT-PSO focuses on the stage of intensification (operations of planer and orbiter) and the corresponding convergence rate is fast, but stagnation at the local optimum is prevented by the balance of diversification (operations of conjugator and cycler), which is proven by the results in
Figure 5a,b. However, from
Figure 5c to
Figure 5d, as the dataset size grows, diversification (operations of conjugator and cycler) dominates the early search to provide more possible candidates and the intensification (operations of planer and orbiter) guarantees that GT-PSO would finally converge in the late search. Thus, the implication of adaptive control of GT-PSO convergence is interpreted and summarized.
For the rest of alternative methods in
Figure 5, the performance curve of PSO (in black) is similar to GT-PSO (in red) because GT-PSO is an extended and refined version of PSO, so naturally our proposed method outperforms the original PSO. GA (brown curve) suffers from the drawback of early maturing performance, which is stagnation at the local optimum and inadequate solution. The reason behind this phenomenon is probably the complex procedure of selection, crossover, mutation, and termination, with enormous parameters in each step. Sometimes, ACO (green curve) has a slower convergence rate than others and this may be caused by the positive feedback of accumulated pheromones on the particular paths, and there are few escape strategies for ants to create a potential new path to the solution, which further causes bad solutions from the local optimum. The performance of DE (blue curve) is very stable and its results are fairly decent due to the foundation of differential evolution approach and the adaptive dynamic turbulence strategy for stagnation at the local optimum. ATSA (purple curve) performs with a rapid convergence rate because of two main adaptive phases at each iteration: the randomly selected tunicate for searching all the space and the best tunicate for improving the search navigation. They cooperate with each other adaptively to boost the search quality. IChOA (yellow curve) has the slowest convergence rate due to non-deterministic turbulence factors caused by the initialization of a Halton list and enhanced non-linear convergence operators. Its performance becomes worse when the complexity is higher.
The time complexity of GT-PSO for the ACS problem is discussed as follows. Assume that
is the number of learning materials in a curriculum sequence,
is the evaluating cost of the objective function,
is the size of the swarm population, and
is the number of iterations. According to Equations (12) to (14),
, since each one calculates the sum of every element in the sequence, so its time complexity is linear to
, and thus
. In the initialization of GT-PSO in
Figure 4, the time complexity is
. In each iteration, the time complexity of each operation is
and the time complexity of one single iteration is
. Finally, the time complexity of GT-PSO is
, and it belongs to polynomial complexity and is acceptable as the complexity of the solutions to NP-hard problems.
The space complexity of GT-PSO for the ACS problem is discussed as follows. Similarly, the space complexity of the objective function is . In the initialization of GT-PSO, the space complexity is , and in each iteration the space complexity of each operation is . No extra space is needed for the rest of the search, so the time complexity of GT-PSO is . It is less complex than the time cost and in practice the storage space is always sufficient. Therefore, the time complexity is the main concern of the GT-PSO algorithm.
Despite the advantages achieved by GT-PSO, there are still some limitations of the existing algorithm. Firstly, the global optimum is not guaranteed to be reached because of the inherent randomness of all metaheuristics. Secondly, it can only deal with the combinatorial problem of discrete optimization. Thirdly, it may cost huge computational time when the objective function is extremely complex.