Optimal Decision Making for Customer-Intensive Services Based on Queuing System Considering the Heterogeneity of Customer Advertising Perception

Abstract

In customer-intensive services, advertising can increase customers’ patience and bring more utility to customers. However, customers’ different perceptions of advertising can affect their utility and indirectly affect the decision making of the service provider. Thus, this paper uses the M/M/1 queueing model to study the optimal decision making of customer-intensive service providers in different markets according to the customers’ heterogeneity. We first classify customers into two categories: high sensitivity and low sensitivity, and then we analyze the consumption behavior of these two types of customers in the service system as the potential customer arrival rate increases. Finally, the optimal decisions of the service provider with different demands are determined. We find that the service provider can benefit from making optimal decisions based on market demand as the potential customer arrival rate increases. If the potential arrival rate exceeds a certain threshold, the service provider has more dominance in the market, and relevant decision making is no longer affected by the potential customer arrival rate. Furthermore, it is not always beneficial for the service provider to serve all customers regardless of whether there are low-sensitivity customers in the service system, and advertising can tap more highly sensitive customers and help to further increase the revenue of service providers. The results also show that ignoring the heterogeneity of customers’ sensitivity to advertising very likely leads to losses in revenue.

1. Introduction

Customer-intensive services refer to services that are highly experienced and patient [1]. Customers have a strong perception of the service rate in the service process. The slower the service rate, the higher the perceived utility of the customers. Customer-intensive services include medical services, financial counseling, psychological counseling, beauty salons, housekeeping services, etc. [2,3,4], so it is of great significance to study customer-intensive services. In medical services, patients can be treated effectively when doctors invest more time and experience. In addition, the advertising and popularity of service providers also have an important impact on the customers’ perceived utility of such services [2] because advertising can make customers fully understand products and services, thereby attracting customers to join the service system.

As studied by Anand et al. [3], the core of customer-intensive services is the service rate, and service providers need to provide high-quality services based on the service rate. Moreover, in modern business, advertising has played a very important role. Service providers use advertising to expand the market, establish service awareness, and improve the perceived utility of customers through the establishment of awareness [2]. Therefore, proper advertising can attract more customers to purchase services, which increases the service provider’s revenue. However, with the rapid changes in the business environment, various kinds of advertisements emerge one after another, which makes customers have different preferences for advertising. To a certain extent, the formation of customer heterogeneity requires the service provider to adjust service decisions in a timely manner to adapt to the service market. In real life, we can easily find that some customers attach great importance to advertising, are keen on the things reflected in the advertisements, and believe that the advertisements represent the quality of products and services. The awareness created by the advertisements makes these customers trust the service provider even more. However, there are always some customers who may not be sensitive to advertising, and they think that the content of advertisements does not represent the specific nature of the product or service. Therefore, it is easy for them to ignore the advertisements. Customers’ different perceptions of advertising make it difficult for the service provider to make decisions, which requires the service provider to conduct corresponding research on the market before making decisions. Based on the research of Cho and Cheon [5], customers’ perception sensitivity to advertising can be obtained through relevant market research, which first solves the problem of advertising perception measurement. Then, Galeotti et al. [6] believe that implementing targeted advertising strategies for different market segments can not only achieve higher returns but also effectively reduce competition among firms. Furthermore, Chen et al. [7] analyze the important role of personalized advertising from the perspective of rational choice theory. It can be seen that it is of great significance to make corresponding decisions according to the heterogeneity in customers’ perception of advertising.

However, in customer-intensive services, advertising is not the core factor affecting customer utility. Therefore, such service providers do not deliberately formulate personalized advertisements to attract more customers (for example, we can hardly see heterogeneous medical advertisements of one hospital). Therefore, for such service providers, the problem that needs to be faced is how to make optimal service decisions for a specific advertising intensity to meet the needs of heterogeneous markets. In addition, customers’ waiting time becomes longer as the potential customer arrival rate increases, and then the service system becomes crowded; hence, the customers with lower perceived utility tend to leave the service system. This has resulted in little success in advertising campaigns by service providers. Thus, the scale of the potential arrival rate and the heterogeneity of customers’ advertising perception make such service providers face the problem of how to make optimal service decisions for different types of customers.

The service provider needs to provide a high service rate and set reasonable prices to optimize revenue based on advertising in customer-intensive services. According to the above background, this paper uses the M/M/1 model to study the optimal service decisions of such service providers with different market demands (potential customer arrival rate) and heterogeneity in customers’ perception of advertising. This paper solves the optimal decision-making problem of such service providers in different market conditions and provides a theoretical basis for gaining optimal revenue. This facilitates the long-term development of customer-intensive services.

The contributions and innovations of this paper can be summarized as follows. (1) As far as we know, this paper is the first to study the impact of the heterogeneity of customers’ advertising perception on the decision making and revenue acquisition of customer-intensive service providers, which makes the decisions of such service providers more consistent with the actual operation situation. (2) In addition, we also study the change in the optimal decisions of customer-intensive service providers with the change in market demand, which can help such service providers adjust decisions according to market demand so as to obtain optimal revenue. (3) We find that advertising can effectively increase the number of highly sensitive customers in the market, thus bringing more revenue to the service provider, which reflects the importance of advertising and market segmentation. At the same time, it enriches the theory of advertising heterogeneity in customer-intensive services.

The rest of this paper is organized as follows. In Section 2, we provide a review of relevant studies on customer-intensive services, advertising effects, and the heterogeneity of advertising perception. In Section 3, we construct a basic model considering the heterogeneity of customers’ advertising perception and analyze the utility function of customers and the revenue function of service providers. In Section 4, we conduct optimal decision analysis for the situation with low-sensitivity customers in the system. In Section 5, we consider the optimal decision when an increase in the customer arrival rate makes the low-sensitivity customers exit the system and only the high-sensitivity customers remain and compare the change in the optimal decision and revenue in the two cases. In Section 6, we further study the impact of ignoring the heterogeneity in customer perception to reflect the significance of considering customer heterogeneity in this paper. In Section 7, we conclude the paper.

2. Literature Review

Our study is primarily concerned with customer-intensive services, advertising effects, and heterogeneity in advertising perception.

Customer-intensive services include medical services, personal care, counseling, etc. [8]. Anand et al. [3] point out that in customer-intensive services, a customer’s perceived utility increases with the service time, but this also leads to an increase in waiting time, thereby reducing the customer’s utility. In addition, we must also pay attention to the impact of waiting costs on customers in such services. Waiting cost includes time cost and discomfort cost, of which discomfort cost mainly refers to the negative psychological and physiological feelings of waiting, which some scholars call anxiety cost [9,10]. Based on the study of anxiety cost, Zhan et al. [2] conclude through their study that advertisements of service providers can reduce customers’ anxiety costs and tap more potential customers by increasing the visibility of service providers. Furthermore, since service time is inversely proportional to the service rate in customer-intensive services, changes in the service rate can affect the effectiveness of corresponding strategies formulated by service providers [11,12]. Li et al. [13] assume that customers’ purchase decisions are forward-looking in customer-intensive services and find that customer heterogeneity would affect optimal decisions, market coverage, and expected returns. Zhao et al. [14] study the pricing strategies of customer-intensive service providers based on online reviews, further explaining the relationship between service quality and the rate of such services. Then, Wang et al. [15] study the problem of agent pooling in customer-intensive services. Through queuing game theory analysis, they show that when agents take strategic behaviors, they may choose to speed up the service rate to try to serve more customers, thus reducing the service quality. Liu et al. [16] develop a strategic queuing model for customer-intensive services and find that under the condition of heterogeneous consumers, no matter whether the number of service providers is large or small, price competition and service competition may be conducted at the same time. This kind of literature on customer-intensive services focuses on analyzing service rate and service competition and does not consider the effect of the heterogeneity of customers’ perception of advertising in customer-intensive services. Therefore, different from such literature, this paper focuses on the impact of heterogeneity in customers’ perception of advertising on the operational decisions of such customer-intensive service providers. Our motivation is to help customer-intensive service providers in the advertising marketing environment to make service rate and price decisions when facing heterogeneous customers, which is conducive to the long-term development of these service providers.

In the literature on advertising effect, Zhan et al. [2] believe that advertising can tap more potential customers. Advertising allows consumers to familiarize themselves with specific goods and services in advance, which means that the information in advertisements has certain promotional benefits [17]. Yu et al. [18] believe that advertising has a threshold effect, so if the advertising level is lower than a certain level, advertising has almost no impact on sales, which means that a high level of advertising is necessary. Liu et al. [19] and SeyedEsfahani et al. [20] study advertising collaboration and cost sharing with online platforms. They believe that advertising on online platforms is more beneficial than traditional forms. In addition, many scholars have also paid attention to how to set reasonable prices to attract customers through advertising [21,22]. Therefore, in this paper, we also pay attention to the impact of the advertising effect on the price setting of service providers. Shapiro [23] analyzes the impact of advertising on the health insurance market and argues that advertising is more effective in counties with poor health. In addition, Tapanainen et al. [24] believe that the development of eWOM has made advertising more influential among consumers. For example, many medical institutions have begun to use the Internet for publicity. Pazoki and Samarghandi [25] construct a framework to analyze optimal pricing and optimal advertising strategies based on word-of-mouth effects through sensitivity analysis using the infectious disease epidemic model (SIS). These literatures find that advertising effects have a significant impact on consumer behavior, even in customer-intensive services. However, in this paper, in order to solve the optimal decision-making problem of customer-intensive service providers in the advertising marketing environment, we analyze the impact of the heterogeneity of customers’ perception of advertising on service providers’ optimal decisions, thus contributing to the literature. In addition, we study the changes in the optimal service rate and price decision of such service providers with the arrival rate of customers with different advertising perception types, which expands the application of advertising effect theory in customer-intensive services.

Not only that but the heterogeneity of customers greatly affects the strategy of service providers [26], and the heterogeneity of customers’ perceptions of advertisements also affects the decision making of service providers. Customer personalization is valuable to service providers, so service providers can often customize pricing for customers [27,28]. This makes us realize the importance of personalized advertising and differentiated advertising. The perceived utility and cost of heterogeneous customers in the waiting process are different, so using the queuing model to explain the purchasing behavior of heterogeneous customers is beneficial to help service providers achieve an appropriate balance between operating costs and service quality [16,27,28]. Li et al. [29] introduce the heterogeneity of waiting cost into customer-intensive services and divide customers into two categories: high waiting cost and low waiting cost. They analyze the optimal strategy of service providers when customers’ waiting costs are heterogeneous. Meanwhile, Nazerzadeh and Randhawa [30] study the pricing problem of customer heterogeneity in the M/M/1 system and point out that dividing customers into two categories is an effective way to optimize decision making and increase revenue. In this paper, we also draw on relevant research and divide customers into two categories: high sensitivity and low sensitivity. Although some scholars have conducted some research on customer heterogeneity, its correlation to advertising heterogeneity in customer-intensive services is still unexplored, which also motivated us to solve such heterogeneity problems. Therefore, in this paper, we analyze the impact of different types of customer behavior on the optimal decision and revenue of customer-intensive service providers with the change in market demand so as to reflect the importance of considering the heterogeneity of customers’ advertising perception in the operation of such service providers.

3. Model Establishment

In customer-intensive services, advertising effects still play a key role. The advertising of service providers can not only establish their own popularity but also improve the perceived utility of customers through the establishment of popularity [2]. Meanwhile, the rapid changes in the business environment make different customers have different preferences for commercial advertisements. Customers who are more concerned about advertising and more sensitive tend to obtain higher utility from advertising, while customers with lower sensitivity do not obtain high utility. Therefore, the same service decision may have different effects on the purchasing behavior of the two types of customers, thereby affecting a service provider’s revenue.

3.1. Customer Utility

We assume that a customer-intensive service provider serves customers with a single server and that the service rule is first-come, first-served. Therefore, the service system satisfies the classic M/M/1 queuing model. M/M/1 has been used in numerous literatures to analyze the waiting behavior of customers and the optimal decision making of service providers [2,3,31].

There are many customer categories in the market, but the focus of this study is on the impact of customer differences on decision making. Therefore, the number of customer categories is not the content of this study. Therefore, in order to simplify the analysis, and according to the classification of customer heterogeneity by Nazerzadeh and Randhawa [30] and Li et al. [12], this paper assumes that there are two types of customers in the market. One type is customers who are highly sensitive to advertisements, called H customers, where their perception coefficient of advertisements is $k_H$ and their proportion is $q$; the other type is customers who are less sensitive to advertisements, called L customers, where their perception coefficient is $k_L$ and their proportion is $\left(1-q\right)$. It should be noted that the difference between the two types of customers in this paper is the difference in the perception of advertising rather than the difference in the waiting cost per unit time. This assumption that customers’ waiting cost per unit time is the same is widely applied in the study of customer-intensive services [2,3,15].

The potential demand (potential arrival rate of customers) in the market is $\mathsf{\Lambda }$, the effective demand (effective arrival rate of customers) is $\lambda$, and customers arrive with a Poisson flow. The service rate provided by the service provider is $\mu$ ($\mu$ satisfies the exponential distribution), the price charged is $P$, and the advertising intensity is $a$.

According to the above assumptions, the system waiting time in the classic M/M/1 queuing model is:

$$W\left(\mu ,\lambda \right)=\{\begin{array}{cc}\frac{1}{\mu -\lambda }& if 0\le \lambda <\mu \\ \infty & otherwise\end{array}$$

(1)

In customer-intensive services, a customer’s perceived utility $V\left(\mu \right)$ increases as the service rate slows ($\mu$ becomes smaller). According to the definition of a customer-intensive service and the description of the utility function by Anand et al. [3], the utility function of a customer based on the service rate can be obtained as follows:

$$V\left(\mu \right)={\left[V_b+\beta {\mu }_b-\beta \mu \right]}^{+}$$

(2)

where $x^{+}=\max \left(0,x\right)$, $V\left(\mu \right)$ represents the customer’s perceived utility to the service rate, $V_b$ represents the benchmark service utility, and ${\mu }_b$ represents the benchmark service rate. $\beta$ represents the customer’s perception of the service rate, that is, the service rate sensitivity. The greater the $\beta$, the greater the customer’s perception of the unit service rate.

Table 1. Summary of notations.

Parameters	Description
$k_i$	$i$ customers’ perception of the advertising effect ($i=H,L$)
$\mathsf{\Lambda }$	The total potential arrival rate of customers (potential market demand)
$\lambda$	The effective arrival rate of customers (effective market demand)
$q$	The percentage of H customers in the system
$\mu$	Service rate
$t$	The average service time
$V\left(\mu \right)$	The utility perceived by customer
$W\left(\mu ,\lambda \right)$	The waiting time in the system
$V_b$	The baseline service utility
${\mu }_b$	The baseline service rate
$\beta$	The degree of customers’ perception of the service rate
$V_{Ni}$	The net utility of $i$ customers ($i=H,L$)
$R\left(\mu ,P\right)$	The revenue of the service provider
$P$	The price that the service provider charges
$a$	The advertising intensity
$m$	The maximum service utility
$c$	The waiting cost per unit time.

shows the parameter definitions.

3.2. Decision Making and Revenue of Service Providers

Customers choose whether to enter the service system according to the net utility. In customer-intensive services, the net utility of customers can be expressed as follows:

$$V_{Ni}\left(\mu ,P\right)=V\left(\mu \right)-P-cW=V_b+\beta \left({\mu }_b-\mu \right)+k_{i}a-P-cW i=H, L$$

(3)

High-sensitivity customers have higher perceived utility. Therefore, when two types of customers choose to join the queue, the net utility of customer H is greater than that of customer L, that is, $V_{NH}\left(\mu ,P\right)>V_{NL}\left(\mu ,P\right)$. Changes in the potential arrival rate may lead to the following four situations:

(1)

There are L customers in the system (Situation $S_L$)

①

Situation $S_{L1}$. All L customers join the system. Since $V_{NH}\left(\mu ,P\right)>V_{NL}\left(\mu ,P\right)$, this effectively means that all H customers also join the service system.

②

Situation $S_{L2}$. A part of L customers join the queue, and $V_{NL}\left(\mu ,P\right)=0$. Since $V_{NH}\left(\mu ,P\right)>V_{NL}\left(\mu ,P\right)$, it means that the utility of H customers is positive, and they will all join the service system.

(2)

There is no L customer in the system (Situation $S_H$)

①

Situation $S_{H1}$. All H customers join the service system, but no L customers join. $V_{NH}\left(\mu ,P\right)>0$, $V_{NL}\left(\mu ,P\right)<0$.

②

Situation $S_{H2}$. Only some H customers join the service system, and $V_{NH}\left(\mu ,P\right)=0$. This means that the net utility of L customers must be negative, and they will not join the service system.

The revenue of the service provider can be expressed as follows:

$$R\left(\mu ,P\right)=P\lambda \left(\mu ,P\right)$$

(4)

In the customer-intensive services, the effective arrival rate of customers is related to the decision making of service providers and the consumption behavior of customers. Therefore, it is necessary to analyze the optimal revenue of service providers under different decisions so as to determine the optimal decision. The revenue optimization of the service provider can be expressed as follows:

$$\underset{\mu \in \left[\underset{\_}{\mu },\overline{\mu }\right],P>0}{\max }R\left(\mu ,P\right)=\underset{\mu \in \left[\underset{\_}{\mu },\overline{\mu }\right]}{\max }\left\{\underset{P>0}{\max }\left\{P\lambda \left(\mu ,P\right)\right\}\right\}$$

(5)

The solution method in this paper is to first solve the optimal price under a certain service rate and then substitute the optimal price into the revenue function and optimize the service rate.

3.3. Service Rate Range

In customer-intensive services, the service rate is the core element to measure service quality. The faster service rate makes the perceived service utility of customers lower, and customers are reluctant to join the queue; although the slower service rate makes the customers have higher utility, it is easy to cause congestion of the service system. Therefore, it is necessary to determine the range of service rates to ensure that customers will not leave the queue due to too-fast service rates or too-long waiting times. This needs to ensure that there are still customers joining the queue when the price $P=0$, that is, $V_N=V_b+\beta \left({\mu }_b-\mu \right)+k_{i}a-P-cW\ge 0$. The range of service rate $\mu$ is as follows:

$$\frac{\left(V_b+\beta {\mu }_b+k_{i}a-\sqrt{{\left(V_b+\beta {\mu }_b+k_{i}a\right)}^2-4\beta c}\right)}{2\beta }\le \mu \le \frac{\left(V_b+\beta {\mu }_b+k_{i}a+\sqrt{{\left(V_b+\beta {\mu }_b+k_{i}a\right)}^2-4\beta c}\right)}{2\beta }$$

(6)

When $\mu <{\underset{\_}{\mu }}_i$, it indicates that the service rate is slow, and customers need to wait for a long time in the service system, so they are reluctant to join the queue. When $\mu >{\overline{\mu }}_i$, it is because the service rate is faster, resulting in less utility for customers. Therefore, in order to keep the benefit from becoming zero, the service rate is specified in the range $\left[{\underset{\_}{\mu }}_i,{\overline{\mu }}_i\right]$. Additionally, ${\mathsf{\Omega }}_L=\left[{\underset{\_}{\mu }}_L,{\overline{\mu }}_L\right]$, ${\mathsf{\Omega }}_H=\left[{\underset{\_}{\mu }}_H,{\overline{\mu }}_H\right]$.

For H customers, they have a higher $k_H$ and a higher perceived utility in the service process. Therefore, the variable range of the service rate formulated by the service provider becomes larger, i.e., ${\underset{\_}{\mu }}_H<{\underset{\_}{\mu }}_L<{\overline{\mu }}_L<{\overline{\mu }}_H$. This shows that with the change in the service rate, when L customers enter the service system, all H customers will enter the system.

4. Decision Making with Low-Sensitivity Customers

4.1. Optimal Decision Making

In the service system, the L customers obtain the utility $V\left(\mu \right)$ based on the service rate and the utility $k_{L}a$ based on the advertisement effect and also need to bear the service price $P$ and the waiting cost $\frac{c}{\mu -\lambda \left(\mu ,P\right)}$. All L customers in $S_{L1}$ can be served. Because $V_{NH}\left(\mu ,P\right)>V_{NL}\left(\mu ,P\right)$, it means that all customers including H customers can enter the service system in this situation. The effective customer arrival rate ${\lambda }_{L1}\left(\mu ,P\right)$ in $S_{L1}$ is the total market demand $\mathsf{\Lambda }$. This also shows that in $S_{L1}$, $\mathsf{\Lambda }$ is small and the net utility of L customers is always positive. However, as $\mathsf{\Lambda }$ increases, the customers’ waiting cost increases, and the net utility of L customers gradually decreases to zero. In this case, only a part of L customers can join the service system. The service system is in situation $S_{L2}$, and $V_{NL}\left(\mu ,P\right)=0$. Based on formula (3) and $V_{NL}\left(\mu ,P\right)=0$, $V\left(\mu \right)-P+k_{L}a-\frac{c}{\mu -\lambda \left(\mu ,P\right)}=0$ can be obtained. Therefore, the effective arrival rate of customers in situation $S_{L2}$ can be obtained:

$${\lambda }_{L2}\left(\mu ,P\right)=\mu -\frac{c}{V\left(\mu \right)+k_{L}a-P}$$

(7)

The effective customer arrival rates in $S_{L1}$ and $S_{L2}$ are as follows:

$$\lambda \left(\mu ,P\right)=\{\begin{array}{cc}{\lambda }_{L1}\left(\mu ,P\right)=\mathsf{\Lambda }& if 0<P\le V\left(\mu \right)+k_{L}a-\frac{c}{\mu -\mathsf{\Lambda }}\\ {\lambda }_{L2}\left(\mu ,P\right)=\mu -\frac{c}{V\left(\mu \right)+k_{L}a-P}& if V\left(\mu \right)+k_{L}a-\frac{c}{\mu -\mathsf{\Lambda }}<P<V\left(\mu \right)+k_{L}a-\frac{c}{\mu -q\mathsf{\Lambda }}\end{array}$$

(8)

According to the above analysis, $S_{L1}$ and $S_{L2}$ are not completely independent but can be converted according to different market demand $\mathsf{\Lambda }$.

On the basis of the above effective customer arrival rate, the revenue function of the service provider can be obtained as follows:

$$R\left(\mu ,P\right)=\{\begin{array}{cc}{R}_{L1}\left(\mu ,P\right)=P\mathsf{\Lambda }& if 0<P\le V\left(\mu \right)+k_{L}a-\frac{c}{\mu -\mathsf{\Lambda }}\\ R_{L2}\left(\mu ,P\right)=P\left(\mu -\frac{c}{V\left(\mu \right)+k_{L}a-P}\right)& if V\left(\mu \right)+k_{L}a-\frac{c}{\mu -\mathsf{\Lambda }}<P<V\left(\mu \right)+k_{L}a-\frac{c}{\mu -q\mathsf{\Lambda }}\end{array}$$

(9)

Using the above revenue function to optimize the service price, the optimal price is obtained as follows:

$$P^{*}\left(\mu \right)=\{\begin{array}{cc}{P}_{\mathrm{L}1}\left(\mu \right)=V\left(\mu \right)+k_{L}a-\frac{c}{\mu -\mathsf{\Lambda }}& if 0<\mathsf{\Lambda }\le {\widehat{\lambda }}_{L2}\left(\mu \right) and S_{L1}\\ P_{L2}\left(\mu \right)=V\left(\mu \right)+k_{L}a-\sqrt{\frac{c\left(V\left(\mu \right)+k_{L}a\right)}{\mu }}& if {\widehat{\lambda }}_{L2}\left(\mu \right)<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{L2}\left(\mu \right)}{q} and S_{L2}\end{array}$$

(10)

The effective arrival rate threshold ${\widehat{\lambda }}_{L2}\left(\mu \right)$ represents the maximum number of customers that the service provider can serve at a given service rate $\mu$ when there are L customers in the service system. When $0<\mathsf{\Lambda }\le {\widehat{\lambda }}_{L2}\left(\mu \right)$, all customers can be served, including L customers and H customers, which is the precondition for making decisions. When ${\widehat{\lambda }}_{L2}\left(\mu \right)<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{L2}\left(\mu \right)}{q}$, only customers of scale ${\widehat{\lambda }}_{L2}\left(\mu \right)$ can actually be served, and ${\widehat{\lambda }}_{L2}\left(\mu \right)$ includes a part of L customers and all H customers. The effective arrival rate in this case is ${\lambda }_e\left(\mu ,P^{*}\left(\mu \right)\right)={\widehat{\lambda }}_{L2}\left(\mu \right)=\mu -\sqrt{\frac{c\mu }{V\left(\mu \right)+k_{L}a}}$.

The effective customer arrival rate at the optimal price is as follows:

$${\lambda }^{*}\left(\mu ,P^{*}\left(\mu \right)\right)=\{\begin{array}{cc}{\lambda }_{L1}^{*}\left(\mu ,P^{*}\left(\mu \right)\right)=\mathsf{\Lambda }\hfill & if 0<\mathsf{\Lambda }\le {\widehat{\lambda }}_{L2}\left(\mu \right) and S_{L1}\\ {\lambda }_{L2}^{*}\left(\mu ,P^{*}\left(\mu \right)\right)={\widehat{\lambda }}_{L2}\left(\mu \right)\hfill & if {\widehat{\lambda }}_{L2}\left(\mu \right)<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{L2}\left(\mu \right)}{q} and S_{L2}\end{array}$$

(11)

Finally, based on $R^{*}\left(\mu \right)=P^{*}\left(\mu \right){\lambda }^{*}\left(\mu ,P^{*}\left(\mu \right)\right)$, the service rate is optimized to obtain the optimal service rate as follows:

$${\mu }^{*}=\{\begin{array}{ll}{\mu }_{L1}^{*}=\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}& if S_{L1}\\ {\mu }_{L2}^{*}=\frac{m+k_{L}a}{2\beta }& if S_{L2}\end{array}$$

(12)

After substituting the optimal service rates back to $P^{*}\left(\mu \right)$ and ${\lambda }^{*}\left(\mu ,P^{*}\left(\mu \right)\right)$, the following proposition can be obtained:

Proposition 1.

i. 

From $0<\mathsf{\Lambda }\le {\widehat{\lambda }}_{L2}$, we know that the effective arrival rate of $S_{L1}$ is less than the effective customer arrival rate of $S_{L2}$.

ii. 

When $\mathsf{\Lambda }$ satisfies $0<\mathsf{\Lambda }\le {\widehat{\lambda }}_{L2}$, that is, situation $S_{L1}$, the optimal decision is: ${\mu }_{L1}^{*}=\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}$, $P_{L1}^{*}\left({\mu }^{*}\right)=m+k_{L}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}$; the optimal effective arrival rate is ${\lambda }_{L1}^{*}\left({\mu }^{*},P^{*}\left({\mu }^{*}\right)\right)=\mathsf{\Lambda }$.

iii. 

When ${\widehat{\lambda }}_{L2}<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{L2}}{q}$, that is, situation $S_{L2}$, a part of L customers can enter the system, and the optimal decision is: ${\mu }_{L2}^{*}=\frac{m+k_{L}a}{2\beta }$, $P_{L2}^{*}\left({\mu }^{*}\right)=\frac{m+k_{L}a-2\sqrt{\beta c}}{2}$; the optimal effective arrival rate is ${\lambda }_{L2}^{*}\left({\mu }^{*},P^{*}\left({\mu }^{*}\right)\right)=\frac{m+k_{L}a-2\sqrt{\beta c}}{2\beta }$. (Proof in Appendix A).

Proposition 1 provides the basis for the optimal decision of service providers. The service provider chooses the decision to adapt to the market to obtain the optimal revenue. When $0<\mathsf{\Lambda }\le {\widehat{\lambda }}_{L2}$, the service rate ${\mu }_{L1}^{*}$ and the optimal price $P_{L1}^{*}$ are formulated according to $\mathsf{\Lambda }$. As $\mathsf{\Lambda }$ increases, when $\mathsf{\Lambda }$ satisfies ${\widehat{\lambda }}_{L2}<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{L2}}{q}$, ${\mu }_{L2}^{*}$ and $P_{L2}^{*}$ are not affected by $\mathsf{\Lambda }$. This shows that with the increase in $\mathsf{\Lambda }$, the service provider gradually has market dominance relative to the L customers, and the corresponding decision making is not affected by $\mathsf{\Lambda }$.

Lemma 1.

When $0<\mathsf{\Lambda }\le {\widehat{\lambda }}_{L2}$, $\frac{\partial {\mu }_{L1}^{*}}{\partial a}=0, \frac{\partial P_{L1}^{*}}{\partial a}>0$; when ${\widehat{\lambda }}_{L2}<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{L2}}{q}$, $\frac{\partial {\mu }_{L2}^{*}}{\partial a}>0,\frac{\partial P_{L2}^{*}}{\partial a}>0$. (Proof in Appendix A).

The above lemma shows that when $0<\mathsf{\Lambda }\le {\widehat{\lambda }}_{L2}$, as the advertising intensity $a$ increases, customers can obtain higher perceived utility from it. However, the market demand is low and does not cause congestion to the service system, so the service provider should keep ${\mu }_{L1}^{*}$ fixed. The service provider can increase the revenue by increasing the optimal price $P_{L1}^{*}$. With the continuous increase in $\mathsf{\Lambda }$, once $a$ increases, more customers are attracted into the service system, resulting in congestion of the service system. Therefore, the service provider should increase the service rate to reduce the congestion of the service system. Meanwhile, based on the increase in customer utility, the service provider can also increase the optimal price $P_{L2}^{*}$.

4.2. Optimal Revenue

In $S_{L1}$, all L customers obtain positive utility access to the system. Since $V_{NH}\left(\mu ,P\right)>V_{NL}\left(\mu ,P\right)$, H customers must obtain positive effect. Therefore, in $S_{L1}$, all H customers and L customers enter the system. The optimal revenue of the service provider can be expressed as follows:

$$R_{L1}^{*}=P_{L1}^{*}\left({\mu }^{*}\right){\lambda }_{L2}^{*}\left({\mu }^{*},P^{*}\left({\mu }^{*}\right)\right)=\left(m+k_{L}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}\right)\mathsf{\Lambda }$$

(13)

Lemma 2.

The maximum value of $R_{L1}^{*}$ is obtained when $\mathsf{\Lambda }={\widehat{\lambda }}_{L2}$, and we can obtain $R_{L1}^{*}\le R_{L2}^{*}$. (Proof in Appendix A).

Lemma 2 shows that with the increase in $\mathsf{\Lambda }$, the situation of serving only a part of L customers brings greater revenue to the service provider. In $S_{L2}$, the service provider only serves a part of L customers. However, due to the large scale of the potential arrival rate, the effective arrival rate of $S_{L2}$ is still greater than that of $S_{L1}$, that is, ${\lambda }_{L2}^{*}\left({\mu }^{*},P^{*}\left({\mu }^{*}\right)\right)>{\lambda }_{L1}^{*}\left({\mu }^{*},P^{*}\left({\mu }^{*}\right)\right)$. This indicates that the increase in the effective arrival rate enables service providers to gain more revenue. In the market corresponding to $S_{L2}$, the service provider makes the corresponding optimal decision, which can bring more revenue than $S_{L1}$ can bring. That is, the market with ${\widehat{\lambda }}_{L2}<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{L2}}{q}$ is more conducive to the service provider to obtain more benefits.

5. Decision Making without Low-Sensitivity Customers

5.1. Optimal Decision Making

Like L customers, H customers obtain utility $V\left(\mu \right)$ based on the service rate and need to bear service price $P$ and waiting cost $\frac{c}{\mu -\lambda \left(\mu ,P\right)}$ in the service system. However, the utility obtained by the H customers is $k_{H}a$, which is higher than the $k_{L}a$ obtained by the L customers, that is, $V_{NH}\left(\mu ,P\right)>V_{NL}\left(\mu ,P\right)$. This means that when $V_{NH}\left(\mu ,P\right)=0$, L customers must not obtain positive service utility and leave the service system. The reason for this phenomenon is the crowding-out effect caused by the higher potential arrival rate. Only customers with higher perceived utility can stay in the service system. Therefore, the customers in the service system are H, and their quantity is $q\mathsf{\Lambda }$; L customers do not exist in the service system.

Based on Formula (3), when $V_{NH}\left(\mu ,P\right)=0$, there is $V\left(\mu \right)-P+k_{H}a-\frac{c}{\mu -\lambda \left(\mu ,P\right)}=0$. The effective arrival rate for customers in $S_{H2}$ can be obtained:

$${\lambda }_{H2}\left(\mu ,P\right)=\mu -\frac{c}{V\left(\mu \right)+k_{H}a-P}$$

(14)

Therefore, we obtain the effective customer arrival rate in the system in $S_H$ as follows:

$$\lambda \left(\mu ,P\right)=\{\begin{array}{cc}{\lambda }_{H1}\left(\mu ,P\right)=q\mathsf{\Lambda }& if V\left(\mu \right)+k_{L}a-\frac{c}{\mu -q\mathsf{\Lambda }}\le P\le V\left(\mu \right)+k_{H}a-\frac{c}{\mu -q\mathsf{\Lambda }}\\ {\lambda }_{H2}\left(\mu ,P\right)=\mu -\frac{c}{V\left(\mu \right)+k_{H}a-P}& if V\left(\mu \right)+k_{H}a-\frac{c}{\mu -q\mathsf{\Lambda }}\le P\le V\left(\mu \right)+k_{H}a-\frac{c}{\mu }\end{array}$$

(15)

The effective arrive rate in $S_H$ is based on the potential arrive rate $q\mathsf{\Lambda }$ of H customers. However, according to $V_{NH}\left(\mu ,P\right)=0$, it can be seen that the potential arrival rate $\mathsf{\Lambda }$ is relatively large, and only customers of scale $q\mathsf{\Lambda }$ can enter the system to obtain non-negative utility. Combined with Formula (5), the service provider revenue function in $S_H$ is obtained as follows:

$$R\left(\mu ,P\right)=\{\begin{array}{cc}{R}_{H1}\left(\mu ,P\right)=Pq\mathsf{\Lambda }& if V\left(\mu \right)+k_{L}a-\frac{c}{\mu -q\mathsf{\Lambda }}\le P\le V\left(\mu \right)+k_{H}a-\frac{c}{\mu -q\mathsf{\Lambda }}\\ R_{H2}\left(\mu ,P\right)=P\left(\mu -\frac{c}{V\left(\mu \right)+k_{H}a-P}\right)& if V\left(\mu \right)+k_{H}a-\frac{c}{\mu -q\mathsf{\Lambda }}\le P\le V\left(\mu \right)+k_{H}a-\frac{c}{\mu }\end{array}$$

(16)

Using the above revenue function to optimize the service price, the optimal price is obtained as follows:

$$P^{*}\left(\mu \right)=\{\begin{array}{cc}{P}_{H1}\left(\mu \right)=V\left(\mu \right)+k_{H}a-\frac{c}{\mu -q\mathsf{\Lambda }}\hfill & if\frac{{\widehat{\lambda }}_{L2}\left(\mu \right)}{q}<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{H2}\left(\mu \right)}{q} and S_{H1}\\ P_{H2}\left(\mu \right)=V\left(\mu \right)+k_{H}a-\sqrt{\frac{c\left(V\left(\mu \right)+k_{H}a\right)}{\mu }}\hfill & if\frac{{\widehat{\lambda }}_{H2}\left(\mu \right)}{q}<\mathsf{\Lambda } and S_{H2}\end{array}$$

(17)

The effective arrival rate threshold ${\widehat{\lambda }}_{H2}\left(\mu \right)$ represents the maximum number of customers that the service provider can serve under a given service rate $\mu$ when all the customers in the service system are H. When $\frac{{\widehat{\lambda }}_{L2}\left(\mu \right)}{q}<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{H2}\left(\mu \right)}{q}$, all H customers can be served; when $\frac{{\widehat{\lambda }}_{H2}\left(\mu \right)}{q}<\mathsf{\Lambda }$, only H customers of a quantity of ${\widehat{\lambda }}_{H2}\left(\mu \right)$ can be served. The effective arrival rate in this case is ${\lambda }^{*}\left(\mu ,P^{*}\left(\mu \right)\right)={\widehat{\lambda }}_{H2}\left(\mu \right)=\mu -\sqrt{\frac{c\mu }{V\left(\mu \right)+k_{H}a}}$.

Therefore, the effective customer arrival rate in a service system without L customers is as follows:

$${\lambda }^{*}\left(\mu ,P^{*}\left(\mu \right)\right)=\{\begin{array}{cc}{\lambda }_{H1}^{*}\left(\mu ,P^{*}\left(\mu \right)\right)=q\mathsf{\Lambda }& if \frac{{\widehat{\lambda }}_{L2}\left(\mu \right)}{q}<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{H2}\left(\mu \right)}{q} and S_{H1}\\ {\lambda }_{H2}^{*}\left(\mu ,P^{*}\left(\mu \right)\right)=\mu -\sqrt{\frac{c\mu }{V\left(\mu \right)+k_{H}a}}& if \frac{{\widehat{\lambda }}_{H2}\left(\mu \right)}{q}<\mathsf{\Lambda } and S_{H2}\end{array}$$

(18)

Finally, based on $R^{*}\left(\mu \right)=P^{*}\left(\mu \right){\lambda }^{*}\left(\mu ,P^{*}\left(\mu \right)\right)$, the optimal service rate in the service system with only H customers can be obtained as follows:

$${\mu }^{*}=\{\begin{array}{cc}{\mu }_{H1}^{*}=q\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}& if S_{H1}\\ {\mu }_{H2}^{*}=\frac{m+k_{H}a}{2\beta }& if S_{H2}\end{array}$$

(19)

Proposition 2.

i. 

As the potential arrival rate increases further, the L customers’ utility continues to decrease, and they exit the system completely.

ii. 

At ${\widehat{\lambda }}_{L2}<q\mathsf{\Lambda }\le {\widehat{\lambda }}_{H2}(\frac{{\widehat{\lambda }}_{L2}}{q}<\mathsf{\Lambda }\le \frac{{\widehat{\lambda }}_{H2}}{q}$), all H customers are served in $S_{H1}$. The optimal service rate and price are ${\mu }_{H1}^{*}=q\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}, P_{H1}^{*}\left({\mu }^{*}\right)=m+k_{H}a-q\beta \mathsf{\Lambda }-2\sqrt{\beta c}$; the optimal effective arrival rate is ${\lambda }_{H1}^{*}\left({\mu }^{*},P^{*}\left({\mu }^{*}\right)\right)=q\mathsf{\Lambda }$.

iii. 

At $q\mathsf{\Lambda }>{\widehat{\lambda }}_{H2}$($\mathsf{\Lambda }>\frac{{\widehat{\lambda }}_{H2}}{q}$), only some customers in $S_{H2}$ can obtain positive net utility. The optimal service rate and price are ${\mu }_{H2}^{*}=\frac{m+k_{H}a}{2\beta }$, $P_{H2}^{*}\left({\mu }^{*}\right)=\frac{m+k_{H}a-2\sqrt{\beta c}}{2}$; the optimal effective arrival rate is ${\lambda }_{H2}^{*}\left({\mu }^{*},P^{*}\left({\mu }^{*}\right)\right)=\frac{m+k_{H}a-2\sqrt{\beta c}}{2\beta }$. (Proof in Appendix A).

Proposition 2 gives the corresponding optimal decision that the service provider can make when the service system is full of H customers as the market demand continues to increase. When $\frac{{\widehat{\lambda }}_{L2}}{q}<\mathsf{\Lambda }\le \frac{{\widehat{\lambda }}_{H2}}{q}$, the formulation of the optimal service rate ${\mu }_{H1}^{*}$ depends on the total number $q\mathsf{\Lambda }$ of H customers in the service system. The larger the ratio $q$ is, the more the service provider should formulate a faster service rate and reduce the corresponding price $P_{H2}^{*}$. At $\mathsf{\Lambda }>\frac{{\widehat{\lambda }}_{H2}}{q}$, the scaling factor $q$ no longer affects the formulation of ${\mu }_{H2}^{*}$ and $P_{H2}^{*}$. That is, when $\mathsf{\Lambda }$ exceeds $\frac{{\widehat{\lambda }}_{H2}}{q}$, the service provider also has a certain dominance in the market relative to H customers, and the number of H customers no longer directly affects the decision making of service providers.

Lemma 3.

When $\frac{{\widehat{\lambda }}_{L2}}{q}<\mathsf{\Lambda }\le \frac{{\widehat{\lambda }}_{H2}}{q}$, $\frac{\partial {\mu }_{H1}^{*}}{\partial a}=0$, $\frac{\partial P_{H1}^{*}}{\partial a}>0$; when $\mathsf{\Lambda }>\frac{{\widehat{\lambda }}_{H2}}{q}$, $\frac{\partial {\mu }_{H2}^{*}}{\partial a}>0$, $\frac{\partial P_{H2}^{*}}{\partial a}>0$. Combining with Lemma 1, it can be seen that with the gradual increase in $\mathsf{\Lambda }$, the change in the service rate with the advertising intensity $a$ is first fixed, then increased, then fixed, and finally continues to increase. (Proof in Appendix A).

When there are only H customers in the service system, it means that there are more H customers in this case, and L customers are squeezed out of the service system. At ${\widehat{\lambda }}_{L2}<q\mathsf{\Lambda }\le {\widehat{\lambda }}_{H2}$, the increase in advertising intensity does not bring a higher degree of congestion to the system (because L customers have left the system). Therefore, the service provider only needs to increase the price to reduce the degree of congestion but does not need to increase the service rate. Once the number of H customers is too large in $q\mathsf{\Lambda }>{\widehat{\lambda }}_{H2}$, higher $a$ requires service providers to provide faster service rates and higher prices to reduce system congestion. In the whole process of $\mathsf{\Lambda }$’s change, the service provider first relies on the utility function of the L customers to make decisions, and then when the L customers completely exit the system, it relies on the H customers’ utility function to make decisions. This is equivalent to H customers replacing L customers in the decision-making process.

5.2. Optimal Revenue

In contrast with the case of $\mathsf{\Lambda }>\frac{{\widehat{\lambda }}_{L2}}{q}$, H customers squeeze all L customers out of the service system. Therefore, the service provider needs to make decisions for H customers. The optimal revenue can be expressed as follows:

$$R_{H1}^{*}=P_{H1}^{*}\left({\mu }^{*}\right){\lambda }_{H2}^{*}\left({\mu }^{*},P^{*}\left({\mu }^{*}\right)\right)=\left(m+k_{H}a-q\beta \mathsf{\Lambda }-2\sqrt{\beta c}\right)q\mathsf{\Lambda }$$

(20)

Lemma 4.

The maximum value of $R_{H1}^{*}$ is obtained at $\mathsf{\Lambda }={\widehat{\lambda }}_{H2}$, and we obtain $R_{H1}^{*}\le R_{H2}^{*}$. (Proof in Appendix A).

Lemma 4 shows that regardless of whether there are L customers in the service system, serving a part of customers brings higher revenue. This is due to the continuous increase in market demand. When the service provider can only serve some customers, it means that the potential arrival rate far exceeds the maximum upper limit of the number of customers that the service system can serve. In this case, the service provider should change the service decision of serving all customers (L customers or H customers) as soon as possible, follow the relationship between the market demand and the upper limit of the service system, and make the service decision to serve a part of customers. This coincides with the conclusion of Li et al. [12] on the study of the heterogeneous waiting cost model. This reflects that in customer-intensive services, when there are differences in customers, with the increase in total market demand, serving a part of customers can often have more benefits. Based on the definition of the development stage of service providers by Zhan et al. [2], service providers at the stage of higher total market demand can often obtain optimal revenue by adjusting decisions. Coincidentally, our study of heterogeneity in advertising sensitivity also verifies this notion.

5.3. Comparison of Revenue

No matter whether there are L customers in the service system, the service provider serving a part of L customers or a part of H customers can obtain higher revenue with the change in the potential arrival rate in the market. However, in general, is the situation in which there are no L customers in the service system less profitable than the situation in which there are L customers? In this section, we will analyze this issue.

(1) Comparison of the revenue in $S_{H1}$ and $S_{L1}$

In $S_{H1}$, all H customers can be served, while in $S_{L1}$, all L customers can be served. Since $V_{NH}\left(\mu ,P\right)>V_{NL}\left(\mu ,P\right)$, in $S_{L1}$, all L customers and H customers can enter the system. The difference between them is that $S_{H1}$’s effective customer arrival rate is greater than $S_{L1}$’s effective customer arrival rate. The minimum value of the difference between the payoffs in $S_{H1}$ and $S_{L1}$ is as follows:

$$min∆R_1=min{R}_{H1}^{*}-max{R}_{L1}^{*}=\frac{\left(m+2k_{H}a-k_{L}a-2\sqrt{\beta c}\right)\left(m+k_{L}a-2\sqrt{\beta c}\right)}{4\beta }-\frac{{\left(m+k_{L}a-2\sqrt{\beta c}\right)}^2}{4\beta }$$

(21)

Since $(2k_{H}a-k_{L}a)>k_{H}a>k_{L}a$, $min∆R_1>0$, then $min{R}_{H1}^{*}>max{R}_{L1}^{*}$, that is, the revenue in $S_{H1}$ is greater than that in $S_{L1}$. This shows that with the increase in the potential customer arrival rate $\mathsf{\Lambda }$, only serving all H customers can obtain higher benefits than serving all H and L customers. Because of the increase in $\mathsf{\Lambda }$, only serving all H customers can not only alleviate the congestion of the system but also lead to H customers having higher perceived utility so that the service provider has more room to adjust decision making. Meanwhile, since $max{R}_{L1}^{*}=R_{L2}^{*}$, we can obtain $min{R}_{H1}^{*}>R_{L2}^{*}$, which indicates that $S_{H1}$’s revenue is also greater than $S_{L2}$’s.

(2) Comparison of the revenue in $S_{H2}$ and $S_{L2}$

In $S_{H2}$, some H customers are served, while in $S_{L2}$, some L customers are served. Since $V_{NH}\left(\mu ,P\right)>V_{NL}\left(\mu ,P\right)$, all H customers in $S_{L2}$ also join the system. The difference between the revenue in the two situations is expressed as follows:

$$∆R_2=R_{H2}^{*}-R_{L2}^{*}=\frac{{\left(m+k_{H}a-2\sqrt{\beta c}\right)}^2}{4\beta }-\frac{{\left(m+k_{L}a-2\sqrt{\beta c}\right)}^2}{4\beta }$$

(22)

Since $k_H>k_L$, $∆R_2>0$ can be obtained, that is, $R_{H2}^{*}>R_{L2}^{*}$. It can be seen that serving some H customers can have higher benefits than serving all H and some L customers. Although the service provider in $S_{L2}$ not only serves some L customers but also all H customers, due to the increase in $\mathsf{\Lambda }$, the effective customer arrival rate ${\lambda }_{H2}^{*}$ of $S_{H2}$ is significantly higher than that of ${\lambda }_{L2}^{*}$. The improvement of the effective arrival rate increases the revenue of service providers. Combining $R_{H1}^{*}\le R_{H2}^{*}$, $R_{L1}^{*}\le R_{L2}^{*}$, and $min{R}_{H1}^{*}>R_{L2}^{*}$ in the final analysis of Formula (21), we can obtain the following lemma.

Lemma 5.

With the continuous increase in $\mathsf{\Lambda }$, the service provider makes corresponding optimal decisions under different market conditions. In each market situation, the size of revenue satisfies $R_{H2}^{*}\ge R_{H1}^{*}>R_{L2}^{*}\ge R_{L1}^{*}$.

The above lemma means that with the increase in $\mathsf{\Lambda }$, the revenue obtained by the service provider implementing the corresponding optimal decision in each market condition will gradually increase. This also shows that the increase in $\mathsf{\Lambda }$ in the market is extremely beneficial for customer-intensive service providers. Advertising is one of the most beneficial ways to increase $\mathsf{\Lambda }$ in a market [2]. When the service provider conducts advertising, it first taps more potential customers; secondly, according to the effective customer arrival rate threshold ${\widehat{\lambda }}_{L2}=\frac{m+k_{L}a-2\sqrt{\beta c}}{2\beta }$ and ${\widehat{\lambda }}_{H2}=\frac{m+k_{H}a-2\sqrt{\beta c}}{2\beta }$, it can be seen that advertising $a$ also increases the upper limit of the number of customers that the service system can serve, which effectively improves the service provider’s revenue. Not only that but $R_{H2}^{*}\ge R_{H1}^{*}>R_{L2}^{*}\ge R_{L1}^{*}$ actually indicates that there are more highly sensitive customers in the market, which is more beneficial for the service provider. Advertising is an effective way to tap these highly sensitive customers. Although this paper only divides the customers in the market into two categories, the research results can generally show that no matter how many kinds of customers there are in the market, service providers should advertise as much as possible to find more highly sensitive customers. This is conducive to increasing revenue.

5.4. Simulation

Numerical simulation analysis is used to illustrate the change in the service provider’s optimal decision and optimal revenue with $\mathsf{\Lambda }$, and we assign parameters $a=5$, $V_b=10, {\mu }_b=2$, $\beta =1$, $c=1$, $k_L=0.5$, $k_H=1$, and $q=0.5$ according to the research of Zhan et al. [2]. According to the formula for the effective arrival rate in Proposition 1 and Proposition 2, it can be known that ${\lambda }_{L2}^{*}=6.25$ and ${\lambda }_{H2}^{*}=7.5$, so it can be assumed that $\mathsf{\Lambda }\in \left[0,20\right]$. 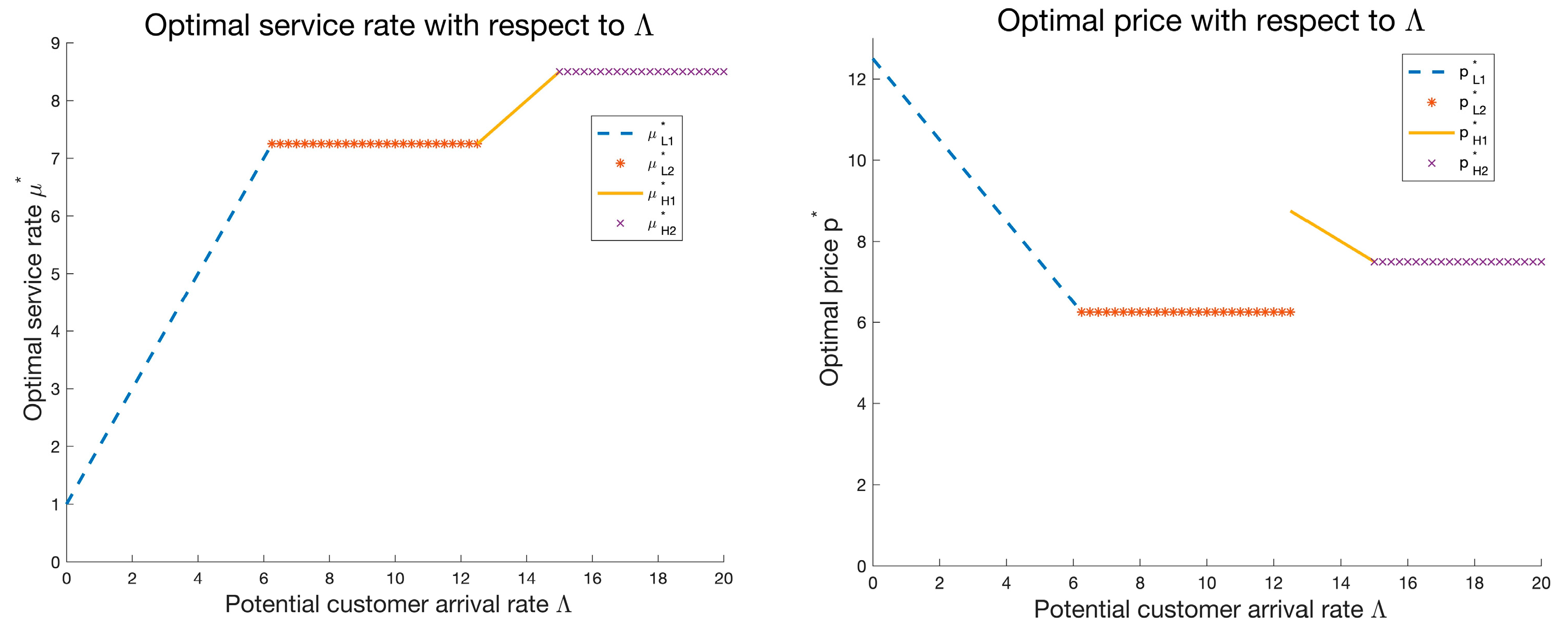Figure 1 illustrates the optimal service rate and the optimal price with respect to $\mathsf{\Lambda }$. 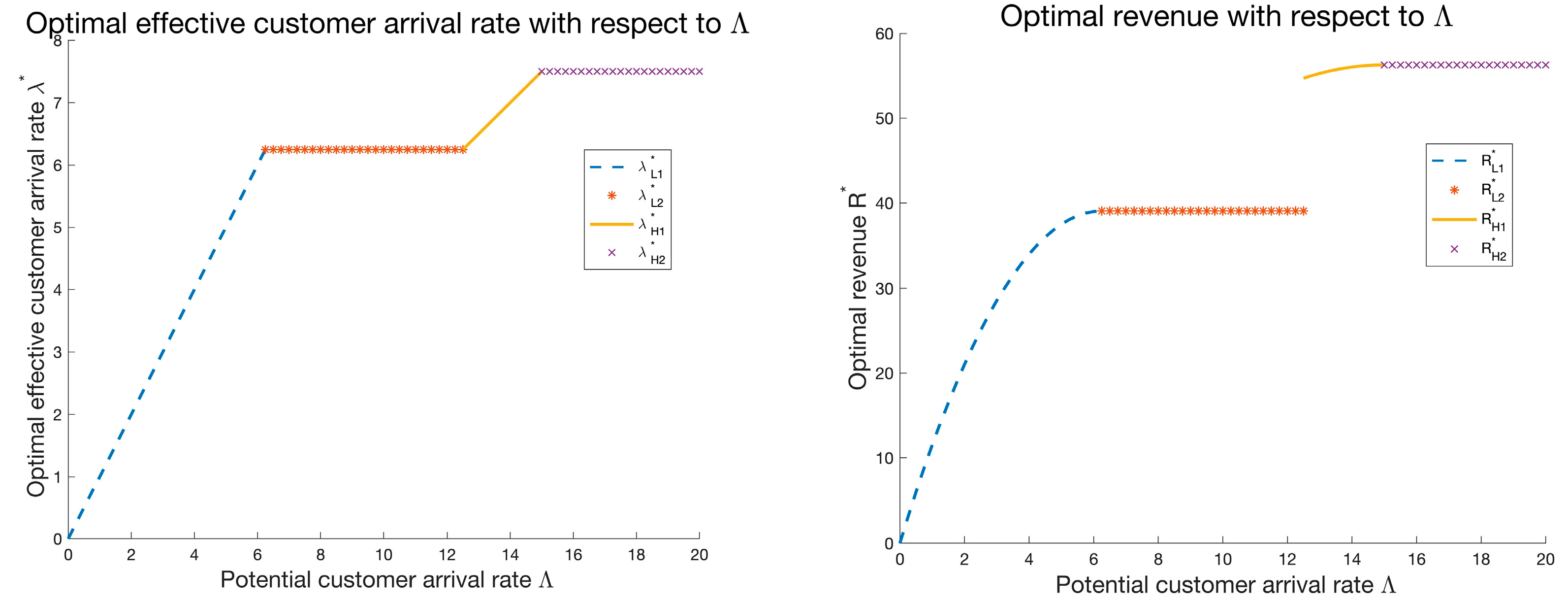Figure 2 illustrates the optimal effective customer arrival rate and the optimal revenue with respect to $\mathsf{\Lambda }$.

Figure 1 shows that as $\mathsf{\Lambda }$ increases, the optimal service rate generally shows an upward trend, and ${\mu }_H^{*}$ is always higher than ${\mu }_L^{*}$. As for the price, the price in $S_{L1}$ decreases with $\mathsf{\Lambda }$, and then the price in $S_{L2}$ remains constant. The service price then jumps up in $S_{H1}$ as L customers drop out of the market, then decreases as $\mathsf{\Lambda }$ increases, and remains constant in $S_{H2}$. The constant $P_{H2}^{*}$ is still greater than $P_{L2}^{*}$, indicating that the increase in high-sensitivity customers helps service providers to increase prices.

Figure 2 shows that with the increase in $\mathsf{\Lambda }$, the effective customer arrival rate also generally shows an upward trend. However, due to the limitation of the service capacity of the service system, the increase in $\mathsf{\Lambda }$ brings the service provider a smaller and smaller increase in revenue. When $\mathsf{\Lambda }>{\lambda }_{L2}^{*}=6.25$, in $S_{L2}$, some L customers and all H customers can be served. In this case, the increase in $\mathsf{\Lambda }$ can no longer improve the revenue of the service provider. This shows that an increase in customers is not always beneficial for such service providers because, in customer-intensive services, there are thresholds ${\widehat{\lambda }}_{L2}$ and ${\widehat{\lambda }}_{H2}$ for the number of people that service providers can serve. Although the continuous increase in $\mathsf{\Lambda }$ eventually makes the service provider’s revenue no longer increase, $R_{H2}^{*}$ is still higher than $R_{L2}^{*}$. This means that by distinguishing customers’ advertising sensitivity differences, it can help service providers to make optimal decisions that match them under different market conditions, thereby increasing revenue. This also shows the importance of market segmentation—the more detailed the classification of target customers, the more precise decisions can be made.

6. Extensions: The Impact of Ignoring Heterogeneity

According to the previous analysis, the service provider needs to make different optimal decisions as the demand increases. However, some service providers in reality cannot or do not use different decisions according to customer heterogeneity and potential customer arrival rate. For example, some service providers with poor decision-making and market research abilities, such as hair and beauty salons, do not spend too much effort on decision making; hence, they usually assume that customers are homogeneous. Although such a rough assumption reduces the tediousness of decision making and the difficulty of market research, it makes them unable to adapt to the changes in the market and affects the revenue in the meantime. For the sake of discussion and without loss of generality, we assume that once the service provider believes that all customers are homogeneous, there are three cases, in which the service provider believes that the customers in the market are all homogeneous L customers, homogeneous M customers, or homogeneous H customers. The advertising sensitivity of M customers is between $k_L$ and $k_H$.

6.1. All Homogeneous L Customers

In this section, when the service provider considers all customers as homogeneous L customers, there exists a threshold of the effective customer arrival rate ${\widehat{\lambda }}_L=\frac{m+k_{L}a-2\sqrt{\beta c}}{2\beta }$. Then, the decisions of the service provider can be described as follows.

Homogeneous L decision ①: when $0\le \mathsf{\Lambda }\le {\widehat{\lambda }}_L$, the optimal decisions are ${\mu }_L^{*}=\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}, P_L^{*}\left({\mu }^{*}\right)=m+k_{L}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}$, and the service provider can serve all customers.

Homogeneous L decision ②: when $\mathsf{\Lambda }>{\widehat{\lambda }}_L$, the optimal decisions are ${\mu }_L^{*}=\frac{m+k_{L}a}{2\beta }, P_L^{*}\left({\mu }^{*}\right)=\frac{m+k_{L}a-2\sqrt{\beta c}}{2}$, and the service provider serves only a part of the customers.

When $0\le \mathsf{\Lambda }\le {\widehat{\lambda }}_L$, the service provider intends to serve all L customers. Furthermore, the optimal decisions are the same as those in $S_{L1}$, and therefore, the revenue is also the same. If ${\widehat{\lambda }}_L<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_L}{q}$, the optimal decisions of the service provider are also the same as those in $S_{L2}$. However, once $q\mathsf{\Lambda }>\widehat{\lambda }$, the number of H customers exceeds the threshold of the effective arrival rate of all customers, resulting in only H customers being in the system. Thus, the optimal decisions in $S_{L2}$ are no longer applicable, and they have an impact on revenue in this case.

In homogeneous L decision ②, the optimal decisions are ${\mu }_L^{*}=\frac{m+k_{L}a}{2\beta }, P_L^{*}\left({\mu }^{*}\right)=\frac{m+k_{L}a-2\sqrt{\beta c}}{2}$ at $q\mathsf{\Lambda }>\widehat{\lambda }$. According to Equation (14), the threshold of the effective customer arrival rate can be calculated as

$${\widehat{\lambda }}_{LH}=\frac{m+k_{L}a}{2\beta }-\frac{c}{k_{H}a-k_{L}a+\sqrt{\beta c}},$$

(23)

if $q\mathsf{\Lambda }\le {\widehat{\lambda }}_{LH}$, the effective arrival rate of customers ${\lambda }_{LH1}^{*}=q\mathsf{\Lambda }$; once $q\mathsf{\Lambda }>{\widehat{\lambda }}_{LH}$, the effective arrival rate of customers ${\lambda }_{LH2}^{*}={\widehat{\lambda }}_{LH}$. Thus, we obtain the following proposition.

Proposition 3.

In homogeneous L decision ②, if $q\mathsf{\Lambda }\le {\widehat{\lambda }}_{LH}$, the revenue of the service provider is $R_{LH1}^{*}=P_L^{*}{\lambda }_{LH1}^{*}=\frac{m+k_{L}a-2\sqrt{\beta c}}{2}q\mathsf{\Lambda }$. Once $q\mathsf{\Lambda }>{\widehat{\lambda }}_{LH}$, the revenue of service provider is $R_{LH2}^{*}=P_L^{*}{\lambda }_{LH2}^{*}=\frac{m+k_{L}a-2\sqrt{\beta c}}{2}\left(\frac{m+k_{L}a}{2\beta }-\frac{c}{k_{H}a-k_{L}a+\sqrt{\beta c}}\right)$. (Proof in Appendix A).

From the Proposition 3, it can be seen that when the potential demand in the service system is different, the service providers obtain different revenues by implementing homogeneous L decision ②. The differences between homogenous and heterogeneous strategies are shown in Figure 3 of Section 6.4.

6.2. All Homogeneous M Customers

If the service provider considers all customers in the market as M customers, and their sensitivity to advertising $k_M$ is between $k_L$ and $k_H$, there exists a threshold of the effective arrival rate of customers ${\widehat{\lambda }}_M=\frac{m+k_{M}a-2\sqrt{\beta c}}{2\beta }$, and the optimal decisions can be expressed as follows.

Homogeneous M decision$①$: when $\mathsf{\Lambda }\le {\widehat{\lambda }}_M$, the optimal decisions are ${\mu }_M^{*}=\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }},P_M^{*}\left({\mu }^{*}\right)=m+k_{M}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}$, and the service provider can serve all customers.

Homogeneous M decision ②: when $\mathsf{\Lambda }>{\widehat{\lambda }}_M$, the optimal decisions are ${\mu }_M^{*}=\frac{m+k_{M}a}{2\beta },P_M^{*}\left({\mu }^{*}\right)=\frac{m+k_{M}a-2\sqrt{\beta c}}{2}$.

(1) In homogeneous M decision $①$, the service provider can serve all M customers at $\mathsf{\Lambda }\le {\widehat{\lambda }}_M$. Because $V_{NH}\left(\mu ,P\right)>V_{NM}\left(\mu ,P\right)>V_{NL}\left(\mu ,P\right)$, in reality, all H customers obtain positive utility and enter the service system, and a part of L customers also enter the system in the meantime. Thus, the effective customer arrival rate in the queue can be calculated by

$${\lambda }_{ML}^{*}=\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}-\frac{c}{\sqrt{\beta c}+k_{L}a-k_{M}a},$$

(24)

and then the revenue of the service provider can be expressed as

$$R_{ML}^{*}=P_M^{*}{\lambda }_{ML}^{*}=\left(m+k_{M}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}\right)\left(\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}-\frac{c}{\sqrt{\beta c}+k_{L}a-k_{M}a}\right).$$

(25)

(2) In homogeneous M decision ②, the service provider can serve only a part of M customers at $\mathsf{\Lambda }>{\widehat{\lambda }}_M$. Furthermore, all L customers cannot obtain positive utility; hence, the actual target customers are in fact H customers. Then, the threshold of the effective customer arrival rate can be expressed as

$${\widehat{\lambda }}_{MH}=\frac{m+k_{M}a}{2\beta }-\frac{c}{k_{H}a-k_{M}a+\sqrt{\beta c}}.$$

(26)

If $q\mathsf{\Lambda }\le {\widehat{\lambda }}_{MH}$, the effective customer arrival rate is ${\lambda }_{MH1}^{*}=q\mathsf{\Lambda }$. Once $q\mathsf{\Lambda }>{\widehat{\lambda }}_{MH}$, the effective customer arrival rate is ${\lambda }_{MH2}^{*}={\widehat{\lambda }}_{MH}$. Thus, we can obtain Proposition 4 as follows.

Proposition 4.

In homogeneous M decision ②, if $q\mathsf{\Lambda }\le {\widehat{\lambda }}_{MH}$, the revenue of service provider is $R_{MH1}^{*}=P_M^{*}{\lambda }_{MH1}^{*}=\frac{m+k_{M}a-2\sqrt{\beta c}}{2}q\mathsf{\Lambda }$. Once $q\mathsf{\Lambda }>{\widehat{\lambda }}_{MH}$, the revenue of service provider is $R_{MH2}^{*}=P_M^{*}{\lambda }_{MH2}^{*}=\frac{m+k_{M}a-2\sqrt{\beta c}}{2}\left(\frac{m+k_{M}a}{2\beta }-\frac{c}{k_{H}a-k_{M}a+\sqrt{\beta c}}\right)$. (Proof in Appendix A).

Proposition 4 is similar to Proposition 3, both of which indicate that customer-intensive service providers obtain different revenues from implementing homogeneous decision ② under different potential demand scales. This difference is mainly due to the difference in the effective customer arrival rate in the system rather than the difference in price.

6.3. All Homogeneous H customers

If a service provider considers all customers in the market as H customers, there exists a threshold of the effective customer arrival rate ${\widehat{\lambda }}_H=\frac{m+k_{H}a-2\sqrt{\beta c}}{2\beta }$, and the optimal decisions of the service provider can be expressed as follows.

Homogeneous H decision ①: when $\mathsf{\Lambda }\le {\widehat{\lambda }}_H$, the optimal decisions are ${\mu }_H^{*}=\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }},P_H^{*}\left({\mu }^{*}\right)=m+k_{H}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}$, and the service provider can serve all customers.

Homogeneous H decision ②: when $\mathsf{\Lambda }>{\widehat{\lambda }}_H$, the optimal decisions are ${\mu }_H^{*}=\frac{m+k_{H}a}{2\beta },P_H^{*}\left({\mu }^{*}\right)=\frac{m+k_{H}a-2\sqrt{\beta c}}{2}$, and the service provider can serve only a part of the customers.

(1) In homogeneous H decision $①$, the service provider’s original purpose is to serve all H customers. However, in fact, there are L customers in the service system, and a part of them will likely be served. Thus, these L customers actually are the target customers (which means that the decision is designed for L customers), and the effective customer arrival rate can be expressed by

$${\lambda }_{HL}^{*}=\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}-\frac{c}{\sqrt{\beta c}+k_{L}a-k_{H}a},$$

(27)

The above equation is the effective customer arrival rate when the service provider makes homogeneous H decision for H customers but the actual target customers are L customers. If $\sqrt{\beta c}+k_{L}a-k_{H}a\ge 0$, L customers can obtain non-negative utility; hence, ${\lambda }_{HL}^{*}$ includes both H and L customers. However, once $\sqrt{\beta c}+k_{L}a-k_{H}a<0$, it means that L customers can only obtain negative utility, and there are only H customers in the service system; therefore, the actual target customers are only H customers in this case.

If $\sqrt{\beta c}+k_{L}a-k_{H}a\ge 0$, it indicates that the difference between $k_H$ and $k_L$ is small. Meanwhile, the effective customer arrival rate is ${\lambda }_{HL}^{*}$; thus, the revenue can be expressed as

$$R_{HL}^{*}=P_H^{*}{\lambda }_{HL}^{*}=\left(m+k_{H}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}\right)\left(\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}-\frac{c}{\sqrt{\beta c}+k_{L}a-k_{H}a}\right).$$

(28)

However, once $\sqrt{\beta c}+k_{L}a-k_{H}a<0$, the difference between $k_H$ and $k_L$ is large, and there are only H customers in the service system. Thus, the effective arrival rate equals $q\mathsf{\Lambda }$, and L customers are no longer the target customers; then, the revenue can be expressed by

$$R_{HH1}^{*}=P_H^{*}{\lambda }_{HH1}^{*}=\left(m+k_{H}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}\right)q\mathsf{\Lambda }.$$

(29)

$R_{HH1}^{*}$ denotes the revenue when the service provider makes homogeneous H decision $①$ while the actual target customers are only H customers.

(2) If $\mathsf{\Lambda }>{\widehat{\lambda }}_H$, the service provider’s original purpose is to serve only a part of the H customers in homogeneous H strategy ②. The threshold of the effective customer arrival rate is ${\widehat{\lambda }}_H={\lambda }_H^{*}=\frac{m+k_{H}a-2\sqrt{\beta c}}{2\beta }$. However, according to Proposition 2, the effective arrival rate equals $\frac{m+k_{H}a-2\sqrt{\beta c}}{2\beta }$ at $q\mathsf{\Lambda }>{\lambda }_{H2}^{*}={\lambda }_H^{*}$; hence, the revenue in the homogeneous H decision is the same as that in $S_{H2}$. When ${\widehat{\lambda }}_H<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_H}{q}$, all H customers can obtain non-negative utility, that is, the effective customer arrival rate can be expressed by ${\lambda }_{HH2}^{*}=q\mathsf{\Lambda }$. Then, the revenue of the service provider can be calculated as

$$R_{HH2}^{*}=\frac{m+k_{H}a-2\sqrt{\beta c}}{2}q\mathsf{\Lambda }.$$

(30)

On the basis of the above analysis, we can conclude the following propositions.

Proposition 5.

i. 

In homogeneous H decision ①, if $\sqrt{\beta c}+k_{L}a-k_{H}a\ge 0$, the revenue is $R_{HL}^{*}=P_H^{*}{\lambda }_{HL}^{*}=\left(m+k_{H}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}\right)\left(\mathsf{\Lambda }+\sqrt{\frac{c}{\beta }}-\frac{c}{\sqrt{\beta c}+k_{L}a-k_{H}a}\right)$; once $\sqrt{\beta c}+k_{L}a-k_{H}a<0$, the revenue is $R_{HH1}^{*}=P_H^{*}{\lambda }_{HH1}^{*}=\left(m+k_{H}a-\beta \mathsf{\Lambda }-2\sqrt{\beta c}\right)q\mathsf{\Lambda }$.

ii. 

In homogeneous H strategy ②, if $\mathsf{\Lambda }>{\widehat{\lambda }}_H$, the revenue in the homogeneous H decision is the same as that in $S_{H2}$. When ${\widehat{\lambda }}_H<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_H}{q}$, the revenue of the service provider is $R_{HH2}^{*}=\frac{m+k_{H}a-2\sqrt{\beta c}}{2}q\mathsf{\Lambda }$.

The difference between the revenue in the above proposition and those in the implementation of the heterogeneous decision in Chapter 5 is represented in the corresponding Figures of Section 6.4.

6.4. Simulation

In order to show the impact of ignoring heterogeneity on the revenue of service providers, we study the difference between the revenue of service providers with and without the heterogeneity of consumers’ advertising perception through numerical analysis. Figure 3 illustrates the revenue between the homogeneous L decision and the heterogeneous decision. Figure 4 illustrates the revenue between the homogeneous M decision and the heterogeneous decision at different $k_{\mathrm{M}}$. Figure 5 illustrates the revenue between the homogeneous H decision and the heterogeneous decision. Figure 6 illustrates the revenue between the homogeneous H decision and the heterogeneous decision at different $k_H$.

In $S_{L1}$ or $S_{L2}$, the service provider’s belief that all customers in the system are L customers will not affect its revenue. However, Figure 3 illustrates that the service provider’s decision that ignores customer heterogeneity and considers all customers as L customers affects its revenue in $S_{H1}$ or $S_{H2}$. Such a “wrong” decision makes the actual revenue lower than that when customer heterogeneity is taken into account in $S_{H1}$ or $S_{H2}$.

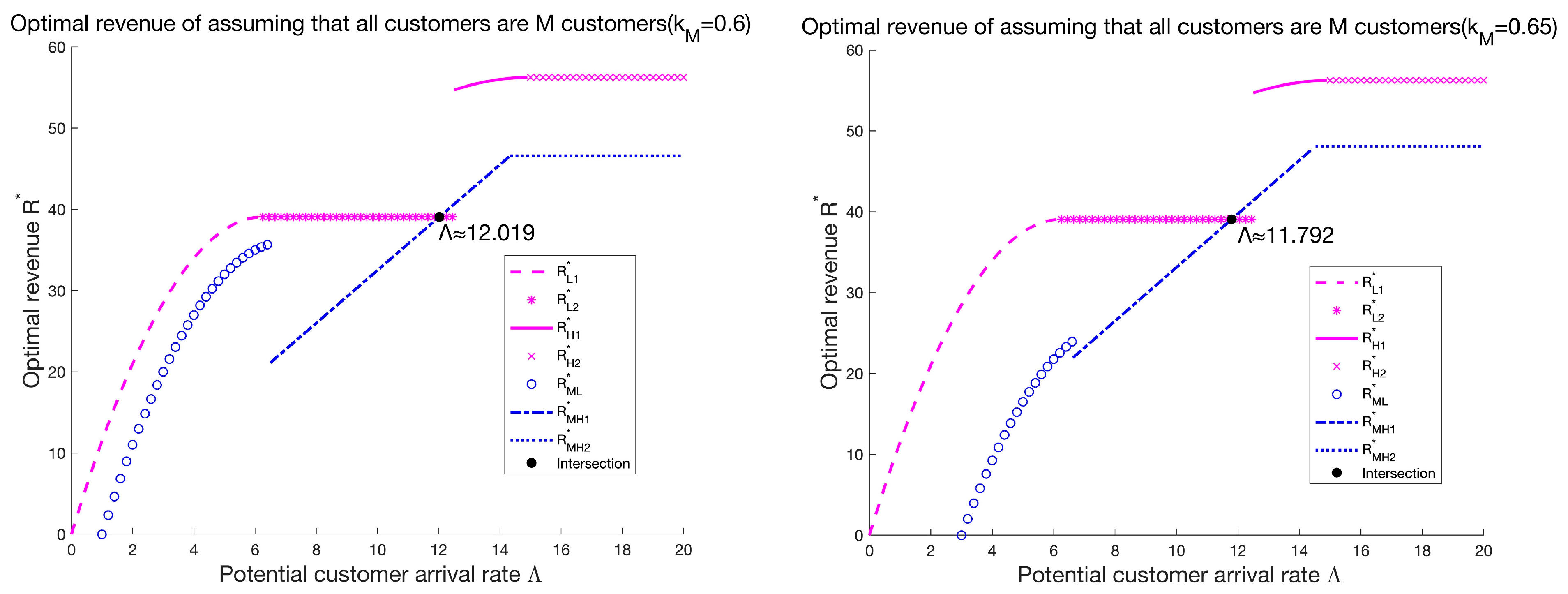
From Figure 4, we can know that once the service provider mistakenly believes that all customers in the market are M customers, such a “wrong” decision has an impact on the service provider’s revenue throughout. In general, the actual revenue in the homogeneous M decision is lower than that in the heterogeneous decision. However, the revenue in the homogeneous M decision is higher than that in $S_{L2}$ at a small section of range of $\mathsf{\Lambda }$. The reason lies in the fact that the effective arrival rate in $S_{L2}$ is not affected by $\mathsf{\Lambda }$, while the effective arrival rate in the homogeneous M decision increases as $\mathsf{\Lambda }$ increases. In addition, if $\mathsf{\Lambda }>{\widehat{\lambda }}_M$, $P_M^{*}$ is greater than that the service price in $S_{L2}$. Hence, the continuous increase in $\mathsf{\Lambda }$ is likely to lead to $R_{MH1}^{*}$ being greater than $R_{L2}^{*}$.

Moreover, the increase in $k_{\mathrm{M}}$ makes the intersection value between $R_{L2}^{*}$ and $R_{MH1}^{*}$ smaller, indicating that $R_{MH1}^{*}$ becomes faster to be greater than $R_{L2}^{*}$. This is because the increase in $k_{\mathrm{M}}$ leads to the increase in $P_M^{*}$ in $\mathsf{\Lambda }>{\widehat{\lambda }}_M$, resulting in a faster increase in $R_{MH1}^{*}$.

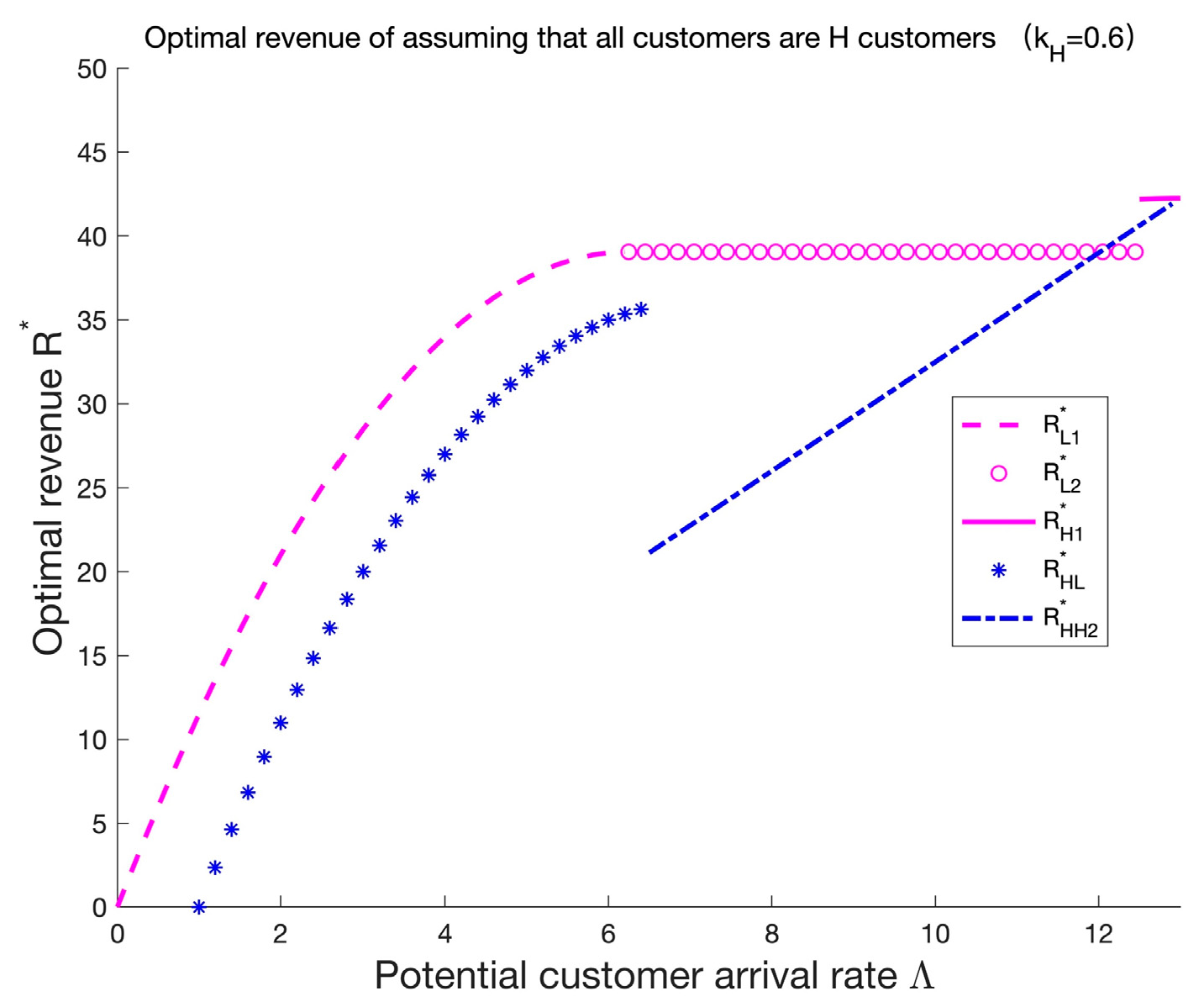
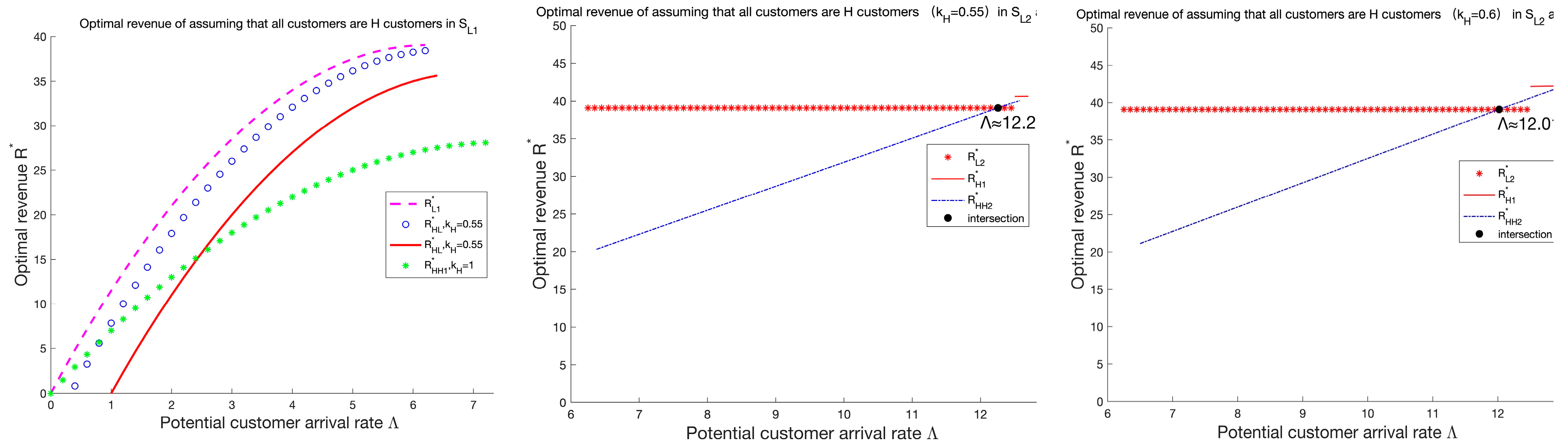
The above figure illustrates that $R_{HL}^{*}$ is significantly lower than $R_{L1}^{*}$, and $R_{HH2}^{*}$ is also lower than $R_{H1}^{*}$ in the homogeneous H decision. However, $R_{HH2}^{*}$ is lower than $R_{L2}^{*}$ at first as $\mathsf{\Lambda }$ increases, but then it briefly becomes higher than $R_{L2}^{*}$ after the intersection of the two lines. To analyze more specifically the difference between the revenue in the homogeneous H decision and $R_{L1}^{*}$, $R_{L2}^{*}$, and $R_{H1}^{*}$, we performed further numerical analysis. In different cases ($k_H=0.55$, $k_H=0.6$, and $k_H=1$), we analyze the difference between $R_{HL}^{*}$ and $R_{L1}^{*}$. In addition, we also compare $R_{HH2}^{*}$ with the revenue in $S_{L2}$ and $S_{H1}$ at $k_H=0.55$ or $k_H=0.6$.

The left figure above shows that the revenue in homogeneous H decision ① is lower than that in $S_{L1}$. Furthermore, when the difference between $k_H$ and $k_L$ is relatively large, the difference between $R_{HL}^{*}$ and $R_{L1}^{*}$ increases as $k_H$ increases, indicating that if the gap between heterogeneous customers is larger, such a “wrong” homogeneous H decision affects the revenue to a greater extent. Once the difference between $k_H$ and $k_L$ expands to the point where $\sqrt{\beta c}+k_{L}a-k_{H}a<0$, only H customers remain in the system, and $R_{HH1}^{*}$ is higher than $R_{HL}^{*}$ at first due to the higher service price. However, the increase in $R_{HH1}^{*}$ gradually slows down, and eventually, it becomes significantly lower than $R_{HL}^{*}$ as $\mathsf{\Lambda }$ increases.

The middle and right figures illustrate that $R_{HH2}^{*}$ is lower than $R_{L2}^{*}$ at first and then briefly becomes greater than $R_{L2}^{*}$ after the intersection of the two lines. Meanwhile, the $\mathsf{\Lambda }$ value of this intersection point becomes smaller as $k_H$ increases, indicating that $R_{HH2}^{*}$ becomes faster to be greater than $R_{L2}^{*}$. The reason is that the effective customer arrival rate in $S_{L2}$ is not affected by $\mathsf{\Lambda }$, while the effective customer arrival rate in the homogeneous H decision increases with $\mathsf{\Lambda }$, so $P_H^{*}$ is greater than that in $S_{L2}$ at $\mathsf{\Lambda }>{\widehat{\lambda }}_H$; thus, the continuous increase in $\mathsf{\Lambda }$ is likely to lead to $R_{HH2}^{*}$ is greater than $R_{L2}^{*}$. Furthermore, a higher $k_H$ motivates the service provider to set higher $P_H^{*}$; hence, the increase in $R_{HH2}^{*}$ is more rapid.

7. Conclusions

7.1. Conclusions and Remarks

Since there are differences in customers’ perception of advertising, this paper uses the M/M/1 model to study the optimal decision making of customer-intensive service providers under different market conditions based on customer heterogeneity. This paper determines the optimal decisions in different potential customer arrival rates and provides a theoretical basis for the acquisition of optimal revenue for service providers. This paper also finds that:

(1)

With the increase in the potential arrival rate, the service provider’s revenue from serving a part of customers is higher than that from serving all customers regardless of whether there are L customers in the service system.

(2)

The service provider has more dominance in the market when the potential arrival rate exceeds the effective arrival rate threshold (${\widehat{\lambda }}_{L2}<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{L2}}{q}$ and $\mathsf{\Lambda }>\frac{{\widehat{\lambda }}_{H2}}{q}$); this is manifested in the fact that the decision making of the service provider is no longer affected by the potential customer arrival rate $\mathsf{\Lambda }$.

(3)

The revenue is further improved with the increase in the number of highly sensitive customers, which reflects the importance of advertising and market segmentation. Advertising can effectively increase the number of highly sensitive customers in the market, thereby bringing more revenue to the service provider.

(4)

Once the service provider adopts a homogeneous decision, it reduces the revenue in a large range, which shows that it is extremely necessary for the service provider to conduct market segmentation.

7.2. Management Implication

(1)

When there are L customers in the market, the potential arrival rate $\mathsf{\Lambda }$ in the market must be low. In $0<\mathsf{\Lambda }\le {\widehat{\lambda }}_{L2}$, the decision making of service providers must be made according to the scale of $\mathsf{\Lambda }$. The potential arrival rate is low and advertising does not cause system congestion, so there is no need to change the service rate. However, in the case of ${\widehat{\lambda }}_{L2}<\mathsf{\Lambda }<\frac{{\widehat{\lambda }}_{L2}}{q}$, due to the increase in the potential arrival rate, the system congestion caused by advertising requires the service provider to increase the service rate.

(2)

When $\mathsf{\Lambda }$ is high, H customers have a crowding-out effect on L customers. In ${\widehat{\lambda }}_{L2}<q\mathsf{\Lambda }\le {\widehat{\lambda }}_{H2}$, the decision of service providers should be made according to the scale of $\mathsf{\Lambda }$ and the proportion $q$. When there are few H customers, the service provider only needs to control the crowding degree of the system through price. In $q\mathsf{\Lambda }>{\widehat{\lambda }}_{H2}$, since there are many H customers, the service provider not only needs to control the congestion of the system through higher prices but also needs to formulate a higher service rate.

(3)

Customer-intensive service providers should segment the target market, determine the general number of various customers through market research, and make optimal decisions accordingly. Meanwhile, service providers should tap more high-sensitivity customers through advertising so as to further improve service providers’ revenue. It also shows that forgoing some low-sensitivity customers often leads to higher revenue.

7.3. Innovation and Contribution

This paper introduces the heterogeneity of customers’ advertising perception in customer-intensive services for the first time and analyzes how the service provider adjusts the optimal service rate decision and price decision according to the change in market demand scale and the number of different types of customers in the system. Therefore, the innovation and contribution of this article have the following two aspects.

Theoretical aspect: Compared with the research of Zhan et al. [2] and Anand et al. [3], this paper studies for the first time the impact of the heterogeneity of customer advertising perception on the decision making and revenue acquisition of customer-intensive service providers. We analyze how such service providers should adjust the optimal service rate decision and price decision according to the customer category in the system with the growth of market potential demand. We introduce customer heterogeneity and advertising effect to expand the optimal decision theory of customer-intensive service providers.

Practical aspect: Through the establishment of theoretical models and numerical analysis, we find that advertising can effectively increase the number of highly sensitive customers in the market, thus bringing more revenue to service providers, which reflects the importance of advertising and market segmentation. This conclusion was not mentioned in the research of Zhan et al. [2] and Li et al. [13]. At the same time, it also indicates that customer-intensive service providers can tap more potential customers through higher-intensity advertising and only serve some highly sensitive customers, which can bring higher profits to such service providers and contribute to the long-term development of service providers.

7.4. Future Research

Although we have studied the impact of advertising effects on such service providers, we have not included advertising costs in the decision making of service providers, and the existence of advertising costs is a key factor affecting the final profits of service providers. Meanwhile, customers’ perception of the advertising intensity in this study is regarded as linear to simplify the calculation. However, in fact, the perception of customers may be nonlinear, which will also be the focus of our future research.