Abstract
Quality function deployment (QFD) is a customer-driven quality management tool that can improve system quality, promote innovation, and enhance the core competitiveness of enterprises. Nonetheless, the traditional QFD method has defects in handling the experts’ assessments, measuring customer requirement importance, and prioritizing engineering characteristics, which affect its efficiency and limit its application in the real world. In this study, a new QFD approach based on spherical fuzzy sets (SFSs) and a combined compromise solution (CoCoSo) method is proposed to overcome the shortcomings associated with the traditional QFD. To be specific, the linguistic relationship assessments between the customer requirements and engineering characteristics provided by the experts were described by the SFSs, the relative weights of the customer requirements were obtained via the decision-making trial and evaluation laboratory (DEMATEL) method, and the importance ranking orders of the engineering characteristics were determined with an improved CoCoSo method. The feasibility and effectiveness of the proposed QFD approach are illustrated by an empirical case of accommodation service design. The results show that the new QFD approach provides a useful and practical way to represent the relationship assessment information of experts and determine the priority of engineering characteristics in product development.
1. Introduction
Quality function deployment (QFD) is a typical customer-driven quality management tool originally developed by Akao [1]. It facilitates product design and improvement with a systematic operation mechanism for translating customer requirements (CRs) into corresponding engineering characteristics (ECs). Compared with other quality management methods, the QFD can quantitatively incorporate CRs into different phases of product design to maximize customer satisfaction [2]. As a result, it enables companies to raise customer satisfaction, shorten the product development cycle, reduce the number of changes with product design, lower manufacturing costs, and improve communication and collaboration between departments [3,4]. Due to these inherent advantages, the QFD method has been applied in various fields (e.g., for the cellphone closed-loop supply chain optimization [5], the economic indicator analysis of sustainable supply chain [6], the Healthcare 4.0 implementation assessment [7], the service quality improvement in radiology centers [8], and the CNC machine tool development [9]).
Normally, a QFD framework can be separated into four interlinked stages: product planning, part deployment, process planning, and production planning [10]. In each stage, the correlatives between inputs (WHATs) and outputs (HOWs) are formulated by a correlative matrix called the house of quality (HOQ). As the core of QFD, the HOQ integrates the CRs into the whole process of product development in the form of consecutive ‘‘input–output’’ translation [11]. In the product planning stage, six components are included, which include CRs, ECs, the importance weights of CRs, relationships between CRs and ECs, interrelations among ECs, and the importance prioritization of ECs [12]. Although the QFD has been widely used for quality improvement, many drawbacks have been pointed out for the classical HOQ method. First, numerical values are used to evaluate the relationship between CRs and ECs, which increases the difficulty for experts to express their assessments and reduces the accuracy of outcomes [13,14,15]. Second, the importance rankings of ECs are determined by using a simple weighted averaging method. It is a compensatory method and may result in a biased ranking result of ECs in practical applications [15,16,17]. Third, the weights of CRs are determined by directly ignoring their internal correlations. In real-world situations, there may exist interrelationships and dependence among CRs due to the complexity of QFD problems [11,15,17].
In the real product development process, it is often hard for experts to assess the relationships between CRs and ECs based on crisp values due to the inherent vagueness and uncertainty in human judgements [15,18]. The classical QFD method has difficulty in resolving this fuzzy and uncertainty [11,19]. As one of the latest extensions of the fuzzy set theory, the spherical fuzzy sets (SFSs) were introduced by Gündoǧdu and Kahraman [20]. In a SFS, membership, non-membership, and hesitant degrees are defined independently and the squared sum of them can be between zero and one [21]. It defines membership functions on a spherical surface and the hesitant degree is not determined by the values of membership and non-membership degrees [22,23]. Accordingly, the SFSs provide a wider range for expressing the decision-makers’ opinions than other fuzzy sets [24,25]. Recently, the SFS theory has been applied to address various decision-making problems such as the efficiency evaluation of airports [26], logistic autonomous vehicle assessment [24], internal audit planning [27], road safety assessment [28], logistics hub location [29], and emergency hospital investment analysis [30]. Therefore, it is promising to employ the SFS to express the experts’ vague and uncertain evaluations on the relationships between CRs and ECs in QFD.
In QFD, determining the importance ranking of ECs against multiple CRs can be reviewed as a complex multi-criteria decision -making (MCDM) problem [31,32]. Therefore, a lot of MCDM methods have been adopted to overcome the shortcomings and improve the performance of traditional QFD in the literature [19,33,34,35]. As a new MCDM method, the combined compromise solution (CoCoSo) approach was originally proposed by Yazdani et al. [36] to determine the best alternative by integrating simple additive weighting and exponentially weighted product models. It incorporates three different compromise aggregation functions to compute the final compromise score and can acquire the optimum alternative without counterintuitive phenomena [37,38]. Compared with other MCDM methods, the CoCoSo approach promotes the exactitude of a decision-making system and has a higher resolution in distinguishing alternatives [39,40,41]. Because of its advantages, the CoCoSo method has been employed to deal with many decision-making problems in recent years, which include energy system planning [42], occupational health and safety risk assessment [43], eco-friendly packaging evaluation [44], failure mode risk analysis [45], public transportation management [46], and urban transport planning [47]. Hence, it is expected to apply the CoCoSo technique to derive the importance priority of the identified ECs in QFD.
Considering the advantages of the SFSs and the CoCoSo method, in this study, we combined them to develop a new integrated model for improving the performance of traditional QFD. To sum up, the contributions of this study to the literature are as follows. First, the SFSs were utilized to capture the uncertainty and fuzziness of relationship evaluation information between CRs and ECs provided by experts. Second, an extended CoCoSo method was introduced to acquire the importance ranking of ECs in product or service development. Third, the importance ratings of CRs were derived by using the decision-making trial and evaluation laboratory (DEMATEL) method by considering their cause and effect relations and interactions. Additionally, a practical case regarding the service design for tourism accommodation is provided to illustrate the feasibility and practicability of the proposed new QFD approach.
The rest of the article is structured as follows. Section 2 briefly reviews the current research on QFD improvement. Section 3 presents the basic concepts and definitions of the SFS theory. In Section 4, a new integrated QFD approach using SFSs and the CoCoSo method is proposed. In Section 5, a practical case is provided to demonstrate the proposed QFD approach. Finally, Section 6 presents our conclusions and discusses potential future research directions.
2. Literature Review
To eliminate the deficiencies and strengthen the capability of traditional QFD, a variety of improved methods have been developed in the past decades [31]. On one hand, many QFD methods based on uncertainty theories and MCDM methods were proposed. For example, Yang et al. [3] proposed a large group decision-making method that integrated proportional hesitant fuzzy linguistic term sets (PHFLTSs) and the cumulative prospect theory (CPT) to determine the ranking priority of ECs in QFD. Liu et al. [15] constructed a large group QFD model based on an extended TODIM (Portuguese acronym for interactive multi-criteria decision making) method under the interval type-2 fuzzy environment. Shi et al. [2] provided a QFD approach using double hierarchy hesitant linguistic term sets (DHHLTSs) and the ORESTE (organísation, rangement et Synthèse de données relarionnelles, in French) method for the EC prioritization. Ping et al. [11] presented an approach for QFD based on linguistic Pythagorean fuzzy sets (LPFSs) and an alternative queuing method. In [16], an integrated QFD model was developed, in which the rough cloud model was utilized to treat uncertain information and an extended technique for order preference by similarity to an ideal solution (TOPSIS) was introduced for ranking ECs. In [14], an integrated QFD framework was constructed, in which the hesitant fuzzy linguistic term sets (HFLTSs) were used to handle the experts’ uncertain assessments and the TOPSIS was extended to compute the importance degrees of ECs. In [34], the authors reported a QFD method in which the extended HFLTSs were applied for the elicitation of hesitant assessment information and the prospect theory was employed to derive the ranking orders of ECs.
On the other hand, in recent years, multiple different methods and theories have been integrated to enhance the performance of normal QFD. For instance, Xiao et al. [10] suggested a consensus-based QFD to derive the consensual importance ratings of ECs, where linguistic distributions were used to express the relationship assessments between CRs and ECs and a minimum–maximum adjustment consensus model was used to assist experts in deriving a consensual relationship assessment. Wang et al. [17] put forward a QFD method to rate ECs based on interval-valued intuitionistic fuzzy sets, a continuous ordered weighted averaging operator, Choquet integral, K-additive measures, and mixed integer programming. Haktanir and Kahraman [4] proposed a QFD approach using interval-valued intuitionistic fuzzy sets, Z-fuzzy numbers, and Chebyshev’s inequality for new product design. Kulcsár et al. [9] combined the QFD with network science to propose a network-based QFD method to support a CNC machine tool development. In addition, Wang et al. [19] applied double hierarchy hesitant linguistic term sets (DHHLTSs), maximizing the consensus method and axiomatic design approach to enhance the performance of the classical QFD. Mao et al. [33] employed the linguistic Z-numbers, evaluation based on distance from average solution (EDAS), and stepwise weight assessment ratio analysis (SWARA) to improve the effectiveness of QFD. Wu et al. [35] adopted the multi-objective optimization by ratio analysis plus the full multiplicative form (MULTIMOORA) method, cloud model theory, and a maximizing deviation method to overcome the deficiencies of the traditional QFD. In [48], the PHFLTSs, prospect theory, and best–worst method were combined to improve the QFD.
From the above literature review, it can be seen that a great many generalized fuzzy methods have been employed in QFD to handle the imprecise and vague relationship assessments between CRs and ECs. Nevertheless, due to the increasing complexities of practical QFD problems, it is often difficult to acquire sufficient and accurate relationship data and the current fuzzy methods are not effective to express vague and uncertain information comprehensively. In addition, many MCDM methods have been adopted to determine the importance ranking orders of ECs in QFD. However, no study has been conducted to improve the QFD on the basis of the CoCoSo method. To fill these gaps, the aim of this paper was to develop a new approach by integrating the SFSs and an extended CoCoSo method to determine the importance priority of ECs in QFD. The proposed QFD approach is capable of handling more uncertainty and ambiguity of the relationship evaluation information provided by experts, and can provide more practical and reliable solutions to derive the most significant ECs for designing or improving products.
3. Preliminaries
The SFSs were first proposed by Gündoǧdu and Kahraman [20] to better express the uncertainty and fuzziness evaluation information given by the decision-makers.
Definition 1
[20]. Let X be a fixed non-empty universe of discourse. An SFSover X is described by
whereare the degrees of membership, non-membership, and hesitancy of x to , respectively. They satisfy the condition that. For convenience,can be briefly denoted as a triplet form .
Example 1.
If an expert assessed the relationship between a CR and an EC on three dimensions as high (membership), not high (non-membership), and indeterminacy (hesitancy), among which high is 0.8, not high is 0.3, and indeterminacy is 0.2. Then, the evaluation result can be expressed as an SFS = (0.8, 0.3, 0.2).
Definition 2
[20]. Letand be any two SFSs and, then the basic operational laws of SFSs are given as follows:
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
Example 2.
Let and be two SFSs and , then we have
; ;
; .
Definition 3
[20]. Suppose that there are two SFSs and , then their score function and the accuracy function are defined by
Based on the score and accuracy functions, the comparison rules of SFSs are as follows: > , if and only if it satisfies: (1) or (2) and .
Example 3.
Let and be two SFSs, then, by using Equations (2) and (3), we have and . Thus, > according to the comparison rules of SFSs.
Definition 4
[20]. Letbe a set of SFSs and be their associated weights with. Then, the spherical fuzzy weighted averaging (SFWA) operator is defined as:
Example 4.
Let, , , and be any four SFSs andbe their weight vector. Then, by using Equation (4), we have.
4. The Proposed QFD Approach
In this section, an integrated methodology based on SFSs and the CoCoSo method was devised to prioritize the ECs in QFD. In particular, the SFSs were utilized to express the experts’ vague assessments on the interrelationships between CRs and ECs, the DEMATEL method was introduced to derive the comparative weights of CRs, and an extended CoCoSo method was utilized to determine the importance orders of ECs. A flowchart of the proposed QFD approach comprising three phases is depicted in Figure 1.
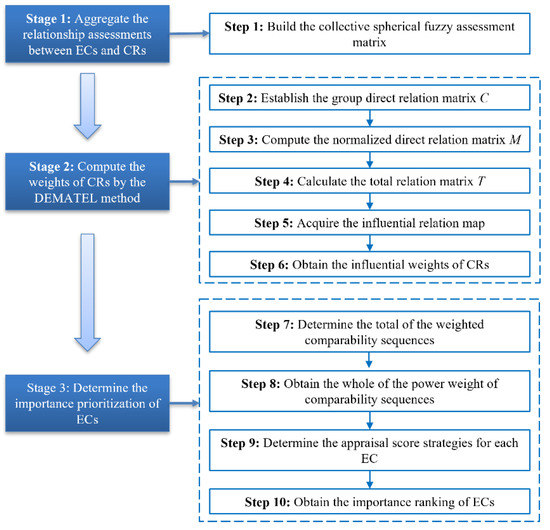
Figure 1.
Flowchart of the proposed QFD approach.
Suppose that a QFD problem consists of m engineering characteristics and n customer requirements . Assume that l experts are involved to evaluate the correlations between the CRs and ECs of the QFD problem, and each expert is assigned a weight satisfying > 0 and . Let be the spherical fuzzy assessment matrix of the kth expert, where is the spherical fuzzy rating of ECi with respect to CRj provided by the expert Ek.
In what follows, the detailed steps of the proposed QFD approach are explained.
Stage 1: Aggregate the relationship assessments between ECs and CRs.
Step 1: Build the collective spherical fuzzy assessment matrix .
By using the SFWA operator, the individual spherical fuzzy assessment matrices can be aggregated to obtain the collective spherical fuzzy assessment matrix . That is,
Stage 2: Compute the weights of CRs by the DEMATEL method.
The DEMATEL method, originally developed by the Geneva Research Center of the Battelle Memorial Institute, is an effective technique to analyze the relationships as well as the interdependence intensity among system elements [49]. It can help decision-makers and analysts understand the interdependence of factors through matrices or digraphs and restrict the relations that reflect characteristics within an essential systemic and developmental trend [50]. Due to its simplicity and effectiveness, the DEMATEL method is more suitable in real-life applications and has been widely used in various decision-making problems [51,52,53,54]. Therefore, in this study, we employed the DEMATEL method to obtain the weights of CRs by analyzing the correlations among them.
Step 2: Establish the group direct relation matrix C.
Suppose that h customers are involved to determine the extent to which a specific CR affects another one. The direct relation matrix for each customer, denoted as , in which represents how CRi influences the CRj. The value of is taken as an integer score, in which 0 denotes “no influence”, 1 denotes “very low influence”, 2 denotes “low influence”, 3 denotes “high influence”, and 4 denotes “very high influence”.
The group direct relation matrix can be calculated by
Step 3: Compute the normalized direct relation matrix M.
With the group direct relation matrix C, the normalized direct relation matrix M can be derived by the following formula
where .
Step 4: Calculate the total relation matrix T.
Based on the normalized direct-relation matrix M, the total relation matrix T is computed by
in which I stands for an identity matrix.
Step 5: Acquire the influential relation map.
Let R represent the sum of rows of the matrix T and D denote the sum of columns of the matrix T, in which R and D can be determined by the following equations
Furthermore, an influential relation map can be depicted on the basis of the ordered pairs in which is named after ‘Prominence’ and is called ‘Relation’.
Step 6: Obtain the influential weights of CRs.
According to [55], the influential weights of CRs wj (j = 1, 2, …, n) can be calculated with the following equations
Stage 3: Determine the importance prioritization of ECs.
Step 7: Determine the total of the weighted comparability sequence Si.
In this step, the total of the weighted comparability sequences Ui (i = 1, 2, …, m) can be derived from the following equation
Step 8: Obtain the whole of the power weight of the comparability sequence Pi.
Similarly, the whole of the power weight of the comparability sequence Pi (i = 1, 2, …, m) can be computed by
Step 9: Determine the appraisal score strategies for each EC.
This step is to calculate the three appraisal score strategies Kia, Kib, and Kic for each EC by using the following equations
In Equation (17), ϑ is determined by experts to balance the model scores between the weighted sum method and the weighted product method. Generally, it can take the value of 0.5.
Step 10: Obtain the importance ranking of ECs.
Finally, the importance index values of the m ECs Ki (i = 1, 2, …, m) are computed by
The most critical EC has the highest importance index value. Thus, the given m ECs can be ranked according to the decreased order of their importance index values Ki (i = 1, 2, …, m).
5. Illustrative Example
In this part, an illustrative example regarding the accommodation service design [56] is presented to show the applicability and effectiveness of our proposed QFD approach.
5.1. Implementation and Results
As tourism plays a crucial role in the national economy, accommodation service quality is of significance for tourists. Weizhou Island, located in Beihai, Guangxi Zhuang Autonomous Region, is a famous scenic spot for its well-preserved natural landscape. Providing accommodation services is incumbent for each tourist visiting the island. Thus, the service product design for accommodation is essential to secure competitive advantages for accommodation service suppliers. To determine the importance degrees of service designs, an effective QFD approach should be employed for the service product design to fulfill customer needs with the highest possible quality.
In the service product design problem, the critical service designs (i.e., ECs) are obtained via the ratings of service attributes (i.e., CRs) and the relationships between ECs and CRs. When applying the proposed QFD approach, appropriate CRs and ECs have to be identified first. The main CRs to be considered in the case were identified from a preliminary survey, which was performed through direct interviews with 100 tourists visiting Weizhou Island. Through in-depth interviews with managers of famous international hotels, seven possible ECs when customer needs related to service design or management requirements were found. Furthermore, the managers added four ECs based on the literature analysis and accommodation service characteristics. As a result, eight CRs and eleven ECs were determined for the accommodation service design in Weizhou Island, which are listed in Table 1.

Table 1.
The CRS and ECS identified in the case study.
For the QFD problem, four experts were invited to give their assessments on the correlations between ECs and CRs. These were senior managers from different departments of the international hotels including the engineering department, food and beverage department, housekeeping department, and front office department. All the experts had professional knowledge in the accommodation management domain and had worked in their relevant fields for more than three years. The experts adopted SFSs to express their relationship ratings and the linguistic term sets used are shown in Table 2. Specifically, E1 adopts S1, E2 and E3 adopt S2, and E4 adopts S4 to elicit their assessments on the relationships between ECs and CRs. The linguistic assessment information obtained from the four experts is shown in Table 3, Table 4, Table 5 and Table 6. By converting them into the corresponding SFSs, the individual spherical fuzzy assessment matrices can be determined.

Table 2.
The linguistic term sets used by the four experts.

Table 3.
Linguistic assessments of expert E1.

Table 4.
Linguistic assessments of expert E2.

Table 5.
Linguistic assessments of expert E3.

Table 6.
Linguistic assessments of expert E4.
Next, the steps of the proposed QFD approach were conducted to determine the most important ECs for the given case study.
Step 1: By using Equation (5), the individual spherical fuzzy assessment matrices are aggregated to obtain the collective spherical fuzzy assessment matrix , as shown in Table 7. In this case, the weight of each expert is assumed to be equal, that is, λk = 0.25 for k = 1, 2, 3, 4.

Table 7.
The collective spherical fuzzy assessment matrix .
Step 2: Five tourists (h = 5) were invited to determine the direct relation matrices of CRs . Due to the space limitations, only the assessment of the first tourist is presented here:
Then, via Equation (6), the group direct relation matrix C is acquired as
Step 3: The normalized direct relation matrix M is calculated by Equation (7) as
Step 4: The total relation matrix T is calculated via Equation (8) as follows:
Step 5: Using Equations (9) and (10), the vectors R and D are calculated as follows:
Step 6: By using Equations (11) and (12), the influential weights of CRs are obtained as:
Step 7: The total of the weighted comparability sequences Si (i = 1, 2, …, 11) are computed via Equation (13) and presented in Table 8.

Table 8.
Computational results by the CoCoSo method.
Step 8: The whole of the power weight of comparability sequence Pi (i = 1, 2, …, 11) is computed via Equation (14), as shown in Table 8.
Step 9: According to Equations (15)–(17), the appraisal score strategies Kia, Kib, and Kic (i = 1, 2, …, 11) are calculated and given in Table 8.
.
Based on the decreased order in the importance index values Ki (i = 1, 2, …, 11), the 11 ECs could be ranked and their ranking orders were determined as: EC3 > EC1 > EC4 > EC8 > EC6 > EC11 > EC7 > EC2 > EC9 > EC10 > EC5. This implies that complaint handling (EC3) occupies the most vital position among the considered ECs, which should be given more attention in the service design process, followed by relations (EC1) and cleanliness (EC4).
5.2. Comparative Analysis
To further illustrate the advantages of the proposed QFD approach, this section performed a comparative analysis with the traditional QFD, the linguistic QFD [33], and the multigranular linguistic QFD [56] methods based on the above case study. The ranking results of the ECs determined by the listed methods are exhibited in Figure 2.
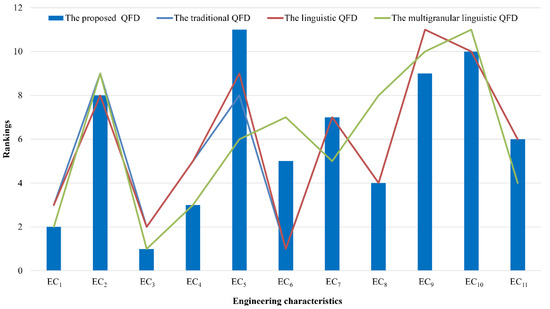
Figure 2.
The EC ranking results of the comparative analysis.
As can be seen from Figure 2, the top three ECs obtained by the proposed approach were the same as the ones determined by the multigranular linguistic QFD method. Since the case example was adopted from [56], the priority of ECs acquired by the multigranular linguistic QFD can be considered as a benchmark. Moreover, the ranking orders of five ECs with the proposed approach were consistent with those by the linguistic QFD method. Therefore, the applicability and feasibility of the proposed QFD approach were proven.
However, there was a significant difference between the two sets of EC priority rankings produced by the proposed QFD and the traditional QFD. This can be explained by the shortcomings associated with the traditional QFD method, as indicated in the Introduction. Furthermore, there were some differences in the importance rankings of ECs obtained via the proposed QFD and the linguistic QFD methods. For example, EC4 was ranked in third place by the proposed approach, whereas via the linguistic QFD method, EC1 was ranked in third place. Additionally, EC6 was ranked in fifth place via the proposed approach, which was different from the one derived by the linguistic QFD method. The inconsistent results may be caused by the reasons as follows. First, in the linguistic QFD method, the linguistic Z numbers are used to describe the experts’ relationship assessments between the CRs and ECs, which are unable to capture the uncertainty and fuzziness of the evaluation information comprehensively. Second, in the linguistic QFD method, the EDAS method is used to determine the prioritization of ECs, which has low resolution in differentiating the ECs in QFD.
In addition, there exist inconsistent ranking orders of ECs derived by the proposed approach and the multigranular linguistic QFD method. For instance, EC8 ranked in fourth place by the proposed approach, while it was ranked eighth by the multigranular linguistic QFD. Moreover, EC6 was ranked in fifth place in the proposed approach, whereas it was ranked seventh by the multigranular linguistic QFD. These differences can be explained by the following facts. First, the multigranular unbalanced linguistic term sets were used to capture the experts’ relationship ratings in the multigranular linguistic QFD, which were unable to handle the uncertainty and ambiguity of the relationship assessments given by the experts. Second, a combined structure that combined maximizing the deviation and the best–worst method was employed for the determination of the ranking of ECs. The method is unable to promote the exactitude of the QFD process and may obtain the most significant ECs with counterintuitive phenomena.
From the comparative analysis, it can be concluded that the importance ranking result of ECs acquired by our proposed QFD approach based on SFSs and the CoCoSo method is reasonable and reliable. Compared with the traditional QFD and its improvements, the advantages of the proposed QFD approach are summarized below:
- (1)
- Based on the SFSs, the proposed approach is capable of handling more uncertainty and ambiguity in the relationship assessments between CRs and ECs. Thus, the QFD team members were more flexible in expressing their opinions in complex or ill-defined situations.
- (2)
- The DEMATEL method was used to compute the importance weights of CRs in QFD. As a result, the proposed approach could determine appropriate weights of CRs by analyzing the inter-relationships and cause–effect relationships among them.
- (3)
- An extended CoCoSo method was introduced to obtain the importance ranking of ECs, which can promote the exactitude of the QFD process and has a higher resolution in distinguishing ECs. Therefore, the proposed approach is able to provide a credible prioritization of the identified ECs and offer a more reasonable solution for product optimization.
6. Conclusions
QFD is a customer-driven product development tool to efficiently translate customer needs into design requirements in order to achieve higher customer satisfaction. Although showing much attractiveness, the traditional HOQ method still suffers from some important weaknesses concerning the rationality of the approach. Thus, this paper proposed a new improved QFD approach by combining the SFSs and the CoCoSo method to enhance the performance of the traditional QFD. It could effectively deal with the ambiguous and uncertain relationship assessment information between CRs and ECs with the SFSs and determine a more accurate and credible ranking of ECs for product development based on the CoCoSo method. The practical application and advantages of the proposed QFD were illustrated by an empirical case of accommodation service design. It was shown that the proposed approach allows for the identification of service attributes perceived to affect the service design performance from the tourist’s point of view, enabling the assessment of possible gaps between the tourists’ and hotel’s perception of service delivery.
Future studies will focus on the following directions. First, the consensus among experts was not considered and adequately handled in this study. Therefore, endeavors should be devoted to improve the proposed QFD by addressing the consensus issue of experts in future studies. Second, in the proposed QFD, the weights of the CRs were derived by the DEMATEL method with crisp numbers. In the future, advanced DEMATEL methods can be used to weight CRs due to the impreciseness and vagueness of the experts’ judgements. In addition, a decision support system needs be constructed in the future to help quality managers reduce the calculation process of the proposed QFD in real-life applications.
Author Contributions
Conceptualization, X.-G.X. and L.Z.; Methodology, L.Z. and L.-X.M.; Writing—original draft preparation, L.Z. and L.-X.M.; Writing—review and editing, X.-G.X. and K.L.; Visualization, K.L.; Supervision, X.-G.X. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 72001196) and the Fundamental Research Funds for the Central Universities (No. 22120220035).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| CoCoSo | Combined compromise solution |
| CPT | Cumulative prospect theory |
| CRs | Customer requirements |
| DEMATEL | Decision-making trial and evaluation laboratory |
| DHHLTSs | Double hierarchy hesitant linguistic term sets |
| ECs | Engineering characteristics |
| EDAS | Evaluation based on distance from average solution |
| HFLTSs | Hesitant fuzzy linguistic term sets |
| HOQ | House of quality |
| LPFSs | Linguistic Pythagorean fuzzy sets |
| MCDM | Multi-criteria decision making |
| MULTIMOORA | Multi-objective optimization by ratio analysis plus the full multiplicative form |
| ORESTE | Organísation, rangement et Synthèse de données relarionnelles, in French |
| PHFLTSs | Proportional hesitant fuzzy linguistic term sets |
| QFD | Quality function deployment |
| SFSs | Spherical fuzzy sets |
| SFWA | Spherical fuzzy weighted averaging |
| SWARA | Stepwise weight assessment ratio analysis |
| TODIM | Portuguese acronym for interactive multi-criteria decision making |
| TOPSIS | Technique for order preference by similarity to an ideal solution |
References
- Akao, Y. New product development and quality assurancequality deployment system. Stand. Qual. Control 1972, 25, 7–14. [Google Scholar]
- Shi, H.; Mao, L.X.; Li, K.; Wang, X.H.; Liu, H.C. Engineering characteristics prioritization in quality function deployment using an improved ORESTE method with double hierarchy hesitant linguistic information. Sustainability 2022, 14, 9771. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, Z.S.; Chan, C.Y.P.; Pedrycz, W.; Martínez, L.; Skibniewski, M.J. Large-scale group decision-making for prioritizing engineering characteristics in quality function deployment under comparative linguistic environment. Appl. Soft Comput. 2022, 127, 109359. [Google Scholar] [CrossRef]
- Haktanir, E.; Kahraman, C. New product design using chebyshev’s inequality based interval-valued intuitionistic Z-fuzzy QFD method. Informatica 2022, 33, 1–33. [Google Scholar] [CrossRef]
- Allehashemi, T.; Amin, S.H.; Zolfaghari, S. A proposed multi-objective model for cellphone closed-loop supply chain optimization based on fuzzy QFD. Expert Syst. Appl. 2022, 210, 118577. [Google Scholar] [CrossRef]
- Goharshenasan, A.; Sheikh Aboumasoudi, A.; Shahin, A.; Ansari, A. Prioritizing the economic indicators of SSC: An integrative QFD approach of performance prism and BSC. Benchmarking 2022, 29, 522–550. [Google Scholar] [CrossRef]
- Tortorella, G.L.; Fogliatto, F.S.; Sunder, M.V.; Cawley Vergara, A.M.; Vassolo, R. Assessment and prioritisation of Healthcare 4.0 implementation in hospitals using quality function deployment. Int. J. Prod. Res. 2022, 60, 3147–3169. [Google Scholar] [CrossRef]
- Gavahi, S.S.; Hosseini, S.M.H.; Moheimani, A. An application of quality function deployment and SERVQUAL approaches to enhance the service quality in radiology centres. Benchmarking 2022. [Google Scholar] [CrossRef]
- Kulcsár, E.; Gyurika, I.G.; Csiszér, T. Network-based—Quality Function Deployment (NB-QFD): The combination of traditional QFD with network science approach and techniques. Comput. Ind. 2022, 136, 103592. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, X.; Zhang, H. Coping with diversity ratings in prioritizing design requirements in quality function deployment: A consensus-based approach with minimum-maximum adjustments. Comput. Ind. Eng. 2022, 163, 107799. [Google Scholar] [CrossRef]
- Ping, Y.J.; Liu, R.; Wang, Z.L.; Liu, H.C. New approach for quality function deployment with an extended alternative queuing method under linguistic Pythagorean fuzzy environment. Eur. J. Ind. Eng. 2022, 16, 349–370. [Google Scholar] [CrossRef]
- Karasan, A.; Ilbahar, E.; Cebi, S.; Kahraman, C. Customer-oriented product design using an integrated neutrosophic AHP & DEMATEL & QFD methodology. Appl. Soft Comput. 2022, 118, 108445. [Google Scholar]
- Finger, G.S.W.; Lima-Junior, F.R. A hesitant fuzzy linguistic QFD approach for formulating sustainable supplier development programs. Int. J. Prod. Econ. 2022, 247, 108428. [Google Scholar] [CrossRef]
- Erol, I.; Murat Ar, I.; Peker, I.; Searcy, C. Alleviating the impact of the barriers to circular economy adoption through blockchain: An investigation using an integrated MCDM-based QFD with hesitant fuzzy linguistic term sets. Comput. Ind. Eng. 2022, 165, 107962. [Google Scholar] [CrossRef]
- Liu, H.C.; Shi, H.; Li, Z.; Duan, C.Y. An integrated behavior decision-making approach for large group quality function deployment. Inf. Sci. 2022, 582, 334–348. [Google Scholar] [CrossRef]
- Fang, H.; Li, J.; Song, W. A new method for Quality Function Deployment based on rough cloud model theory. IEEE Trans. Eng. Manag. 2022, 69, 2842–2856. [Google Scholar] [CrossRef]
- Wang, L.; Yu, L.; Ni, Z. A novel IVIF QFD considering both the correlations of customer requirements and the ranking uncertainty of technical attributes. Soft Comput. 2022, 26, 4199–4213. [Google Scholar] [CrossRef]
- Kutlu Gündoğdu, F.; Kahraman, C. A novel spherical fuzzy QFD method and its application to the linear delta robot technology development. Eng. Appl. Artif. Intell. 2020, 87, 103348. [Google Scholar] [CrossRef]
- Wang, Z.L.; Liu, H.C.; Xu, J.Y.; Ping, Y.J. A new method for quality function deployment using double hierarchy hesitant fuzzy linguistic term sets and axiomatic design approach. Qual. Eng. 2021, 33, 511–522. [Google Scholar] [CrossRef]
- Gündoǧdu, F.K.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, G.; Chen, X. SF-GRA method based on cumulative prospect theory for multiple attribute group decision making and its application to emergency supplies supplier selection. Eng. Appl. Artif. Intell. 2022, 110, 104679. [Google Scholar] [CrossRef]
- Garg, H.; Sharaf, I.M. A new spherical aggregation function with the concept of spherical fuzzy difference for spherical fuzzy EDAS and its application to industrial robot selection. Comput. Appl. Math. 2022, 41, 1–26. [Google Scholar] [CrossRef]
- Donyatalab, Y.; Kutlu Gündoğdu, F.; Farid, F.; Seyfi-Shishavan, S.A.; Farrokhizadeh, E.; Kahraman, C. Novel spherical fuzzy distance and similarity measures and their applications to medical diagnosis. Expert Syst. Appl. 2022, 191, 116330. [Google Scholar] [CrossRef]
- Rahnamay Bonab, S.; Jafarzadeh Ghoushchi, S.; Deveci, M.; Haseli, G. Logistic autonomous vehicles assessment using decision support model under spherical fuzzy set integrated Choquet Integral approach. Expert Syst. Appl. 2023, 214, 119205. [Google Scholar] [CrossRef]
- Ozceylan, E.; Ozkan, B.; Kabak, M.; Dagdeviren, M. A state-of-the-art survey on spherical fuzzy sets. J. Intell. Fuzzy Syst. 2022, 42, 195–212. [Google Scholar] [CrossRef]
- Yilmaz, M.K.; Kusakci, A.O.; Aksoy, M.; Hacioglu, U. The evaluation of operational efficiencies of Turkish airports: An integrated spherical fuzzy AHP/DEA approach. Appl. Soft Comput. 2022, 119, 108620. [Google Scholar] [CrossRef]
- Menekse, A.; Camgoz-Akdag, H. Internal audit planning using spherical fuzzy ELECTRE. Appl. Soft Comput. 2022, 114, 108155. [Google Scholar] [CrossRef]
- Jafarzadeh Ghoushchi, S.; Shaffiee Haghshenas, S.; Memarpour Ghiaci, A.; Guido, G.; Vitale, A. Road safety assessment and risks prioritization using an integrated SWARA and MARCOS approach under spherical fuzzy environment. Neural Comput. Appl. 2022. [Google Scholar] [CrossRef]
- Gocer, F.; Sener, N. Spherical fuzzy extension of AHP-ARAS methods integrated with modified k-means clustering for logistics hub location problem. Expert Syst. 2022, 39, e12886. [Google Scholar] [CrossRef]
- Bolturk, E.; Seker, S. Spherical fuzzy present worth analysis method for emergency hospital investment analysis. IEEE Trans. Eng. Manag. 2022. [Google Scholar] [CrossRef]
- Huang, J.; Mao, L.X.; Liu, H.C.; Song, M.S. Quality function deployment improvement: A bibliometric analysis and literature review. Qual. Quant. 2022, 56, 1347–1366. [Google Scholar] [CrossRef]
- Sivasamy, K.; Arumugam, C.; Devadasan, S.R.; Murugesh, R.; Thilak, V.M.M. Advanced models of quality function deployment: A literature review. Qual. Quant. 2016, 50, 1399–1414. [Google Scholar] [CrossRef]
- Mao, L.X.; Liu, R.; Mou, X.; Liu, H.C. New approach for quality function deployment using linguistic Z-numbers and EDAS method. Informatica 2021, 32, 565–582. [Google Scholar] [CrossRef]
- Liu, H.C.; Wu, S.M.; Wang, Z.L.; Li, X.Y. A new method for quality function deployment with extended prospect theory under hesitant linguistic environment. IEEE Trans. Eng. Manag. 2021, 68, 442–451. [Google Scholar] [CrossRef]
- Wu, S.M.; You, X.Y.; Liu, H.C.; Wang, L.E. Improving quality function deployment analysis with the cloud MULTIMOORA method. Int. Trans. Oper. Res. 2020, 27, 1600–1621. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Kazimieras Zavadskas, E.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Sindhwani, R.; Singh, P.L.; Behl, A.; Afridi, M.S.; Sammanit, D.; Tiwari, A.K. Modeling the critical success factors of implementing net zero emission (NZE) and promoting resilience and social value creation. Technol. Forecast. Soc. Chang. 2022, 181, 121759. [Google Scholar] [CrossRef]
- Ghasemi, K.; Behzadfar, M.; Borhani, K.; Nouri, Z. Geographic information system based combined compromise solution (CoCoSo) method for exploring the spatial justice of accessing urban green spaces, a comparative study of district 22 of Tehran. Ecol. Indic. 2022, 144, 109455. [Google Scholar] [CrossRef]
- Zhang, F.; Song, W. Sustainability risk assessment of blockchain adoption in sustainable supply chain: An integrated method. Comput. Ind. Eng. 2022, 171, 108378. [Google Scholar] [CrossRef]
- Peng, X.; Garg, H. Intuitionistic fuzzy soft decision making method based on CoCoSo and CRITIC for CCN cache placement strategy selection. Artif. Intell. Rev. 2022, 55, 1567–1604. [Google Scholar] [CrossRef]
- Pamucar, D.; Faruk Görçün, Ö. Evaluation of the European container ports using a new hybrid fuzzy LBWA-CoCoSo’B techniques. Expert Syst. Appl. 2022, 203, 117463. [Google Scholar] [CrossRef]
- Ali, T.; Aghaloo, K.; Chiu, Y.R.; Ahmad, M. Lessons learned from the COVID-19 pandemic in planning the future energy systems of developing countries using an integrated MCDM approach in the off-grid areas of Bangladesh. Renew. Energy 2022, 189, 25–38. [Google Scholar] [CrossRef]
- Chen, Q.Y.; Liu, H.C.; Wang, J.H.; Shi, H. New model for occupational health and safety risk assessment based on Fermatean fuzzy linguistic sets and CoCoSo approach. Appl. Soft Comput. 2022, 126, 109262. [Google Scholar] [CrossRef]
- Tavana, M.; Shaabani, A.; Di Caprio, D.; Bonyani, A. A novel Interval Type-2 Fuzzy best-worst method and combined compromise solution for evaluating eco-friendly packaging alternatives. Expert Syst. Appl. 2022, 200, 117188. [Google Scholar] [CrossRef]
- Yousefi, S.; Valipour, M.; Gul, M. Systems failure analysis using Z-number theory-based combined compromise solution and full consistency method. Appl. Soft Comput. 2021, 113, 107902. [Google Scholar] [CrossRef]
- Deveci, M.; Pamucar, D.; Gokasar, I.; Delen, D.; Martínez, L. A fuzzy Einstein-based decision support system for public transportation management at times of pandemic. Knowl. Based Syst. 2022, 252, 109414. [Google Scholar] [CrossRef]
- Simić, V.; Ivanović, I.; Đorić, V.; Torkayesh, A.E. Adapting urban transport planning to the COVID-19 pandemic: An integrated fermatean fuzzy model. Sustain. Cities Soc. 2022, 79, 103669. [Google Scholar] [CrossRef]
- Huang, J.; You, X.Y.; Liu, H.C.; Si, S.L. New approach for quality function deployment based on proportional hesitant fuzzy linguistic term sets and prospect theory. Int. J. Prod. Res. 2019, 57, 1283–1299. [Google Scholar] [CrossRef]
- Gabus, A.; Fontela, E. World problems, an invitation to further thought within the framework of DEMATEL. Battelle Geneva Res. Cent. Geneva Switz. 1972. [Google Scholar]
- Si, S.L.; You, X.Y.; Liu, H.C.; Zhang, P. DEMATEL technique: A systematic review of the state-of-the-art literature on methodologies and applications. Math. Probl. Eng. 2018, 2018, 3696457. [Google Scholar] [CrossRef]
- Lu, J.; Rong, D.; Lev, B.; Liang, M.; Zhang, C.; Gao, Y. Constraints affecting the promotion of waste incineration power generation project in China: A perspective of improved technology acceptance model. Technol. Forecast. Soc. Chang. 2023, 186, 122165. [Google Scholar] [CrossRef]
- Yorulmaz, M.; Karabulut, K. Analyzing the factors determining the effectiveness of the international safety management code applied on ships through the fuzzy DEMATEL method. Saf. Sci. 2022, 155, 105872. [Google Scholar] [CrossRef]
- Kassem, M.; Ahmed, A.L. Digital transformation through Building Information Modelling: Spanning the macro-micro divide. Technol. Forecast. Soc. Chang. 2022, 184, 122006. [Google Scholar] [CrossRef]
- Digalwar, A.K.; Saraswat, S.K.; Rastogi, A.; Thomas, R.G. A comprehensive framework for analysis and evaluation of factors responsible for sustainable growth of electric vehicles in India. J. Clean. Prod. 2022, 378, 134601. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Lu, C.; Chen, Y.Z. Evaluating health-care waste treatment technologies using a hybrid multi-criteria decision making model. Renew. Sustain. Energy Rev. 2015, 41, 932–942. [Google Scholar] [CrossRef]
- Tian, Z.P.; Nie, R.X.; Wang, J.Q.; Li, L. Group multigranular linguistic QFD for prioritizing service designs with combined weighting method. Expert Syst. 2019, 36, e12419. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).