Transfer EEG Emotion Recognition by Combining Semi-Supervised Regression with Bipartite Graph Label Propagation
Abstract
:1. Introduction
- The semi-supervised label propagation method based on sample-feature bipartite graph and semi-supervised regression method are combined to form a unified framework for joint common subspace optimization and emotion recognition. We first achieve better data feature distribution alignment through EEG feature transfer, based on which we then construct a better sample-feature bipartite graph and sample-label mapping matrix to promote the estimation of EEG emotional state in the target domain;
- The EEG emotional state in the target domain is estimated by a bi-model fusion strategy. First, a sample-feature bipartite graph is constructed based on the premise that similar samples have similar feature distributions. This graph is used to characterize the sample-feature connections between the source and the target domain for label propagation, as shown by the ‘Bi-graph label propagation’ part of Figure 1. Furthermore, a semi-supervised regression is used to learn a mapping matrix to describe the intra-domain connections between samples and labels, which aims to estimate the EEG emotional state of the target domain. By fusing both models, the EEG emotional state of the target domain is estimated from the perspective of similar feature distributions should be shared by samples from the same emotional state;
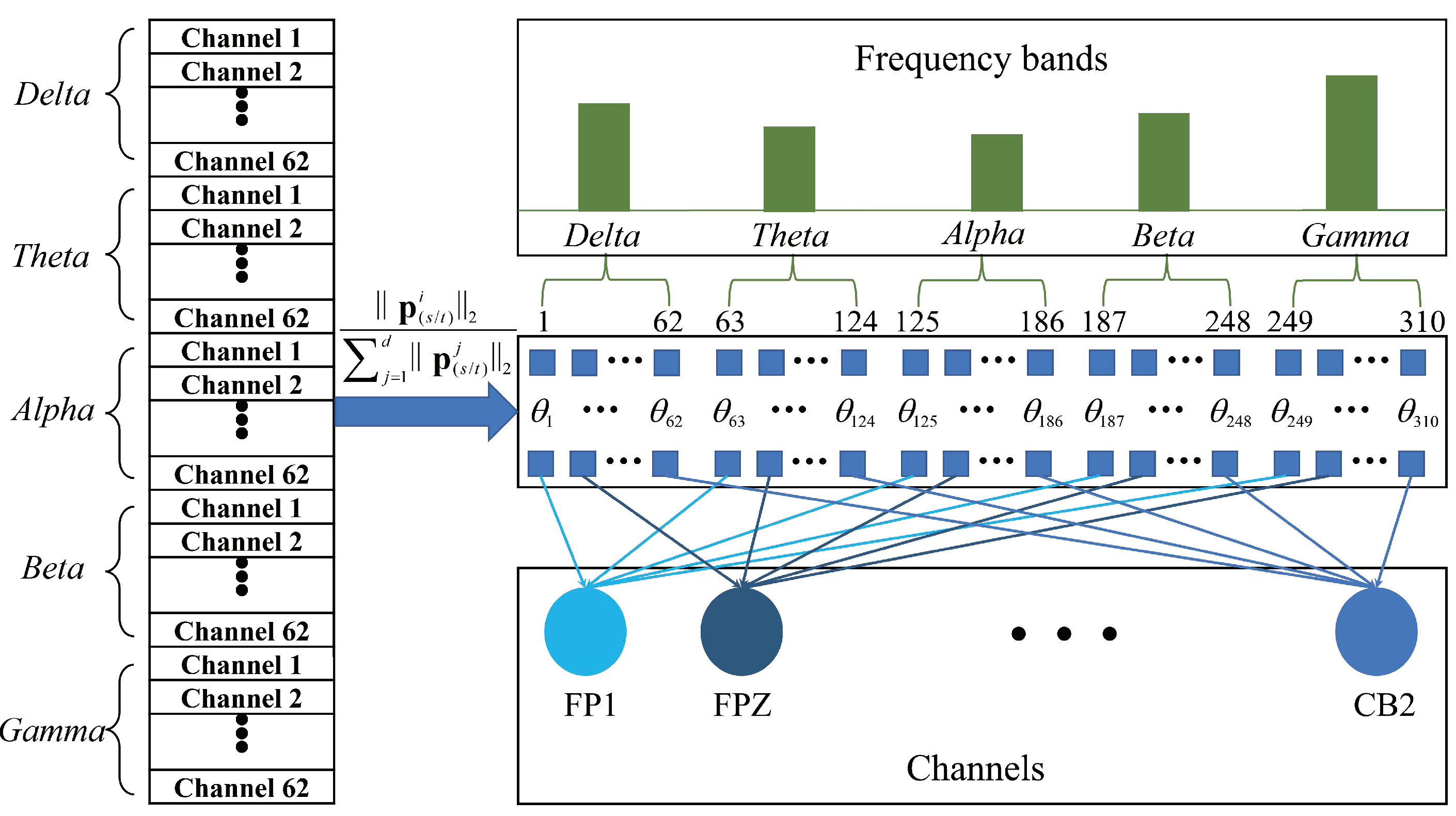
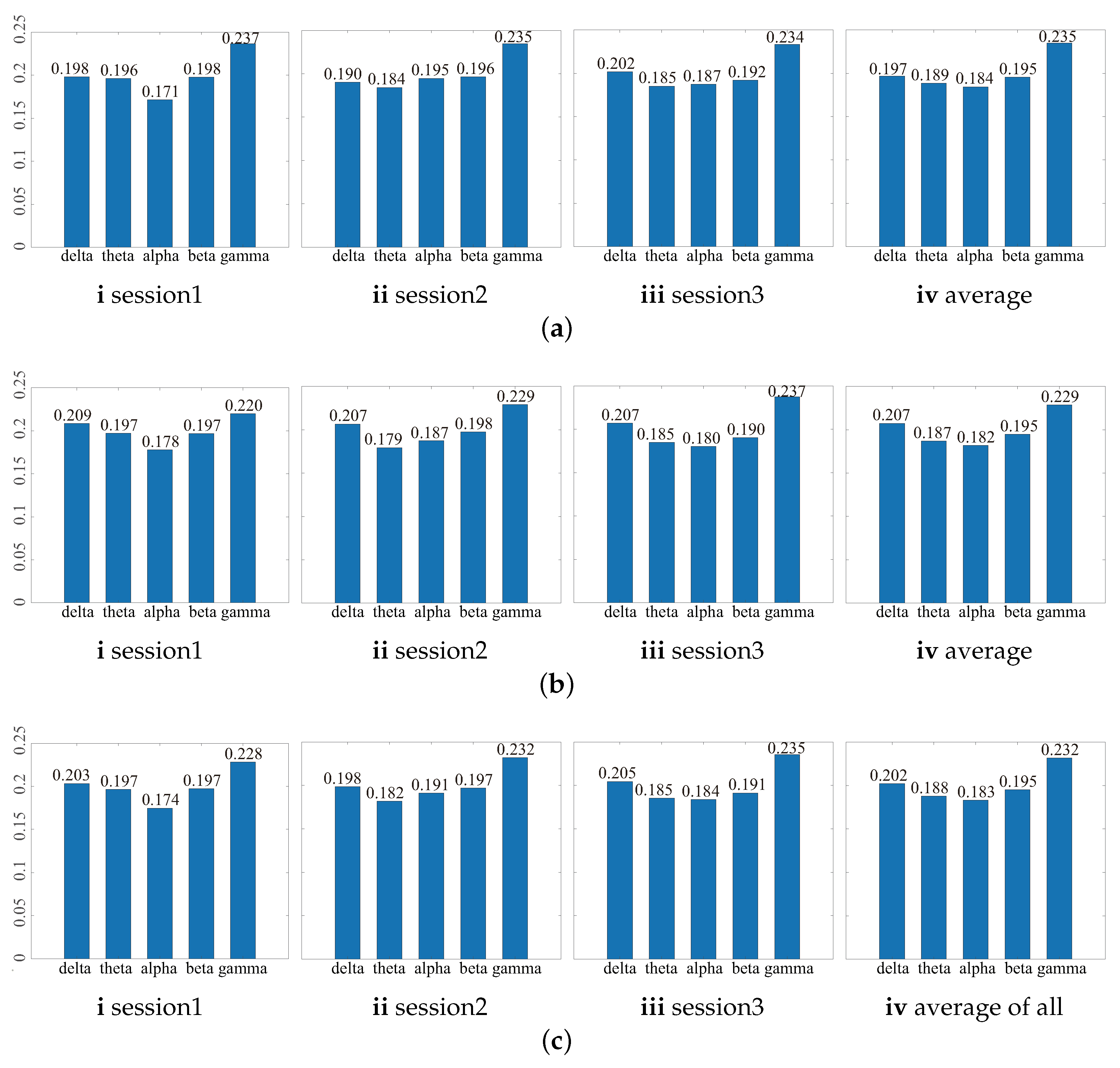
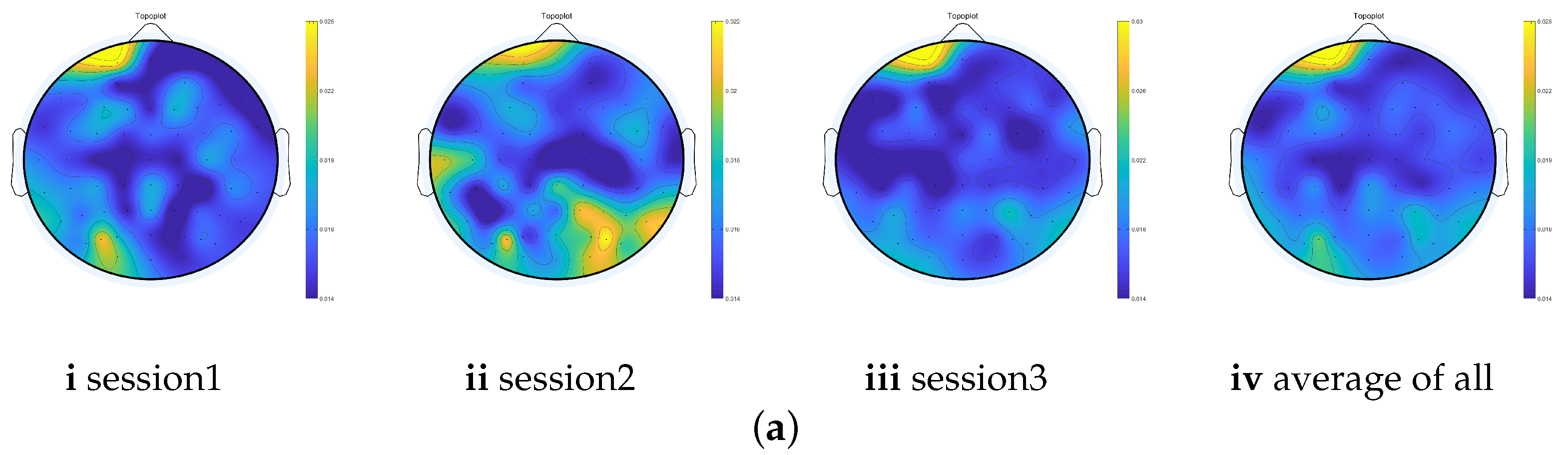
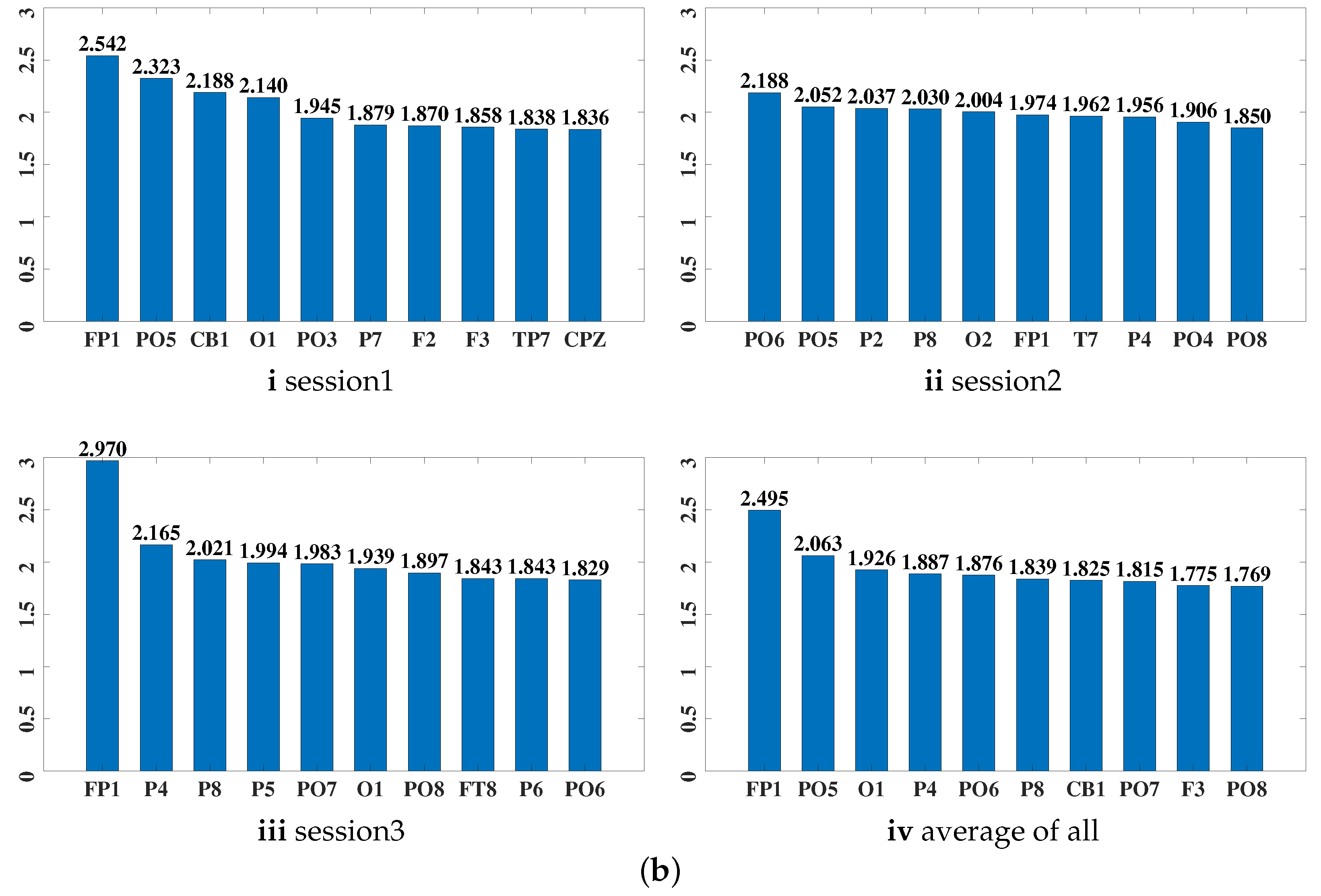
- We explore the EEG emotion activation patterns from the learned common subspace shared by source and target domains, which is based on the rationality that the subspace should retain the common features of the source and the target domain and inhibit the non-common features. We measure the importance of each EEG feature dimension by the normalized -norm of each row of the projection matrix. Based on the coupling correspondence between EEG features and the frequency bands and channels, the importance of frequency bands and brain regions in EEG emotion recognition are quantified.
2. Methodology
2.1. Problem Definition
2.2. Domain Alignment
2.3. Label Estimation
2.3.1. Bipartite Label Propagation
2.3.2. Semi-Supervised Regression
2.3.3. Fused Label Estimation Model
2.4. Overall Objective Function
2.5. Optimization
- Update . The objective function in terms of variable is
- Update . The objective function in terms of variable is
- Update . The corresponding objective function is
- Update . The objective function in terms of variable is
- Update . The objective function in terms of variable is
| Algorithm 1 The procedure for TSRBG framework |
|
2.6. Computational Complexity
3. Experiments
3.1. Dataset
3.2. Experimental Settings
3.3. Recognition Results and Analysis
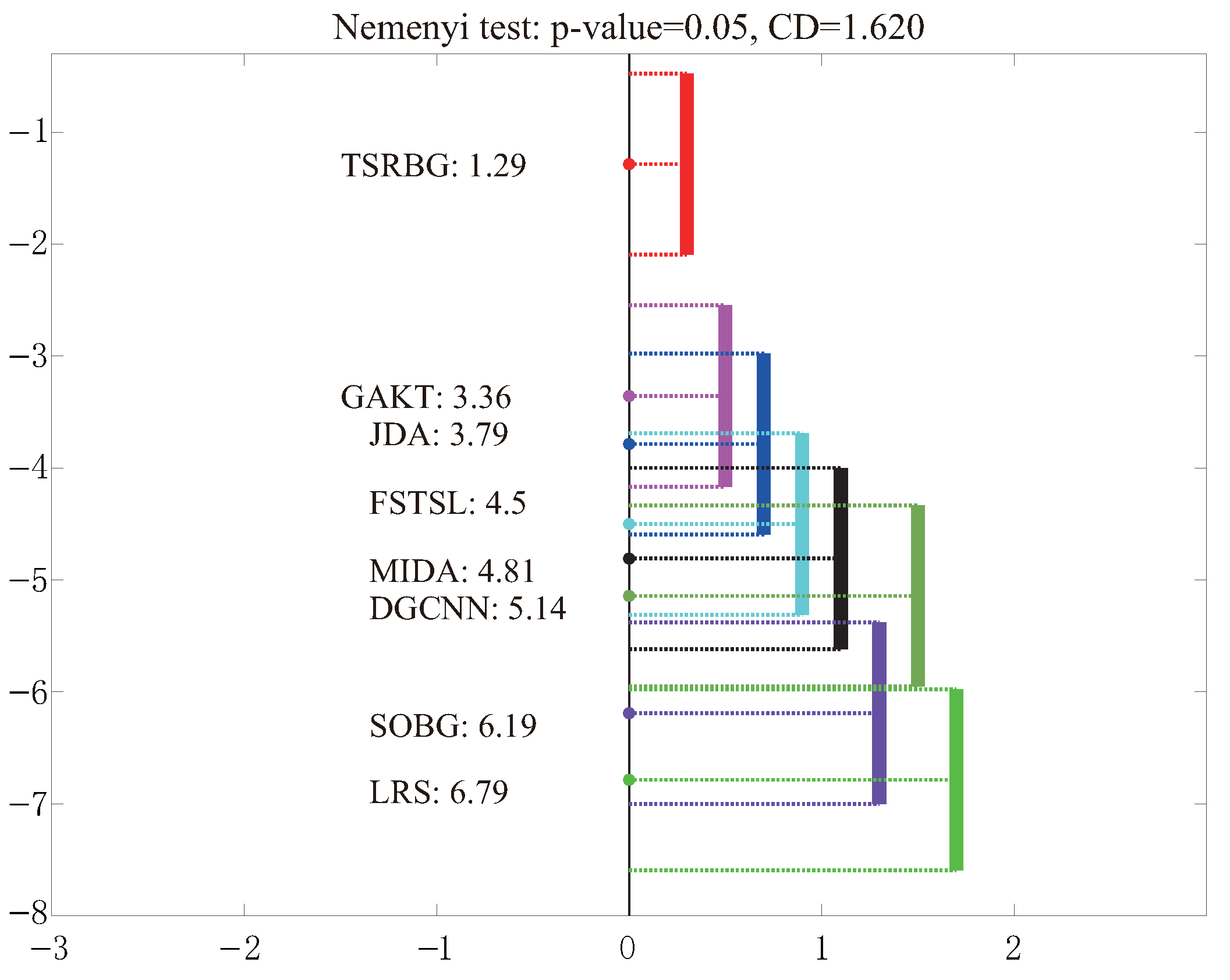
- TSRBG has achieved better EEG emotional state recognition accuracy than the other compared models in most cases. The highest recognition accuracy is the 15th subject of session 2, which is 88.58%. The average recognition accuracy of the three sessions are better than the other seven models, which are 72.83%, 76.49%, and 77.50%, respectively. On the whole, it verifies that the proposed TSRBG model is effective.
- By comparing the average recognition accuracy of the eight models in three sessions, it can be found that the joint optimization of semi-supervised EEG emotional states estimation and EEG feature transfer alignment in a tight coupling way can obtain better recognition accuracy. By setting GAKT and TSRBG as control groups, we find that the accuracy of TSRBG is significantly better than that of GAKT, and the main difference between them is the semi-supervised EEG emotion state estimation process. GAKT constructs an undirected graph based on the unaligned original data and this graph will not be updated with the data distribution alignment. In the double projection feature alignment subspace, it fails to well describe the sample association between the two domains. As a result, it cannot accurately estimate the EEG emotion state in the target domain, which affects the alignment effect of conditional distribution. However, TSRBG estimates the EEG emotional states of target domain by a bi-model fusing method. One model is used to construct a sample-feature bipartite graph to characterize inter-domain associations for label propagation. The initialized graph is dynamically updated based on the data subspace representations. The other model is the semi-supervised regression, which can effectively build the connection between subspace data representations and the label indicator matrix.
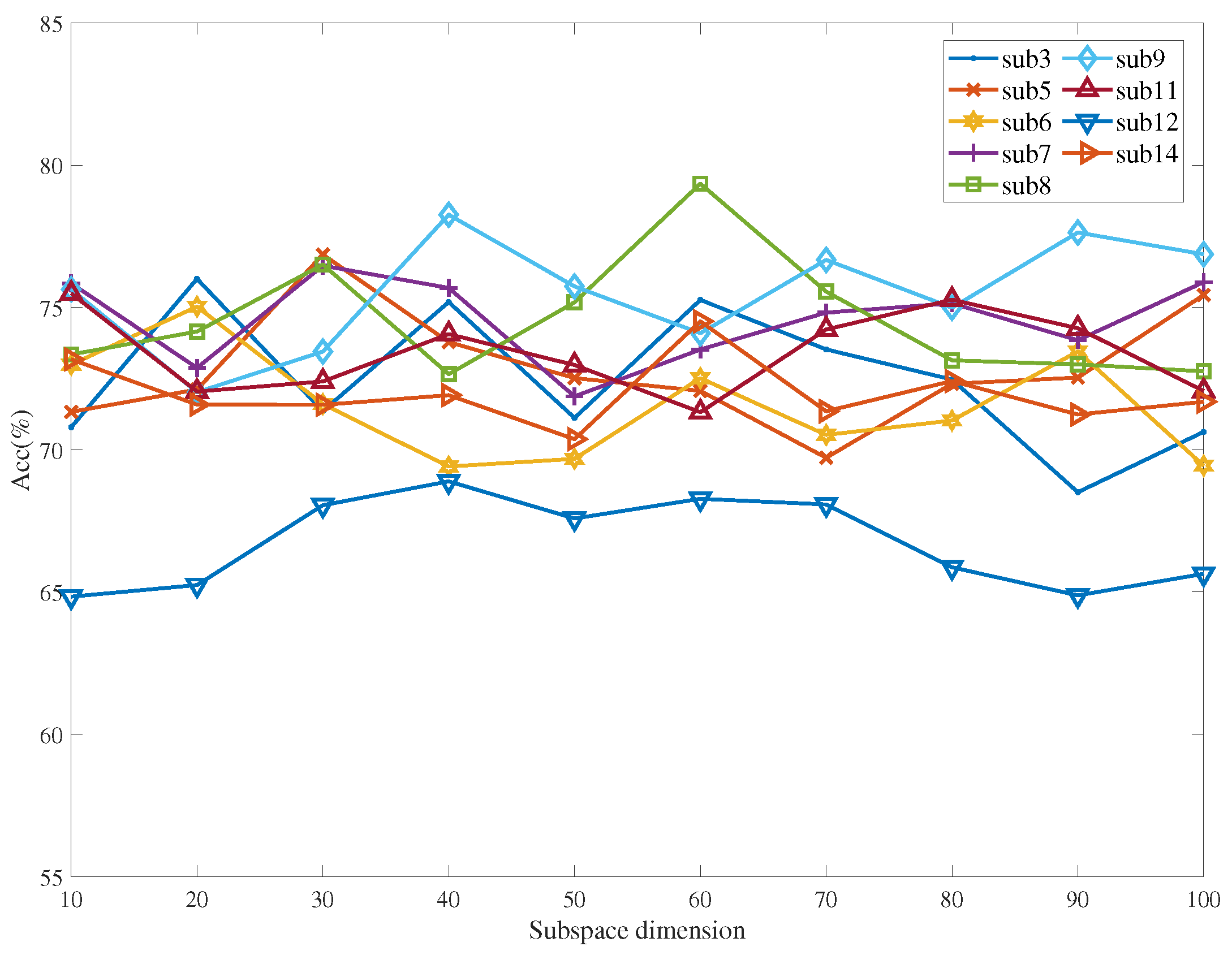
3.4. Subspace Analysis and Mining
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beldoch, M. Sensitivity to expression of emotional meaning in three modes of communication. In The Communication of Emotional Meaning; McGraw-Hill: New York, NY, USA, 1964; pp. 31–42. [Google Scholar]
- Salovey, P.; Mayer, J.D. Emotional intelligence. Imagin. Cogn. Personal. 1990, 9, 185–211. [Google Scholar] [CrossRef]
- Chen, L.; Wu, M.; Pedrycz, W.; Hirota, K. Emotion Recognition and Understanding for Emotional Human-Robot Interaction Systems; Springer: Cham, Switzerland, 2020; pp. 1–247. [Google Scholar]
- Papero, D.; Frost, R.; Havstad, L.; Noone, R. Natural systems thinking and the human family. Systems 2018, 6, 19. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Huan, W.; Hou, B.; Tian, Y.; Zhang, Z.; Song, A. Can emotion be transferred?—A review on transfer learning for EEG-Based Emotion Recognition. IEEE Trans. Cogn. Dev. Syst. 2021. [Google Scholar] [CrossRef]
- Nie, Z.; Wang, X.; Duan, R.; Lu, B. A survey of emotion recognition based on EEG. Chin. J. Biomed. Eng. 2012, 31, 12. [Google Scholar]
- Ko, B.C. A brief review of facial emotion recognition based on visual information. Sensors 2018, 18, 401. [Google Scholar] [CrossRef] [PubMed]
- Akçay, M.B.; Oğuz, K. Speech emotion recognition: Emotional models, databases, features, preprocessing methods, supporting modalities, and classifiers. Speech Commun. 2020, 116, 56–76. [Google Scholar] [CrossRef]
- Alswaidan, N.; Menai, M.E.B. A survey of state-of-the-art approaches for emotion recognition in text. Knowl. Inf. Syst. 2020, 62, 2937–2987. [Google Scholar] [CrossRef]
- Khare, S.K.; Bajaj, V.; Sinha, G.R. Adaptive tunable Q wavelet transform-based emotion identification. IEEE Trans. Instrum. Meas. 2020, 69, 9609–9617. [Google Scholar] [CrossRef]
- Becker, H.; Fleureau, J.; Guillotel, P.; Wendling, F.; Merlet, I.; Albera, L. Emotion recognition based on high-resolution EEG recordings and reconstructed brain sources. IEEE Trans. Affect. Comput. 2020, 11, 244–257. [Google Scholar] [CrossRef]
- Wang, H.; Pei, Z.; Xu, L.; Xu, T.; Bezerianos, A.; Sun, Y.; Li, J. Performance enhancement of P300 detection by multiscale-CNN. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Hondrou, C.; Caridakis, G. Affective, natural interaction using EEG: Sensors, application and future directions. In Lecture Notes in Computer Science, Proceedings of the Artificial Intelligence: Theories and Applications—7th Hellenic Conference on AI (SETN 2012), Lamia, Greece, 28–31 May 2012; Maglogiannis, I., Plagianakos, V.P., Vlahavas, I.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7297, pp. 331–338. [Google Scholar] [CrossRef] [Green Version]
- Marei, A.; Yoon, S.A.; Yoo, J.U.; Richman, T.; Noushad, N.; Miller, K.; Shim, J. Designing feedback systems: Examining a feedback approach to facilitation in an online asynchronous professional development course for high school science teachers. Systems 2021, 9, 10. [Google Scholar] [CrossRef]
- Mammone, N.; De Salvo, S.; Bonanno, L.; Ieracitano, C.; Marino, S.; Marra, A.; Bramanti, A.; Morabito, F.C. Brain network analysis of compressive sensed high-density EEG signals in AD and MCI subjects. IEEE Trans. Ind. Inform. 2018, 15, 527–536. [Google Scholar] [CrossRef]
- Murugappan, M.; Rizon, M.; Nagarajan, R.; Yaacob, S.; Hazry, D.; Zunaidi, I. Time-frequency analysis of EEG signals for human emotion detection. In Proceedings of the 4th Kuala Lumpur International Conference on Biomedical Engineering 2008, Kuala Lumpur, Malaysia, 25–28 June 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 262–265. [Google Scholar]
- Thejaswini, S.; Ravi Kumar, K.M.; Aditya Nataraj, J.L. Analysis of EEG based emotion detection of DEAP and SEED-IV databases using SVM. SSRN Electron. J. 2019, 8, 576–581. [Google Scholar]
- Li, X.; Song, D.; Zhang, P.; Zhang, Y.; Hou, Y.; Hu, B. Exploring EEG features in cross-subject emotion recognition. Front. Neurosci. 2018, 12, 162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ali Olamat, P.O.; Atasever, S. Deep learning methods for multi-channel EEG-based emotion recognition. Int. J. Neural Syst. 2022, 32, 2250021. [Google Scholar] [CrossRef]
- Lew, W.C.L.; Wang, D.; Shylouskaya, K.; Zhang, Z.; Lim, J.H.; Ang, K.K.; Tan, A.H. EEG-based emotion recognition using spatial-temporal representation via Bi-GRU. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 116–119. [Google Scholar]
- Gong, S.; Xing, K.; Cichocki, A.; Li, J. Deep learning in EEG: Advance of the last ten-year critical period. IEEE Trans. Cogn. Dev. Syst. 2022, 14, 348–365. [Google Scholar] [CrossRef]
- Li, J.; Qiu, S.; Du, C.; Wang, Y.; He, H. Domain adaptation for EEG emotion recognition based on latent representation similarity. IEEE Trans. Cogn. Dev. Syst. 2020, 12, 344–353. [Google Scholar] [CrossRef]
- Gong, B.; Shi, Y.; Sha, F.; Grauman, K. Geodesic flow kernel for unsupervised domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2066–2073. [Google Scholar]
- Yan, K.; Kou, L.; Zhang, D. Learning domain-invariant subspace using domain features and independence maximization. IEEE Trans. Cybern. 2018, 48, 288–299. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Fu, B.; Li, F.; Shi, G.; Zheng, W. A novel transferability attention neural network model for EEG emotion recognition. Neurocomputing 2021, 447, 92–101. [Google Scholar] [CrossRef]
- Zheng, W.L.; Lu, B.L. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks. IEEE Trans. Auton. Ment. Dev. 2015, 7, 162–175. [Google Scholar] [CrossRef]
- Zheng, W.L.; Zhu, J.Y.; Lu, B.L. Identifying stable patterns over time for emotion recognition from EEG. IEEE Trans. Affect. Comput. 2017, 10, 417–429. [Google Scholar] [CrossRef] [Green Version]
- Quan, X.; Zeng, Z.; Jiang, J.; Zhang, Y.; Lu, B.; Wu, D. Physiological signals based affective computing: A systematic review. Acta Autom. Sin. 2021, 47, 1769–1784. (In Chinese) [Google Scholar]
- Suhaimi, N.S.; Mountstephens, J.; Teo, J. EEG-based emotion recognition: A state-of-the-art review of current trends and opportunities. Comput. Intell. Neurosci. 2020, 2020, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Lu, B.; Zhang, Y.; Zheng, W. A survey of affective brain-computer interface. Chin. J. Intell. Sci. Technol. 2021, 3, 36–48. (In Chinese) [Google Scholar]
- Niu, S.; Liu, Y.; Wang, J.; Song, H. A decade survey of transfer learning (2010–2020). IEEE Trans. Artif. Intell. 2020, 1, 151–166. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Zheng, W.L.; Lu, B.L. Personalizing EEG-based affective models with transfer learning. In Proceedings of the 25th International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 2732–2738. [Google Scholar]
- Zhou, R.; Zhang, Z.; Yang, X.; Fu, H.; Zhang, L.; Li, L.; Huang, G.; Dong, Y.; Li, F.; Liang, Z. A novel transfer learning framework with prototypical representation based pairwise learning for cross-subject cross-session EEG-based emotion recognition. arXiv 2022, arXiv:2202.06509. [Google Scholar]
- Bahador, N.; Kortelainen, J. Deep learning-based classification of multichannel bio-signals using directedness transfer learning. Biomed. Signal Process. Control 2022, 72, 103300. [Google Scholar] [CrossRef]
- Jayaram, V.; Alamgir, M.; Altun, Y.; Scholkopf, B.; Grosse-Wentrup, M. Transfer learning in brain-computer interfaces. IEEE Comput. Intell. Mag. 2016, 11, 20–31. [Google Scholar] [CrossRef] [Green Version]
- Ding, Z.; Li, S.; Shao, M.; Fu, Y. Graph adaptive knowledge transfer for unsupervised domain adaptation. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 37–52. [Google Scholar]
- Lan, Z.; Sourina, O.; Wang, L.; Scherer, R.; Müller-Putz, G.R. Domain adaptation techniques for EEG-based emotion recognition: A comparative study on two public datasets. IEEE Trans. Cogn. Dev. Syst. 2019, 11, 85–94. [Google Scholar] [CrossRef]
- Cui, J.; Jin, X.; Hu, H.; Zhu, L.; Ozawa, K.; Pan, G.; Kong, W. Dynamic Distribution Alignment with Dual-Subspace Mapping For Cross-Subject Driver Mental State Detection. IEEE Trans. Cogn. Dev. Syst. 2021. [Google Scholar] [CrossRef]
- Gretton, A.; Sriperumbudur, B.; Sejdinovic, D.; Strathmann, H.; Balakrishnan, S.; Pontil, M.; Fukumizu, K. Optimal kernel choice for large-scale two-sample tests. In Curran Associates, Incorporated, Proceedings of the 26th Annual Conference on Neural Information Processing Systems (NIPS 2012); Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates, Incorporated: Lake Tahoe, NV, USA, 2012; Volume 25, pp. 1205–1213. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Bartels, R.H.; Stewart, G.W. Solution of the matrix equation AX + XB = C [F4]. Commun. ACM 1972, 15, 820–826. [Google Scholar] [CrossRef]
- Peng, Y.; Zhu, X.; Nie, F.; Kong, W.; Ge, Y. Fuzzy graph clustering. Inf. Sci. 2021, 571, 38–49. [Google Scholar] [CrossRef]
- Zheng, W.L.; Liu, W.; Lu, Y.; Lu, B.L.; Cichocki, A. Emotionmeter: A multimodal framework for recognizing human emotions. IEEE Trans. Cybern. 2018, 49, 1110–1122. [Google Scholar] [CrossRef]
- Long, M.; Wang, J.; Ding, G.; Sun, J.; Yu, P.S. Transfer feature learning with joint distribution adaptation. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 2200–2207. [Google Scholar]
- Song, P.; Zheng, W. Feature selection based transfer subspace learning for speech emotion recognition. IEEE Trans. Affect. Comput. 2018, 11, 373–382. [Google Scholar] [CrossRef]
- Nie, F.; Wang, X.; Deng, C.; Huang, H. Learning a structured optimal bipartite graph for co-clustering. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4132–4141. [Google Scholar]
- Song, T.; Zheng, W.; Song, P.; Cui, Z. EEG Emotion Recognition Using Dynamical Graph Convolutional Neural Networks. IEEE Trans. Affect. Comput. 2020, 11, 532–541. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z. Machine Learning Beijing; Tsinghua University Press: Beijing, China, 2016; pp. 42–44. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Peng, Y.; Qin, F.; Kong, W.; Ge, Y.; Nie, F.; Cichocki, A. GFIL: A unified framework for the importance analysis of features, frequency bands and channels in EEG-based emotion recognition. IEEE Trans. Cogn. Dev. Syst. 2021. [Google Scholar] [CrossRef]
- Nie, F.; Huang, H.; Cai, X.; Ding, C. Efficient and robust feature selection via joint ℓ2,1-norms minimization. In Proceedings of the 23rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; Volume 2, pp. 1813–1821. [Google Scholar]



| Subject | JDA | GAKT | MIDA | FSTSL | SOBG | DGCNN | LRS | TSRBG |
|---|---|---|---|---|---|---|---|---|
| sub2 | 57.81 | 73.09 | 67.69 | 66.51 | 35.02 | 54.64 | 49.12 | 73.68 |
| sub3 | 64.75 | 62.63 | 58.40 | 59.93 | 63.69 | 57.46 | 39.25 | 67.33 |
| sub4 | 68.27 | 58.99 | 44.77 | 60.52 | 50.53 | 58.99 | 42.89 | 71.33 |
| sub5 | 48.53 | 39.72 | 46.53 | 56.99 | 48.53 | 49.12 | 32.67 | 73.44 |
| sub6 | 51.59 | 53.11 | 47.83 | 46.53 | 49.24 | 40.42 | 21.39 | 67.57 |
| sub7 | 70.15 | 58.87 | 54.99 | 54.76 | 44.54 | 48.18 | 42.66 | 75.32 |
| sub8 | 65.45 | 62.51 | 66.39 | 42.30 | 43.95 | 51.12 | 47.59 | 80.96 |
| sub9 | 64.86 | 63.69 | 53.35 | 61.69 | 45.95 | 62.98 | 43.24 | 74.74 |
| sub10 | 65.69 | 51.12 | 63.81 | 55.11 | 47.47 | 42.66 | 46.77 | 78.73 |
| sub11 | 51.94 | 62.16 | 59.34 | 47.83 | 47.24 | 51.00 | 42.42 | 73.80 |
| sub12 | 54.29 | 59.34 | 59.11 | 48.06 | 50.18 | 55.93 | 63.34 | 71.21 |
| sub13 | 62.98 | 64.28 | 50.65 | 54.05 | 52.64 | 52.29 | 33.49 | 68.51 |
| sub14 | 55.58 | 65.45 | 43.95 | 49.82 | 49.59 | 53.23 | 40.89 | 68.86 |
| sub15 | 69.10 | 52.41 | 46.65 | 57.58 | 33.73 | 53.82 | 33.73 | 74.15 |
| Avg. | 60.79 | 59.10 | 54.53 | 54.41 | 47.31 | 52.27 | 41.39 | 72.83 |
| Subject | JDA | GAKT | MIDA | FSTSL | SOBG | DGCNN | LRS | TSRBG |
|---|---|---|---|---|---|---|---|---|
| sub2 | 90.75 | 68.03 | 66.83 | 74.88 | 50.12 | 65.87 | 78.13 | 78.49 |
| sub3 | 69.59 | 61.54 | 69.23 | 68.99 | 78.73 | 68.99 | 80.41 | 81.25 |
| sub4 | 60.49 | 79.57 | 63.82 | 51.56 | 55.05 | 59.38 | 31.85 | 74.52 |
| sub5 | 58.89 | 63.22 | 71.03 | 67.55 | 48.32 | 56.13 | 55.05 | 74.04 |
| sub6 | 61.78 | 56.49 | 41.47 | 54.09 | 36.66 | 52.28 | 36.18 | 75.84 |
| sub7 | 64.54 | 68.87 | 69.59 | 77.28 | 42.91 | 64.54 | 52.04 | 78.13 |
| sub8 | 78.49 | 68.63 | 66.35 | 54.81 | 68.39 | 49.76 | 50.12 | 77.16 |
| sub9 | 59.13 | 54.33 | 60.46 | 41.83 | 61.42 | 54.81 | 37.02 | 76.92 |
| sub10 | 41.11 | 82.33 | 62.14 | 50.00 | 67.19 | 60.34 | 59.38 | 76.56 |
| sub11 | 63.58 | 72.00 | 51.58 | 60.82 | 32.81 | 53.00 | 42.91 | 74.28 |
| sub12 | 56.49 | 44.59 | 41.11 | 68.87 | 49.88 | 47.72 | 27.76 | 69.23 |
| sub13 | 62.98 | 64.90 | 53.37 | 60.34 | 32.81 | 49.16 | 58.41 | 71.75 |
| sub14 | 46.51 | 50.48 | 49.04 | 44.71 | 48.32 | 61.66 | 52.28 | 74.16 |
| sub15 | 77.76 | 88.82 | 55.53 | 84.01 | 61.18 | 60.46 | 57.57 | 88.58 |
| Avg. | 63.72 | 65.99 | 58.68 | 61.41 | 51.27 | 58.77 | 51.34 | 76.49 |
| Subject | JDA | GAKT | MIDA | FSTSL | SOBG | DGCNN | LRS | TSRBG |
|---|---|---|---|---|---|---|---|---|
| sub2 | 54.62 | 60.10 | 87.96 | 88.93 | 45.99 | 64.60 | 55.96 | 79.56 |
| sub3 | 64.11 | 65.57 | 76.76 | 70.07 | 42.09 | 49.51 | 49.27 | 72.26 |
| sub4 | 57.66 | 69.34 | 43.92 | 63.26 | 57.06 | 56.08 | 43.19 | 81.14 |
| sub5 | 63.75 | 67.64 | 74.33 | 61.19 | 39.54 | 46.35 | 39.05 | 79.68 |
| sub6 | 57.66 | 62.65 | 57.42 | 54.99 | 40.88 | 72.14 | 41.85 | 84.91 |
| sub7 | 66.99 | 79.93 | 47.49 | 72.63 | 55.60 | 59.49 | 18.86 | 77.86 |
| sub8 | 62.41 | 59.85 | 76.64 | 64.72 | 47.93 | 69.10 | 58.76 | 73.24 |
| sub9 | 75.18 | 50.24 | 50.97 | 47.20 | 51.82 | 50.61 | 37.35 | 73.11 |
| sub10 | 51.09 | 69.34 | 41.73 | 58.64 | 32.60 | 50.24 | 45.13 | 76.64 |
| sub11 | 57.06 | 81.75 | 54.14 | 56.08 | 40.63 | 61.92 | 58.76 | 75.79 |
| sub12 | 45.50 | 57.54 | 56.69 | 61.31 | 53.77 | 59.37 | 54.62 | 70.32 |
| sub13 | 55.72 | 61.44 | 46.59 | 46.72 | 42.34 | 50.00 | 42.70 | 76.28 |
| sub14 | 56.45 | 77.25 | 57.06 | 77.62 | 50.85 | 53.41 | 27.01 | 79.56 |
| sub15 | 70.32 | 85.28 | 52.19 | 62.04 | 56.45 | 54.01 | 23.60 | 84.67 |
| Avg. | 59.89 | 67.71 | 58.85 | 63.24 | 46.97 | 56.92 | 42.58 | 77.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Peng, Y. Transfer EEG Emotion Recognition by Combining Semi-Supervised Regression with Bipartite Graph Label Propagation. Systems 2022, 10, 111. https://doi.org/10.3390/systems10040111
Li W, Peng Y. Transfer EEG Emotion Recognition by Combining Semi-Supervised Regression with Bipartite Graph Label Propagation. Systems. 2022; 10(4):111. https://doi.org/10.3390/systems10040111
Chicago/Turabian StyleLi, Wenzheng, and Yong Peng. 2022. "Transfer EEG Emotion Recognition by Combining Semi-Supervised Regression with Bipartite Graph Label Propagation" Systems 10, no. 4: 111. https://doi.org/10.3390/systems10040111
APA StyleLi, W., & Peng, Y. (2022). Transfer EEG Emotion Recognition by Combining Semi-Supervised Regression with Bipartite Graph Label Propagation. Systems, 10(4), 111. https://doi.org/10.3390/systems10040111







