Bifactor Models for Predicting Criteria by General and Specific Factors: Problems of Nonidentifiability and Alternative Solutions
Abstract
:1. Introduction
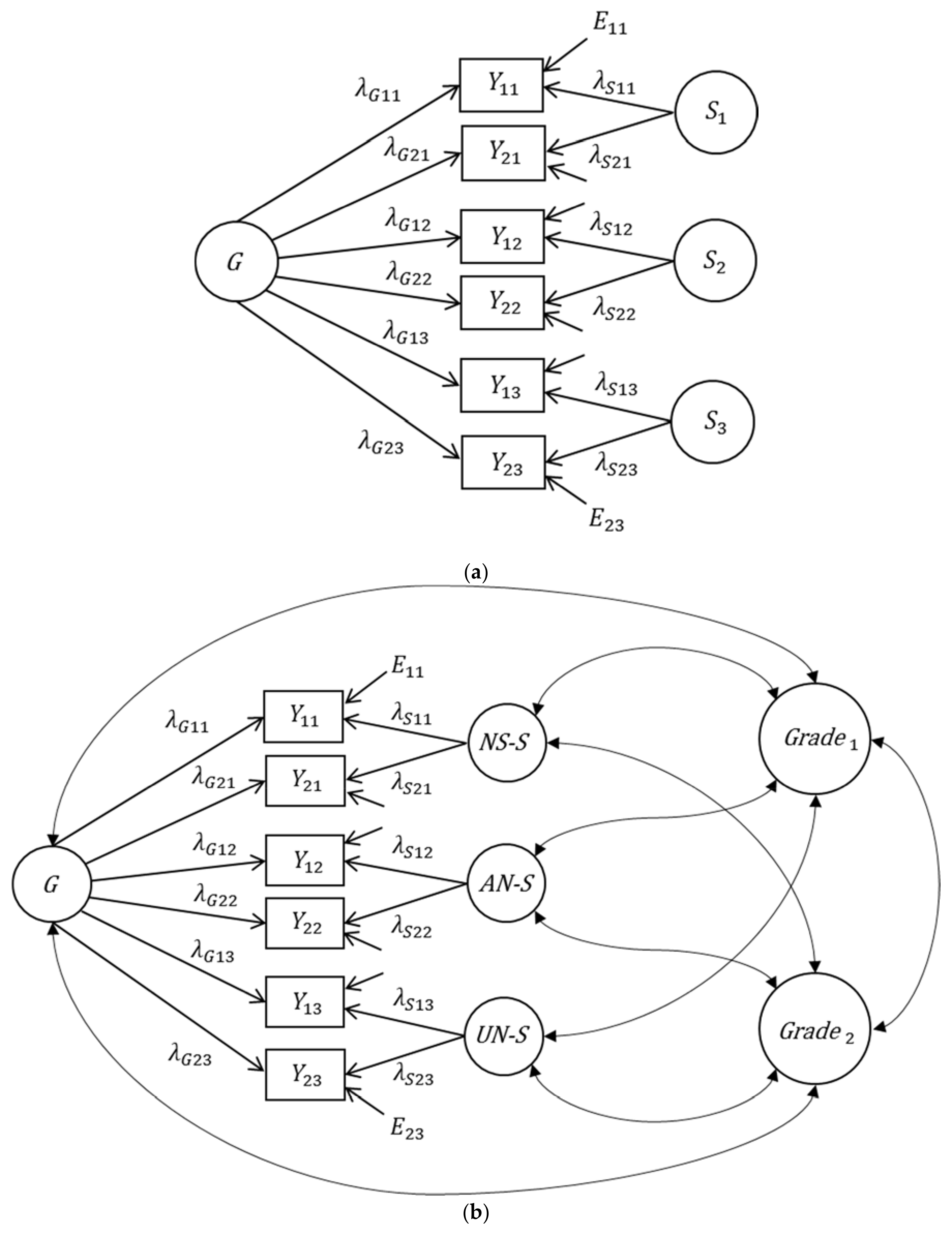
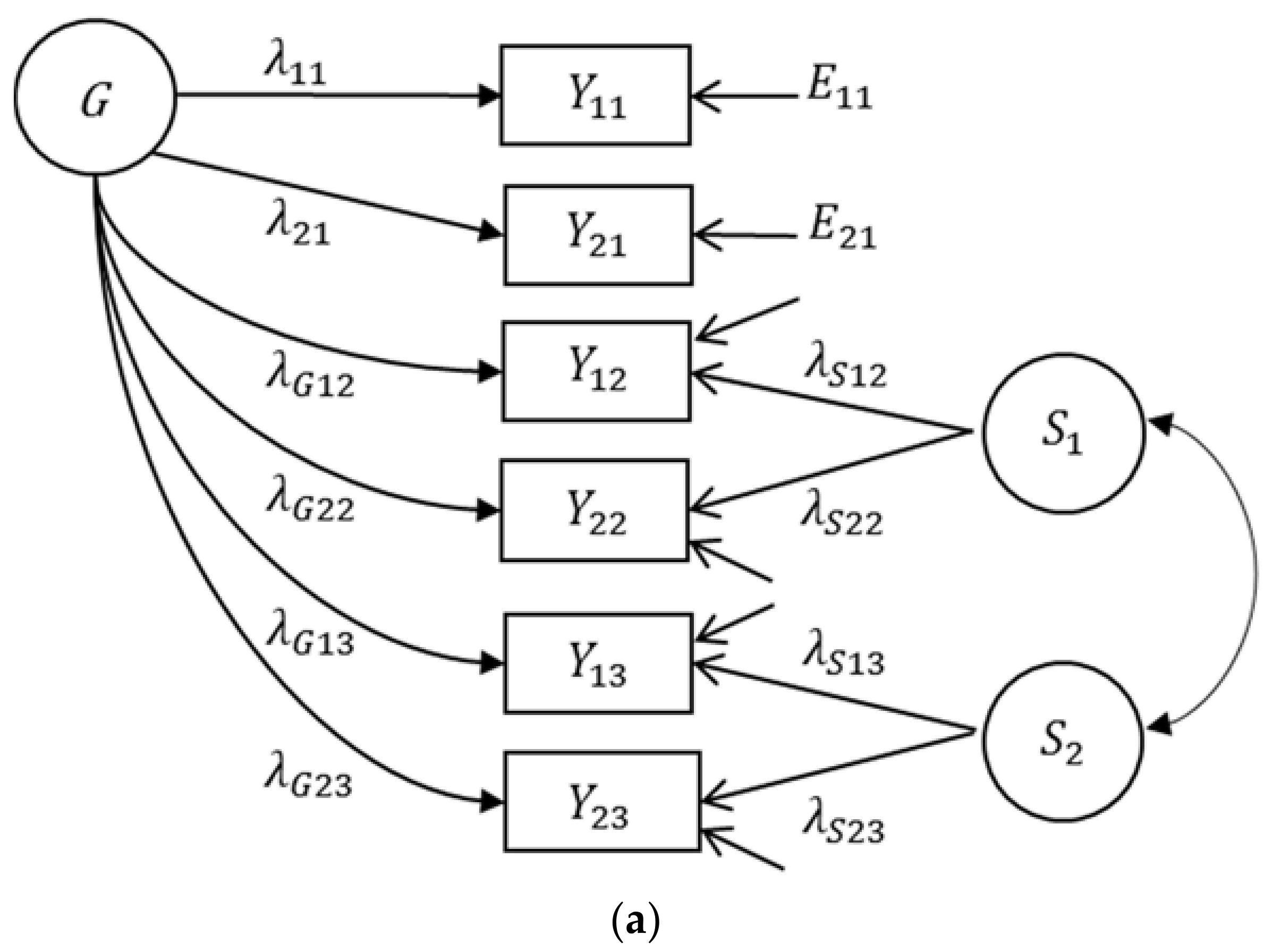
Bifactor Model
2. Description of the Empirical Study
2.1. Participants and Materials
2.2. Data Analysis
2.3. Application of the Bifactor Model
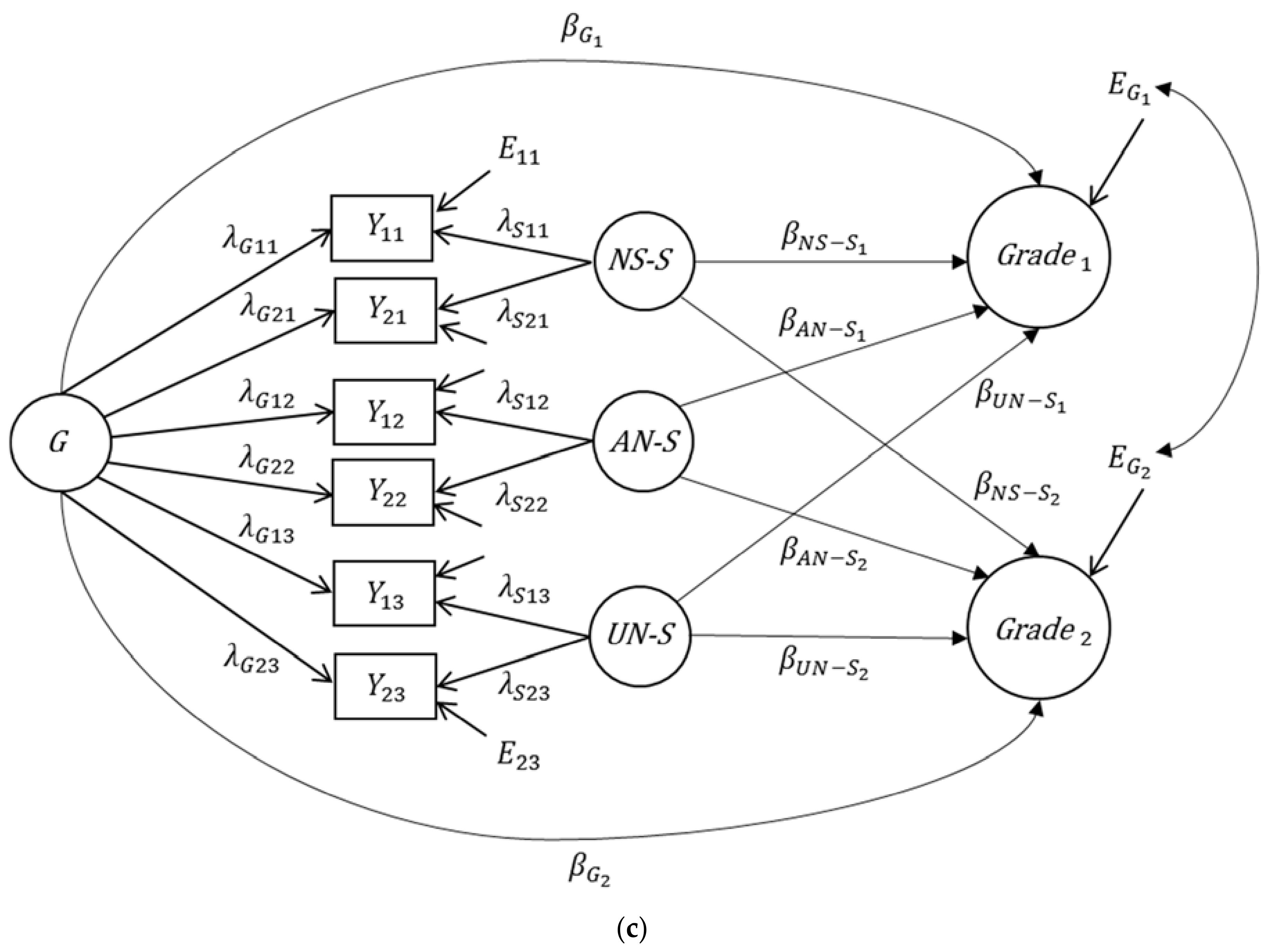
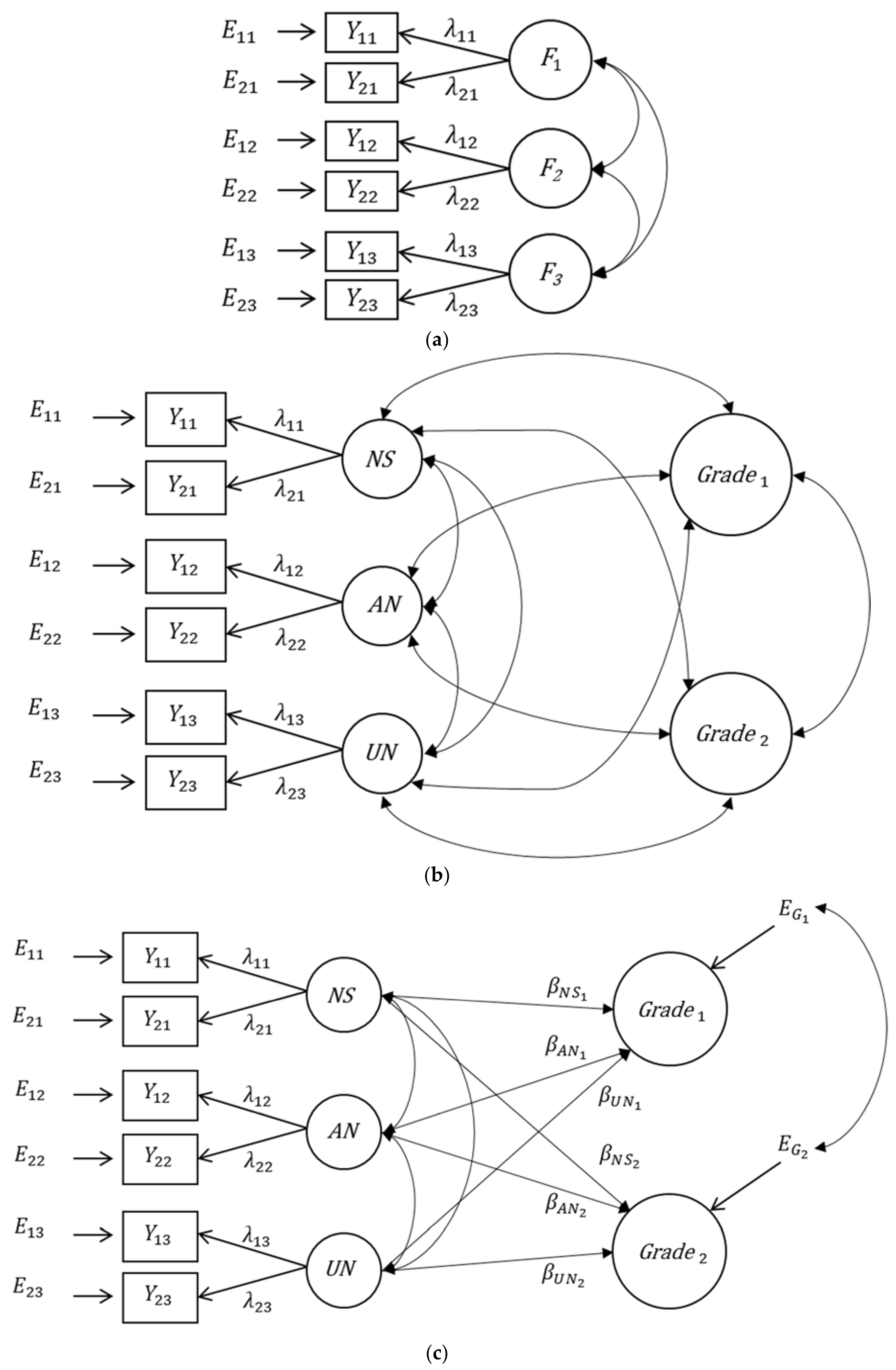
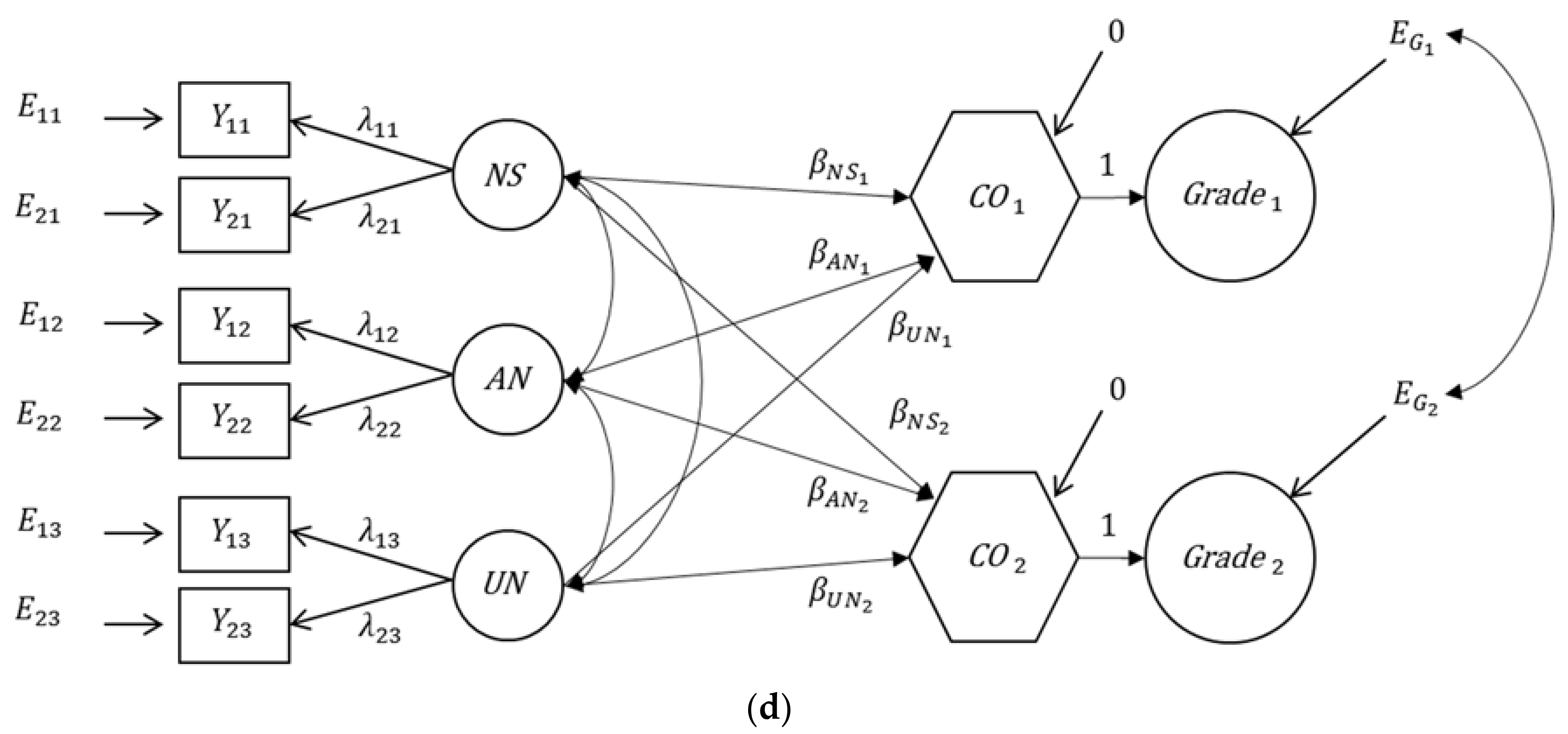
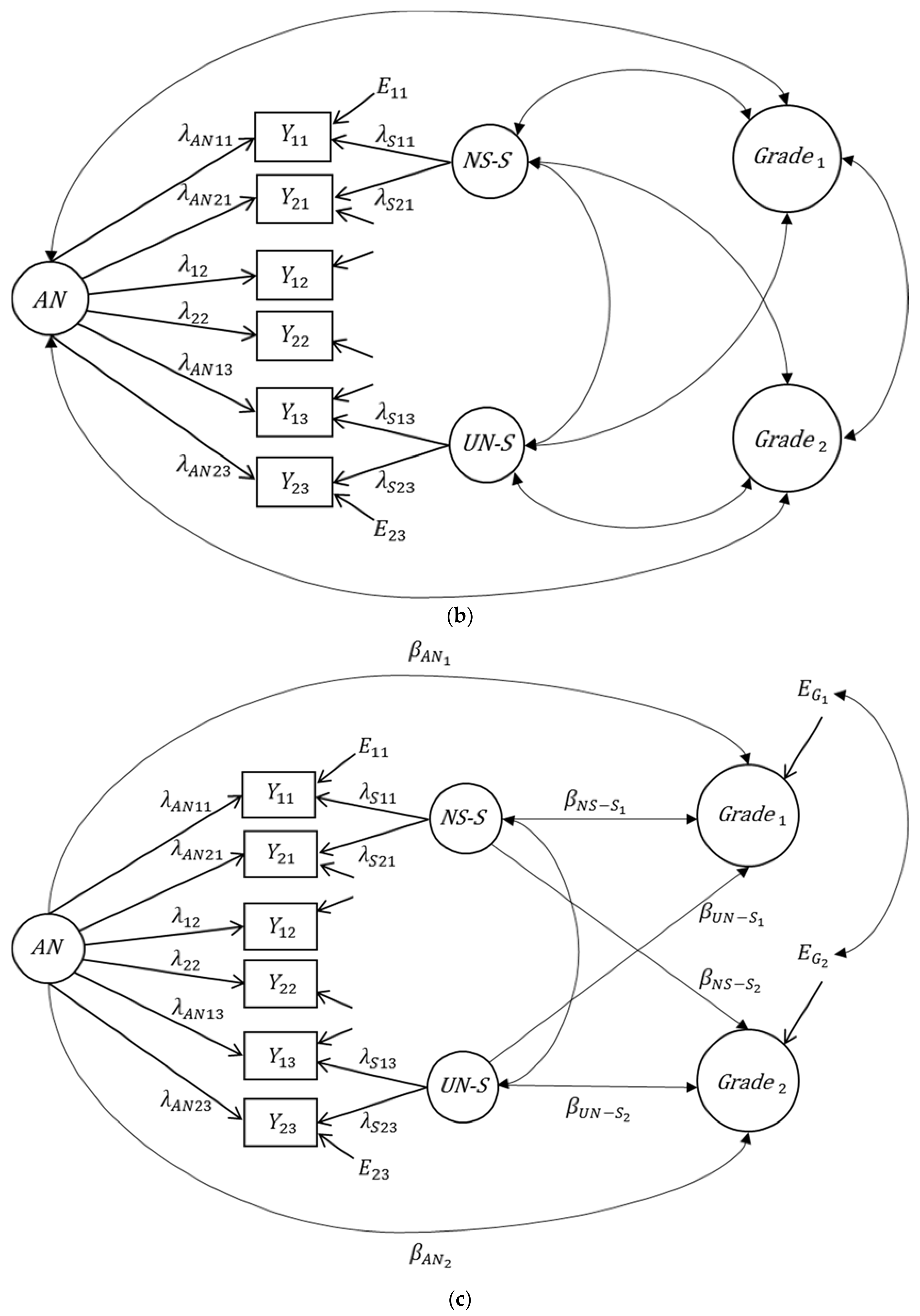
3. Alternatives to Extended Bifactor Models
3.1. Application of the Extended First-Order Factor Model
3.2. Application of the Bifactor(S-1) Model
4. Discussion
5. Conclusions and Recommendations
Author Contributions
Conflicts of Interest
Appendix A
References
- Spearman, C. General Intelligence objectively determined and measured. Am. J. Psychol. 1904, 15, 201–293. [Google Scholar] [CrossRef]
- Gustafsson, J.E.; Balke, G. General and specific abilities as predictors of school achievement. Multivar. Behav. Res. 1993, 28, 407–434. [Google Scholar] [CrossRef] [PubMed]
- Kuncel, N.R.; Hezlett, S.A.; Ones, D.S. Academic performance, career potential, creativity, and job performance: Can one construct predict them all? J. Pers. Soc. Psychol. 2004, 86, 148–161. [Google Scholar] [CrossRef] [PubMed]
- Kell, H.J.; Lang, J.W.B. Specific abilities in the workplace: More important than g? J. Intell. 1993, 5, 13. [Google Scholar] [CrossRef]
- Carretta, T.R.; Ree, M.J. General and specific cognitive and psychomotor abilities in personnel selection: The prediction of training and job performance. Int. J. Sel. Assess. 2000, 8, 227–236. [Google Scholar] [CrossRef]
- Ree, M.J.; Earles, J.A.; Teachout, M.S. Predicting job performance: Not much more than g. J. Appl. Psychol. 1994, 79, 518–524. [Google Scholar] [CrossRef]
- Ree, J.M.; Carretta, T.R. G2K. Hum. Perform. 2002, 15, 3–23. [Google Scholar]
- Murphy, K. What can we learn from “Not much more than g”? J. Intell. 2017, 5, 8–14. [Google Scholar] [CrossRef]
- Lang, J.W.B.; Kersting, M.; Hülsheger, U.R.; Lang, J. General mental ability, narrower cognitive abilities, and job performance: The perspective of the nested-factors model of cognitive abilities. Pers. Psychol. 2010, 63, 595–640. [Google Scholar] [CrossRef]
- Rindermann, H.; Neubauer, A.C. Processing speed, intelligence, creativity, and school performance: Testing of causal hypotheses using structural equation models. Intelligence 2004, 32, 573–589. [Google Scholar] [CrossRef]
- Goertz, W.; Hülsheger, U.R.; Maier, G.W. The validity of specific cognitive abilities for the prediction of training success in Germany: A meta-analysis. J. Pers. Psychol. 2014, 13, 123. [Google Scholar] [CrossRef]
- Ziegler, M.; Dietl, E.; Danay, E.; Vogel, M.; Bühner, M. Predicting training success with general mental ability, specific ability tests, and (un)structured interviews: A meta-analysis with unique samples. Int. J. Sel. Assess. 2011, 19, 170–182. [Google Scholar] [CrossRef]
- Holzinger, K.; Swineford, F. The bi-factor method. Psychometrika 1937, 2, 41–54. [Google Scholar] [CrossRef]
- Beaujean, A.A.; Parkin, J.; Parker, S. Comparing Cattewll-Horn-Carroll factor models: Differences between bifactor and higher order factor models in predicting language achievement. Psychol. Assess. 2014, 26, 789–805. [Google Scholar] [CrossRef] [PubMed]
- Benson, N.F.; Kranzler, J.H.; Floyd, R.G. Examining the integrity of measurement of cognitive abilities in the prediction of achievement: Comparisons and contrasts across variables from higher-order and bifactor models. J. Sch. Psychol. 2016, 58, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Betts, J.; Pickard, M.; Heistad, D. Investigating early literacy and numeracy: Exploring the utility of the bifactor model. Sch. Psychol. Q. 2011, 26, 97–107. [Google Scholar] [CrossRef]
- Brunner, M. No g in education? Learn. Individ. Differ. 2008, 18, 152–165. [Google Scholar] [CrossRef]
- Christensen, A.P.; Silvia, P.J.; Nusbaum, E.C.; Beaty, R.E. Clever people: Intelligence and humor production ability. Psychol. Aesthet. Creat. Arts 2018, 12, 136–143. [Google Scholar] [CrossRef]
- Immekus, J.C.; Atitya, B. The predictive validity of interim assessment scores based on the full-information bifactor model for the prediction of end-of-grade test performance. Educ. Assess. 2016, 21, 176–195. [Google Scholar] [CrossRef]
- McAbee, S.T.; Oswald, F.L.; Connelly, B.S. Bifactor models of personality and college student performance: A broad versus narrow view. Eur. J. Pers. 2014, 28, 604–619. [Google Scholar] [CrossRef]
- Saß, S.; Kampa, N.; Köller, O. The interplay of g and mathematical abilities in large-scale assessments across grades. Intelligence 2017, 63, 33–44. [Google Scholar] [CrossRef]
- Schult, J.; Sparfeldt, J.R. Do non-g factors of cognitive ability tests align with specific academic achievements? A combined bifactor modeling approach. Intelligence 2016, 59, 96–102. [Google Scholar] [CrossRef]
- Silvia, P.J.; Beaty, R.E.; Nusbaum, E.C. Verbal fluency and creativity: General and specific contributions of broad retrieval ability (Gr) factors to divergent thinking. Intelligence 2013, 41, 328–340. [Google Scholar] [CrossRef]
- Silvia, P.J.; Thomas, K.S.; Nusbaum, E.C.; Beaty, R.E.; Hodges, D.A. How does music training predict cognitive abilities? A bifactor approach to musical expertise and intelligence. Psychol. Aesthet. Creat. Arts 2016, 10, 184–190. [Google Scholar] [CrossRef]
- Gunnell, K.E.; Gaudreau, P. Testing a bi-factor model to disentangle general and specific factors of motivation in self-determination theory. Pers. Individ. Differ. 2015, 81, 35–40. [Google Scholar] [CrossRef]
- Stefansson, K.K.; Gestsdottir, S.; Geldhof, G.J.; Skulason, S.; Lerner, R.M. A bifactor model of school engagement: Assessing general and specific aspects of behavioral, emotional and cognitive engagement among adolescents. Int. J. Behav. Dev. 2016, 40, 471–480. [Google Scholar] [CrossRef]
- Wang, M.-T.; Fredericks, J.A.; Ye, F.; Hofkens, T.L.; Schall Linn, J. The math and science engagement scales: Scale development, validation, and psychometric properties. Learn. Instr. 2016, 43, 16–26. [Google Scholar] [CrossRef]
- Byllesby, B.M.; Elhai, J.D.; Tamburrino, M.; Fine, T.H.; Cohen, C.; Sampson, L.; Shirley, E.; Chan, P.K.; Liberzon IGalea, S.; Calabrese, J.R. General distress is more important than PTSD’s cognition and mood alterations factor in accounting for PTSD and depression’s comorbidity. J. Affect. Disord. 2017, 211, 118–123. [Google Scholar] [CrossRef] [PubMed]
- Ogg, J.A.; Bateman, L.; Dedrick, R.F.; Suldo, S.M. The relationship between life satisfaction and ADHD symptoms in middle school students: Using a bifactor model. J. Atten. Disord. 2016, 20, 390–399. [Google Scholar] [CrossRef] [PubMed]
- Subica, A.M.; Allen, J.G.; Frueh, B.C.; Elhai, J.D.; Fowler, C.J. Disentangling depression and anxiety in relation to neuroticism, extraversion, suicide, and self-harm among adult psychiatric inpatients with serious mental illness. Br. J. Clin. Psychol. 2015, 55, 349–370. [Google Scholar] [CrossRef] [PubMed]
- Furtner, M.R.; Rauthmann, J.F.; Sachse, P. Unique self-leadership: A bifactor model approach. Leadership 2015, 11, 105–125. [Google Scholar] [CrossRef]
- Chen, F.F.; Hayes, A.; Carver, C.S.; Laurenceau, J.P.; Zhang, Z. Modeling general and specific variance in multifaceted constructs: A comparison of the bifactor model to other approaches. J. Pers. 2012, 80, 219–251. [Google Scholar] [CrossRef] [PubMed]
- Debusscher, J.; Hofmans, J.; De Fruyt, F. The multiple face(t)s of state conscientiousness: Predicting task performance and organizational citizenship behavior. J. Res. Pers. 2017, 69, 78–85. [Google Scholar] [CrossRef]
- Chiu, W.; Won, D. Relationship between sport website quality and consumption intentions: Application of a bifactor model. Psychol. Rep. 2016, 118, 90–106. [Google Scholar] [CrossRef] [PubMed]
- Eid, M.; Geiser, C.; Koch, T.; Heene, M. Anomalous results in g-factor models: Explanations and alternatives. Psychol. Methods 2017, 22, 541–562. [Google Scholar] [CrossRef] [PubMed]
- Brunner, M.; Nagy, G.; Wilhelm, O. A tutorial on hierarchically structured constructs. J. Pers. 2012, 80, 796–846. [Google Scholar] [CrossRef] [PubMed]
- Reise, S.P. The rediscovery of the bifactor measurement models. Multivar. Behav. Res. 2012, 47, 667–696. [Google Scholar] [CrossRef] [PubMed]
- Kell, H.J.; Lang, J.W.B. The great debate: General abilitiy and specific abilities in the prediction of important outcomes. J. Intell. 2018, 6, 24. [Google Scholar]
- Kersting, M.; Althoff, K.; Jäger, A.O. WIT-2. Der Wilde-Intelligenztest. Verfahrenshinweise; Hogrefe: Göttingen, Germany, 2008. [Google Scholar]
- Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 8th ed.; Muthén & Muthén: Los Angeles, CA, USA, 1998. [Google Scholar]
- Roth, B.; Becker, N.; Romeyke, S.; Schäfer, S.; Domnick, F.; Spinath, F.M. Intelligence and school grades: A meta-analysis. Intelligence 2015, 53, 118–137. [Google Scholar] [CrossRef]
- Bollen, K.A.; Bauldry, S. Three Cs in measurement models: Causal indicators, composite indicators, and covariates. Psychol. Methods 2011, 16, 265–284. [Google Scholar] [CrossRef] [PubMed]
- Grace, J.B.; Bollen, K.A. Representing general theoretical concepts in structural equation models: The role of composite variables. Environ. Ecol. Stat. 2008, 15, 191–213. [Google Scholar] [CrossRef]
- Cronbach, L.J. Essentials of Psychological Testing, 3rd ed.; Harper & Row: New York, NY, USA, 1970. [Google Scholar]
- Kane, M.T. Validating the interpretations and uses of test scores. J. Educ. Meas. 2013, 50, 1–73. [Google Scholar] [CrossRef]
- Messick, S. Validity. In Educational Measurement, 3rd ed.; Linn, R.L., Ed.; Macmillan: New York, NY, USA, 1989; pp. 13–103. [Google Scholar]
- Newton, P.; Shaw, S. Validity in Educational and Psychological Assessment; Sage: Thousand Oaks, CA, USA, 2014. [Google Scholar]
- Geiser, C.; Eid, M.; Nussbeck, F.W. On the meaning of the latent variables in the CT-C(M–1) model: A comment on Maydeu-Olivares & Coffman (2006). Psychol. Methods 2008, 13, 49–57. [Google Scholar] [PubMed]
- Holzinger, K.J.; Swineford, F. The relationship of two bi-factors to achievement in geometry and other subjects. J. Educ. Psychol. 1946, 27, 257–265. [Google Scholar] [CrossRef]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Test; University of Chicago Press: Chicago, IL, USA, 1980. [Google Scholar]
- Baumert, J.; Brunner, M.; Lüdtke, O.; Trautwein, U. Was messen internationale Schulleistungsstudien?—Resultate kumulativer Wissenserwerbsprozesse [What are international school achievement studies measuring? Results of cumulative acquisition of knowledge processes]. Psychol. Rundsch. 2007, 58, 118–145. [Google Scholar] [CrossRef]
- Johnson, W.; Bouchard, T.J., Jr.; Krueger, R.F.; McGue, M.; Gottesman, I.I. Just one g: Consistent results from three test batteries. Intelligence 2004, 32, 95–107. [Google Scholar] [CrossRef]
- Johnson, W.; Te Nijenhuis, J.; Bouchard, T.J., Jr. Still just 1 g: Consistent results from five test batteries. Intelligence 2008, 36, 81–95. [Google Scholar] [CrossRef]
- Steyer, R.; Mayer, A.; Geiser, C.; Cole, D.A. A theory of states and traits: Revised. Annu. Rev. Clin. Psychol. 2015, 11, 71–98. [Google Scholar] [CrossRef] [PubMed]
| 1 | For reasons of parsimony, we present standard errors and significance tests only for unstandardized solutions (across all analyses included in this paper). The corresponding information for the standardized solutions leads to the same conclusions. |
| 2 | From a historical point of view this early paper is also interesting for the debate on the role of general and specific factors. It showed that achievements in school subjects that do not belong to the science or language spectrum such as shops and crafts as well as drawing were more strongly correlated with the specific spatial ability factor (r = 0.461 and r = 0.692) than with the general factor (r = 0.219 and r = 0.412), whereas the g factor was more strongly correlated with all other school domains (between r = 0.374 and r = 0.586) than the specific factor (between r = −0.057 and r = 0.257). |
| NS1 | NS2 | AN1 | AN2 | UN1 | UN2 | Math | Eng | |
|---|---|---|---|---|---|---|---|---|
| NS1 | 4.456 | |||||||
| NS2 | 0.787 | 4.487 | ||||||
| AN1 | 0.348 | 0.297 | 4.496 | |||||
| AN2 | 0.376 | 0.347 | 0.687 | 4.045 | ||||
| UN1 | 0.383 | 0.378 | 0.295 | 0.366 | 5.168 | |||
| UN2 | 0.282 | 0.319 | 0.224 | 0.239 | 0.688 | 5.539 | ||
| Math | 0.349 | 0.350 | 0.289 | 0.378 | 0.302 | 0.275 | ||
| Eng | 0.225 | 0.205 | 0.263 | 0.241 | 0.135 | 0.097 | 0.469 | |
| Means | 4.438 | 3.817 | 4.196 | 4.018 | 4.900 | 4.411 | ||
| Proportions of the grades | 1: 0.123 2: 0.311 3: 0.297 4: 0.174 5: 0.096 | 1: 0.059 2: 0.393 3: 0.338 4: 0.174 5: 0.037 |
| G-Factor Loadings | S-Factor Loadings | Residual Variances | Rel | Covariances | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| G | NS-S | AN-S | UN-S | Math | Eng | ||||||
| NS1 | 1 0.651 | 1 0.615 | 0.882 (0.176) 0.198 | 0.802 | G | 1.887 (0.481) | 0 | 0 | 0 | 0.286 | 0.150 |
| NS2 | 0.971 (0.098) 0.630 | 1 0.613 | 1.022 (0.199) 0.228 | 0.772 | NS-S | 0 | 1.687 (0.331) | 0 | 0 | 0.272 | 0.194 |
| AN1 | 0.759 (0.161) 0.492 | 1 0.620 | 1.681 (0.255) 0.374 | 0.626 | AN-S | 0 | 0 | 1.726 (0.316) | 0 | 0.283 | 0.270 |
| AN2 | 0.838 (0.162) 0.573 | 1 0.653 | 0.993 (0.217) 0.245 | 0.755 | UN-S | 0 | 0 | 0 | 2.207 (0.441) | 0.212 | 0.058 |
| UN1 | 1.000 (0.199) 0.604 | 1 0.653 | 1.074 (0.215) 0.208 | 0.792 | Math | 0.393 (0.456) | 0.353 (0.445) | 0.371 (0.353) | 0.315 (0.428) | ||
| UN2 | 0.781 (0.198) 0.456 | 1 0.631 | 2.181 (0.334) 0.394 | 0.606 | Eng | 0.206 (0.470) | 0.252 (0.475) | 0.355 (0.384) | 0.086 (0.460) | 0.469 (0.055) | |
| Mathematics (R2 = 0.284) | English (R2 = 0.113) | |||
|---|---|---|---|---|
| b | bs | B | bs | |
| G | 0.205 (0.234) | 0.282 | 0.115 (0.246) | 0.158 |
| NS-S | 0.213 (0.264) | 0.276 | 0.143 (0.283) | 0.186 |
| AN-S | 0.218 (0.207) | 0.286 | 0.200 (0.223) | 0.264 |
| UN-S | 0.145 (0.198) | 0.216 | 0.035 (0.208) | 0.051 |
| Factor Loadings | Residual Variances | Rel | Covariances | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NS | AN | UN | Math | Eng | |||||
| NS1 | 1 0.889 | 0.938 (0.200) 0.211 | 0.789 | NS | 3.519 (0.425) | 0.464 | 0.461 | 0.394 | 0.242 |
| NS2 | 1 0.886 | 0.967 (0.197) 0.215 | 0.785 | AN | 1.490 (0.274) | 2.927 (0.394) | 0.408 | 0.400 | 0.304 |
| AN1 | 1 0.807 | 1.569 (0.290) 0.349 | 0.651 | UN | 1.661 (0.302) | 1.338 (0.277) | 3.680 (0.493) | 0.349 | 0.142 |
| AN2 | 1 0.851 | 1.118 (0.257) 0.276 | 0.724 | Math | 0.740 (0.127) | 0.685 (0.126) | 0.669 (0.134) | 0.469 | |
| UN1 | 1 0.844 | 1.487 (0.365) 0.288 | 0.712 | Eng | 0.455 (0.136) | 0.520 (0.128) | 0.272 (0.133) | 0.469 | |
| UN2 | 1 0.815 | 1.859 (0.390) 0.336 | 0.664 | ||||||
| Mathematics (R2 = 0.233) | English (R2 = 0.106) | |||
|---|---|---|---|---|
| b | bs | b | bs | |
| NS | 0.113 ** (0.039) | 0.213 | 0.073 (0.046) | 0.137 |
| AN | 0.140 ** (0.046) | 0.239 | 0.146 ** (0.050) | 0.250 |
| UN | 0.080 * (0.037) | 0.153 | −0.012 (0.041) | −0.023 |
| G-Factor Loadings | S-Factor Loadings | Residual Variances | Rel | Covariances | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NS-S | AN | UN-S | Math | Eng | ||||||
| NS1 | 0.509 (0.083) 0.412 | 1 0.787 | 0.938 (0.200) 0.211 | 0.789 | NS-S | 2.760 (0.333) | 0 | 0.337 | 0.235 | 0.114 |
| NS2 | 0.509 (0.083) 0.411 | 1 0.784 | 0.968 (0.197) 0.216 | 0.784 | AN | 0 | 2.928 (0.394) | 0 | 0.400 | 0.304 |
| AN1 | 1 0.807 | 1.568 (0.290) 0.349 | 0.651 | UN-S | 0.980 (0.244) | 0 | 3.069 (0.442) | 0.203 | 0.020 | |
| AN2 | 1 0.851 | 1.117 (0.257) 0.276 | 0.724 | Math | 0.391 (0.110) | 0.685 (0.126) | 0.356 (0.124) | |||
| UN1 | 0.457 (0.084) 0.344 | 1 0.771 | 1.487 (0.365) 0.288 | 0.712 | Eng | 0.190 (0.121) | 0.520 (0.128) | 0.035 (0.123) | 0.469 (0.055) | |
| UN2 | 0.781 (0.084) 0.332 | 1 0.744 | 1.858 (0.390) 0.336 | 0.664 | ||||||
| Mathematics (R2 = 0.233) | English (R2 = 0.106) | |||
|---|---|---|---|---|
| b | bs | b | bs | |
| AN | 0.234 ** (0.038) | 0.400 | 0.178 ** (0.040) | 0.304 |
| NS-S | 0.113 ** (0.046) | 0.188 | 0.073 (0.046) | 0.122 |
| UN-S | 0.080 * (0.037) | 0.140 | −0.012 (0.041) | −0.021 |
| Mathematics (R2 = 0.233) | English (R2 = 0.106) | |||
|---|---|---|---|---|
| b | bs | b | bs | |
| NS | 0.210 ** (0.031) | 0.394 | 0.129 ** (0.037) | 0.242 |
| AN-S | 0.140 ** (0.046) | 0.212 | 0.146 ** (0.050) | 0.221 |
| UN-S | 0.080 * (0.037) | 0.136 | −0.012 (0.041) | −0.021 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eid, M.; Krumm, S.; Koch, T.; Schulze, J. Bifactor Models for Predicting Criteria by General and Specific Factors: Problems of Nonidentifiability and Alternative Solutions. J. Intell. 2018, 6, 42. https://doi.org/10.3390/jintelligence6030042
Eid M, Krumm S, Koch T, Schulze J. Bifactor Models for Predicting Criteria by General and Specific Factors: Problems of Nonidentifiability and Alternative Solutions. Journal of Intelligence. 2018; 6(3):42. https://doi.org/10.3390/jintelligence6030042
Chicago/Turabian StyleEid, Michael, Stefan Krumm, Tobias Koch, and Julian Schulze. 2018. "Bifactor Models for Predicting Criteria by General and Specific Factors: Problems of Nonidentifiability and Alternative Solutions" Journal of Intelligence 6, no. 3: 42. https://doi.org/10.3390/jintelligence6030042
APA StyleEid, M., Krumm, S., Koch, T., & Schulze, J. (2018). Bifactor Models for Predicting Criteria by General and Specific Factors: Problems of Nonidentifiability and Alternative Solutions. Journal of Intelligence, 6(3), 42. https://doi.org/10.3390/jintelligence6030042




