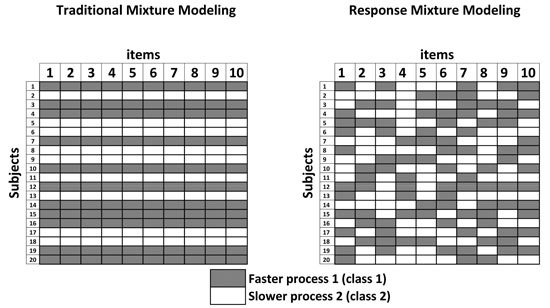
Response Mixture Modeling of Intraindividual Differences in Responses and Response Times to the Hungarian WISC-IV Block Design Test
Abstract
:1. Introduction
2. Methods
2.1. Item Response Theory Modeling of Response Times
2.2. An Extension to Model Intraindividual Differences
Special Cases
2.3. Conditional Dependence
2.4. Estimation
3. Simulated Data Application
3.1. Data Generation
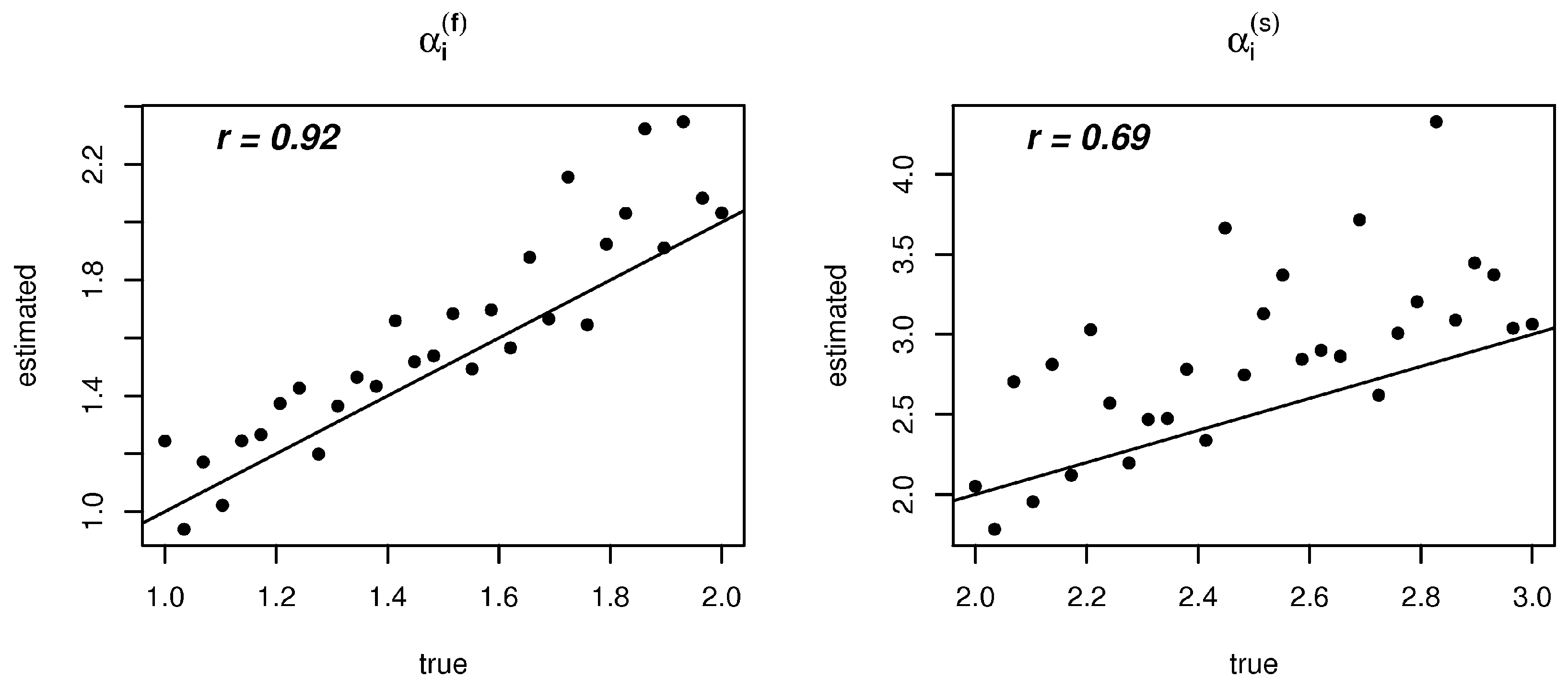
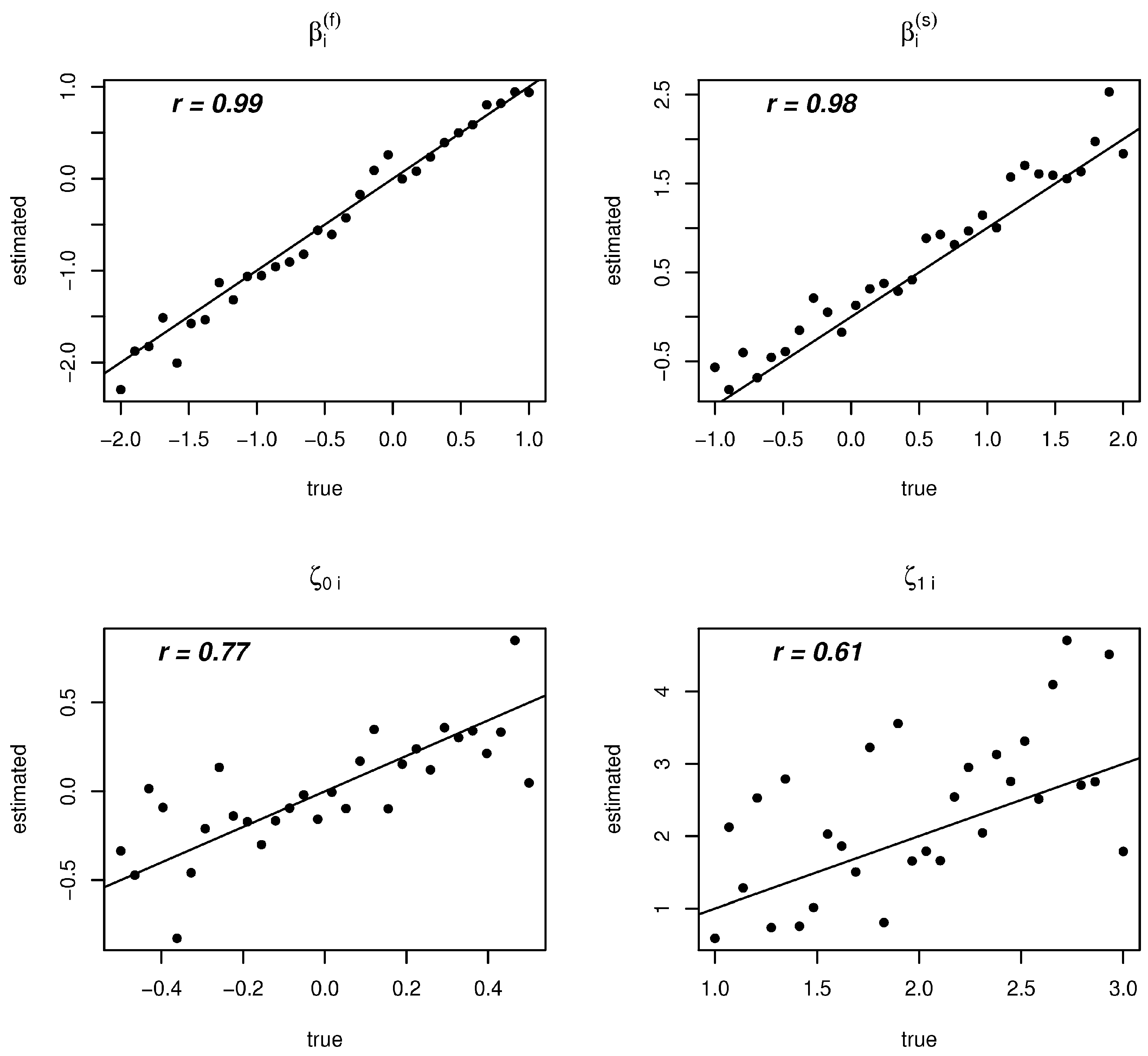
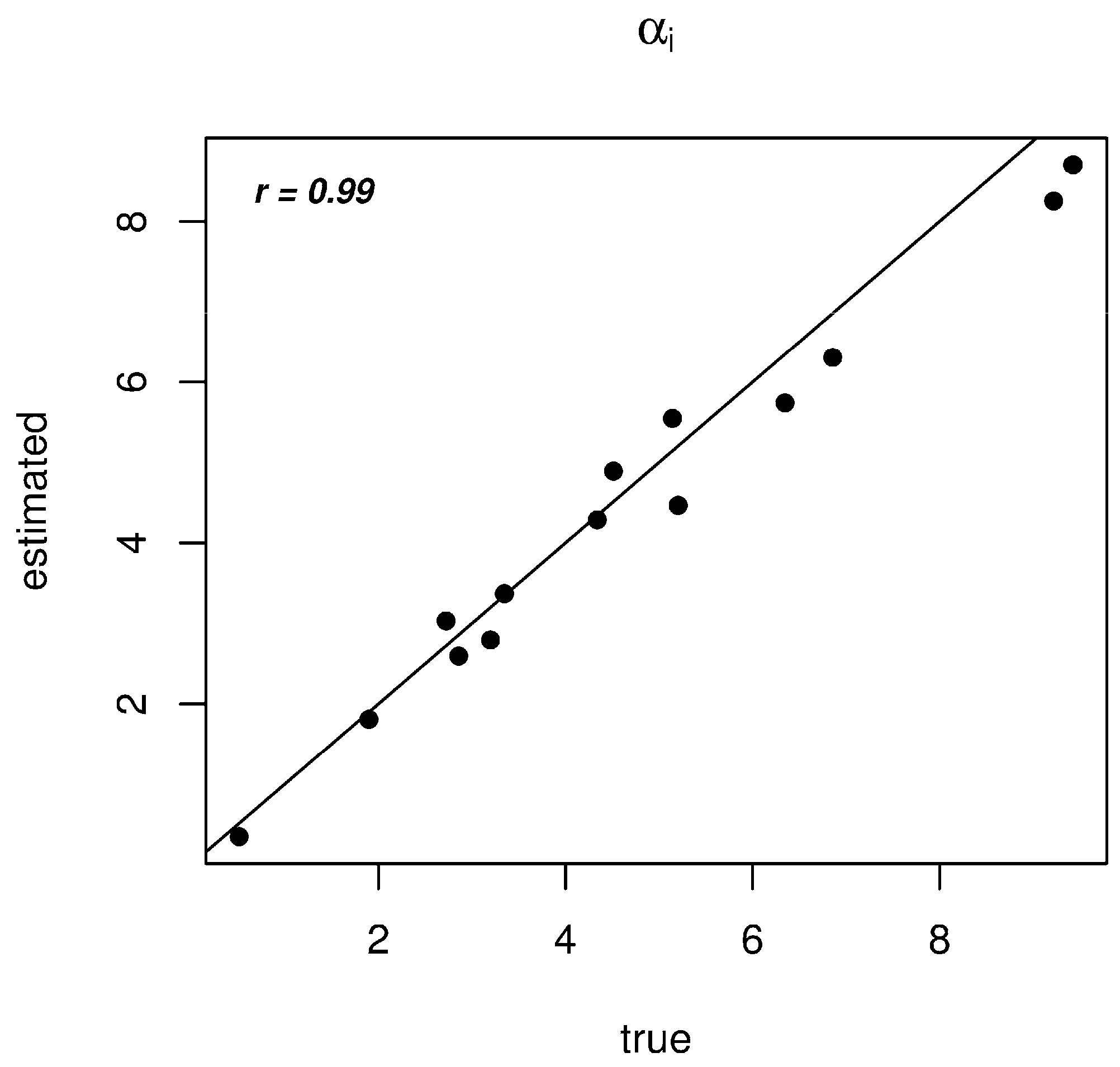
3.2. Results
4. Application to the Wechsler Intelligence Scale for Children-Fourth Edition (WISC-IV) Block Design Test
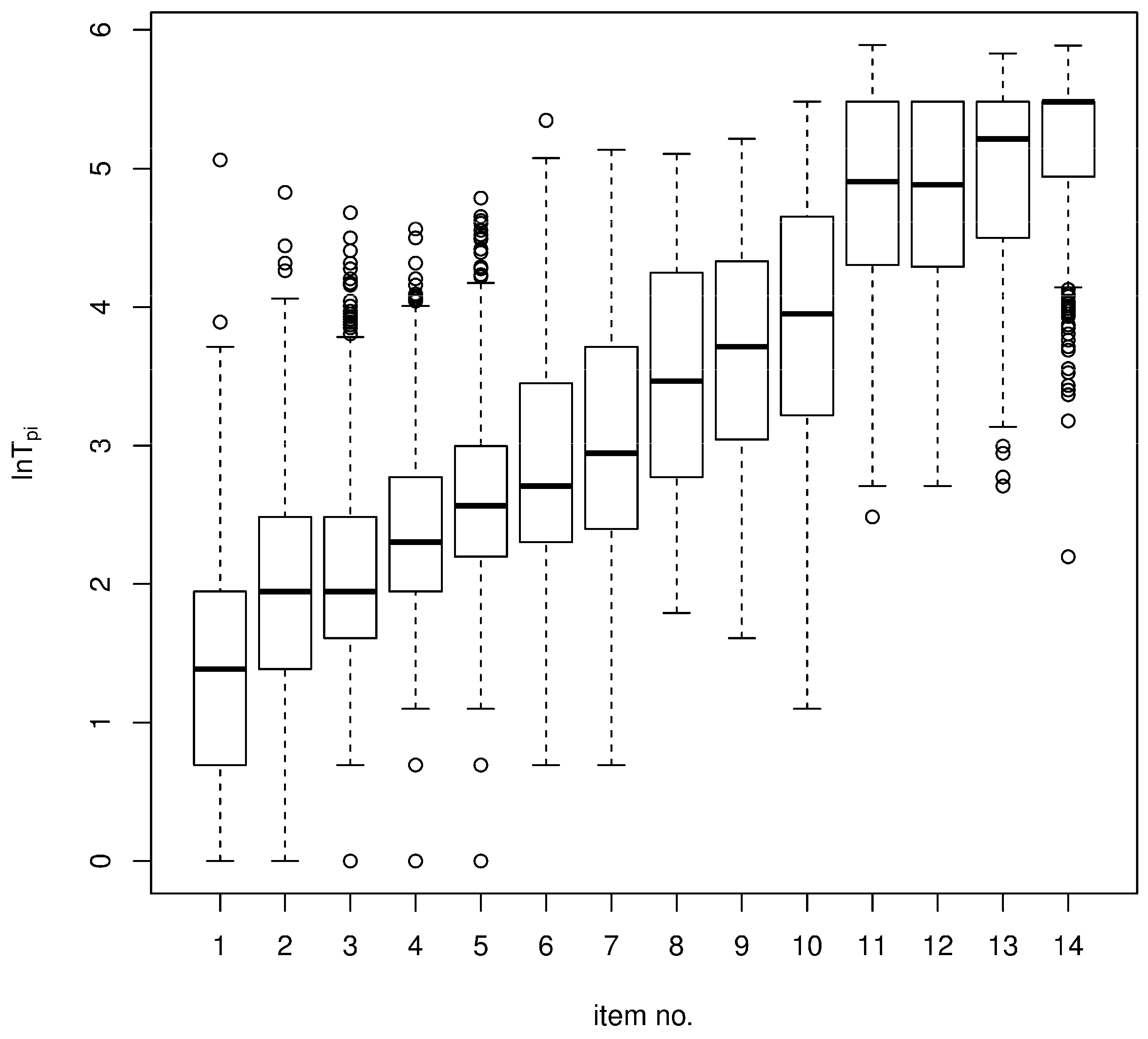
4.1. Data
4.2. Results
4.2.1. Conditional Independence
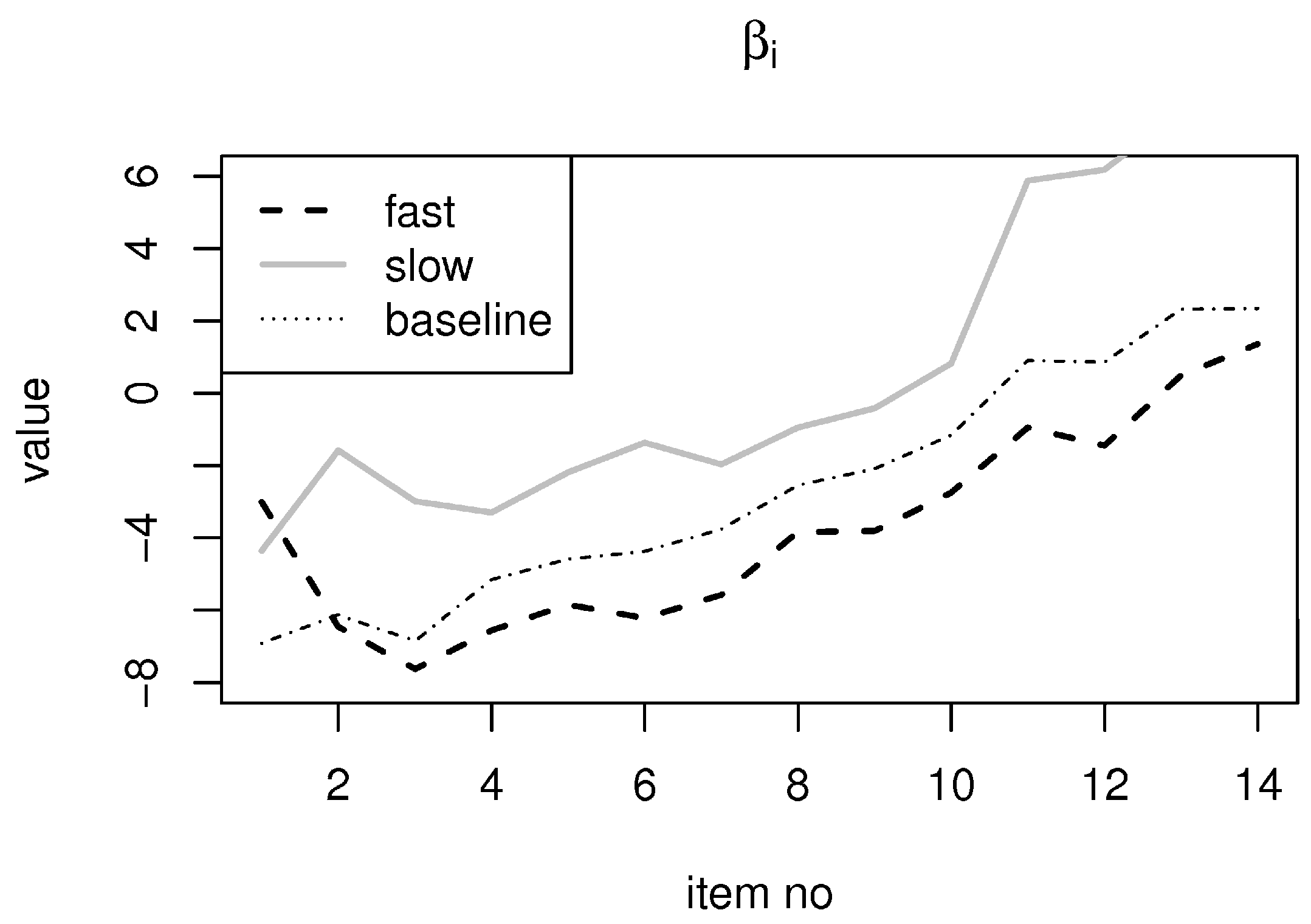
4.2.2. Response Mixture Models
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Raven, J.C. Advanced Progressive Matrices; HK Lewis: London, UK, 1962. [Google Scholar]
- Carpenter, P.A.; Just, M.A.; Shell, P. What one intelligence test measures: A theoretical account of the processing in the Raven Progressive Matrices Test. Psychol. Rev. 1990, 97, 404–431. [Google Scholar] [CrossRef] [PubMed]
- Galton, F. Hereditary Genius: An Inquiry into its Laws and Consequences; Macmillan: Fontana, CA, USA; London, UK, 1869. [Google Scholar]
- Galton, F. Inquiries into Human Faculty and its Development; AMS Press: New York, NY, USA, 1883. [Google Scholar]
- Jensen, A.R. Galton’s legacy to research on intelligence. J. Biosoc. Sci. 2002, 34, 145–172. [Google Scholar] [CrossRef] [PubMed]
- Jensen, A.R. Clocking the Mind: Mental Chronometry and Individual Differences; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Van Ravenzwaaij, D.; Brown, S.; Wagenmakers, E.J. An integrated perspective on the relation between response speed and intelligence. Cognition 2011, 119, 381–393. [Google Scholar] [CrossRef] [PubMed]
- Ratcliff, R.; Schmiedek, F.; McKoon, G. A diffusion model explanation of the worst performance rule for reaction time and IQ. Intelligence 2008, 36, 10–17. [Google Scholar] [CrossRef] [PubMed]
- Ratcliff, R. A theory of memory retrieval. Psychol. Rev. 1978, 85, 59–108. [Google Scholar] [CrossRef]
- Wagenmakers, E.-J. Methodological and empirical developments for the Ratcliff diffusion model of response times and accuracy. Eur. J. Cogn. Psychol. 2009, 21, 641–671. [Google Scholar] [CrossRef]
- Van der Maas, H.L.J.; Molenaar, D.; Maris, G.; Kievit, R.A.; Borsboom, D. Cognitive psychology meets psychometric theory: On the relation between process models for decision making and latent variable models for individual differences. Psychol. Rev. 2011, 118, 339–356. [Google Scholar] [CrossRef] [PubMed]
- Molenaar, D. The value of response times in item response modeling. Measurement 2015, 13, 177–181. [Google Scholar] [CrossRef]
- Borsboom, D.; Mellenbergh, G.J.; van Heerden, J. The concept of validity. Psychol. Rev. 2004, 111, 1061–1071. [Google Scholar] [CrossRef] [PubMed]
- Hamaker, E.L.; Nesselroade, J.R.; Molenaar, P.C. The integrated trait-state model. J. Res. Personal. 2007, 41, 295–315. [Google Scholar] [CrossRef]
- Molenaar, P.C.M. A manifesto on psychology as idiographic science: Bringing the person back into scientific psychology, this time forever. Measurement 2004, 2, 201–218. [Google Scholar] [CrossRef]
- Van der Maas, H.L.; Dolan, C.V.; Grasman, R.P.; Wicherts, J.M.; Huizenga, H.M.; Raijmakers, M.E. A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychol. Rev. 2006, 113, 842–861. [Google Scholar] [CrossRef] [PubMed]
- Shiffrin, R.M.; Schneider, W. Controlled and automatic human information processing: II. Perceptual learning, automatic attending and a general theory. Psychol. Rev. 1977, 84, 127–190. [Google Scholar] [CrossRef]
- Goldhammer, F.; Naumann, J.; Stelter, A.; Tóth, K.; Rölke, H.; Klieme, E. The time on task effect in reading and problem solving is moderated by task difficulty and skill: Insights from a computer-based large-scale assessment. J. Educ. Psychol. 2014, 106, 608–626. [Google Scholar] [CrossRef]
- Grabner, R.H.; Ansari, D.; Koschutnig, K.; Reishofer, G.; Ebner, F.; Neuper, C. To retrieve or to calculate? Left angular gyrus mediates the retrieval of arithmetic facts during problem solving. Neuropsychologia 2009, 47, 604–608. [Google Scholar] [CrossRef] [PubMed]
- Ericsson, K.A.; Staszewski, J.J. Skilled memory and expertise: Mechanisms of exceptional performance. In Complex Information Processing: The Impact of Herbert A. Simon; Klahr, D., Kotovsky, K., Eds.; Erlbaum: Hillsdale, MI, USA, 1989. [Google Scholar]
- Van Harreveld, F.; Wagenmakers, E.J.; van der Maas, H.L. The effects of time pressure on chess skill: An investigation into fast and slow processes underlying expert performance. Psychol. Res. 2007, 71, 591–597. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, K.; Scheerer, M. Abstract and concrete behavior an experimental study with special tests. Psychol. Monogr. 1941, 53, 1–151. [Google Scholar] [CrossRef]
- Jones, R.S.; Torgesen, J.K. Analysis of behaviours involved in performance of the block design subtest of the WICS-R. Intelligence 1981, 5, 321–328. [Google Scholar] [CrossRef]
- Schorr, D.; Bower, G.H.; Kiernan, R. Stimulus variables in the block design task. J. Consult. Clin. Psychol. 1982, 50, 479–487. [Google Scholar] [CrossRef] [PubMed]
- Partchev, I.; de Boeck, P. Can fast and slow intelligence be differentiated? Intelligence 2012, 40, 23–32. [Google Scholar] [CrossRef]
- Jeon, M.; de Boeck, P. A generalized item response tree model for psychological assessments. Behav. Res. Methods 2015, in press. [Google Scholar] [CrossRef] [PubMed]
- DiTrapani, J.; Jeon, M.; De Boeck, P.; Partchev, I. Attempting to differentiate fast and slow intelligence: Using generalized item response trees to examine the role of speed on intelligence tests. Intelligence 2016, 56, 82–92. [Google Scholar] [CrossRef]
- Larson, G.E.; Alderton, D.L. Reaction time variability and intelligence: A “worst performance” analysis of individual differences. Intelligence 1990, 14, 309–325. [Google Scholar] [CrossRef]
- Molenaar, D.; de Boeck, P. Response mixture modeling: Accounting for different measurement properties of faster and slower item responses. Psychometrika 2016. under review. [Google Scholar]
- Wechsler, D. Wechsler Intelligence Scale for Children-Fourth Edition (WISC-IV); The Psychological Corporation: San Antonio, TX, USA, 2003. [Google Scholar]
- Nagyné Réz, I.; Lányiné Engelmayer, Á.; Kuncz, E.; Mészáros, A.; Mlinkó, R.; Bass, L.; Rózsa, S.; Kő, N. WISC-IV: A Wechsler Gyermek Intelligenciateszt Legújabb Változata; Hungarian Version of the Wechsler Intelligence Scale for Children—Fourth Edition (WISC—IV); OS Hungary Tesztfejlesztő: Budapest, Hungary, 2008. (In Hungarian) [Google Scholar]
- Van der Linden, W.J. A hierarchical framework for modeling speed and accuracy on test items. Psychometrika 2007, 72, 287–308. [Google Scholar] [CrossRef]
- Van der Linden, W.J. Conceptual issues in response-time modeling. J. Educ. Meas. 2009, 46, 247–272. [Google Scholar] [CrossRef]
- Loeys, T.; Legrand, C.; Schettino, A.; Pourtois, G. Semi-parametric proportional hazards models with crossed random effects for psychometric response times. Br. J. Math. Stat. Psychol. 2014, 67, 304–327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molenaar, D.; Tuerlinckx, F.; van der Maas, H.L.J. A generalized linear factor model approach to the hierarchical framework for responses and response times. Br. J. Math. Stat. Psychol. 2015, 68, 197–219. [Google Scholar] [CrossRef] [PubMed]
- Ranger, J.; Ortner, T. The case of dependency of responses and response times: A modeling approach based on standard latent trait models. Psychol. Test. Assess. Model. 2012, 54, 128–148. [Google Scholar]
- Wang, C.; Chang, H.H.; Douglas, J.A. The linear transformation model with frailties for the analysis of item response times. Br. J. Math. Stat. Psychol. 2013, 66, 144–168. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Fan, Z.; Chang, H.H.; Douglas, J.A. A semiparametric model for jointly analyzing response times and accuracy in computerized testing. J. Educ. Behav. Stat. 2013, 38, 381–417. [Google Scholar] [CrossRef]
- Roskam, E.E. Toward a psychometric theory of intelligence. In Progress in Mathematical Psychology; Roskam, E.E., Suck, R., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1987; pp. 151–171. [Google Scholar]
- Wang, T.; Hanson, B.A. Development and calibration of an item response model that incorporates response time. Appl. Psychol. Meas. 2005, 29, 323–339. [Google Scholar] [CrossRef]
- Luce, R.D. Response Times; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Van der Linden, W.J.; Guo, F. Bayesian procedures for identifying aberrant response-time patterns in adaptive testing. Psychometrika 2008, 73, 365–384. [Google Scholar] [CrossRef]
- Van der Linden, W.J.; Glas, C.A. Statistical tests of conditional independence between responses and/or response times on test items. Psychometrika 2010, 75, 120–139. [Google Scholar] [CrossRef]
- Gilks, W.R.; Richardson, S.; Spiegelhalter, D.J. Introducing Markov chain Monte Carlo. In Markov Chain Monte Carlo in Practice; Springer: New York, NY, USA, 1996; pp. 1–19. [Google Scholar]
- Thomas, A.; Hara, B.O.; Ligges, U.; Sturtz, S. Making BUGS Open. R News 2006, 6, 12–17. [Google Scholar]
- Rozencwajg, P.; Corroyer, D. Strategy development in a block design task. Intelligence 2002, 30, 1–25. [Google Scholar] [CrossRef]
- Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 5th ed.; Muthén & Muthén: Los Angeles, CA, USA, 2007. [Google Scholar]
- Bolsinova, M.; Maris, G. A test for conditional independence between response time and accuracy. Br. J. Math. Stat. Psychol. 2016, 69, 62–79. [Google Scholar] [CrossRef] [PubMed]
- Bolsinova, M.; Tijmstra, J. Posterior predictive checks for conditional independence between response time and accuracy. J. Educ. Behav. Stat. 2016, 41, 123–145. [Google Scholar] [CrossRef]
- Aitchison, J.; Silvey, S.D. Maximum-likelihood estimation of parameters subject to restraints. Ann. Math. Stat. 1958, 29, 813–828. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; van der Linde, A. Bayesian measures of model complexity and fit (with discussion). J. Roy. Stat. Soc. Ser. B 2002, 64, 583–640. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Greven, S.; Kneib, T. On the behaviour of marginal and conditional AIC in linear mixed models. Biometrika 2010, 97, 773–789. [Google Scholar] [CrossRef]
- Vaida, F.; Blanchard, S. Conditional Akaike information for mixed-effects models. Biometrika 2005, 92, 351–370. [Google Scholar] [CrossRef]
- Unsworth, N.; Redick, T.S.; Lakey, C.E.; Young, D.L. Lapses in sustained attention and their relation to executive control and fluid abilities: An individual differences investigation. Intelligence 2010, 38, 111–122. [Google Scholar] [CrossRef]
- Goldhammer, F. Measuring ability, speed, or both? Challenges, psychometric solutions, and what can be gained from experimental control. Measurement 2015, 13, 133–164. [Google Scholar] [CrossRef] [PubMed]
- Holden, R.R.; Kroner, D.G. Relative efficacy of differential response latencies for detecting faking on a self-report measure of psychopathology. Psychol. Assess. 1992, 4, 170–173. [Google Scholar] [CrossRef]
- McLeod, L.; Lewis, C.; Thissen, D. A Bayesian method for the detection of item preknowledge in computerized adaptive testing. Appl. Psychol. Meas. 2003, 27, 121–137. [Google Scholar] [CrossRef]
- Rabbitt, P. How old and young subjects monitor and control responses for accuracy and speed. Br. J. Psychol. 1979, 70, 305–311. [Google Scholar] [CrossRef]
- Mollenkopf, W.G. An experimental study of the effects on item-analysis data of changing item placement and test time limit. Psychometrika 1950, 15, 291–315. [Google Scholar] [CrossRef] [PubMed]
- Goldhammer, F.; Kroehne, U. Controlling individuals’ time spent on task in speeded performance measures: Experimental time limits, posterior time limits, and response time modeling. Appl. Psychol. Meas. 2014, 38, 255–267. [Google Scholar] [CrossRef]
- 1Specifically, πi(s) is obtained by integrating out εpi from Equation (9). That is, πi(s) = , where ω( ) is a logistic function and ( ) is the standard normal density function.
- 2Specifically, the mAIC and mBIC use the same penalty of the deviance as the AIC and BIC, but in contrast with the traditional AIC and BIC, the deviance is averaged over the samples of the MCMC procedure instead of evaluated at the maximum likelihood estimates of the parameters.
| Item | Mod. | Cor. |
|---|---|---|
| 1 | 28.59 | 0.35 |
| 2 | 1.41 | −0.16 |
| 3 | 7.87 | −0.12 |
| 4 | 6.06 | −0.07 |
| 5 | 14.24 | −0.11 |
| 6 | 13.14 | −0.15 |
| 7 | 8.41 | −0.13 |
| 8 | 5.59 | −0.11 |
| 9 | 12.44 | −0.14 |
| 10 | 7.44 | −0.11 |
| 11 | 14.37 | −0.13 |
| 12 | 14.99 | −0.13 |
| 13 | 24.46 | −0.16 |
| 14 | 70.64 | −0.16 |
| i | αi | βi | ||
|---|---|---|---|---|
| mean | sd | mean | sd | |
| 1 | 0.56 | 0.43 | −6.91 | 0.91 |
| 2 | 1.74 | 0.39 | −6.13 | 0.68 |
| 3 | 2.79 | 0.48 | −6.84 | 0.83 |
| 4 | 2.76 | 0.33 | −5.16 | 0.47 |
| 5 | 3.05 | 0.32 | −4.59 | 0.39 |
| 6 | 3.42 | 0.37 | −4.37 | 0.41 |
| 7 | 3.54 | 0.35 | −3.76 | 0.35 |
| 8 | 4.56 | 0.43 | −2.55 | 0.28 |
| 9 | 3.99 | 0.36 | −2.09 | 0.24 |
| 10 | 4.58 | 0.41 | −1.16 | 0.22 |
| 11 | 5.32 | 0.57 | 0.90 | 0.25 |
| 12 | 5.62 | 0.62 | 0.86 | 0.26 |
| 13 | 4.42 | 0.48 | 2.32 | 0.30 |
| 14 | 1.82 | 0.20 | 2.34 | 0.19 |
| Model | Restriction(s) | DIC | mAIC | mBIC |
|---|---|---|---|---|
| 1 | – | 25,850 | 30,464 | 33,494 |
| 2 | αi(s) = αi(f) | 25,690 | 30,389 | 33,407 |
| 3 | αi(s) = αi(f); βi(s) = βi(f) | 25,900 | 30,474 | 33,479 |
| 4 | αi(s) = αi(f); ζ1i = ζ1 | 25,570 | 30,232 | 33,236 |
| 5 | αi(s) = αi(f); ζ1i = ζ1; ζ0i = ζ0 | 25,940 | 30,339 | 33,329 |
| Model | Restriction(s) | Correlations | σθ(s) | µθ(s) | ||
|---|---|---|---|---|---|---|
| θ(s), θ(f) | τ, θ(s) | τ, θ(f) | ||||
| 0 | – | – | −0.90 1 | – | – | – |
| 1 | – | 0.95 | −0.90 | −0.86 | 1 * | 0 * |
| 2 | αi(s) = αi(f) | 0.95 | −0.90 | −0.86 | 1.20 (0.16) | 0 * |
| 3 | αi(s) = αi(f); βi(s) = βi(f) | 0.96 | −0.89 | −0.87 | 1.05 (0.06) | −0.97 (0.06) |
| 4 | αi(s) = αi(f); ζ1i = ζ1 | 0.93 | −0.91 | −0.86 | 1.18 (0.14) | 0 * |
| 5 | αi(s) = αi(f); ζ1i = ζ1; ζ0i = ζ0 | 0.96 | −0.89 | −0.87 | 0.98 (0.09) | 0 * |
| i | αi | βi(f) | βi(s) | ζ0i | πi(s) | ||||
|---|---|---|---|---|---|---|---|---|---|
| mean | sd | mean | sd | mean | sd | mean | sd | ||
| 1 | 0.51 | 0.40 | −3.01 | 4.21 | −4.36 | 3.83 | −0.39 | 3.99 | 0.65 |
| 2 | 1.90 | 0.47 | −6.45 | 1.56 | −1.58 | 2.81 | 2.30 | 1.93 | 0.01 |
| 3 | 2.72 | 0.54 | −7.62 | 1.02 | −2.99 | 1.86 | 1.33 | 0.26 | 0.10 |
| 4 | 2.86 | 0.45 | −6.55 | 0.80 | −3.30 | 0.69 | 0.54 | 0.10 | 0.30 |
| 5 | 3.35 | 0.44 | −5.85 | 0.61 | −2.19 | 0.67 | 0.63 | 0.09 | 0.27 |
| 6 | 4.34 | 0.55 | −6.22 | 0.70 | −1.37 | 0.94 | 1.01 | 0.08 | 0.16 |
| 7 | 4.51 | 0.56 | −5.58 | 0.63 | −1.97 | 0.74 | 0.74 | 0.10 | 0.23 |
| 8 | 5.21 | 0.59 | −3.84 | 0.47 | −0.95 | 0.59 | 0.52 | 0.10 | 0.30 |
| 9 | 5.14 | 0.60 | −3.81 | 0.47 | −0.42 | 0.55 | 0.46 | 0.10 | 0.33 |
| 10 | 6.35 | 0.82 | −2.75 | 0.47 | 0.82 | 0.64 | 0.42 | 0.09 | 0.34 |
| 11 | 9.42 | 1.35 | −0.95 | 0.50 | 5.88 | 1.31 | 0.32 | 0.06 | 0.38 |
| 12 | 9.22 | 1.23 | −1.45 | 0.51 | 6.18 | 1.22 | 0.28 | 0.05 | 0.39 |
| 13 | 6.86 | 0.97 | 0.49 | 0.41 | 7.81 | 1.30 | 0.13 | 0.05 | 0.45 |
| 14 | 3.20 | 0.47 | 1.36 | 0.30 | 7.68 | 1.27 | 0.11 | 0.04 | 0.46 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molenaar, D.; Bolsinova, M.; Rozsa, S.; De Boeck, P. Response Mixture Modeling of Intraindividual Differences in Responses and Response Times to the Hungarian WISC-IV Block Design Test. J. Intell. 2016, 4, 10. https://doi.org/10.3390/jintelligence4030010
Molenaar D, Bolsinova M, Rozsa S, De Boeck P. Response Mixture Modeling of Intraindividual Differences in Responses and Response Times to the Hungarian WISC-IV Block Design Test. Journal of Intelligence. 2016; 4(3):10. https://doi.org/10.3390/jintelligence4030010
Chicago/Turabian StyleMolenaar, Dylan, Maria Bolsinova, Sandor Rozsa, and Paul De Boeck. 2016. "Response Mixture Modeling of Intraindividual Differences in Responses and Response Times to the Hungarian WISC-IV Block Design Test" Journal of Intelligence 4, no. 3: 10. https://doi.org/10.3390/jintelligence4030010
APA StyleMolenaar, D., Bolsinova, M., Rozsa, S., & De Boeck, P. (2016). Response Mixture Modeling of Intraindividual Differences in Responses and Response Times to the Hungarian WISC-IV Block Design Test. Journal of Intelligence, 4(3), 10. https://doi.org/10.3390/jintelligence4030010