Preventing Response Elimination Strategies Improves the Convergent Validity of Figural Matrices
Abstract
:1. Introduction
1.1. Components of Figural Matrices

1.2. Models of the Solution Process for Figural Matrices
1.3. Differences in Solution Strategy Outcomes
1.4. Response Format Design
1.4.1. Response Formats that Use Distractors
1.4.2. Item Formats that Work without Distractors

1.5. Goals
2. Experimental Section
2.1. Sample
2.2. Procedure
2.3. Test Methods
2.3.1. Matrices Tests
2.3.2. Distractor-Free Version
2.3.3. Conceptual Distractor Version
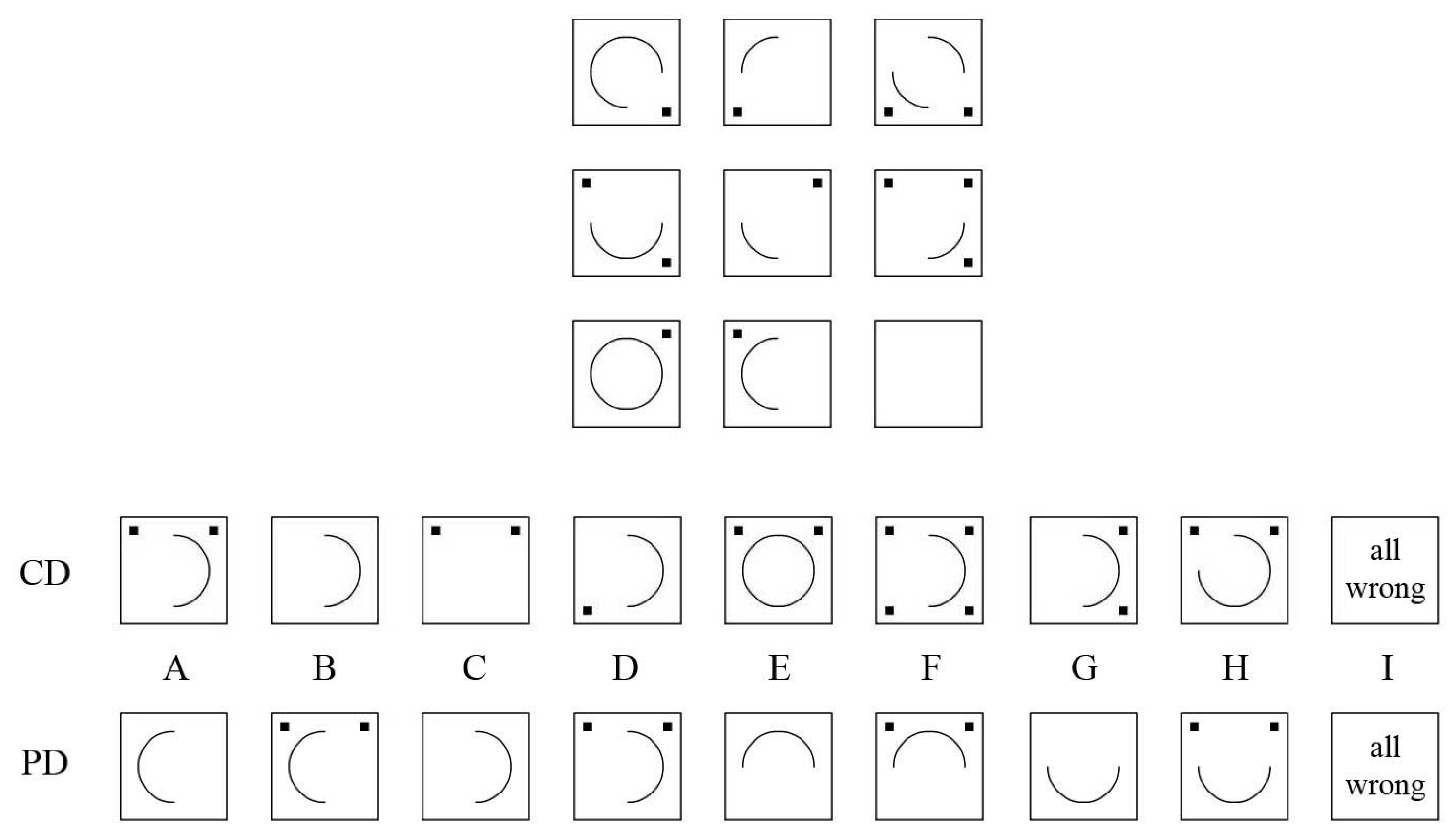
2.3.4. Perceptual Distractor Version
2.3.5. Working Memory Battery
2.3.6. Intelligence Test
2.4. Statistical Procedure
2.5. Software
3. Results
3.1. Internal Consistency
3.2. Item Difficulties
| Item | Rules | p(DF) | p(CD) | p(PD) |
|---|---|---|---|---|
| 1 | 1 | 0.75 | 0.80 | 0.76 |
| 2 | 1 | 0.91 | 0.88 | 0.89 |
| 3 | 1 | 1.00 | 1.00 | 0.96 |
| 4 | 1 | 0.86 | 0.80 | 0.82 |
| 5 | 1 | 0.16 | 0.14 | 0.22 |
| 6 | 1 | 0.14 | 0.12 | 0.22 |
| 7 | 2 | 0.41 | 0.54 | 0.47 |
| 8 | 2 | 0.70 | 0.58 | 0.71 |
| 9 | 2 | 0.70 | 0.64 | 0.76 |
| 10 | 2 | 0.73 | 0.58 | 0.76 |
| 11 | 2 | 0.16 | 0.26 | 0.29 |
| 12 | 2 | 0.45 | 0.46 | 0.53 |
| 13 | 2 | 0.30 | 0.68 | 0.62 |
| 14 | 2 | 0.48 | 0.66 | 0.53 |
| 15 | 2 | 0.38 | 0.50 | 0.51 |
| 16 | 2 | 0.14 | 0.44 | 0.27 |
| 17 | 2 | 0.14 | 0.28 | 0.38 |
| 18 | 2 | 0.55 | 0.68 | 0.71 |
| 19 | 2 | 0.77 | 0.78 | 0.76 |
| 20 | 2 | 0.66 | 0.78 | 0.87 |
| 21 | 2 | 0.54 | 0.46 | 0.53 |
| 22 | 3 | 0.41 | 0.52 | 0.58 |
| 23 | 3 | 0.13 | 0.38 | 0.31 |
| 24 | 3 | 0.54 | 0.62 | 0.69 |
| 25 | 3 | 0.34 | 0.60 | 0.67 |
| 26 | 3 | 0.48 | 0.64 | 0.60 |
| 27 | 3 | 0.44 | 0.62 | 0.76 |
| 28 | 3 | 0.29 | 0.44 | 0.44 |
| 29 | 3 | 0.38 | 0.58 | 0.44 |
| 30 | 3 | 0.39 | 0.62 | 0.56 |
| 31 | 3 | 0.70 | 0.68 | 0.69 |
| 32 | 4 | 0.07 | 0.40 | 0.62 |
| 33 | 4 | 0.25 | 0.30 | 0.67 |
| 34 | 4 | 0.39 | 0.50 | 0.58 |
| 35 | 4 | 0.23 | 0.38 | 0.33 |
| 36 | 4 | 0.27 | 0.32 | 0.38 |
| 37 | 5 | 0.23 | 0.36 | 0.56 |
| 38 | 5 | 0.21 | 0.38 | 0.58 |
| M(p) | – | 0.44 | 0.54 | 0.58 |
| SD(p) | – | 0.25 | 0.20 | 0.19 |
3.3. Correlations with Intelligence and Working Memory Capacity
| Test | DF | CD | PD | DF vs. CD | DF vs. PD | CD vs. PD |
|---|---|---|---|---|---|---|
| ISTV | r = 0.64 ** | r = 0.34 * | r = 0.30 | z = 1.57 | z = 1.63 * | z = 0.17 |
| ISTN | r = 0.46 ** | r = 0.15 | r = 0.63 ** | z = 1.34 | z = 0.89 | z = 2.27 ** |
| ISTF | r = 0.53 ** | r = −0.14 | r = 0.12 | z = 2.84 ** | z = 1.71 * | z = 1 |
| ISTG | r = 0.61 ** | r = 0.12 | r = 0.53 ** | z = 2.28 ** | z = 0.43 | z = 1.8 * |
| WMV | r = 0.45 ** | r = 0.20 | r = 0.30 * | z = 1.41 | z = 0.85 | z = 0.5 |
| WMN | r = 0.48 ** | r = 0.18 | r = 0.32 * | z = 1.7 * | z = 0.93 | z = 0.7 |
| WMF | r = 0.44 ** | r = 0.26 | r = 0.20 | z = 1.03 | z = 1.3 ** | z = 0.3 |
| WMG | r = 0.54 ** | r = 0.25 | r = 0.35 * | z = 1.74 * | z = 1.16 | z = 0.52 |
3.4. Multiple-Group Comparisons
| Matrices + Working Memory | ||||||||
| Model | χ2 | df | p(χ2) | CFI | RMSEA | Δχ2 | Δdf | p(Δχ2) |
| Configural | 32.81 | 24 | 0.11 | 0.98 | 0.09 | – | – | – |
| Weak | 37.00 | 32 | 0.25 | 0.99 | 0.06 | 4.19 | 8 | 0.84 |
| Strong | 47.86 | 40 | 0.18 | 0.98 | 0.06 | 10.86 | 8 | 0.21 |
| Strict | 55.98 | 52 | 0.33 | 0.99 | 0.04 | 8.12 | 12 | 0.78 |
| Matrices + Intelligence | ||||||||
| Model | χ2 | df | p(χ2) | CFI | RMSEA | Δχ2 | Δdf | p(Δχ2) |
| Configural | 38.37 | 24 | 0.03 | 0.95 | 0.14 | – | – | – |
| Weak | 62.07 | 32 | <0.01 | 0.90 | 0.17 | 23.71 | 8 | <0.01 |
| Strong | 86.39 | 40 | <0.01 | 0.84 | 0.19 | 24.32 | 8 | <0.01 |
| Strict | 108.83 | 52 | <0.01 | 0.81 | 0.19 | 22.44 | 12 | 0.03 |
4. Discussion
| Rules | DF | CD | PD |
|---|---|---|---|
| 1 | M(p) = 0.64 | M(p) = 0.62 | M(p) = 0.65 |
| SD(p) = 0.39 | SD(p) = 0.39 | SD(p) = 0.34 | |
| 2 | M(p) = 0.47 | M(p) = 0.55 | M(p) = 0.58 |
| SD(p) = 0.22 | SD(p) = 0.16 | SD(p) = 0.18 | |
| 3 | M(p) = 0.41 | M(p) = 0.57 | M(p) = 0.57 |
| SD(p) = 0.15 | SD(p) = 0.09 | SD(p) = 0.14 | |
| 4 | M(p) = 0.24 | M(p) = 0.38 | M(p) = 0.52 |
| SD(p) = 0.11 | SD(p) = 0.08 | SD(p) = 0.15 | |
| 5 | M(p) = 0.22 | M(p) = 0.37 | M(p) = 0.57 |
| SD(p) = 0.01 | SD(p) = 0.01 | SD(p) = 0.01 |
5. Limitations
6. Conclusions
Acknowledgments
Author Contributions
Conflict of Interest
References
- Carpenter, P.A.; Just, M.A.; Shell, P. What one intelligence test measures: A theoretical account of the processing in the Raven Progressive Matrices Test. Psychol. Rev. 1990, 97, 404–431. [Google Scholar] [CrossRef] [PubMed]
- Bethell-Fox, C.E.; Lohman, D.F.; Snow, R.E. Adaptive reasoning: Componential and eye movement analysis of geometric analogy performance. Intelligence 1984, 8, 205–238. [Google Scholar] [CrossRef]
- Hayes, T.R.; Petrov, A.A.; Sederberg, P.B. A novel method for analyzing sequential eye movements reveals strategic influence on Raven’s Advanced Progressive Matrices. J. Vis. 2011, 11, 10. [Google Scholar] [CrossRef] [PubMed]
- Jarosz, A.F.; Wiley, J. Why does working memory capacity predict RAPM performance? A possible role of distraction. Intelligence 2012, 40, 427–438. [Google Scholar] [CrossRef]
- Putz-Osterloh, W. Problemlöseprozesse und Intelligenztestleistung; Huber: Bern, Switzerland, 1981. (In German) [Google Scholar]
- Vigneau, F.; Caissie, A.F.; Bors, D.A. Eye-movement analysis demonstrates strategic influences on intelligence. Intelligence 2006, 34, 261–272. [Google Scholar] [CrossRef]
- Mitchum, A.L.; Kelley, C.M. Solve the problem first: Constructive solution strategies can influence the accuracy of retrospective confidence judgments. J. Exp. Psychol. Learn. Mem. Cogn. 2010, 36, 699–710. [Google Scholar] [CrossRef] [PubMed]
- Primi, R. Complexity of geometric inductive reasoning tasks. Intelligence 2002, 30, 41–70. [Google Scholar] [CrossRef]
- Arendasy, M.E.; Sommer, M. Reducing response elimination strategies enhances the construct validity of figural matrices. Intelligence 2013, 41, 234–243. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive load theory, learning difficulty, and instructional design. Learn. Instr. 1994, 4, 295–312. [Google Scholar] [CrossRef]
- Paas, F.; Renkl, A.; Sweller, J. Cognitive load theory: Instructional implications of the interaction between information structures and cognitive architecture. Instr. Sci. 2004, 32, 1–8. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive load theory. Psychol. Learn. Motiv. Cogn. Educ. 2011, 55, 37–76. [Google Scholar]
- Embretson, S.E. The role of working memory capacity and general control processes in intelligence. Intelligence 1995, 20, 169–189. [Google Scholar] [CrossRef]
- Rasmussen, D.; Eliasmith, C. A Neural Model of Rule Generation in Inductive Reasoning. Top. Cogn. Sci. 2011, 3, 140–153. [Google Scholar] [CrossRef] [PubMed]
- Babcock, R.L. Analysis of age differences in types of errors on the Raven’s Advanced Progressive Matrices. Intelligence 2002, 30, 485–503. [Google Scholar] [CrossRef]
- Raven, J.; Raven, J.C.; Court, J.H. Manual for Raven’s Progressive Matrices and Vocabulary Scales; Harcourt Assessment: San Antonio, TX, USA, 1998. [Google Scholar]
- Arendasy, M.E. Automatisierte Itemgenerierung und Psychometrische Qualitätssicherung am Beispiel des Matrizentests GEOM; Universität Wien: Wien, Austria, 2004. (In German) [Google Scholar]
- Guttman, L.; Schlesinger, I.M. Systematic Construction of Distractors for Ability and Achievement Test Items. Educ. Psychol. Meas. 1967, 27, 569–580. [Google Scholar] [CrossRef]
- Ward, W.C.; Bennett, R.E. Construction Versus Choice in Cognitive Measurement: Issues in Constructed Response, Performance Testing, and Portfolio Assessment; Lawrence Earlbaum Associates: Hillsdale, MI, USA, 1993. [Google Scholar]
- Stevenson, C.E.; Hickendorff, M.; Resing, W.C.M.; Heiser, W.J.; de Boeck, P.A.L. Explanatory item response modeling of children’s change on a dynamic test of analogical reasoning. Intelligence 2013, 41, 157–168. [Google Scholar] [CrossRef]
- Piskernik, B.; Debelak, R. Free Response Matrices; Schuhfried: Mödling, Austria, 2013. [Google Scholar]
- Becker, N.; Preckel, F.; Karbach, J.; Raffel, N.; Spinath, F.M. Die Matrizenkonstruktionsaufgabe: Validierung eines distraktorfreien Aufgabenformats zur Vorgabe figuraler Matrizen. Diagnostica 2015, 61, 22–33. (In German) [Google Scholar] [CrossRef]
- Becker, N.; Spinath, F.M. Design a Matrix Test. Ein Distraktorfreier Matrizentest zur Erfassung der Allgemeinen Intelligenz (DESIGMA); Hogrefe: Göttingen, Germany, 2014. [Google Scholar]
- Preckel, F. Diagnostik Intellektueller Hochbegabung. Testentwicklung zur Erfassung der Fluiden Intelligenz; Hogrefe: Göttingen, Germany, 2003. (In German) [Google Scholar]
- Gittler, G. Dreidimensionaler Würfeltest (3DW); Beltz: Weinheim, Germany, 1990. (In German) [Google Scholar]
- Wilhelm, O.; Hildebrandt, A.; Oberauer, K. What is working memory capacity, and how can we measure it? Front. Psychol. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Conway, A.R.A.; Kane, M.J.; Bunting, M.F.; Hambrick, D.Z.; Wilhelm, O.; Engle, R.W. Working memory span tasks: A methodological review and user’s guide. Psychon. Bull. Rev. 2005, 12, 769–786. [Google Scholar] [CrossRef] [PubMed]
- Liepmann, D.; Beauducel, A.; Brocke, R.; Amthauer, R. Intelligenz-Struktur-Test 2000 R (I-S-T 2000 R); Hogrefe: Göttingen, Germany, 2007. (In German) [Google Scholar]
- Millsap, R.E.; Zalkind, S.S.; Xenos, T. Quick-Reference Tables to Determine the Significance of the Difference between Two Correlation Coefficients from Two Independent Samples. Educ. Psychol. Meas. 1990, 50, 297–307. [Google Scholar] [CrossRef]
- Brown, T.A. Confirmatory Factor Analysis for Applied Research; Guilford Press: New York, NY, USA, 2006. [Google Scholar]
- Hirschfeld, G.; von Brachel, R. Multiple-Group confirmatory factor analysis in R–A tutorial in measurement invariance with continuous and ordinal indicators. Pract. Assess. Res. Eval. 2014, 19, No. 7. [Google Scholar]
- Chen, F.F. What happens if we compare chopsticks with forks? The impact of making inappropriate comparisons in cross-cultural research. J. Personal. Soc. Psychol. 2008, 95, 1005–1018. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Wien, Austria, 2015. [Google Scholar]
- Rosseel, Y. Lavaan: An R package for structural equation modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Pornprasertmanit, S.; Miller, P.; Schoemann, A.; Rosseel, Y.; Quick, C.; Garnier-Villarreal, M.; Selig, J.; Boulton, A.; Preacher, K.; Coffman, D.; et al. semTools: Useful Tools for Structural Equation Modeling; R Foundation for Statistical Computing: Wien, Austria, 2015. [Google Scholar]
- Robinson, N.M.; Janos, P.M. The contribution of intelligence tests to the understanding of special children. In Intelligence and Exceptionality: New Directions for Theory, Assessment, and Instructional Practices; Day, J.D., Borkowski, J.G., Eds.; Ablex Publishing: Westport, CT, USA, 1987; pp. 21–55. [Google Scholar]
- Ackerman, P.L.; Beier, M.E.; Boyle, M.D. Individual differences in working memory within a nomological network of cognitive and perceptual speed abilities. J. Exp. Psychol. Gen. 2002, 131, 567–589. [Google Scholar] [CrossRef] [PubMed]
- Preckel, F.; Thiemann, H. Online- versus paper-pencil-version of a high potential intelligence test. Swiss J. Psychol. 2003, 62, 131–138. [Google Scholar] [CrossRef]
- Preckel, F.; Freund, P.A. Accuracy, latency, and confidence in abstract reasoning: The influence of fear of failure and gender. Psychol. Sci. 2005, 47, 230–245. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker, N.; Schmitz, F.; Falk, A.M.; Feldbrügge, J.; Recktenwald, D.R.; Wilhelm, O.; Preckel, F.; Spinath, F.M. Preventing Response Elimination Strategies Improves the Convergent Validity of Figural Matrices. J. Intell. 2016, 4, 2. https://doi.org/10.3390/jintelligence4010002
Becker N, Schmitz F, Falk AM, Feldbrügge J, Recktenwald DR, Wilhelm O, Preckel F, Spinath FM. Preventing Response Elimination Strategies Improves the Convergent Validity of Figural Matrices. Journal of Intelligence. 2016; 4(1):2. https://doi.org/10.3390/jintelligence4010002
Chicago/Turabian StyleBecker, Nicolas, Florian Schmitz, Anke M. Falk, Jasmin Feldbrügge, Daniel R. Recktenwald, Oliver Wilhelm, Franzis Preckel, and Frank M. Spinath. 2016. "Preventing Response Elimination Strategies Improves the Convergent Validity of Figural Matrices" Journal of Intelligence 4, no. 1: 2. https://doi.org/10.3390/jintelligence4010002
APA StyleBecker, N., Schmitz, F., Falk, A. M., Feldbrügge, J., Recktenwald, D. R., Wilhelm, O., Preckel, F., & Spinath, F. M. (2016). Preventing Response Elimination Strategies Improves the Convergent Validity of Figural Matrices. Journal of Intelligence, 4(1), 2. https://doi.org/10.3390/jintelligence4010002




