1. Introduction
Direct current to direct current (DC–DC) power converters are devices that control the output voltage and act as bridges to transfer energy between sources and loads. These power converters are now used in multiple applications [
1], such as computer power sources, distributed power systems, electric vehicles, aircraft, etc. Several types of DC–DC power converters, such as boost, buck, or buck–boost converters, are now used for different purposes in the power grid. The interest in this research is to work with the boost converter, which is a step-up DC–DC power converter, and its implementation is relatively simple. In most cases, the boost converter applications are oriented to conditioning power sources, such as photovoltaic systems [
2].
In the 1980s, sliding mode controllers were designed for this type of system [
3]. In [
4], the authors designed a controller based on sliding mode control and defined it as a surface given by a linear combination of the error and derived from the error. However, the design generated chattering in the system, which increased the ripple and distortion at the output of the circuit. Therefore, it is expected theoretically that the switch operates a finite number of times per period for implementing a converter.
In 2000, the zero average dynamics (ZAD) technique was reported for the first time, which consists of defining a switching surface and forcing the dynamic system that governs the converter to evolve, on average, over the surface [
5]. This technique obtained a fixed switching frequency and it was designed with an auxiliary output based on a digital control action to guarantee an average output signal in each iteration [
6]. Recently, ZAD was used to control DC motors [
7], and the authors of [
8] presented the experimental implementation of a buck converter with quasi-sliding mode control combined with a loss estimator function. A trigger signal was used to implement the centered pulse-width modulation (CPWM) and synchronize the sampling of analogical signals from the buck converter, allowing the use of a lower sampling frequency and ensuring the measurements at the right time.
The presence of bifurcation [
9] and chaos phenomena [
10] in DC–DC converters was demonstrated, due, among other things, to the nonlinear switching action (determined by the type of controller used) [
11,
12,
13]. For example, the chaos phenomenon was confirmed in electronic circuits in the 1980s [
14,
15]. Then, the chaos phenomenon was experimentally confirmed in a buck converter in 1990 [
16]. Moreover, a study of nonlinear phenomena in power converters that includes stability analysis, routes to chaos, and converter analysis in discontinuous driving mode, can be found in [
10,
17,
18].
In [
19], the authors studied the behavior of a two-dimensional system defined by a boost converter controlled with ZAD, where saturated periodic orbits and a period addition phenomenon are found. In [
20], a boost converter was controlled, chaos control was carried out with TDAS, and the period addition phenomenon was demonstrated in a model where parasitic resistances were included, making it closer to the experimental model. Additionally, in [
21], it was considered a switching surface that includes the current in the capacitor, chaos control was achieved with FPIC and some branches were classified. In [
22], the (ZAD) control technique applied to a boost converter for power factor correction was presented. In [
23], the authors presented the design, robustness analysis, and implementation of a ZAD and sliding mode control (ZAD–SMC) for a multiphase step-down converter. The controllers were implemented in a Field Programmable Gate Arrays (FPGA), and experimental results validated the transient response, robustness, and fixed switching frequency. FPGAs allow avoiding delays produced by sampling and PWM generation, using sequential algorithms on a microprocessor.
Unlike previous work, this paper presents the performance of a boost converter controlled with a zero average dynamics technique to regulate DC signals. Furthermore, the main contributions in this paper are defined as follows:
The state-space model is presented in a compact form and variable change is performed to depend only on the parameter .
The ZAD control technique is designed using a new sliding surface, where all the variables of the system are considered.
It is analytically demonstrated that the piecewise linear approximation of the switching surface is a good technique because the error can be considerably reduced. In addition, the maximum and minimum errors in the approximation occur precisely at the ends of the sub-intervals.
It is shown numerically that the system presents good voltage and current regulations and low relative error with respect to the reference signals.
The existence of the birth of a chaotic attractor is shown numerically for the boost converter controlled with ZAD.
A large regulation area with low errors is found based on a parametric diagram that depends on and , confirming the good performance of the boost converter controlled with ZAD.
The remainder of the paper is organized into three sections. First,
Section 2 presents the materials and methods, where the mathematical formulation of the problem is included. Then,
Section 3 presents the results and analysis. Finally,
Section 4 presents the conclusions.
2. Materials and Methods
This section presents the mathematical expressions to study the dynamics of the boost converter controlled with ZAD. Equations for the boost system, the control strategy, and the duty cycle are included. Furthermore, dynamics of the boost system related to the switching surface are formulated. Moreover, the piecewise linear approximation applied to the switching surface to obtain an explicit form of the duty cycle is expressed.
2.1. Boost Converter
This study is based on the differential equations of the system described by two state-space configurations, as shown in Equation (
1).
where the terms
,
, and
. In addition, the control variable
u takes values in the set
, depends on time, and its value is specified according to the type of control implemented for the system. Moreover, as the matrices
and
are different, the vector field
f is discontinuous. This type of discontinuity is responsible for inducing nonlinear effects when modeling a power converter.
A compact way of writing the system presented in Equation (
1) is now expressed in Equation (
2):
which can be also written as in Equation (
3):
The last expression is known as the control system, where
is the control variable or system input [
24]. From the point of view of the control theory, the system presented in Equation (
2) is not linear because the control variable multiplies the vector of state variables.
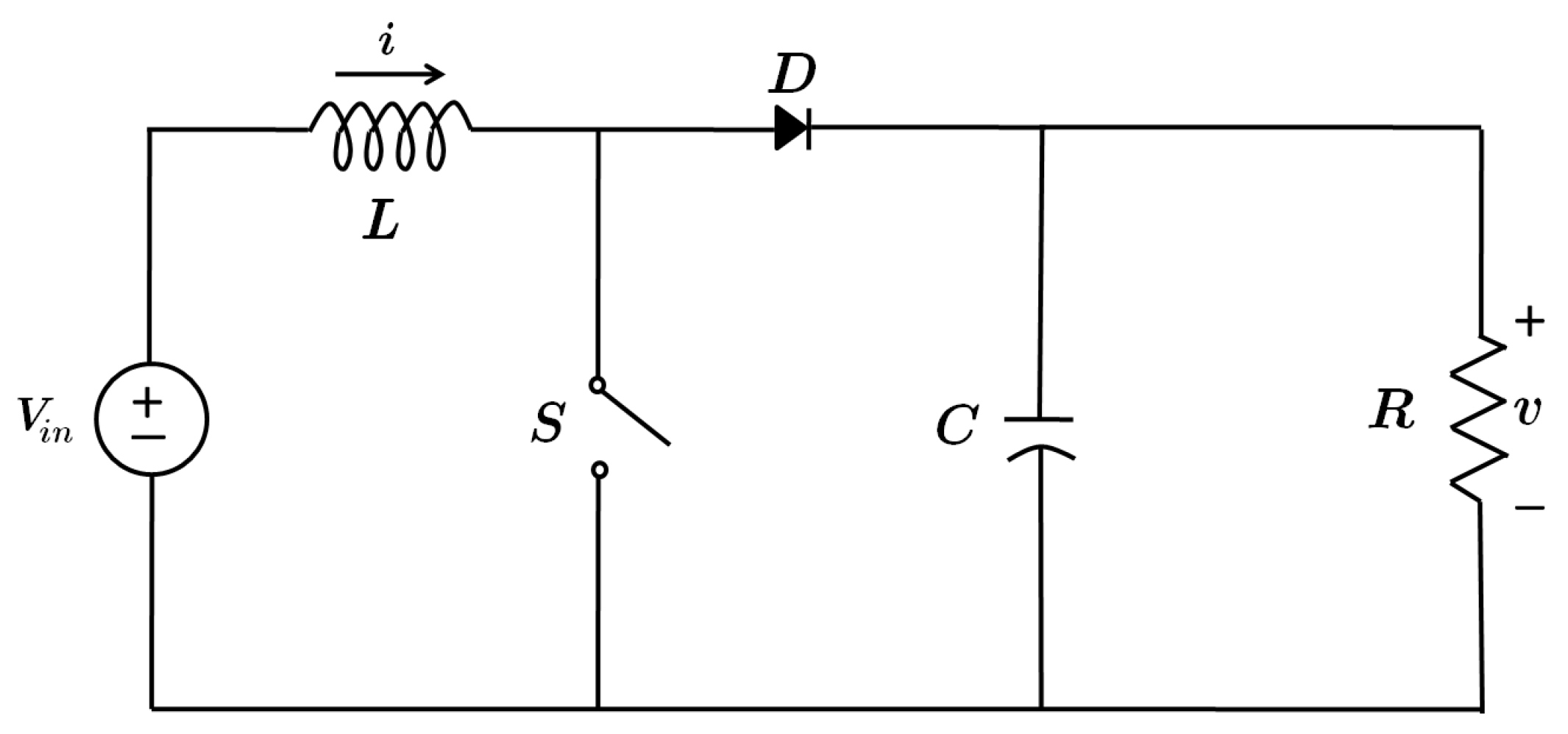
The control system that defines the boost converter is simplified, assuming that
. Then, the basic scheme of a boost converter is displayed in
Figure 1. In this figure,
is the input voltage,
i is the inductance current,
L is the inductor,
S is the switch,
D is the diode,
C is the capacitor, and
v is the output voltage. When the switch
S is closed (state ON), the coil
L stores energy from the voltage source
, while the load is fed by the capacitor
C. In addition, when the switch is open (state OFF), the current can only pass through diode
D and feed capacitor
C and the load.
The boost converter is governed by the following differential equations:
Consequently, the state space in which the system evolves is a subset
(where
is a unit circle). Performing changes in system variables, the following expressions are obtained as presented in Equations (
6)–(
8).
The system shows a unique parameter
in the following way:
A boost converter is a step-up power converter that obtains
with
. Therefore, when simulating the system, the initial voltage condition is assumed strictly to be more than 1. Now, Equations (
10) and (
11) are obtained when
u changes in the set
, as follows:
where:
This is a system with differential equations given by Equation (
1), which can be written compactly as in Equation (
15):
The solution for each topology is obtained as follows [
25]:
where
and
After considering each topology and calculating the exponential matrices, Equations (
19) and (
20) are obtained:
where
is a two-by-two identity matrix.
In terms of each of the components, the solutions of the system presented in Equation (
9) are as follows:
For the topology 1 (
),
For the topology 2 (
),
where
. Herein, an evaluation of
must be considered to avoid unwanted solutions.
If
, Topology 3 is obtained as follows:
However, the discontinuous conduction mode presented in Topology 3 is not obtained in this paper and thus will be not evaluated.
To validate the mathematical model described in (
15), a more exact model is simulated in MATLAB where parameters of an experimental circuit are included, with the following parameters:
V,
,
f,
mH,
,
and
. Herein, the term
is the inductor internal resistance, and
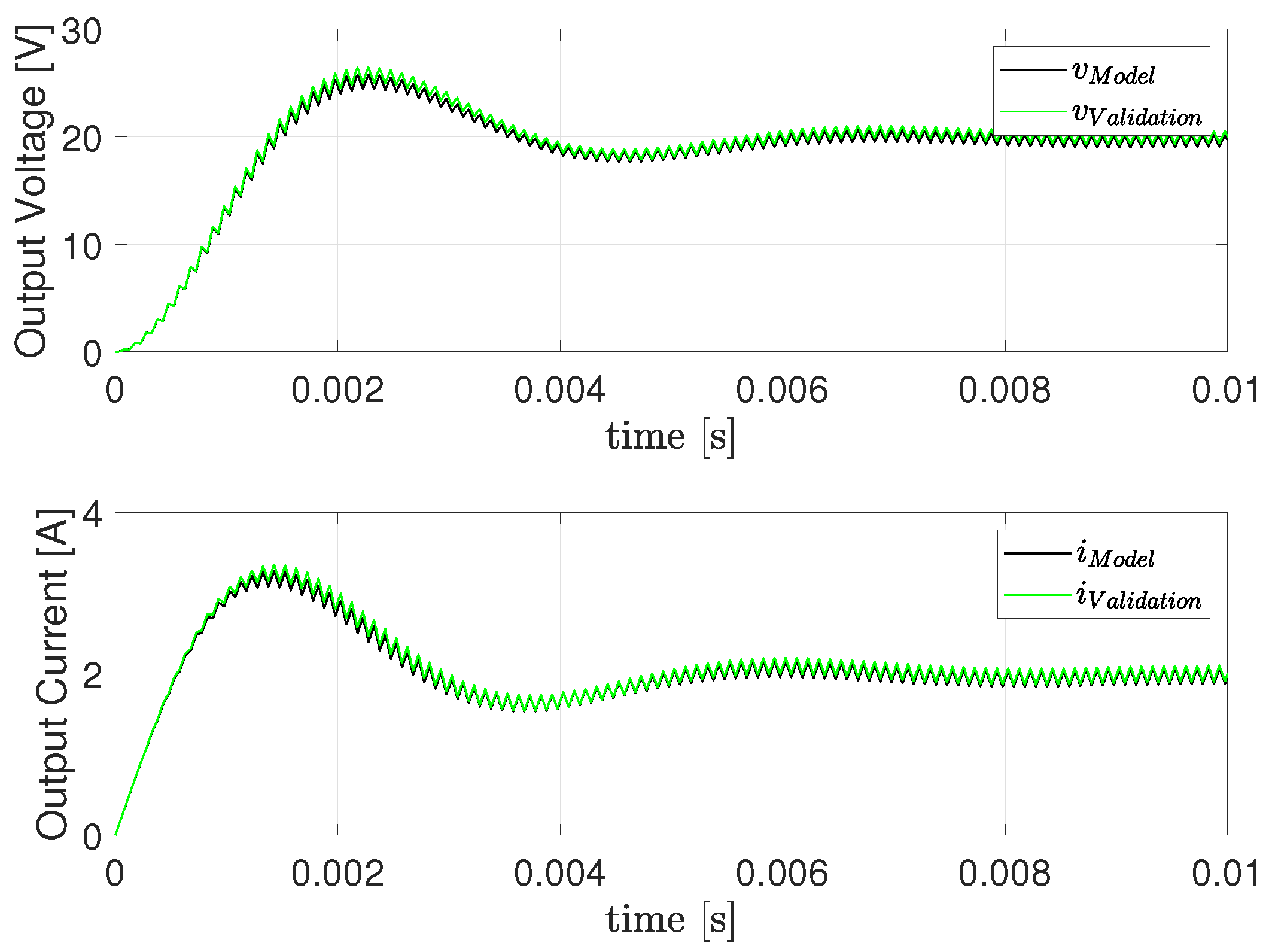
is the static drain-to-source on-resistance. The behavior in time of the open-loop system with a reference of
V is shown in
Figure 2. The results show that in both the transient state and steady-state operations, the two models behave similarly, concluding that Equation (
15) is a good mathematical representation of the boost converter.
2.2. Pulse-Width Modulation
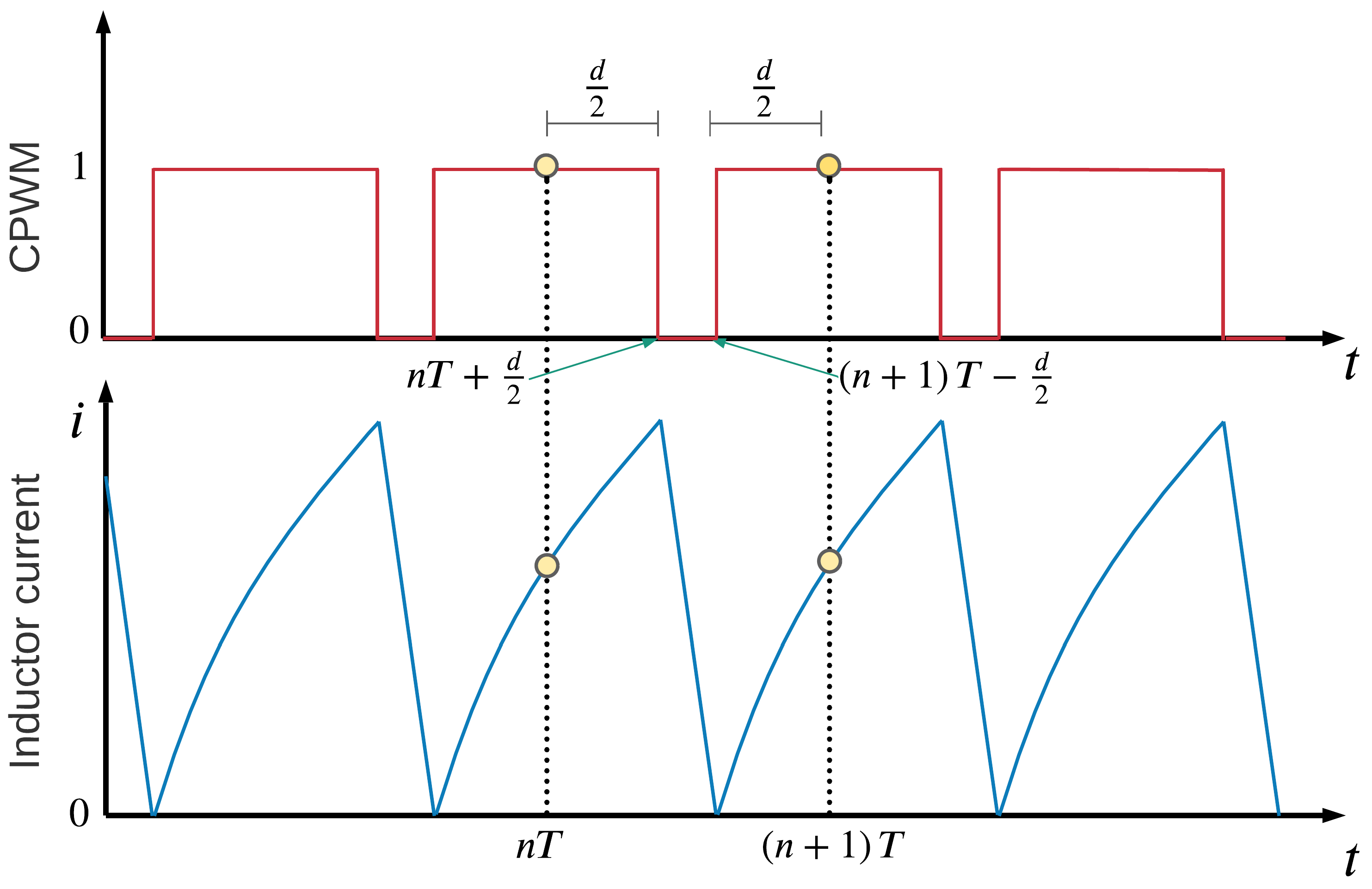
In this research, the CPWM is used. In period
T, two commutations are made in such a way that a time interval
is divided into three sub-intervals, where the first and last have the same length (
Figure 3).
Switching is carried out according to the scheme . In general, the duty cycle varies from period to period due to continuous ON–OFF switching, where the traditional way of calculating the duty cycle d is by using a reference ramp.
2.3. Zero Average Dynamics Technique
The duty cycle is calculated with the ZAD technique, defining the time that the switch is open or closed. In this control technique, sampling is performed for the capacitor voltage (v) and the inductor current (i). These two variables are measured at and (where no transients are presented). The sampling process must be synchronized in such a way that all variables are measured simultaneously.
This technique consists of the following:
The last condition guarantees that only there will be a finite switching number per period, as the control was designed with that intention.
2.4. Piecewise Linear Approximation of the Switching Surface
As a CPWM is used, the control variable
u that is applied to the system can be defined as follows:
The calculation of the duty cycle through Equation (
28), implies the solution of a transcendent equation. A piecewise linear function is used to approximate the switching surface and to produce an elementary equation from which the duty cycle can be calculated analytically. Therefore, this approach is performed by considering the following assumptions [
26]:
The dynamics of the error or switching surface behaves like a piecewise linear function.
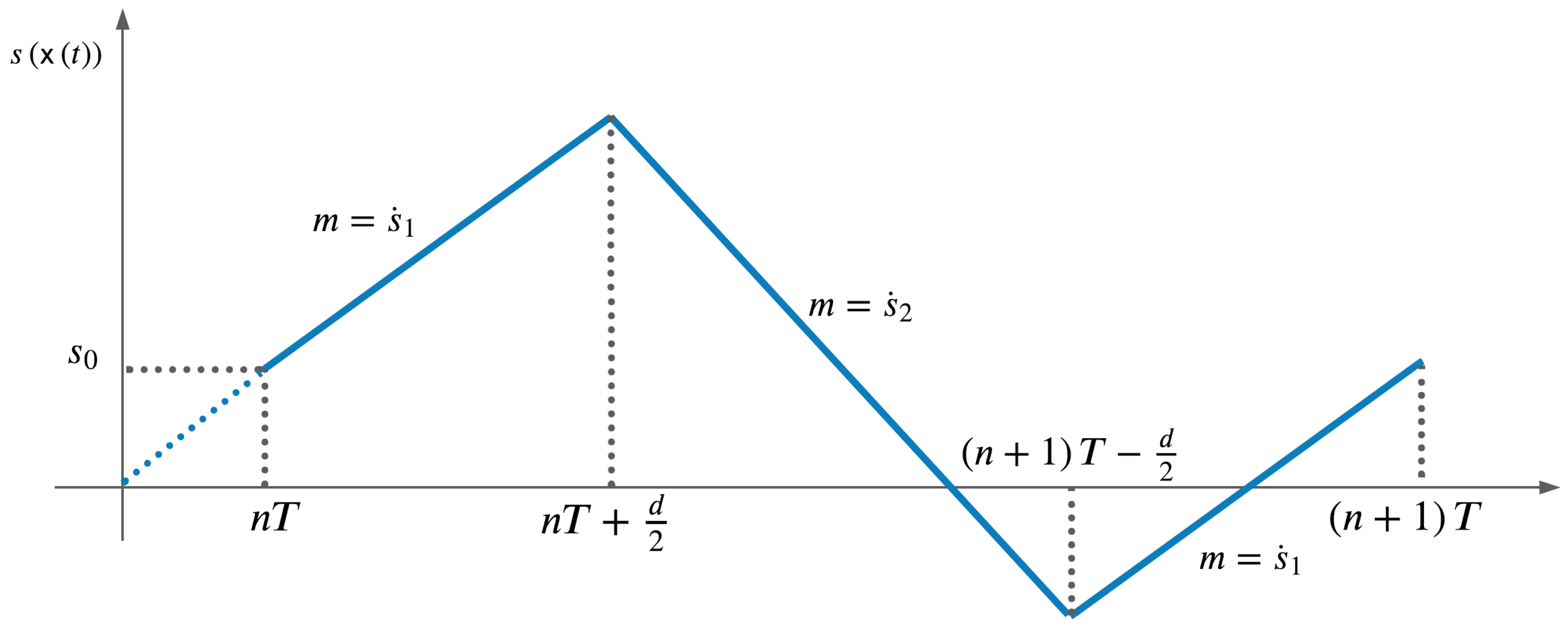
The slopes of the dynamic error at each section are determined by the slopes calculated at the switching time, assuming that the slope at the beginning of the period, noted as , is the same as at the end. That means that in the sections between and , the slope of is , which corresponds to the derivative of the switching surface with respect to time for the case . Furthermore, in the section the slope of is and corresponds to the derivative of the switching surface with respect to time for the case .
Figure 4 shows the piecewise linear approximation of the switching surface.
From the assumptions and the figure presented above, the following mathematical expressions are obtained as shown in Equations (
29)–(
31):
To validate Equation (
27), another approximation technique is selected. For instance, the Weierstrass approximation theorem states that for all real and continuous function
f [
27], defined in the compact interval
, no degenerated and for each real number
, there is a polynomial expression
p that depends on the
as follows:
for each
. In other words, the function
f can be approximated as uniform by the polynomial expression
p. Therefore, choosing the
as small as preferred, the relationship is established in Equation (
27). Then, the following holds:
Indeed, from the triangular inequality is obtained the following:
and as follows:
Considering the following:
Despite this polynomial approximation, the problem that arises is when solving the duty cycle
d from Equation (
33). However,
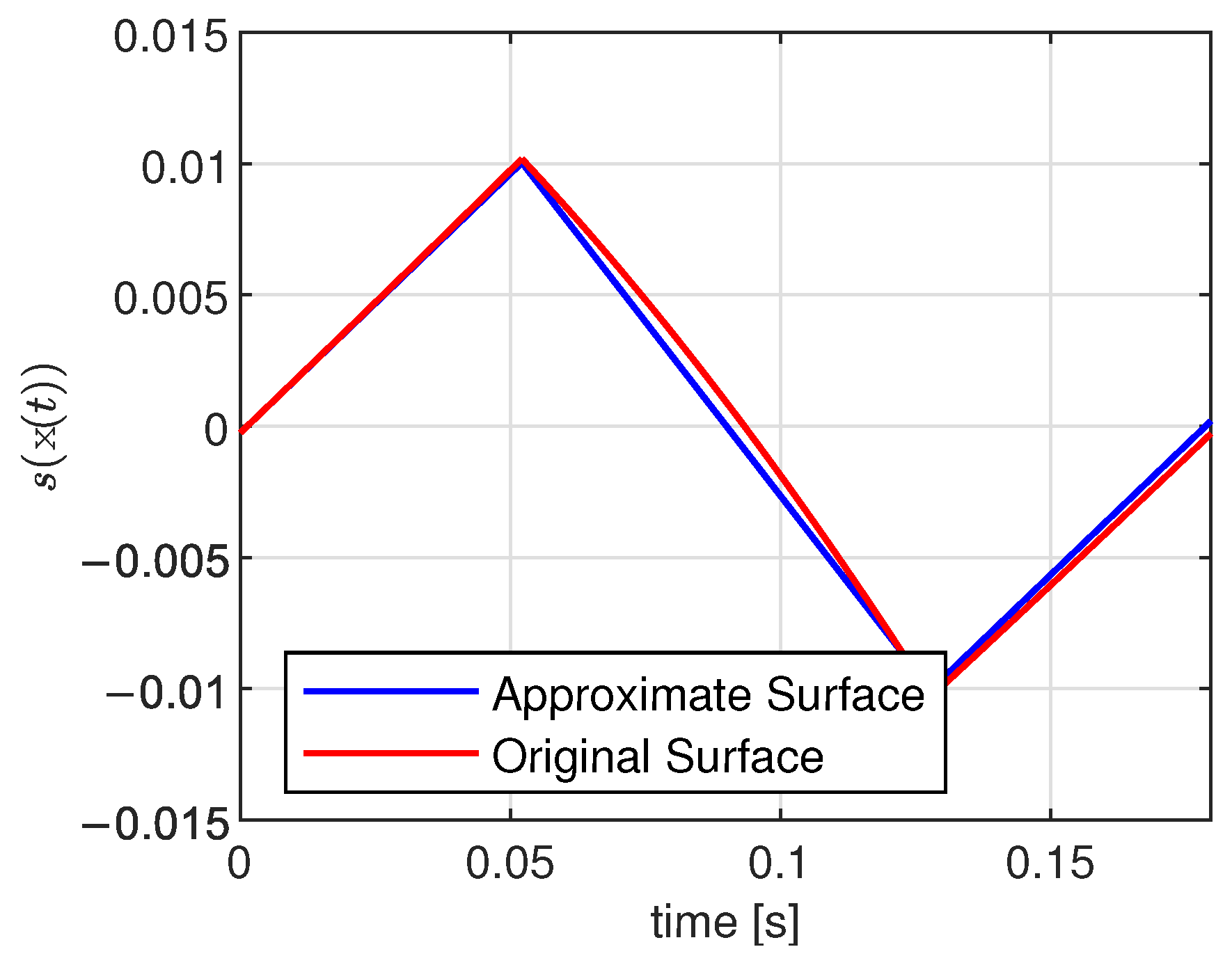
Figure 5 shows that the piecewise linear approximation of the switching surface is good.
Therefore, using the approximation of
obtained with the piecewise linear technique, the following expression is obtained:
, or the following:
Now, according to the different topologies, the following expressions are obtained:
Using the system solutions in each topology, considering the -periodic orbits; then the following holds:
For Topology 1, given
, if the following expression is chosen:
then:
For Topology 2, the following holds:
with
Therefore, given
, the following expression is chosen:
where
. Now, the following expression is obtained:
The simulation of the system, implemented in MATLAB, shows that the approximation is good, and that it is better for the topology corresponding to than for .
Now,
is the linear approximation of
. For the topology
, the following mathematical expression is obtained:
and it is null for
, from which the maximum and minimum values occur at the extremes of the intervals (precisely at switching).
Now, we have the following:
A minimum value is obtained when and have the same signs, and a maximum value when and have opposite signs.
From Equation (
49), it is obtained that
and for
, the maximum and minimum values obtained with the piecewise linear approximation of the switching surface depend on the switching instant
.
2.5. Duty Cycle
The duty cycle is calculated using the ZAD technique by approximating the switching surface with a piecewise linear function and using the equality presented in Equation (
27). Hence, using Equations (
29)–(
31) and the integral given by Equation (
27), the following mathematical expression is obtained:
When equating to zero, the duty cycle (
d) is then obtained as the following:
Values of the duty cycle could be or . In either of these two cases, the system saturates, even for the next election in each period. For instance, we have the following:
If , the system is forced to evolve according to Topology 1.
If , the system is forced to evolve according to Topology 2.
If denominator of Equation (
51), defined now as
, is equal to zero, then two possibilities are defined: (a) the system is forced to evolve according to Topology 1 if the numerator
; (b) the system is forced to evolve according to Topology 2 if
.
3. Results and Analysis
In this section, the performance of the ZAD technique is presented, considering voltage regulation and the presence of chaotic behavior. This analysis is performed by approximating the switching surface with a piecewise linear function.
3.1. ZAD with Piecewise Linear Approximation
Figure 6 shows the state space of the system simulated with the constant parameters
and
. For each figure,
,
s, and
are kept constant.
Figure 6 shows that the system evolves to the stable fixed point
of the Poincaré plot. This result shows the presence of
periodic orbit in the dynamic system, defined in Equation (
9). This simulation considers
and
.
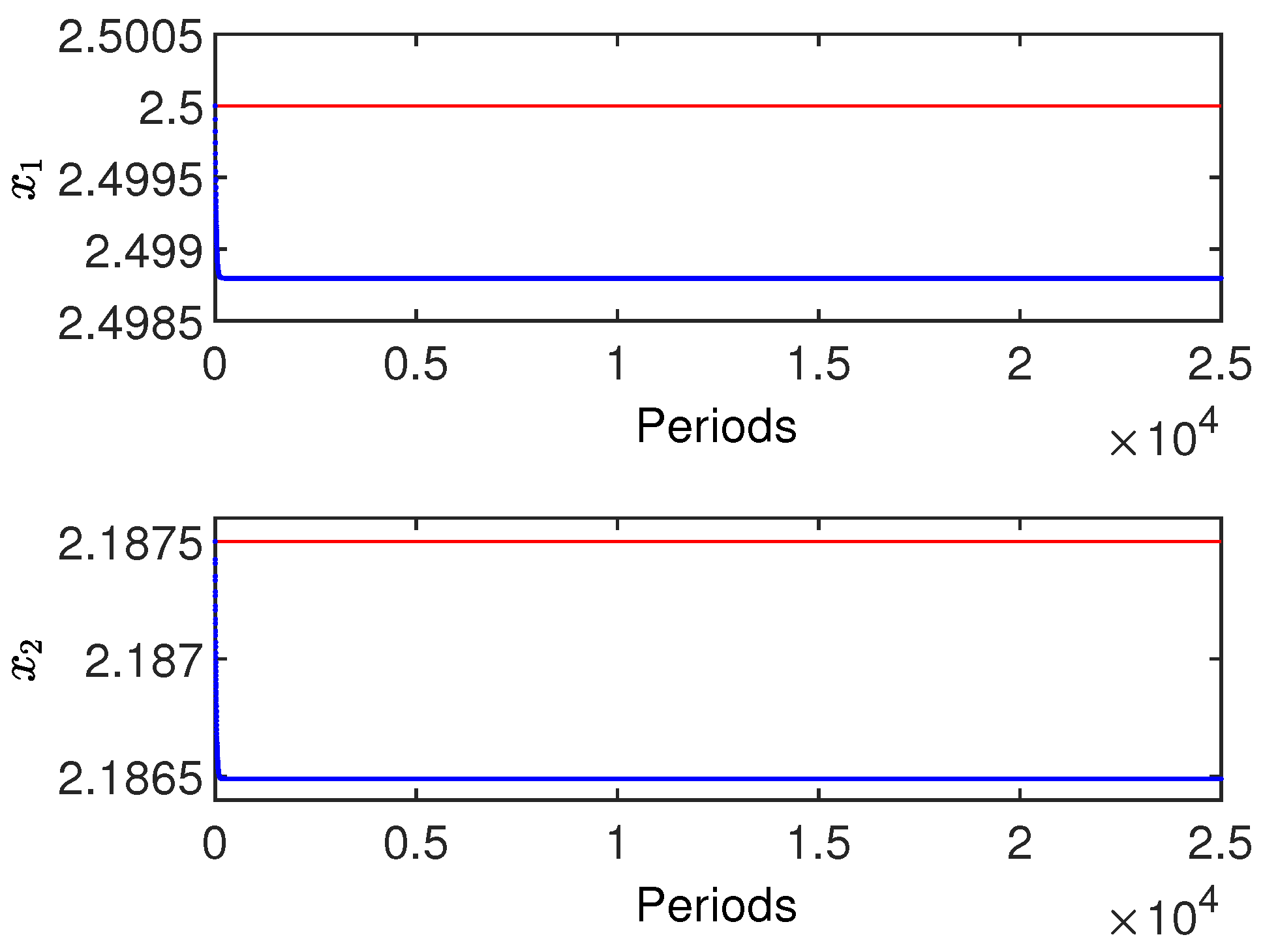
Figure 7 shows the regulation of the voltage and current variables, identified as
and
, respectively. The red lines correspond to the voltage and current references, and the blue lines are the measured variables. This simulation considers
and
. The result shows that the system presents excellent regulation in both current and voltage variables. The differences between the references and the measured values are obtained for the voltage as
and the current as
. These last calculations give a relative voltage regulation error of
and a current regulation error of
.
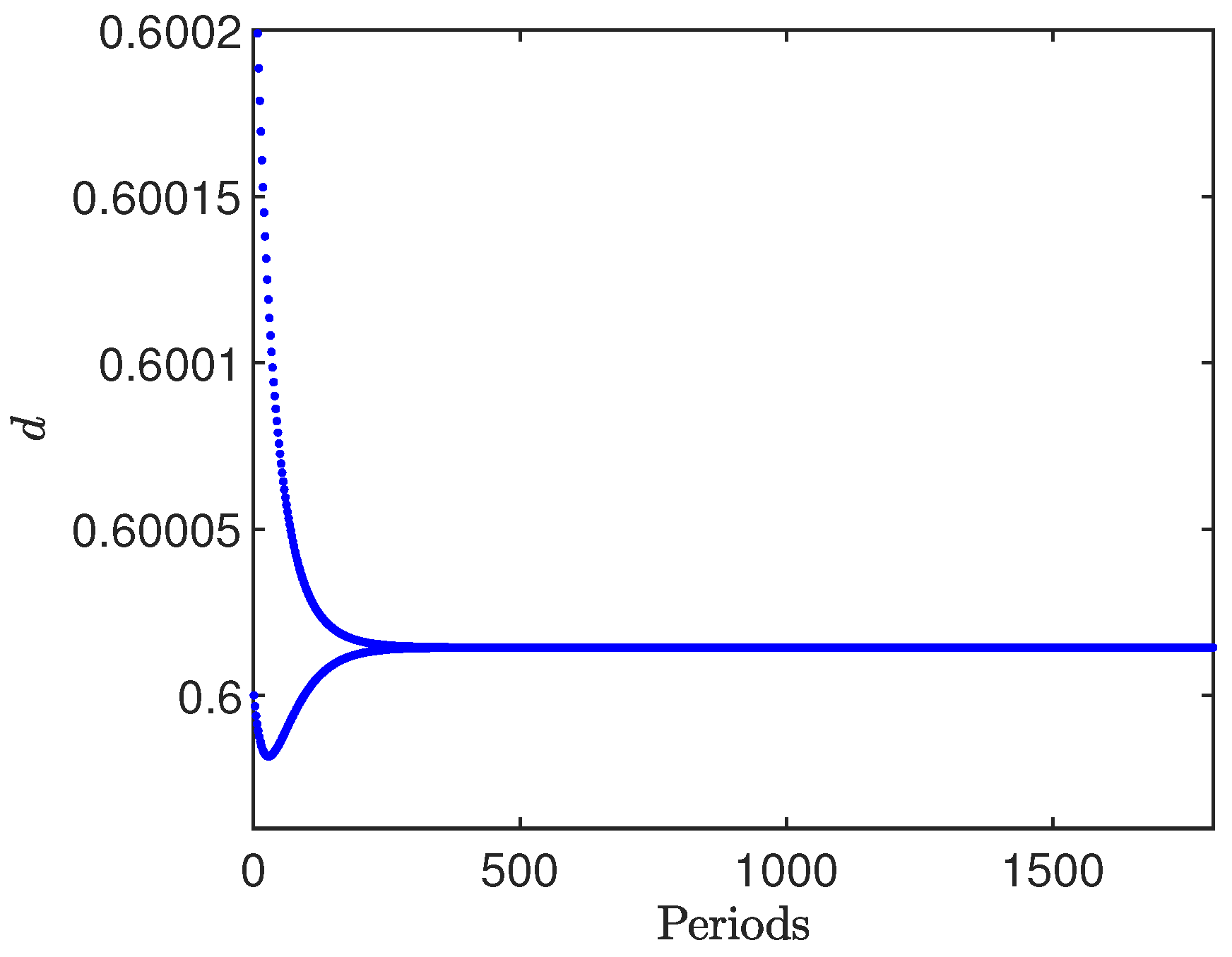
Figure 8 shows that the duty cycle stabilizes quickly at a value of
. The duty cycle is normalized to changes between 0 and 1. This simulation considers
and
. In this case, the duty cycle is unsaturated and with fixed switching frequency [
28], complying with the characteristics of this type of control presented in [
5,
23], which validates the veracity of these results.
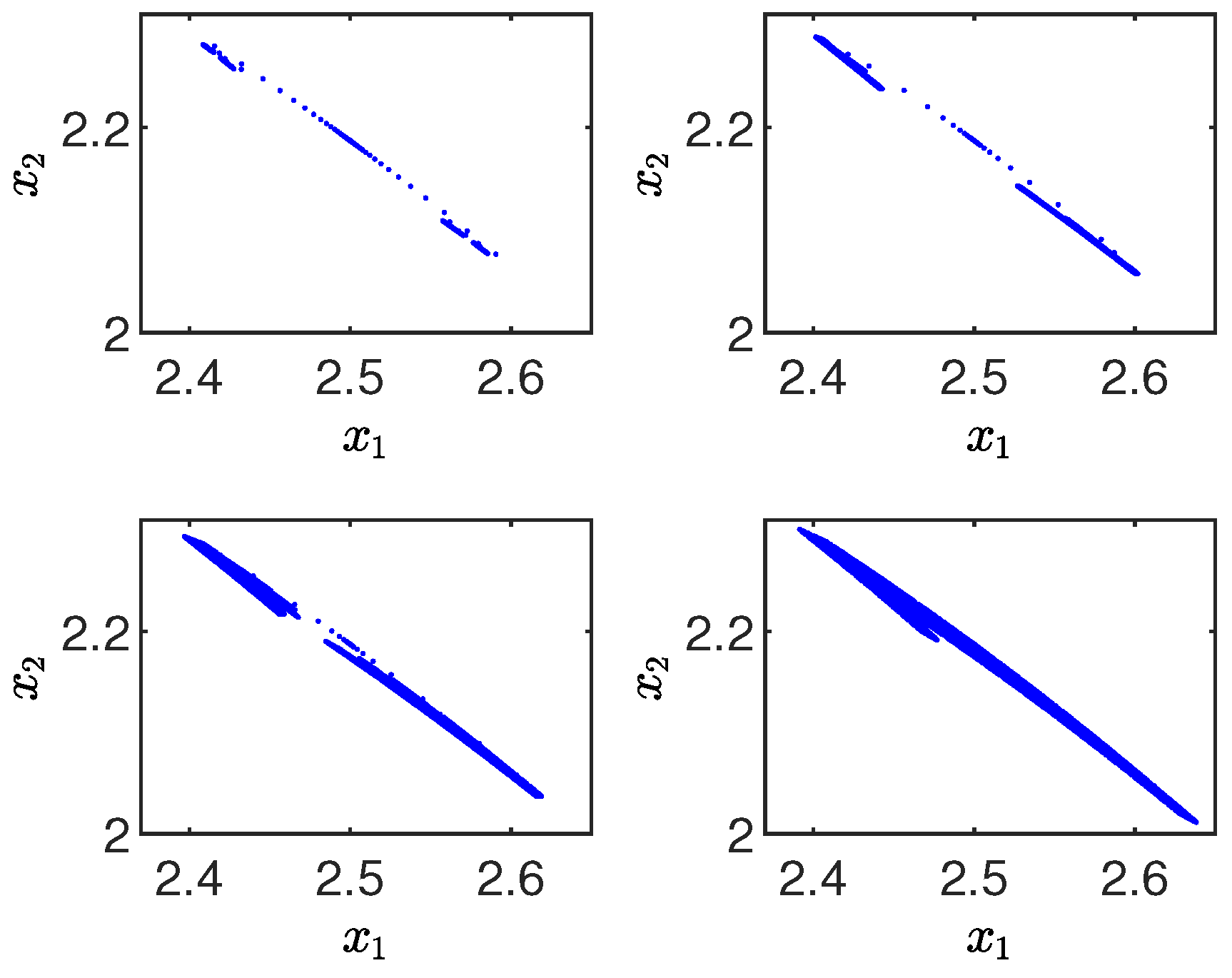
A chaotic attractor, identified with the letter
A, is shown in
Figure 9. For each graph in
Figure 9, the following value is selected:
. In the first figure,
; in the second,
; in the third,
; and in the last (corresponding to the attractor), the chosen value is
. It is difficult to find the exact value of
that causes a chaotic attractor.
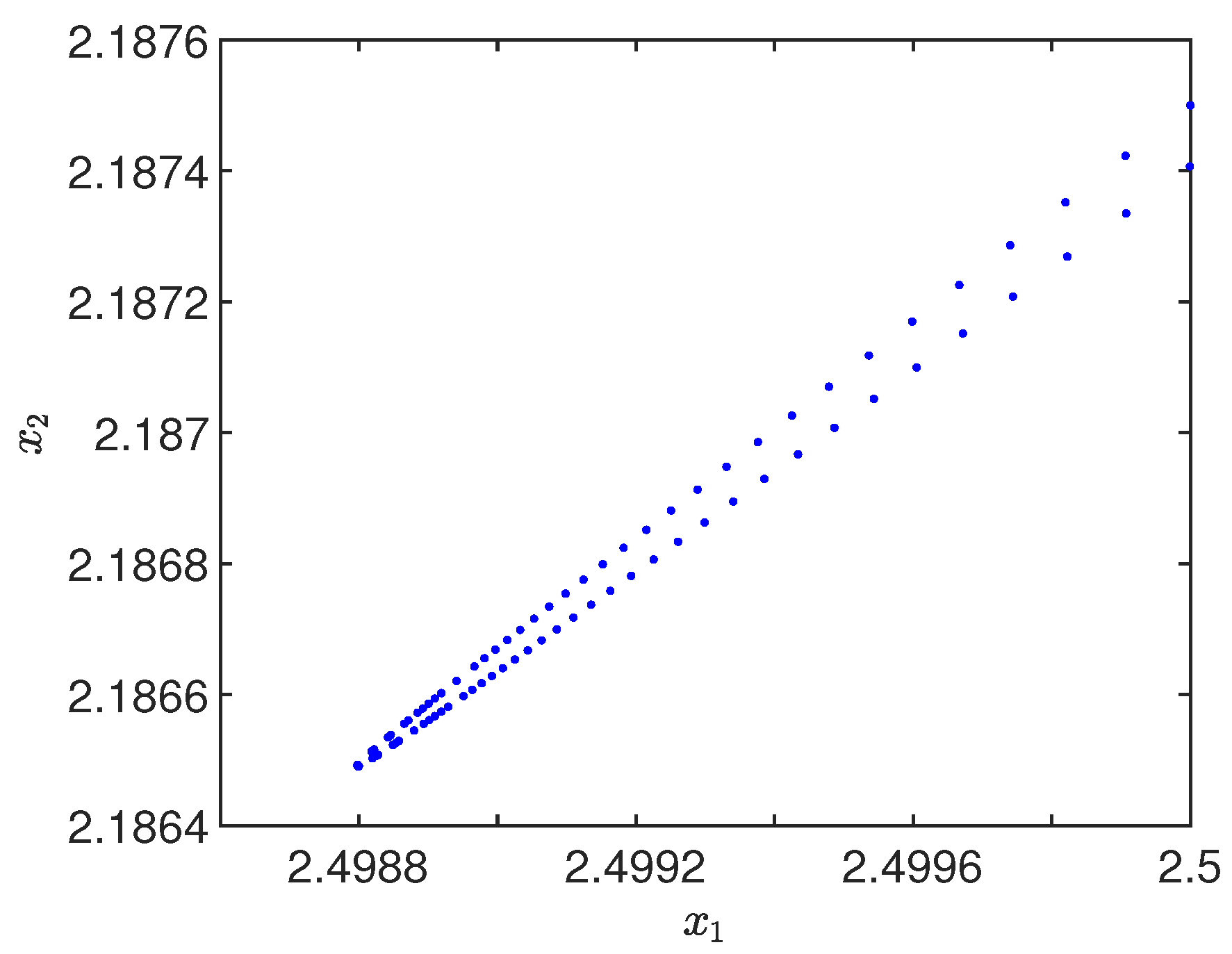
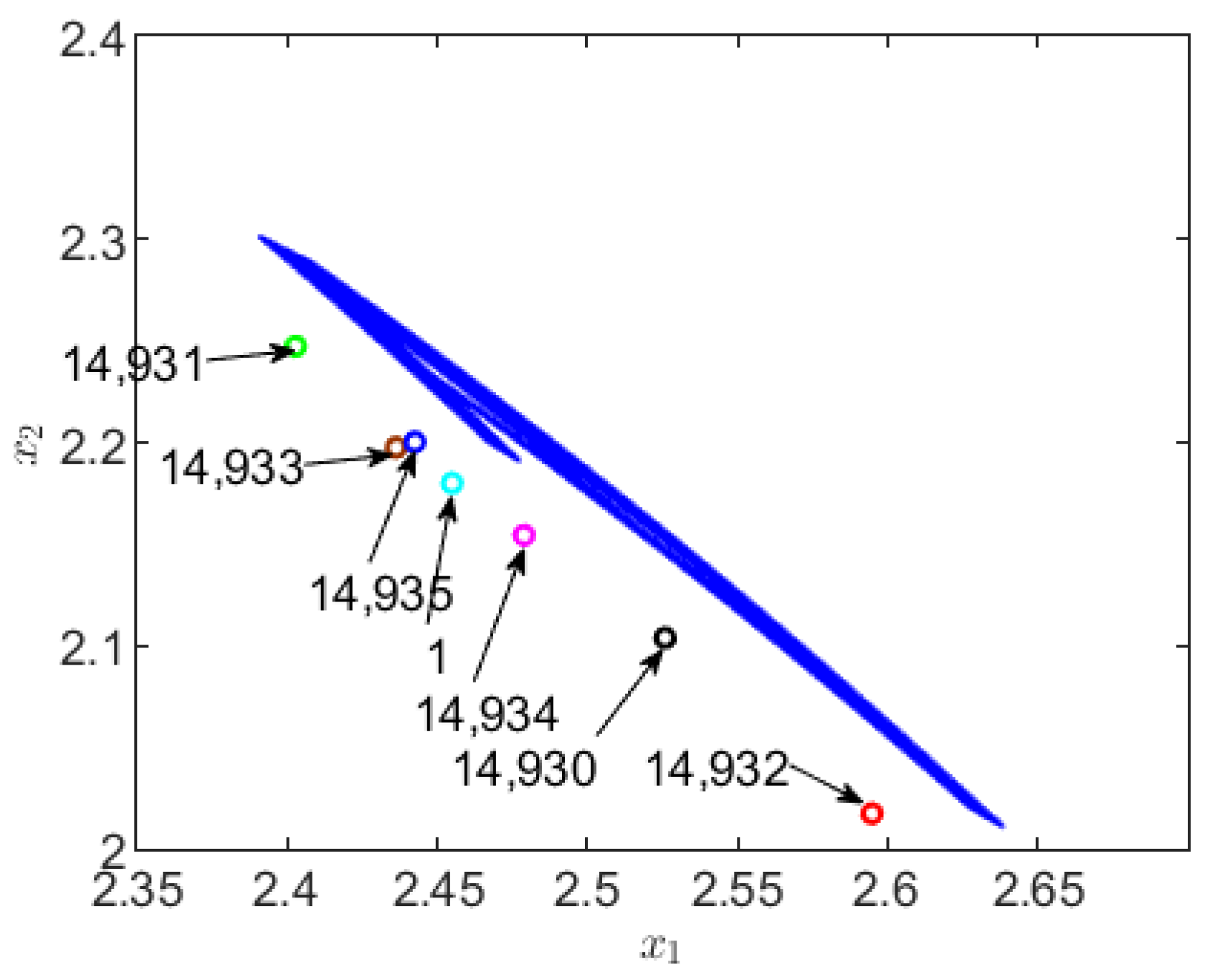
Figure 10 corresponds to an extension of the chaotic attractor. Note that as a subset of the state space, the attractor
A is contained, for example, in the ball centered at
and radius 1, which means that
A is bounded.
This figure shows the first iteration of the Poincaré map and iterations from 14,930 to 14,935 corresponding to an initial condition
, which is close to
or the set
A. In addition, it is observed that these iterations oscillate without a certain pattern. Set
A has a sensitive dependence on the initial conditions [
29].
Using the Euclidean metric, the distance between the previous iterations and set A is estimated. This distance is less than (where u represents the units) and it is calculated by constructing a perpendicular line to the set A and passing through the point corresponding to iteration 14,932. Then, a right triangle is constructed with a vertex in this iteration and hypotenuse in the perpendicular line. Numerically, set A attracts from a certain iteration all the iterations that follow. The generation of set A is carried out with 30,000 iterations of the Poincaré map.
Choosing other initial conditions close to
, the result shows that set
A is indeed a chaotic attractor. Then, with the calculation of the Lyapunov exponents,
A is found in an area where the system exhibits chaotic behavior.
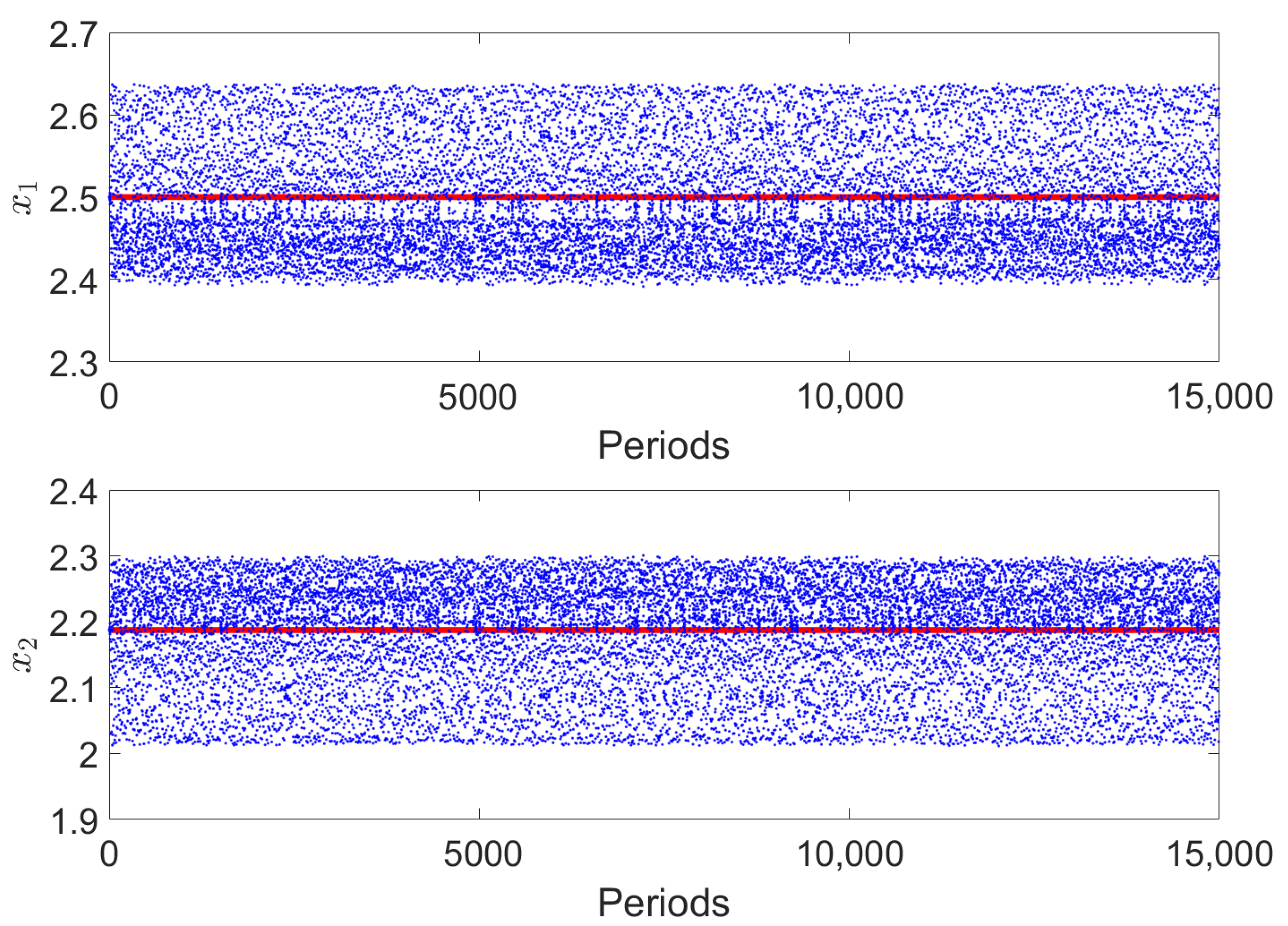
Figure 11 shows that, even though it operates in a chaotic regime, the system presents good regulation in both the voltage and current. Indeed,
and
. The relative voltage error of
and the relative current error of
are obtained.
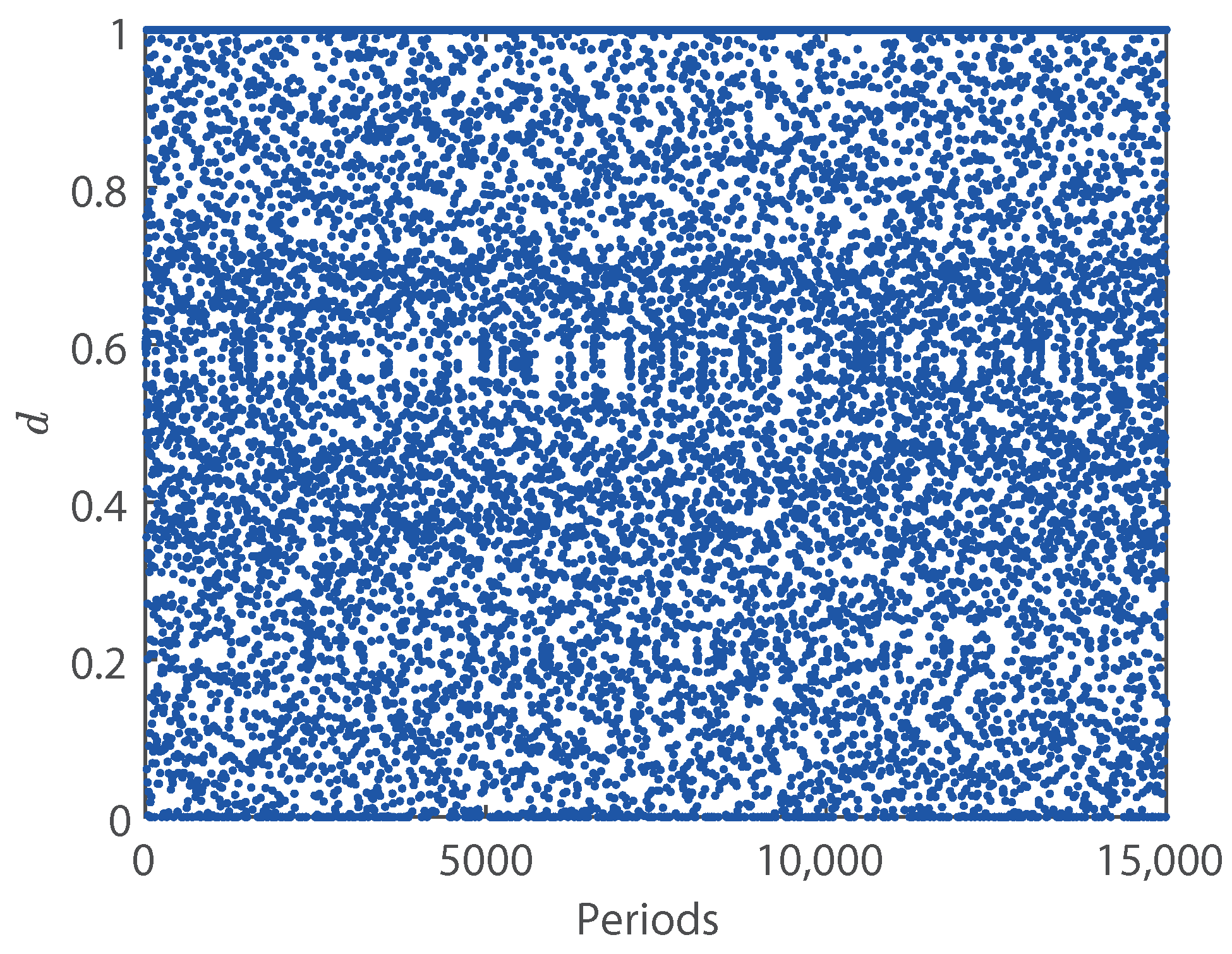
The scattered points in
Figure 12 correspond to the evolution of the duty cycle, and they confirm that the system is operating in a chaotic regime.
3.2. Regulation
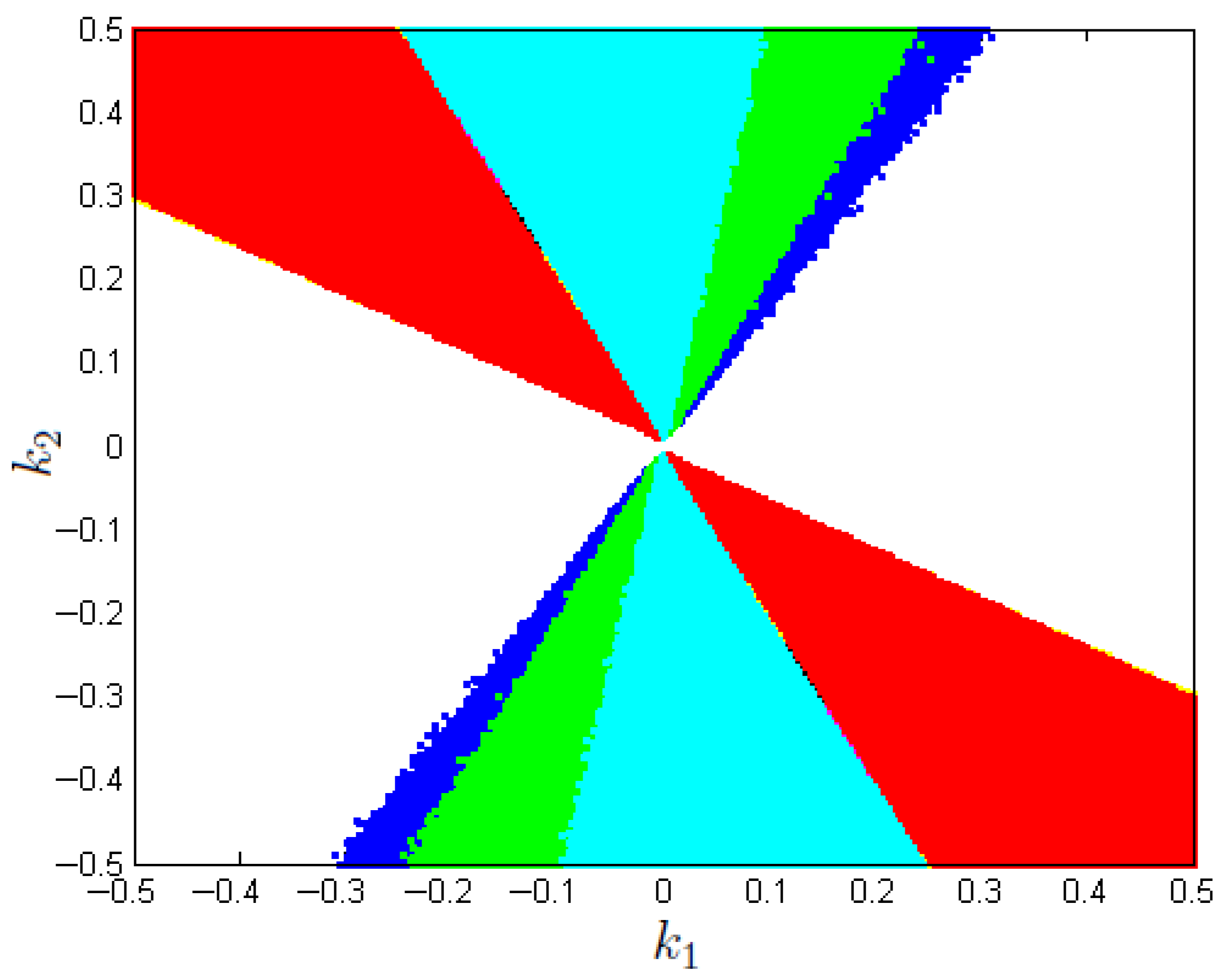
This section analyzes the ability of the ZAD and boost converter to follow a constant reference signal (system regulation) with changes in the switching surface parameters
). Hence,
Figure 13 shows different regulation zones in the bi-parametric space diagram graphed in the planes
and
. These results show that the system regulates the voltage magnitude from
to
. The reference signal to follow is constant and equal to
.
The regulation error is greater than in the white zones, which means that the operation is not good. Furthermore, in the blue zones, the regulation error is ; in the green zones, it is ; and in the cyan zones, it is . Moreover, in the magenta zones, the regulation error is ; in the black zones, it is ; in the yellow zones, it is ; and in the red zones, it is . Therefore, these results show a wide area where the system is regulating well with errors from to .