Response of Viscoelastic Turbulent Pipeflow Past Square Bar Roughness: The Effect on Mean Flow
Abstract
1. Introduction
2. Problem Description
3. Results and Discussion
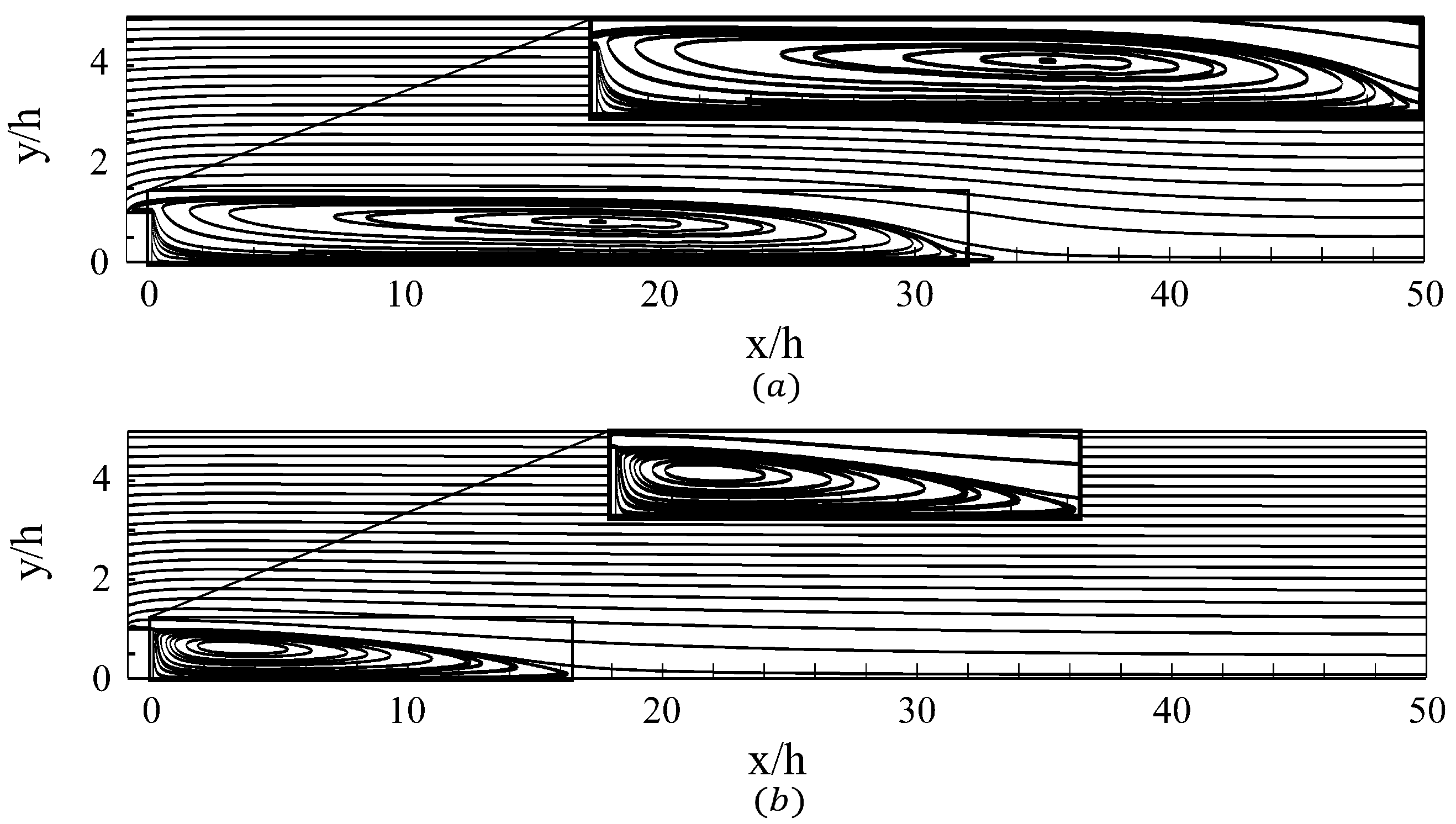
3.1. Flow Response
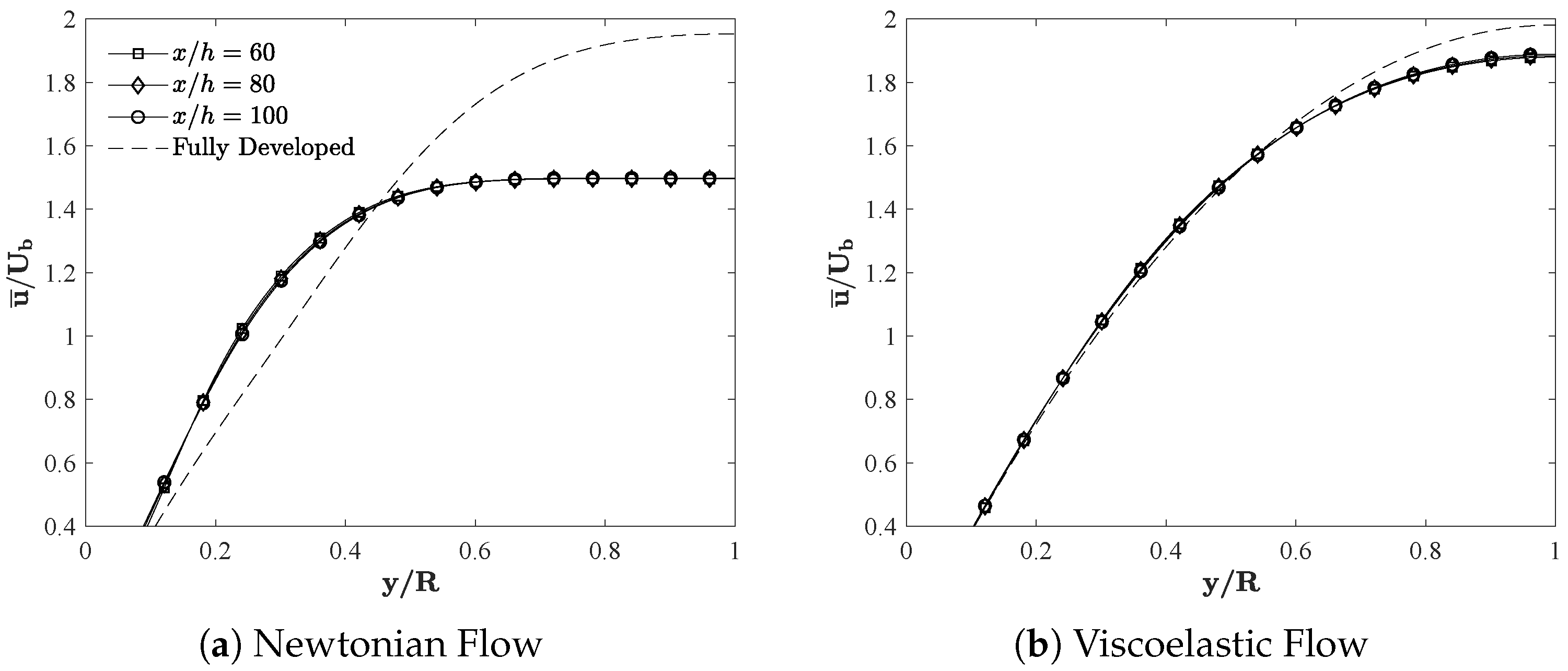
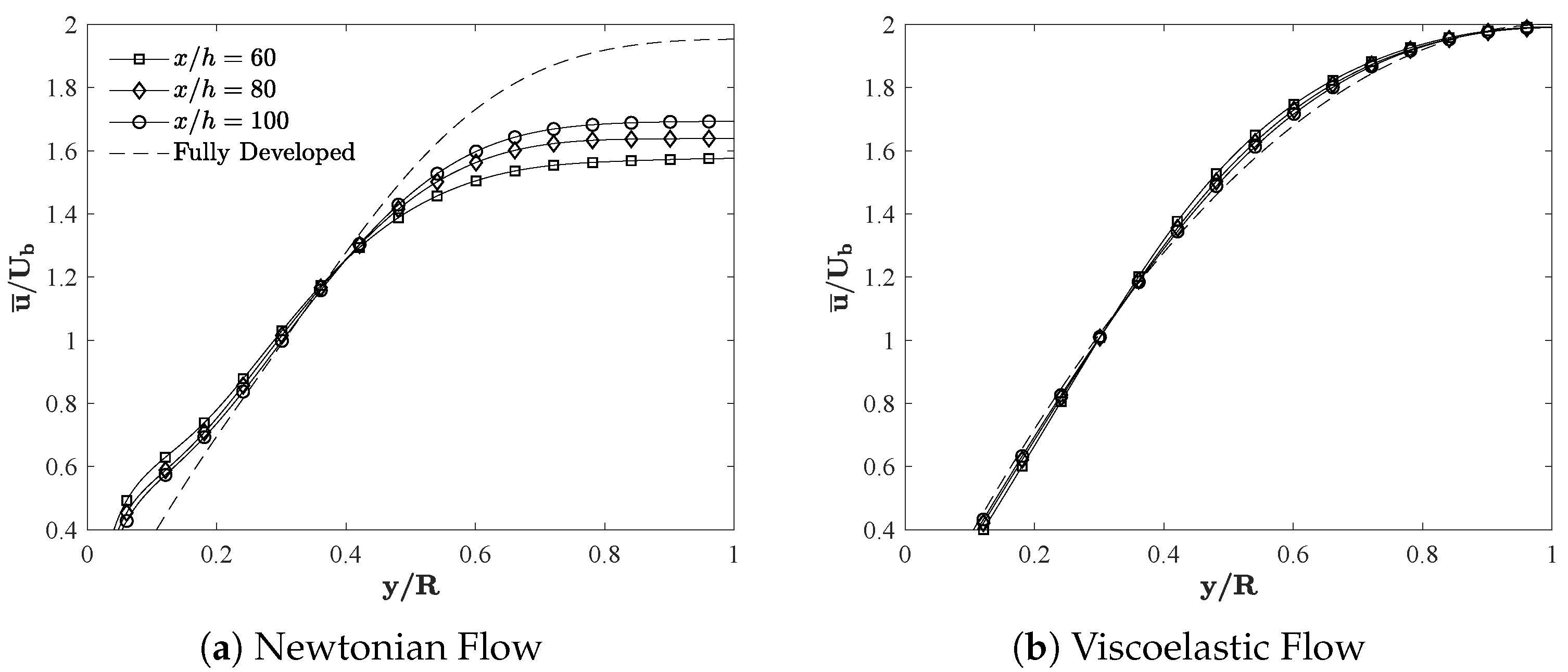
3.2. Flow Recovery
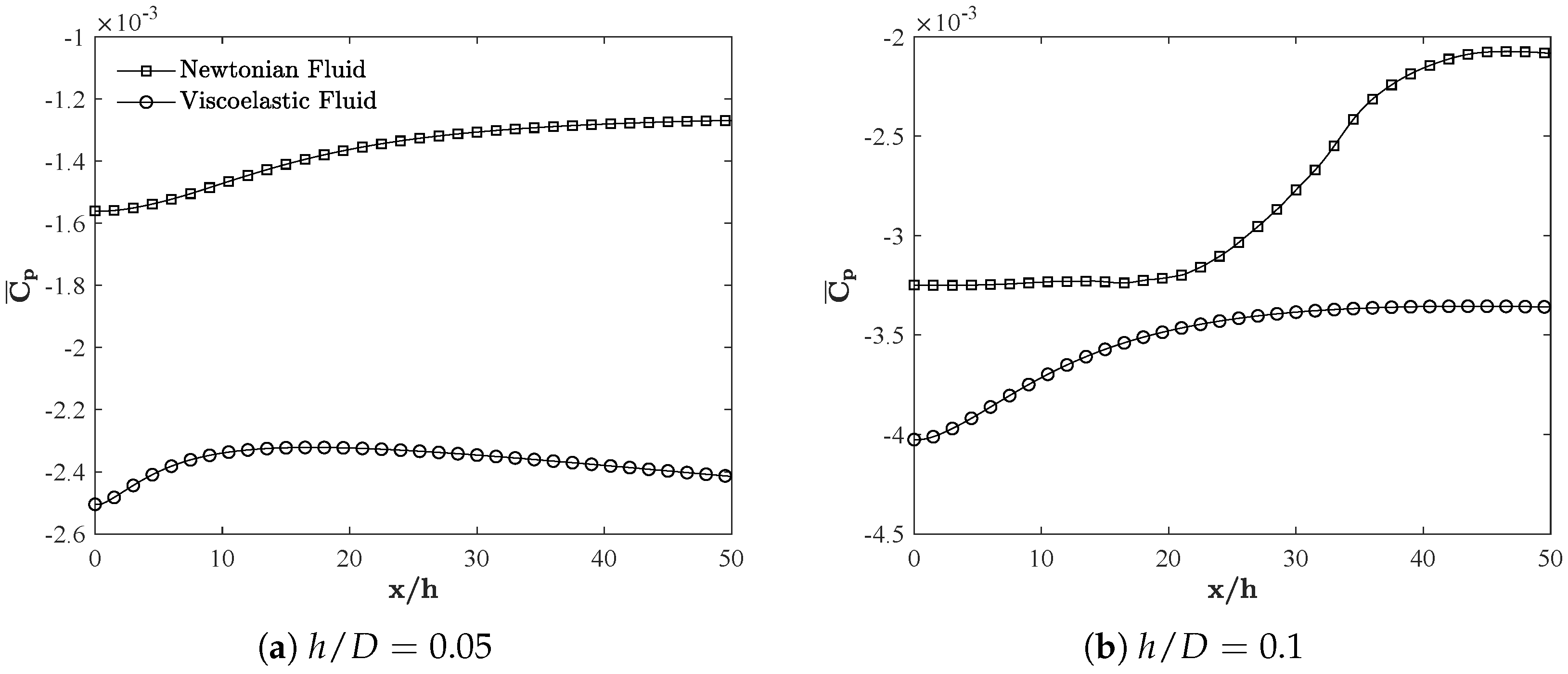
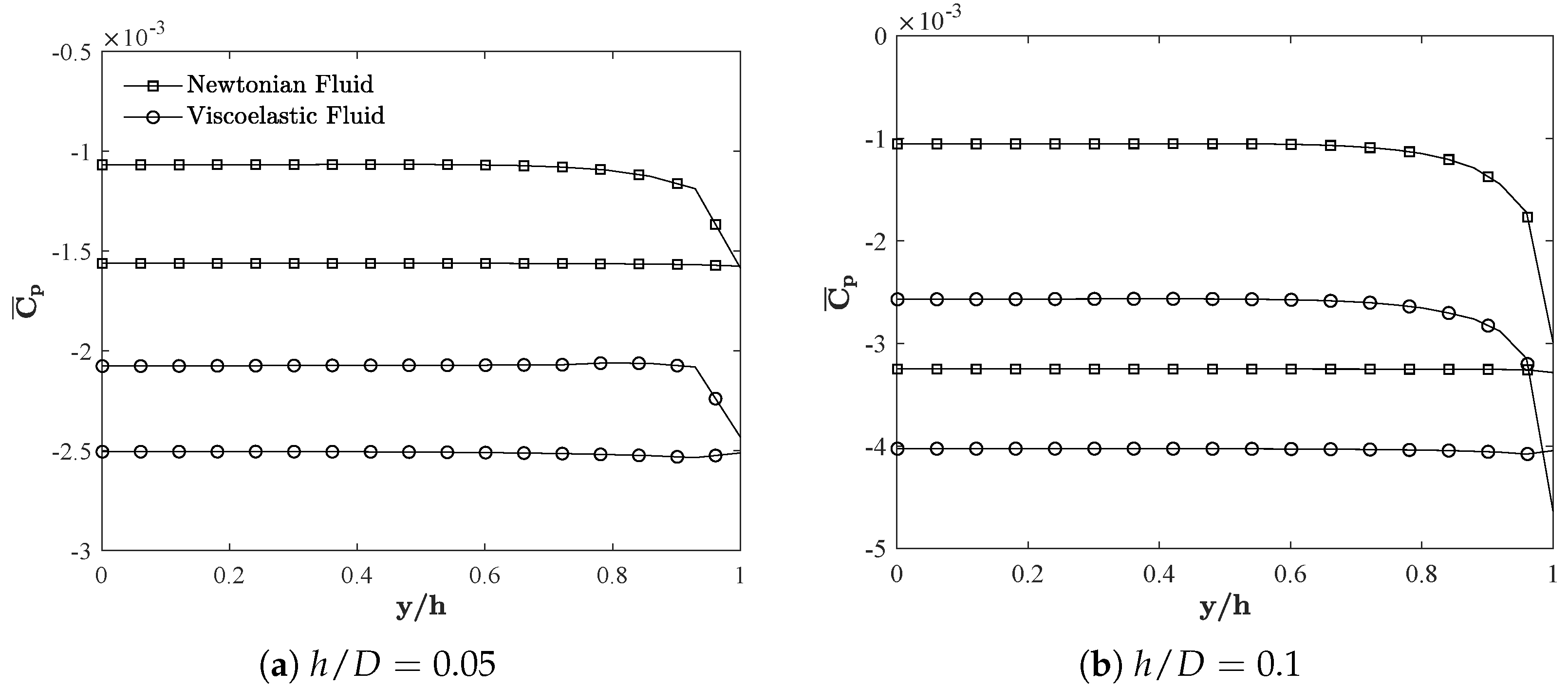
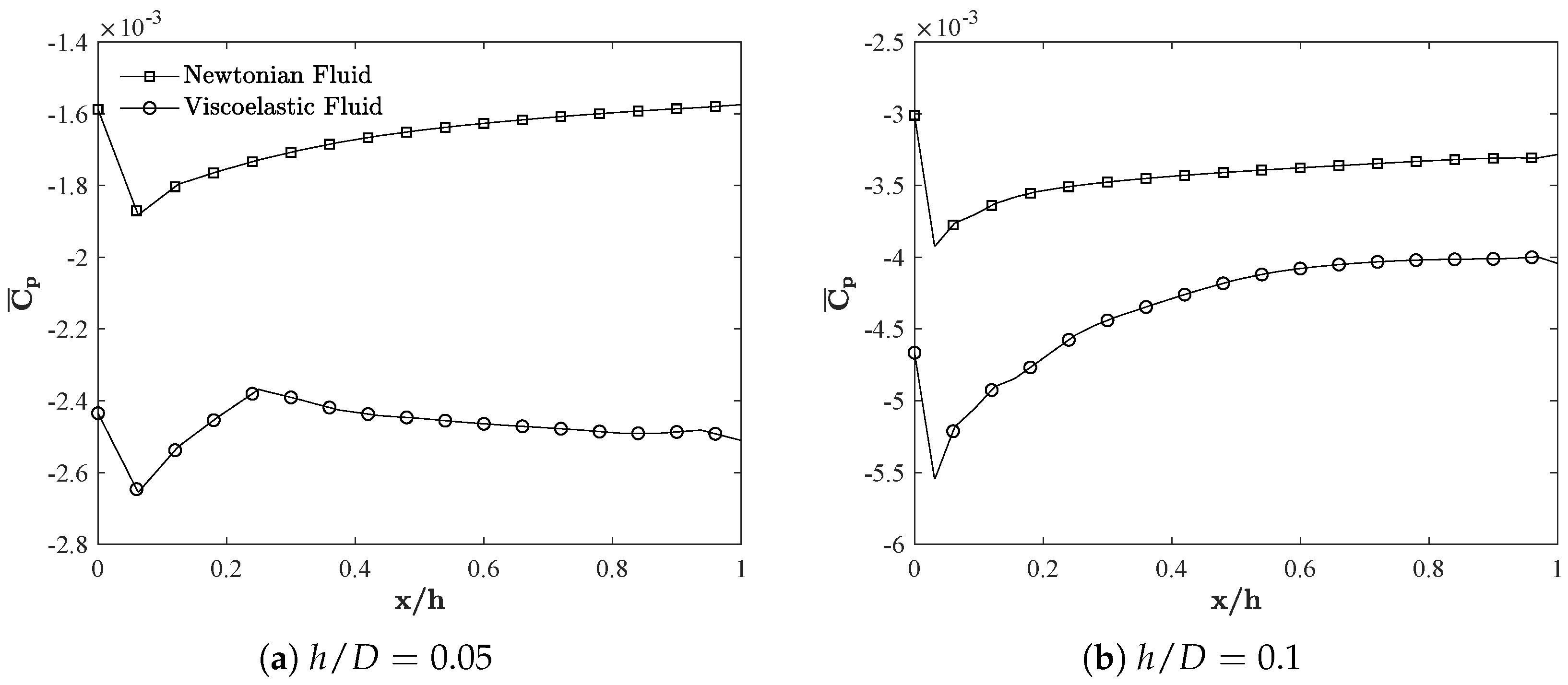
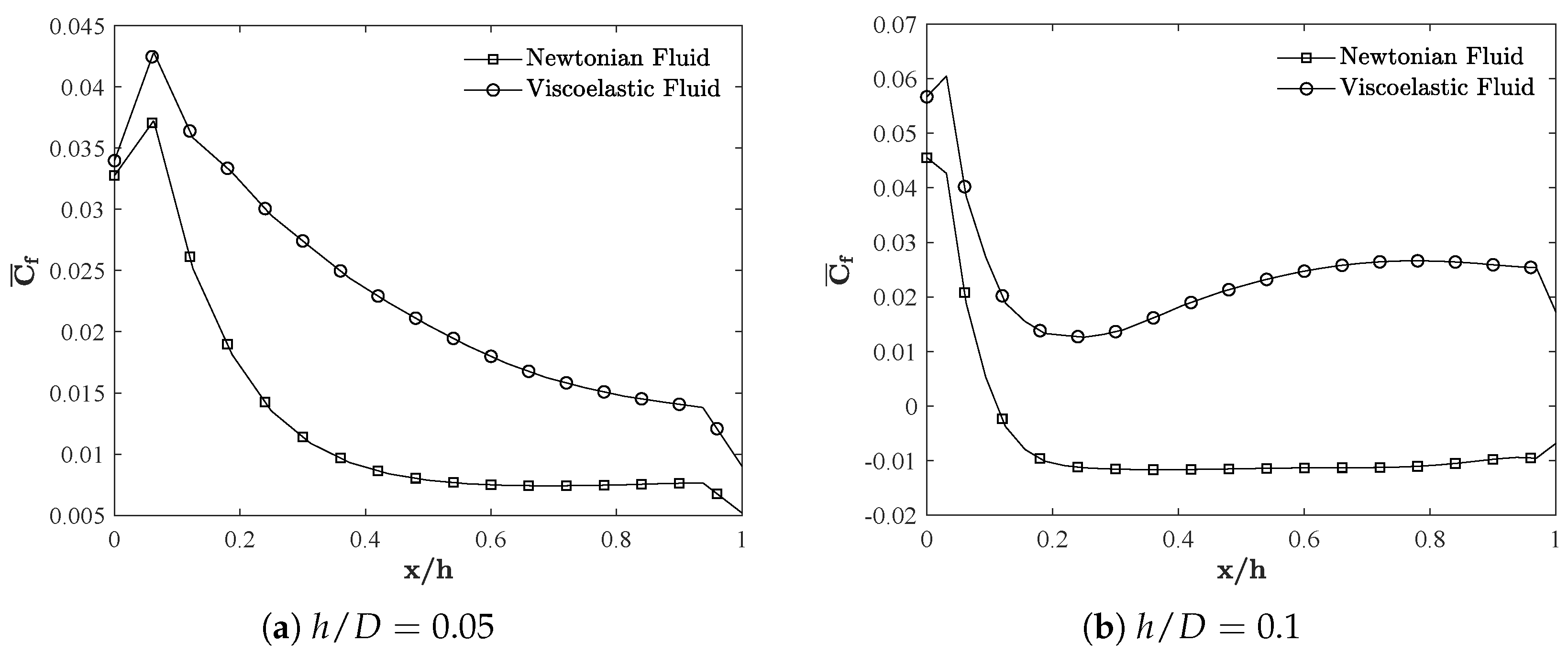
3.3. Distribution of Pressure and Wall Shear Stresses
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hart, A. A review of technologies for transporting heavy crude oil and bitumen via pipelines. J. Pet. Explor. Prod. Technol. 2014, 4, 327–336. [Google Scholar] [CrossRef]
- Abdul-Hadi, A.A.; Khadom, A.A. Studying the effect of some surfactants on drag reduction of crude oil flow. Chin. J. Eng. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- White, C.M.; Mungal, M.G. Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 2008, 40, 235–256. [Google Scholar] [CrossRef]
- White, C.M.; Somandepalli, V.S.R.; Mungal, M.G. The turbulence structure of drag-reduced boundary layer flow. Exp. Fluids 2004, 36, 62–69. [Google Scholar] [CrossRef]
- Toms, B.A. Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. Proc. Inf. Cong. Rheol. 1948, 1948, 135. [Google Scholar]
- Hanks, R.W. Fluid Dynamics (Chemical Engineering); Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Burger, E.D.; Munk, W.R.; Wahl, H.A. Flow increase in the Trans Alaska Pipeline through use of a polymeric drag-reducing additive. J. Pet. Technol. 1982, 34, 377–386. [Google Scholar] [CrossRef]
- Takeuchi, H. Demonstration test of energy conservation of central air conditioning system at the Sapporo City Office Building—Reduction of pump power by flow drag reduction using surfactant. Synth. Engl. Ed. 2012, 4, 136–143. [Google Scholar]
- Sellin, R.H.J. Drag reduction in sewers: First results from a permanent installation. J. Hydraul. Res. 1978, 16, 357–371. [Google Scholar] [CrossRef]
- Fabula, A.G. Fire-Fighting Benefits of Polymeric Friction Reduction. J. Basic Eng. 1971, 93, 453–455. [Google Scholar] [CrossRef]
- Verma, S.; Hemmati, A. Performance of Overset Mesh in Modeling the Wake of Sharp-Edge Bodies. Computation 2020, 8, 66. [Google Scholar] [CrossRef]
- Smits, A.J.; Young, S.T.B.; Bradshaw, P. The effect of short regions of high surface curvature on turbulent boundary layers. J. Fluid Mech. 1979, 94, 209–242. [Google Scholar] [CrossRef]
- Durst, F.; Wang, A.B. Experimental and numerical investigations of the axisymmetric, turbulent pipe flow over a wall-mounted thin obstacle. In Proceedings of the 7th Symposium on Turbulent Shear Flows, Stanford, CA, USA, 21–23 August 1989; Volume 1, pp. 4–10. [Google Scholar]
- Dimaczek, G.; Tropea, C.; Wang, A.B. Turbulent flow over two-dimensional, surface-mounted obstacles: Plane and axisymmetric geometries. In Advances in Turbulence 2; Springer: Berlin/Heidelberg, Germany, 1989; pp. 114–121. [Google Scholar]
- Jiménez, J. Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 2004, 36, 173–196. [Google Scholar] [CrossRef]
- Smits, A.; Ding, L.; Van Buren, T. Flow over a square bar roughness. In Proceedings of the 11th International Symposium on Turbulence and Shear Flow Phenomena, Southampton, UK, 30 July–2 August 2019. [Google Scholar]
- Leonardi, S.; Orlandi, P.; Smalley, R.J.; Djenidi, L.; Antonia, R.A. Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 2003, 491, 229. [Google Scholar] [CrossRef]
- Hemmati, A.; Wood, D.H.; Martinuzzi, R.J. Wake dynamics and surface pressure variations on two-dimensional normal flat plates. AIP Adv. 2019, 9, 045209. [Google Scholar] [CrossRef]
- Goswami, S.; Hemmati, A. Response of turbulent pipeflow to multiple square bar roughness elements at high Reynolds number. Phys. Fluids 2020, 32, 075110. [Google Scholar] [CrossRef]
- Goswami, S.; Hemmati, A. Evolution of turbulent pipe flow recovery over a square bar roughness element at a range of Reynolds numbers. Phys. Fluids 2021, 33, 035113. [Google Scholar] [CrossRef]
- Favero, J.L.; Secchi, A.R.; Cardozo, N.S.M.; Jasak, H. Viscoelastic flow analysis using the software OpenFOAM and differential constitutive equations. J. Non-Newton. Fluid Mech. 2010, 165, 1625–1636. [Google Scholar] [CrossRef]
- Tsukahara, T.; Kawase, T.; Kawaguchi, Y. DNS of viscoelastic turbulent channel flow with rectangular orifice at low Reynolds number. Int. J. Heat Fluid Flow 2011, 32, 529–538. [Google Scholar] [CrossRef][Green Version]
- Holmes, L.; Favero, J.; Osswald, T. Numerical simulation of three-dimensional viscoelastic planar contraction flow using the software OpenFOAM. Comput. Chem. Eng. 2012, 37, 64–73. [Google Scholar] [CrossRef]
- Azaiez, J.; Guénette, R.; Ait-Kadi, A. Numerical simulation of viscoelastic flows through a planar contraction. J. Non-Newton. Fluid Mech. 1996, 62, 253–277. [Google Scholar] [CrossRef]
- Dubief, Y.; Terrapon, V.E.; Soria, J. On the mechanism of elasto-inertial turbulence. Phys. Fluids 2013, 25, 110817. [Google Scholar] [CrossRef]
- Resende, P.R.; Pinho, F.T.; Younis, B.A.; Kim, K.; Sureshkumar, R. Development of a Low-Reynolds-number k-ω Model for FENE-P Fluids. Flow, Turbul. Combust. 2013, 90, 69–94. [Google Scholar] [CrossRef]
- Resende, P.R.; Kim, K.; Younis, B.A.; Sureshkumar, R.; Pinho, F.T. A FENE-P k-ε turbulence model for low and intermediate regimes of polymer-induced drag reduction. J. Non-Newton. Fluid Mech. 2011, 166, 639–660. [Google Scholar] [CrossRef]
- Tsukahara, T.; Motozawa, M.; Tsurumi, D.; Kawaguchi, Y. PIV and DNS analyses of viscoelastic turbulent flows behind a rectangular orifice. Int. J. Heat Fluid Flow 2013, 41, 66–79. [Google Scholar] [CrossRef]
- Shaban, S.; Azad, M.; Trivedi, J.; Ghaemi, S. Investigation of near-wall turbulence in relation to polymer rheology. Phys. Fluids 2018, 30, 125111. [Google Scholar] [CrossRef]
- Samanta, D.; Dubief, Y.; Holzner, M.; Schäfer, C.; Morozov, A.N.; Wagner, C.; Hof, B. Elasto-inertial turbulence. Proc. Natl. Acad. Sci. USA 2013, 110, 10557–10562. [Google Scholar] [CrossRef] [PubMed]
- Quinzani, L.M.; Armstrong, R.C.; Brown, R.A. Birefringence and laser-Doppler velocimetry (LDV) studies of viscoelastic flow through a planar contraction. J. Non-Newton. Fluid Mech. 1994, 52, 1–36. [Google Scholar] [CrossRef]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1950, 200, 523–541. [Google Scholar]
- Giesekus, H. A simple constitutive equation for polymer fluids based on the concept of deformation-dependent tensorial mobility. J. Non-Newton. Fluid Mech. 1982, 11, 69–109. [Google Scholar] [CrossRef]
- Phan-Thien, N. A nonlinear network viscoelastic model. J. Rheol. 1978, 22, 259–283. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids: Fluid Mechanics, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1987; Volume 1. [Google Scholar]
- Macosko, C.W. Rheology: Principles, Measurements, and Applications; VCH Publishers Inc.: New York, NY, USA, 1994. [Google Scholar]
- Sureshkumar, R.; Beris, A.N.; Handler, R.A. Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 1997, 9, 743–755. [Google Scholar] [CrossRef]
- Warner, H.R., Jr. Kinetic theory and rheology of dilute suspensions of finitely extendible dumbbells. Ind. Eng. Chem. Fundam. 1972, 11, 379–387. [Google Scholar] [CrossRef]
- Rothstein, J.P.; McKinley, G.H. The axisymmetric contraction–expansion: The role of extensional rheology on vortex growth dynamics and the enhanced pressure drop. J. Non-Newton. Fluid Mech. 2001, 98, 33–63. [Google Scholar] [CrossRef]
- Poole, R.J.; Escudier, M.P. Turbulent flow of non-Newtonian liquids over a backward-facing step: Part II, Viscoelastic and shear-thinning liquids. J. Non-Newton. Fluid Mech. 2003, 109, 193–230. [Google Scholar] [CrossRef]
- Oliveira, P.J. Asymmetric flows of viscoelastic fluids in symmetric planar expansion geometries. J. Non-Newton. Fluid Mech. 2003, 114, 33–63. [Google Scholar] [CrossRef]
- Poole, R.J.; Escudier, M.P.; Afonso, A.; Pinho, F.T. Laminar flow of a viscoelastic shear-thinning liquid over a backward-facing step preceded by a gradual contraction. Phys. Fluids 2007, 19, 093101. [Google Scholar] [CrossRef]
- Xiong, Y.L.; Bruneau, C.H.; Kellay, H. A numerical study of two dimensional flows past a bluff body for dilute polymer solutions. J. Non-Newton. Fluid Mech. 2013, 196, 8–26. [Google Scholar] [CrossRef][Green Version]
- Tsukahara, T.; Tanabe, M.; Kawaguchi, Y. Effect of fluid viscoelasticity on turbulence and large-scale vortices behind wall-mounted plates. Adv. Mech. Eng. 2014, 6, 823138. [Google Scholar] [CrossRef]
- Tsukahara, T.; Kawase, T.; Kawaguchi, Y. DNS on turbulent heat transfer of viscoelastic fluid flow in a plane channel with transverse rectangular orifices. Prog. Comput. Fluid Dyn. Int. J. 2013, 13, 212–223. [Google Scholar] [CrossRef]
- Yamagata, T.; Ito, A.; Sato, Y.; Fujisawa, N. Experimental and numerical studies on mass transfer characteristics behind an orifice in a circular pipe for application to pipe-wall thinning. Exp. Therm. Fluid Sci. 2014, 52, 239–247. [Google Scholar] [CrossRef]
- Hemmati, A.; Wood, D.H.; Martinuzzi, R.J. On simulating the flow past a normal thin flat plate. J. Wind. Eng. Ind. Aerodyn. 2018, 174, 170–187. [Google Scholar] [CrossRef]
- Ashrafian, A.; Andersson, H.I.; Manhart, M. DNS of turbulent flow in a rod-roughened channel. Int. J. Heat Fluid Flow 2004, 25, 373–383. [Google Scholar] [CrossRef]
- McKeon, B.J.; Swanson, C.J.; Zagarola, M.V.; Donnelly, R.J.; Smits, A.J. Friction factors for smooth pipe flow. J. Fluid Mech. 2004, 511, 41–44. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. In International Workshop on Coupled Methods in Numerical Dynamics; IUC Dubrovnik Croatia: Dubrovnik, Croatia, 2007; Volume 1000, pp. 1–20. [Google Scholar]
- Hultmark, M.; Vallikivi, M.; Bailey, S.C.C.; Smits, A.J. Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 2012, 108, 094501. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Smits, A.J. Roughness effects in laminar channel flow. J. Fluid Mech. 2019, 876, 1129–1145. [Google Scholar] [CrossRef]
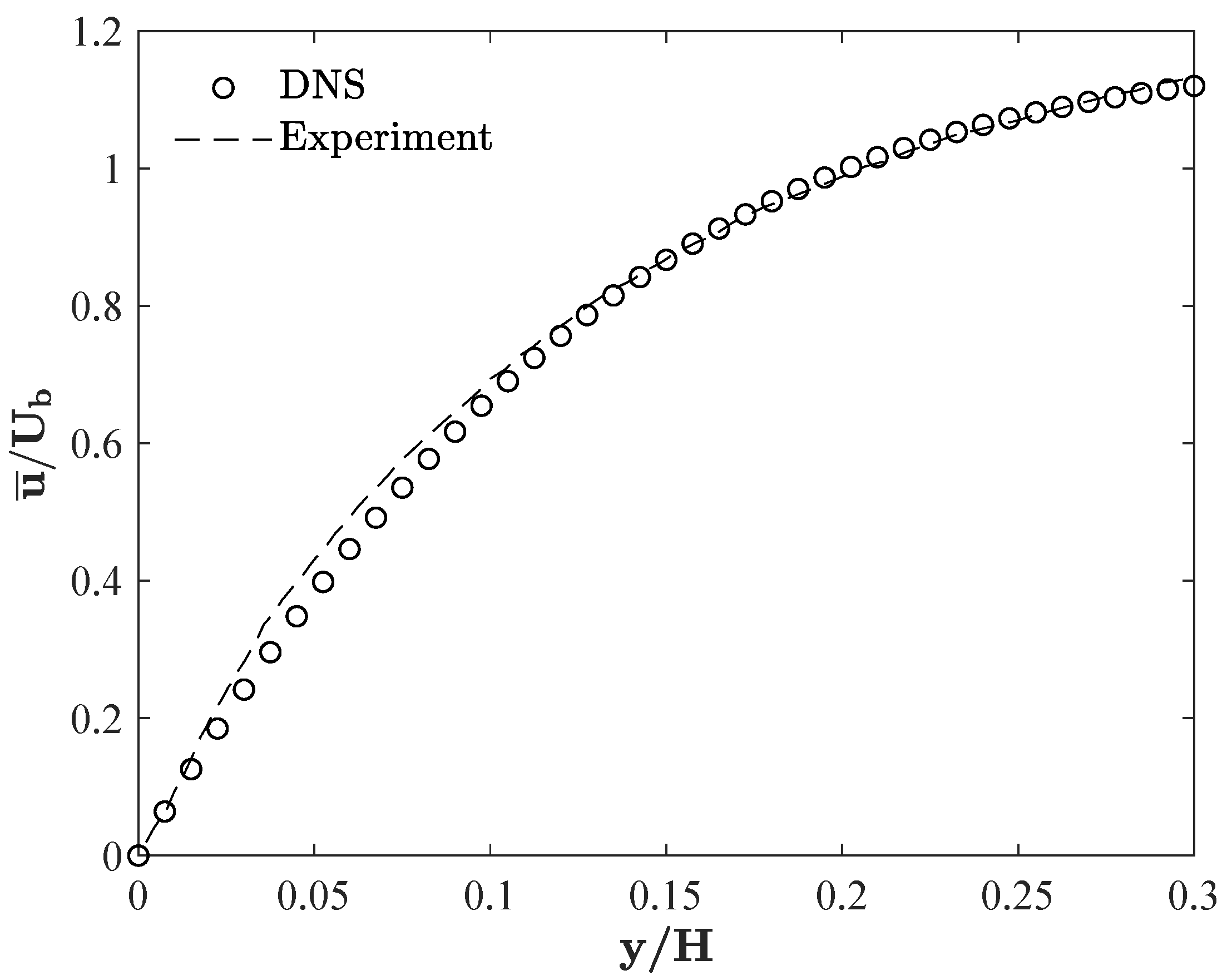
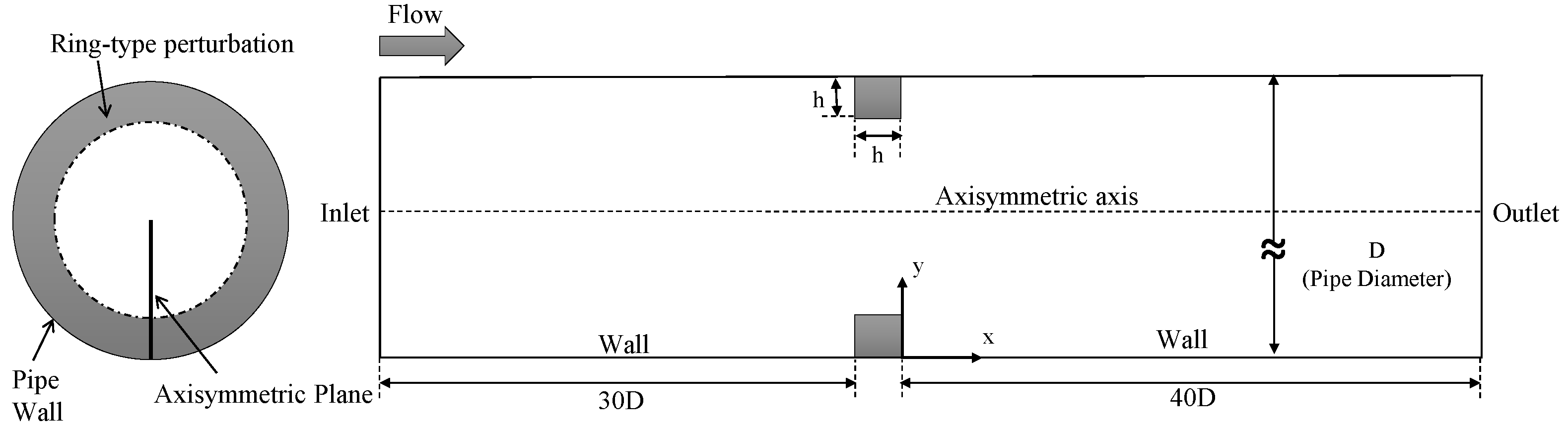
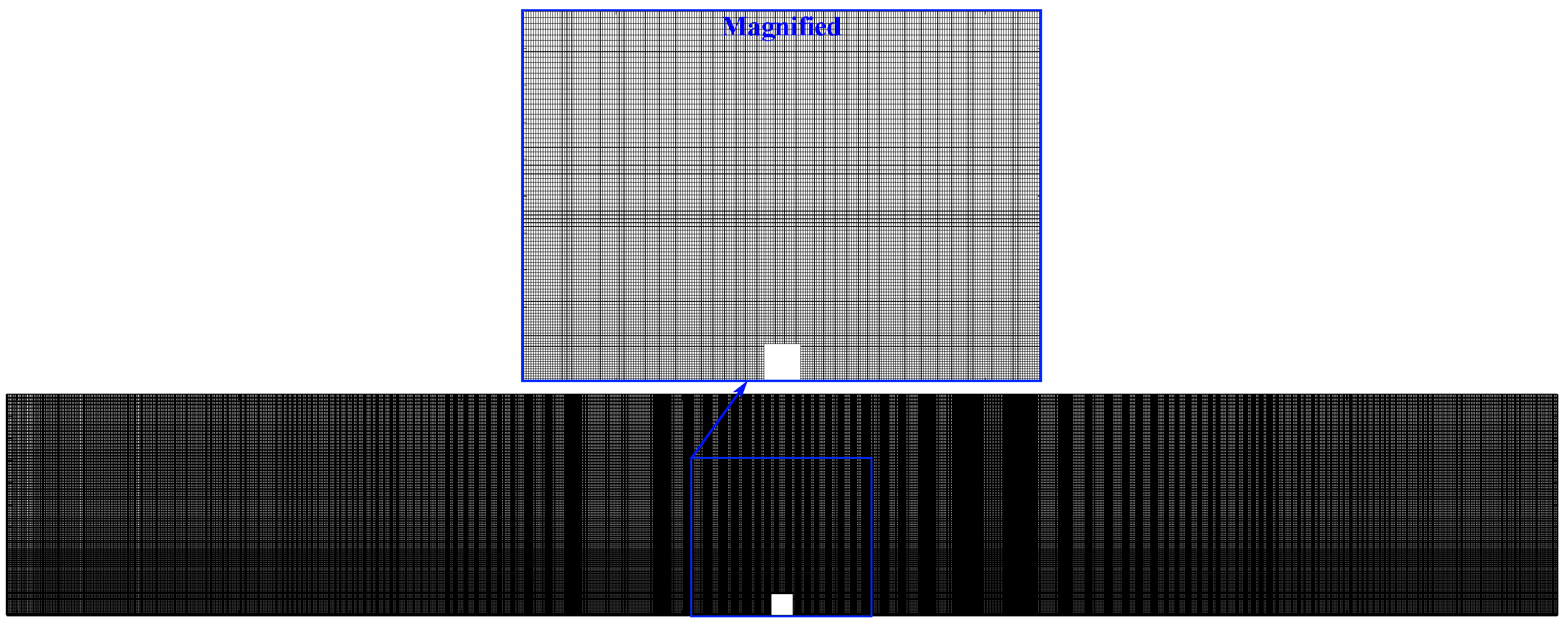
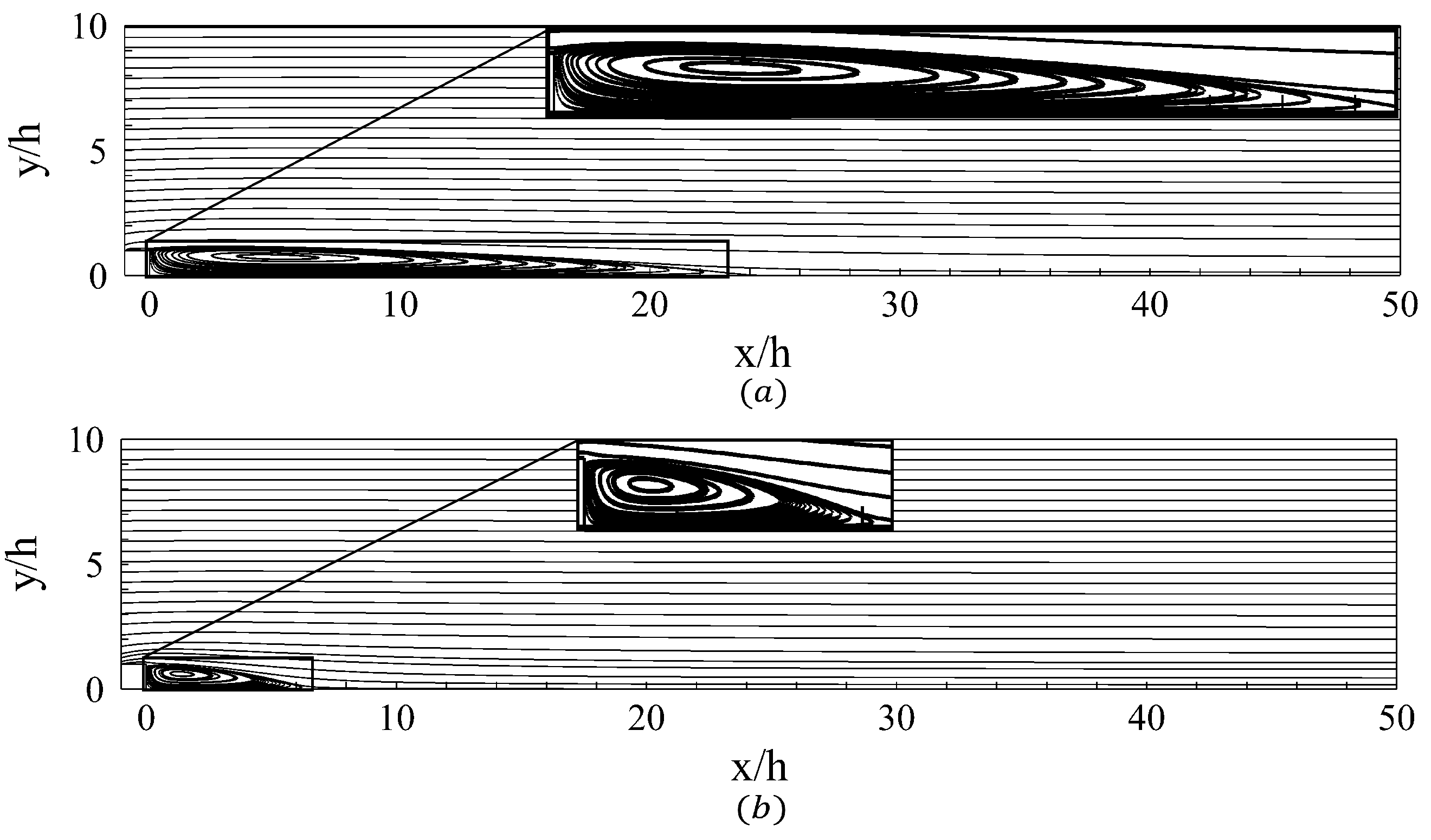
| Case | 1 | 2 | 5 | 8 | |
|---|---|---|---|---|---|
| Current Case | |||||
| Hemmati et al. (2018) [47] | |||||
| Ashrafian et al. (2004) [48] | ≈3.2 | − | − | − | |
| Dubief et al. (2013) [25] | ≈2.3 | − | − | − |
| Parameter | Value |
|---|---|
| Extensibility of the polymer, | 200 |
| Ratio of solvent to zero-shear viscosity, | |
| Polymer relations time, (s) | |
| Reynolds number, | 5000 |
| Frictional Reynolds number, | 384 |
| Study | |||
|---|---|---|---|
| Newtonian | − | ||
| Viscoelastic | 73 | ||
| Newtonian | − | ||
| Viscoelastic |
| Study | |||
|---|---|---|---|
| Newtonian | 350 | − | |
| Viscoelastic | 100 | 71 | |
| Newtonian | 200 | − | |
| Viscoelastic | 60 | 70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goswami, S.; Hemmati, A. Response of Viscoelastic Turbulent Pipeflow Past Square Bar Roughness: The Effect on Mean Flow. Computation 2021, 9, 85. https://doi.org/10.3390/computation9080085
Goswami S, Hemmati A. Response of Viscoelastic Turbulent Pipeflow Past Square Bar Roughness: The Effect on Mean Flow. Computation. 2021; 9(8):85. https://doi.org/10.3390/computation9080085
Chicago/Turabian StyleGoswami, Shubham, and Arman Hemmati. 2021. "Response of Viscoelastic Turbulent Pipeflow Past Square Bar Roughness: The Effect on Mean Flow" Computation 9, no. 8: 85. https://doi.org/10.3390/computation9080085
APA StyleGoswami, S., & Hemmati, A. (2021). Response of Viscoelastic Turbulent Pipeflow Past Square Bar Roughness: The Effect on Mean Flow. Computation, 9(8), 85. https://doi.org/10.3390/computation9080085






