Performance of Overset Mesh in Modeling the Wake of Sharp-Edge Bodies
Abstract
:1. Introduction
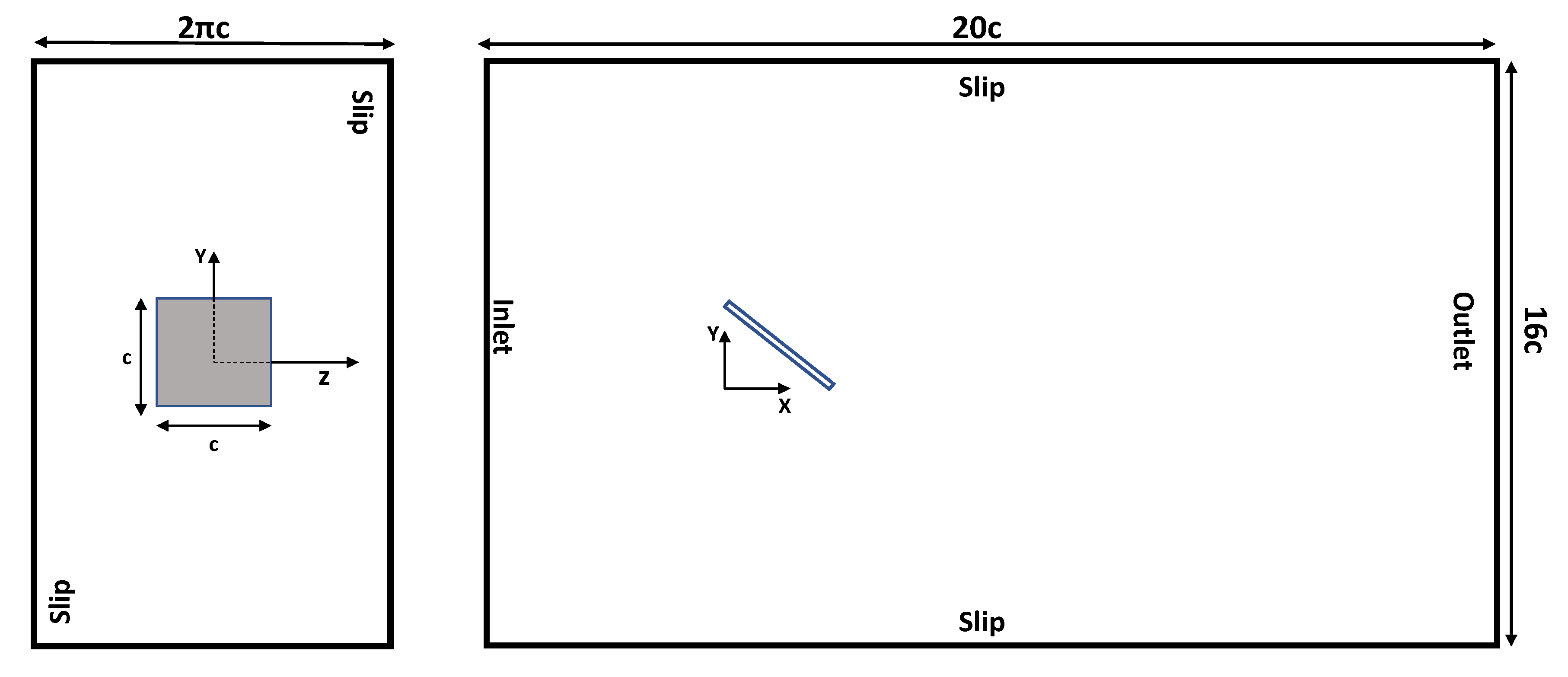
2. Problem Description
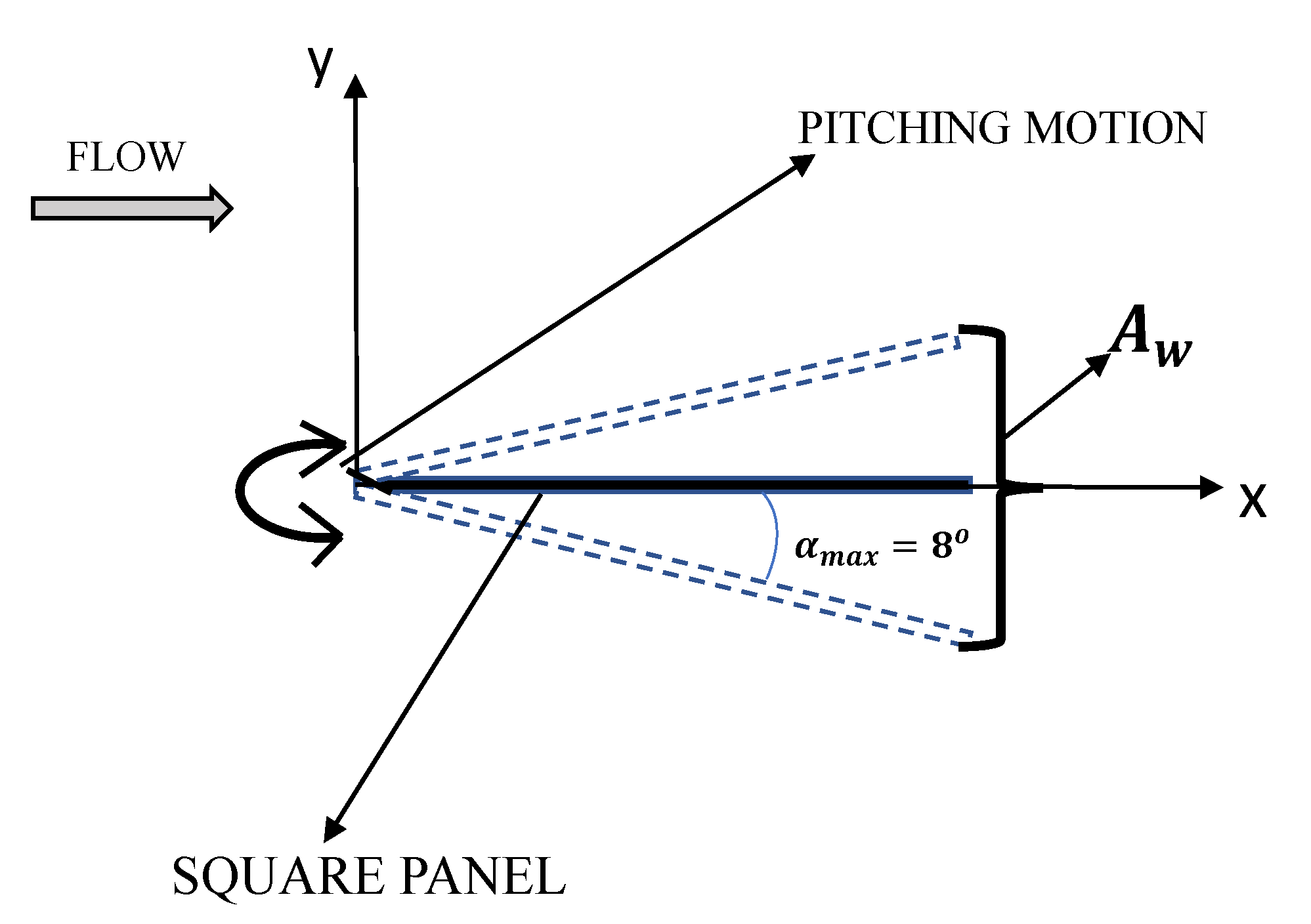
2.1. Cases 1–5
2.2. Cases 6–7
2.3. Governing Equations
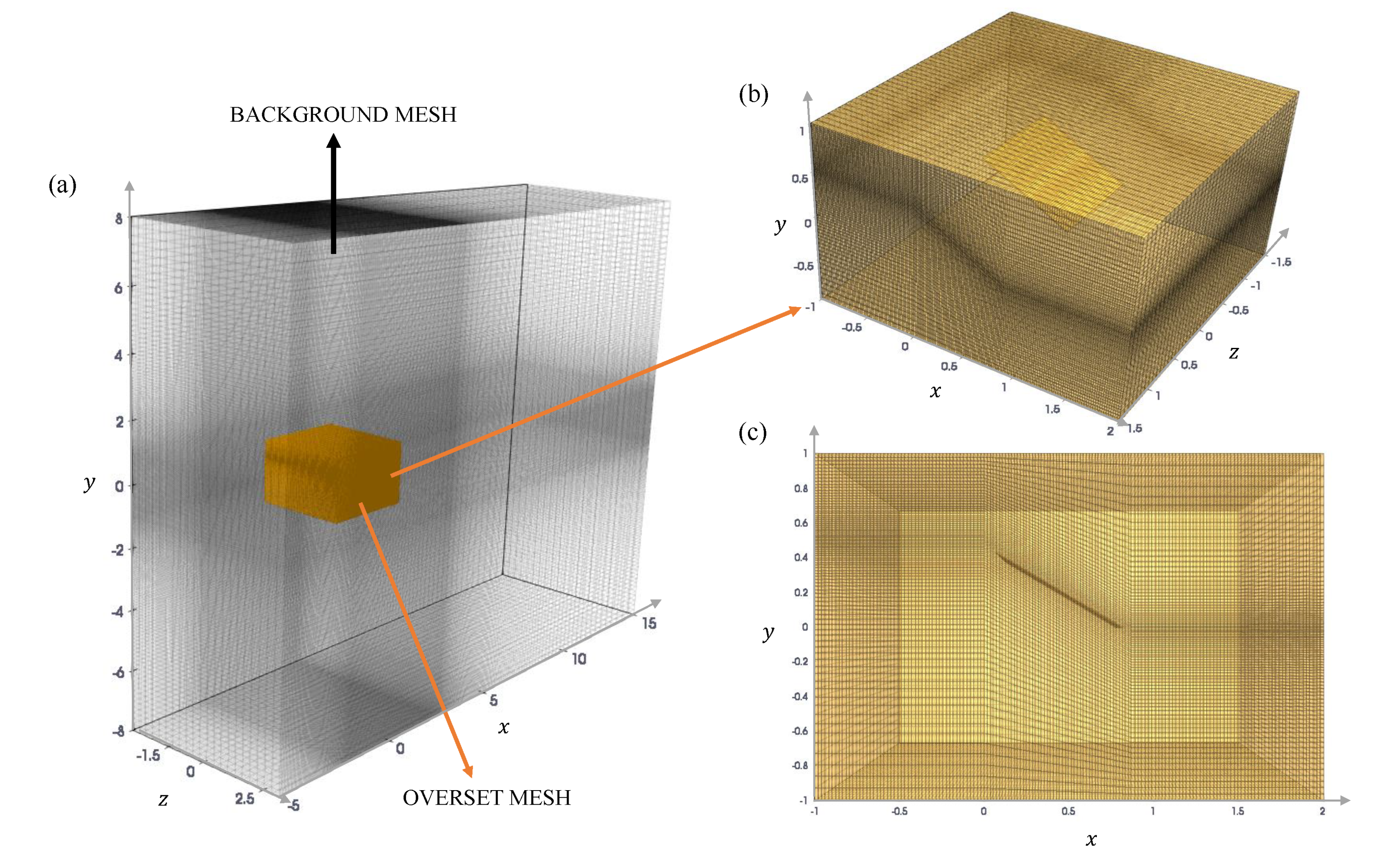
2.4. Computational Setup and Boundary Conditions
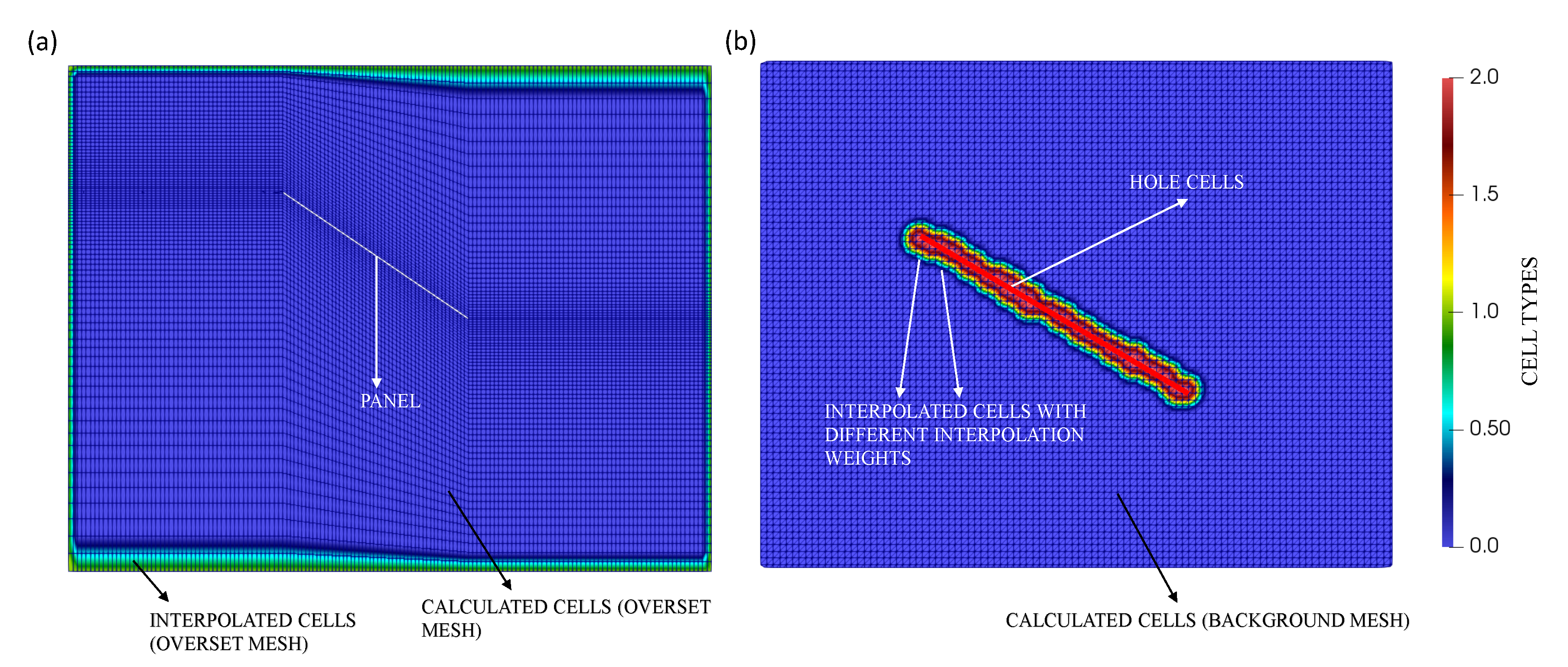
- Step (1): The addressing of all the cells which will act as neighbors (donors) to an acceptor cell is conducted by employing their index number defined within the mesh. The solver also identifies the fields (pressure, velocity and turbulence quantities) that are required for interpolation in acceptor cells on the background and the overset grids.
- Step (2): Hole, interpolated and calculated cells are then set by the solver. Hole cells are generally identified in the underlying background or overset grid, which could be stationary or prescribed to execute a motion. They are governed by the secondary (overlapping) grid, which approximates the representation of wall boundary of moving body. The flow field is not solved within these cells. Interpolated cells require interpolation from donor cells, present on the overlapping regions of mesh, i.e., Interpolated cells lying on the background grid have their donors on overset grid and vice-versa. All the remaining cells that are not identified as interpolated or hole cells are assigned as calculated cells.
- Step (3): The interpolation scheme specified by the user is used by the solver to perform interpolation from field values of identified donor cells. For instance, if the scheme is specified to be inverse distance, a corresponding list of donor cells and their weights (calculated based on the distance between centroid of acceptor and donor cell) is supplied for each interpolated cell.
3. Results and Discussion
3.1. Stationary Panel
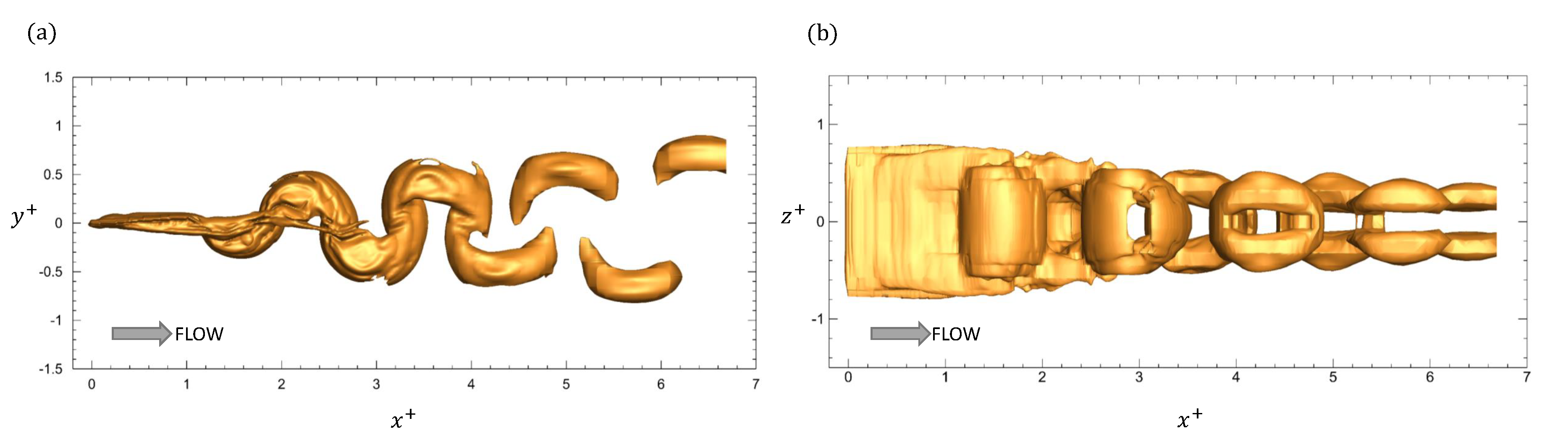
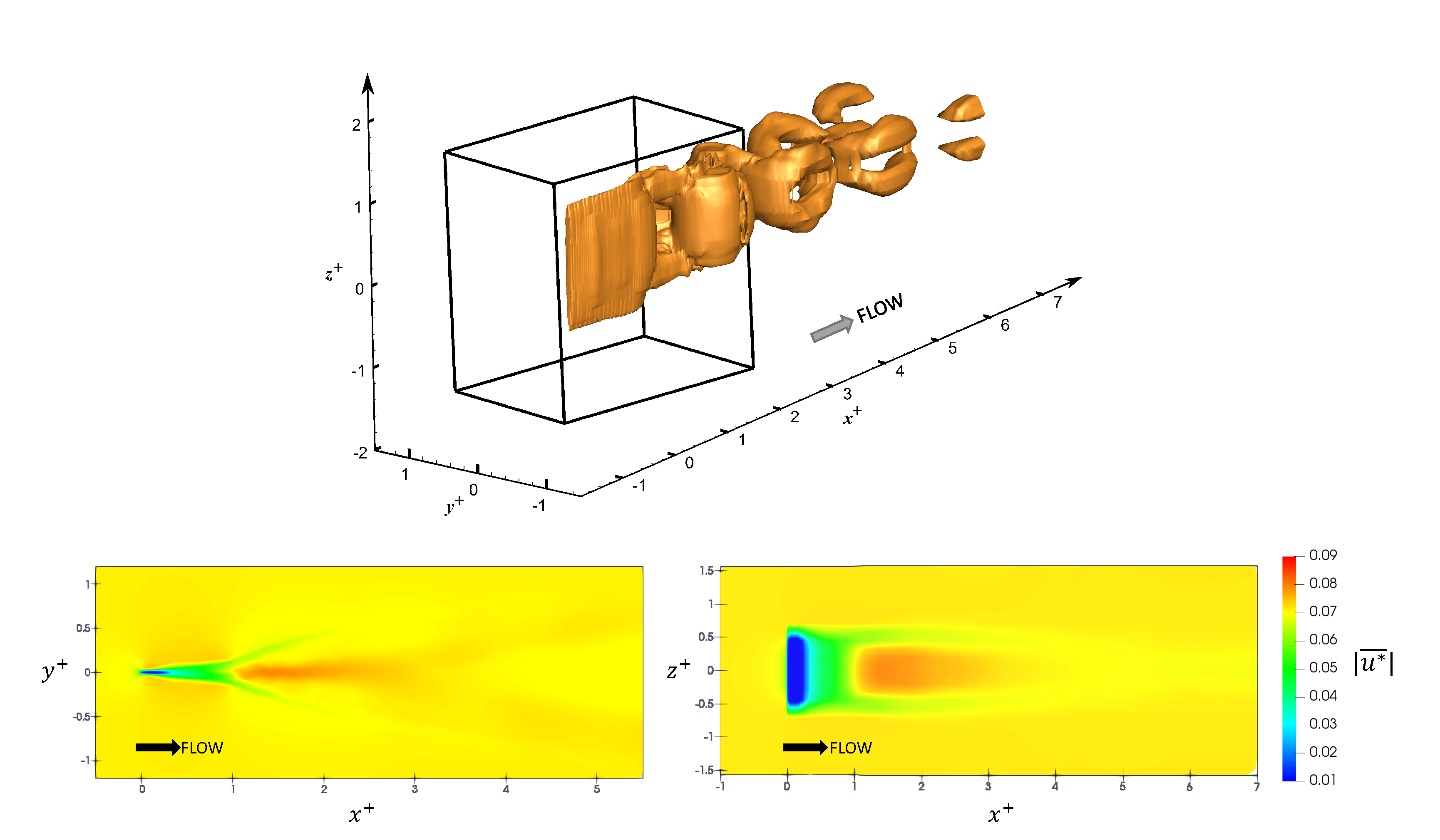
3.2. Pitching Panels (Cases 6–7)
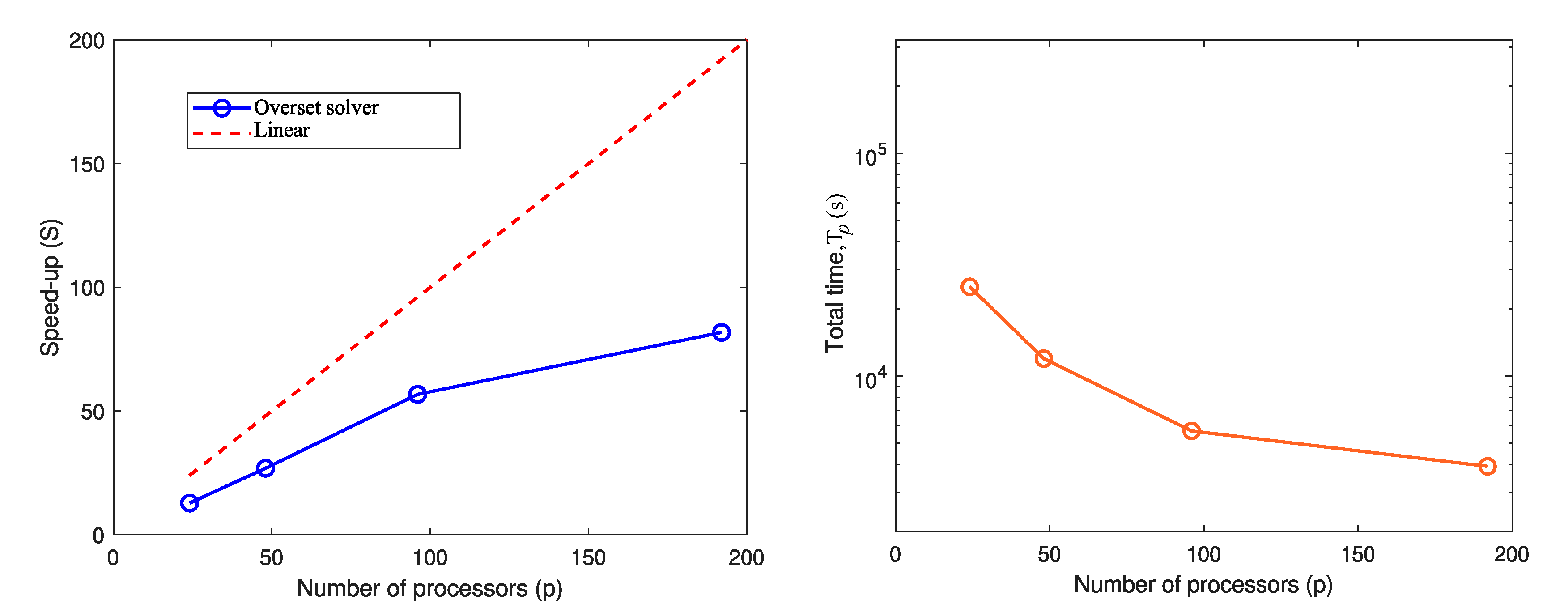
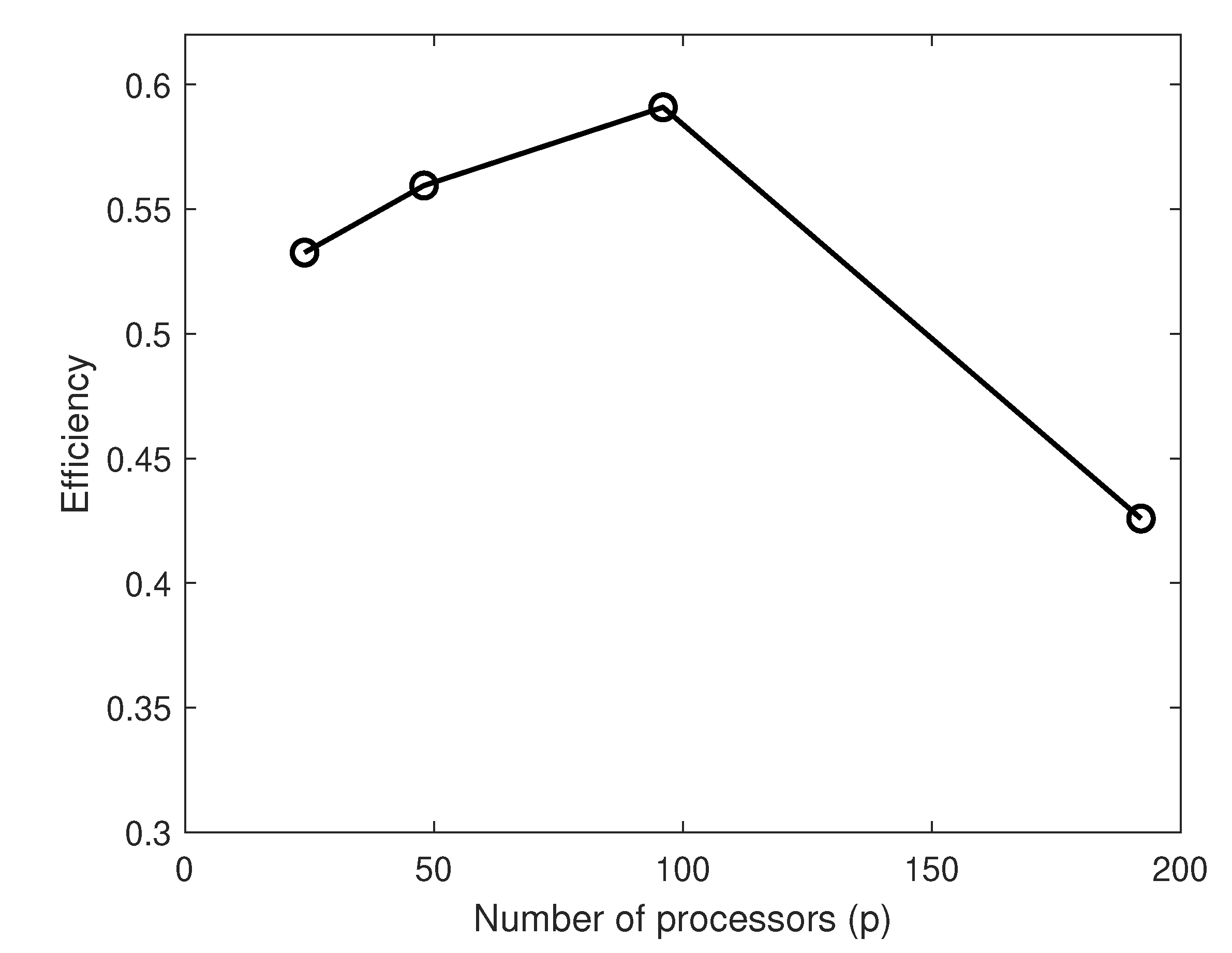
3.3. Scalability Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karman, T.V. On the mechanism of the drag a moving body experiences in a fluid. Prog. Aerosp. Sci. 2013, 59, 13–15. [Google Scholar] [CrossRef]
- Roshko, A. Experiments on flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 1961, 10, 345–356. [Google Scholar] [CrossRef] [Green Version]
- Roshko, A. On the Drag and Shedding Frequency of Two-Dimensional Bluff Bodies; National Advisory Committee for Aeronautics, Technical Note 3169; California Institute of Technology: Pasadena, CA, USA, 1954. [Google Scholar]
- Ellenrieder, K.D.V.; Parker, K.; Soria, J. Flow structures behind a heaving and pitching finite-span wing. J. Fluid Mech. 2003, 490, 129–138. [Google Scholar] [CrossRef]
- Guglielmini, L.; Blondeaux, P. Propulsive efficiency of oscillating foils. Eur. J. Mech. B/Fluids 2004, 23, 255–278. [Google Scholar] [CrossRef]
- Ohmi, K.; Coutanceauz, M.; Daube, O.; Loc, T.P. Further experiments on vortex formation around an oscillating and translating airfoil at large incidences. J. Fluid Mech. 1991, 225, 607–630. [Google Scholar] [CrossRef]
- Buchholz, J.H.J.; Smits, A.J. On the evolution of the wake structure produced by a low-aspect-ratio pitching panel. J. Fluid Mech. 2006, 546, 433–443. [Google Scholar] [CrossRef] [Green Version]
- Fage, A.; Johansen, F.C. On the flow of air behind an inclined flat plate of infinite span. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1927, 116, 170–197. [Google Scholar]
- Von Ellenrieder, K.D.; Parker, K.; Soria, J. Visualization of a three dimensional heaving aerofoil flow. In Proceedings of the 14th Australasian Fluid Mechanics Conference, Adelaide, Australia, 10–14 December 2001. [Google Scholar]
- Blondeaux, P.; Fornarelli, F.; Guglielmini, L.; Triantafyllou, M.S.; Verzicco, R. Numerical experiments on flapping foils mimicking fish-like locomotion. Phys. Fluids 2005, 17, 113601. [Google Scholar] [CrossRef]
- Senturk, U.; Brunner, D.; Jasak, H.; Herzog, N.; Rowley, C.; Smits, A.J. Benchmark simulations of flow past rigid bodies using an open-source, sharp interface immersed boundary method. Prog. Comput. Fluid Dyn. 2019, 19, 205–219. [Google Scholar]
- Senturk, U.; Smits, A.J. Numerical simulations of the flow around a square pitching panel. J. Fluids Struct. 2018, 76, 454–468. [Google Scholar] [CrossRef]
- Lewin, G.C.; Haj-Hariri, H. Modelling thrust generation of a two-dimensional heaving airfoil in a viscous flow. J. Fluid Mech. 2003, 492, 339–362. [Google Scholar] [CrossRef]
- Panahi, R.; Shafieefar, M. Application of Overlapping Mesh in Numerical Hydrodynamics. Pol. Marit. Res. 2009, 16, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Chandar, D. On overset interpolation strategies and conservation on unstructured grids in OpenFOAM. Comput. Phys. Commun. 2019, 239, 72–83. [Google Scholar] [CrossRef]
- Shenoy, R.; Smith, M.J.; Park, M.A. Unstructured Overset Mesh Adaptation with Turbulence Modeling for Unsteady Aerodynamic Interactions. J. Aircr. 2014, 51, 161–174. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, X.; Fan, S.; Wan, D.; Wang, J. Implementation of Overset Grid in OpenFOAM and its validation to PMM model test of a container ship. In Proceedings of the 13th OpenFOAM Workshop (OFW13), Shanghai, China, 24–29 June 2018. [Google Scholar]
- Wang, J.; Wan, D. Wave effects on free running ship in standard zig-zag maneuver. In Proceedings of the 32th Workshop on Water Waves and Floating Bodies, Dalian, China, 23–26 April 2017. [Google Scholar]
- Chandar, D.; Gopalan, H. Comparative Analysis of the Arbitrary Mesh Interface(AMI) and Overset Methods for Dynamic Body Motions in OpenFOAM. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Liu, J.; Akay, H.U.; Ecer, A.; Payli, R.U. Flows around moving bodies using a dynamic unstructured overset-grid method. Int. J. Comput. Fluid Dyn. 2010, 24, 187–200. [Google Scholar] [CrossRef]
- Morris, M.J.; Dutton, J.C.; Addy, A.L. Peak torque characteristics of butterfly valves. Proc. Forum Ind. Appl. Fluid Mech. 1987, 54, 63–66. [Google Scholar]
- Aarnes, J.R.; Jin, T.; Mao, C.; Haugen, N.E.; Luo, K.; Andersson, H.I. Treatment of solid objects in the Pencil Code using an immersed boundary method and overset grids. Geophys. Astrophys. Fluid Dyn. 2018. [Google Scholar] [CrossRef] [Green Version]
- Taira, K.; Colonius, T. Three-dimensional flows around low-aspect-ratio flat-plate wings at low Reynolds numbers. J. Fluid Mech. 2009, 623, 187–207. [Google Scholar] [CrossRef] [Green Version]
- Najjar, F.M.; Balachandar, S. Low frequency unsteadiness in the wake of normal flat plate. J. Fluid Mech. 1998, 370, 101–147. [Google Scholar] [CrossRef]
- Hemmati, A.; Wood, D.H.; Martinuzzi, R.J. Characteristics of distinct flow regimes in the wake of an infinite span normal thin flat plate. Int. J. Heat Fluid Flow 2016, 62, 423–436. [Google Scholar] [CrossRef]
- Dong, H.; Mittal, R.; Najjar, F.M. Wake topology and hydrodynamic performance of low-aspect-ratio flapping foils. J. Fluid Mech. 2006, 566, 309–343. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.; Caulfield, C.P. Three-dimensional transition after wake deflection behind a flapping foil. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 91, 043017. [Google Scholar] [CrossRef]
- Deng, J.; Sun, L.; Shao, X. Dynamical features of the wake behind a pitching foil. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 92, 063013. [Google Scholar] [CrossRef]
- Narasimhamurthy, V.D.; Andersson, H.I. Numerical simulation of the turbulent wake behind a normal flat plate. Int. J. Heat Fluid Flow 2009, 30, 1037–1043. [Google Scholar] [CrossRef]
- Hemmati, A.; Wood, D.H.; Martinuzzi, R.J. On simulating the flow past a normal thin flat plate. J. Wind Eng. Ind. Aerodyn. 2017, 566, 170–187. [Google Scholar] [CrossRef]
- Hemmati, A.; Smits, A.J. The Effect of Pitching Frequency on the Hydrodynamics of Oscillating Foils. ASME J. Appl. Mech. 2019, 86, 101010. [Google Scholar] [CrossRef]
- Hemmati, A.; Buren, T.V.; Smits, A.J. Effects of trailing edge shape on vortex formation by pitching panels of small aspect ratio. Phys. Rev. Fluids 2019, 4, 033101. [Google Scholar] [CrossRef]
- Kim, Y.; Xie, Z.T. Modelling the effect of freestream turbulence on dynamic stall of wind turbine blades. Comput. Fluids 2016, 129, 53–66. [Google Scholar] [CrossRef] [Green Version]
- Petra, T. Description of the overset mesh approach in ESI version of OpenFOAM. In Proceedings of the CFD with OpenSource Software; Nilsson, H., Ed.; Chalmers University of Technology: Gothenburg, Sweden, 2019. [Google Scholar]
- Noack, R.; Boger, D.; Kunz, R.E.; Carrica, P. Sugar++: An improved general overset grid assembly capability. In Proceedings of the 19th AIAA Computational Fluid Dynamics Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar]
- Tay, W.B.; Bijl, H.; van Oudheusden, B.W. Biplane and Tail Effects in Flapping Flight. AIAA J. 2013, 51, 2133–2146. [Google Scholar] [CrossRef]
- Green, M.A.; Smits, A.J. Effects of three-dimensionality on thrust production by a pitching panel. J. Fluid Mech. 2008, 615, 211–220. [Google Scholar] [CrossRef] [Green Version]
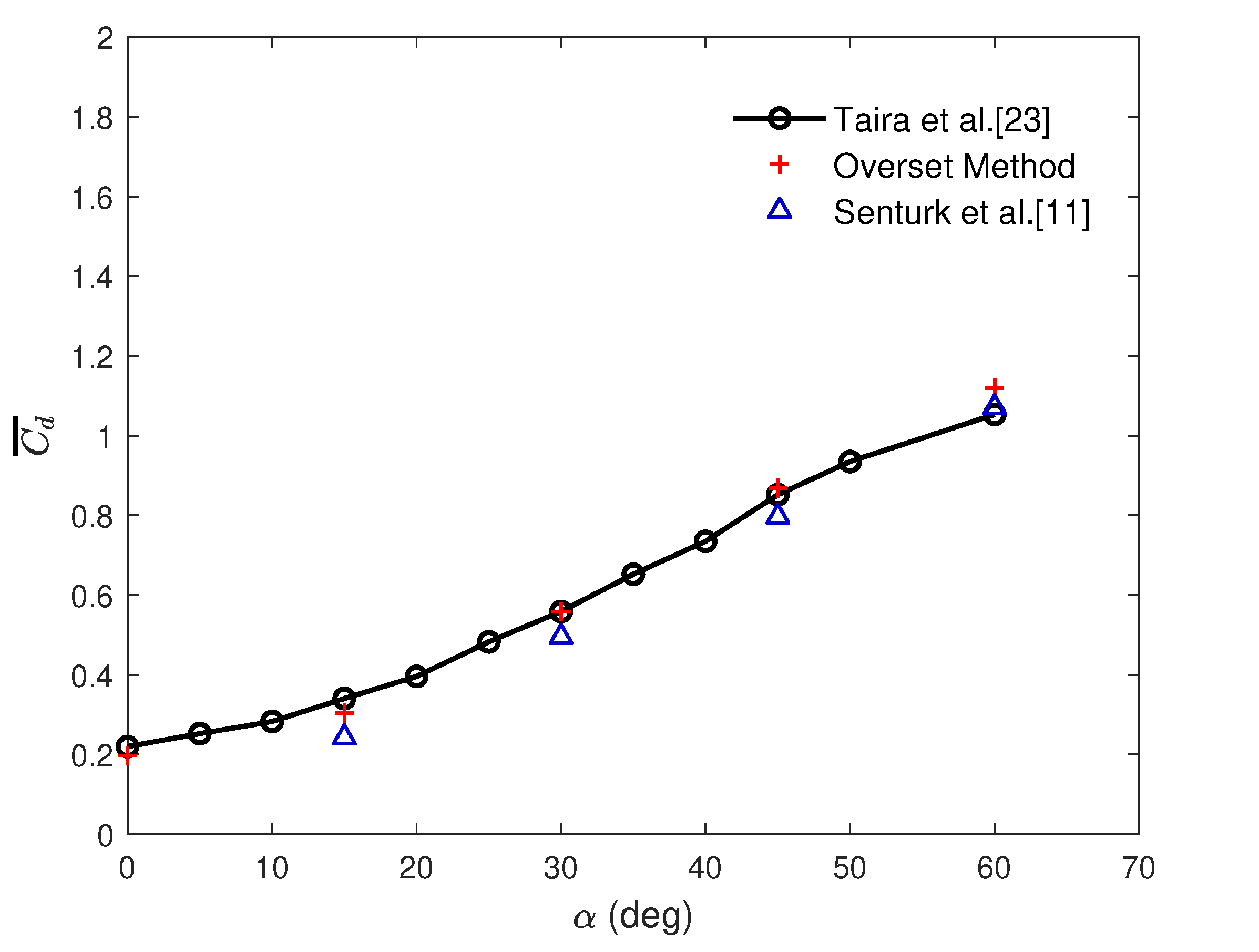
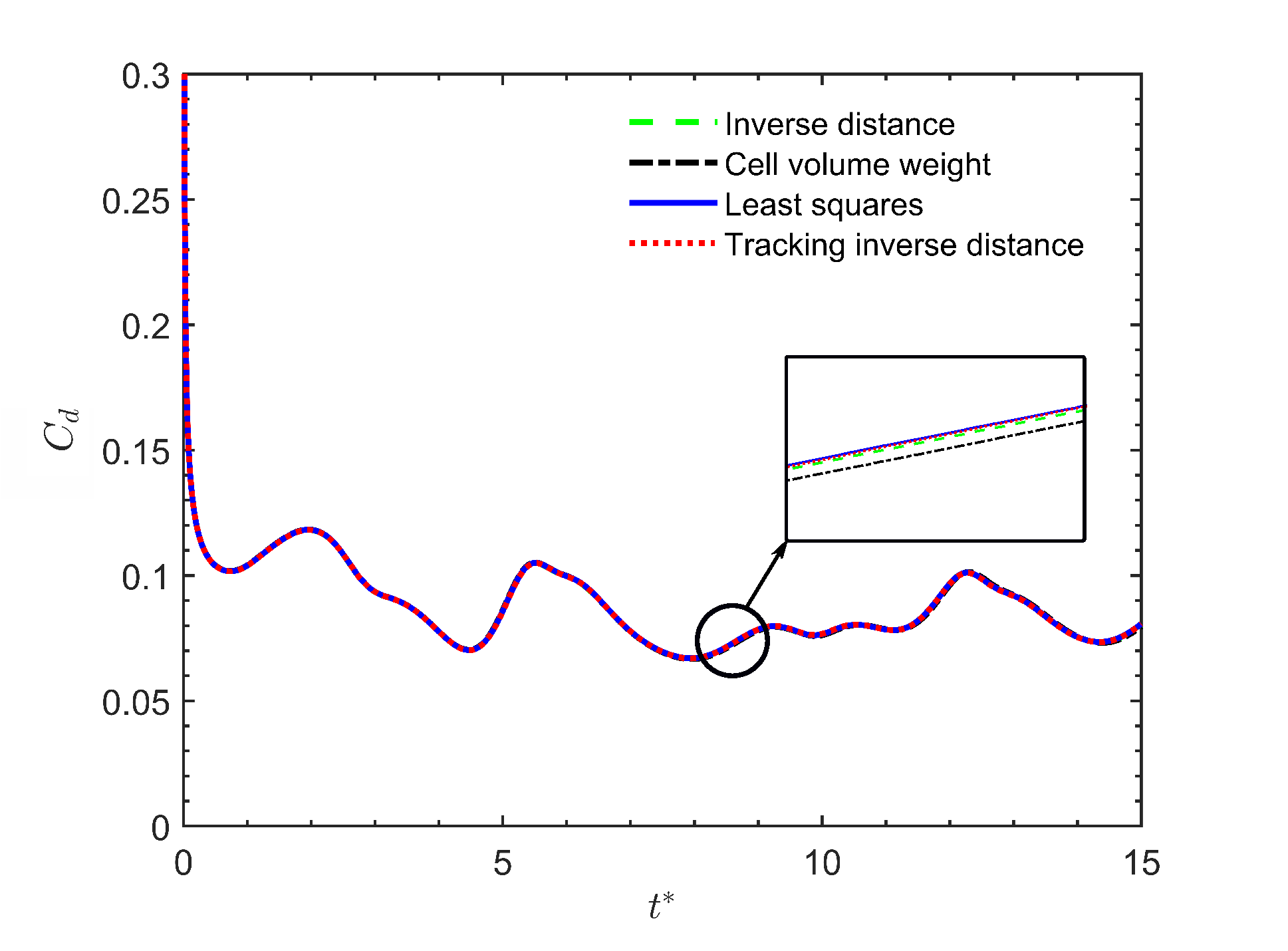
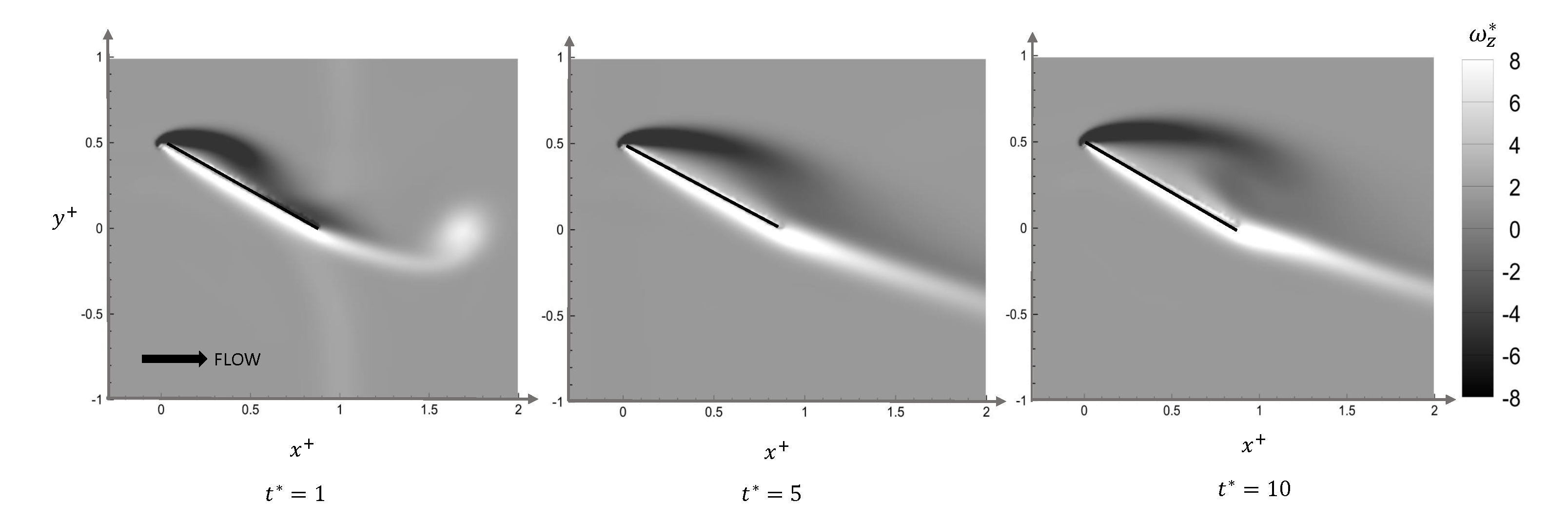
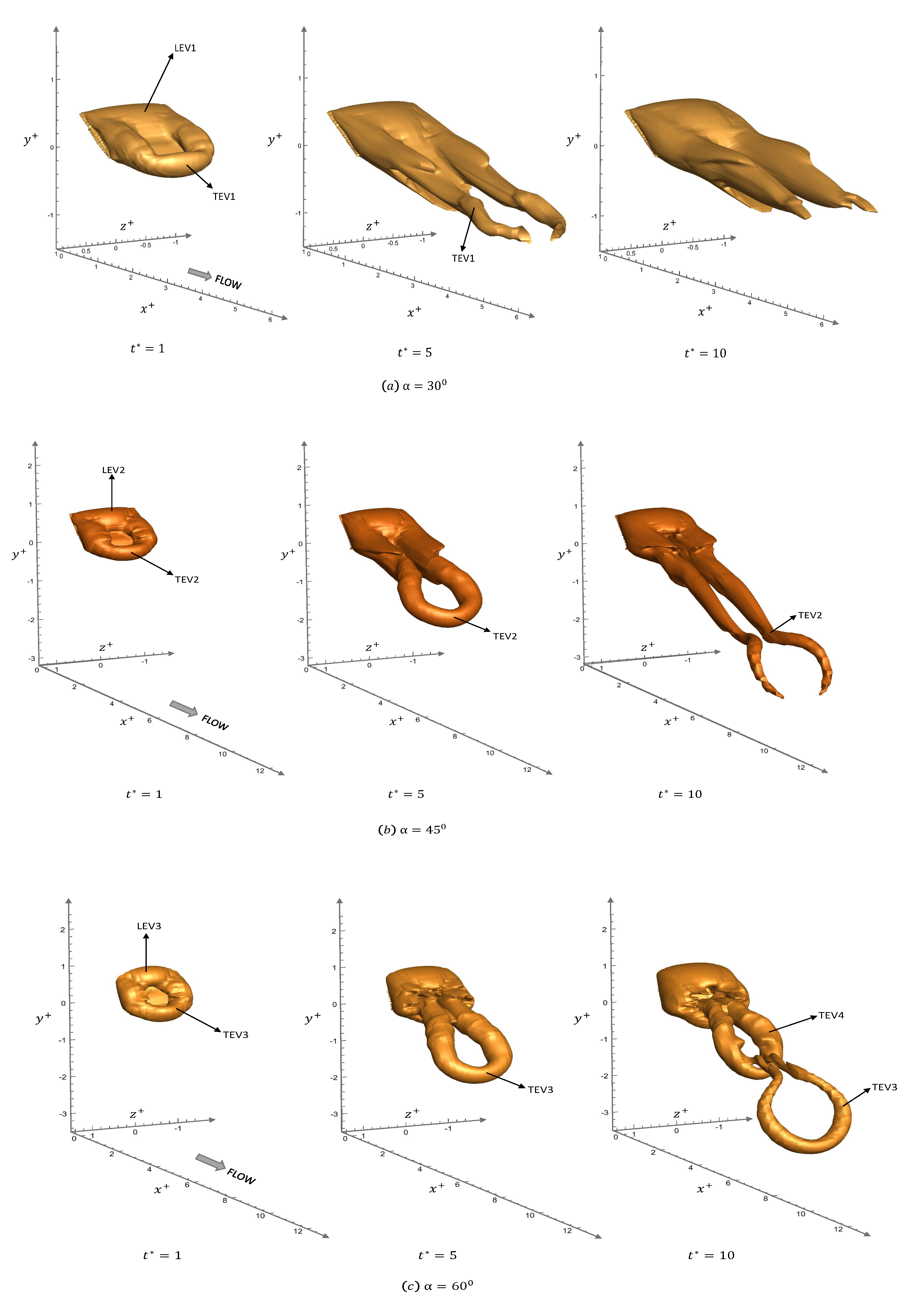
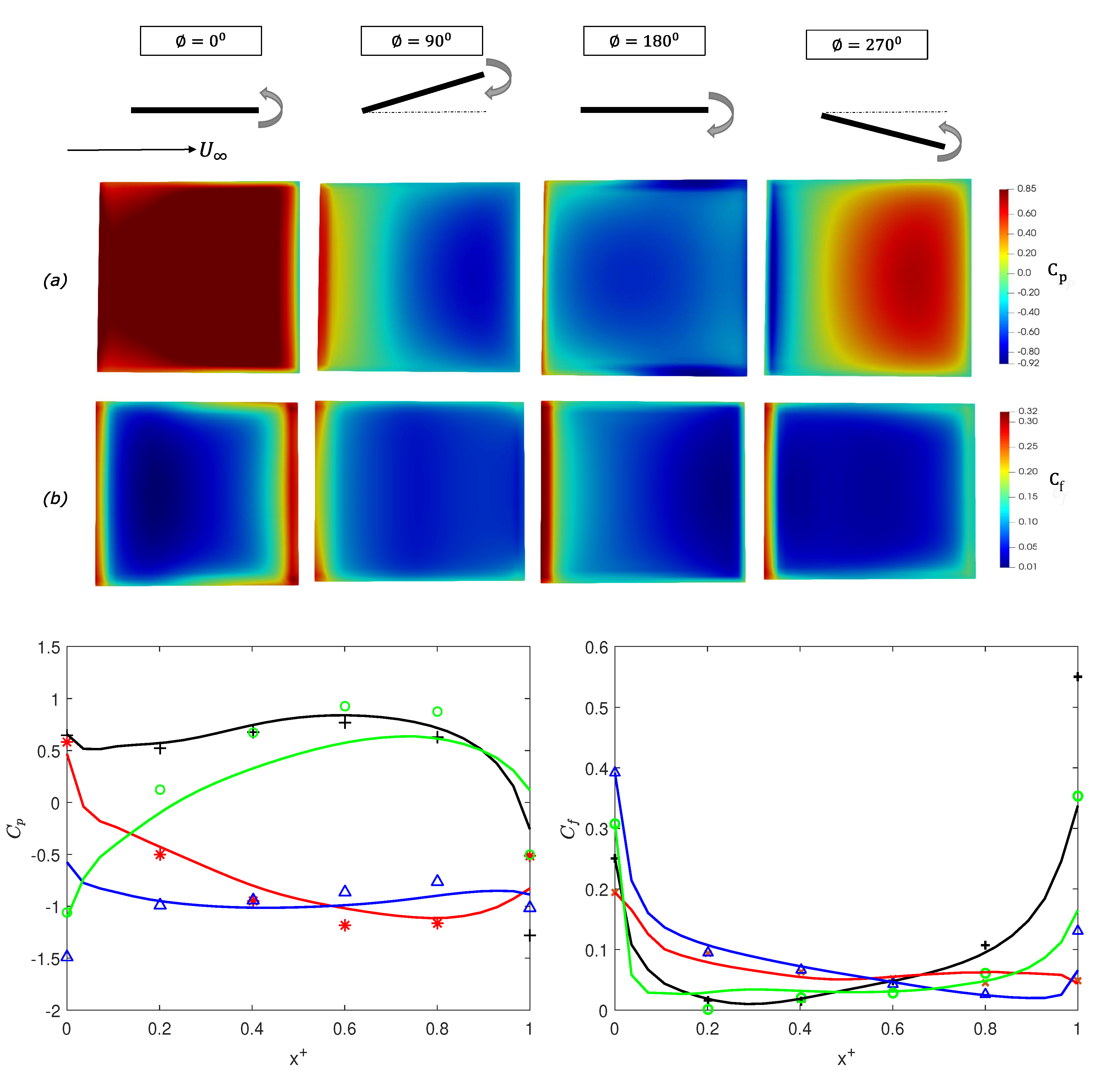
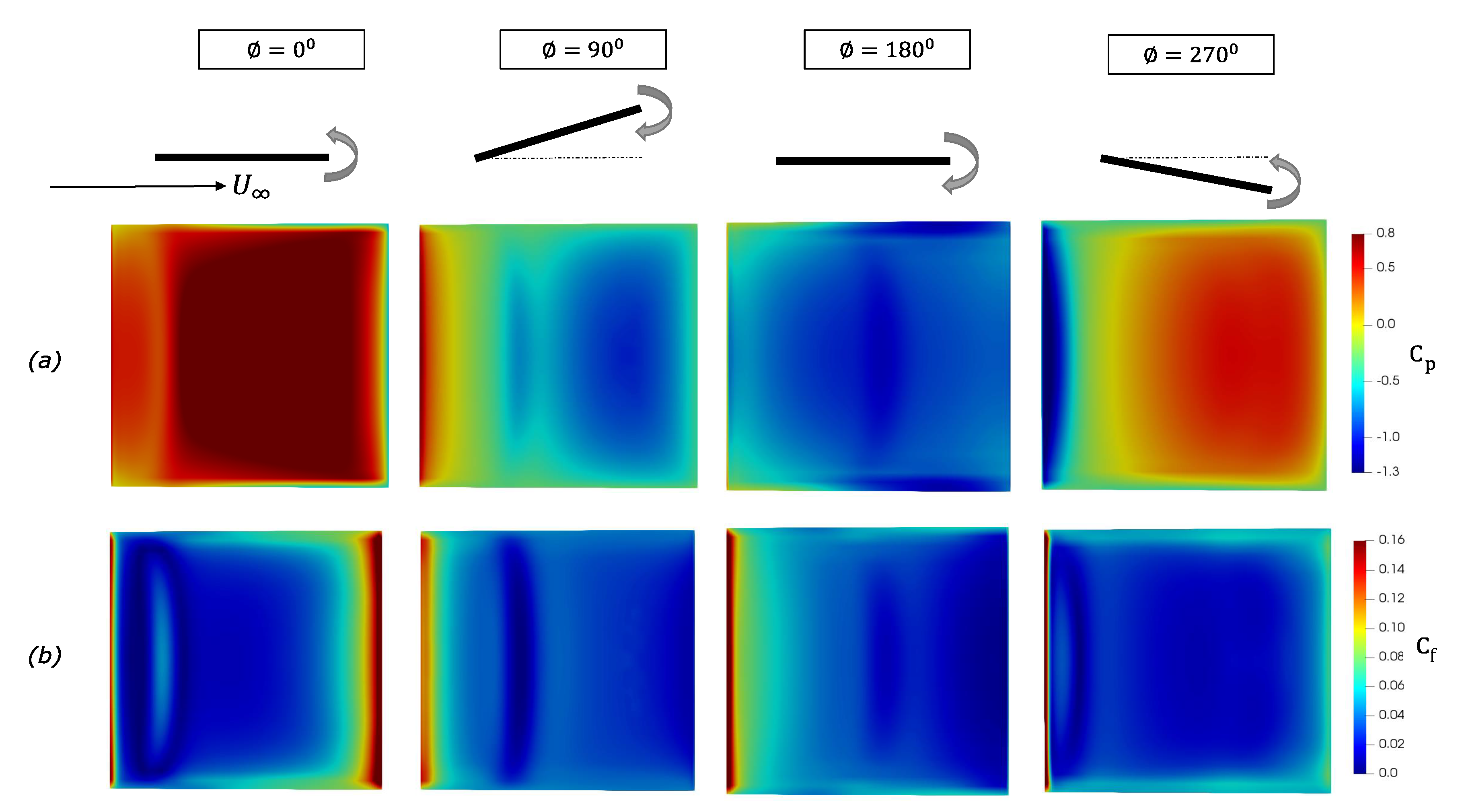
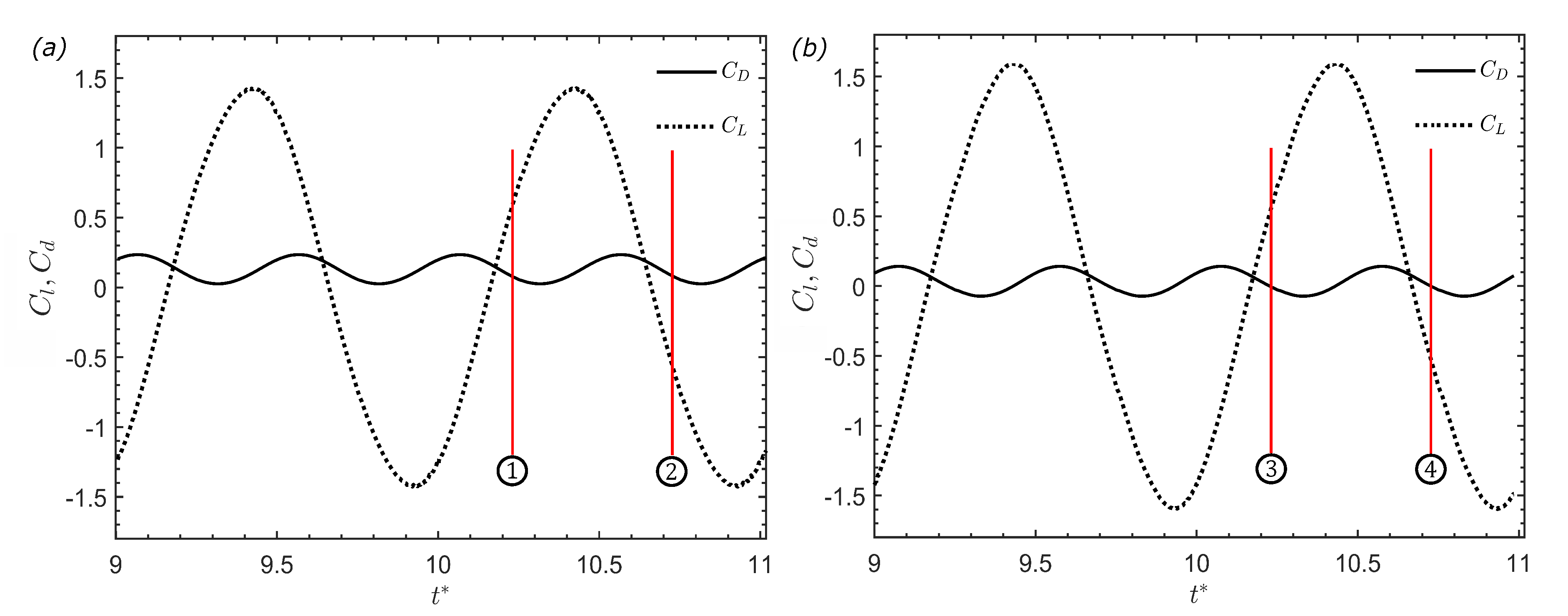
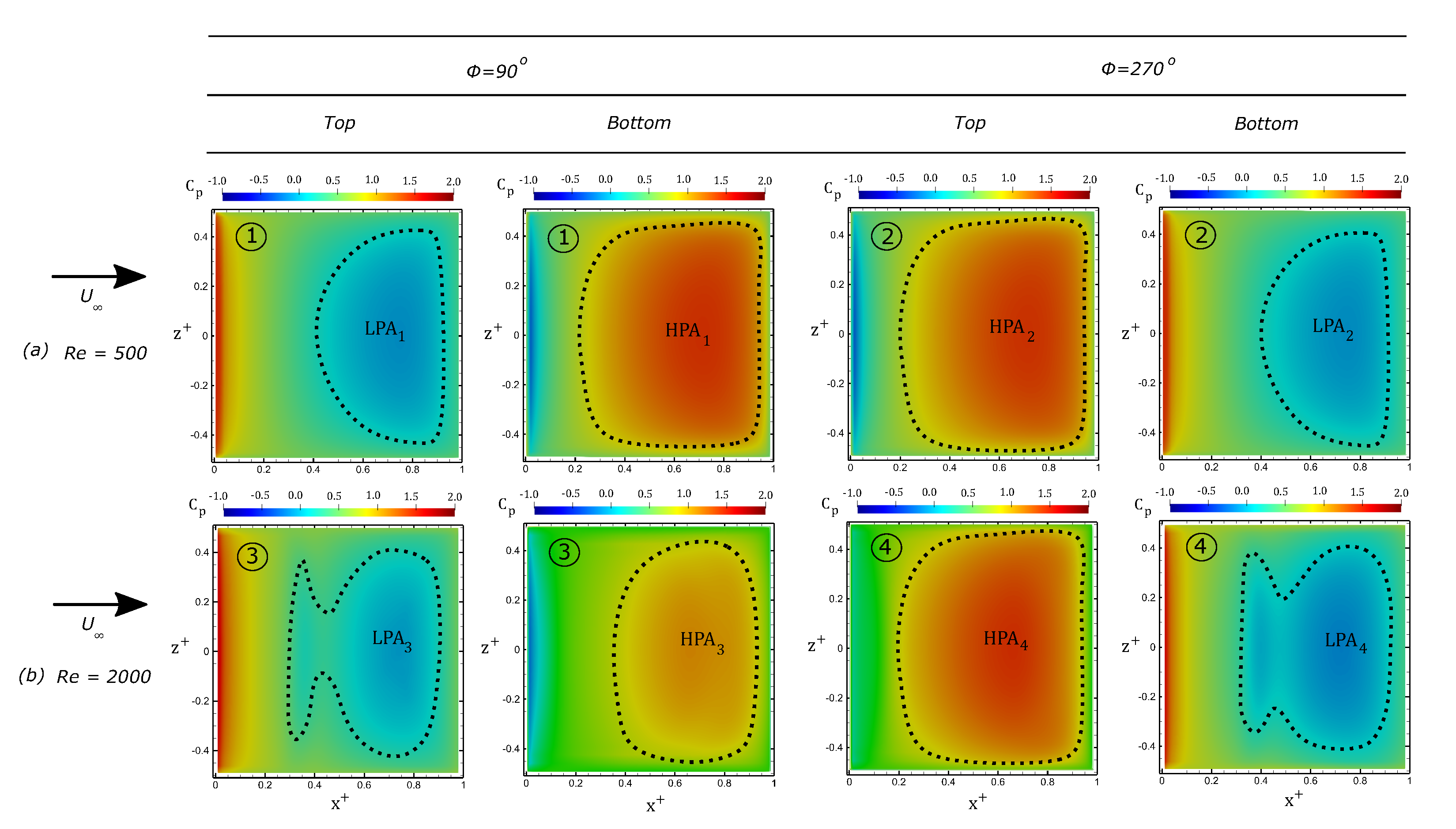
| Case Number | Motion Description | Angle of Attack, [deg] | Maximum Amplitude, A [deg] | Reynolds Number, | Strouhal Number, |
|---|---|---|---|---|---|
| 1 | Stationary | 0 | - | 300 | - |
| 2 | Stationary | 15 | - | 300 | - |
| 3 | Stationary | 30 | - | 300 | - |
| 4 | Stationary | 45 | - | 300 | - |
| 5 | Stationary | 60 | - | 300 | - |
| 6 | Pitching | - | 8 | 500 | 0.2 |
| 7 | Pitching | - | 8 | 2000 | 0.2 |
| Study | Method | Relative Error | (Meshes) | |||
|---|---|---|---|---|---|---|
| Grid-1 | Direct | 0.612 | 9.50% | - | ||
| Grid-2 | Direct | 0.589 | 5.40% | 3.7% | ||
| Grid-3 | Direct | 0.563 | 0.89% | 4.44% | ||
| Grid-4 | Direct | 0.56 | 0.35% | 0.5% | ||
| Taira et al. [23] | Direct | - | 0.558 | - | - |
| Sim. No. | Technique | CPU Time |
|---|---|---|
| 1 | InverseDistance | 11,330.14 |
| 2 | CellVolumeWeight | 40,779.31 |
| 3 | LeastSquares | 15,361.44 |
| 4 | TrackingInverseDistance | 12,619.05 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, S.; Hemmati, A. Performance of Overset Mesh in Modeling the Wake of Sharp-Edge Bodies. Computation 2020, 8, 66. https://doi.org/10.3390/computation8030066
Verma S, Hemmati A. Performance of Overset Mesh in Modeling the Wake of Sharp-Edge Bodies. Computation. 2020; 8(3):66. https://doi.org/10.3390/computation8030066
Chicago/Turabian StyleVerma, Suyash, and Arman Hemmati. 2020. "Performance of Overset Mesh in Modeling the Wake of Sharp-Edge Bodies" Computation 8, no. 3: 66. https://doi.org/10.3390/computation8030066
APA StyleVerma, S., & Hemmati, A. (2020). Performance of Overset Mesh in Modeling the Wake of Sharp-Edge Bodies. Computation, 8(3), 66. https://doi.org/10.3390/computation8030066





