Abstract
Silicene is considered to be the most promising anode material for lithium-ion batteries. In this work, we show that transmutation doping makes silicene substantially more suitable for use as an anode material. Pristine and modified bilayer silicene was simulated on a graphite substrate using the classical molecular dynamics method. The parameters of Morse potentials for alloying elements were determined using quantum mechanical calculations. The main advantage of modified silicene is its low deformability during lithium intercalation and its possibility of obtaining a significantly higher battery charge capacity. Horizontal and vertical profiles of the density of lithium as well as distributions of the most significant stresses in the walls of the channels were calculated both in undoped and doped systems with different gaps in silicene channels. The energies of lithium adsorption on silicene, including phosphorus-doped silicene, were determined. High values of the self-diffusion coefficient of lithium atoms in the silicene channels were obtained, which ensured a high cycling rate. The calculations showed that such doping increased the normal stress on the walls of the channel filled with lithium to 67% but did not provoke a loss of mechanical strength. In addition, doping achieved a greater battery capacity and higher charging/discharging rates.
1. Introduction
Lithium-ion batteries (LIBs) have high energy densities and a long operating life: they do not have a memory effect. These advantages have allowed LIB to take a leading position in the field of energy storage [1]. Currently, they are mainly intended for use as power sources in portable electronic devices. However, modern LIBs do not yet have sufficient power: they need significant reserves to boost their charge capacity and their charging rate. Solving these problems will promote the widespread use of LIBs in the automotive industry. Recently, a search for new materials for an anode has been actively conducted, since almost all previously used materials did not fully meet the requirements for the performance characteristics of the new-generation LIB anode [2]. Silicon has a record charge capacity in relation to the intercalation of lithium (4.4 Li atoms per 1 Si atom), which is many times higher than that of graphite. However, bulk silicon changes its volume greatly during lithiation (up to 400%). Therefore, it does not withstand any long cycling, and it cracks. As a result, the electrode becomes unusable. The use of thin films with a honeycomb structure (for example, silicene, graphene, or transition-metal dichalcogenides) as the anode material can substantially eliminate this drawback [3,4].
Thin films of silicon and (in particular) silicene are the most promising anode materials for lithium-ion batteries [5,6,7]. The advantage of their use in electrochemical devices is that they allow for the maintenance of a high theoretical electrode capacity (4200 mAh/g), which characterizes the intercalation of lithium in bulk silicon. In this case, the electrode remains stable during cycling, and the change in its volume during the intercalation of lithium is sharply reduced. However, silicene does not have the same mechanical strength as graphene. The presence of vacancy defects in silicene increases the capacity of the electrode during lithiation but reduces its mechanical strength [8]. Silicene saturated with tri- and hexavacancies is unsuitable for use as an anode material [9]. Doping silicene can improve its mechanical properties.
There are various experimental methods for doping silicon films with phosphorus. Thin silicon films can be doped with phosphorus to form a p – n junction through irradiation with thermal neutrons [10]. This method is called local neutron transmutation doping (NTD). Silicon films can also be doped using plasma chemical deposition with an electron beam. The conductivity of a phosphorus-doped Si/H film obtained in this way was ~1 Ω·cm–1 [11]. Phosphoric acid can be used as a source of polycrystalline silicon thin film doping [12]. Due to defects introduced during doping, an increase in the electrical resistivity of an n-type Si film was observed at a carrier concentration of 1015 cm−3. Silicon crystal phosphorus doping using NTD is the most effective doping control method. This method effectively removes the nonuniformities of a highly resistive silicon crystal. As a result of irradiation with thermal neutrons, some of Si atoms are transformed into P atoms, and a certain fraction of C atoms is converted into N.
Most often, doping a semiconductor material is used to obtain the properties necessary for applications in electronics. In this case, the strength properties of the material go by the wayside. However, the ability to withstand a prolonged dynamic load is a necessary quality of the anode material. In addition, when using thin-film materials, it is important not to deform them too much when the anode is filled with lithium, as in the case of anodes formed from pure two-layer graphene or silicene [13,14]. The strong deformation of two-layer honeycomb structures can significantly reduce the charge capacity of an electrode.
It has been shown that doping is important when silicene is used both as a material for electronic devices and as a material for layered electrodes [15]. Through first-principle calculations, it has been demonstrated that upon the Al/B doping of silicene, holes were formed, and the lattice constant increased [16]. Two layers of sodium were found to adsorb on doped (with B or Al) silicene. As a result, the capacitance of the electrode increased with respect to single-layer adsorption to 2256 and 1928 mAh/g, respectively. Density functional theory (DFT) calculations predict that Al/B-doped silicene can be effectively used as the electrode material in an LIB. Doping silicene with such elements as phosphorus leads to a decrease in the cohesion energy of this two-dimensional material and to an increase in its strength.
An adequate study of the intercalation of lithium in a silicon material is possible using the classical molecular dynamics model, which allows for calculations for a sufficiently large system and considers the process over a considerable time period. The number of intercalated Li atoms can reach up to 80% of the number of Si atoms in a silicene sheet. For modeling, it is necessary to know the exact potentials of the interatomic interaction. If such potentials were created and widely used for systems with ion–covalent interactions [17,18], then the interactions of Si and C with P and N could be easily described. Unfortunately, interaction potentials are poorly represented, and data on P interaction potentials are almost absent. Therefore, the first part of this study was devoted to the development of such potentials.
The aim of this work was to study the effect of phosphorus-doping silicene using NTD on the ability of lithium to fill channels formed by silicene sheets on a graphite substrate, including a modified silicene, and also to estimate the adequacy of descriptions of interatomic interactions with parameters obtained through Morse potentials.
2. Materials and Methods
2.1. Potential Related to Substrate
For carbon atoms, we applied the traditional Tersoff potential [19,20]. The encapsulation of nitrogen atoms into graphene results in the distortion of its lattice. Lengths, elasticities, and strengths of C–N bonds differ from the corresponding characteristics of C–C bonds. Not all empirical force fields are applicable to the specific case of C–N and N–N interactions on a graphene sheet. To check the traditional boron, nitrogen, carbon (BNC) Tersoff potential [21], we applied it to three small models of nitrogen-doped graphene and compared the results to more accurate density functional theory (DFT) calculations. For these calculations, we used a generalized gradient approximation (GGA) in the form of the van der Waals Density Functional (vdW DF) of Dion et al. [22] with the exchange modification of K. Berland and P. Hyldgaard [23] together with a polarized split-valence double-z (DZP) basis set [24]. A rectangle form of periodic cells was conserved during the geometry optimization, but both in-plain periods were optimized. An out-of-plane period of 80 Å preserved any interlayer interactions. We used a 6×6×4 set of k-points according to the Monkhorst–Pack scheme [25] and a plane-wave cutoff of 300Ry. For carbon and nitrogen atoms, we used nonrelativistic norm-conserving Troullier–Martins pseudopotentials [26,27]. SIESTA software [24] was applied.
The periodic cells of the considered models are shown in Figure 1. For every system, we calculated the mean energy of nitrogen defects, Ed, as follows:
where E(C24) and E(C24-qNq) are the energies of pristine (Figure 1a) and doped (Figure 1b–d) graphene periodic cells; E(C) and E(N) are the energies of carbon and nitrogen atoms, respectively; and q is the number of nitrogen atoms in the unit cells (q = 1, 2, or 6).
Ed = (E(C24-qNq) + E(C) – E(C24) – E(N))/q,
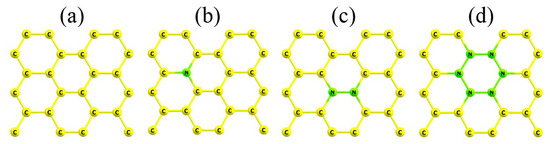
Figure 1.
Periodic cells for the models of pristine (a) and nitrogen-doped (b–d) graphene.
To probe the elastic properties of the regarding systems, we also calculated the energy differences ΔEa, ΔEz, and ΔE between the undistorted system and the system under 2% stretching along the armchair, in a zigzag, or in both directions, respectively. In addition, we calculated the mean lengths of C–N and N–N bonds. The corresponding data are listed in Table 1.

Table 1.
Energies of the nitrogen defects, energy differences, and average bond lengths calculated within the density functional theory and empirical force fields. All energies and lengths are in eV and Å, respectively. DFT: density functional theory.
As is evident from Table 1, the BCN Tersoff potential was completely inadequate for the nitrogen-doped graphene. For example, it predicted the negative energy of the single-nitrogen defect in graphene and of N–N bonds shorter than 1 Å. Thus, we did not use the BCN potential in our study. As an alternative, we combined the traditional Tersoff potential for carbon with an additional pair of Morse terms for C–N and N–N interactions:
where r is the interatomic pair distance; and De, α, and r0 are the fitting parameters. During our simulations, we did not expect the breaking or formation of any new bonds in nitrogen-doped graphene. Therefore, a rather simple Morse potential was sufficient to describe the energy, geometry, and elasticity of the C–N and N–N bonds. Morse potential parameters were fitted to the obtained DFT data. Their values are presented in Table 2. One can see from Table 1 that the combined Tersoff + Morse approach provided the best agreement with the DFT data. The mean absolute deviations of the calculated energies from the corresponding DFT values were equal to 1.23 and 0.02 eV for the BCN Tersoff and Tersoff + Morse approaches, respectively. At the same time, the mean absolute deviation of bond lengths was less than 0.01 Å for both empirical approaches.
Φ(r) = De[exp{–2α(r – re)} – 2exp{–α(r – re)}],

Table 2.
Morse fitting parameters for the interatomic pair interactions. The cutoff distance was 2.0 Å for C–C and C–N interactions and 3.0 Å for Si–P and P–P interactions. The three parameter sets for P–P interactions corresponded to the following cases: (1) each P atom in a pair had only one P neighbor; (2) each P atom in a pair had two or more P neighbors; and (3) the first P atom in a pair had only one P neighbor, but the second one had two or more P neighbors.
To describe the C–C interactions inside the graphite layers (or in the bound graphene), the Tersoff potential with a modified cut-off function [28] was used. Using this potential prevents the overestimation of the rigidity of this material and leads to its realistic mechanical behavior [29].
2.2. Modeling of Intercalation of Lithium in a Silicene Channel
For the Si–P and Si–Si interactions in P-doped silicene, we applied the same combined Tersoff + Morse approach described in the previous section. We used similar model systems for the P-doped silicene (see Figure 1, where one should replace C and Si elements by N and P, respectively). DFT and empirical results are listed in Table 1, and the fitting Morse parameters are presented in Table 2. One can see that the difference between the empirical and DFT data for P-doped silicene was stronger than the corresponding difference for N-doped graphene. The origin of this mismatch was the corrugated structure of silicene, which results in a low value of its rigidity. However, we found that the Tersoff + Morse approach was acceptable for our calculations. Thus, we applied it in our further molecular dynamics simulations.
The interaction between Si atoms located in the same silicene sheet was carried out using the Tersoff potential [20]. Cross-interactions, including the interaction between Si atoms belonging to different sheets of silicene, were carried out on the basis of the application of the Morse potential [30,31,32]. The interactions between atoms of type A and atoms of type B can be described using the Morse potential, whose parameters (AB) are calculated from simple interpolation relations [8]:
De AB = (De A De B)1/2,
α AB = ½ (α A α B),
re AB = (re A re B)1/2.
α AB = ½ (α A α B),
re AB = (re A re B)1/2.
In addition, according to Equation (3), the interactions Li–Li and Li–X were calculated, where X = Si, C, P, N. The parameters of the Morse potential for cross-interactions (not included in Table 2) are presented in Table 3. The parameters of the interatomic interactions Si(1)–Si(2), C(1)–C(2), and Li–Li for this potential are also given here. The superscripts indicate that the atom belongs to one of the sheets (1 or 2) of silicene or graphene.

Table 3.
Morse potential parameters used to describe cross-interactions, including those between Si and C atoms lying in different structural layers as well as interactions between lithium atoms.
2.3. Molecular Dynamic Simulation Technique
Bilayer silicene was considered to be a channel for the intercalation of lithium. Each sheet of silicene contained 300 atoms. Atoms in the lower layer of silicene were located exactly under the center of regular hexagons belonging to the upper layer. The average distance between the nearest Si atoms in the same silicene sheet was 0.233 nm. Hexagonal graphite consisting of four layers with 680 atoms in each layer was used as a substrate. The packing order of graphite planes was determined by alternating layers according to the ABAB type, which was analogous to that of bilayer silicene. The distance between the graphite layers was 0.337 nm, and the distance between the nearest neighboring C atoms in the plane of the layer was 0.242 nm.
Sheets of silicene with a floral structure [5] were arranged horizontally one above the other. The unit cell of silicene had a rhombic shape and contained 18 atoms, 6 of which were elevated relative to the basal plane [33]. The sheets of silicene were oriented with respect to each other so that the protrusions on their surfaces were facing outward. The calculations were performed for six hg gaps between the sheets of silicene, with an initial value of 0.24 nm and a final value of 0.75 nm. The value hg = 0.24 nm was determined in the DFT calculations as a gap in two-layer free-standing silicene [34]. The gap hg = 0.75 nm was used to study the intercalation/deintercalation of lithium in a silicene channel on metal substrates [5,6,7]. The remaining hg values were separated from each other by a distance of 0.1 nm. The lithium atoms in the channel with the gap hg = 0.75 nm could move quite freely along the channels located on the metal (Ag, Al, and Cu) substrates [5,6,7,35]. In the present work, the initial distance between the lower silicene sheet and the graphite substrate was 0.222 nm and corresponded to a similar value determined using the DFT calculations in Reference [36]. The channel did not have material sidewalls but was surrounded by an artificial force barrier, making it difficult for atoms to escape through the side and back surfaces [7]. The model we used corresponded with electrodes in a lithium-ion battery being separated by a solid electrolyte. Through the input (frontal surface), Li+ ions were periodically introduced into the channel at an interval of 1 ps. Ions were introduced one after another and were “drawn” into the channel due to the applied electric field having a strength of 104 V/m. After 1 ps, the Li+ ion entering the channel turned into a lithium atom [7], which subsequently did not “feel” the presence of the electric field. In other words, the intercalation was simulated in the form of ions entering the silicene channel from a solid electrolyte, as is shown in Figure 2. The filling of each channel consisted of 400 starts of Li+ ions. In other words, the intercalation time in the system was 500 ps, or 5 million time steps (Δt = 0.1 fs).
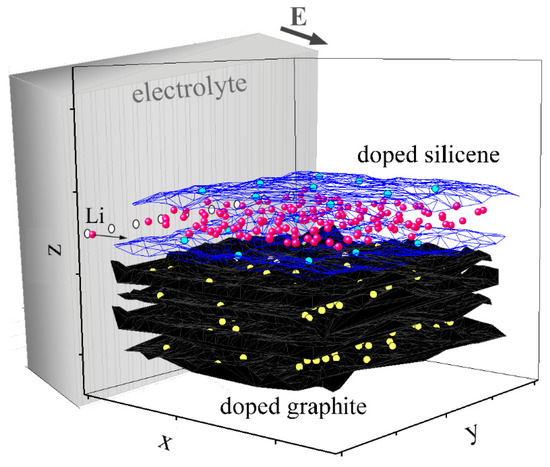
Figure 2.
Schematic diagram of the doped system (“silicene channel on a graphite substrate”), in which the channel was filled with lithium. Lithium ions entered the channel through a solid electrolyte. The walls of the channel are translucent, lithium atoms are shown as red circles, phosphorus atoms are represented by blue circles, and nitrogen atoms are shown as yellow circles.
The walls of the channel were represented either by sheets of perfect silicene or silicene containing defects. Nine defects were approximately evenly distributed on each of the sheets of silicene. Monovacancies were considered to be defects. An ion injection procedure was carried out until the channel was completely filled with lithium. When the limit was reached, the ions could no longer enter the channel and continued their motion beyond it.
The distance between the silicene sheets (from 0.24 nm to 0.75 nm) was a variable parameter in our study. Cell parameters and the number of Si, C, P, and N atoms remained unchanged. However, the number of Li+ ions intercalated in the channel changed depending on the distance between the silicene sheets. All initial parameters used in the simulation are presented in Table 4.

Table 4.
Initial parameters used in the simulation.
2.4. Calculation Formulas
The profile of the Li atom distribution density in the silicene channel was calculated as follows. The total volume of the channel was divided into identical elementary volumes. Further, the number of Li atoms (in the completely lithiated systems) belonging to the elementary volumes was estimated. This procedure was performed along the axes o–x and o–z (horizontal and vertical distribution density). A density profile reflected the final filling of the channel with lithium.
The self-diffusion coefficient of lithium atoms in the system is expressed as
where Γ is the dimension of space, and is the mean square of the displacement of atoms. The coefficient D was determined after the channel was completely filled with lithium in a separate calculation for a time interval of 500 ps. Moreover, the number of initial time instants was t0 = 5.
The filling of the silicene channel with lithium was associated with the appearance of stresses in the channel walls. We calculated the stress tensor arising in silicene during the intercalation of lithium, which characterized the mechanical suitability of this material to act as an anode. The calculated stress tensor was averaged over both channel walls. The components of the stress acting on the l elementary area are expressed as [37]
Here, n denotes the number of atoms in the l-element; Ω represents the volume per atom; Sl is the area of the l element; viα and fαij are α-projections of the velocity and force vector; i and j are the designations of atoms; ui and uj are the current coordinates of the i and j atoms; and the meeting point of the i–j straight line with an l area is indicated by u.
It was of interest to determine the binding strength between the intercalated lithium atoms and the channel walls. The substitution of certain atoms in silicene with phosphorus atoms can lead to a change in the adsorption energy of lithium atoms in the channel walls. In turn, this change will affect the channel occupancy. The adsorption (bonding) energy per lithium atom was calculated according to
where E0 is the total energy of the silicene layer free of adsorbed Li atoms, x is the number of Li atoms adsorbed on silicene, ELi is the energy of the isolated Li atom, and Ex is the total energy of the lithiated structure.
Eb = E0 + xELi − Ex,
In the present work, the standard Large-scale Atomic/Molecular Massively Parallel Simulation (LAMMPS) code for performing molecular dynamics (MD) modeling [38] was supplemented with fragments that made it possible to calculate the kinetic and mechanical properties of the system. The calculations were performed on a Uran cluster-type hybrid computer at the Institute of Mathematics and Mechanics of the Ural Branch (IMM UB) RAS with a peak capacity of 216 Tflop/s and a 1864 CPU.
3. Results
Doping of the system (a silicene channel on a graphite substrate) had a significant effect on the channel filling with lithium. Figure 3 compares the results of the intercalation of lithium into a pristine system and a system subjected to nuclear transmutation doping. In both cases, the initial gap between the sheets of silicene was 0.24 nm.
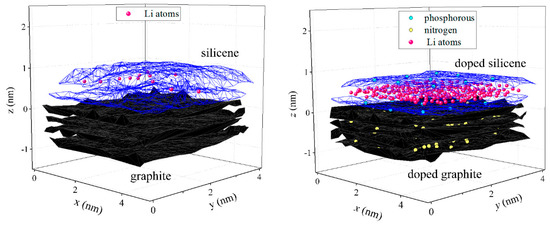
Figure 3.
Filling of a silicene channel (gaps of 0.24 nm) with lithium on a graphite substrate after 500 ps. A pristine system is shown on the left, and a system subjected to nuclear transmutation doping is shown on the right.
After 400 attempts to introduce Li+ ions between the sheets of silicene, 12 Li atoms were found in the pristine system, while the number of Li atoms in the channel of the irradiated system was 244. In the first case, the low channel occupancy was associated with severe deformation of not only the silicene sheets but also the layers of graphite. Both the upper and the lower sheets of silicene after intercalation acquired a convex shape (in the form of a dome). In the second case, the upper layer of graphite had a flatter shape. The lower sheet of silicene had a concave shape (the edges were raised above the substrate), and the upper sheet, on the contrary, had a raised fairly flat central part and edges lowered toward the substrate. This channel shape allowed for the accommodation of a fairly large number of Li atoms. The lithiation dynamical process is submitted in the Supplementary materials.
Table 5 presents the limiting number of Li atoms intercalated into silicene channels with various gaps both in the absence and in the presence of NTD. In almost all cases, with the exception of the channel with the gap hg = 0.75 nm, irradiation with thermal neutrons made it possible to achieve a substantially higher (almost one order of magnitude, and sometimes even higher) channel occupancy during lithium intercalation. This was due to the correct shape of the irradiated channel being maintained during the filling process, whereas pristine silicene underwent severe deformation, which greatly prevented it from filling the channel formed by it and lithium.

Table 5.
Limit number of intercalated lithium atoms in silicene channels with a gap hg (not subjected and subjected to nuclear transmutation doping (NTD)).
Lithium density profiles considered in the direction of the electric field (zigzag) in the irradiated and unirradiated silicene channels with different gaps are shown in Figure 4. Intercalation carried out in a pristine system led not only to an extremely low filling of the channel with lithium but also to extremely uneven filling in the zigzag direction. Channels with the gap hg = 0.75 nm, where a high and uniform degree of lithium filling was observed, were an exception. For the irradiated system, the pattern of filling the channel with lithium was completely different. In this case, for all channel gaps (without exception), a high degree of lithium filling was achieved. As a rule, this filling was fairly uniform. The channels with the narrowest gap (hg = 0.24 nm), where the maximum lithium filling was observed, were a certain exception. In this case, the filling of the first half of the channel in the zigzag direction was noticeably higher than the population of lithium in the second half. This was due to the fact that the almost completely filled narrow channel was continuously filled with lithium when the passage of Li atoms in the second half in the zigzag direction was impossible. In this channel, the largest number of lithium atoms (out of all the considered variants) fit because of the acquisition of an oval shape by the channel. Due to the narrow gap, the exit of Li atoms from the channel during its filling was extremely difficult.
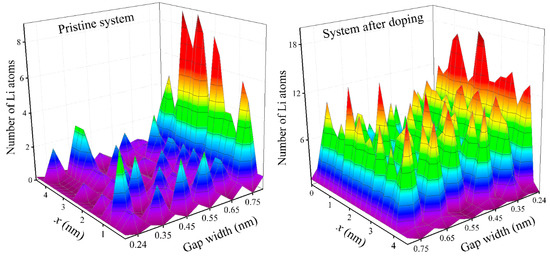
Figure 4.
Density profiles of lithium in a silicene channel in a zigzag direction, obtained as a result of the intercalation of Li+ ions into the channel (with walls of pristine silicene (left) and silicene processed by the NTD method (right)).
The height distribution of Li atoms in the silicene channels is shown in Figure 5, which presents the altitude density profiles of lithium atoms in unirradiated (left) and irradiated (right) channels. Since the gaps in the channels differed significantly, the display of the density profiles depending on the height values is not expressive. Therefore, an interval equal to the size of the entire gap (divided into 20 sections) on one of the horizontal axes is reflected in Figure 5. Here, the variable k shows the section number. The counting of the sections starts from the bottom sheet of silicene, i.e., bottom–up. This representation allows for a more accurate reflection of the altitude profiles of the distribution of lithium atoms in different channels in the same figure. As can be seen in Figure 5, lithium atoms were mainly located near the upper silicene sheet, almost regardless of the size of the gap in the channel. This was manifested to a greater extent for the case of the unirradiated system, in which the lower part of the channel extended upward almost to hg/2 and was not occupied by lithium. In the irradiated system, the value of the lithium-free region in the channel was somewhat reduced. This arrangement of Li atoms in the channel indicated a significant effect of the carbon substrate on the packing of intercalated Li atoms. This effect was reduced in the irradiated system due to an increase in the adsorption capacity of phosphorus-doped silicene. The uniformity of the distribution of Li atoms in the channel increased slightly with the increasing gap.
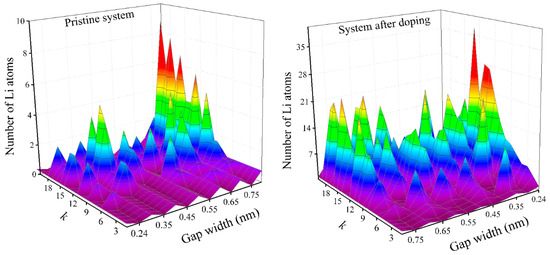
Figure 5.
Vertical density profiles of lithium in the silicene channel obtained as a result of the intercalation of Li+ ions into the channel (with walls of pristine silicene (left) and silicene processed by the NTD method (right)).
Normal to the channel walls stresses σzz are the most significant both for the channel free of lithium and for the channel filled with this metal. Figure 6 shows the distribution of σzz stresses in the silicene sheets in the zigzag and armchair directions. The stress distributions corresponded with the moment of complete filling of the channel for the narrowest gap (0.24 nm) of lithium both for the undoped and for the doped systems. The stresses σzz were negative due to the corresponding direction of the forces fz that stretched the silicene. As a rule, the absolute value of the stress σzz in the walls of the irradiated silicene channel was higher than that in the walls of the unirradiated silicene channel. This was due to the appearance of additional stresses created by the impurity introduced by NTD. The stress distribution σzz in the zigzag direction was more uniform than in the armchair direction.
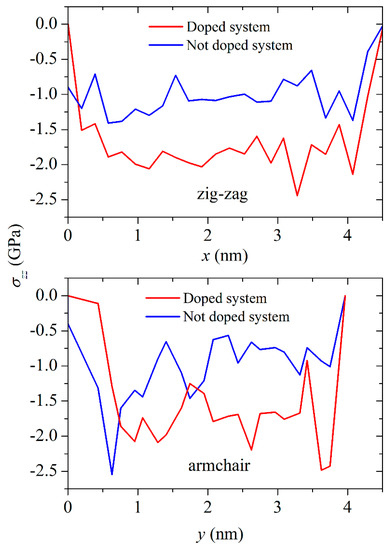
Figure 6.
Distribution of σzz stresses in the zigzag (top) and armchair (bottom) directions for the systems (“silicene channel–carbon substrate”) not subjected to and subjected to NTD when the channel was completely filled with lithium. The channel width was 0.24 nm.
The phosphorus- and nitrogen-doping of silicene and a carbon substrate, respectively, led to an increase in the adsorption energy Eb of lithium on silicene (Figure 7a), which implied a complete filling of the channel with lithium. With gaps in the silicene channel from 0.24 to 0.65 nm, a relatively small change in the adsorption energy occurred both in the doped and in the undoped systems. However, upon a gap change to 0.75 nm, in both cases, there was a sharp increase in the value of Eb. Most likely, with this gap, a significant number of Li atoms occupied, energetically, more favorable places near the channel walls. Such places could be located above or below the centers of hexagonal cells formed by the Si atoms.
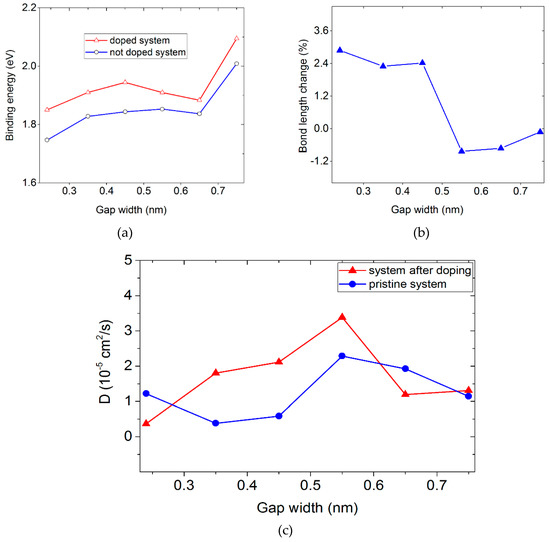
Figure 7.
(a) Binding energy, Eb, of Li as a function of channel gap width for undoped and doped systems; (b) change in the Si–P bond length during the filling of a silicene channel with phosphorus-doped walls as a function of the channel gap; (c) coefficient of the self-diffusion of lithium atoms in the silicene channel with undoped and phosphorus-doped walls.
Filling of the narrow (hg ≤ 0.45 nm) irradiated silicene channel with lithium caused an increase in the stress in the channel walls and an increase in the adsorption energy of the Li atoms. In this case, P atoms embedded in silicene were somewhat distant from the Si atoms. This was expressed in an increase in the length of the Si–P bond by 2.3%–2.9% (Figure 7b). However, a further increase in the channel gap to 0.55 nm led to a decrease in the lithium adsorption energy and a noticeable decrease in the length of the Si–P bond. As a result, the length of the Si–P bond even decreased (by 0.8%) with respect to the corresponding size in the initial state, i.e., in the absence of lithium in the channel. A further increase in the channel gap led to a slight increase in the bond length, but even with the gap of 0.75 nm, it still remained 0.12% below its initial value.
The dependence of the self-diffusion coefficient D of Li atoms when the channel was completely filled with lithium took on a shape resembling a sinusoid (Figure 7c). The D(hg) function of the irradiated silicon material also behaved unpredictably. Both dependences D(hg) had a maximum at hg = 0.55 nm. The D values of the Li atoms in the unirradiated and irradiated channels almost equalized when the gap became 0.75 nm. The values of the gap-averaged D coefficients of lithium for the unirradiated and irradiated systems were 1.25 × 10–5 cm2/s and 1.69 × 10–5 cm2/s, respectively. This was only 5.4 and 4.0 times less than the self-diffusion coefficient of liquid lithium at the melting point (6.8 ± 0.3 × 10–5 cm2/s) [39].
4. Discussion
In References [5,6,7], it was shown that using the same procedure for lithium filling in an identical silicene channel that has no defects and is located on metal substrates (Ag, Al, Cu, and Ni) can achieve the presence of 39 to 74 Li atoms. The best channel occupancy with lithium (91 Li atoms) was achieved in the presence of monovacancies in the channel walls if the channel was placed on the Ni(111) substrate and in the presence of bivacancies (85 Li atoms) in silicene when the channel was on the Cu(111) substrate. The silicene channel with a gap of hg = 0.75 nm (located on the graphite substrate) had a significantly higher degree of lithium filling: 143 Li atoms for the pristine system and 165 Li atoms for the system subjected to NTD processing. As can be seen, with a given channel gap, irradiation ceased to play any role in increasing the channel capacity with respect to its filling with lithium. However, it is noteworthy that the channel on the graphite substrate had a significantly higher capacity (up to four times greater) than similar channels on any other metal surface. The main reason for this was a great change in the shape of the channel on the metal substrate. This made it difficult to access a large number of Li+ ions in the channel.
The phosphorus-doped silicene channel had a significantly better horizontal fillability with lithium than the corresponding channel made of pure silicene. The high horizontal uniformity of the filling of the channel irradiated with thermal neutrons was associated with its weak bending deformation compared to that of the unirradiated channel. This was due to the formation of strong Si–P bonds in the system. A vertical irregularity in the filling of the channel with lithium was also present after irradiation of the system. However, the degree of this unevenness in the doped system decreased. The predominant lithium filling of the upper part of the channel was associated with the presence of a solid substrate, to which the lower wall of the channel adhered tightly. Lithium atoms moving along the channel collided with each other and with Li+ ions introduced into the channel. As a result of these collisions, the direction of the velocity of the atoms changed. Atoms that had a high proportion of a vertical velocity component and that were moving downward collided with the atoms of the lower, rigid, nonbending channel wall and then flew away from it. Due to a much softer interaction with the upper wall, which did not have any support or Li atoms “attached” to it, they fixed themselves to the upper wall or were attached to the atoms deposited on it. This formed a vertical density profile in the channel. Phosphorus doping caused hardening of the upper wall of the channel. In this case, the reaction of the wall to collisions produced by Li atoms was more stringent than in the case of an undoped system. As a result, Li atoms were removed from the upper wall at greater distances, thereby reducing the free space of the lower part of the channel. The low diffusion barriers of Li and a high diffusion rate suggest that silicene on a substrate has an increased charge/discharge rate [40]. Thus, higher values of the coefficient D are necessary to increase the rate of cycling. However, an excessive increase in the self-diffusion coefficient of lithium ions сaused, for example, by strong heating can lead to the occurrence of significant stresses in silicene sheets, which provokes the material’s destruction.
Depending on the channel gap, the lithium adsorption energy varied from 1.75 to 2.05 eV in the case of an undoped system and from 1.85 to 2.10 eV for a doped system. These adsorption energies were in good agreement with the results of first-principle calculations (2.08–2.23 eV) obtained from a study of lithium diffusion in free-standing two-layer silicene [41]. We note that the binding energy of lithium in crystalline silicon (1.62 eV) [42], as well as the energy of lithium adsorption on silicon nanowires (1.6 eV) [43], was inferior to our Eb of bilayer silicene on the carbon substrate. The theoretical specific charging capacity of bilayer silicene is 715 mAh/g [44]. Taking into account the calculated occupancy of the phosphorus-doped silicene channel (hg = 0/24 nm) on the graphite substrate, the chemical activity of silicon with respect to lithium, and the feasibility of using multilayer silicene as an anode material, we could estimate the charge capacity of the modified silicene anode as 776 mAh/g. Thus, phosphorus doping may increase the capacity of the silicene anode by 8.5%.
It has been experimentally established that the hardness of silicon wafers (according to Vickers) increases by 1.2 times after strong phosphorus doping [45]. This result is consistent with our average 4.2% increase in the binding energy of lithium with the substrate after the phosphorus-doping of silicene. The binding energy increased as the contact of Li atoms with the silicene wall of the channel became closer, which was possible when the wall became more rigid.
Local stresses σzz in the channel walls, which appeared during the intercalation of lithium from forces acting perpendicularly to the walls, did not exceed 2.6 GPa both for the unirradiated system and for the system irradiated with thermal neutrons. Similar studies performed for an autonomous silicene membrane showed the possibility of achieving stresses of ~0.72 GPa in the membrane [46]. Such stresses could not cause mechanical damage to silicene, because its fracture strength is ~12.5 GPa at room temperature [47].
5. Conclusions
A method for reconstructing the interatomic interaction potential using quantum mechanical calculations was developed. The parameters of the Morse potential were calculated to describe the interactions of P and N atoms with each other and with Si and C. The use of the developed potentials for modeling the intercalation of phosphorus- and nitrogen-doped two-dimensional silicene systems provided adequate results. For six different channel gaps, classical molecular dynamic modeling of the intercalation of lithium into silicene channels located on a graphite substrate was performed. In the case of doping with phosphorus, the highest filling of the channel with lithium was achieved with the smallest of the considered gaps (hg = 0.24 nm). The use of a graphite substrate was found to increase significantly the number of Li atoms introduced into the channel as opposed to the use of metal substrates. The calculated horizontal density profiles of lithium (in a zigzag direction) indicated an inhomogeneous filling of the undoped silicene channels with lithium and an almost uniform filling of the phosphorus-doped channels. Density profiles in the vertical direction reflected a concentration of Li atoms in the vicinity of the upper silicene sheet both in the case of the undoped and in the case of the doped systems. Moreover, doping with phosphorus led to some stretching of the vertical density profile toward the lower sheet of silicene. Normal to silicene sheets stresses σzz, are the determining stresses in the channel walls when it is completely filled with lithium. The maximum values of σzz both in the case of undoped and in the case of doped systems did not exceed 21% of the stress leading to silicene destruction. The binding energy of lithium with the channel walls increased by 2.5%–6.0% as a result of the silicene phosphorus-doping. Both in the presence of doping and in its absence, the binding energy of lithium with silicene was maximal with the largest (hg = 0.75 nm) of the simulated gaps in the channel. The intercalation of lithium into the channel led to an increase in the length of the Si–P bond if the gap hg < 0.5 nm. Otherwise, the length of the Si–P bond was slightly reduced with respect to its value for the channel that did not undergo the intercalation. For both types of studied channels, fluctuating and mismatching dependencies of the average coefficient of the self-diffusion of lithium atoms on the channel gap were observed. However, at the maximum gap of hg = 0.75 nm, the D values for the channels with doped and undoped silicene walls almost coincided. The data obtained indicate an improvement in the characteristics necessary for the application of silicene as an anode material when it is doped with phosphorus.
Thus, our results show excellent possibilities for using P-doped silicene as an electrode material in a lithium-ion battery.
Supplementary Materials
The following are available online at https://www.mdpi.com/2079-3197/7/4/60/s1.
Author Contributions
A.G. performed the conceptualization, methodology, formal analysis, investigation, writing—original draft preparation, project administration, and funding acquisition. K.I. was engaged in investigation, software, validation, resources, data curation, and formal analysis. K.K. performed the methodology, formal analysis, validation, data curation, and writing—review and editing. M.M. Maslov performed the methodology, formal analysis, validation, data curation, and writing—review and editing.
Funding
This work was supported by the Russian Science Foundation (grant number 16-13-00061).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Galashev, A.E.; Rakhmanova, O.R.; Zaikov, Y.P. Defect silicene and graphene as applied to the anode of lithium-ion batteries: Numerical experiment. Phys. Solid State 2016, 58, 1850–1857. [Google Scholar] [CrossRef]
- Galashev, A.E.; Rakhmanova, O.R. Computer simulation of a forced drift of lithium ions through graphene membranes. High Temp. 2016, 54, 11–19. [Google Scholar] [CrossRef]
- Salah, M.; Murphy, P.; Hall, C.; Francis, C.; Kerr, R.; Fabretto, M. Pure silicon thin-film anodes for lithium-ion batteries: A review. J. Power Sour. 2019, 414, 48–67. [Google Scholar] [CrossRef]
- Luo, X.; Lang, J.; Lv, S.; Li, Z. High-performance sandwich structured Si thin film anodes with LiPON coating. Front. Mater. Sci. 2018, 12, 147–155. [Google Scholar] [CrossRef]
- Galashev, A.Y.; Ivanichkina, K.A. Computer test of a new silicone anode for lithium-ion battery. ChemElectroChem 2019, 6, 1525–1535. [Google Scholar] [CrossRef]
- Galashev, A.Y.; Ivanichkina, K.A. Computer study of atomic mechanisms of intercalation/deintercalation of Li ions in a silicene anode on an Ag (111) substrate. J. Electrochem. Soc. 2018, 165, 1788–1796. [Google Scholar] [CrossRef]
- Galashev, A.Y.; Ivanichkina, K.A. Computational investigation of a promising Si–Cu anode material. Phys. Chem. Chem. Phys. 2019, 21, 12310. [Google Scholar] [CrossRef] [PubMed]
- Galashev, A.E.; Ivanichkina, K.A. Numerical simulation of the structure and mechanical properties of silicene layers on graphite during the lithium ion motion. Phys. Solid State 2019, 61, 233–243. [Google Scholar] [CrossRef]
- Galashev, A.E.; Ivanichkina, K.A.; Vorobev, A.S.; Rakhmanova, O.R. Structure and stability of defective silicene on Ag(001) and Ag(111) substrates: A computer experiment. Phys. Solid State 2017, 59, 1242–1252. [Google Scholar] [CrossRef]
- Yamada, Y.; Yamamoto, H.; Ohba, H.; Sasase, M.; Esaka, F.; Yamaguchi, K.; Udono, H.; Shamoto, S.; Yokogama, A.; Hojou, K. Local neutron transmutation doping using isotopically enriched silicon film. J. Phys. Chem. Solids 2007, 68, 2204–2208. [Google Scholar] [CrossRef]
- Shchukin, V.; Sharafutdinov, R.G.; Konstantinov, V.O. Deposition of silicon films doped with boron and phosphorus by the gas-jet plasma-chemical method. Semiconductors 2019, 53, 127–131. [Google Scholar] [CrossRef]
- Ali, M.K.M.; Ibrahim, K.; Mkawi, E.M.; Salhin, A. Characterization of phosphoric acid doped N-type silicon Thin films printed on ITO coated PET substrate. Int. J. Electrochem. Sci. 2013, 8, 535–547. [Google Scholar]
- Galashev, A.E.; Zaikov, Y.P. Computer simulation of Li+ ion interaction with a graphene sheet. Rus. J. Phys. Chem. A 2015, 89, 2243–2247. [Google Scholar] [CrossRef]
- Galashev, A.E.; Ivanichkina, K.A. Computer modeling of lithium intercalation and deintercalation in a silicene channel. Rus. J. Phys. Chem. A 2019, 93, 765–769. [Google Scholar] [CrossRef]
- Zhu, J.; Gandi, A.N.; Schwingenschlogl, U. Potential of B/Al-doped silicene electrodes in Na/K-ion batteries. Adv. Theory Simulat. 2018, 1, 1800017. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, Y. Density functional theory study of the silicene-like SiX and XSi3 (X = B, C, N, Al, P) honeycomb lattices: The various buckled structures and versatile electronic properties. J. Phys. Chem. C 2013, 117, 18266–18278. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Weber, T.A. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B Condens. Matter. 1985, 31, 5262–5271. [Google Scholar] [CrossRef]
- Tersoff, J. Empirical interatomic potential for carbon, with application to amorphous carbon. Phys. Rev. Lett. 1988, 61, 2879–2882. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B: Condens. Matter. 1989, 39, 5566–5568. [Google Scholar] [CrossRef]
- Kınacı, A.; Haskins, J.B.; Sevik, C.; Çağın, T. Thermal conductivity of BN–C nanostructures. Phys. Rev. B 2012, 86, 115410. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schroder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef] [PubMed]
- Berland, K.; Hyldgaard, P. Exchange functional that tests the robustness of the plasmon description of the van der Waals density functional. Phys. Rev. B 2014, 89, 035412. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter. 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. II. Operators for fast iterative diagonalization. Phys. Rev. B 1991, 43, 8861–8869. [Google Scholar] [CrossRef]
- Gopal, R.; Kumar, R.; Parashar, A. Tersoff potential with improved accuracy for simulating graphene in molecular dynamics environment. Mater. Res. Express 2016, 3, 035011. [Google Scholar]
- Galashev, A.E. Molecular dynamic simulation of the bombardment of a lead film on graphene by Xe13 clusters. Phys. Met. Metallogr. 2016, 117, 246–253. [Google Scholar] [CrossRef]
- Yu, R.; Zhai, P.; Li, G.; Liu, L. Molecular dynamics simulation of the mechanical properties of single-crystal bulk Mg2Si. J. Electron. Mater. 2012, 41, 1465–1469. [Google Scholar] [CrossRef]
- Fang, T.-E.; Wu, J.-H. Molecular dynamics simulations on nanoindentation mechanisms of multilayered films. Comp. Mater. Sci. 2008, 43, 785–790. [Google Scholar] [CrossRef]
- Das, S.K.; Roy, D.; Sengupta, S. Volume change in some substitutional alloys using Morse potential function. J. Phys. F: Metal. Phys. 1977, 7, 5–13. [Google Scholar] [CrossRef]
- Galashev, A.E.; Rakhmanova, O.R.; Ivanichkina, K.A. Graphene and graphite supports for silicene stabilization: A computational study. J. Struct. Chem. 2018, 59, 877–883. [Google Scholar] [CrossRef]
- Rui, W.; Shaofeng, W.; Xiaozhi, W. The stability and charge carriers in bilayer silicene. arXiv 2013, arXiv:1305.4789. [Google Scholar]
- Galashev, A.Y.; Ivanichkina, K.A. Nanoscale simulation of the lithium ion interaction with defective silicene. Phys. Lett. A 2017, 381, 3079–3083. [Google Scholar] [CrossRef]
- Neek-Amal, M.; Sadeghi, A.; Berdiyorov, G.R.; Peeters, F.M. Realization of free-standing silicene using bilayer graphene. Appl. Phys. Lett. 2013, 103, 261904. [Google Scholar] [CrossRef]
- Galashev, A.Y. Computer study of the removal of Cu from the graphene surface using Ar clusters. Comput. Mater. Sci. 2015, 98, 123–128. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Murday, J.S.; Cotts, R.M. Self-diffusion coefficient of liquid lithium. J. Chem. Phys. 1968, 48, 4938–4945. [Google Scholar] [CrossRef]
- Galashev, A.Y.; Zaikov, Y.P. New Si–Cu and Si–Ni anode materials for lithium ion batteries. J. Appl. Elecrtochem. 2019, 49, 1027–1034. [Google Scholar] [CrossRef]
- Lin, X.; Ni, J. Much stronger binding of metal adatoms to silicene than to graphene: A first-principles study. Phys. Rev. B 2012, 86, 075440. [Google Scholar] [CrossRef]
- Tritsaris, G.A.; Zhao, K.; Okeke, O.U.; Kaxiras, E. Diffusion of Lithium in Bulk Amorphous Silicon: A Theoretical Study. J. Phys. Chem. C 2012, 116, 22212–22216. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, W.; Cui, Y.; Wang, E. Lithium insertion in silicon nanowires: An ab initio study. Nano Lett. 2010, 10, 3243–3249. [Google Scholar] [CrossRef] [PubMed]
- Tritsaris, G.A.; Kaxiras, E.; Meng, S.; Wang, E. Adsorption and diffusion of lithium on layered silicon for Li-ion storage. Nano Lett. 2013, 13, 2258–2263. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.; Sun, Y.; Lu, Y.; Liang, X.; Tian, D.; Ma, X.; Yang, D. Comparison on mechanical properties of heavily phosphorus- and arsenic-doped Czochralski silicon wafers. AIP Adv. 2018, 8, 045301. [Google Scholar] [CrossRef]
- Mortazavia, R.; Dianatb, A.; Cunibertib, G.; Rabczuk, T. Application of silicene, germanene and stanene for Na or Li ion storage: A theoretical investigation. Electrochimica Acta. 2016, 213, 865–870. [Google Scholar] [CrossRef]
- Pei, Q.X.; Sha, Z.D.; Zhang, Y.Y.; Zhang, Y.W. Effects of temperature and strain rate on the mechanical properties of silicone. J. Appl. Phys. 2014, 115, 023519. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).