Application of High-Order Compact Difference Scheme in the Computation of Incompressible Wall-Bounded Turbulent Flows
Abstract
1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. Temporal Discretization
2.3. Spatial Discretization
2.4. Inversion of the Semi-Implicit Linear System
2.5. Poisson Equation Solver
- Compute by DFT or DCT.
- Compute modified wavenumbers and .
- Compute in Fourier space by Equation (35).
- Compute in physical space by inverse DFT or DCT of .
3. Validation Tests
3.1. Taylor–Green Vortices
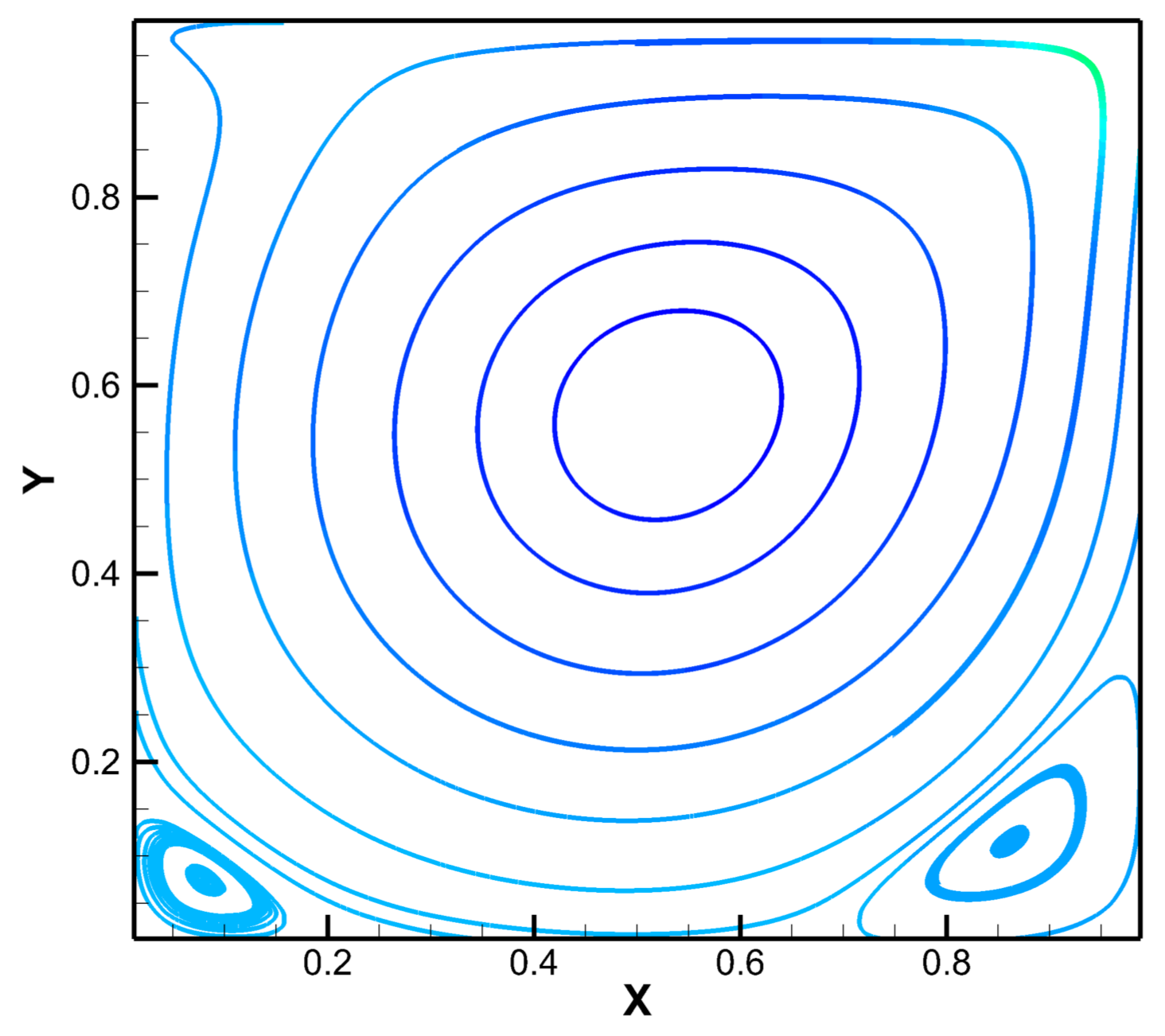
3.2. Burggraf Flow
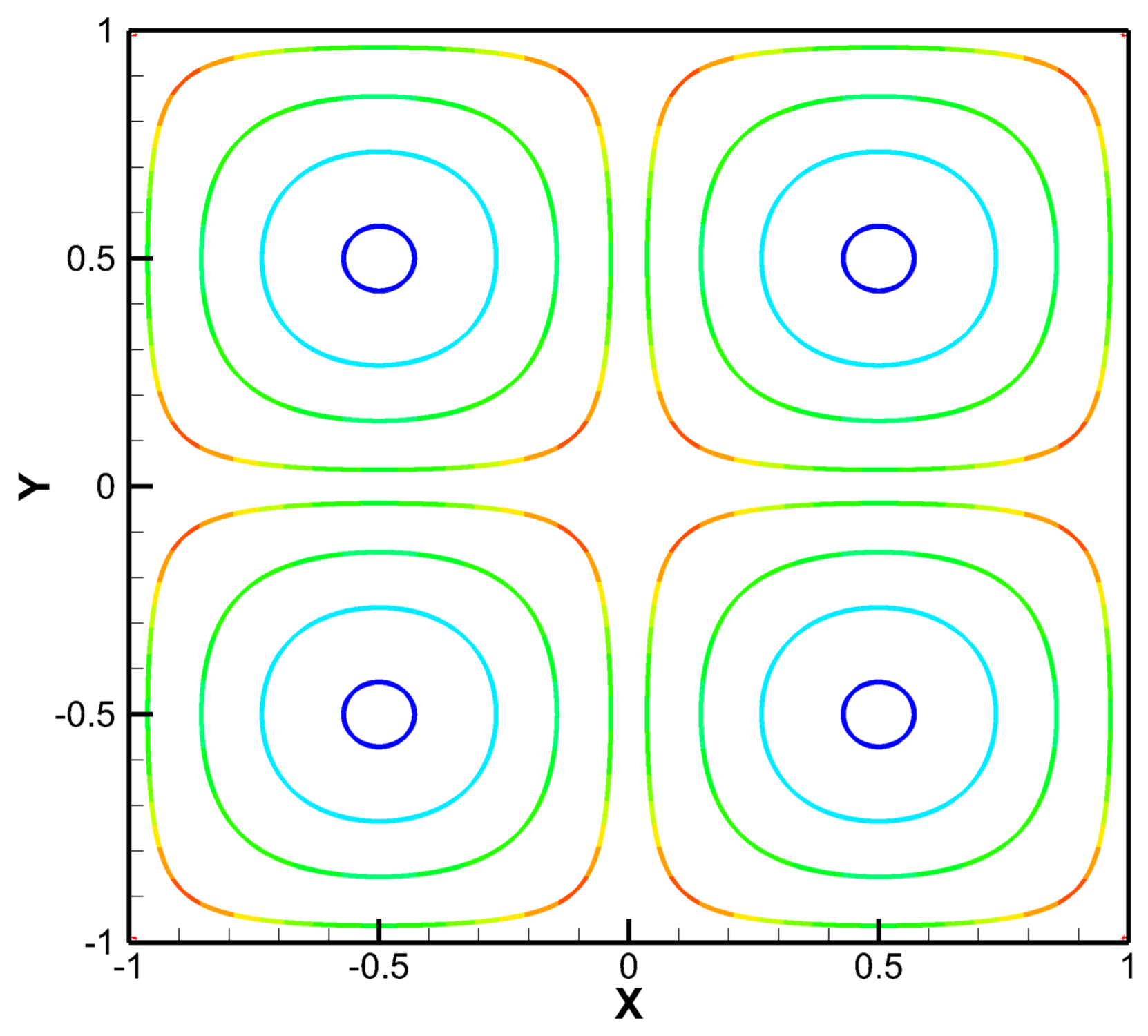
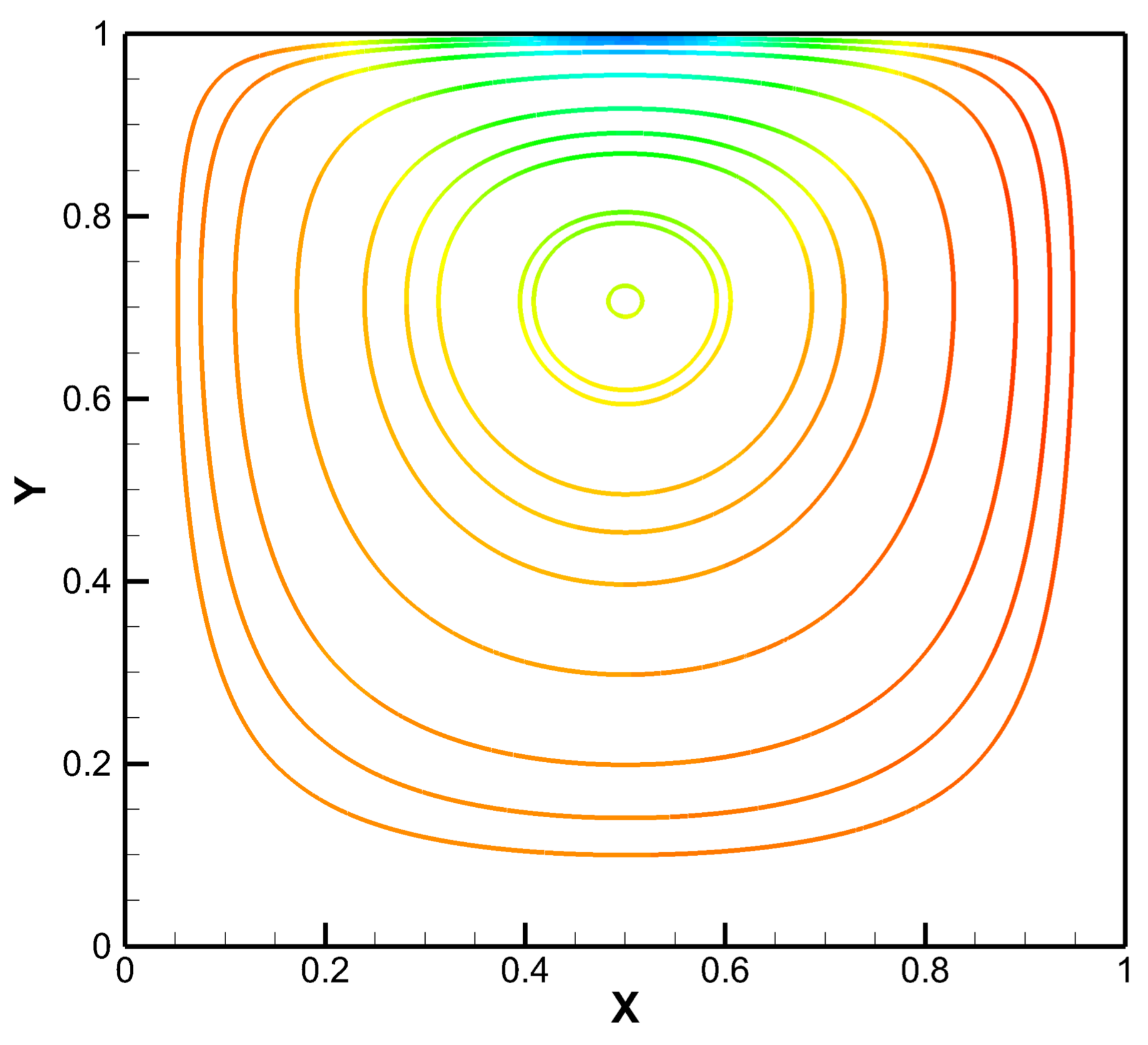
3.3. Lid-Driven Cavity Flow
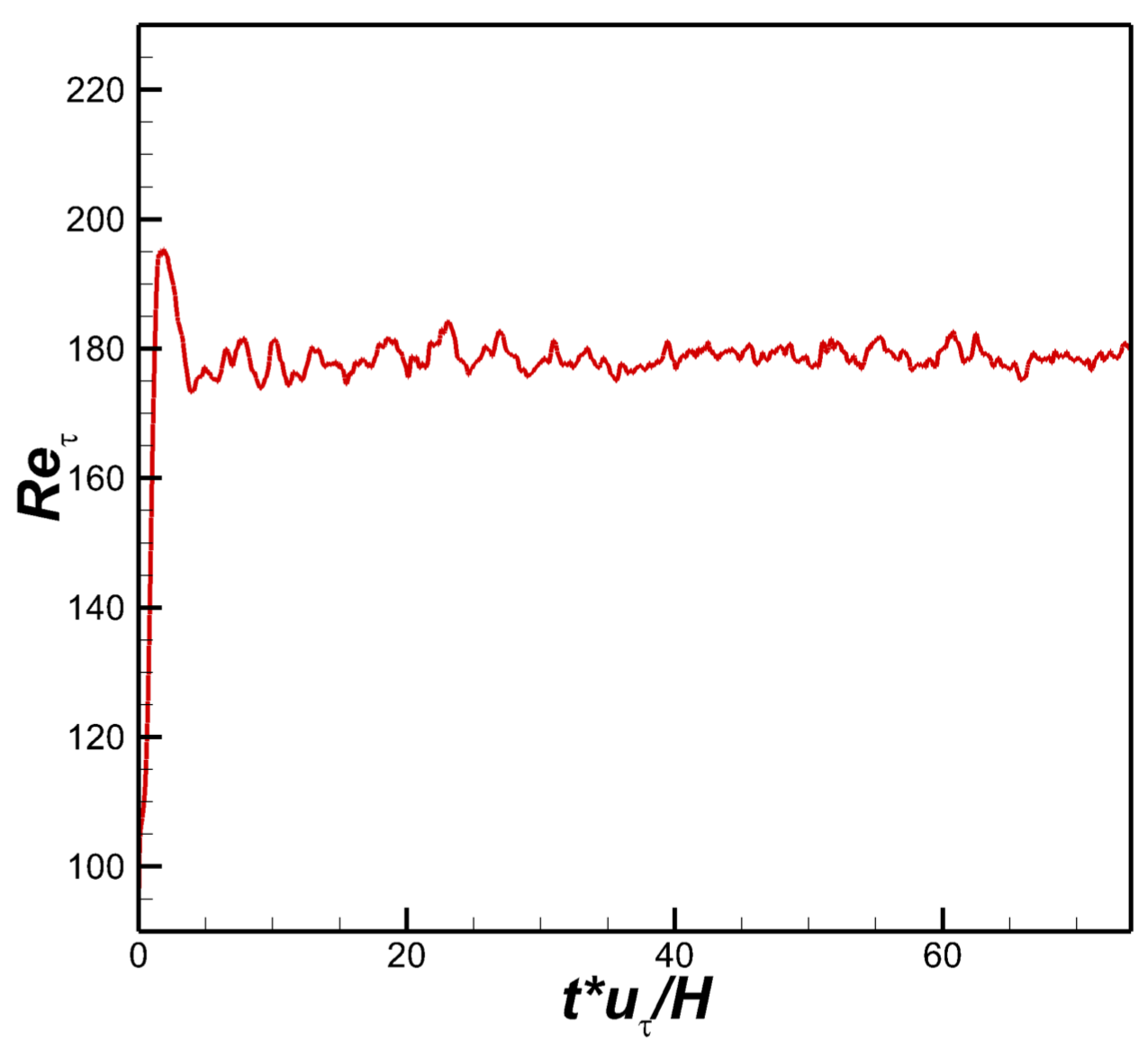
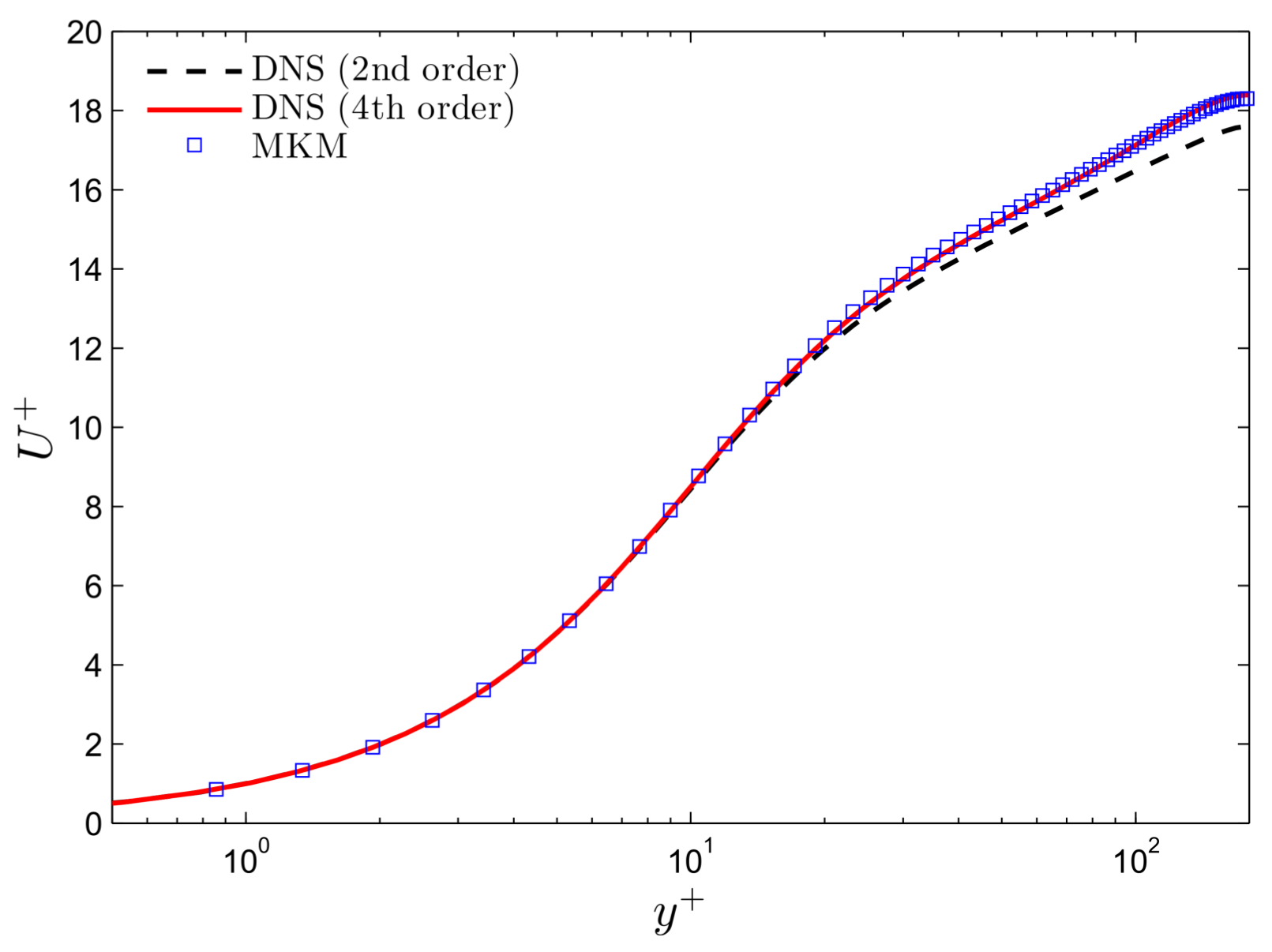
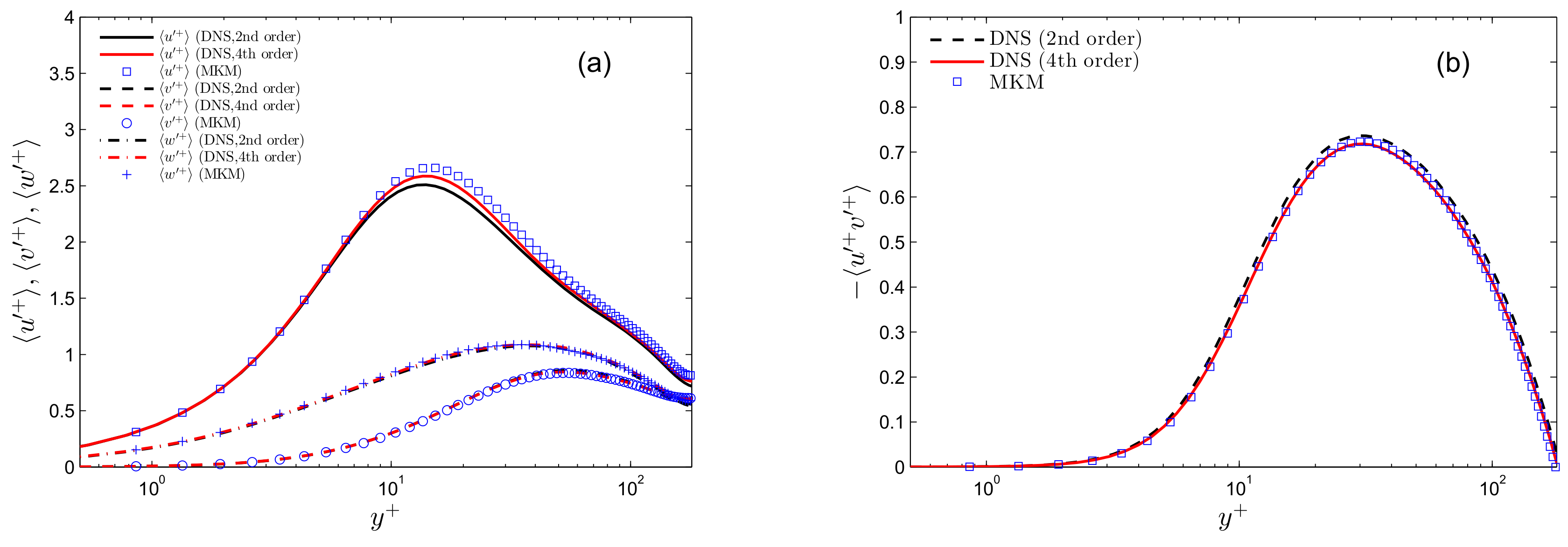
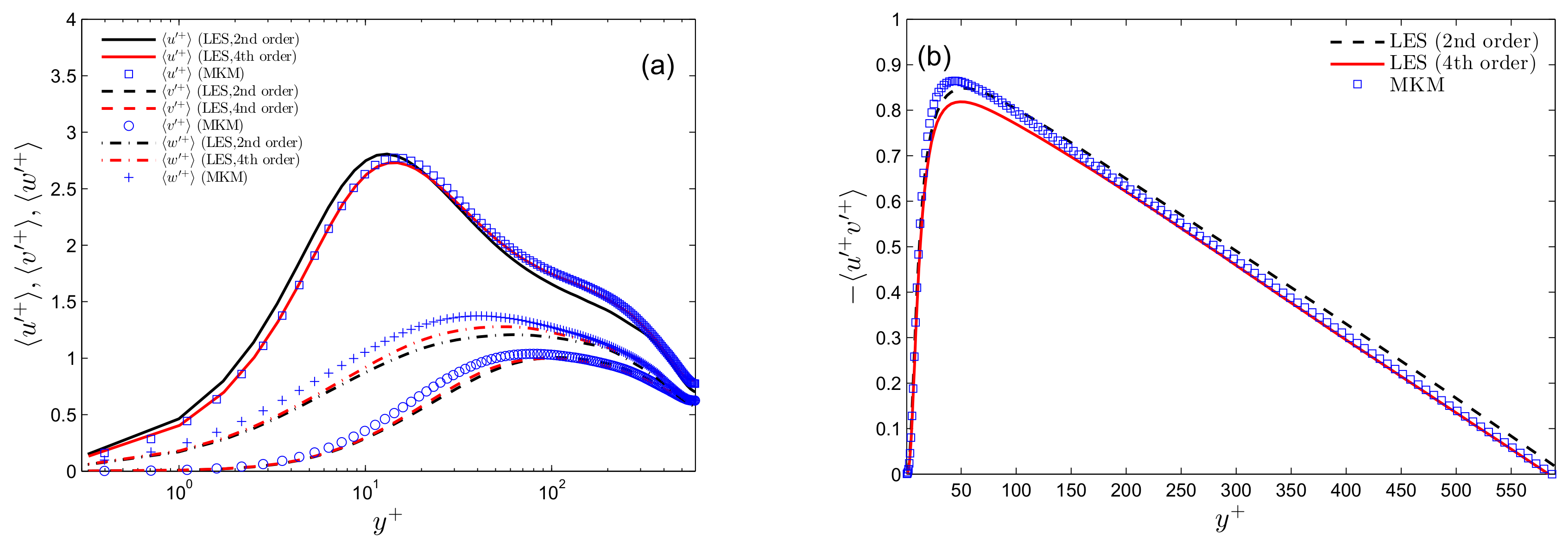
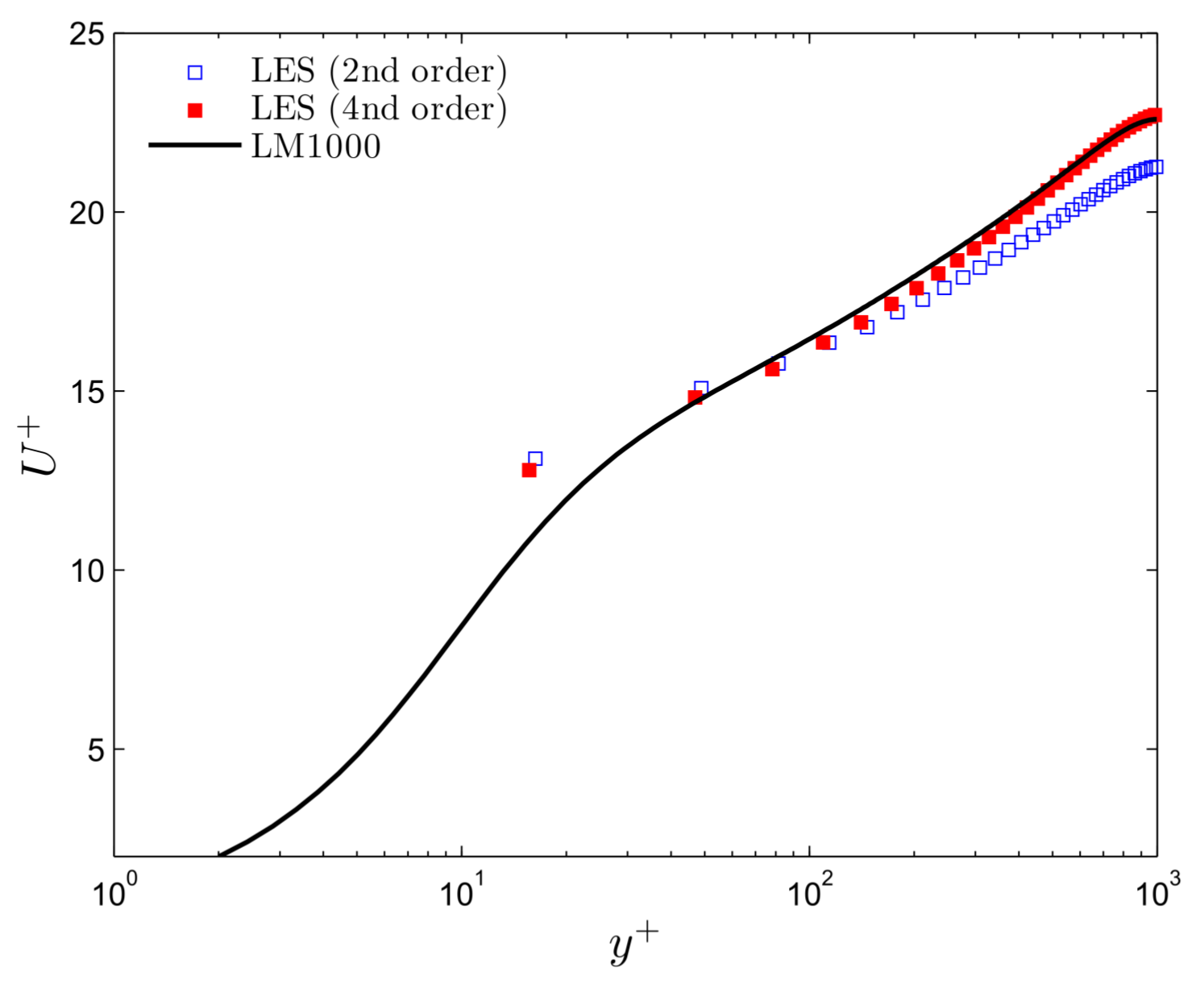
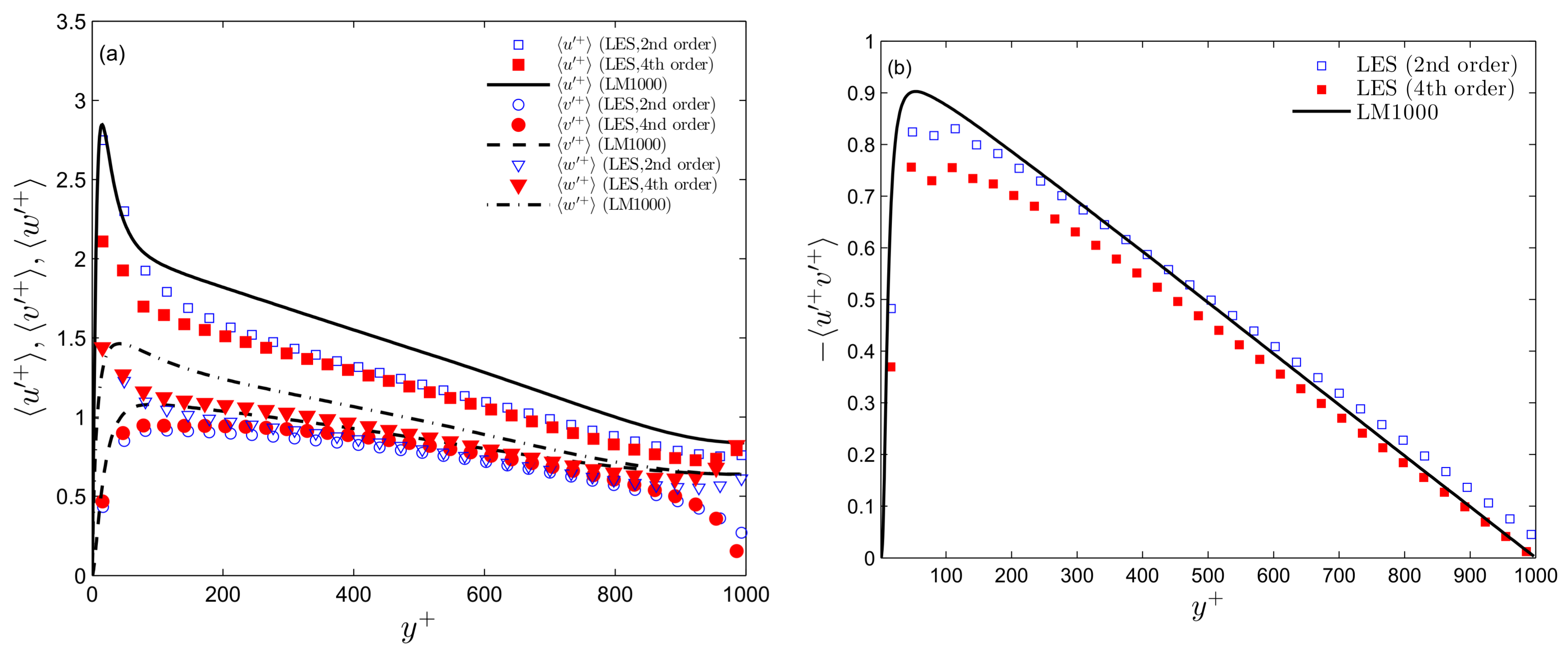
4. Computation of Turbulent Channel Flows
4.1.
4.2.
4.3.
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AP | Approximate Projection |
| CFD | Computational Fluid Dynamics |
| DCT | Discrete Cosine Transform |
| DFT | Discrete Fourier Transform |
| DNS | Direct Numerical Simulation |
| EP | Exact Projection |
| FD | Finite Difference |
| FFT | Fast Fourier Transform |
| FV | Finite Volume |
| HPC | High Performance Computation |
| LES | Large Eddy Simulation |
| LM | Lee and Moser |
| MKM | Moser, Kim and Mansour |
| R.m.s | Root-mean-squared |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equations |
| WMLES | Wall-Modeled Large Eddy Simulation |
References
- Lesieur, M.; Metais, O. New trends in large-eddy simulations of turbulence. Annu. Rev. Fluid Mech. 1996, 28, 45–82. [Google Scholar] [CrossRef]
- Moin, P.; Mahesh, K. Direct numerical simulation: A tool in turbulence research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Meneveau, C.; Katz, J. Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 2000, 32, 1–32. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef]
- Moser, R.; Kim, J.; Mansour, M.N. Direct numerical simulation of turbulent channel flow up to Reτ = 590. Phys. Fluids 1999, 11, 943–945. [Google Scholar] [CrossRef]
- Del Álamo, J.C.; Jiménez, J.; Zandonade, P.; Moser, R.D. Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 2004, 500, 135–144. [Google Scholar] [CrossRef]
- Hoyas, S.; Jiménez, J. Scaling of the velocity fluctuations in turbulent channels up to Reτ = 2003. Phys. Fluids 2006, 18, 011702. [Google Scholar] [CrossRef]
- Lozano-Durán, A.; Jiménez, J. Effect of the computational domain on direct simulations of turbulent channels up to Reτ = 4200. Phys. Fluids 2014, 26, 011702. [Google Scholar] [CrossRef]
- Lee, M.; Moser, R.D. Direct numerical simulation of turbulent channel flow up to Reτ ≈ 5200. J. Fluid Mech. 2015, 774, 943–945. [Google Scholar] [CrossRef]
- Wu, X.; Moin, P. A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 2008, 608, 81–112. [Google Scholar] [CrossRef]
- Chin, C.; Monty, J.P.; Ooi, A. Reynolds number effects in DNS of pipe flow and comparison with channels and boundary layers. Int. J. Heat Fluid Flow 2014, 45, 33–40. [Google Scholar] [CrossRef]
- Wu, X.; Moin, P.; Adrian, R.J.; Baltzer, J.R. Osborne Reynolds pipe flow: Direct simulation from laminar through gradual transition to fully developed turbulence. Proc. Natl. Acad. Sci. USA 2015, 112, 7920–7924. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.; Lee, J.H.; Jin, L.; Kang, J.; Sung, H.J. Direct numerical simulation of a 30R long turbulent pipe flow at Reτ = 3008. Phys. Fluids 2015, 27, 065110. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Bernardini, M.; Pirozzoli, S.; Orlandi, P. Velocity statistics in turbulent channel flow up to Reτ = 4000. J. Fluid Mech. 2014, 742, 171–191. [Google Scholar] [CrossRef]
- Moin, P.; Verzicco, R. On the suitability of second-order accurate discretizations for turbulent flow simulations. Eur. J. Mech. B/Fluids 2016, 55, 242–245. [Google Scholar] [CrossRef]
- Kravchenko, A.G.; Moin, P. On the effect of numerical errors in large eddy simulations of turbulent flows. J. Comput. Phys. 1997, 131, 310–322. [Google Scholar] [CrossRef]
- Morinishi, Y.; Lund, T.S.; Vasilyev, O.V.; Moin, P. Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 1998, 143, 90–124. [Google Scholar] [CrossRef]
- Verstappen, R.W.C.P.; Veldman, A.E.P. Symmetry-preserving discretization of turbulent flow. J. Comput. Phys. 2003, 187, 343–368. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Mahesh, K. A family of high order finite difference schemes with good spectral resolution. J. Comput. Phys. 1998, 145, 332–358. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, H. Developing high-order weighted compact nonlinear schemes. J. Comput. Phys. 2000, 165, 22–44. [Google Scholar] [CrossRef]
- Nagarajan, S.; Lele, S.K.; Ferziger, J.H. A robust high-order compact method for large eddy simulation. J. Comput. Phys. 2003, 191, 392–419. [Google Scholar] [CrossRef]
- Zhou, Q.; Yao, Z.; He, F.; Shen, M. A new family of high-order compact upwind difference schemes with good spectral resolution. J. Comput. Phys. 2007, 227, 1306–1339. [Google Scholar] [CrossRef]
- Rizzetta, D.P.; Visbal, M.R.; Morgan, P.E. A high-order compact finite-difference scheme for large-eddy simulation of active flow control. Prog. Aerosp. Sci. 2008, 44, 397–426. [Google Scholar] [CrossRef]
- Zhang, S.; Jiang, S.; Shu, C.W. Development of nonlinear weighted compact schemes with increasingly higher order accuracy. J. Comput. Phys. 2008, 227, 7294–7321. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 54–73. [Google Scholar]
- Van Doormaal, J.; Raithby, G. Enhancements of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar] [CrossRef]
- Kwak, D.; Chang, J.L.; Shanks, S.P.; Chakravarthy, S.R. A three-dimensional incompressible Navier–Stokes flow solver using primitive variables. AIAA J. 1986, 24, 390–396. [Google Scholar] [CrossRef]
- Drikakis, D.; Govatsos, P.; Papantonis, D. A characteristic-based method for incompressible flows. Int. J. Numer. Methods Fluids 1994, 19, 667–685. [Google Scholar] [CrossRef]
- Shapiro, E.; Drikakis, D. Artificial compressibility, characteristics-based schemes for variable density, incompressible, multi-species flows. Part I: Derivation of different formulations and constant density limit. J. Comput. Phys. 2005, 210, 584–607. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Janenko, N.N. The Method of Fractional Steps; Springer: Berlin, Germany, 1971. [Google Scholar]
- Kim, J.; Moin, P. Application of a fractional-step method to incompressible Navier-Stokes equations. J. Comput. Phys. 1985, 59, 308–323. [Google Scholar] [CrossRef]
- Van Kan, J. A second-order accurate pressure-correction scheme for viscous incompressible flow. SIAM J. Sci. Stat. Comput. 1986, 7, 870–891. [Google Scholar] [CrossRef]
- Bell, J.B.; Colella, P.; Glaz, H.M. A second-order projection method for the incompressible Navier-Stokes equations. J. Comput. Phys. 1989, 85, 257–283. [Google Scholar] [CrossRef]
- Brown, D.L.; Cortez, R.; Minion, M.L. Accurate projection methods for the incompressible Navier-Stokes equations. J. Comput. Phys. 2001, 168, 464–499. [Google Scholar] [CrossRef]
- Drikakis, D.; Rider, W. High-Resolution Methods for Incompressible and Low-Speed Flows; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Ma, Y.; Fu, D.; Kobayashi, T.; Taniguchi, N. Numerical solution of the incompressible Navier–Stokes equations with an upwind compact difference scheme. Int. J. Numer. Methods Fluids 1999, 30, 509–521. [Google Scholar]
- Demuren, A.O.; Wilson, R.V.; Carpenter, M. Higher-order compact schemes for numerical simulation of incompressible flows, Part I: Theoretical development. Numer. Heat Transf. Part B Fundam. 2001, 39, 207–230. [Google Scholar]
- Wilson, R.V.; Demuren, A.O.; Carpenter, M. Higher-order compact schemes for numerical simulation of incompressible flows, part II: Applications. Numer. Heat Transf. Part B Fundam. 2001, 39, 231–255. [Google Scholar]
- Abide, S.; Viazzo, S. A 2D compact fourth-order projection decomposition method. J. Comput. Phys. 2005, 206, 252–276. [Google Scholar] [CrossRef]
- Zhang, K.K.; Shotorban, B.; Minkowycz, W.; Mashayek, F. A compact finite difference method on staggered grid for Navier–Stokes flows. Int. J. Numer. Methods Fluids 2006, 52, 867–881. [Google Scholar] [CrossRef]
- Pandit, S.K.; Kalita, J.C.; Dalal, D. A transient higher order compact scheme for incompressible viscous flows on geometries beyond rectangular. J. Comput. Phys. 2007, 225, 1100–1124. [Google Scholar] [CrossRef]
- Knikker, R. Study of a staggered fourth-order compact scheme for unsteady incompressible viscous flows. Int. J. Numer. Methods Fluids 2009, 59, 1063–1092. [Google Scholar] [CrossRef]
- Laizet, S.; Lamballais, E. High-order compact schemes for incompressible flows: A simple and efficient method with quasi-spectral accuracy. J. Comput. Phys. 2009, 228, 5989–6015. [Google Scholar] [CrossRef]
- Boersma, B.J. A 6th order staggered compact finite difference method for the incompressible Navier–Stokes and scalar transport equations. J. Comput. Phys. 2011, 230, 4940–4954. [Google Scholar] [CrossRef]
- Tyliszczak, A. A high-order compact difference algorithm for half-staggered grids for laminar and turbulent incompressible flows. J. Comput. Phys. 2014, 276, 438–467. [Google Scholar] [CrossRef]
- Reis, G.A.; Tasso, I.V.M.; Souza, L.F.; Cuminato, J.A. A compact finite differences exact projection method for the Navier-Stokes equations on a staggered grid with fourth-order spatial precision. Comput. Fluids 2015, 118, 19–31. [Google Scholar] [CrossRef]
- Sengupta, T.K.; Sengupta, A. A new alternating bi-diagonal compact scheme for non-uniform grids. J. Comput. Phys. 2016, 310, 1–25. [Google Scholar] [CrossRef]
- Abide, S.; Binous, M.; Zeghmati, B. An efficient parallel high-order compact scheme for the 3D incompressible Navier-Stokes equations. Int. J. Comput. Fluid Dyn. 2017, 1–16. [Google Scholar] [CrossRef]
- Dukowicz, J.K.; Dvinsky, A.S. Approximate factorisation as a high order splitting for the incompressible flow equations. J. Comput. Phys. 1992, 102, 336–347. [Google Scholar] [CrossRef]
- Perot, J.B. An analysis of the fractional step method. J. Comput. Phys. 1993, 108, 51–58. [Google Scholar] [CrossRef]
- Kim, K.; Baek, S.J.; Sung, H.J. An implicit velocity decoupling procedure for the incompressible Navier-Stokes equations. Int. J. Numer. Methods Fluids 2002, 38, 125–138. [Google Scholar] [CrossRef]
- Orszag, S.A.; Israeli, M.; Deville, M.O. Boundary conditions for incompressible flows. J. Comput. Phys. 1986, 1, 75–111. [Google Scholar] [CrossRef]
- Gresho, P.M.; Sani, R.L. On pressure boundary conditions for the incompressible Navier–Stokes equations. Int. J. Numer. Methods Fluids 1987, 7, 1111–1145. [Google Scholar] [CrossRef]
- Makhoul, J. A fast cosine transform in one and two dimensions. IEEE Trans. Acoust. Speech Signal Proc. 1980, 28, 27–34. [Google Scholar] [CrossRef]
- Shih, T.M.; Tan, C.H.; Hwang, B.C. Effects of grid staggering on numerical schemes. Int. J. Numer. Methods Fluids 1989, 9, 193–212. [Google Scholar] [CrossRef]
- Ghia, U.; Ghia, K.N.; Shin, C.T. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Xie, S.; Ghaisas, N.; Archer, C.L. Sensitivity issues in finite-difference large-eddy simulations of the atmospheric boundary layer with dynamic subgrid-scale models. Bound. Layer Meteorol. 2015, 157, 421–445. [Google Scholar] [CrossRef]
- Boris, J.; Grinstein, F.; Oran, E.; Kolbe, R. New insights into large eddy simulation. Fluid Dyn. Res. 1992, 10, 199–228. [Google Scholar] [CrossRef]
- Margolin, L.; Rider, W.; Grinstein, F. Modeling turbulent flow with implicit LES. J. Turbul. 2006, N15. [Google Scholar] [CrossRef]
- Hickel, S.; Adams, N. On implicit subgrid-scale modeling in wall-bounded flows. Phys. Fluids 2007, 19, 105106. [Google Scholar] [CrossRef]
- Kokkinakis, I.; Drikakis, D. Implicit large eddy simulation of weakly-compressible turbulent channel flow. Comput. Methods Appl. Mech. Eng. 2015, 287, 229–261. [Google Scholar] [CrossRef]
- Tsoutsanis, P.; Kokkinakis, I.W.; Könözsy, L.; Drikakis, D.; Williams, R.J.; Youngs, D.L. Comparison of structured-and unstructured-grid, compressible and incompressible methods using the vortex pairing problem. Comput. Methods Appl. Mech. Eng. 2015, 293, 207–231. [Google Scholar] [CrossRef]
- Piomelli, U. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Piomelli, U. Wall-layer models for large-eddy simulations. Prog. Aerosp. Sci. 2008, 44, 437–446. [Google Scholar] [CrossRef]
- Schumann, U. Subgrid-scale model for finite difference simulation of turbulent flows in plane channels and annuli. J. Comput. Phys. 1975, 18, 376–404. [Google Scholar] [CrossRef]
- Grötzbach, G. Encyclopedia of Fluid Mechanics; Chapter Direct Numerical and Large Eddy Simulations of Turbulent Channel Flows; Gulf Publishing Company: Houston, TX, USA, 1987; Volume 6, pp. 1337–1391. [Google Scholar]
- Kawai, S.; Larsson, J. Wall-modeling in large eddy simulation: Length scales, grid resolution, and accuracy. Phys. Fluids 2012, 24, 015105. [Google Scholar] [CrossRef]
- Lee, J.; Cho, M.; Choi, H. Large eddy simulations of turbulent channel and boundary layer flows at high Reynolds number with mean wall shear stress boundary condition. Phys. Fluids 2013, 25, 110808. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; Wilczek, M.; Meneveau, C. Large-eddy simulation study of the logarithmic law for second- and higher-order moments in turbulent wall-bounded flow. J. Fluid Mech. 2014, 757, 888–907. [Google Scholar] [CrossRef]
- Chung, D.; McKeon, B.J. Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 2010, 661, 341–364. [Google Scholar] [CrossRef]
- Suzuki, H.; Nagata, K.; Sakai, Y.; Hayase, T.; Hasegawa, Y.; Ushijima, T. An attempt to improve accuracy of higher-order statistics and spectra in direct numerical simulation of incompressible wall turbulence by using the compact schemes for viscous terms. Int. J. Numer. Methods Fluids 2013, 73, 509–522. [Google Scholar] [CrossRef]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, R.; Wang, L.; Wang, P.; Wang, Y.; Zheng, X. Application of High-Order Compact Difference Scheme in the Computation of Incompressible Wall-Bounded Turbulent Flows. Computation 2018, 6, 31. https://doi.org/10.3390/computation6020031
Hu R, Wang L, Wang P, Wang Y, Zheng X. Application of High-Order Compact Difference Scheme in the Computation of Incompressible Wall-Bounded Turbulent Flows. Computation. 2018; 6(2):31. https://doi.org/10.3390/computation6020031
Chicago/Turabian StyleHu, Ruifeng, Limin Wang, Ping Wang, Yan Wang, and Xiaojing Zheng. 2018. "Application of High-Order Compact Difference Scheme in the Computation of Incompressible Wall-Bounded Turbulent Flows" Computation 6, no. 2: 31. https://doi.org/10.3390/computation6020031
APA StyleHu, R., Wang, L., Wang, P., Wang, Y., & Zheng, X. (2018). Application of High-Order Compact Difference Scheme in the Computation of Incompressible Wall-Bounded Turbulent Flows. Computation, 6(2), 31. https://doi.org/10.3390/computation6020031




