First Principles Study of Topochemical Effects and Electronic Structure Relationships between ANCl and A2N2Se (A = Zr, Ce) Assimilated to Pseudo-Binaries: {AN}Cl and {A2N2}Se
Abstract
:1. Introduction
2. Computational Framework
3. Geometry Optimization and Energy Dependent Results
3.1. Charge Transfer
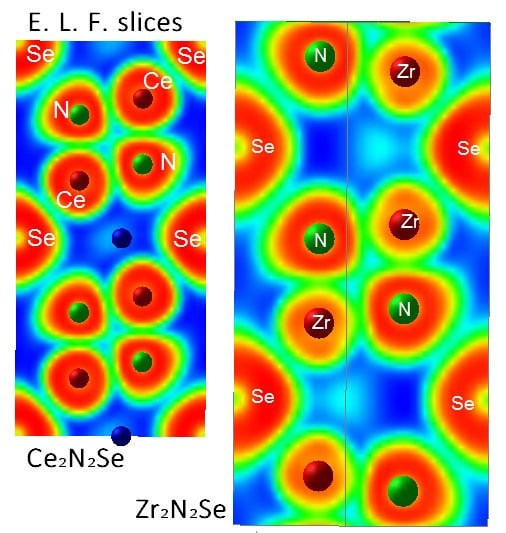
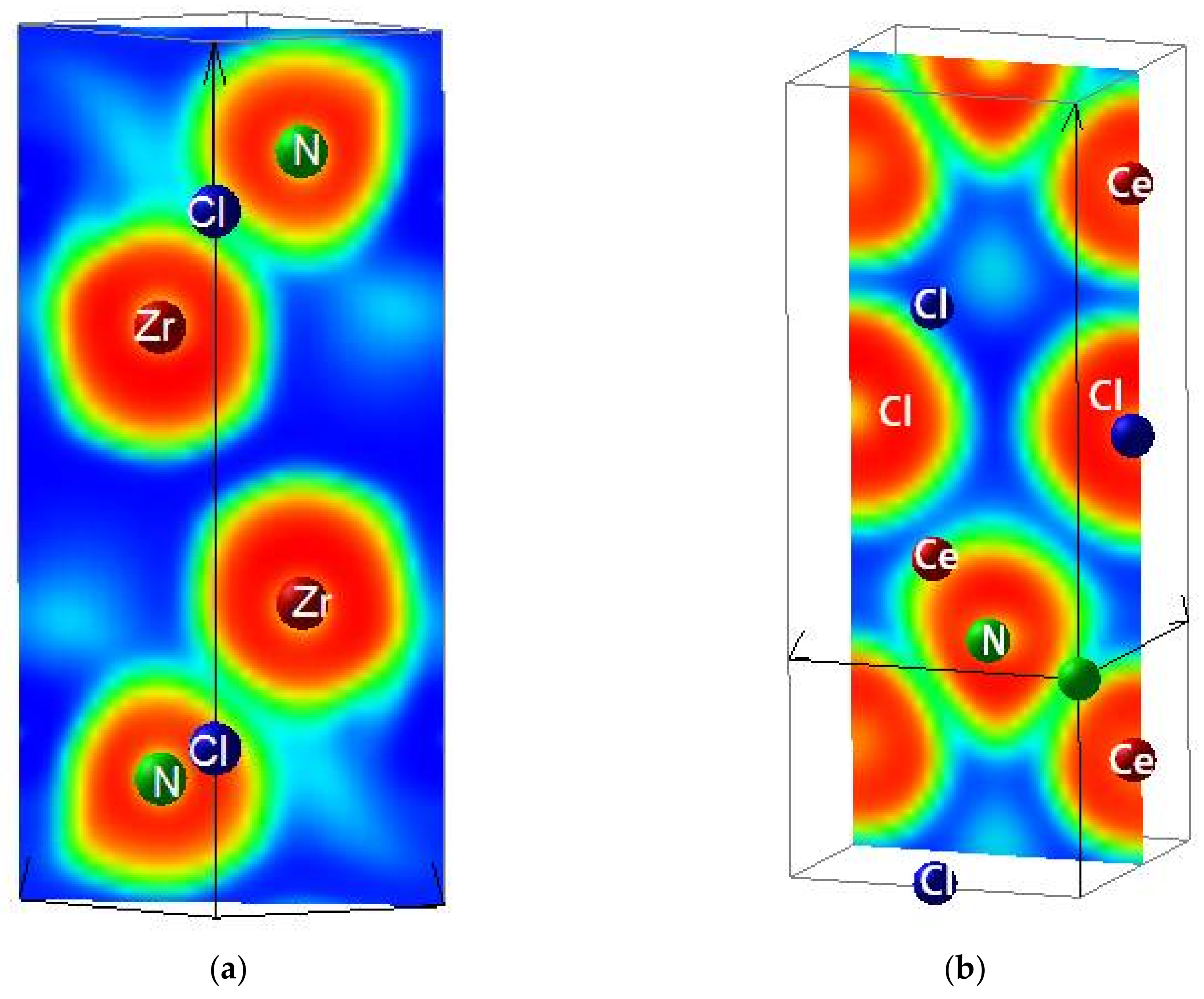
3.2. Electron Localization Function ELF
4. Electronic Structure and Chemical Bonding
4.1. Electronic Density of States
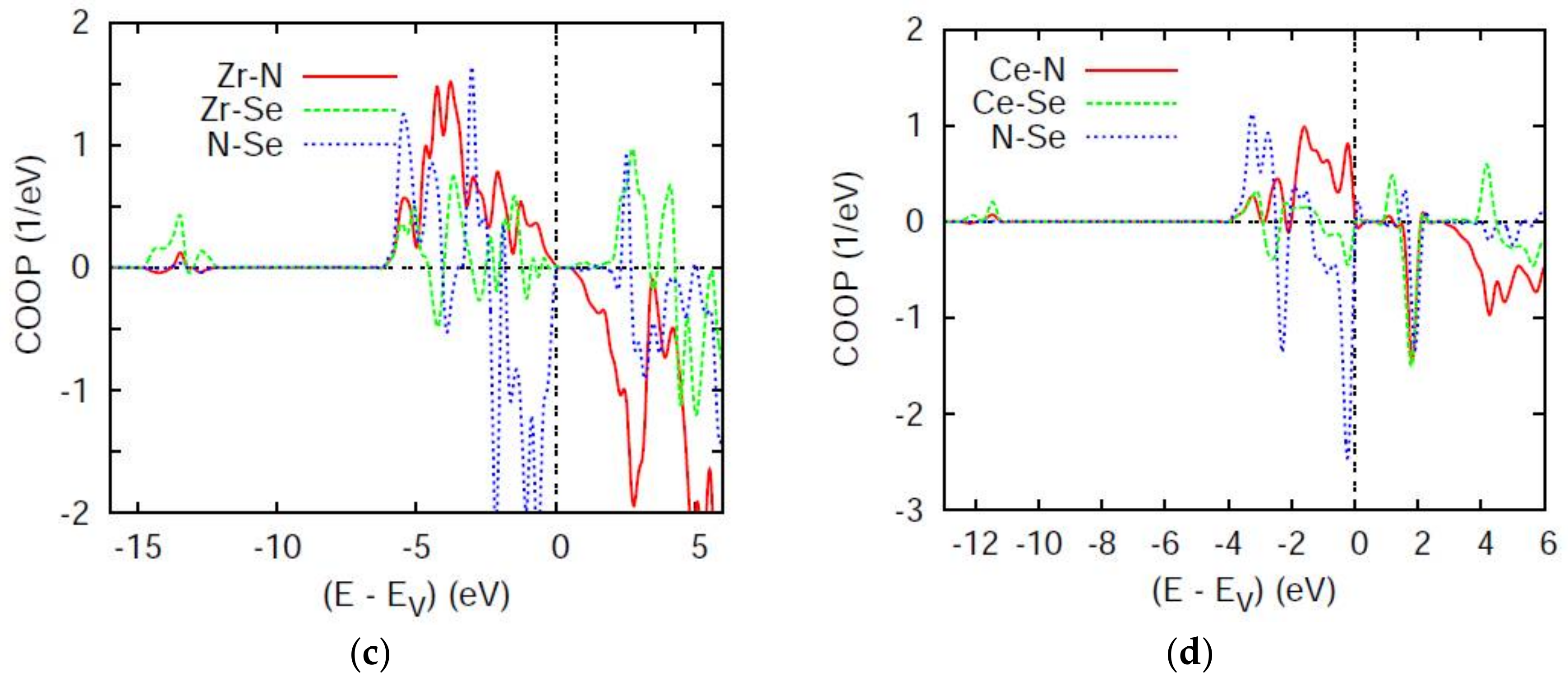
4.2. Chemical Bonding
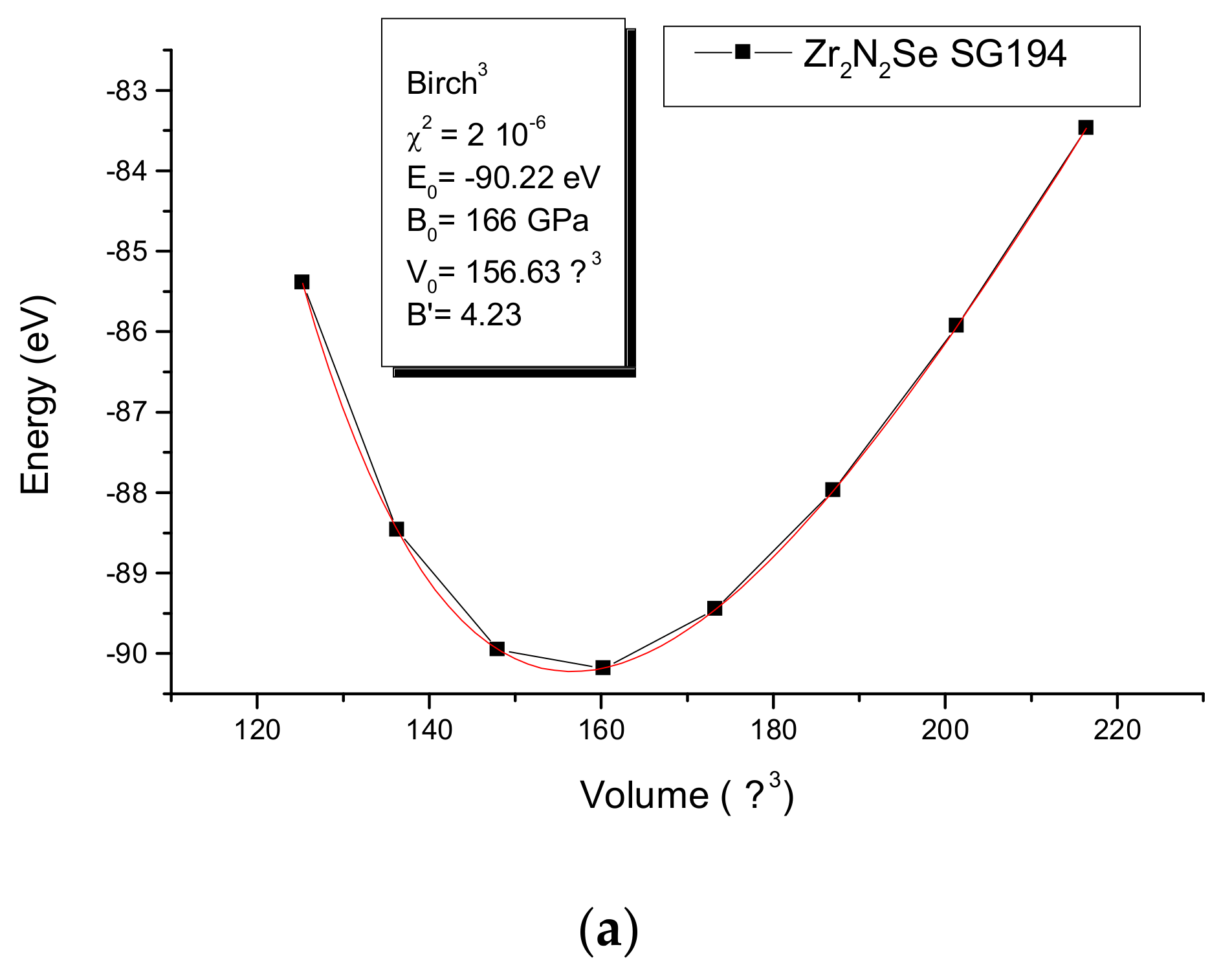
5. A2N2Se: Mechanical Properties from the Energy-Volume Equations of States EOS
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Matar, S.F.; Etourneau, J. (CaO)nIrO2 (n = 1, 2, 4) family: Chemical scissors effects of CaO on structural characteristics correlated to physical properties. Ab initio study. J. Solid State Chem. 2017, 255, 82–88. [Google Scholar] [CrossRef]
- Matar, S.F.; Eyert, V.; Villesuzanne, A.; Whangbo, M.-H. First-principles study of the electronic and magnetic structures of the tetragonal and orthorhombic phases of Ca3Mn2O7. Phys. Rev. B 2007, 76, 054403. [Google Scholar] [CrossRef]
- Juza, R.; Friedrichsen, H. Die Kristallstruktur von β-ZrNCl und β-ZrNBr. Z. Anorg. Allg. Chem. 1964, 332, 173–178. [Google Scholar]
- Ehrlich, G.M.; Badding, M.E.; Brese, N.E.; Trail, S.S.; DiSalvo, F.J. New cerium nitride chlorides: Ce6Cl12N2 and CeNCl. J. Alloys Compd. 1994, 206, 95–101. [Google Scholar] [CrossRef]
- Lissner, F.; Hack, B.; Lerch, M.; Schleid, T. Zr2N2Se: The First Zirconium(IV) Nitride Selenide by the Oxi- dation of Zirconium(III) Nitride with Selenium. Z. Anorg. Allg. Chem. 2012, 638, 1407–1410. [Google Scholar] [CrossRef]
- Yongkwan, D.; DiSalvo, F.J. Ce2SeN2: Ternary selenide nitride containing tetravalent Ce in the Ce2SO2 structure type. Solid State Sci. 2011, 13, 19–22. [Google Scholar]
- Boldyrev, V.V. Topochemistry and topochemical reactions. React. Solids 1990, 8, 231–246. [Google Scholar] [CrossRef]
- Stoltz, C.; Ramesha, K.; Sirchio, S.A.; Gönen, Z.S.; Eichhorn, B.W.; Salamanca-Riba, L.; Gopalakrishnan, J. Topochemical Anion Metathesis Routes to the Zr2N2S Phases and the Na2S and ACl Derivatives (A: Na, K, Rb). J. Am. Chem. Soc. 2003, 125, 4285–4292. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. A 1965, 140, A1133. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. B 1964, 136, B864. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, J. From ultra-soft pseudo-potentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Blöchl, P.E.; Jepsen, O.; Anderson, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Bader, R. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Eyert, V. Basic Notions and Applications of the Augmented Spherical Wave Method. Int. J. Quantum Chem. 2000, 77, 1007–10031. [Google Scholar] [CrossRef]
- Eyert, V. The Augmented Spherical Wave Method—A Comprehensive Treatment; Lecture Notes in Physics; Springer: Heidelberg, Germany, 2007. [Google Scholar]
- Hoffmann, R. How Chemistry and Physics Meet in the Solid State. Angew. Chem. Int. Ed. 1987, 26, 846–878. [Google Scholar] [CrossRef]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
- Matar, S.F.; Chevalier, B.; Pöttgen, R. Intermediate cerium valence intermetallics Ce4RuMg, Ce23Ru7Mg4, CeRu2Mg5, and Ce2Ru4Mg17: Electronic structures and chemical bonding from DFT. Intermetallics 2012, 31, 88–93. [Google Scholar] [CrossRef]
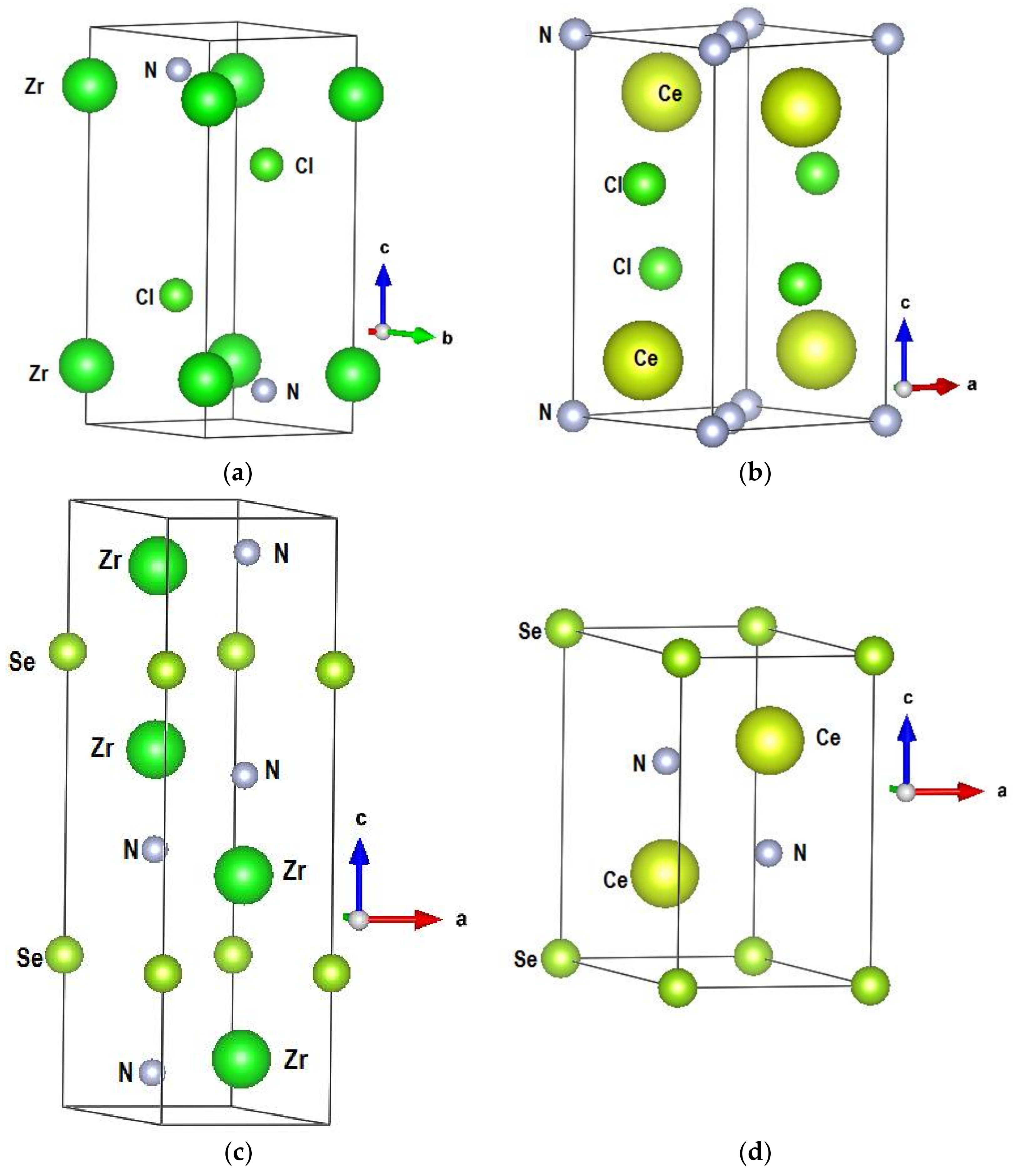




| Experimental [3] and (Calculated) Crystal Data of β ZrNCl | Experimental [4] and Calculated Crystal Data of CeNCl | Experimental [8] and (Calculated) Crystal Data of Zr2N2Se | Experimental [6] and (Calculated) Crystal Data of Ce2N2Se | |||||
|---|---|---|---|---|---|---|---|---|
| Space group | P-3m1 N°164 | P4/nmm N°129 | P63/mmc N°194 | P-3m1 N°164 | ||||
| Particular atomic positions | Cr (2a) 0, 0, 0 N1 (2b) ½, 0, 0 | N (2a) 0, 0, 0 | Se (2b) 0, 0, ¼ | Se (2a) 0, 0, 0 | ||||
| Lattice parameters | a = 3.604 (3.454) Å c = 9.234 (11.0) Å V(cell) = 103.87 (107.89) Å3 Zr (2c) 0,0,z; z = 0.147 (0.178) N and Cl (2d) 1/3, 2/3, z | a = 4.08 (4.01) Å c = 6.84 (6.93) Å V(cell) = 113.76 (111.76) Å3 Ce and Cl (2c) 0, ½, z | a = 3.6398 (3.822) Å c = 13. 1641 (12.623) Å V(cell) = 151.035 (159.69) Å3 Zr and N (4f) 1/3, 2/3, z | a = 4.0772 (4. 13) Å c = 7.048 (7.30) Å V (cell) = 101.462 (107.89) Å3 Ce and N (2d) 1/3, 2/3, z | ||||
| Atoms (2d) | z | Atoms (2c) | z | Atoms (4f) | z | Atoms (2d) | z | |
| Atomic coordinates | Cl | 0.332 (0.292) | Ce | 0.166 (0.194) | Zr | 0.9013 (0.9354) | Ce | 0.2847 (0.292) |
| N | 0.625 (0.621) | Cl | 0.628 (0.624) | N | 0.0661 (0.066) | N | 0.6256 (0.625) | |
| Distances | d(Zr–N) = 2.09 (2.10) Å, d(Zr-Cl) = 2.69 (2.72) Å | d(Ce–N) = 2.17 (2.16)Å, d(Ce-Cl) = 2.89 (3.13) Å | d(Zr–N) = 2.17 (2.18) Å, d(Zr–Se) = 2.89 (2.90)Å | d(Ce–N) = 2.4 (2.43) Å, d(Ce–Se) = 3.09 (3.2) Å | ||||
| Binary Oxides | ||||
| ZrO2 | CeO2 | |||
| QA | +2.55 | +2.425 | ||
| QO | −1.275 | −1.212 | ||
| ±ΔQ | ±2.55 | ±2.425 | ||
| Ternary Compounds | ||||
| ZrNCl | Zr2N2Se | CeNCl | Ce2N2Se | |
| QA | +2.22 | +2.17 | +1.97 | +1.83 |
| QN | −1.56 | −1.60 | −1.21 | −1.30 |
| QCl | −0.66 | - | -0.76 | - |
| QSe | - | −1.14 | - | −1.06 |
| ±ΔQ | ±2.22 | ±2.17 | ±1.97 | ±1.83 |
| ±ΔQcmplx | ±0.66 | ±1.14 | ±0.76 | ±1.06 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matar, S.F. First Principles Study of Topochemical Effects and Electronic Structure Relationships between ANCl and A2N2Se (A = Zr, Ce) Assimilated to Pseudo-Binaries: {AN}Cl and {A2N2}Se. Computation 2018, 6, 30. https://doi.org/10.3390/computation6020030
Matar SF. First Principles Study of Topochemical Effects and Electronic Structure Relationships between ANCl and A2N2Se (A = Zr, Ce) Assimilated to Pseudo-Binaries: {AN}Cl and {A2N2}Se. Computation. 2018; 6(2):30. https://doi.org/10.3390/computation6020030
Chicago/Turabian StyleMatar, Samir F. 2018. "First Principles Study of Topochemical Effects and Electronic Structure Relationships between ANCl and A2N2Se (A = Zr, Ce) Assimilated to Pseudo-Binaries: {AN}Cl and {A2N2}Se" Computation 6, no. 2: 30. https://doi.org/10.3390/computation6020030
APA StyleMatar, S. F. (2018). First Principles Study of Topochemical Effects and Electronic Structure Relationships between ANCl and A2N2Se (A = Zr, Ce) Assimilated to Pseudo-Binaries: {AN}Cl and {A2N2}Se. Computation, 6(2), 30. https://doi.org/10.3390/computation6020030